Measuring Complexity in Financial Data

The stock market is a canonical example of a complex system, in which a large number of interacting agents lead to joint evolution of stock returns and the collective market behavior exhibits emergent properties. However, quantifying complexity in stock market data is a challenging task. In this report, we explore four different measures for characterizing the intrinsic complexity by evaluating the structural relationships between stock returns. The first two measures are based on linear and non-linear co-movement structures (accounting for contemporaneous and Granger causal relationships), the third is based on algorithmic complexity, and the fourth is based on spectral analysis of interacting dynamical systems. Our analysis of a dataset comprising daily prices of a large number of stocks in the complete historical data of NASDAQ (1972–2018) shows that the third and fourth measures are able to identify the greatest global economic downturn in 2007–09 and associated spillovers substantially more accurately than the first two measures. We conclude this report with a discussion of the implications of such quantification methods for risk management in complex systems.

1. Introduction

How can complexity in financial markets be measured? Although financial markets are routinely thought of as complex systems, exact characterization of their embedded complexity seems non-existent, as pointed out in Brunnermeier and Oehmke [1]. In various contexts, different characterizations and underlying mechanisms have been proposed; explanations include the emergence of macroscopic properties from microscopic interactions [2, 3], the presence of power laws and/or long memory in fluctuations [4], and scaling behavior in growth rates of economic and financial entities [5], to name a few.

In this brief research report we investigate the following question: Given the realized dynamical behavior of a system, can we find the degree of complexity embedded in the system? We note that in the case of financial markets, while interactions between economic agents can be non-linear in nature (due to heterogeneity in behavioral aspects, institutional properties, or information processing abilities), a complete enumeration of all such non-linearities is almost impossible. In this work we do not attempt to find a microfoundation of complexity based on traders' behavior; instead, we aim to quantify complexity in terms of a summary statistic inferred from observed behavior that potentially evolves over time.

We consider four main candidate measures of complexity in multivariate financial asset return data. The dataset we analyze is extracted from complete historical data between 1972 and 2018 of NASDAQ (National Association of Securities Dealers Automated Quotations), which is one of the largest stock markets in the world in terms of trading volume. We divide the whole time evolution into overlapping windows of 4 years long. To fix ideas, let N be the number of stocks in the stock market and T the number of return data points within each time window, where N ≪ T (in the actual implementation for each window of data, N = 300 and T ≥ 1, 000, which corresponds to 4 years of trading in NASDAQ; we elaborate on the data structure and sample selection in section 2.1). The first measure is based on mutual information across stocks. Mutual information is an entropy-based measure that generalizes the linear co-movement structure to non-linear co-movements. The second measure is based on dispersion in systemic risk captured via Granger causal relationships across stocks; Granger causality captures lagged co-movement structure in the data. The third measure is based on algorithmic complexity evaluated on the projection of the N-dimensional data onto a two-dimensional space. The fourth measure is based on a vector autoregression estimation of N-dimensional data. This measure is motivated by the famous May-Wigner result that characterizes the instability of many-dimensional heterogeneous interacting systems. We compute each of these measures on 4-years windows and study how the measure evolves when we move the windows by 1 year (from 1972 to 2018 there are 44 such windows).

We assess the usefulness of the measures by seeing whether they can identify the only major financial crisis in the time period under consideration (1972–2018), which occurred during 2007–09 (for an overview of the economic and financial impacts and the implications of the crisis, readers can consult [6, 7] and references therein). During this crisis, the housing market meltdown in the USA led to an avalanche of collapse in the global financial market. Therefore, if any of the four measures of complexity show an increase in magnitude during this time period (or around it), we will take this as a sign of increased instability and hence embedded complexity.

To summarize the results, we find that the first two measures do not exhibit any unusual behavior during or around 2007–09. However, the third and fourth measures (based on algorithmic complexity and heterogeneity of interactions, respectively) do show a substantial increase in magnitude during the crisis period.

Our work is related to several strands of the existing literature. First, it is related to an early attempt of Bonanno et al. to characterize levels of complexity in financial data [8]. They graded complexity in three levels: the lowest level has time series properties (such as volatility clustering); level two contains cross-correlations; and level three is characterized by extreme movements in the collective dynamics, signifying the highest level of complexity. The present work is an attempt toward numerically quantifying the third level, i.e., the highest level of complexity as described in Bonanno et al. [8]. Second, we note that the goal of finding complexity measures for financial data based on techniques from physics, economics, evolutionary biology, etc. has often been discussed, for example in Johnson and Lux [9] and references therein; however, to the best of our knowledge, currently there is still no measure available (apart from sudden changes in volatility) that can accurately identify periods of large-scale financial distress from only asset return data. We note that this goal is different from that of seeking statistical precursors to financial crises (or even identifying mechanisms correlated with financial crises), toward which some work has already been done (see e.g., [10, 11]).

There is large volume of work on construction and inference of network structures from multivariate stock return data (see [12–14] and references therein). Our first measure is based on non-linear relationships between stock returns, for which we adopt an entropy-based measure of mutual information (previously used in the context of financial time series, such as in Fiedor [15]), and we compare the dynamics of the corresponding eigenspectrum with that obtained from linear correlation matrices [16]. We see that there is an overall increase in the degree of correlation over time between what can be inferred from non-linear and from linear relationships, along with a cyclic oscillation in explanatory power. This indicates that a non-linear relationship between assets does not necessarily convey more information than a linear relationship.

Next, we quantify the behavior of a directional Granger causal network over time. The spread in centralities of the nodes in the directional lagged co-movement network (captured by Granger causation) remains fairly stable over time. This analysis is motivated by two influential papers in which the systemic risks of assets were constructed from return data (see [17, 18]). There is a related literature on characterizing shock spillover in a multi-dimensional return network. However, here we do not consider those constructions, since they do not directly relate to instability of the financial system.

We then implement a non-parametric, information-theoretic measure of complexity that is based on algebraic complexity [19–24]. Zenil et al. [25] applied an algorithmic measure of complexity to financial data. We adapt their measure to many-dimensional data by transforming the data through multi-dimensional scaling. This dimension-reduction technique makes the method very generally applicable to time series data, and the measure is able to accurately identify times of crisis.

Finally, the fourth measure is based on the ecology-inspired dynamical systems theory proposed by Robert May [26]. In reference [27] an adaptation of the original May-Wigner result is proposed in the context of a discrete-time vector autoregression model and applied to a limited set of data from the New York Stock Exchange. We adopt the same approach and construct the implied heterogeneity index of stock interactions, which exhibits sharp transitions during the crisis and also in the post-crisis period, indicating lagged effects.

2. Materials and Methods

In this section we describe the data and the methods. All background material and a step-by-step description of the computational procedure are given in the Supplementary Material.

2.1. Data Description

We collected daily NASDAQ stock return data over a period of 47 years, from 1972 to 2018 [obtained from the Center for Research in Security Prices (CRSP) database, http://www.crsp.org/, accessed through Wharton Research Data Services (WRDS), https://wrds-www.wharton.upenn.edu/]. Let 𝕋 denote the length of the entire data series in years, so 𝕋 = 47. We considered moving windows of width equal to 4 years, i.e., 1972–75, 1973–76, and so on until 2015–18, with the windows indexed by k = 1, 2, …, 44¹. For each window, we calculated the market capitalization of all stocks at the end of the period and selected the top N = 300, with the restriction that the data for chosen stocks cannot have more than 5% missing values within a window (which we fill with zeros). This dataset covers pre-crisis, crisis, and post-crisis periods (the crisis period was 2007–09).

We denote each price series by $S_i^k(t)$, where i is the stock, t is the time period within a window, and k is the window. A 4-years window has ~1,000 days (each year has slightly more than 250 trading days) and is denoted by T_k. All our analyses were conducted on the log-return data, defined as

$\begin{array}{ll}{G}_i^k(t)=log{S}_i^k(t+1)-log{S}_i^k(t).& (1)\end{array}$

Next, we normalize the log-return data as follows:

$\begin{array}{ll}{g}_i^k(t)=\frac{G_i^k(t)-\langle G_i^k(t)\rangle }{{\sigma }_i^k},& (2)\end{array}$

where 〈·〉 denotes the sample average and ${\sigma }_i^k$ is the sample standard deviation of G_i.

2.2. Quantification of Linear and Non-linear Relationships

In this subsection we compare the information content in linear and non-linear relationships.

2.2.1. Correlation Matrix

We construct the cross-correlation matrix C^k as

$\begin{array}{ll}{C}_{ij}^k=\langle g_i^k(t)g_j^k(t)\rangle & (3)\end{array}$

for all i, j ≤ N for the kth window, where k = 1, …, 𝕋. For the {i, j}th pair we construct a distance measure in the form of (this form is widely used; see e.g., [13]).

$\begin{array}{ll}{D}_{ij}^k=\sqrt{2(1-C_{ij}^k)}.& (4)\end{array}$

2.2.2. Entropy and Mutual Information Matrix

First we need to define entropy. For the probability distribution p(x) of a discrete variable X defined over a domain [x₁, x₂, …, x_N], the Shannon entropy is given by [23]

$\begin{array}{ll}H(X)=-{\displaystyle \sum _i}p(x_i){log}_{2}p(x_i).& (5)\end{array}$

For two discrete variables X and Y with probability distributions p(x) and p(y), the joint entropy is given by [23]

$\begin{array}{ll}H(X,Y)=-{\displaystyle \sum _i}{\displaystyle \sum _j}p(x_i,y_j){log}_{2}p(x_i,y_j),& (6)\end{array}$

where p(x_i, y_j) denotes joint probability. Mutual information is an entropy-based measure that is defined for two variables X and Y having probability distributions p(x) and p(y) [23]:

$\begin{array}{ll}I(X;Y)={\displaystyle \sum _{i,j}}p(x_i,y_j){log}_2\frac{p(x_i,y_j)}{p(y_j)p(x_i)},& (7)\end{array}$

which is always guaranteed to be non-negative and symmetric. We construct the mutual information matrix M^k for each window k, where the element $M_{ij}^k$ of the matrix is defined as

$\begin{array}{ll}{M}_{ij}^k=I(g_i^k;g_j^k).& (8)\end{array}$

By construction, M has all non-negative elements and is symmetric. We have used the Freedman-Diaconis rule here [28] to discretize the data. Further details are available in the Supplementary Material.

2.2.3. Comparison of Linear and Non-linear Relationships

We conduct an eigendecomposition of both the distance and the mutual information matrices for every window k = 1, 2, …, 𝕋. First we carry out eigendecompositions of the distance matrix D (from Equation 4) and the mutual information matrix M (from Equation 8):

$\begin{array}{ll}D={\displaystyle \sum _{i=1}^N}{v}_i^D{(v_i^D)}^{\prime }{\lambda }_i^D\text{\hspace{1em}and\hspace{1em}}M={\displaystyle \sum _{i=1}^N}{v}_i^M{(v_i^M)}^{\prime }{\lambda }_i^M,& (9)\end{array}$

where λ_i is the ith eigenvalue, v_i is the corresponding eigenvector, and a prime represents transpose. Since the dominant eigenvector represents the contribution of each asset to the aggregate interaction matrix, we extract the dominant eigenvectors from both the distance and the mutual information matrices for every window and regress the eigenvector obtained from the kth mutual information matrix (v^{mi, k}) on that obtained from the corresponding kth distance matrix (v^{D, k}):

$\begin{array}{ll}{v}_j^{\text{mi},k}=\alpha +\beta v_j^{D,k}+{ϵ}_j\text{\hspace{1em}for\hspace{1em}}j=1,\dots ,N,& (10)\end{array}$

where α and β are constants and ϵ_j is an error term. The explained variation (i.e., the R² of the regression) over 47 windows is plotted in Figure 1. High explanatory power would indicate that the information content is similar in the two measures. Two features stand out from the results. First, there is substantial time variation and an almost cyclic oscillation in the explanatory power. Second, there seems to be a general increase over time in the degree of relationship, indicating that the information content is becoming more similar, at least for pairwise relationships. The mutual information estimates were computed by discretizing the data, with each series converted into an ordinal categorical series with b classes, where b = 8, 12, and 16, utilizing the useful property that mutual information is a probability-based measure. Upon varying number of bins, the results are similar in all cases [29]. Therefore, the information content seems to be captured well by linear correlation matrices, which are much less computationally intensive.

FIGURE 1

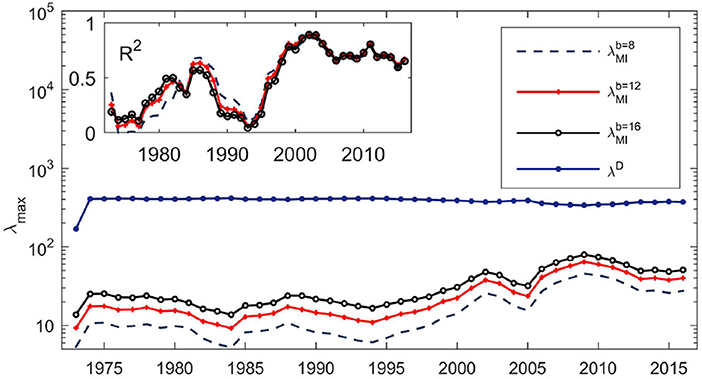
Figure 1. Evolution of the dominant eigenvalues of the distance matrices (λ^D) and the mutual information matrices (${\lambda }_{\text{MI}}^b$ with b = 8, 12, 16) over the time period 1972–2018. The dominant eigenvalues of the mutual information matrices (for three bin choices) show variation over time in the semi-log plot. Due to scaling, the variation in the dominant eigenvalue of the distance matrix is subdued. Inset: Time series of R² obtained from regressing the dominant eigenvector of the mutual information matrix on the dominant eigenvector of the distance matrix over the period 1972–2018 comprising 44 time windows. The choice of the number of bins b seems to have a negligible effect (results are shown for b = 8, 12, and 16). The dominant eigenvectors representing market modes in the distance matrices D and the mutual information matrices M became strongly correlated after the year 2000.

2.3. Complexity Through Dispersion in Systemic Risk

The spread in systemic risk across different stocks may indicate the degree of complexity. A high spread would imply that some assets are extremely risky while other assets are safe; a low spread would indicate a similar risk profile for all stocks. We quantify systemic risk following the method proposed in Yun et al. [17], which uses the Granger causal network as the fundamental building block.

We construct the Granger causal network (GCN) for each window of data (excluding the first window as its network size was not comparable with that of the rest). Each network is constructed as follows. If the jth asset's return Granger causes the ith asset's return, then there exists an edge from j to i:

$\begin{array}{ll}{r}_{it}=\alpha +{\beta }_{ii}{r}_{i,t-1}+{\beta }_{ij}{r}_{j,t-1}+{ϵ}_{it}\text{\hspace{1em}for }i,j=1,\dots ,N,& (11)\end{array}$

where α is a constant, β_ij is the parameter of interest, and ϵ_it is an error term. In the estimated model, if β_ij is significantly different from zero (evaluated at the standard 5% level of significance, with estimation done using the lmtest package in R), we connect i and j. We do the same for all i, j = 1, …, N and create a full Granger causal matrix G_N×N. A visual example is shown in Figure 2A. High dispersion in the degree connectivity is evident.

FIGURE 2

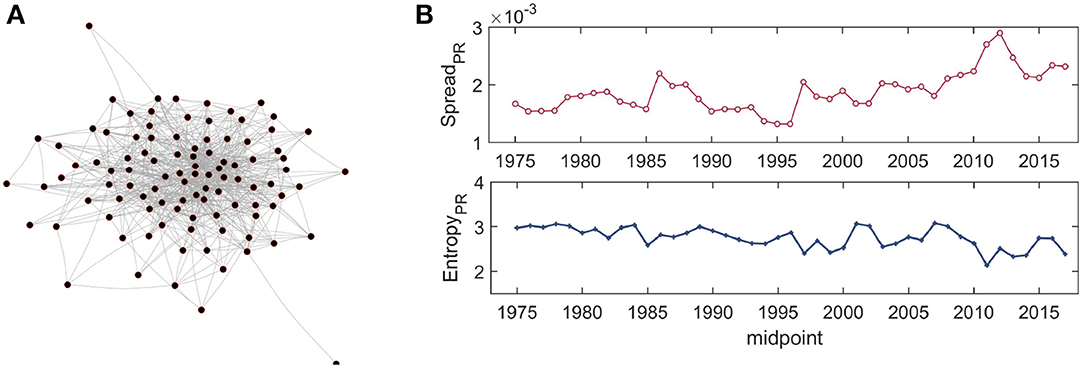
Figure 2. (A) Illustrative example of a Granger causal network of 100 firms (nodes) with greatest market capitalization in the last window of data (2015–2018) from NASDAQ; an edge represents Granger causality between a pair of return time series. (B) Evolution of the spread in systemic risk as measured by PageRank computed on Granger causality: the top panel shows the evolution of the standard deviation of PageRank for the nodes; the bottom panel shows the evolution of the differential entropy (Jaynes' method). The spread in centrality of assets remained stable over time, with a large spike occurring around 2013 in the standard deviation, while the entropy remains quite stable.

Once the network is created, we find the PageRank [30] of the matrix as a measure of the systemic risk [17, 18]. The interpretation is that a high PageRank would imply a higher propensity of lagged movement with respect to other assets and, therefore, higher risk of spillover from other stocks (see the Supplementary Material).

We study the evolution of the influence of assets in the GCN by calculating the dispersion in PageRank. High dispersion would indicate high inequality in influence. We present the evolution of the standard deviation and the differential entropy, two well-known measures of dispersion, in Figure 2B. Both series seem to be quite stable, indicating low spread in the influence of assets in the predictive GCN, except for the high inequality around 2013 shown by the first series (the estimate for 2013 represents data from the window 2012–15).

2.4. Algorithmic Measures Based on Information Theory

In this subsection we treat the problem of defining complexity in the financial network from the point of view of replicability of the emergent pattern. Although the present approach is different, we note that in Zenil and Delahaye [25] it was proposed to apply an algorithmic complexity measure to financial price data. The authors analyzed deviation of financial markets from log-normal behavior in a parametric setup under distributional assumptions. Here we use a non-parametric formulation and study the time series behavior of the implied complexity measure.

Our main idea is as follows. Given financial time series data for a certain window, we first create a correlation matrix (as in Equation 3), and from that we construct a distance matrix in the form of an identity matrix minus the correlation matrix. Then, based on a clustering technique (multi-dimensional scaling, a non-linear dimension-reduction technique for information visualization that creates a pattern of the relative positions of a number of objects in a dataset; we employed Euclidean distance for the present implementation [31] using the sklearn.manifold package in Python), we project the distance matrix onto a two-dimensional plane. This step generates a data cloud on the two-dimensional plane.

By defining a fine grid on the plane, we convert the data cloud into a binary matrix, where each cell is evaluated according to whether or not it contains an asset's projection. Thus, we get a pattern on a two-dimensional grid. Given this binary matrix pattern, we can construct a complexity measure [21, 22, 32] based on how complex the pattern is that emerges on the matrix. Our main object of study is the evolution of this complexity measure (see the Supplementary Material).

Given this binary representation, one way to construct a complexity measure would be to employ a lossless compression method that captures statistical regularities related to information-theoretic measures, such as Shannon entropy, instead of algorithmic measures [22, 33]. A key limitation of such approaches is that they are not invariant with respect to different descriptions of the same object, while methods in algorithmic complexity, such as the “invariance theorem,” can overcome this difficulty [32]. In the following we adopt an algorithm (the block decomposition method, BDM for short) developed in Zenil et al. [21, 22, 32] to construct a complexity measure which in our view is a potential candidate.

The algorithmic complexity of a string can be defined in terms of the shortest algorithm that generates that string [34–36]. The algorithmic complexity K(s) of a string s is the length of the shortest program p that generates s when executed on a universal Turing machine U (prefix-free; for details see [37, 38]), which can be formally expressed as

$\begin{array}{ll}{K}_U(s)=min\{|p|:U(p)=s\}.& (12)\end{array}$

In the following we apply BDM estimation of the complexity of the projection of the data on a two-dimensional grid. For a complete discussion of the methodology of complexity calculations and the background, which is a vast literature in itself, one can consult [34, 35, 39, 40, 40–43].

2.5. Interactive Dynamics: Complexity Through Heterogeneity

Next, we explore an ecology-inspired [9] characterization of economic complexity in terms of the stability of interlinked dynamical systems [44], which comes from the work of Robert May. The result (which goes by the name of the May-Wigner result) is based on prior theoretical work done by E. Wigner on random matrices. The key idea is that as a first-order dynamical system defined on a vector of variables X_N×1 with random heterogeneous connections becomes larger (i.e., N increases), the system tends to be become unstable [26]. Formally, if Γ is an N × N interaction matrix with elements γ_ij such that Prob(γ_ij = 0) = c and ${\gamma }_{ij}=f(0,{\sigma }^2)$ for all other elements, where f is some distribution with mean zero and variance σ², then in the limit N → ∞, the probability that the linear system

$\begin{array}{ll}\dot{X}=\Gamma X_t& (13)\end{array}$

is stable tends to 1 if Ncσ² < 1 and tends to 0 if Ncσ² > 1 [44]. Importantly, for us σ represents the heterogeneity in the strengths of connections of the interaction matrix Γ. In Rai et al. [27] this idea was applied to the stock market with a discrete-time formulation in the form of a vector autoregression ($X_t=\tilde{\Gamma }{X}_{t-1}+{ϵ}_t$, where one allows for a constant vector c in the vector autoregression estimation; see the Supplementary Material). It is shown that during times of crisis the estimated heterogeneity parameter (σ obtained from the estimated $\tilde{\Gamma }$ matrix) increases substantially. However, the data considered in Rai et al. [27] was limited (spanning the 16 years 2002–17), the time windows were non-overlapping, and the analysis was done only on data from the New York Stock Exchange. In the present paper, we perform a complementary analysis with the same technique, using NASDAQ data from 1972 to 2018 with overlapping windows. We fit the vector autoregression model to the data and estimate the $\tilde{\Gamma }$ matrix for each window; then we compute the standard deviation of the estimated parameters in the $\tilde{\Gamma }$ matrix, which represents the degree of heterogeneity in the interaction strengths.

2.6. Decomposability of Complexity Measures

We also explore whether a feature that we find at the level of raw data can be decomposed in terms of slices of data obtained via eigendecomposition. For this purpose, we consider singular value decomposition,

$\begin{array}{ll}g=U\Sigma V^{*}& (14)\end{array}$

where the return matrix g (of size T × N) is expressed as a product of three matrices, namely a T × T matrix U, an N × N orthonormal matrix V, such that V = V^*, and a T × N rectangular diagonal matrix Σ which contains non-negative numbers on the diagonal. In the present context, T > N.

After de-meaning the data matrix g, we consider the matrix Σ′ which contains only a subset of entries on the diagonal while the rest of the entries are replaced by zeros. The original matrix Σ would have N entries on the diagonal. For Σ′, we take the subsets to be the first to fourth singular values and the fifth to fifteenth singular values, implying that we can reconstruct the return series associated with the first four and the next eleven values by simply constructing

$\begin{array}{ll}{g}^{\prime }=U{\Sigma }^{\prime }{V}^{*}.& (15)\end{array}$

We implement the complexity measures on these reconstructed data matrices as well, to see whether a complexity measure calculated from the whole data can be decomposed into complexity measures pertaining to the dominant eigenmodes in the data. We note that for the vector autoregression model estimation, the estimated interaction matrices would have only k non-trivial columns if we select k eigenmodes to construct the data slices.

3. Results

In Figure 3 we plot the complexity measure for rolling windows using the BDM for the whole data. The results were obtained by employing the multi-dimensional scaling method for fixed axes using the scikit library in Python [45]. Fixing the axes is required because the multi-dimensional scaling algorithm does not always compute the projection in the same way since the technique is invariant under rotation in the two-dimensional plane, whereas the complexity measure is not invariant under rotation. The BDM results were obtained using the Python module developed by the AlgoDyn Development team (publicly available at https://pybdm-docs.readthedocs.io/en/latest/index.html). For the present purposes, we used the 2D implementation and two symbols. For the heterogeneity estimates following the May-Wigner theory, in Figure 4 we plot the evolution of the heterogeneity in the interaction matrix. The analysis was done using the VARS package in the R programming language. Both of the above analyses were complemented by computing the evolution of the same measures on the first four and the next eleven eigenmodes using the singular value decomposition (implemented using quantmod in R), as shown in the insets of Figures 3, 4.

FIGURE 3

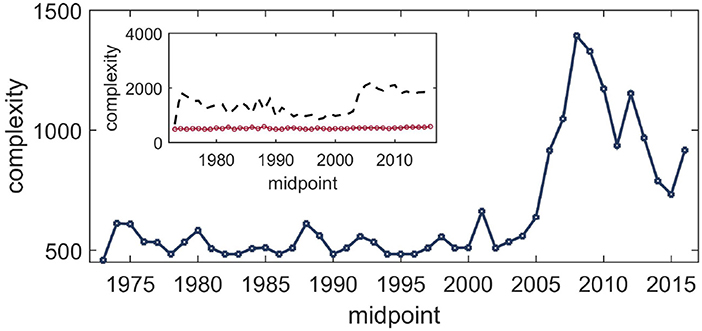
Figure 3. Evolution of the complexity of financial linkages among the stocks over the period 1972–2018 obtained from the BDM. The dimension of the financial linkage data was reduced by mapping the dissimilarity matrices (constructed from the cross-correlation matrix ρ_N×N as I_N×N − ρ_N×N) onto two-dimensional grids using a multi-dimensional scaling technique, and the complexity measure was then evaluated on these. The measured value peaks around the crisis period. Inset: Result of the same procedure applied to data slices corresponding to the first four eigenmodes (black dashed line) and the next eleven eigenmodes (red circles).

FIGURE 4

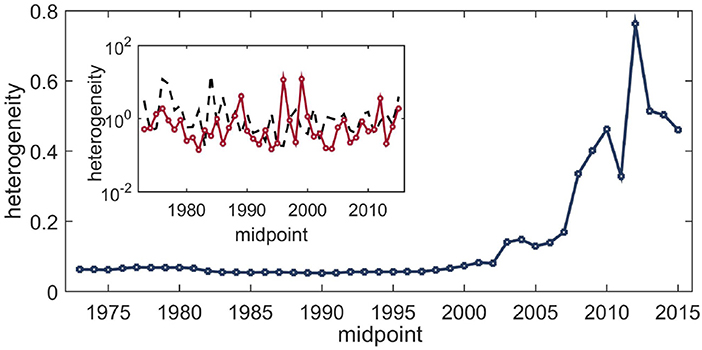
Figure 4. Evolution of the heterogeneity in interaction strengths among the stocks over the period 1972–2018 obtained from the vector autoregression model. Each point estimate corresponds to a 4-years data slice. The x-axis plots the midpoints of the windows. Inset: Result of the same procedure applied to data slices corresponding to the first four eigenmodes (black dashed line) and the next eleven eigenmodes (red circles). No particular pattern emerges from the decomposition, but at the aggregate level heterogeneity increases substantially during the time of the crisis and rises further in the post-crisis period.

The main takeaway from these results is that both of the complexity measures correctly indicate the time of crisis. The BDM-based measure computes an analog of the dispersion in the clustering of data (even with normalized return data), whereas the vector autoregression-based measure captures the dispersion in terms of the strength of interactions. Interestingly, when we apply the same techniques to slices of data corresponding to different eigenmodes, similar features are absent. Therefore, these complexity measures, while reasonably correct at the aggregate level, do not seem to be decomposable.

4. Summary and Discussion

The goal of this work was to extract statistical features from time-varying data that indicate evolution of complexity. Financial systems are thought of as canonical examples of complex systems in terms of interaction, emergence, evolution, and non-stationarity. Here we have analyzed historical financial data on a comprehensive set of stocks from NASDAQ, which is one of the three most followed indices of the US stock market and consists mostly of non-financial tech-oriented firms.

We have estimated four indices of complexity: a measure based on the information content of non-linear co-movements, a systemic risk-based measure constructed from Granger causal networks, an algorithmic complexity measure based on multi-dimensional scaling, and a heterogeneity-based measure motivated by dynamical systems theory. To summarize, the first two measures do not seem to indicate the crisis period (2007–09) clearly, whereas the third and fourth measures perform substantially better and are more accurate. However, neither of the latter two measures is decomposable, in the sense that for each of them the sum of the complexities of decomposed data is not the same as the complexity of the original data.

Some caveats and future directions for research are as follows. First, the results indicate that the information content of the mutual information matrix and that of the correlation matrix become quite similar after the year 2000, so a non-linear measure, such as mutual information is not very useful. There are, however, some new measures of association, with different asymptotic theory (e.g., [46]), that could be explored in future work. Second, an open problem relating to the construction of the Granger causal matrix from pairwise regression is that it does not test for joint significance and there can be type I error due to multiple testing, leading to false discovery of edges [47]. In future work we intend to explore this issue in more detail. Third, for the BDM-based measure of complexity, implementation with more symbols may yield better results, although this would be computationally quite costly. Fourth, following Rai et al. [27] we have shown that the heterogeneity of interaction strengths among the stocks significantly increases during the crisis period and attains an even higher level in the post-crisis period. Two major differences between our results and those of Rai et al. [27] are that (i) in the present work, the spike in heterogeneity has a much larger magnitude than that found in Rai et al. [27]; and (ii) in our results the greatest spike in heterogeneity occurs shortly after the crisis (rather than during the crisis as in the analysis of NYSE data in Rai et al. [27]) and seems to continue for a long time without tapering off.

Management of risk in complex systems, such as financial markets requires clear quantification of the complexity. The measures proposed in this paper complement the existing statistical finance literature on describing evolution of markets during crisis and non-crisis periods [11, 48–51]. In this work we have used the word complexity to mean emergent instability, similar to Kuyyamudi et al. [11]. It would be interesting to see whether similar ideas can be applied to other complex systems [12]. In the context of financial markets, such quantification of complexity brings us closer to answering the question of what factors (economic or financial) drive the evolution of complexity. A causal explanation of the mechanisms can inform policy-making with regard to complex financial systems.

Data Availability Statement

The data can be accessed through WRDS (Wharton Research Data Services) by paying the required fees. Requests to access these datasets should be directed to the Center for Research in Security Prices: http://www.crsp.org/, WRDS: https://wrds-www.wharton.upenn.edu/.

Author Contributions

AC designed the research. GY and AG carried out the numerical computations. AC and GY prepared the figures. All authors were involved in writing the paper.

Funding

This research was partially supported by an institute grant, IIM Ahmedabad.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank the HPC lab at IIM Ahmedabad for computational support and the Vikram Sarabhai Library for providing the data used in this research. We would like to thank three reviewers, Guiseppe Brandi, Bikas K. Chakrabarti, Anirban Chakraborti, Diptesh Ghosh, Sitabhra Sinha, and Hector Zenil for useful discussions and for providing helpful references. We are grateful to Abinash Mishra for helping us with the collection and processing of the data. Jalshayin Bhachech and Abinash Mishra provided excellent research assistance. All remaining errors are ours.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2020.00339/full#supplementary-material

Footnotes

1. ^Because of missing data, the first window contains 124 stocks.

References

1. Brunnermeier M, Oehmke M. Complexity in Financial Markets. Working paper. Princeton, NJ: Princeton University (2009).

Google Scholar

2. Di Guilmi C, Gallegati M, Landini S. Interactive Macroeconomics: Stochastic Aggregate Dynamics With Heterogeneous and Interacting Agents. Cambridge: Cambridge University Press (2017).

3. Gallegati M. Complex Agent-Based Models. Berlin: Springer (2018).

Google Scholar

4. Lillo F, Mantegna RN. Power-law relaxation in a complex system: Omori law after a financial market crash. Phys Rev E. (2003) 68:016119. doi: 10.1103/PhysRevE.68.016119

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Stanley MH, Amaral LA, Buldyrev SV, Havlin S, Leschhorn H, Maass P, et al. Scaling behaviour in the growth of companies. Nature. (1996) 379:804–6. doi: 10.1038/379804a0

CrossRef Full Text | Google Scholar

6. Kashyap A, Zingales L. The 2007-8 financial crisis: Lessons from corporate finance. J Financ Econ. (2010) 97:303–488. doi: 10.1016/j.jfineco.2010.05.010

CrossRef Full Text | Google Scholar

7. Foster J, Magdoff F. The Great Financial Crisis: Causes and Consequences. New York, NY: NYU Press (2008).

Google Scholar

8. Bonanno G, Lillo F, Mantegna RN. Levels of complexity in financial data. Phys A. (2001) 299:16–27. doi: 10.1016/S0378-4371(01)00279-5

CrossRef Full Text | Google Scholar

9. Johnson N, Lux T. Ecology and economics. Nature. (2011) 469:302–3. doi: 10.1038/469302a

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Sornette D, Zhou W. Predictability of large future changes in major financial indices. Int J Forecast. (2006) 22:153–68. doi: 10.1016/j.ijforecast.2005.02.004

CrossRef Full Text | Google Scholar

11. Kuyyamudi C, Chakrabarti AS, Sinha S. Emergence of frustration signals systemic risk. Phys Rev E. (2019) 99:052306. doi: 10.1103/PhysRevE.99.052306

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Newman ME. The structure and function of complex networks. SIAM Rev. (2003) 45:167–256. doi: 10.1137/S003614450342480

CrossRef Full Text | Google Scholar

13. Mantegna RN, Stanley HE. Introduction to Econophysics: Correlations and Complexity in Finance. Cambridge: Cambridge University Press (1999).

Google Scholar

14. Farmer JD, Lo AW. Frontiers of finance: evolution and efficient markets. Proc Natl Acad Sci USA. (1999) 96:9991–2. doi: 10.1073/pnas.96.18.9991

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Fiedor P. Networks in financial markets based on the mutual information rate. Phys Rev E. (2014) 89:052801. doi: 10.1103/PhysRevE.89.052801

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Sinha S, Chatterjee A, Chakraborti A, Chakrabarti BK. Econophysics: An Introduction. John Wiley & Sons (2010).

Google Scholar

17. Yun T, Jeong D, Park S. “Too central to fail” systemic risk measure using PageRank algorithm. J Econ Behav Organ. (2019) 162:251–72. doi: 10.1016/j.jebo.2018.12.021

CrossRef Full Text | Google Scholar

18. Billio M, Getmansky M, Lo A, Pelizzon L. Econometric measures of connectedness and systemic risk in the finance and insurance sectors. J Financ Econ. (2012) 104:535–59. doi: 10.1016/j.jfineco.2011.12.010

CrossRef Full Text | Google Scholar

19. Nirenberg S, Carcieri SM, Jacobs AL, Latham PE. Retinal ganglion cells act largely as independent encoders. Nature. (2001) 411:698. doi: 10.1038/35079612

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Williams PL, Beer RD. Generalized measures of information transfer. arXiv. (2011) 1102.1507.

Google Scholar

21. Zenil H, Kiani NA, Zea AA, Tegnér J. Causal deconvolution by algorithmic generative models. Nat Mach Intell. (2019) 1:58. doi: 10.1038/s42256-018-0005-0

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Zenil H, Kiani NA, Tegnér J. Low-algorithmic-complexity entropy-deceiving graphs. Phys Rev E. (2017) 96:012308. doi: 10.1103/PhysRevE.96.012308

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Cover TM, Thomas JA. Elements of Information Theory. John Wiley & Sons (2012).

24. Shannon CE. A mathematical theory of communication. Bell Syst Tech J. (1948) 27:379–423.

Google Scholar

25. Zenil H, Delahaye JP. An algorithmic information theoretic approach to the behaviour of financial markets. J Econ Surv. (2011) 25:431–63. doi: 10.1111/j.1467-6419.2010.00666.x

CrossRef Full Text | Google Scholar

26. May RM. Will a large complex system be stable? Nature. (1972) 238:413–4. doi: 10.1038/238413a0

CrossRef Full Text | Google Scholar

27. Rai A, Bansal A, Chakrabarti AS. Statistical estimation of time-varying complexity in financial networks. Eur Phys J B. (2019) 92:239. doi: 10.1140/epjb/e2019-100161-1

CrossRef Full Text | Google Scholar

28. Freedman D, Diaconis P. On the histogram as a density estimator: L2 theory. Z Wahrsch Verwandte Geb. (1981) 57:453–76. doi: 10.1007/BF01025868

CrossRef Full Text | Google Scholar

29. Paiva AR, Park I, Príncipe JC. A comparison of binless spike train measures. Neural Comput Appl. (2010) 19:405–19. doi: 10.1007/s00521-009-0307-6

CrossRef Full Text | Google Scholar

30. Newman M. Networks. Oxford: Oxford University Press (2018).

Google Scholar

31. Borg I, Groenen P. Modern multidimensional scaling: theory and applications. J Educ Meas. (2003) 40:277–80. doi: 10.1111/j.1745-3984.2003.tb01108.x

CrossRef Full Text | Google Scholar

32. Zenil H, Badillo L, Hernández-Orozco S, Hernández-Quiroz F. Coding-theorem like behaviour and emergence of the universal distribution from resource-bounded algorithmic probability. Int J Parallel Emerg Distrib Syst. (2019) 34:161–80. doi: 10.1080/17445760.2018.1448932

CrossRef Full Text | Google Scholar

33. Cilibrasi R, Vitányi PM. Clustering by compression. IEEE Trans Inform Theory. (2005) 51:1523–45. doi: 10.1109/TIT.2005.844059

CrossRef Full Text | Google Scholar

34. Levin LA. Laws of information conservation (nongrowth) and aspects of the foundation of probability theory. Probl Pered Inform. (1974) 10:30–5.

Google Scholar

35. Chaitin GJ. On the length of programs for computing finite binary sequences. J ACM. (1966) 13:547–69. doi: 10.1145/321356.321363

CrossRef Full Text | Google Scholar

36. Kolmogorov AN. Three approaches to the quantitative definition of information. Probl Inform Transm. (1965) 1:1–7.

Google Scholar

37. Li M, Vitányi P. An Introduction to Kolmogorov Complexity and Its Applications, Vol. 3. Springer (2008).

PubMed Abstract | Google Scholar

38. Calude CS, Salomaa K, Roblot TK. Finite state complexity. Theor Comput Sci. (2011) 412:5668–77. doi: 10.1016/j.tcs.2011.06.021

CrossRef Full Text | Google Scholar

39. Solomonoff RJ. A formal theory of inductive inference. Part I. Inform Control. (1964) 7:1–22. doi: 10.1016/S0019-9958(64)90223-2

CrossRef Full Text | Google Scholar

40. Soler-Toscano F, Zenil H, Delahaye J-P, Gauvrit N. Calculating kolmogorov complexity from the output frequency distributions of small turing machines. PLoS ONE. (2014) 9:e96223. doi: 10.1371/journal.pone.0096223

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Delahaye JP, Zenil H. Numerical evaluation of algorithmic complexity for short strings: a glance into the innermost structure of randomness. Appl Math Comput. (2012) 219:63–77. doi: 10.1016/j.amc.2011.10.006

CrossRef Full Text | Google Scholar

42. Rado T. On non-computable functions. Bell Syst Tech J. (1962) 41:877–84. doi: 10.1002/j.1538-7305.1962.tb00480.x

CrossRef Full Text | Google Scholar

43. Zenil H, Hernández-Orozco S, Kiani NA, Soler-Toscano F, Rueda-Toicen A, Tegnér J. A decomposition method for global evaluation of shannon entropy and local estimations of algorithmic complexity. Entropy. (2018) 20:605. doi: 10.3390/e20080605

CrossRef Full Text | Google Scholar

44. Sinha S. Complexity vs. stability in small-world networks. Phys A Stat Mech Appl. (2005) 346:147–53. doi: 10.1016/j.physa.2004.08.062

CrossRef Full Text | Google Scholar

45. Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, et al. Scikit-learn: machine learning in Python. J Mach Learn Res. (2011) 12:2825–30.

Google Scholar

46. Chatterjee S. A new coefficient of correlation. J Am Stat Assoc. (2020) 1–21. doi: 10.1080/01621459.2020.1758115

CrossRef Full Text | Google Scholar

47. Drton M, Perlman MD. Multiple testing and error control in gaussian graphical model selection. Stat Sci. (2007) 22:430–49. doi: 10.1214/088342307000000113

CrossRef Full Text | Google Scholar

48. Verma A, Buonocore RJ, Di Matteo T. A cluster driven log-volatility factor model: a deepening on the source of the volatility clustering. Quant Finance. (2019) 19:981–96. doi: 10.1080/14697688.2018.1535183

CrossRef Full Text | Google Scholar

49. Kenett DY, Raddant M, Lux T, Ben-Jacob E. Evolvement of uniformity and volatility in the stressed global financial village. PLoS ONE. (2012) 7:e31144. doi: 10.1371/journal.pone.0031144

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Namaki A, Shirazi AH, Jafari GR. Network analysis of a financial market based on genuine correlation and threshold method. Phys A. (2011) 390:3835–41. doi: 10.1016/j.physa.2011.06.033

CrossRef Full Text | Google Scholar

51. Namaki A, Lai ZK, Jafari GR, Raei R, Tehrani R. Comparing emerging and mature markets during times of crises: a non-extensive statistical approach. Phys A. (2011) 392:3039–44. doi: 10.1016/j.physa.2013.02.008

CrossRef Full Text | Google Scholar