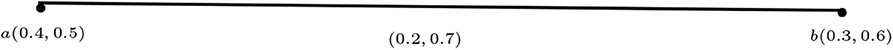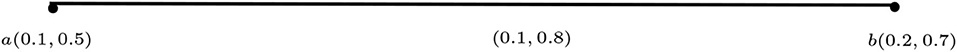Certain Concepts of Vague Graphs With Applications to Medical Diagnosis

Shao, Zehui; Kosari, Saeed; Shoaib, Muhammad; Rashmanlou, Hossein

doi:10.3389/fphy.2020.00357

ORIGINAL RESEARCH article

Front. Phys., 11 November 2020

Sec. Statistical and Computational Physics

Volume 8 - 2020 | https://doi.org/10.3389/fphy.2020.00357

This article is part of the Research Topic Mathematical Treatment of Nanomaterials and Neural Networks View all 28 articles

$\nZehui Shao$ Zehui Shao¹

Saeed Kosari¹^*

Muhammad Shoaib²

Hossein Rashmanlou³

¹Institute of Computing Science and Technology, Guangzhou University, Guangzhou, China
²Department of Mathematics, University of the Punjab, New Campus, Lahore, Pakistan
³Mazandaran Adib Institute of Higher Education, Sari, Iran

The purpose of this research study is to present and explore the key properties of some new operations on vague graphs, including rejection, maximal product, symmetric difference, and residue product. This article introduces the notions of degree of a vertex and total degree of a vertex in a vague graph. As well, this study outlines the specific conditions required for obtaining the degrees of vertices in vague graphs under the operations of maximal product, symmetric difference, and rejection. The article also discusses applications of vague sets in medical diagnosis.

1. Introduction

Graph theory is an extremely useful tool for solving combinatorial problems in a wide range of fields, including geometry, algebra, number theory, topology, operations research, biology, and social systems. Graph theory also has many applications of great scope, such as in networking, image capture, clustering, handling uncertainty, image segmentation, finding communities in networks, bioscience, information technology, operations research, and social science networks consisting of points connected by lines. In fact, graph theory studies connections between objects, such as vertices and edges and the various relations between them. Fuzzy graph theory is finding an increasing number of applications in modeling real-time systems, where the amount of information inherent in the system varies with different levels of precision. In 1965, Zadeh [1] first proposed the theory of fuzzy sets. The fuzzy graph, with the approximate reasoning, enables many combinatorial problems in fields, such as topology and algebra to be solved more easily. The concept of fuzzy graphs is discussed by Rosenfeld [2] as well as by Bhattacharya [3, 4]. Fuzzy graphs date back to the nineteenth century, and their use has grown tremendously in recent years [5, 6]. Gau and Buehrer [7] proposed the concept of vague set in 1993, which replaces the value of an element in a set with a subinterval of [0, 1]. Specifically, a true-membership function t_v(x) and a false-membership function f_v(x) are used to describe the boundaries of the membership degree. Descriptions of real-world problems can be improved by using the theory of vague sets. Researchers have applied this theory to several real-world situations, such as decision-making and fuzzy control. The theory of vague sets is also helpful for fault diagnosis and knowledge discovery. Interval-valued fuzzy sets have a case vague set, which has been applied in different fields of mathematics. Ramakrishna [8] introduced the concept of vague graph and also studied related properties. Vague graphs have numerous applications in geometry and operations research and are also useful in many areas of computer science. Rashmanlou and Borzooei [9] studied new concepts relating to vague graphs, product vague graphs [10], regularity of vague graphs [11], and vague competition graphs [12]. Krishna and Lavanya [13] developed new concepts of coloring in vague graphs. Besides the membership degree, the non-membership degree has been introduced as well, which is presented by Atanassove [14] in an intuitionistic fuzzy set, a type of extension of a fuzzy set. Parvathi and Karunambigai [15] discussed intuitionistic fuzzy graphs. Devi et al. [16] presented new concepts regarding intuitionistic fuzzy labeling graphs.

In this study we outline and explore the key properties of some new operations on vague graphs, including rejection, maximal product, symmetric difference, and residue product. We introduce new notions, such as degree of a vertex and total degree of a vertex in a vague graph. We also outline specific conditions for obtaining the degrees of vertices in vague graphs under the operations of maximal product, symmetric difference, and rejection. Furthermore, we explore applications of vague sets in medical diagnosis.

2. Preliminaries

In this section we introduce the key preliminary notions and definitions that are used in this study.

Definition 2.1 ([17]). A graph is an ordered pair G = (V, E), where V is the set of vertices of G and E is the set of all edges, arcs, or lines, which are two-element subsets of V (that is, an edge is related to two vertices and the relation is represented as an unordered pair {m, n} of those vertices).

Note that for an edge {m, n}, graph theorists usually use the somewhat shorter notation mn. Two vertices m and n in an undirected graph G are said to be adjacent in G if mn is an edge of G. An edge whose endpoints are the same is called a loop. A graph without loops is called a simple graph.

Definition 2.2 ([7]). A vague set M is a pair (T_M; F_M) of functions on a set V, where T_M and F_M are real-valued V → [0, 1] functions such that T_M(m) + F_M(m) < 1 for all m ∈ V. The interval [T_M(m), 1 − F_M(m)] is known as the vague value of m in M.

In this definition, for m in M, T_M(m) is the lower bound for the degree of membership and F_M(m) is the lower bound for the negative of the degree of membership. Therefore, the degree of membership of m ∈ M is given by the interval [T_M(m), 1 − F_M(m)].

Definition 2.3 ([8]). Let G = (V, E) be a crisp graph. A pair G = (M, N) is called a vague graph defined on the crisp graph G = (V, E) if M = (T_M, F_M) is a vague set on V and N = (T_N, F_N) is vague set on E ⊆ V × V such that T_N(mn) ≤ min(T_M(m), T_M(n)) and F_N(mn) ≥ max(F_M(m), F_M(n)) for each edge mn in E.

Definition 2.4 ([9]). A vague graph G is said to be strong if T_N(mn) = min(T_M(m), T_M(n)) and F_N(mn) = max(F_M(m), F_M(n)) for all m, n ∈ V.

Definition 2.5 ([9]). A vague graph G is said to be complete if T_N(mn) = min(T_M(m), T_M(n)) and F_N(mn) = max(F_M(m), F_M(n)) for all mn ∈ E.

Definition 2.6 ([11]). A vague graph G is said to be connected if $T_{N}^{\infty} (m_{i} m_{j}) > 0$ and $F_{N}^{\infty} (m_{i} m_{j}) < 1$ for all m_i, m_j ∈ V. Also, we have

\begin{array}{r} T_{N}^{\infty} (m n) = sup {T_{N} (m n_{1}) \land T_{N} (n_{1} n_{2}) \land T_{N} (n_{2} n_{3}) \land \dots \\ \land T_{N} (n_{k - 1} n) ∣ m, n_{1}, n_{2}, \dots, n_{k - 1}, n \in V} \end{array}

and

\begin{array}{r} F_{N}^{\infty} (m n) = inf {F_{N} (m n_{1}) \lor F_{N} (n_{1} n_{2}) \lor F_{N} (n_{2} n_{3}) \lor \dots \\ \lor F_{N} (n_{k - 1} n) ∣ m, n_{1}, n_{2}, \dots, n_{k - 1}, n \in V} . \end{array}

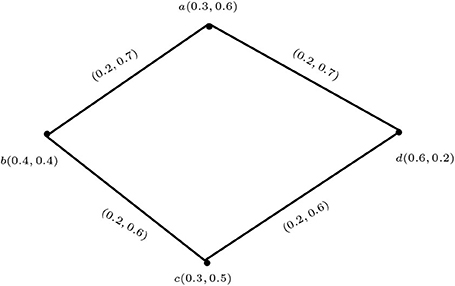
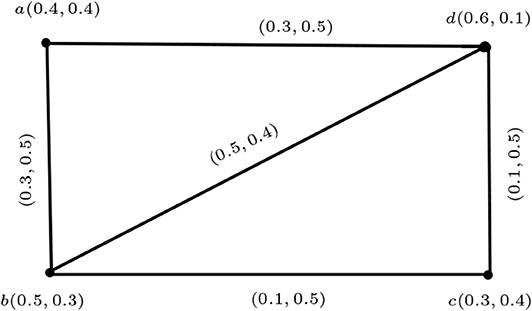
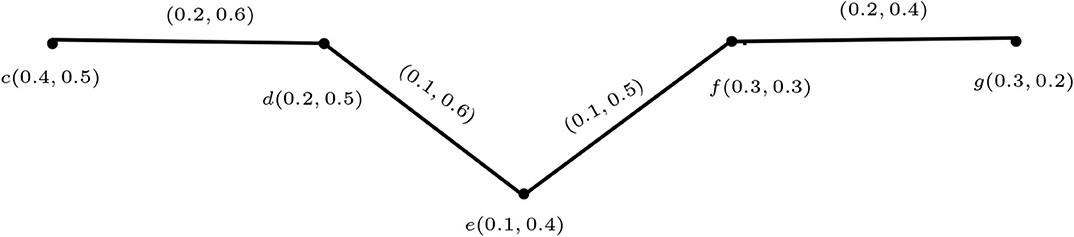
Example 2.7. Consider a vague graph G such that V = {a, b, c}, E = {ab, bc, cd, ad}, $M = 〈 (\frac{a}{0.3}, \frac{b}{0.4}, \frac{c}{0.3}, \frac{d}{0.6}), (\frac{a}{0.6}, \frac{b}{0.4}, \frac{c}{0.5}, \frac{a}{0.2}) 〉$ , and $N = 〈 (\frac{a b}{0.2}, \frac{b c}{0.2}, \frac{c d}{0.2}, \frac{a d}{0.2}), (\frac{a b}{0.7}, \frac{b c}{0.6}, \frac{c d}{0.6}, \frac{a d}{0.7}) 〉$ .

By routine computations, it is easy to show that G is a vague graph (Figure 1).

FIGURE 1

Figure 1. The vague graph G in Example 2.7.

3. Operations on Vague Graphs

In this section we define four new kinds of operations on vague graphs: the maximal product, residue product, rejection, and symmetric difference. We show that the maximal product, residue product, or rejection of two vague graphs is again a vague graph.

Definition 3.1. The maximal product G₁ * G₂ = (M₁*M₂, N₁*N₂) of two vague graphs G₁ = (M₁, N₁) and G₂ = (M₂, N₂) is defined by

\begin{array}{l} (i) (T_{M_{1}} * T_{M_{2}}) ((m_{1}, m_{2})) = max {T_{M_{1}} (m_{1}), T_{M_{2}} (m_{2})}, \\ (F_{M_{1}} * F_{M_{2}}) ((m_{1}, m_{2})) = min {F_{M_{1}} (m_{1}), F_{M_{2}} (m_{2})} \\ \forall (m_{1}, m_{2}) \in (V_{1} \times V_{2}); \end{array}

\begin{array}{l} (ii) (T_{M_{1}} * T_{M_{2}}) ((m, m_{2}) (m, n_{2})) = max {T_{M_{1}} (m), T_{N_{2}} (m_{2} n_{2})}, \\ (F_{M_{1}} * F_{M_{2}}) ((m, m_{2}) (m, n_{2})) = min {F_{M_{1}} (m), F_{N_{2}} (m_{2} n_{2})} \\ \forall m \in V_{1} and m_{2} n_{2} \in E_{2}; \end{array}

\begin{array}{l} (iii) (T_{M_{1}} * T_{M_{2}}) ((m_{1}, z) (n_{1}, z)) = max {T_{N_{1}} (m_{1} n_{1}), T_{M_{2}} (z)}, \\ (F_{M_{1}} * F_{M_{2}}) ((m_{1}, z) (n_{1}, z)) = min {F_{N_{1}} (m_{1} n_{1}), F_{M_{2}} (z)} \\ \forall z \in V_{2} and m_{1} n_{1} \in E_{1} . \end{array}

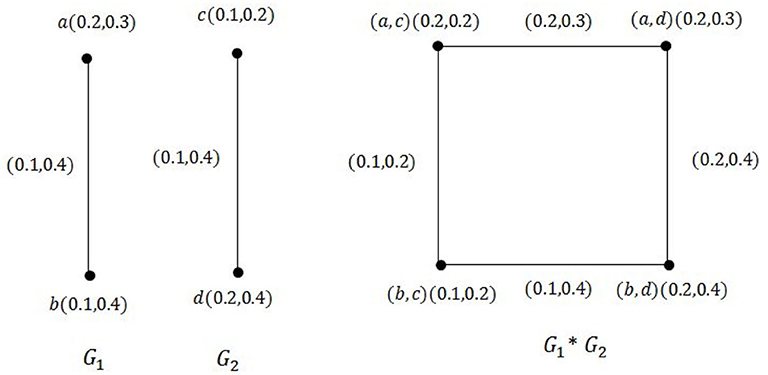
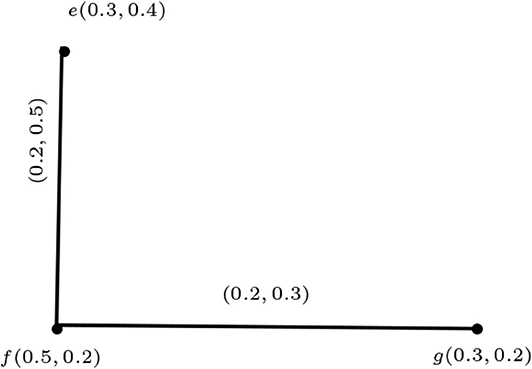
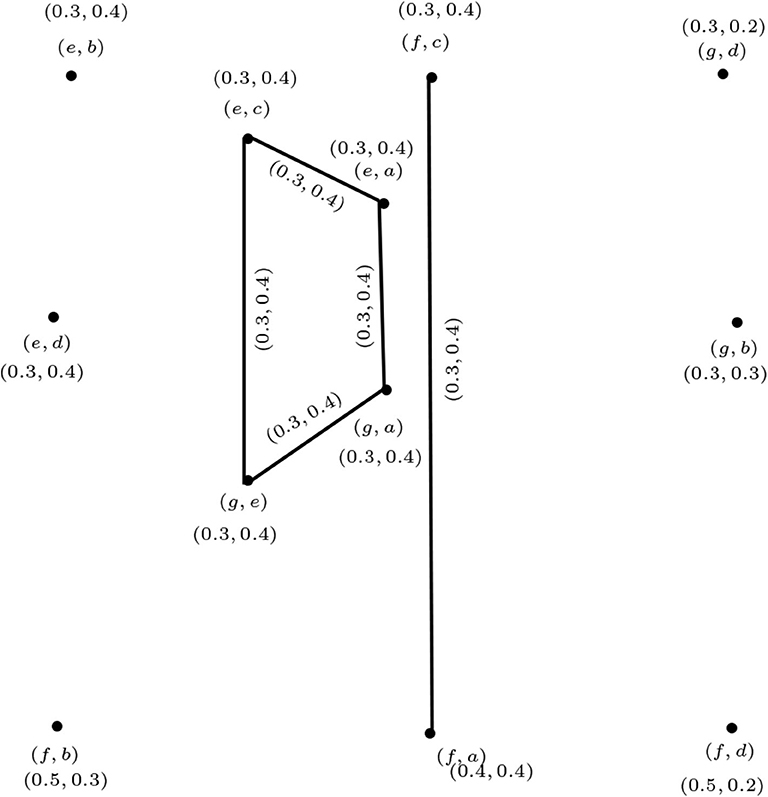
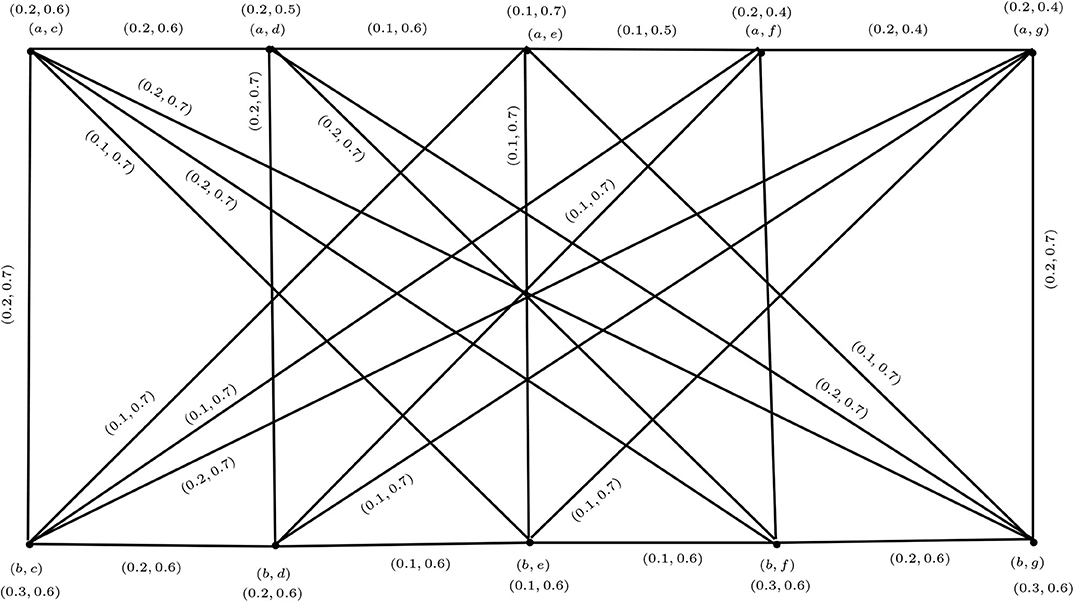
Example 3.2. Consider the two vague graphs G₁ and G₂ shown in Figures 2, 3. Their maximal product G₁ * G₂ is shown in Figure 4.

FIGURE 2

Figure 2. G₁.

FIGURE 3

Figure 3. G₂.

FIGURE 4

Figure 4. G₁ * G₂.

For the vertex (a, d), we find the membership and non-membership values as follows:

\begin{array}{l} (T_{M_{1}} * T_{M_{2}}) ((a, d)) = max {T_{M_{1}} (a), T_{M_{2}} (d)} \\ = max {0.4, 0.1} = 0.4, \\ (F_{M_{1}} * F_{M_{2}}) ((a, d)) = min {F_{M_{1}} (a), F_{M_{2}} (d)} \\ = min {0.5, 0.3} = 0.3, \\ for a \in V_{1} and d \in V_{2} . \end{array}

For the edge (a, d)(a, e), we find the following membership and non-membership values:

\begin{array}{l} (T_{M_{1}} * T_{M_{2}}) ((a, d) (a, e)) = max {T_{M_{1}} (a), T_{N_{2}} (d e)} \\ = max {0.4, 0.1} = 0.4, \\ (F_{M_{1}} * F_{M_{2}}) ((a, d) (a, e)) = min {F_{M_{1}} (a), F_{N_{2}} (d e)} \\ = min {0.5, 0.6} = 0.5, \\ for a \in V_{1} and d e \in E_{2} . \end{array}

Now, for edge (a, g)(b, g) we have

\begin{array}{l} (T_{M_{1}} * T_{M_{2}}) ((a, g) (b, g)) = max {T_{N_{1}} (a b), T_{M_{2}} (g)} \\ = max {0.2, 0.3} = 0.3, \\ (F_{M_{1}} * F_{M_{2}}) ((a, g) (b, g)) = min {F_{N_{1}} (a b), F_{M_{2}} (g)} \\ = min {0.7, 0.4} = 0.4, \\ for g \in V_{2} and a b \in E_{1} . \end{array}

Similarly, we can find the membership and non-membership values for all the remaining vertices and edges.

Proposition 3.3. The maximal product of two vague graphs G₁ and G₂ is a vague graph.

Proof: Let G₁ = (M₁, N₁) and G₂ = (M₂, N₂) be two vague graphs on crisp graphs G₁ = (V₁, E₁) and G₂ = (V₂, E₂), respectively, and let ((m₁, m₂)(n₁, n₂)) ∈ E₁ × E₂. Then by Definition 3.1 we have two cases:

(i) If m₁ = n₁ = m, then

\begin{array}{l} (T_{N_{1}} * T_{N_{2}}) ((m, m_{2}) (m, n_{2})) = max {T_{M_{1}} (m), T_{N_{2}} (m_{2} n_{2})} \\ \leq max {T_{M_{1}} (m), min {T_{M_{2}} (m_{2}), T_{M_{2}} (n_{2})}} \\ = min {max {{T_{M_{1}} (m), T_{M_{2}} (m_{2})}, max {{T_{M_{1}} (m), T_{M_{2}} (n_{2})}} \\ = min {(T_{M_{1}} * T_{M_{2}}) (m, m_{2}), (T_{M_{1}} * T_{M_{2}}) (m, n_{2})}, \\ (F_{N_{1}} * F_{N_{2}}) ((m, m_{2}) (m, n_{2})) = min {F_{M_{1}} (m), F_{N_{2}} (m_{2} n_{2})} \\ \geq min {F_{M_{1}} (m), max {F_{M_{2}} (m_{2}), F_{M_{2}} (n_{2})}} \\ = max {min {{F_{M_{1}} (m), F_{M_{2}} (m_{2})}, min {{F_{M_{1}} (m), F_{M_{2}} (n_{2})}} \\ = max {(F_{M_{1}} * F_{M_{2}}) (m, m_{2}), (F_{M_{1}} * F_{M_{2}}) (m, n_{2})} . \end{array}

(ii) If m₂ = n₂ = z, then

\begin{array}{l} (T_{N_{1}} * T_{N_{2}}) ((m_{1}, z) (n_{1}, z)) = max {T_{N_{1}} (m_{1} n_{1}), T_{M_{2}} (z)} \\ \leq max {min {T_{N_{1}} (m_{1} n_{1}), T_{M_{2}} (z)} \\ = min {max {{T_{N_{1}} (m_{1}), T_{M_{2}} (z)}, max {{T_{M_{1}} (n_{1}), T_{M_{2}} (z)}} \\ = min {(T_{M_{1}} * T_{M_{2}}) (m_{1}, z), (T_{M_{1}} * T_{M_{2}}) (n_{1}, z)}, \\ (F_{N_{1}} * F_{N_{2}}) ((m_{1}, z) (n_{1}, z)) = min {F_{N_{1}} (m_{1} n_{1}), F_{M_{2}} (z)} \\ \geq min {max {F_{N_{1}} (m_{1} n_{1}), F_{M_{2}} (z)} \\ = max {min {{F_{M_{1}} (m_{1}), F_{M_{2}} (z)}, min {{F_{M_{1}} (n_{1}), F_{M_{2}} (z)}} \\ = max {(F_{M_{1}} * F_{M_{2}}) (m_{1}, z), (F_{M_{1}} * F_{M_{2}}) (n_{1}, z)} . \end{array}

Therefore, G₁ * G₂ is a vague graph. □

Theorem 3.4. The maximal product of two strong vague graphs G₁ and G₂ is a strong vague graph.

Proof: Let G₁ = (M₁, N₁) and G₂ = (M₂, N₂) be two strong vague graphs on crisp graphs G₁ = (V₁, E₁) and G₂ = (V₂, E₂), respectively, and let ((m₁, m₂)(n₁, n₂)) ∈ E₁ × E₂. Then, by Proposition 3.3, G₁ * G₂ is a vague graph. Now we have two cases:

(i) If m₁ = n₁ = m, then

\begin{array}{l} (T_{N_{1}} * T_{N_{2}}) ((m, m_{2}) (m, n_{2})) = max {T_{M_{1}} (m), T_{N_{2}} (m_{2} n_{2})} \\ = max {T_{M_{1}} (m), min {T_{M_{2}} (m_{2}), T_{M_{2}} (n_{2})}} \\ = min {max {{T_{M_{1}} (m), T_{M_{2}} (m_{2})}, max {{T_{M_{1}} (m), T_{M_{2}} (n_{2})}} \\ = min {(T_{M_{1}} * T_{M_{2}}) (m, m_{2}), (T_{M_{1}} * T_{M_{2}}) (m, n_{2})}, \\ (F_{N_{1}} * F_{N_{2}}) ((m, m_{2}) (m, n_{2})) = min {F_{M_{1}} (m), F_{N_{2}} (m_{2} n_{2})} \\ = min {F_{M_{1}} (m), max {F_{M_{2}} (m_{2}), F_{M_{2}} (n_{2})}} \\ = max {min {{F_{M_{1}} (m), F_{M_{2}} (m_{2})}, min {{F_{M_{1}} (m), F_{M_{2}} (n_{2})}} \\ = max {(F_{M_{1}} * F_{M_{2}}) (m, m_{2}), (F_{M_{1}} * F_{M_{2}}) (m, n_{2})} . \end{array}

(ii) If m₂ = n₂ = z, then

\begin{array}{l} (T_{N_{1}} * T_{N_{2}}) ((m_{1}, z) (n_{1}, z)) = max {T_{N_{1}} (m_{1} n_{1}), T_{M_{2}} (z)} \\ = max {min {T_{N_{1}} (m_{1} n_{1}), T_{M_{2}} (z)} \\ = min {max {{T_{N_{1}} (m_{1}), T_{M_{2}} (z)}, max {{T_{M_{1}} (n_{1}), T_{M_{2}} (z)}} \\ = min {(T_{M_{1}} * T_{M_{2}}) (m_{1}, z), (T_{M_{1}} * T_{M_{2}}) (n_{1}, z)}, \\ (F_{N_{1}} * F_{N_{2}}) ((m_{1}, z) (n_{1}, z)) = min {F_{N_{1}} (m_{1} n_{1}), F_{M_{2}} (z)} \\ = min {max {F_{N_{1}} (m_{1} n_{1}), F_{M_{2}} (z)} \\ = max {min {{F_{M_{1}} (m_{1}), F_{M_{2}} (z)}, min {{F_{M_{1}} (n_{1}), F_{M_{2}} (z)}} \\ = max {(F_{M_{1}} * F_{M_{2}}) (m_{1}, z), (F_{M_{1}} * F_{M_{2}}) (n_{1}, z)} . \end{array}

Therefore, G₁ * G₂ is a strong vague graph. □

Example 3.5. Consider the strong vague graphs G₁ and G₂ as in Figure 5.

FIGURE 5

Figure 5. Vague graphs G₁, G₂, and G₁ * G₂.

It is easy to see that G₁ * G₂ is a strong vague graph too.

Remark 3.1. If the maximal product of two vague graphs G₁ = (M₁, N₁) and G₂ = (M₂, N₂) is a strong vague graph, G₁ and G₂ need not be strong in general.

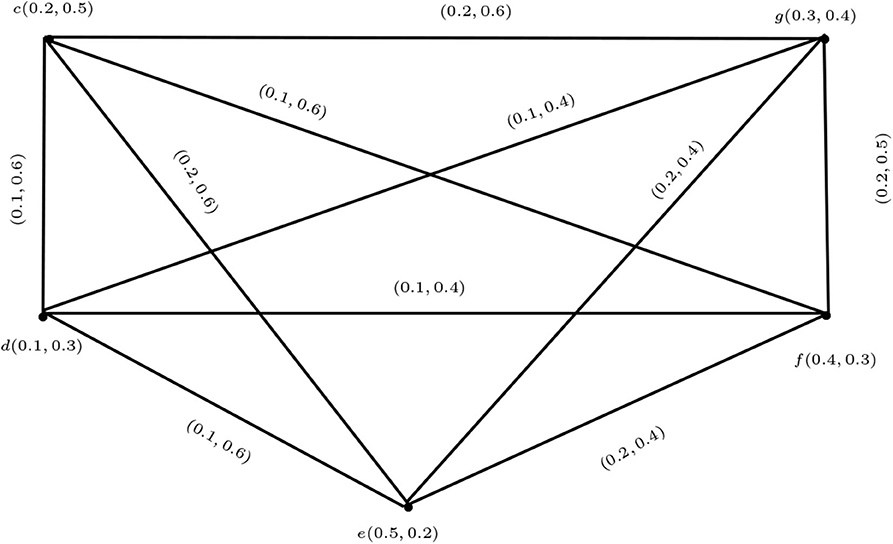
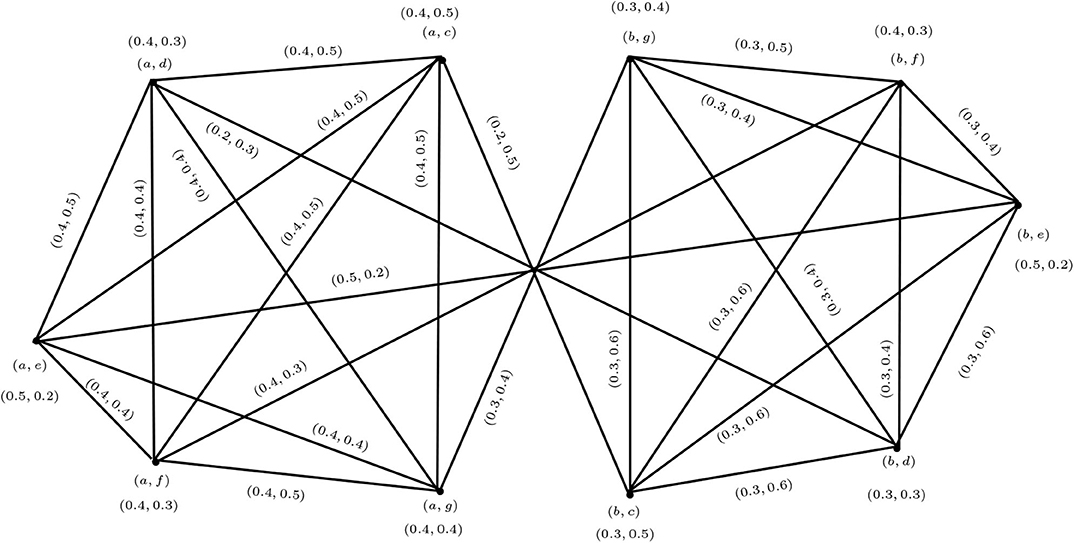
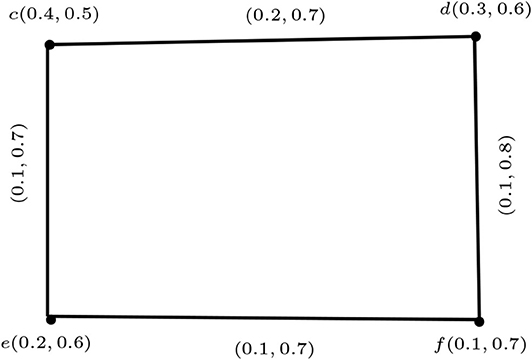
Example 3.6. Consider the vague graphs G₁ and G₂ as in Figures 6, 7. The maximal product of G₁ and G₂ is G₁ * G₂ shown in Figure 8.

FIGURE 6

Figure 6. G₁.

FIGURE 7

Figure 7. G₂.

FIGURE 8

Figure 8. G₁ * G₂.

We can see that G₁ and G₁ * G₂ are strong vague graphs, but G₂ is not strong: since T_N₂(m₂, n₂) = 0.1 but min{T_M₂(m₂), T_M₂(n₂} = min{0.2, 0.2} = 0.2, we have T_N₂(m₂, n₂) ≠ min{T_M₂(m₂), T_M₂(n₂}.

Theorem 3.7. The maximal product of two connected vague graphs is a connected vague graph.

Proof: Let G₁ = (M₁, N₁) and G₂ = (M₂, N₂) be two connected vague graphs on crisp graphs G₁ = (V₁, E₁) and G₂ = (V₂, E₂), respectively, where V₁ = {m₁, m₂, …, m_k} and V₂ = {n₁, n₂, …, n_s}. Then $T_{N_{1}}^{\infty} (m_{i} m_{j}) > 0$ for all m_i, m_j ∈ V₁ and $T_{N_{2}}^{\infty} (n_{i} n_{j}) > 0$ for all n_i, n_j ∈ V₂ (or $F_{N_{1}}^{\infty} (m_{i} m_{j}) < 1$ for all m_i, m_j ∈ V₁ and $F_{N_{2}}^{\infty} (n_{i} n_{j}) < 1$ for all n_i, n_j ∈ V₂). The maximal product of G₁ = (M₁, N₁) and G₂ = (M₂, N₂) can be taken as G = (M, N). Now, consider the k subgraphs of G with the vertex set {(m_i, n₁), (m_i, n₂), …, (m_i, n_s)} for i = 1, 2, …, k. Each of these subgraphs of G is connected, since the m_i's are the same and G₂ is connected, so that each n_i is adjacent to at least one of the vertices in V₂. Also, since G₁ is connected, each x_i is adjacent to at least one of the vertices in V₁.

Hence, there exists at least one edge between any pair of the above k subgraphs. Thus, we have $T_{N}^{\infty} ((m_{i}, n_{j}) (m_{m}, n_{n})) > 0$ (or $F_{N}^{\infty} ((m_{i}, n_{j}) (m_{m}, n_{n})) < 1$ ) for all ((m_i, n_j)(m_m, n_n)) ∈ E. Therefore, G is a connected vague graph. □

Remark 3.2. The maximal product of two complete vague graphs is not a complete vague graph in general. This is because we do not include the case where (m₁, m₂) ∈ E₁ and (n₁, n₂) ∈ E₂ in the definition of the maximal product of two vague graphs.

Remark 3.3. The maximal product of two complete vague graphs is a strong vague graph.

Example 3.8. Consider the complete vague graphs G₁ and G₂ in Figure 5. A simple calculation yields that G₁ * G₂ is a strong vague graph.

Definition 3.9. Let G₁ = (M₁, N₁) and G₂ = (M₂, N₂) be two vague graphs. For any vertex (m₁, m₂) ∈ V₁ × V₂ we define

\begin{array}{l} {(d_{T})}_{G_{1} * G_{2}} (m_{1}, m_{2}) = \sum_{(m_{1}, m_{2}) (n_{1}, n_{2}) \in E_{1} \times E_{2}} (T_{N_{1}} * T_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) \\ = \sum_{m_{1} = n_{1}, m_{2} n_{2} \in E_{2}} max {T_{M_{1}} (m_{1}), T_{N_{2}} (m_{2} n_{2})} \\ + \sum_{m_{1} n_{1} \in E_{1}, m_{2} = n_{2}} max {T_{N_{1}} (m_{1} n_{1}), T_{M_{2}} (m_{2})}, \\ {(d_{F})}_{G_{1} * G_{2}} (m_{1}, m_{2}) = \sum_{(m_{1}, m_{2}) (n_{1}, n_{2}) \in E_{1} \times E_{2}} (F_{N_{1}} * F_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) \\ = \sum_{m_{1} = n_{1}, m_{2} n_{2} \in E_{2}} min {F_{M_{1}} (m_{1}), F_{N_{2}} (m_{2} n_{2})} \\ + \sum_{m_{1} n_{1} \in E_{1}, m_{2} = n_{2}} min {F_{N_{1}} (m_{1} n_{1}), F_{M_{2}} (m_{2})} . \end{array}

Theorem 3.10. Let G₁ = (M₁, N₁) and G₂ = (M₂, N₂) be two vague graphs. If T_M₁ ≥ T_N₂, F_M₁ ≤ F_N₂, T_M₂ ≥ T_N₁, and F_M₂ ≤ F_N₁, then (_{d_T)G₁ * G₂}(m₁, m₂) = (d)_G₂(m₂)T_M₁(m₁) + (d)_G₁(m₁)T_M₂(m₂) and (_{d_F)G₁ * G₂}(m₁, m₂) = (d)_G₂(m₂)F_M₁(m₁) + (d)_G₁(m₁)F_M₂(m₂).

Proof: From the definition of a vertex in the cartesian product, we have

\begin{array}{l} {(d_{T})}_{G_{1} * G_{2}} (m_{1}, m_{2}) = \sum_{(m_{1}, m_{2}) (n_{1}, n_{2}) \in E_{1} \times E_{2}} (T_{N_{1}} * T_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) \\ = \sum_{m_{1} = n_{1}, m_{2} n_{2} \in E_{2}} max {T_{M_{1}} (m_{1}), T_{N_{2}} (m_{2} n_{2})} \\ + \sum_{m_{1} n_{1} \in E_{1}, m_{2} = n_{2}} max {T_{N_{1}} (m_{1} n_{1}), T_{M_{2}} (m_{2})} \\ = \sum_{m_{2} n_{2} \in E_{2}, m_{1} = n_{1}} T_{N_{2}} (m_{2} n_{2}) + \sum_{m_{1} n_{1} \in E_{1}, m_{2} = n_{2}} T_{N_{1}} (m_{1} n_{1}) \\ = {(d)}_{G_{2}} (m_{2}) T_{M_{1}} (m_{1}) + {(d)}_{G_{1}} (m_{1}) T_{M_{2}} (m_{2}), \end{array}

\begin{array}{l} {(d_{F})}_{G_{1} * G_{2}} (m_{1}, m_{2}) = \sum_{(m_{1}, m_{2}) (n_{1}, n_{2}) \in E_{1} \times E_{2}} (F_{N_{1}} * F_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) \\ = \sum_{m_{1} = n_{1}, m_{2} n_{2} \in E_{2}} min {F_{M_{1}} (m_{1}), F_{N_{2}} (m_{2} n_{2})} \\ + \sum_{m_{1} n_{1} \in E_{1}, m_{2} = n_{2}} min {F_{N_{1}} (m_{1} n_{1}), F_{M_{2}} (m_{2})} \\ = \sum_{m_{2} n_{2} \in E_{2}, m_{1} = n_{1}} F_{N_{2}} (m_{2} n_{2}) + \sum_{m_{1} n_{1} \in E_{1}, m_{2} = n_{2}} F_{N_{1}} (m_{1} n_{1}) \\ = {(d)}_{G_{2}} (m_{2}) F_{M_{1}} (m_{1}) + {(d)}_{G_{1}} (m_{1}) F_{M_{2}} (m_{2}), \end{array}

as claimed. □

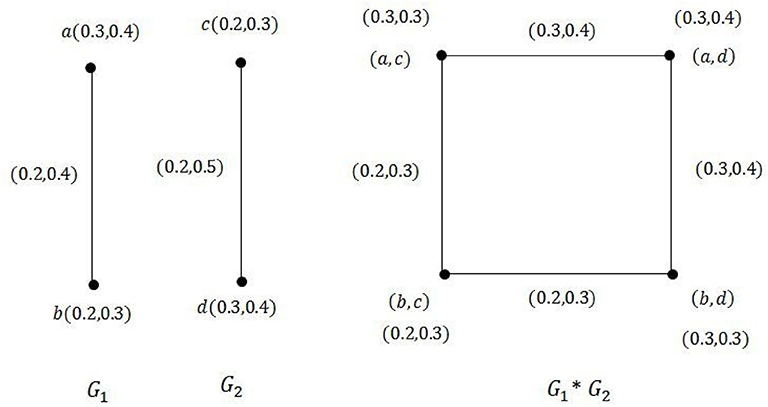
Example 3.11. Consider the vague graphs G₁, G₂, and G₁ * G₂ as in Figure 9. Since T_M₁ ≥ T_N₂, F_M₁ ≤ F_N₂, T_M₂ ≥ T_N₁, and F_M₂ ≤ F_N₁, by Theorem 3.10 we have

\begin{array}{l} {(d_{T})}_{G_{1} * G_{2}} (a, c) = {(d)}_{G_{2}} (c) T_{M_{1}} (a) + {(d)}_{G_{1}} (a) T_{M_{2}} (c) = 1 \cdot (0.3) \\ + 1 \cdot (0.2) = 0.5, \\ {(d_{F})}_{G_{1} * G_{2}} (a, c) = {(d)}_{G_{2}} (c) F_{M_{1}} (a) + {(d)}_{G_{1}} (a) F_{M_{2}} (c) = 1 \cdot (0.4) \\ + 1 \cdot (0.3) = 0.7 . \\ {(d_{T})}_{G_{1} * G_{2}} (a, d) = {(d)}_{G_{2}} (d) T_{M_{1}} (a) + {(d)}_{G_{1}} (a) T_{M_{2}} (d) = 1 \cdot (0.3) \\ + 1 \cdot (0.3) = 0.6, \\ {(d_{F})}_{G_{1} * G_{2}} (a, d) = {(d)}_{G_{2}} (d) F_{M_{1}} (a) + {(d)}_{G_{1}} (a) F_{M_{2}} (d) = 1 \cdot (0.4) \\ + 1 \cdot (0.4) = 0.8 . \\ {(d_{T})}_{G_{1} * G_{2}} (b, c) = {(d)}_{G_{2}} (c) T_{M_{1}} (b) + {(d)}_{G_{1}} (b) T_{M_{2}} (c) = 1 \cdot (0.2) \\ + 1 \cdot (0.2) = 0.4, \\ {(d_{F})}_{G_{1} * G_{2}} (b, c) = {(d)}_{G_{2}} (c) F_{M_{1}} (b) + {(d)}_{G_{1}} (b) F_{M_{2}} (c) = 1 \cdot (0.3) \\ + 1 \cdot (0.3) = 0.6 . \\ \begin{array}{l} {(d_{T})}_{G_{1} * G_{2}} (b, d) = {(d)}_{G_{2}} (d) T_{M_{1}} (b) + {(d)}_{G_{1}} (b) T_{M_{2}} (d) = 1 \cdot (0.2) \\ + 1 \cdot (0.3) = 0.5, \\ {(d_{F})}_{G_{1} * G_{2}} (b, d) = {(d)}_{G_{2}} (d) F_{M_{1}} (b) + {(d)}_{G_{1}} (b) F_{M_{2}} (d) = 1 \cdot (0.3) \\ + 1 \cdot (0.4) = 0.7 . \end{array} \end{array}

FIGURE 9

Figure 9. Vague graphs G₁, G₂, and G₁ * G₂.

By direct calculations we obtain

\begin{array}{l} {(d_{T})}_{G_{1} * G_{2}} (a, c) = 0.3 + 0.2 = 0.5, \\ {(d_{F})}_{G_{1} * G_{2}} (a, c) = 0.4 + 0.3 = 0.7, \\ {(d_{T})}_{G_{1} * G_{2}} (a, d) = 0.3 + 0.3 = 0.6, \\ {(d_{F})}_{G_{1} * G_{2}} (a, d) = 0.4 + 0.4 = 0.8, \\ {(d_{T})}_{G_{1} * G_{2}} (b, c) = 0.2 + 0.2 = 0.4, \\ {(d_{F})}_{G_{1} * G_{2}} (b, c) = 0.3 + 0.3 = 0.6, \\ {(d_{T})}_{G_{1} * G_{2}} (b, d) = 0.3 + 0.2 = 0.5, \\ {(d_{F})}_{G_{1} * G_{2}} (b, d) = 0.3 + 0.4 = 0.7 . \end{array}

It is clear that the degrees of vertices calculated using the formula in Theorem 3.10 and by the direct method are the same.

Definition 3.12. Let G₁ = (M₁, N₁) and G₂ = (M₂, N₂) be two vague graphs. For any vertex (m₁, m₂) ∈ V₁ × V₂ we define

\begin{array}{l} {(t d_{T})}_{G_{1} * G_{2}} (m_{1}, m_{2}) = \sum_{(m_{1}, m_{2}) (n_{1}, n_{2}) \in E_{1} \times E_{2}} (T_{N_{1}} * T_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) \\ + (T_{M_{1}} * T_{M_{2}}) (m_{1}, m_{2}) \\ = \sum_{m_{1} = n_{1}, m_{2} n_{2} \in E_{2}} max {T_{M_{1}} (m_{1}), T_{N_{2}} (m_{2} n_{2})} \\ + \sum_{m_{1} n_{1} \in E_{1}, m_{2} = n_{2}} max {T_{N_{1}} (m_{1} n_{1}), T_{M_{2}} (m_{2})} \\ + max {T_{M_{1}} (m_{1}), T_{M_{2}} (m_{2})}, \\ {(t d_{F})}_{G_{1} * G_{2}} (m_{1}, m_{2}) = \sum_{(m_{1}, m_{2}) (n_{1}, n_{2}) \in E_{1} \times E_{2}} (F_{N_{1}} * F_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) \\ + (F_{M_{1}} * F_{M_{2}}) (m_{1}, m_{2}) \\ = \sum_{m_{1} = n_{1}, m_{2} n_{2} \in E_{2}} min {F_{M_{1}} (m_{1}), F_{N_{2}} (m_{2} n_{2})} \\ + \sum_{m_{1} n_{1} \in E_{1}, m_{2} = n_{2}} min {F_{N_{1}} (m_{1} n_{1}), F_{M_{2}} (m_{2})} \\ + min {F_{M_{1}} (m_{1}), F_{M_{2}} (m_{2})} . \end{array}

Example 3.13. In this example we find the degree and the total degree of vertices (a, c) and (a, d) in Example 3.2:

\begin{array}{l} {(d_{T})}_{G_{1} * G_{2}} (a, c) = {(d)}_{G_{2}} (a) T_{M_{1}} (c) + {(d)}_{G_{1}} (c) T_{M_{2}} (a) \\ = 1 (0.2) + 4 (0.4) = 0.2 + 1.6 = 1.8, \\ {(d_{F})}_{G_{1} * G_{2}} (a, c) = {(d)}_{G_{2}} (a) F_{M_{1}} (c) + {(d)}_{G_{1}} (c) F_{M_{2}} (a) \\ = 1 (0.5) + 4 (0.5) = 0.3 + 1.2 = 1.5 . \end{array}

Therefore, d_{G₁ * G₂}(a, c) = (1.8, 1.5). In addition, by the definition of the total vertex degree in the maximal product,

\begin{array}{l} {(t d_{T})}_{G_{1} * G_{2}} (a, c) = {(d)}_{G_{2}} (a) T_{M_{1}} (c) + {(d)}_{G_{1}} (c) T_{M_{2}} (a) \\ + max {T_{M_{1}} (a), T_{M_{2}} (c)} \\ = 1 (0.2) + 4 (0.4) + max (0.2, 0.4) = 2.2, \\ {(t d_{F})}_{G_{1} * G_{2}} (a, c) = {(d)}_{G_{2}} (a) F_{M_{1}} (c) + {(d)}_{G_{1}} (c) F_{M_{2}} (a) \\ + min {F_{M_{1}} (a), F_{M_{2}} (c)} \\ = 1 (0.5) + 4 (0.5) + min (0.3, 0.4) = 1.8 . \end{array}

Therefore, td_{G₁ * G₂}(a, c) = (2.2, 1.8).

We also have

\begin{array}{l} {(d_{T})}_{G_{1} * G_{2}} (a, d) = {(d)}_{G_{2}} (a) T_{M_{1}} (d) + {(d)}_{G_{1}} (d) T_{M_{2}} (a) \\ = 1 (0.1) + 4 (0.4) = 0.1 + 1.6 = 1.7, \\ {(d_{F})}_{G_{1} * G_{2}} (a, d) = {(d)}_{G_{2}} (a) F_{M_{1}} (d) + {(d)}_{G_{1}} (d) F_{M_{2}} (a) \\ = 1 (0.3) + 4 (0.5) = 0.3 + 2 = 2.3, \end{array}

\begin{array}{l} {(t d_{T})}_{G_{1} * G_{2}} (a, d) = {(d)}_{G_{2}} (a) T_{M_{1}} (d) + {(d)}_{G_{1}} (d) T_{M_{2}} (a) \\ + max {T_{M_{1}} (a), T_{M_{2}} (d)} \\ = 1 (0.1) + 4 (0.4) + max (0.4, 0.1) = 2.1, \\ {(t d_{F})}_{G_{1} * G_{2}} (a, d) = {(d)}_{G_{2}} (a) F_{M_{1}} (d) + {(d)}_{G_{1}} (d) F_{M_{2}} (a) \\ + min {F_{M_{1}} (a), F_{M_{2}} (d)} \\ = 1 (0.3) + 4 (0.5) + min (0.5, 0.3) = 2.6 . \end{array}

Hence, d_{G₁ * G₂}(a, d) = (1.7, 2.3) and td_{G₁ * G₂}(a, d) = (2.1, 2.6).

Similarly, we can find the degree and the total degree of all vertices in G₁ * G₂.

Theorem 3.14. Let G₁ = (M₁, N₁) and G₂ = (M₂, N₂) be two vague graphs. If T_M₁ ≥ T_N₂, F_M₁ ≤ F_N₂, T_M₂ ≥ T_N₁, and F_M₂ ≤ F_N₁, then (t_{d_T)G₁ * G₂}(m₁, m₂) = (d)_G₂(m₂)T_M₁(m₁) + (d)_G₁(m₁)T_M₂(m₂) + max{T_M₁(m₁), T_M₂(m₂)} and (t_{d_F)G₁ * G₂}(m₁, m₂) = (d)_G₂(m₂)F_M₁(m₁) + (d)_G₁(m₁)F_M₂(m₂) + min{F_M₁(m₁), F_M₂(m₂)}.

Proof: From Definition 3.12 we have

\begin{array}{l} {(t d_{T})}_{G_{1} * G_{2}} (m_{1}, m_{2}) = \sum_{(m_{1}, m_{2}) (n_{1}, n_{2}) \in E_{1} \times E_{2}} (T_{N_{1}} * T_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) \\ + (T_{M_{1}} * T_{M_{2}}) (m_{1}, m_{2}) \\ = \sum_{m_{1} = n_{1}, m_{2} n_{2} \in E_{2}} max {T_{M_{1}} (m_{1}), T_{N_{2}} (m_{2} n_{2})} \\ + \sum_{m_{1} n_{1} \in E_{1}, m_{2} = n_{2}} max {T_{N_{1}} (m_{1} n_{1}), T_{M_{2}} (m_{2})} \\ + max {T_{M_{1}} (m_{1}), T_{M_{2}} (m_{2})} \\ = \sum_{m_{2} n_{2} \in E_{2}, m_{1} = n_{1}} T_{N_{2}} (m_{2} n_{2}) + \sum_{m_{1} n_{1} \in E_{1}, m_{2} = n_{2}} T_{N_{1}} (m_{1} n_{1}) \\ + max {T_{M_{1}} (m_{1}), T_{M_{2}} (m_{2})} \\ = {(d)}_{G_{2}} (m_{2}) T_{M_{1}} (m_{1}) + {(d)}_{G_{1}} (m_{1}) T_{M_{2}} (m_{2}) \\ + max {T_{M_{1}} (m_{1}), T_{M_{2}} (m_{2})} \end{array}

and

\begin{array}{l} {(t d_{F})}_{G_{1} * G_{2}} (m_{1}, m_{2}) = \sum_{(m_{1}, m_{2}) (n_{1}, n_{2}) \in E_{1} \times E_{2}} (F_{N_{1}} * F_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) \\ + (F_{M_{1}} * F_{M_{2}}) (m_{1}, m_{2}) \\ = \sum_{m_{1} = n_{1}, m_{2} n_{2} \in E_{2}} min {F_{M_{1}} (m_{1}), F_{N_{2}} (m_{2} n_{2})} \\ + \sum_{m_{1} n_{1} \in E_{1}, m_{2} = n_{2}} min {F_{N_{1}} (m_{1} n_{1}), F_{M_{2}} (m_{2})} \\ + min {F_{M_{1}} (m_{1}), F_{M_{2}} (m_{2})} \\ = \sum_{m_{2} n_{2} \in E_{2}, m_{1} = n_{1}} F_{N_{2}} (m_{2} n_{2}) + \sum_{m_{1} n_{1} \in E_{1}, m_{2} = n_{2}} F_{N_{1}} (m_{1} n_{1}) \\ + min {F_{M_{1}} (m_{1}), F_{M_{2}} (m_{2})} \\ = {(d)}_{G_{2}} (m_{2}) F_{M_{1}} (m_{1}) + {(d)}_{G_{1}} (m_{1}) F_{M_{2}} (m_{2}) \\ + min {F_{M_{1}} (m_{1}), F_{M_{2}} (m_{2})}, \end{array}

as asserted.

Example 3.15. Consider the vague graphs G₁, G₂, and G₁ * G₂ in Figure 9. The total degree of the vertex in the maximal product is calculated by the following formula:

\begin{array}{l} {(t d_{T})}_{G_{1} * G_{2}} (m_{1}, m_{2}) = {(d)}_{G_{2}} (m_{2}) T_{M_{1}} (m_{1}) + {(d)}_{G_{1}} (m_{1}) T_{M_{2}} (m_{2}) \\ + max {T_{M_{1}} (m_{1}), T_{M_{2}} (m_{2})}, \\ {(t d_{F})}_{G_{1} * G_{2}} (m_{1}, m_{2}) = {(d)}_{G_{2}} (m_{2}) F_{M_{1}} (m_{1}) + {(d)}_{G_{1}} (m_{1}) F_{M_{2}} (m_{2}) \\ + min {F_{M_{1}} (m_{1}), F_{M_{2}} (m_{2})} . \end{array}

Using the formula we find that

\begin{array}{l} {(t d_{T})}_{G_{1} * G_{2}} (a, c) = {(d)}_{G_{2}} (c) T_{M_{1}} (a) + {(d)}_{G_{1}} (a) T_{M_{2}} (c) \\ + max {T_{M_{1}} (a), T_{M_{2}} (c)} \\ = 1 \cdot (0.3) + 1 \cdot (0.2) + max {0.2, 0.3} \\ = 0.3 + 0.2 + 0.3 = 0.8, \\ {(t d_{F})}_{G_{1} * G_{2}} (a, c) = {(d)}_{G_{2}} (c) F_{M_{1}} (a) + {(d)}_{G_{1}} (a) F_{M_{2}} (c) \\ + min {F_{M_{1}} (a), F_{M_{2}} (c)} \\ = 1 \cdot (0.4) + 1 \cdot (0.3) + min {0.3, 0.4} \\ = 0.4 + 0.3 + 0.3 = 1 . \\ {(t d_{T})}_{G_{1} * G_{2}} (a, d) = {(d)}_{G_{2}} (d) T_{M_{1}} (a) + {(d)}_{G_{1}} (a) T_{M_{2}} (d) \\ + max {T_{M_{1}} (a), T_{M_{2}} (d)} \\ = 1 \cdot (0.3) + 1 \cdot (0.3) + max {0.3, 0.3} \\ = 0.3 + 0.3 + 0.3 = 0.9, \\ {(t d_{F})}_{G_{1} * G_{2}} (a, d) = {(d)}_{G_{2}} (d) F_{M_{1}} (a) + {(d)}_{G_{1}} (a) F_{M_{2}} (d) \\ + min {F_{M_{1}} (a), F_{M_{2}} (d)} \\ = 1 \cdot (0.4) + 1 \cdot (0.4) + min {0.4, 0.4} \\ = 0.4 + 0.4 + 0.4 = 1.2 . \\ \begin{array}{l} {(t d_{T})}_{G_{1} * G_{2}} (b, c) = {(d)}_{G_{2}} (c) T_{M_{1}} (b) + {(d)}_{G_{1}} (b) T_{M_{2}} (c) \\ + max {T_{M_{1}} (b), T_{M_{2}} (c)} \\ = 1 \cdot (0.2) + 1 \cdot (0.2) + max {0.2, 0.2} \\ = 0.2 + 0.2 + 0.2 = 0.6, \\ {(t d_{F})}_{G_{1} * G_{2}} (b, c) = {(d)}_{G_{2}} (c) F_{M_{1}} (b) + {(d)}_{G_{1}} (b) F_{M_{2}} (c) \\ + min {F_{M_{1}} (b), F_{M_{2}} (c)} \\ = 1 \cdot (0.3) + 1 \cdot (0.3) + min {0.3, 0.3} \\ = 0.3 + 0.3 + 0.3 = 0.9 . \\ {(t d_{T})}_{G_{1} * G_{2}} (b, d) = {(d)}_{G_{2}} (d) T_{M_{1}} (b) + {(d)}_{G_{1}} (b) T_{M_{2}} (d) \\ + max {T_{M_{1}} (b), T_{M_{2}} (d)} \\ = 1 \cdot (0.2) + 1 \cdot (0.3) + max {0.2, 0.3} \\ = 0.2 + 0.3 + 0.3 = 0.8, \\ {(t d_{F})}_{G_{1} * G_{2}} (b, d) = {(d)}_{G_{2}} (d) F_{M_{1}} (b) + {(d)}_{G_{1}} (b) F_{M_{2}} (d) \\ + min {F_{M_{1}} (b), F_{M_{2}} (d)} \\ = 1 \cdot (0.3) + 1 \cdot (0.4) + min {0.3, 0.4} \\ = 0.3 + 0.4 + 0.3 = 1 . \end{array} \end{array}

On the other hand, by direct calculations we obtain

\begin{array}{l} {(t d_{T})}_{G_{1} * G_{2}} (a, c) = 0.3 + 0.2 + 0.3 = 0.8, \\ {(t d_{F})}_{G_{1} * G_{2}} (a, c) = 0.4 + 0.3 + 0.3 = 1, \\ {(t d_{T})}_{G_{1} * G_{2}} (a, d) = 0.3 + 0.3 + 0.3 = 0.9, \\ {(t d_{F})}_{G_{1} * G_{2}} (a, d) = 0.4 + 0.4 + 0.4 = 1.2, \\ {(t d_{T})}_{G_{1} * G_{2}} (b, c) = 0.2 + 0.2 + 0.2 = 0.6, \\ {(t d_{F})}_{G_{1} * G_{2}} (b, c) = 0.3 + 0.3 + 0.3 = 0.9, \\ {(t d_{T})}_{G_{1} * G_{2}} (b, d) = 0.3 + 0.2 + 0.3 = 0.8, \\ {(t d_{F})}_{G_{1} * G_{2}} (b, d) = 0.4 + 0.3 + 0.3 = 1 . \end{array}

It is thus clear that the total degrees of vertices calculated using the formula and by the direct method are the same.

Definition 3.16. The rejection G₁|G₂ = (M₁|M₂, N₁|N₂) of two vague graphs G₁ = (M₁, N₁) and G₂ = (M₂, N₂) is defined as follows:

\begin{array}{l} (i) (T_{M_{1}} | T_{M_{2}}) ((m_{1}, m_{2})) = min {T_{M_{1}} (m_{1}), T_{M_{2}} (m_{2})}, \\ (F_{M_{1}} | F_{M_{2}}) ((m_{1}, m_{2})) = max {F_{M_{1}} (m_{1}), F_{M_{2}} (m_{2})} \\ \forall (m_{1}, m_{2}) \in (V_{1} \times V_{2}); \end{array}

\begin{array}{l} (ii) (T_{N_{1}} | T_{N_{2}}) ((m, m_{2}) (m, n_{2})) = min {T_{M_{1}} (m), T_{M_{2}} (m_{2}), T_{M_{2}} (n_{2})}, \\ (F_{N_{1}} | F_{N_{2}}) ((m, m_{2}) (m, n_{2})) = max {F_{M_{1}} (m), F_{M_{2}} (m_{2}), F_{M_{2}} (n_{2})} \\ \forall m \in V_{2} and m_{2} n_{2} \in E_{2}; \end{array}

\begin{array}{l} (iii) (T_{N_{1}} | T_{N_{2}}) ((m, m_{2}) (m, n_{2})) = min {T_{M_{1}} (m), T_{M_{2}} (m_{2}), T_{M_{2}} (n_{2})} \\ (F_{N_{1}} | F_{N_{2}}) ((m, m_{2}) (m, n_{2})) = max {F_{M_{1}} (m), F_{M_{2}} (m_{2}), F_{M_{2}} (n_{2})} \\ \forall m \in V_{2} and m_{1} n_{1} \in E_{1}; \end{array}

\begin{array}{l} (iv) (T_{N_{1}} | T_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) = min {T_{M_{1}} (m_{1}), T_{M_{1}} (n_{1}), T_{M_{2}} (m_{2}), T_{M_{2}} (n_{2})}, \\ (F_{N_{1}} | F_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) = max {F_{M_{1}} (m_{1}), F_{M_{1}} (n_{1}), F_{M_{2}} (m_{2}), F_{N_{2}} (n_{2})} \\ \forall m_{1} n_{1} \in E_{1} and m_{2} n_{2} \in E_{2} . \end{array}

Example 3.17. Consider the vague graphs G₁ and G₂ in Figures 10, 11. The rejection of G₁ and G₂, i.e., G₁|G₂, is shown in Figure 12.

FIGURE 10

Figure 10. G₁.

FIGURE 11

Figure 11. G₂.

FIGURE 12

Figure 12. G₁|G₂.

For the vertex (a, e), we find the membership and non-membership values as follows:

\begin{array}{l} (T_{M_{1}} | T_{M_{2}}) ((a, e)) = min {T_{M_{1}} (a), T_{M_{2}} (e)} \\ = min {0.4, 0.3} = 0.3, \\ (F_{M_{1}} | F_{M_{2}}) ((a, e)) = max {F_{M_{1}} (a), F_{M_{2}} (e)} \\ = max {0.4, 0.4} = 0.4 \end{array}

for a ∈ V₁ and e ∈ V₂.

For the edge (e, c)(e, a), the membership and non-membership values are given by

\begin{array}{l} (T_{N_{1}} | T_{N_{2}}) ((e, c) (e, a)) = min {T_{M_{1}} (e), T_{M_{2}} (c), T_{M_{2}} (a)} \\ = min {0.3, 0.3, 0.4} = 0.3, \\ (F_{N_{1}} | F_{N_{2}}) ((e, c) (e, a)) = max {F_{M_{1}} (e), F_{M_{2}} (c), F_{M_{2}} (a)} \\ = max {0.4, 0.4, 0.4} = 0.4 \end{array}

for e ∈ V₂ and ac ∉ E₁.

For the edge (e, c)(e, g) we have

\begin{array}{l} (T_{N_{1}} | T_{N_{2}}) ((e, c) (e, g)) = min {T_{M_{1}} (e), T_{M_{2}} (c), T_{M_{2}} (g)} \\ = min {0.3, 0.3, 0.3} = 0.3, \\ (F_{N_{1}} | F_{N_{2}}) ((e, c) (e, g)) = max {F_{M_{1}} (e), F_{M_{2}} (c), F_{M_{2}} (g)} \\ = max {0.4, 0.4, 0.2} = 0.4 \end{array}

for e ∈ V₂ and cg ∉ E₂.

Similarly, we can find the membership and non-membership values for all the remaining vertices and edges.

Proposition 3.18. The rejection of two vague graphs G₁ and G₂ is a vague graph.

Proof: Let G₁ = (M₁, N₁) and G₂ = (M₂, N₂) be two vague graphs on crisp graphs G₁ = (V₁, E₁) and G₂ = (V₂, E₂), respectively, and let ((m₁, m₂)(n₁, n₂)) ∈ E₁ × E₂. Then by Definition 3.16 we have the following:

(i) If m₁ = n₁ and m₂n₂ ∉ E₂, then

\begin{array}{l} (T_{N_{1}} | T_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) = min {T_{M_{1}} (m_{1}), T_{M_{2}} (m_{2}), T_{M_{2}} (n_{2})} \\ = min {min {T_{M_{1}} (m_{1}), T_{M_{2}} (m_{2})}, min {T_{M_{1}} (n_{1}), T_{M_{2}} (n_{2})}} \\ = min {(T_{M_{1}} | T_{M_{2}}) (m_{1}, m_{2}), (T_{M_{1}} | T_{M_{2}}) (n_{1}, n_{2})}, \\ (F_{N_{1}} | F_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) = max {F_{M_{1}} (m_{1}), F_{M_{2}} (m_{2}), F_{M_{2}} (n_{2})} \\ = max {max {F_{M_{1}} (m_{1}), F_{M_{2}} (m_{2})}, max {F_{M_{1}} (n_{1}), F_{M_{2}} (n_{2})}} \\ = max {(F_{M_{1}} | F_{M_{2}}) (m_{1}, m_{2}), (F_{M_{1}} | F_{M_{2}}) (n_{1}, n_{2})} . \end{array}

(ii) If m₂ = n₂ and m₁n₁ ∉ E₁, then

\begin{array}{l} (T_{N_{1}} | T_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) = min {T_{M_{1}} (m_{1}), T_{M_{1}} (n_{1}), T_{M_{2}} (m_{2})} \\ = min {min {T_{M_{1}} (m_{1}), T_{M_{2}} (m_{2})}, min {T_{M_{1}} (n_{1}), T_{M_{2}} (n_{2})}} \\ = min {(T_{M_{1}} | T_{M_{2}}) (m_{1}, m_{2}), (T_{M_{1}} | T_{M_{2}}) (n_{1}, n_{2})}, \\ (F_{N_{1}} | F_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) = max {F_{M_{1}} (m_{1}), F_{M_{1}} (n_{1}), F_{M_{2}} (m_{2})} \\ = max {max {F_{M_{1}} (m_{1}), F_{M_{2}} (m_{2})}, max {F_{M_{1}} (n_{1}), F_{M_{2}} (n_{2})}} \\ = max {(F_{M_{1}} | F_{M_{2}}) (m_{1}, m_{2}), (F_{M_{1}} | F_{M_{2}}) (n_{1}, n_{2})} . \end{array}

(iii) If m₁n₁ ∉ E₁ and m₂n₂ ∉ E₂, then

\begin{array}{l} (T_{N_{1}} | T_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) = min {T_{M_{1}} (m_{1}), T_{M_{1}} (n_{1}), T_{M_{2}} (m_{2}), T_{M_{2}} (n_{2})} \\ = min {min {T_{M_{1}} (m_{1}), T_{M_{2}} (m_{2})}, min {T_{M_{1}} (n_{1}), T_{M_{2}} (n_{2})}} \\ = min {(T_{M_{1}} | T_{M_{2}}) (m_{1}, m_{2}), (T_{M_{1}} | T_{M_{2}}) (n_{1}, n_{2})}, \\ (F_{N_{1}} | F_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) = max {F_{M_{1}} (m_{1}), F_{M_{1}} (n_{1}), F_{M_{2}} (m_{2}), T_{M_{2}} (n_{2})} \\ = max {max {F_{M_{1}} (m_{1}), F_{M_{2}} (m_{2})}, max {F_{M_{1}} (n_{1}), F_{M_{2}} (n_{2})}} \\ = max {(F_{M_{1}} | F_{M_{2}}) (m_{1}, m_{2}), (F_{M_{1}} | F_{M_{2}}) (n_{1}, n_{2})} . \end{array}

Therefore, G₁|G₂ = (M₁|M₂, N₁|N₂) is a vague graph. □

Remark 3.4. The rejection of two complete vague graphs G₁ = (M₁, N₁) and G₂ = (M₂, N₂) is a complete vague graph.

Definition 3.19. Let G₁ = (M₁, N₁) and G₂ = (M₂, N₂) be two vague graphs. For any vertex (m₁, m₂) ∈ V₁ × V₂ we define

\begin{array}{l} {(d_{T})}_{G_{1} | G_{2}} (m_{1}, m_{2}) = \sum_{(m_{1}, m_{2}) (n_{1}, n_{2}) \in E_{1} \times E_{2}} (T_{N_{1}} | T_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) \\ = \sum_{m_{1} = n_{1}, m_{2} n_{2} \notin E_{2}} min {T_{M_{1}} (m_{1}), T_{M_{2}} (m_{2}), T_{M_{2}} (n_{2})} \\ + \sum_{m_{2} = n_{2}, m_{1} n_{1} \notin E_{1}} min {T_{M_{1}} (m_{1}), T_{M_{1}} (n_{1}), T_{M_{2}} (m_{2})} \\ + \sum_{m_{1} n_{1} \notin E_{1} and m_{2} n_{2} \notin E_{2}} min {T_{M_{1}} (m_{1}), T_{M_{1}} (n_{1}), T_{M_{2}} (m_{2}), T_{M_{2}} (n_{2})}, \end{array}

\begin{array}{l} {(d_{F})}_{G_{1} | G_{2}} (m_{1}, m_{2}) = \sum_{(m_{1}, m_{2}) (n_{1}, n_{2}) \in E_{1} \times E_{2}} (F_{N_{1}} | F_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) \\ = \sum_{m_{1} = n_{1}, m_{2} n_{2} \notin E_{2}} max {F_{M_{1}} (m_{1}), F_{M_{2}} (m_{2}), F_{M_{2}} (n_{2})} \\ + \sum_{m_{2} = n_{2}, m_{1} n_{1} \notin E_{1}} max {F_{M_{1}} (m_{1}), F_{M_{1}} (n_{1}), F_{M_{2}} (m_{2})} \\ + \sum_{m_{1} n_{1} \notin E_{1} and m_{2} n_{2} \notin E_{2}} max {F_{M_{1}} (m_{1}), F_{M_{1}} (n_{1}), F_{M_{2}} (m_{2}), F_{M_{2}} (n_{2})} . \end{array}

Definition 3.20. Let G₁ = (M₁, N₁) and G₂ = (M₂, N₂) be two vague graphs. For any vertex (m₁, m₂) ∈ V₁ × V₂ we define

\begin{array}{l} {(t d_{T})}_{G_{1} | G_{2}} (m_{1}, m_{2}) = \sum_{(m_{1}, m_{2}) (n_{1}, n_{2}) \in E_{1} \times E_{2}} (T_{N_{1}} | T_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) \\ + (T_{M_{1}} | T_{M_{2}}) (m_{1}, m_{2}) \\ = \sum_{m_{1} = n_{1}, m_{2} n_{2} \notin E_{2}} min {T_{M_{1}} (m_{1}), T_{M_{2}} (m_{2}), T_{M_{2}} (n_{2})} \\ + \sum_{m_{2} = n_{2}, m_{1} n_{1} \notin E_{1}} min {T_{M_{1}} (m_{1}), T_{M_{1}} (n_{1}), T_{M_{2}} (m_{2})} \\ + \sum_{m_{1} n_{1} \notin E_{1} and m_{2} n_{2} \notin E_{2}} min {T_{M_{1}} (m_{1}), T_{M_{1}} (n_{1}), T_{M_{2}} (m_{2}), T_{M_{2}} (n_{2})}, \end{array}

\begin{array}{l} {(t d_{F})}_{G_{1} | G_{2}} (m_{1}, m_{2}) = \sum_{(m_{1}, m_{2}) (n_{1}, n_{2}) \in E_{1} \times E_{2}} (F_{N_{1}} | F_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) \\ + (F_{M_{1}} | F_{M_{2}}) (m_{1}, m_{2}) \\ = \sum_{m_{1} = n_{1}, m_{2} n_{2} \notin E_{2}} max {F_{M_{1}} (m_{1}), F_{M_{2}} (m_{2}), F_{M_{2}} (n_{2})} \\ + \sum_{m_{2} = n_{2}, m_{1} n_{1} \notin E_{1}} max {F_{M_{1}} (m_{1}), F_{M_{1}} (n_{1}), F_{M_{2}} (m_{2})} \\ + \sum_{m_{1} n_{1} \notin E_{1} and m_{2} n_{2} \notin E_{2}} max {F_{M_{1}} (m_{1}), F_{M_{1}} (n_{1}), F_{M_{2}} (m_{2}), F_{M_{2}} (n_{2})} . \end{array}

Example 3.21. In this example we find the degree and total degree of the vertex (e, a) in Example 3.17:

\begin{array}{l} {(d_{T})}_{G_{1} | G_{2}} (e, a) = min {T_{M_{2}} (e), T_{M_{1}} (a), T_{M_{1}} (c)} \\ + min {T_{M_{2}} (e), T_{M_{1}} (a), T_{M_{2}} (g)} \\ = min {0.3, 0.4, 0.3} + min {0.3, 0.4, 0.3} \\ = 0.3 + 0.3 \\ = 0.6, \\ \begin{array}{l} {(d_{F})}_{G_{1} | G_{2}} (e, a) = max {F_{M_{2}} (e), F_{M_{1}} (a), F_{M_{1}} (c)} \\ + max {F_{M_{2}} (e), F_{M_{1}} (a), F_{M_{2}} (g) \\ = max {0.4, 0.4, 0.4} + max {0.4, 0.4, 0.2} \\ = 0.4 + 0.4 \\ = 0.8. \end{array} \end{array}

Therefore, d_G₁|G₂(a, c)= (0.6,0.8).

In addition, by the definition of the total vertex degree in the maximal product,

\begin{array}{l} {(t d_{T})}_{G_{1} | G_{2}} (e, a) = min {T_{M_{2}} (e), T_{M_{1}} (a), T_{M_{1}} (c)} \\ + min {T_{M_{2}} (e), T_{M_{1}} (a), T_{M_{2}} (g)} \\ + min {T_{M_{2}} (e), T_{M_{1}} (a)} \\ = min {0.3, 0.4, 0.3} + min {0.3, 0.4, 0.3} \\ + min {0.3, 0.4} \\ = 0.3 + 0.3 + 0.3 \\ = 0.9, \\ {(t d_{F})}_{G_{1} | G_{2}} (e, a) = max {F_{M_{2}} (e), F_{M_{1}} (a), F_{M_{1}} (c)} \\ + max {F_{M_{2}} (e), F_{M_{1}} (a), F_{M_{2}} (g)} \\ + max {F_{M_{2}} (e), F_{M_{1}} (a)} \\ = max {0.4, 0.4, 0.4} + max {0.4, 0.4, 0.2} \\ + max {0.3, 0.4} \\ = 0.4 + 0.4 + 0.4 \\ = 1.2 . \end{array}

Therefore, td_G₁|G₂(a, c)= (0.9,1.2).

Similarly, we can find the degree and the total degree of all vertices in G₁|G₂.

Definition 3.22. The symmetric difference G₁ ⊕ G₂ = (M₁ ⊕ M₂, N₁ ⊕ N₂) of two vague graphs G₁ = (M₁, N₁) and G₂ = (M₂, N₂) is defined as follows:

\begin{array}{l} (i) (T_{M_{1}} \oplus T_{M_{2}}) ((m_{1}, m_{2})) = min {T_{M_{1}} (m_{1}), T_{M_{2}} (m_{2})}, \\ (F_{M_{1}} \oplus F_{M_{2}}) ((m_{1}, m_{2})) = max {F_{M_{1}} (m_{1}), F_{M_{2}} (m_{2})} \\ \forall (m_{1}, m_{2}) \in (V_{1} \times V_{2}); \end{array}

\begin{array}{l} (ii) (T_{N_{1}} \oplus T_{N_{2}}) ((m, m_{2}) (m, n_{2})) = min {T_{M_{1}} (m), T_{N_{2}} (m_{2} n_{2})}, \\ (F_{N_{1}} \oplus F_{N_{2}}) ((m, m_{2}) (m, n_{2})) = max {F_{M_{1}} (m), F_{N_{2}} (m_{2} n_{2})} \\ \forall m \in V_{1} and m_{2} n_{2} \in E_{2}; \end{array}

\begin{array}{l} (iii) (T_{N_{1}} \oplus T_{N_{2}}) ((m_{1}, z) (n_{1}, z)) = min {T_{N_{1}} (m_{1} n_{1}), T_{M_{2}} (z)}, \\ (F_{N_{1}} \oplus F_{N_{2}}) ((m_{1}, z) (n_{1}, z)) = max {F_{N_{1}} (m_{1} n_{1}), F_{M_{2}} (z)} \\ \forall z \in V_{2} and m_{1} n_{1} \in E_{1}; \end{array}

\begin{array}{l} (iv) (T_{N_{1}} \oplus T_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) = {\begin{array}{r} min {T_{M_{1}} (m_{1}), T_{M_{1}} (n_{1}), T_{N_{2}} (m_{2} n_{2})} \\ \forall m_{1} n_{1} \in E_{1} and m_{2} n_{2} \in E_{2}, \\ min {T_{M_{2}} (m_{2}), T_{M_{2}} (n_{2}), T_{N_{1}} (m_{1} n_{1})} \\ \forall m_{1} n_{1} \in E_{1} and m_{2} n_{2} \in E_{2}, \end{array} \\ (F_{N_{1}} \oplus F_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) = {\begin{array}{r} max {F_{M_{1}} (m_{1}), F_{M_{1}} (n_{1}), F_{N_{2}} (m_{2} n_{2})} \\ \forall m_{1} n_{1} \in E_{1} and m_{2} n_{2} \in E_{2}, \\ max {F_{M_{2}} (m_{2}), F_{M_{2}} (n_{2}), F_{N_{1}} (m_{1} n_{1})} \\ \forall m_{1} n_{1} \in E_{1} and m_{2} n_{2} \in E_{2} . \end{array} \end{array}

Example 3.23. Consider the vague graphs G₁ and G₂ as in Figures 13, 14. The symmetric difference of G₁ and G₂, i.e., G₁ ⊕ G₂, is shown in Figure 15.

FIGURE 13

Figure 13. G₁.

FIGURE 14

Figure 14. G₂.

FIGURE 15

Figure 15. G₁ ⊕ G₂.

For the vertex (a, f), we find the membership and non-membership values as follows:

\begin{array}{l} (T_{M_{1}} \oplus T_{M_{2}}) ((a, f)) = min {T_{M_{1}} (a), T_{M_{2}} (f)} \\ = min {0.2, 0.3} = 0.2, \\ (F_{M_{1}} \oplus F_{M_{2}}) ((a, f)) = max {F_{M_{1}} (a), F_{M_{2}} (f)} \\ = max {0.4, 0.3} = 0.4 \end{array}

for a ∈ V₁ and f ∈ V₂.

For the edge (a, d)(a, e), the membership and non-membership values are given by

\begin{array}{l} (T_{N_{1}} \oplus T_{N_{2}}) ((a, d) (a, e)) = min {T_{M_{1}} (a), T_{N_{2}} (d e)} \\ = min {0.2, 0.1} = 0.1, \\ (F_{N_{1}} \oplus F_{N_{2}}) ((a, d) (a, e)) = max {F_{M_{1}} (a), F_{N_{2}} (d e)} \\ = max {0.4, 0.6} = 0.6 \end{array}

for a ∈ V₁ and de ∈ E₂.

For the edge (a, d)(b, d) we have

\begin{array}{l} (T_{N_{1}} \oplus T_{N_{2}}) ((a, d) (b, d)) = min {T_{N_{1}} (a b), T_{M_{2}} (d)} \\ = min {0.2, 0.2} = 0.2, \\ (F_{N_{1}} \oplus F_{N_{2}}) ((a, d) (b, d)) = max {F_{N_{1}} (a b), F_{M_{2}} (d)} \\ = max {0.7, 0.4} = 0.7 \end{array}

for ab ∈ E₁ and d ∈ V₂.

For the edge (a, c)(b, f), the membership and non-membership values are

\begin{array}{l} (T_{N_{1}} \oplus T_{N_{2}}) ((a, c) (b, f)) = min {T_{M_{2}} (c), T_{M_{2}} (f), T_{N_{1}} (a b)} \\ = min {0.4, 0.3, 0.2} = 0.2, \\ (F_{N_{1}} \oplus F_{N_{2}}) ((a, c) (b, f)) = max {F_{M_{2}} (c), F_{M_{2}} (f), F_{N_{1}} (a b)} \\ = max {0.5, 0.3, 0.7} = 0.7 \end{array}

for ab ∈ E₁ and cf ∉ E₂.

In the same way, we can find the membership and non-membership values for all remaining vertices and edges.

Proposition 3.24. The symmetric difference of two vague graphs G₁ and G₂ is a vague graph.

Proof: Let G₁ = (M₁, N₁) and G₂ = (M₂, N₂) be two vague graphs on crisp graphs G₁ = (V₁, E₁) and G₂ = (V₂, E₂), respectively, and let ((m₁, m₂)(n₁, n₂)) ∈ E₁ × E₂. Then by Definition 3.22 we have the following cases:

(i) If m₁ = n₁ = m, then

\begin{array}{l} (T_{N_{1}} \oplus T_{N_{2}}) ((m, m_{2}) (m, n_{2})) = min {T_{M_{1}} (m), T_{N_{2}} (m_{2} n_{2})} \\ \leq min {T_{M_{1}} (m), min {T_{M_{2}} (m_{2}), T_{M_{2}} (n_{2})}} \\ = min {min {T_{M_{1}} (m), T_{M_{2}} (m_{2})}, min {T_{M_{1}} (m), T_{M_{2}} (n_{2})}} \\ = min {(T_{M_{1}} \oplus T_{M_{2}}) (m, m_{2}), (T_{M_{1}} \oplus T_{M_{2}}) (m, n_{2})}, \\ (F_{N_{1}} \oplus F_{N_{2}}) ((m, m_{2}) (m, n_{2})) = max {F_{M_{1}} (m), F_{N_{2}} (m_{2} n_{2})} \\ \geq max {F_{M_{1}} (m), max {F_{M_{2}} (m_{2}), F_{M_{2}} (n_{2})}} \\ = max {max {F_{M_{1}} (m), F_{M_{2}} (m_{2})}, max {F_{M_{1}} (m), F_{M_{2}} (n_{2})}} \\ = max {(F_{M_{1}} \oplus F_{M_{2}}) (m, m_{2}), (F_{M_{1}} \oplus F_{M_{2}}) (m, n_{2})} . \end{array}

(ii) If m₂ = n₂ = z, then

\begin{array}{l} (T_{N_{1}} \oplus T_{N_{2}}) ((m_{1}, z) (n_{1}, z)) = min {T_{N_{1}} (m_{1} n_{1}), T_{M_{2}} (z)} \\ \leq min {min {T_{N_{1}} (m_{1} n_{1}), T_{M_{2}} (z)} \\ = min {min {T_{M_{1}} (m_{1}), T_{M_{2}} (z)}, min {T_{M_{1}} (n_{1}), T_{M_{2}} (z)}} \\ = min {(T_{M_{1}} \oplus T_{M_{2}}) (m_{1}, z), (T_{M_{1}} \oplus T_{M_{2}}) (n_{1}, z)}, \\ (F_{N_{1}} \oplus F_{N_{2}}) ((m_{1}, z) (n_{1}, z)) = max {F_{N_{1}} (m_{1} n_{1}), F_{M_{2}} (z)} \\ \geq max {max {F_{N_{1}} (m_{1} n_{1}), F_{M_{2}} (z)} \\ = max {max {F_{M_{1}} (m_{1}), F_{M_{2}} (z)}, max {F_{M_{1}} (n_{1}), F_{M_{2}} (z)}} \\ = max {(F_{M_{1}} \oplus F_{M_{2}}) (m_{1}, z), (F_{M_{1}} \oplus F_{M_{2}}) (n_{1}, z)} . \end{array}

(iii) If m₁n₁ ∉ E₁ and m₂n₂ ∈ E₂, then

\begin{array}{l} (T_{N_{1}} \oplus T_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) = min {T_{M_{1}} (m_{1}), T_{M_{1}} (n_{1}), T_{N_{2}} (m_{2} n_{2})} \\ \leq min {T_{M_{1}} (m_{1}), T_{M_{1}} (n_{1}), m i n {T_{M_{2}} (m_{2}) T_{M_{2}} (n_{2})}} \\ = min {min {T_{M_{1}} (m_{1}), T_{M_{2}} (m_{2})}, {T_{M_{1}} (m_{1}), T_{M_{2}} (n_{2})}} \\ = min {(T_{M_{1}} \oplus T_{M_{2}}) (m_{1}, m_{2}), (T_{M_{1}} \oplus T_{M_{2}}) (n_{1}, n_{2})}, \\ (F_{N_{1}} \oplus F_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) = max {F_{M_{1}} (m_{1}), F_{M_{1}} (n_{1}), F_{N_{2}} (m_{2} n_{2})} \\ \geq max {F_{M_{1}} (m_{1}), F_{M_{1}} (n_{1}), max {F_{M_{2}} (m_{2}) F_{M_{2}} (n_{2})}} \\ = max {max {F_{M_{1}} (m_{1}), F_{M_{2}} (m_{2})}, {F_{M_{1}} (m_{1}), F_{M_{2}} (n_{2})}} \\ = max {(F_{M_{1}} \oplus F_{M_{2}}) (m_{1}, m_{2}), (F_{M_{1}} \oplus F_{M_{2}}) (n_{1}, n_{2})} . \end{array}

(iv) If m₁n₁ ∈ E₁ and m₂n₂ ∉ E₂, then

\begin{array}{l} (T_{N_{1}} \oplus T_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) = min {T_{M_{2}} (m_{2}), T_{M_{2}} (n_{2}), T_{N_{1}} (m_{1} n_{1})} \\ \leq min {T_{M_{2}} (m_{2}), T_{M_{2}} (n_{2}), min {T_{M_{1}} (m_{1}) T_{M_{1}} (n_{1})}} \\ = min {min {T_{M_{1}} (m_{1}), T_{M_{2}} (m_{2})}, {T_{M_{1}} (n_{1}), T_{M_{2}} (n_{2})} \\ = min {(T_{M_{1}} \oplus T_{M_{2}}) (m_{1}, m_{2}), (T_{M_{1}} \oplus T_{M_{2}}) (n_{1}, n_{2})}, \\ (F_{N_{1}} \oplus F_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) = max {F_{M_{2}} (m_{2}), F_{M_{2}} (n_{2}), F_{N_{1}} (m_{1} n_{1})} \\ \geq max {F_{M_{2}} (m_{2}), F_{M_{2}} (n_{2}), max {F_{M_{1}} (m_{1}) F_{M_{1}} (n_{1})}} \\ = max {max {F_{M_{2}} (m_{2}), F_{M_{1}} (m_{1})}, {F_{M_{2}} (m_{2}), F_{M_{1}} (n_{1})} \\ = max {(F_{M_{1}} \oplus F_{M_{2}}) (m_{1}, m_{2}), (F_{M_{1}} \oplus F_{M_{2}}) (n_{1}, n_{2})} . \end{array}

Hence G₁ ⊕ G₂ is a vague graph. □

Remark 3.5. The symmetric difference of two connected vague graphs G₁ = (M₁, N₁) and G₂ = (M₂, N₂) is connected, because we include the case where (m₁, m₂) ∈ E₁ and (n₁, n₂) ∈ E₂ in the definition of the symmetric difference of two vague graphs.

Definition 3.25. Let G₁ = (M₁, N₁) and G₂ = (M₂, N₂) be two vague graphs. For any vertex (m₁, m₂) ∈ V₁ × V₂ we define

\begin{array}{l} {(d_{T})}_{G_{1} \oplus G_{2}} (m_{1}, m_{2}) = \sum_{(m_{1}, m_{2}) (n_{1}, n_{2}) \in E_{1} \times E_{2}} (T_{N_{1}} \oplus T_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) \\ = \sum_{m_{1} = n_{1}, m_{2} n_{2} \in E_{2}} min {T_{M_{1}} (m_{1}), T_{N_{2}} (m_{2} n_{2})} \\ + \sum_{m_{1} n_{1} \in E_{1}, m_{2} = n_{2}} min {T_{N_{1}} (m_{1} n_{1}), T_{M_{2}} (m_{2})} \\ + \sum_{m_{1} n_{1} \notin E_{1} and m_{2} n_{2} \in E_{2}} min {T_{M_{1}} (m_{1}), T_{M_{1}} (n_{1}), T_{N_{2}} (m_{2} n_{2})} \\ + \sum_{m_{1} n_{1} \in E_{1} and m_{2} n_{2} \notin E_{2}} min {T_{N_{1}} (m_{1} n_{1}), T_{M_{2}} (m_{2}), T_{M_{2}} (n_{2})} \end{array}

and

\begin{array}{l} {(d_{F})}_{G_{1} \oplus G_{2}} (m_{1}, m_{2}) = \sum_{(m_{1}, m_{2}) (n_{1}, n_{2}) \in E_{1} \times E_{2}} (F_{N_{1}} \oplus F_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) \\ = \sum_{m_{1} = n_{1}, m_{2} n_{2} \in E_{2}} max {F_{M_{1}} (m_{1}), F_{N_{2}} (m_{2} n_{2})} \\ + \sum_{m_{1} n_{1} \in E_{1}, m_{2} = n_{2}} max {F_{N_{1}} (m_{1} n_{1}), F_{M_{2}} (m_{2})} \\ + \sum_{m_{1} n_{1} \notin E_{1} and m_{2} n_{2} \in E_{2}} max {F_{M_{1}} (m_{1}), F_{M_{1}} (n_{1}), F_{N_{2}} (m_{2} n_{2})} \\ + \sum_{m_{1} n_{1} \in E_{1} and m_{2} n_{2} \notin E_{2}} max {F_{N_{1}} (m_{1} n_{1}), F_{M_{2}} (m_{2}), F_{M_{2}} (n_{2})} . \end{array}

Theorem 3.26. Let G₁ = (M₁, N₁) and G₂ = (M₂, N₂) be two vague graphs. If T_M₁ ≥ T_N₂, F_M₁ ≤ F_N₂, T_M₂ ≥ T_N₁, and F_M₂ ≤ F_N₁, then for every (m₁, m₂) ∈ V₁ × V₂ we have (d)_{G₁ ⊕ G₂}(m₁, m₂) = q(d)_G₁(m₁) + s(d)_G₂(m₂), where s = |V₁| − (d)_G₁(m₁) and q = |V₂| − (d)_G₂(m₂).

Proof: Using Definition 3.25,

\begin{array}{l} {(d_{T})}_{G_{1} \oplus G_{2}} (m_{1}, m_{2}) = \sum_{(m_{1}, m_{2}) (n_{1}, n_{2}) \in E_{1} \times E_{2}} (T_{N_{1}} \oplus T_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) \\ = \sum_{m_{1} = n_{1}, m_{2} n_{2} \in E_{2}} min {T_{M_{1}} (m_{1}), T_{N_{2}} (m_{2} n_{2})} \\ + \sum_{m_{1} n_{1} \in E_{1}, m_{2} = n_{2}} min {T_{N_{1}} (m_{1} n_{1}), T_{M_{2}} (m_{2})} \\ + ​​​​​​​ \sum_{m_{1} n_{1} \in E_{1} and m_{2} n_{2} \in E_{2}} ​ ​​​​​​min {T_{M_{1}} (m_{1}), T_{M_{1}} (n_{1}), T_{N_{2}} (m_{2} n_{2})} \\ + ​​​​​​​ \sum_{m_{1} n_{1} \in E_{1} and m_{2} n_{2} \in E_{2}} ​ ​​​​​​min {T_{N_{1}} (m_{1} n_{1}), T_{M_{2}} (m_{2}), T_{M_{2}} (n_{2})} \\ = \sum_{m_{2} n_{2} \in E_{2}} T_{N_{2}} (m_{2} n_{2}) + \sum_{m_{1} n_{1} \in E_{1}} T_{N_{1}} (m_{1} n_{1}) \\ + ​​​​​​​​​ \sum_{m_{1} n_{1} \in E_{1} and m_{2} n_{2} \in E_{2}} ​ ​​​​​​​​​​ T_{N_{2}} (m_{2} n_{2})} + ​​​​​​​​​​​ \sum_{m_{1} n_{1} \in E_{1} and m_{2} n_{2} \in E_{2}} ​ ​​​​​​​​​​​​ T_{N_{1}} (m_{1} n_{1}) \\ = q {(d_{T})}_{G_{1}} (m_{1}) + s {(d_{T})}_{G_{2}} (m_{2}), \end{array}

\begin{array}{l} {(d_{F})}_{G_{1} \oplus G_{2}} (m_{1}, m_{2}) = \sum_{(m_{1}, m_{2}) (n_{1}, n_{2}) \in E_{1} \times E_{2}} (F_{N_{1}} \oplus F_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) \\ = \sum_{m_{1} = n_{1}, m_{2} n_{2} \in E_{2}} max {F_{M_{1}} (m_{1}), F_{N_{2}} (m_{2} n_{2})} \\ + \sum_{m_{1} n_{1} \in E_{1}, m_{2} = n_{2}} max {F_{N_{1}} (m_{1} n_{1}), F_{M_{2}} (m_{2})} \\ + \sum_{m_{1} n_{1} \notin E_{1} and m_{2} n_{2} \in E_{2}} max {F_{M_{1}} (m_{1}), F_{M_{1}} (n_{1}), F_{N_{2}} (m_{2} n_{2})} \\ + \sum_{m_{1} n_{1} \in E_{1} and m_{2} n_{2} \notin E_{2}} max {F_{N_{1}} (m_{1} n_{1}), F_{M_{2}} (m_{2}), F_{M_{2}} (n_{2})} \\ = \sum_{m_{2} n_{2} \in E_{2}} F_{N_{2}} (m_{2} n_{2}) + \sum_{m_{1} n_{1} \in E_{1}} F_{N_{1}} (m_{1} n_{1}) \\ + \sum_{m_{1} n_{1} \notin E_{1} and m_{2} n_{2} \in E_{2}} F_{N_{2}} (m_{2} n_{2})} + \sum_{m_{1} n_{1} \in E_{1} and m_{2} n_{2} \notin E_{2}} F_{N_{1}} (m_{1} n_{1}) \\ = q {(d_{F})}_{G_{1}} (m_{1}) + s {(d_{F})}_{G_{2}} (m_{2}), \end{array}

and hence the result is proved. □

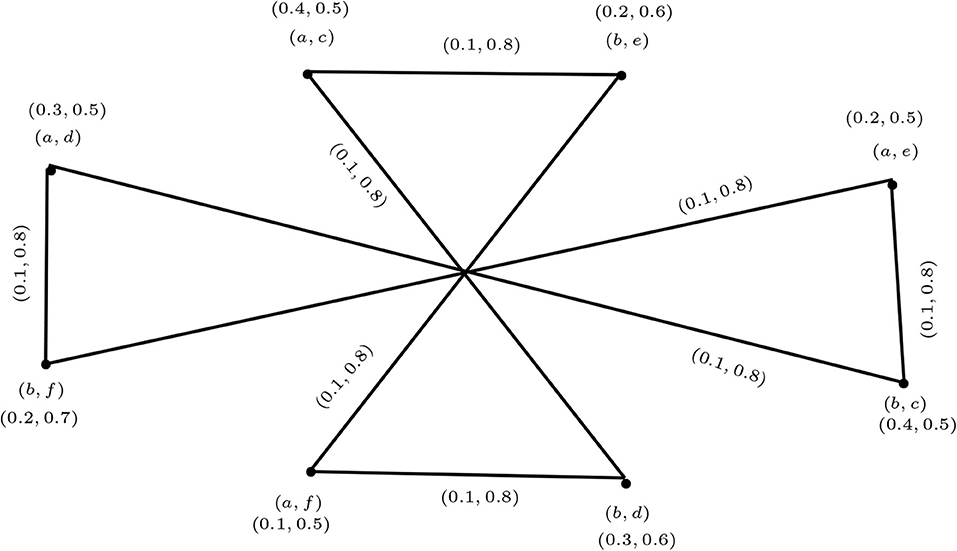
Example 3.27. Consider the two vague graphs G₁ and G₂ in Figure 9 and their symmetric difference in Figure 16. In Figure 9, T_M₁ ≥ T_N₂, F_M₁ ≤ F_N₂, T_M₂ ≥ T_N₁, and F_M₂ ≤ F_N₁. Then, the total degree of a vertex in the symmetric difference is calculated by the following formula:

\begin{array}{l} {(d_{T})}_{G_{1} \oplus G_{2}} (m_{1}, m_{2}) = q {(d_{T})}_{G_{1}} (m_{1}) + s {(d_{T})}_{G_{2}} (m_{2}), \\ {(d_{F})}_{G_{1} \oplus G_{2}} (m_{1}, m_{2}) = q {(d_{F})}_{G_{1}} (m_{1}) + s {(d_{F})}_{G_{2}} (m_{2}) . \end{array}

FIGURE 16

Figure 16. G₁ ⊕ G₂ of the vague graphs in Figure 9.

Using the formula we find that

\begin{array}{l} {(d_{T})}_{G_{1} \oplus G_{2}} (a, c) = 1 \cdot (0.2) + 1 \cdot (0.2) = 0.4, \\ {(d_{F})}_{G_{1} \oplus G_{2}} (a, c) = 1 \cdot (0.4) + 1 \cdot (0.5) = 0.9, \\ {(d_{T})}_{G_{1} \oplus G_{2}} (a, d) = 1 \cdot (0.2) + 1 \cdot (0.2) = 0.4, \\ {(d_{F})}_{G_{1} \oplus G_{2}} (a, d) = 1 \cdot (0.4) + 1 \cdot (0.5) = 0.9 . \end{array}

Hence, (d)_{G₁ ⊕ G₂}(a, c) = (0.4, 0.9) and (d)_{G₁ ⊕ G₂}(a, d) = (0.4, 0.9).

In the same way, we can show that (d)_{G₁ ⊕ G₂}(b, c) = (d)_{G₁ ⊕ G₂}(b, d) = (0.4, 0.9). Direct calculations give

\begin{array}{l} {(d_{T})}_{G_{1} \oplus G_{2}} (a, c) = 0.2 + 0.2 = 0.4, \\ {(d_{F})}_{G_{1} \oplus G_{2}} (a, c) = 0.4 + 0.5 = 0.9, \\ {(d_{T})}_{G_{1} \oplus G_{2}} (a, d) = 0.2 + 0.2 = 0.4, \\ {(d_{F})}_{G_{1} \oplus G_{2}} (a, d) = 0.4 + 0.5 = 0.9, \\ {(d_{T})}_{G_{1} \oplus G_{2}} (b, c) = 0.2 + 0.2 = 0.4, \\ {(d_{F})}_{G_{1} \oplus G_{2}} (b, c) = 0.4 + 0.5 = 0.9, \\ {(d_{T})}_{G_{1} \oplus G_{2}} (b, d) = 0.2 + 0.2 = 0.4, \\ {(d_{F})}_{G_{1} \oplus G_{2}} (b, d) = 0.4 + 0.5 = 0.9 . \end{array}

It is obvious from the above that the degrees of vertices calculated using the formula and by the direct method are the same.

Definition 3.28. Let G₁ = (M₁, N₁) and G₂ = (M₂, N₂) be two vague graphs. For any vertex (m₁, m₂) ∈ V₁ × V₂ we define

\begin{array}{l} {(t d_{T})}_{G_{1} \oplus G_{2}} (m_{1}, m_{2}) = \sum_{(m_{1}, m_{2}) (n_{1}, n_{2}) \in E_{1} \times E_{2}} (T_{N_{1}} \oplus T_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) \\ + (T_{M_{1}} \oplus T_{M_{2}} (m_{1}, m_{2}) \\ = \sum_{m_{1} = n_{1}, m_{2} n_{2} \in E_{2}} min {T_{M_{1}} (m_{1}), T_{N_{2}} (m_{2} n_{2})} \\ + \sum_{m_{1} n_{1} \in E_{1}, m_{2} = n_{2}} min {T_{N_{1}} (m_{1} n_{1}), T_{M_{2}} (m_{2})} \\ + \sum_{m_{1} n_{1} \notin E_{1} and m_{2} n_{2} \in E_{2}} min {T_{M_{1}} (m_{1}), T_{M_{1}} (n_{1}), T_{N_{2}} (m_{2} n_{2})} \\ + \sum_{m_{1} n_{1} \in E_{1} and m_{2} n_{2} \notin E_{2}} min {T_{N_{1}} (m_{1} n_{1}), T_{M_{2}} (m_{2}), T_{M_{2}} (n_{2})} \\ + min {T_{M_{1}} (m_{1}), T_{M_{2}} (m_{2})} \end{array}

and

\begin{array}{l} {(t d_{F})}_{G_{1} \oplus G_{2}} (m_{1}, m_{2}) = \sum_{(m_{1}, m_{2}) (n_{1}, n_{2}) \in E_{1} \times E_{2}} (F_{N_{1}} \oplus F_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) \\ + (F_{M_{1}} \oplus F_{M_{2}} (m_{1}, m_{2}) \\ = \sum_{m_{1} = n_{1}, m_{2} n_{2} \in E_{2}} max {F_{M_{1}} (m_{1}), F_{N_{2}} (m_{2} n_{2})} \\ + \sum_{m_{1} n_{1} \in E_{1}, m_{2} = n_{2}} max {F_{N_{1}} (m_{1} n_{1}), F_{M_{2}} (m_{2})} \\ + \sum_{m_{1} n_{1} \notin E_{1} and m_{2} n_{2} \in E_{2}} max {F_{M_{1}} (m_{1}), F_{M_{1}} (n_{1}), F_{N_{2}} (m_{2} n_{2})} \\ + \sum_{m_{1} n_{1} \in E_{1} and m_{2} n_{2} \notin E_{2}} max {F_{N_{1}} (m_{1} n_{1}), F_{M_{2}} (m_{2}), F_{M_{2}} (n_{2})} \\ + max {F_{M_{1}} (m_{1}), F_{M_{2}} (m_{2})} . \end{array}

Example 3.29. In this example we find the degree and total degree of the vertex (a, e) in Example 3.23. We have

\begin{array}{l} s = | V_{1} | - {(d)}_{G_{1}} (a) \\ = 2 - 1 = 1 \end{array}

and, similarly,

\begin{array}{l} q = | V_{2} | - {(d)}_{G_{2}} (e) \\ = 5 - 2 = 3 . \end{array}

Therefore

\begin{array}{l} {(d_{T})}_{G_{1} \oplus G_{2}} (a, e) = q {(d_{T})}_{G_{1}} (a) + s {(d_{T})}_{G_{2}} (e) \\ = 3 (0.2) + 1 (0.1 + 0.1) = 0.6 + 0.2 = 0.8, \\ {(d_{F})}_{G_{1} \oplus G_{2}} (a, e) = q {(d_{F})}_{G_{1}} (a) + s {(d_{F})}_{G_{2}} (e) \\ = 3 (0.4) + 1 (0.6 + 0.5) = 1.2 + 1.1 = 2.3 . \end{array}

So

\begin{array}{l} {(d)}_{G_{1} \oplus G_{2}} (a, e) = (0.8, 2.3) . \end{array}

In addition, by Definition 3.28 we have

\begin{array}{l} {(t d_{T})}_{G_{1} \oplus G_{2}} (a, e) = q {(t d_{T})}_{G_{1}} (a) + s {(t d_{T})}_{G_{2}} (e) \\ - (s - 1) T_{G_{2}} (e) - (q - 1) T_{G_{1}} (a) \\ - max {T_{G_{1}} (a), T_{G_{2}} (e)} \\ = 3 (0.2 + 0.2) + 1 (0.1 + 0.1 + 0.1) \\ - (1 - 1) (0.1) - (3 - 1) (0.2) - max {0.2, 0.1} \\ = 3 (0.4) + 0.3 - 0.4 - 0.2 = 0.9, \\ {(t d_{F})}_{G_{1} \oplus G_{2}} (a, e) = q {(t d_{F})}_{G_{1}} (a) + s {(t d_{F})}_{G_{2}} (e) \\ - (s - 1) F_{G_{2}} (e) - (q - 1) F_{G_{1}} (a) \\ - min {F_{G_{1}} (a), F_{G_{2}} (e)} \\ = 3 (0.2 + 0.2) + 1 (0.4 + 0.5 + 0.6) \\ - (1 - 1) (0.4) - (3 - 1) (0.4) - min {0.4, 0.4} \\ = 3 (0.4) + 1.5 - 0.8 - 0.4 = 1.5 . \end{array}

Therefore,

\begin{array}{l} {(t d)}_{G_{1} \oplus G_{2}} (a, e) = (0.9, 1.5) . \end{array}

Similarly, we can find the degree and total degree of all vertices in G₁ ⊕ G₂.

Theorem 3.30. Let G₁ = (M₁, N₁) and G₂ = (M₂, N₂) be two vague graphs.

(i) If T_M₁ ≥ T_N₂ and T_M₂ ≥ T_N₁, then for all (m₁, m₂) ∈ V₁ × V₂,

\begin{array}{c} {(t d_{T})}_{G_{1} \oplus G_{2}} (m_{1}, m_{2}) = q {(t d_{T})}_{G_{1}} (m_{1}) + s {(t d_{T})}_{G_{2}} (m_{2}) \\ - (q - 1) T_{G_{1}} (m_{1}) - max {T_{G_{1}} (m_{1}), T_{G_{2}} (m_{2})} . \end{array}

(ii) If F_M₁ ≤ F_N₂ and F_M₂ ≤ F_N₁, then for all (m₁, m₂) ∈ V₁ × V₂,

\begin{array}{c} {(t d_{F})}_{G_{1} \oplus G_{2}} (m_{1}, m_{2}) = q {(t d_{F})}_{G_{1}} (m_{1}) + s {(t d_{F})}_{G_{2}} (m_{2}) \\ - (q - 1) F_{G_{1}} (m_{1}) - min {F_{G_{1}} (m_{1}), F_{G_{2}} (m_{2})} . \end{array}

Here s = |V₁|−(d)_G₁(m₁) and q = |V₂|−(d)_G₂(m₂).

Proof: For all (m₁, m₂) ∈ V₁ × V₂ we have

\begin{array}{l} {(t d_{T})}_{G_{1} \oplus G_{2}} (m_{1}, m_{2}) = \sum_{(m_{1}, m_{2}) (n_{1}, n_{2}) \in E_{1} \times E_{2}} (T_{N_{1}} \oplus T_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) \\ + (T_{M_{1}} \oplus T_{M_{2}}) (m_{1}, m_{2}) \\ = \sum_{m_{1} = n_{1}, m_{2} n_{2} \in E_{2}} min {T_{M_{1}} (m_{1}), T_{N_{2}} (m_{2} n_{2})} \\ + \sum_{m_{1} n_{1} \in E_{1}, m_{2} = n_{2}} min {T_{N_{1}} (m_{1} n_{1}), T_{M_{2}} (m_{2})} \\ + \sum_{m_{1} n_{1} \notin E_{1} and m_{2} n_{2} \in E_{2}} min {T_{M_{1}} (m_{1}), T_{M_{1}} (n_{1}), T_{N_{2}} (m_{2} n_{2})} \\ + \sum_{m_{1} n_{1} \in E_{1} and m_{2} n_{2} \notin E_{2}} min {T_{N_{1}} (m_{1} n_{1}), T_{M_{2}} (m_{2}), T_{M_{2}} (n_{2})} \\ + max {T_{M_{1}} (m_{1}), T_{M_{2}} (m_{2})} \\ = \sum_{m_{2} n_{2} \in E_{2}} T_{N_{2}} (m_{2} n_{2}) + \sum_{m_{1} n_{1} \in E_{1}} T_{N_{1}} (m_{1} n_{1}) \\ + \sum_{m_{1} n_{1} \notin E_{1} and m_{2} n_{2} \in E_{2}} T_{N_{2}} (m_{2} n_{2})} + \sum_{m_{1} n_{1} \in E_{1} and m_{2} n_{2} \notin E_{2}} T_{N_{1}} (m_{1} n_{1}) \\ + max {T_{M_{1}} (m_{1}), T_{M_{2}} (m_{2})} \\ = \sum_{m_{2} n_{2} \in E_{2}} T_{N_{2}} (m_{2} n_{2}) + \sum_{m_{1} n_{1} \in E_{1}} T_{N_{1}} (m_{1} n_{1}) \\ + \sum_{m_{1} n_{1} \notin E_{1} and m_{2} n_{2} \in E_{2}} T_{N_{2}} (m_{2} n_{2})} \\ + \sum_{m_{1} n_{1} \in E_{1} and m_{2} n_{2} \notin E_{2}} T_{N_{1}} (m_{1} n_{1}) + T_{M_{1}} (m_{1}) + T_{M_{2}} (m_{2}) \\ - max {T_{M_{1}} (m_{1}), T_{M_{2}} (m_{2})} \\ = q {(t d_{T})}_{G_{1}} (m_{1}) + s {(t d_{T})}_{G_{2}} (m_{2}) \\ - (q - 1) T_{G_{1}} (m_{1}) - max {T_{G_{1}} (m_{1}), T_{G_{2}} (m_{2})}, \end{array}

\begin{array}{l} {(t d_{F})}_{G_{1} \oplus G_{2}} (m_{1}, m_{2}) = \sum_{(m_{1}, m_{2}) (n_{1}, n_{2}) \in E_{1} \times E_{2}} (F_{N_{1}} \oplus F_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) \\ + (F_{M_{1}} \oplus F_{M_{2}}) (m_{1}, m_{2}) \\ = \sum_{m_{1} = n_{1}, m_{2} n_{2} \in E_{2}} max {F_{M_{1}} (m_{1}), F_{N_{2}} (m_{2} n_{2})} \\ + \sum_{m_{1} n_{1} \in E_{1}, m_{2} = n_{2}} max {F_{N_{1}} (m_{1} n_{1}), F_{M_{2}} (m_{2})} \\ + \sum_{m_{1} n_{1} \notin E_{1} and m_{2} n_{2} \in E_{2}} max {F_{M_{1}} (m_{1}), F_{M_{1}} (n_{1}), F_{N_{2}} (m_{2} n_{2})} \\ + \sum_{m_{1} n_{1} \in E_{1} and m_{2} n_{2} \notin E_{2}} max {F_{N_{1}} (m_{1} n_{1}), F_{M_{2}} (m_{2}), F_{M_{2}} (n_{2})} \\ + min {F_{M_{1}} (m_{1}), F_{M_{2}} (m_{2})} \\ = \sum_{m_{2} n_{2} \in E_{2}} F_{N_{2}} (m_{2} n_{2}) + \sum_{m_{1} n_{1} \in E_{1}} F_{N_{1}} (m_{1} n_{1}) \\ + \sum_{m_{1} n_{1} \notin E_{1} and m_{2} n_{2} \in E_{2}} F_{N_{2}} (m_{2} n_{2})} \\ + \sum_{m_{1} n_{1} \in E_{1} and m_{2} n_{2} \notin E_{2}} F_{N_{1}} (m_{1} n_{1}) \\ + min {F_{M_{1}} (m_{1}), F_{M_{2}} (m_{2})} \\ = \sum_{m_{2} n_{2} \in E_{2}} F_{N_{2}} (m_{2} n_{2}) + \sum_{m_{1} n_{1} \in E_{1}} F_{N_{1}} (m_{1} n_{1}) \\ + \sum_{m_{1} n_{1} \notin E_{1} and m_{2} n_{2} \in E_{2}} F_{N_{2}} (m_{2} n_{2})} \\ + \sum_{m_{1} n_{1} \in E_{1} and m_{2} n_{2} \notin E_{2}} F_{N_{1}} (m_{1} n_{1}) + F_{M_{1}} (m_{1}) + F_{M_{2}} (m_{2}) \\ - min {F_{M_{1}} (m_{1}), F_{M_{2}} (m_{2})} \\ = q {(t d_{F})}_{G_{1}} (m_{1}) + s {(t d_{F})}_{G_{2}} (m_{2}) \\ - (q - 1) F_{G_{1}} (m_{1}) - min {F_{G_{1}} (m_{1}), F_{G_{2}} (m_{2})}, \end{array}

where s = |V₁|−(d)_G₁(m₁) and q = |V₂|−(d)_G₂(m₂). □

Example 3.31. In this example, we calculate the total degree of the vertices in Example 3.27.

The total degree of a vertex in the symmetric difference is given by

\begin{array}{l} {(t d_{T})}_{G_{1} \oplus G_{2}} (m_{1}, m_{2}) = q {(t d_{T})}_{G_{1}} (m_{1}) + s {(t d_{T})}_{G_{2}} (m_{2}) \\ - (q - 1) T_{G_{1}} (m_{1}) - max {T_{G_{1}} (m_{1}), T_{G_{2}} (m_{2})}, \\ {(t d_{F})}_{G_{1} \oplus G_{2}} (m_{1}, m_{2}) = q {(t d_{F})}_{G_{1}} (m_{1}) + s {(t d_{F})}_{G_{2}} (m_{2}) \\ - (q - 1) F_{G_{1}} (m_{1}) - min {F_{G_{1}} (m_{1}), F_{G_{2}} (m_{2})} . \end{array}

Using the above formula, we calculate

\begin{array}{l} {(t d_{T})}_{G_{1} \oplus G_{2}} (a, c) = 1 \cdot (0.5) + 1 \cdot (0.4) - (1 - 1) \cdot (0.3) \\ - max {0.2, 0.3} = 0.6, \\ {(t d_{F})}_{G_{1} \oplus G_{2}} (a, c) = 1 \cdot (0.8) + 1 \cdot (0.8) - (1 - 1) \cdot (0.4) \\ - min {0.3, 0.4} = 1.3, \\ {(t d_{T})}_{G_{1} \oplus G_{2}} (a, d) = 1 \cdot (0.5) + 1 \cdot (0.5) - (1 - 1) \cdot (0.3) \\ - max {0.3, 0.3} = 0.7, \\ {(t d_{F})}_{G_{1} \oplus G_{2}} (a, d) = 1 \cdot (0.8) + 1 \cdot (0.9) - (1 - 1) \cdot (0.4) \\ - min {0.4, 0.4} = 1.3, \\ {(t d_{T})}_{G_{1} \oplus G_{2}} (b, c) = 1 \cdot (0.4) + 1 \cdot (0.4) - (1 - 1) \cdot (0.2) \\ - max {0.2, 0.2} = 0.6, \\ {(t d_{F})}_{G_{1} \oplus G_{2}} (b, c) = 1 \cdot (0.7) + 1 \cdot (0.8) - (1 - 1) \cdot (0.2) \\ - min {0.3, 0.3} = 1.2, \\ {(t d_{T})}_{G_{1} \oplus G_{2}} (b, d) = 1 \cdot (0.4) + 1 \cdot (0.5) - (1 - 1) \cdot (0.2) \\ - max {0.2, 0.3} = 0.6, \\ {(t d_{F})}_{G_{1} \oplus G_{2}} (b, d) = 1 \cdot (0.7) + 1 \cdot (0.9) - (1 - 1) \cdot (0.2) \\ - min {0.3, 0.4} = 1.3 . \end{array}

By direct calculations, we find

\begin{array}{l} {(t d_{T})}_{G_{1} \oplus G_{2}} (a, c) = 0.2 + 0.2 + 0.2 = 0.6, \\ {(t d_{F})}_{G_{1} \oplus G_{2}} (a, c) = 0.4 + 0.5 + 0.4 = 1.3, \\ {(t d_{T})}_{G_{1} \oplus G_{2}} (a, d) = 0.2 + 0.2 + 0.3 = 0.7, \\ {(t d_{F})}_{G_{1} \oplus G_{2}} (a, d) = 0.4 + 0.5 + 0.4 = 1.3, \\ {(t d_{T})}_{G_{1} \oplus G_{2}} (b, c) = 0.2 + 0.2 + 0.2 = 0.6, \\ {(t d_{F})}_{G_{1} \oplus G_{2}} (b, c) = 0.4 + 0.5 + 0.3 = 1.2, \\ {(t d_{T})}_{G_{1} \oplus G_{2}} (b, d) = 0.2 + 0.2 + 0.2 = 0.6, \\ {(t d_{F})}_{G_{1} \oplus G_{2}} (b, d) = 0.4 + 0.5 + 0.4 = 1.3 . \end{array}

It is clear that the total degrees of vertices calculated using the formula and by the direct method are the same.

Definition 3.32. The residue product G₁ • G₂ = (M₁ • M₂, N₁ • N₂) of two vague graphs G₁ = (M₁, N₁) and G₂ = (M₂, N₂) is defined as follows:

\begin{array}{l} (i) (T_{M_{1}} • T_{M_{2}}) ((m_{1}, m_{2})) = max {T_{M_{1}} (m_{1}), T_{M_{2}} (m_{2})}, \\ (F_{M_{1}} • F_{M_{2}}) ((m_{1}, m_{2})) = min {F_{M_{1}} (m_{1}), F_{M_{2}} (m_{2})} \\ \forall (m_{1}, m_{2}) \in (V_{1} \times V_{2}); \end{array}

\begin{array}{l} (ii) (T_{N_{1}} • T_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) = T_{N_{1}} (m_{1} n_{1}), \\ (F_{N_{1}} • F_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) = F_{N_{1}} (m_{1} n_{1}) \\ \forall m_{1} n_{1} \in E_{1}, m_{2} \neq n_{2} . \end{array}

Example 3.33. Consider the vague graphs G₁ and G₂ in Figures 17, 18. The residue product of G₁ and G₂, i.e., G₁ • G₂, is shown in Figure 19.

FIGURE 17

Figure 17. G₁.

FIGURE 18

Figure 18. G₂.

FIGURE 19

Figure 19. G₁ • G₂.

For the vertex (b, e), we find the membership and non-membership values as follows:

\begin{array}{l} (T_{M_{1}} • T_{M_{2}}) ((b, e)) = max {T_{M_{1}} (b), T_{M_{2}} (e)} \\ = max {0.2, 0.2} = 0.2, \\ (F_{M_{1}} • F_{M_{2}}) ((b, e)) = min {F_{M_{1}} (b), F_{M_{2}} (e)} \\ = min {0.7, 0.6} = 0.6 \end{array}

for b ∈ V₁ and e ∈ V₂.

For the edge (a, c)(b, d), we calculate the membership and non-membership values to be

\begin{array}{l} (T_{N_{1}} • T_{N_{2}}) ((a, c) (b, d)) = T_{N_{1}} (a b) = 0.1, \\ (F_{N_{1}} • F_{N_{2}}) ((a, c) (b, d)) = F_{N_{1}} (a b) = 0.8 \end{array}

for ab ∈ E₁ and c ≠ d.

Similarly, we can find the membership and non-membership values for all the remaining vertices and edges.

Proposition 3.34. The residue product of two vague graphs G₁ and G₂ is a vague graph.

Proof: Let G₁ = (M₁, N₁) and G₂ = (M₂, N₂) be two vague graphs on crisp graphs G₁ = (V₁, E₁) and G₂ = (V₂, E₂), respectively, and let ((m₁, m₂)(n₁, n₂)) ∈ E₁ × E₂. If m₁n₁ ∈ E₁ and m₂ ≠ n₂, then

\begin{array}{l} (T_{N_{1}} • T_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) = T_{N_{1}} (m_{1} n_{1}) \\ \leq min {T_{M_{1}} (m_{1}), T_{M_{1}} (n_{1})} \\ \leq max {min {T_{M_{1}} (m_{1}), T_{M_{1}} (n_{1})}, min {T_{M_{2}} (m_{2}), T_{M_{2}} (n_{2})}} \\ = min {max {T_{M_{1}} (m_{1}), T_{M_{1}} (n_{1})}, max {T_{M_{2}} (m_{2}), T_{M_{2}} (n_{2})}} \\ = min {(T_{M_{1}} • T_{M_{2}}) (m_{1}, m_{2}), (T_{M_{1}} • T_{M_{2}}) (n_{1}, n_{2})}, \\ (F_{N_{1}} • F_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) = F_{N_{1}} (m_{1} n_{1}) \\ \geq max {F_{M_{1}} (m_{1}), F_{M_{1}} (n_{1})} \\ \geq min {max {F_{M_{1}} (m_{1}), F_{M_{1}} (n_{1})}, max {F_{M_{2}} (m_{2}), F_{M_{2}} (n_{2})}} \\ = max {min {F_{M_{1}} (m_{1}), F_{M_{1}} (n_{1})}, min {F_{M_{2}} (m_{2}), F_{M_{2}} (n_{2})}} \\ = max {(F_{M_{1}} • F_{M_{2}}) (m_{1}, m_{2}), (F_{M_{1}} • F_{M_{2}}) (n_{1}, n_{2})}, \end{array}

which completes the proof. □

Definition 3.35. Let G₁ = (M₁, N₁) and G₂ = (M₂, N₂) be two vague graphs. For any vertex (m₁, m₂) ∈ V₁ × V₂ we define

\begin{array}{l} {(d_{T})}_{G_{1} • G_{2}} (m_{1}, m_{2}) = \sum_{(m_{1}, m_{2}) (n_{1}, n_{2}) \in E_{1} \times E_{2}} (T_{N_{1}} • T_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) \\ = \sum_{m_{1} n_{1} \in E_{1}, m_{2} \neq n_{2}} T_{N_{1}} (m_{1} n_{1}) \\ = {(d_{T})}_{G_{1}} (m_{1}), \end{array}

\begin{array}{l} {(d_{F})}_{G_{1} • G_{2}} (m_{1}, m_{2}) = \sum_{(m_{1}, m_{2}) (n_{1}, n_{2}) \in E_{1} \times E_{2}} (F_{N_{1}} • F_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) \\ = \sum_{m_{1} n_{1} \in E_{1}, m_{2} \neq n_{2}} F_{N_{1}} (m_{1} n_{1}) \\ = {(d_{F})}_{G_{1}} (m_{1}) . \end{array}

Definition 3.36. Let G₁ = (M₁, N₁) and G₂ = (M₂, N₂) be two vague graphs. For any vertex (m₁, m₂) ∈ V₁ × V₂ we define

\begin{array}{l} {(t d_{T})}_{G_{1} • G_{2}} (m_{1}, m_{2}) = \sum_{(m_{1}, m_{2}) (n_{1}, n_{2}) \in E_{1} \times E_{2}} (T_{N_{1}} • T_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) \\ + (T_{M_{1}} • T_{M_{2}}) (m_{1}, m_{2}) \\ = \sum_{m_{1} n_{1} \in E_{1}, m_{2} \neq n_{2}} T_{N_{1}} (m_{1} n_{1}) + min {T_{M_{1}} (m_{1}), T_{M_{2}} (m_{2})} \\ = \sum_{m_{1} n_{1} \in E_{1}, m_{2} \neq n_{2}} T_{N_{1}} (m_{1} n_{1}) + T_{M_{1}} (m_{1}) + T_{M_{2}} (m_{2}) \\ - max {T_{M_{1}} (m_{1}), T_{M_{2}} (m_{2})} \\ = {(t d_{T})}_{G_{1}} (m_{1}) + T_{M_{2}} (m_{2}) - max {T_{M_{1}} (m_{1}), T_{M_{2}} (m_{2})}, \end{array}

\begin{array}{l} {(t d_{F})}_{G_{1} • G_{2}} (m_{1}, m_{2}) = \sum_{(m_{1}, m_{2}) (n_{1}, n_{2}) \in E_{1} \times E_{2}} (F_{N_{1}} • F_{N_{2}}) ((m_{1}, m_{2}) (n_{1}, n_{2})) \\ + (F_{M_{1}} • F_{M_{2}}) (m_{1}, m_{2}) \\ = \sum_{m_{1} n_{1} \in E_{1}, m_{2} \neq n_{2}} F_{N_{1}} (m_{1} n_{1}) + max {F_{M_{1}} (m_{1}), F_{M_{2}} (m_{2})} \\ = \sum_{m_{1} n_{1} \in E_{1}, m_{2} \neq n_{2}} F_{N_{1}} (m_{1} n_{1}) + F_{M_{1}} (m_{1}) + F_{M_{2}} (m_{2}) \\ - min {F_{M_{1}} (m_{1}), F_{M_{2}} (m_{2})} \\ = {(t d_{F})}_{G_{1}} (m_{1}) + F_{M_{2}} (m_{2}) - min {F_{M_{1}} (m_{1}), F_{M_{2}} (m_{2})} . \end{array}

Example 3.37. In this example we find the degree and total degree of the vertex (b, e) in Example 3.33:

\begin{array}{l} {(d_{T})}_{G_{1} • G_{2}} (b, e) = {(d_{T})}_{G_{1}} (b) \\ = 0.1 + 0.1 = 0.2, \\ {(d_{F})}_{G_{1} • G_{2}} (b, e) = {(d_{F})}_{G_{1}} (b) \\ = 0.8 + 0.8 = 1.6 . \end{array}

Therefore,

{(d)}_{G_{1} • G_{2}} (b, e) = (0.2, 1.6) .

The total degree of (b, e) is given by

\begin{array}{l} {(t d_{T})}_{G_{1} • G_{2}} (b, e) = {(t d_{T})}_{G_{1}} (b) + T_{M_{2}} (e) - max {T_{M_{1}} (b), T_{M_{2}} (e)} \\ = (0.2 + 0.2) + 0.2 - max (0.2, 0.2) \\ = 0.4, \\ {(t d_{F})}_{G_{1} • G_{2}} (b, e) = {(t d_{F})}_{G_{1}} (b) + F_{M_{2}} (e) - min {F_{M_{1}} (b), F_{M_{2}} (e)} \\ = (0.8 + 0.8) + 0.6 - min (0.7, 0.6) \\ = 1.6 . \end{array}

Therefore,

\begin{array}{l} {(t d)}_{G_{1} • G_{2}} (b, e) = (0.4, 1.6) . \end{array}

Similarly, we can find the degree and total degree of all vertices in G₁ • G₂.

4. Application of Vague Sets to Medical Diagnosis

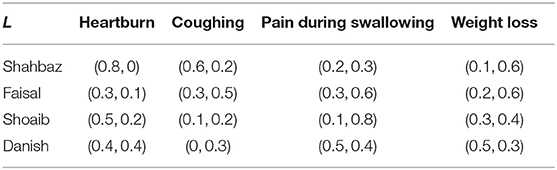
Following the approach outlined by De et al. [18], we will apply vague sets to medical diagnosis by using a max-min-max composition in terms of vague relations. First, we use vague sets to define the disease symptoms. Then, we describe medical knowledge in terms of vague relations. Finally, we determine a diagnosis on the basis of vague relations. Consider four patients named Shahbaz, Shoaib, Faisal, and Danish, and define the set of patients P = {Shahbaz, Shoaib, Faisal, Danish}. Let the set of symptoms under consideration be S = {heartburn, coughing, pain during swallowing, weight loss}. A vague relation L is available from set P to set S, and this is summarized in Table 1.

TABLE 1

Table 1. The vague relation L(P → S).

Cancer is a group of dangerous and prevalent diseases, and represents one of humankind's greatest medical challenges. Many people are diagnosed with late-stage cancer that is difficult or impossible to treat because of a lack of awareness of the disease symptoms. Mathematical models involving vague sets can be used to determine the most likely diagnosis given a set of symptoms that a patient presents with.

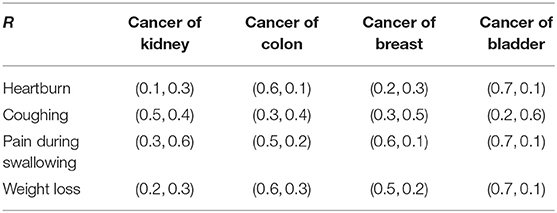
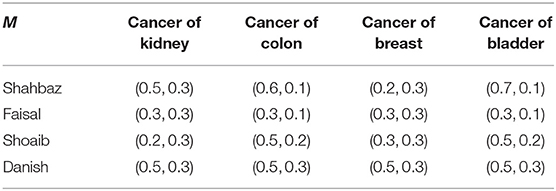
There are many different types of cancers; here we focus on a few of the more life-threatening kinds: (1) kidney cancer, (2) colon cancer, (3) breast cancer, and (4) bladder cancer. We define the set of diagnoses to be D = {cancer of kidney, cancer of colon, cancer of breast, cancer of bladder}. The vague relation R(S → D) from the set of symptoms to the set of diagnoses is given in Table 2. The composition M(P → D) of the vague relations L and R is shown in Table 3; it gives the diagnosis for each patient via the formulas

\begin{array}{l} T_{M} (p_{i}, d_{k}) = \underset{s \in S}{\lor} [T_{L} (p_{i}, s) \land T_{R} (s, d_{k})], \\ F_{M} (p_{i}, d_{k}) = \underset{s \in S}{\land} [F_{L} (p_{i}, s) \lor F_{R} (s, d_{k})], \end{array}

where p_i denotes the patients, d_k denotes the different diagnoses, ∧ = min, and ∨ = max.

TABLE 2

Table 2. The vague relation R(S → D).

TABLE 3

Table 3. The composition M(P → D) of vague relations L and R.

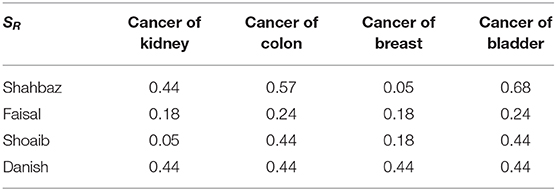
Shown in Table 4 is S_R, the best version of diagnosis for this set of patients, which is determined by the formula S_R = T_R − F_Rπ_R. It is very important because the max-min-max rule alone fails to provide exact information.

TABLE 4

Table 4. S_R, the best version of R determined by the formula S_R = T_R − F_Rπ_R.

5. Conclusion

Compared with fuzzy models, vague models offer greater compatibility and flexibility. A vague graph is a type of extension of a fuzzy graph, and is used widely in the field of computer science. We have defined four new operations of a vague graph, called the maximal product, rejection, symmetric difference, and residue product. We have discussed their properties and provided examples on finding the degree of a vertex and the total degree of vertices of graphs that meet specific conditions. We have formulated and proved theorems for these graphs by using the concept of degree of a vertex and total degree of a vertex of a graph. Furthermore, we have presented an application of vague sets to the medical diagnosis of four types of cancer. In future work we will explore further properties relating to vague graphs and bipolar vague graphs.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Funding

This work was supported by the National Key R&D Program of China (grant no. 2019YFA0706402), the Natural Science Foundation of Guangdong Province (grant no. 2018A0303130115), and the Guangzhou Academician and Expert Workstation (no. 20200115-9).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Zadeh L. Fuzzy sets. Inform Control. (1965) 8:338–53.

Google Scholar

2. Rosenfeld A. Fuzzy graphs. In: Zadeh LA, Fu KS, Shimura M, , editors. Fuzzy Sets and Their Application. New York, NY: Academic Press (2006). p. 77–95.

Google Scholar

3. Bhattacharya P. Some remarks on fuzzy graphs. Pattern Recogn Lett. (1987) 6:297–302.

Google Scholar

4. Bhattacharya P, Suraweera F. An Algorithm to compute the max-min powers and a property of fuzzy graphs. Pattern Recogn Lett. (1991) 12:413–20.

Google Scholar

5. Nagoor Gani A, Latha SR. On irregular fuzzy graphs. Appl Math Sci. (2012) 6:517–23.

Google Scholar

6. Nagoor Gani A, Basheer Ahamed M. Order and size in fuzzy graphs. Bull Pure Appl Sci. (2003) 22:145–8.

Google Scholar

7. Gau WL, Buehrer DJ. Vague sets. IEEE Trans Syst Man Cybernet. (1993) 23:610–4.

Google Scholar

8. Ramakrishna N. Vague graphs. Int J Comput Cogn. (2009) 7:51–8.

9. Borzooei RA, Rashmanlou H. New concepts of vague graphs. Int J Mach Learn Cybernet. (2015) 8:1081–92. doi: 10.1007/s13042-015-0475-x

CrossRef Full Text | Google Scholar

10. Rashmanlou H, Borzooei RA. Product vague graphs and its applications. J Intell Fuzzy Syst. (2016) 30:371–82. doi: 10.3233/IFS-151762

CrossRef Full Text | Google Scholar

11. Boorzooei RA, Rashmanlou H, Samanta S, Pal M. Regularity of vague graphs. J Intell Fuzzy Syst. (2016) 30:3681–9. doi: 10.3233/IFS-162114

CrossRef Full Text | Google Scholar

12. Borzooei RA, Rashmanlou H, Samanta S, Pal M. New concepts of vague competition graphs. J Intell Fuzzy Syst. (2016) 31:69–75. doi: 10.3233/IFS-162121

CrossRef Full Text | Google Scholar

13. Kumar K, Lavanya S, Broumi S, Rashmanlou H. New concepts of coloring in vague graphs with application. J Intell Fuzzy Syst. (2017) 33:1715–21. doi: 10.3233/JIFS-17489

CrossRef Full Text | Google Scholar

14. Atanassov K. Intuitionistic fuzzy sets. Fuzzy Sets Syst. (1986) 20:87–96.

Google Scholar

15. Parvathi R, Karunambigai MG. Intuitionistic fuzzy graphs, computational intelligence, theory and applications. In: International Conference in Germany. Berlin (2006). p. 18–20.

16. Devi M, Ameenal Bibi K, Rashmanlou H. New concepts in intuitionistic fuzzy labeling graphs. Int J Adv Intell Paradigms. (2020).

Google Scholar

17. Berge C. Graphs and Hyper Graphs. Amsterdam: North-Holland Publishing Company (1973).

Google Scholar

18. De SK, Biswas R, Roy AR. An application of intuitionistic fuzzy sets in medical diagnosis. Fuzzy Sets Syst. (2001) 117:209–13. doi: 10.1016/S0165-0114(98)00235-8

CrossRef Full Text | Google Scholar

Keywords: vague set, maximal product, rejection, symmetric difference, residue product, application

Citation: Shao Z, Kosari S, Shoaib M and Rashmanlou H (2020) Certain Concepts of Vague Graphs With Applications to Medical Diagnosis. Front. Phys. 8:357. doi: 10.3389/fphy.2020.00357

Received: 17 May 2020; Accepted: 27 July 2020;
Published: 11 November 2020.

Edited by:

Muhammad Javaid, University of Management and Technology, Pakistan

Reviewed by:

Anouar Ben Mabrouk, University of Kairouan, Tunisia
Ndolane Sene, Cheikh Anta Diop University, Senegal

Copyright © 2020 Shao, Kosari, Shoaib and Rashmanlou. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.

*Correspondence: Saeed Kosari, c2FlZWRrb3NhcmkzOCYjeDAwMDQwO3lhaG9vLmNvbQ==

Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.