ESERK Methods to Numerically Solve Nonlinear Parabolic PDEs in Complex Geometries: Using Right Triangles

In this paper Extrapolated Stabilized Explicit Runge-Kutta methods (ESERK) are proposed to solve nonlinear partial differential equations (PDEs) in right triangles. These algorithms evaluate more times the function than a standard explicit Runge–Kutta scheme (n_t times per step), and these extra evaluations do not increase the order of convergence but the stability region grows with ${O}(n_t^2)$. Hence, the total computational cost is ${O}(n_t)$ times lower than with a traditional explicit algorithm. Thus, these algorithms have been traditionally considered to solve stiff PDEs in squares/rectangles or cubes. In this paper, for the first time, ESERK methods are considered in a right triangle. It is demonstrated that such type of codes keep the convergence and the stability properties under certain conditions. This new approach would allow to solve nonlinear parabolic PDEs with stabilized explicit Runge–Kutta schemes in complex domains, that would be decomposed in rectangles and right triangles.

1. Introduction

Let us suppose that we have to solve a nonlinear PDE with dominating diffusion:

$\begin{array}{ll}{u}_t=d(u_{\bar{x}\bar{x}}+u_{ȳȳ})+f(t,\bar{x},ȳ,u)(\bar{x},ȳ)\in \Omega \subset {ℝ}^2,& (1)\end{array}$

subject to traditional initial and Dirichlet boundary conditions:

$\begin{array}{ll}u(0,\bar{x},ȳ)=g_1(\bar{x},ȳ)(\bar{x},ȳ)\in \Omega ,& (2)\end{array}$

and

$\begin{array}{ll}u(t,\bar{x},ȳ)=g_2(\bar{x},ȳ)(\bar{x},ȳ)\in \partial (\Omega ).& (3)\end{array}$

These types of problems are very common in a large amount of areas such as atmospheric phenomena, biology, chemical reactions, combustion, financial mathematics, industrial engineering, laser modeling, malware propagation, medicine, mechanics, molecular dynamics, nuclear kinetics, etc., see [1–9], to mention a few.

A widely-used approach for solving these time-dependent and multi-dimensional PDEs is to first discretize the space variables (with finite difference or spectral methods) to obtain a very large system of ODEs of the form

$\begin{array}{ll}{y}^{\prime }=f(t,y);y(t_0)=y_0;& (4)\end{array}$

where $y,y_0\in {ℝ}^n$, t ≥ t₀, and f(t, y) takes value in ℝⁿ, this procedure is well-known as the method of lines (MOL). But these systems of ODEs not only have a huge dimension, additionally they might become very stiff problems.

Hence, traditional explicit methods are usually very slow, due to absolute stability, it is necessary to use very small length steps, see [6, 7] and references therein. Therefore, these schemes are not usually considered.

Implicit schemes based on BDF and Runge–Kutta methods have much better stability properties. However, since the dimension of the ODE system is very high, then it is necessary to solve very large nonlinear systems at each iteration.

Other numerous techniques have also been proposed based on ETD schemes (but it is necessary to approximate operators including matrix exponentials), alternating direction implicit methods (they have limitations on the order of convergence) and explicit-implicit algorithms. However, in any case the number of operations is huge when the system dimension is high.

For those cases where it is known that the Jacobian eigenvalues of the function are all real negative or are very close to this semi-axis, there is another option: stabilized explicit Runge–Kutta methods (they are also called Runge-Kutta-Chebyshev methods). This happens, for example, when diffusion dominates in the PDE, when the Laplacian is discretized using finite differences or some spectral techniques, then the associated matrix has this type of eigenvalues.

These types of algorithms are totally explicit, but they have regions of stability extended along the real negative axis. These schemes typically have order 2 or 4 [8, 10–16]. Recently, we propose a new procedure combined with Richardson extrapolation to obtain methods with other orders of convergence [17, 18], but in all these methods, these integrators have many more stages than the order of convergence. Most of these extra stages seek to extend as much as possible the region of stability along the negative real axis. Regions of stability increase quadratically with the number of stages. Thus, the cost per step is greater than in a classic Runge–Kutta, because it is necessary to evaluate the function in Equation (4) n_t times. However, the number of steps reduce proportionally with $n_t^2$, thus the total computational cost is reduced proportionally with n_t.

These schemes have been traditionally considered in squares/rectangles or cubes. But this makes difficult to apply them in PDEs with complex geometries, which happens in most of the cases. Some different strategies have been proposed to apply them when the original domain is not a square nor a cube (see [3–5]). They implemented stabilized Runge–Kutta methods after using adaptive multiresolution techniques or fixed mesh codes in space. But simulations in complex geometries constitute a very challenging problem, see (section 4, [5]), where they stated for their results based on adaptive multiresolution techniques that they “will only present here 2D and 3D simulations in simplified geometries for the sake of assessing our results and perspectives in the field.”

As far as we know, stabilized explicit Runge–Kutta methods have not been tested in triangles yet. For this reason, in this paper, we are analysing how ESERK methods can be employed to solve nonlinear PDEs in these types of regions and their convergence.

In this paper, a summary on ESERK4 methods is provided in section 2. The major advance of our contribution is given in section 3: it is explained how ESERK4 can be utilized for (1) when Ω is a right triangle. After some linear transformations and spatial discretizations ESERK4 is numerically stable and fourth-order convergence in time, and second-order in space is obtained. This allows a new way to numerically approach parabolic nonlinear PDEs in complex domains in the plane, which can be easier decomposed in a sum of triangles and rectangles. Finally, some conclusions and future goals are outlined.

2. ESERK4 Methods

2.1. Construction of First-Order Stabilized Explicit Methods

In [17], ESERK4 schemes were developed for nonlinear PDEs in several dimensions with good stability properties and numerical results in squares and cubes. The idea is quite simple: first-order stabilized explicit Runge–Kutta (SERK) methods are derived using Chebyshev polynomials of the first kind:

$\begin{array}{ll}{T}_0(x)=1,T_1(x)=x,T_s(x)=2x{T}_{s-1}(x)-T_{s-2}(x),& (5)\end{array}$

s being the number of stages of the first-order method.

If we consider

$\begin{array}{ll}{R}_s(z)=\frac{T_s(w_{0,s}+w_{1,s}z)}{T_s(w_{0,s})},w_{0,s}=1+\frac{{\mu }_4}{s^2},w_{1,s}=\frac{T_s(w_{0,s})}{T_s^{\prime }(w_{0,s})},& (6)\end{array}$

then |R_s(z)| oscillates between −λ₄ and λ₄ (for a value 0 < λ₄ = 0.311688 < 1 that we will calculate later) in a region which is O(s²), and $R_s(z)=1+z+O(z^2)$.

We can construct Runge–Kutta schemes with |R_s(z)| as stability functions by just changing $x=1+{\alpha }_p\bar{x}$ (and considering that 1, T_s(x) and $\bar{x}$ are the stability functions of Identity operator, g_s, and hf(·), and writing R_s(z) as a linear combination of the Chebyshev polynomials, see Theorem 1 [12] for more details).

2.2. Construction of Higher-Order ESERK Schemes

Once first-order SERK methods have been derived, they approximate the solution of the initial value problem (4), by performing n_i steps with constant step size h_i at x₀ + h, i.e., y_hi(x₀ + h): = S_{i, 1}, with step sizes h₁ > h₂ > h₃ > … (taking h_i = h/n_i, n_i = 1, …, 4).

Finally

$\begin{array}{l}{S}_{4,4}=\frac{-S_{1,1}+24S_{2,1}-81S_{3,1}+64S_{4,1}}{6}=\\ =\frac{64y_{h/4}(x_0+h)-81y_{h/3}(x_0+h)+24y_{h/2}(x_0+h)-y_h(x_0+h)}{6}& (7)\end{array}$

is a fourth-order approximation with

$\begin{array}{ll}\begin{array}{c}{P}_{4s}(z)=\\ \frac{-R_s(z)+24{(R_s(z/2))}^2-81{(R_s(z/3))}^3+64{(R_s(z/4))}^4}{6}.\end{array}& (8)\end{array}$

as its stability function. Additionally, we have that

$|P_{4s}(z)|\le \frac{|R_s(z)|+24|R_s(z/2){|}^2+81|R_s(z/3){|}^3+64|R_s(z/4){|}^4}{6}.$

The positive real solution of

$\frac{x+24x^2+81x^3+64x^4}{6}=0.95$

is λ₄ = 0.311688. Hence, whenever |R_s(z)| < 0.311688, then |P_4s(z)| < 0.95. Taking ${\mu }_4=\frac{27}{16}$, it can be checked numerically that |R_{s, 4}(z)| ≤ 0.311688 for z ∈ [−s², −1] and 9 ≤ s ≤ 4000, and therefore the ESERK4 methods derived in this way are fourth-order approximations and numerically stable in a region including [−s², 0].

2.3. Parallel, Variable-Step, and Number of Stages Algorithm

In [17], we constructed a variable-step and number of stages algorithm combining all the schemes derived there, with s up to 4,000. The idea is quite simple: (i) First, we select the step size in order to control the local error; the best results were obtained using techniques considered for standard extrapolation methods (see Equations (8–11) in [17]). (ii) Later the minimum s is chosen so that the absolute stability is satisfied.

Recently, we are working developing the parallel version of this code (see [19]). Using 4 threads, CPU times are up to 2.5 times smaller than in the previous sequential algorithm. The new parallel code also has a decreasing memory demand, and therefore it is possible to solve problems with higher dimension in regular PCs.

3. Decomposition of Complex Geometries Into Right Triangles

Complex geometric shapes are ubiquitous in our natural environment. In this paper, we are interested in numerically solving partial differential equations (PDEs) in such types of geometries, which are very common in problems related with human bodies, materials, or simply a complicated engine in classical engineering applications.

One very well-known strategy, within a finite element context, is to build the necessary modifications in the vicinity of the boundary. Such an approach is studied in the composite finite element method (FEM). Those methods based on finite element are usually proposed only for linear PDEs. FEM is a numerical method for solving problems of engineering and mathematical physics (typical problems include structural analysis, heat transfer, fluid flow, mass transport, or electromagnetic potential, because these problems generally require numerically approximating the solution of linear partial differential equations). The finite element method allows the transformation of the problem in a system of algebraic equations. Unfortunately, it is more difficult to employ these techniques with nonlinear parabolic PDEs in several dimensions, although some results have been obtained to know when the resulting discrete Galerkin equations have a unique solution in [20]. However, for some problems, some of these techniques are not easy to be employed numerically, they are computationally very expensive because they require solving nonlinear systems with huge dimension at every step, or it is difficult to demonstrate that the numerical schemes have unique solution in a general case.

On the other hand, Implicit–Explicit (IMEX) methods have been employed to solve a very stiff nonlinear system of ODEs coming from the spatial discretization of nonlinear parabolic PDEs that appeared in the modelization of an ischemic stroke in [5]. The authors employed an adaptive multiresolution approach and a finite volume strategy for the spatial discretizations. And a Strang splitting method in time, combining ROCK4, an explicit Stalized Explicit Runge–Kutta scheme for the diffusion part, and Radau5, an implicit A-stable method for the reaction. These methods were previously analyzed in [3] for streamer discharge simulations, and the authors demonstrated second-order convergence in time. Later, they employed similar strategies for different physical problems in [4, 21]. As the authors state, some of these procedures are complicated except in simple domains like squares and cubes, and only second-order convergence in time is possible. However, there are complex problems where nonlinear terms have potentially large stiffness, and at the same time, it is necessary to efficiently solve the model with small errors. This motivates to derive high-order schemes with good internal stability properties.

In what follows we will explain a new strategy to numerically solve the nonlinear parabolic PDE given by Equation (1) where Ω is any right triangle, and therefore any researcher can combine the theory (utilized with FEM) to spatially decomposed any complex geometry into triangles (since any acute triangle and obtuse triangle can be decomposed into two right triangles), and later employing the method described in this paper. Additionally, schemes proposed in this work are fourth-order ODE solvers (in time), and numerical spatial approximations will be second-order (although fourth-order formulae can be explored except for the closest points to vertices).

3.1. Higher-Order Spatial Approximations in the Triangle

Without loss of generality we can consider that our right triangle is T_R, the one with vertices (0, 1), (0, 0), (1, 0). Otherwise we first use a linear transformation of the right triangle with vertices $P_1=({\bar{x}}_1,{ȳ}_1)$, $P_0=({\bar{x}}_0,{ȳ}_0)$, $P_2=({\bar{x}}_2,{ȳ}_2)$ [where $({\bar{x}}_0,{ȳ}_0)$ is the vertex of the right angle]:

$\begin{array}{ll}(x,y)=L(\bar{x},ȳ)=(a_1(\bar{x}-{\bar{x}}_0)+a_2(ȳ-{ȳ}_0),b_1(\bar{x}-{\bar{x}}_0)+b_2(ȳ-{ȳ}_0)),& (9)\end{array}$

where the parameters a₁, a₂, b₁, b₂ can be computed easily as

$\begin{array}{ll}\begin{array}{c}{a}_1=\frac{{ȳ}_2-{ȳ}_0}{\text{Det}},a_2=\frac{{\bar{x}}_0-{\bar{x}}_2}{\text{Det}},\\ b_1=\frac{{ȳ}_0-{ȳ}_1}{\text{Det}},a_2=\frac{{\bar{x}}_0-{\bar{x}}_1}{\text{Det}},\end{array}& (10)\end{array}$

where

$\begin{array}{ll}\text{Det}=\left|\begin{array}{ccc}1& 1& 1\\ {\bar{x}}_0& {\bar{x}}_1& {\bar{x}}_2\\ {ȳ}_0& {ȳ}_1& {ȳ}_2\end{array}\right|& (11)\end{array}$

and it is easy to check that Det ≠ 0 if and only the three points are not in a line (but we always have a triangle).

The main reason of decomposing our general region Ω∈R² into right triangles (and not other triangles) is, that after this linear transformation given by Equations (9) and (10), our PDE given by Equation (1) transforms into the Equation

$\begin{array}{ll}{u}_t=c_1{u}_{xx}+c_2{u}_{yy}+f(t,x,y,u)(x,y)\in T_R,& (12)\end{array}$

subject to (traditional) initial and Dirichlet boundary conditions. Therefore, let us first study Equation (12), together with

$\begin{array}{ll}u(0,x,y)=g_1(x,y)(x,y)\in T_R,& (13)\end{array}$

and

$\begin{array}{ll}u(t,x,y)=g_2(x,y)(x,y)\in \partial (T_R),& (14)\end{array}$

where ∂(T_R) is the border of the triangle with vertices (0, 1), (0, 0), (1, 0). One positive issue is that, after the traditional spatial discretization described below, the matrix obtained from the diffusion term has all the eigenvalues real, and therefore we can utilize the ESERK methods proposed in the previous section 2.

Now, let us define the spatial discretization of our continuous problem provided by Equation (12), the problem domain T_R is discretized by the grid points (x_i, y_j), where

$\begin{array}{l}{x}_i=i·h,i=0,1,\dots ,N,N=\frac{1}{h},y_j=j·h,\\ j=0,1,\dots ,N-i,h=\Delta x=\Delta y,& (15)\end{array}$

since x_i+y_j ≤ 1.

With this semidiscretizations we will approximate u_xx and u_yy at point (x_i, y_j) with the following second-order formulae:

$\begin{array}{ll}\frac{{\partial }^2{u}_{i,j}}{\partial x^2}=\frac{u_{i+1,j}-2u_{i,j}+u_{i-1,j}}{h^2},\frac{{\partial }^2{u}_{i,j}}{\partial y^2}=\frac{u_{i,j+1}-2u_{i,j}+u_{i,j-1}}{h^2}.& (16)\end{array}$

After the linear transformation given by Equations (9) and (10), our PDE given by Equation (1) may transform into one Equation where one term in u_xy would appear. Normally, this term can be approximated in the square or the rectangle through the formula

$\begin{array}{l}\frac{{\partial }^2{u}_{i,j}}{\partial x\partial y}\\ =\frac{u_{i+1,j+1}-u_{i,j+1}-u_{i+1,j}+2u_{i,j}-u_{i-1,j}-u_{i,j-1}+u_{i-1,j-1}}{2h^2},& (17)\end{array}$

however, in T_R, we can obtain that the point (x_i, y_j) is in T_R, i.e., x_i + y_j < 1, but the point (x_{i + 1}, y_{j + 1}) might not satisfy that x_{i + 1} + y_{j + 1} ≤ 1, and therefore we cannot employ these finite difference formulae if a term in u_xy appears. Fortunately, we will check that this term cancels after this transformation [given by Equations (9 and 10)] whenever the original triangle with vertices $({\bar{x}}_1,{ȳ}_1),({\bar{x}}_0,{ȳ}_0),\text{and }({\bar{x}}_2,{ȳ}_2)$ is a right triangle and $({\bar{x}}_0,{ȳ}_0)$ is the vertex of the right angle. This fact is explained in Figure 1. If we would need to approximate $\frac{{\partial }^2{u}_{2,1}}{\partial x\partial y}$, then it would be necessary to obtain an approximation of u_{3, 2}, but this point is outside of the T_R, the region of study.

FIGURE 1

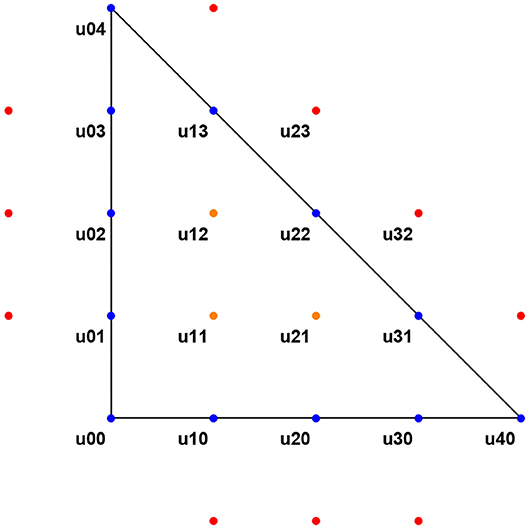
Figure 1. Spatial discretization in the right triangle T_R. We need to approximate partial derivatives of u in the interior (orange points), and therefore we have obtained in the previous steps approximations of the function in the interior, and the points in the border (blue points), but we do not have these values outside of T_R (red points).

In this work, we are employing only second-order approximations in space. In other works, for example [13], we have also employed SERK codes after higher-order discretizations in space, but in rectangles. Normally, in rectangles, we can use formulae similar to

$\begin{array}{l}\frac{{\partial }^2{u}_{i,j}}{\partial x^2}=\frac{-u_{i+2,j}+16u_{i+1,j}-30u_{i,j}+16u_{i-1,j}-u_{i-2,j}}{12h^2},\\ i=2,\dots ,N-2,& (18)\end{array}$

and in the lower edge

$\begin{array}{ll}\frac{{\partial }^2{u}_{1,j}}{\partial x^2}=\frac{10u_{0,j}-15u_{1,j}-4u_{2,j}+14u_{3,j}-6u_{4,j}+u_{5,j}}{12h^2}.& (19)\end{array}$

However, in the triangle, again we can observe in Figure 1, that we would need to approximate the solution in points outside T_R before we can calculate (19) near the vertex (0, 1). Obviously, one possible idea for the future is considering the decomposition of complex regions into bigger rectangles in the interior, and small right triangles near the border of the complex region where it is necessary to solve the PDE.

Now, we are ready to understand why we chose right triangles in the decomposition of complex regions. The main reason is, that simple calculations give us [after linear transformations given by Equations (9–11)]:

$\begin{array}{l}{u}_{\bar{x}\bar{x}}+u_{ȳȳ}=a_1(a_1{u}_{xx}+b_1{u}_{xy})+b_1(a_1{u}_{xy}+b_1{u}_{yy})\\ +a_2(a_2{u}_{xx}+b_2{u}_{xy})+b_2(a_2{u}_{xy}+b_2{u}_{yy}),& (20)\end{array}$

and therefore, after this linear transformation, $u_{\bar{x}\bar{x}}+u_{ȳȳ}$ has the following term in u_xy

$\begin{array}{ll}(2a_1{b}_1+2a_2{b}_2)u_{xy}.& (21)\end{array}$

If we change a₁, a₂, b₁, and b₂ for their values given by Equation (10)

$\begin{array}{ll}{a}_1{b}_1+a_2{b}_2=\frac{{ȳ}_2-{ȳ}_0}{Det}\frac{{\bar{x}}_0-{\bar{x}}_2}{Det}+\frac{{ȳ}_0-{ȳ}_1}{Det}\frac{{\bar{x}}_0-{\bar{x}}_1}{Det}& (22)\end{array}$

which is 0 if and only if the vectors $\overrightarrow{P_2{P}_0}$ and $\overrightarrow{P_0{P}_1}$ are orthogonal, i.e., if they form a right angle at P₀.

Thus, if the original triangle has a right angle at P₀, there is not a term in u_xy, and we can use the second-order approximations in space, with the spatial discretization described above. Additionally, the following theorem guarantee that ESERK methods can be employed (with numerical stability and good results) in this right triangle to solve the PDE given by Equations (1)–(3) after the linear transformation given by Equations (9)–(11) and the spatial discretization given by Equation (15):

Theorem: Let Equations (1)–(3) be the PDE to be solved, and Ω a right triangle with a right angle at P₀. After linear transformation given by Equations (9) and (10), this PDE transforms into Equations (12)–(14), which can be discretized by Equations (15) and (16), transforming into the system of ODEs

$\begin{array}{ll}{\left(\begin{array}{c}{u}_{11}\\ u_{21}\\ ⋮\\ u_{N-21}\\ u_{12}\\ ⋮\\ u_{N-32}\\ ⋮\\ u_{1N-2}\end{array}\right)}^{\prime }=A\left(\begin{array}{c}{u}_{11}\\ u_{21}\\ ⋮\\ u_{N-21}\\ u_{12}\\ ⋮\\ u_{N-32}\\ ⋮\\ u_{1N-2}\end{array}\right)+\left(\begin{array}{c}F\left(t,x_1,y_1,u_{11}\right)\\ F\left(t,x_2,y_1,u_{21}\right)\\ ⋮\\ F\left(t,x_{N-2},y_1,u_{N-21}\right)\\ F\left(t,x_1,y_2,u_{12}\right)\\ ⋮\\ F\left(t,x_{N-3},y_2,u_{N-32}\right)\\ ⋮\\ F\left(t,x_1,y_{N-2},u_{1N-2}\right)\end{array}\right),& (23)\end{array}$

F(t, x_i, y_j, u_ij) being the sum of f(t, x, y, u) at the grid points plus the function given by the spatial discretization of the derivatives at the boundary.

The associate matrix, A, to the terms c₁u_xx + c₂u_yy (with c₁, c₂ ≥ 0) is real and symmetric, and therefore all the eigenvalues of this matrix are negative and real. Hence, Extrapolated Stabilized Explicit Runge–Kutta are numerically stable whenever ∂_u[F(t, x, y, u)] does not modify this type of eigenvalues (real and negative) in the Jacobian function and $s>\sqrt{4\Delta t(\mu +\sigma )}$ (μ being $\frac{c_1}{h^2}$ and $\sigma =\frac{c_2}{h^2}$). Therefore, ESERK4 methods can solve Equations (1)–(3) with a fourth-order convergence in time, and second in space.

Proof: It only remains to study the associate matrix A.

But simple calculations allow us to obtain that

$\begin{array}{ll}A=\left(\begin{array}{cccccc}{B}_{N-2}& C_{N-2,N-3}& 0_{N-2,N-4}& \dots & 0_{N-2,2}& 0_{N-2,1}\\ C_{N-2,N-3}^t& B_{N-3}& C_{N-3,N-4}& \dots & 0_{N-3,2}& 0_{N-2,1}\\ 0_{N-4,N-2}& C_{N-3,N-4}^t& B_{N-4}& \ddots & ⋮& ⋮\\ ⋮& ⋮& \ddots & \ddots & \ddots & \ddots \\ 0_{2,N-2}& 0_{2,N-3}& \dots & \dots & B_2& C_{2,1}\\ 0_{1,N-2}& 0_{1,N-3}& \dots & \dots & C_{2,1}^t& B_1\end{array}\right),& (24)\end{array}$

where B_i is the square matrix with dimension i

$\begin{array}{ll}{B}_i=\left(\begin{array}{ccccc}-2\mu -2\sigma & \mu & 0& \dots & 0\\ \mu & -2\mu -2\sigma & \mu & \ddots & 0\\ 0& \mu & -2\mu -2\sigma & \ddots & ⋮\\ ⋮& \ddots & \ddots & \ddots & \mu \\ 0& 0& \dots & \mu & -2\mu -2\sigma \end{array}\right),& (25)\end{array}$

$C_{i+1,i}=\left(\begin{array}{c}\sigma {\text{Id}}_i\\ 0_{i,1}\end{array}\right),$

0_{i, j} is the i × j matrix with all the values equal 0, Id_i is the identity matrix of dimension i, $\mu =\frac{c_1}{h^2}$ and $\sigma =\frac{c_2}{h^2}$, and therefore A is a symmetric real matrix.

Finally, it is well-known that all the eigenvalues of any symmetric real matrix A are real. Let us suppose that (λ, v) is a complex pair of A, i.e., an eigenvector v = x+ yi ∈ℂⁿ, where x, y ∈ ℝⁿ and λ = a + bi ∈ ℂ is the corresponding eigenvalue with a, b ∈ ℝ. Therefore,

$\begin{array}{ll}Ax+iAy=Av=\lambda v=(ax-by)+i(bx+ay).& (26)\end{array}$

Hence, equalizing real and imaginary parts, we have

$\begin{array}{ll}Ax=(ax-by),Ay=(bx+ay),& (27)\end{array}$

and therefore

$\begin{array}{ll}Ax·y=a(x·y)-b\left|\right|y|{|}^2,x·Ay=b|\left|x\right|{|}^2+a(x·y).& (28)\end{array}$

In this way we can conclude that

$\begin{array}{ll}0=x·Ay-Ax·y=b(||x|{|}^2+||y|{|}^2),& (29)\end{array}$

and, since ||x||²+||y||²≠0, then b = 0 and λ = a∈ℝ

Additionally, since σ, μ ≥ 0, the Gershgoring theorem guarantees for all the eigenvalues of A that 4(μ + σ) ≤ λ_i ≤ 0.

Therefore, whenever the nonlinear part does not modify this type of eigenvalues (real and negative) in the Jacobian function, a bound of the spectral radius of the Jacobian is 4(μ+σ), and we merely need to use an ESERK method with $s>\sqrt{4\Delta t(\mu +\sigma )}$ to guarantee numerical stability.

4. Numerical Example

Let us now study the numerical behavior of ESERK methods in a right triangle with one example. We will consider

$\begin{array}{ll}{u}_t=\frac{5}{{\pi }^2}(u_{\bar{x}\bar{x}}+u_{ȳȳ})+{(1-u)}^3+f(t,\bar{x},ȳ)(\bar{x},ȳ)\in \Omega \subset {ℝ}^2,& (30)\end{array}$

where

$f(t,\bar{x},ȳ)=e^{-3t}{\left(sin\left(\frac{\pi \left(ȳ-2\bar{x}-3\right)}{5}\right)-e^t\right)}^3,$

Ω is the triangle with vertices (−1, 1), (−3, 2), and (0, 3) and initial and boundary conditions are taken such that $u(t,\bar{x},ȳ)=e^{-t}sin\left(\frac{\pi (ȳ-2\bar{x}-3)}{5}\right)$ is its solution.

Hence, we first consider the linear transformation given by Equations (9) and (10), i.e., a₁ = −2/5, a₂ = 1/5, b₁ = 1/5, b₂ = 2/5. In this way Equation (30) transforms into the Equation

$\begin{array}{ll}{u}_t=\frac{1}{{\pi }^2}(u_{xx}+u_{yy})+{(1-u)}^3+f(t,x,y)(x,y)\in T_R,& (31)\end{array}$

where

$f(t,x,y)=e^{-3t}{(sin(\pi x)-e^t)}^3,$

and initial and boundary conditions are taken such that u(t, x, y) = e^−tsin(πx) is its solution.

Now, it is possible to utilize second-order approximations in space, as it was explained in the previous section. ESERK4 with s = 100 and 150 where considered for this numerical experiment with different values of h = Δx = Δy and k = Δt. Numerical convergence at several points was analyzed with both methods, and numerical errors at two points [p₁ = (t, x, y) = (1, 0.15, 0.15) and p₂ = (t, x, y) = (1, 0.5, 0.25)] are shown in Tables 1, 2.

TABLE 1

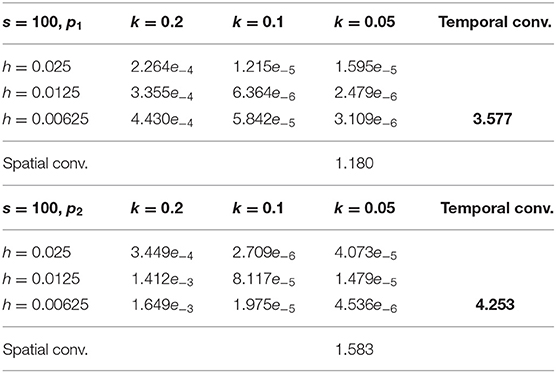
Table 1. Analysis of the numerical convergence at points p₁ = (t, x, y) = (1, 0.15, 0.15) (top) and p₂ = (t, x, y) = (1, 0.5, 0.25) (bottom) for the ESERK4 algorithm with s = 100 with k = Δt = 0.2, 0.1 and 0.05, and h = Δx = Δy = 0.025, 0.0125, and 0.00625.

TABLE 2

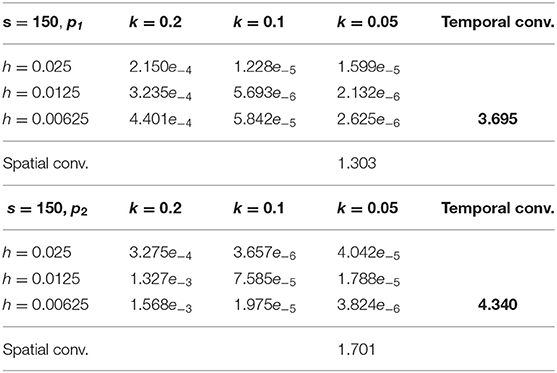
Table 2. Analysis of the numerical convergence at points p₁ = (t, x, y) = (1, 0.15, 0.15) (top) and p₂ = (t, x, y) = (1, 0.5, 0.25) (bottom) for the ESERK4 algorithm with s = 150 with k = Δt = 0.2, 0.1 and 0.05, and h = Δx = Δy = 0.025, 0.0125, and 0.00625.

First of all, we calculated all the eigenvalues of the matrix A after spatial discretization. As it was demonstrated in Theorem 23, they are real and negative, and they are inside the intervals [−1, 292, 0] for h = 0.025; [−5, 183, 0] for h = 0.0125; and [−20, 746, 0] for h = 0.00625. In the three cases, the bound 4(μ+σ) given by Gershgoring theorem is a good approximation for the spectral radius [4(μ+σ) is 1296.91 for h = 0.025, 5187.64 for h = 0.0125, and 20750.6 for h = 0.00625, less than a 1% over the real values].

ESERK4 schemes are stable in [−s², 0] therefore any ESERK method with $s>\sqrt{20750.6k}\ge \sqrt{4150.2}=64.4214$ (since our bigger k = 0.2) is stable in this numerical example.

In both Tables 1, 2, if we take k = 0.2 (also with k = 0.1), we can observe that errors are similar with the three different values h = 0.025, 0.0125, and 0.00625 at many of the points. In this case, most of the error is due to the temporal discretization. Actually, in L₂ norm, errors with constant k = 0.2 grow when h decrease for the three step lengths in space, this is because there are more points and they are close to the border.

If we take h = 0.025 constant, and we vary k = 0.2, 0.1, and k = 0.05, in general we observe that errors in most of the points decrease between k = 0.2 and 0.1, however, if we only compare the errors with h = 0.025, k = 0.1 and k = 0.05, errors are similar at most points (and also in L₂ norm). Obviously, this is because, with h = 0.025, k = 0.1, or k = 0.05, part of the error is due to the spatial discretization.

Therefore, it is not so easy to observe 4−th order convergence in time and 2−nd in space. If we choose h = 0.00625, then most of the error with k₁ = 0.2, k₂ = 0.1, and k₃ = 0.05 is due to temporal discretization. Hence, calculating ${log}_{k_1/k_3}\left(\frac{er{r}_1}{er{r}_3}\right)$ (these values are called Temporal convergence in Tables 1, 2, err₁ being the error with k₁, and err₃ being the error with k₃) we can observe numerical rates in the range 3.6–4.3 in general, which gives us a good idea of the fourth-order convergence in time of ESERK4 schemes.

Now, if we fix k = 0.05, and we repeat the process with h₁ = 0.025, h₂ = 0.0125, and h₃ = 0.00625, we observe that between h₁ and h₂ errors divide (more or less) by 4 which gives us a good idea of the second order in space of the discretization proposed for the right triangle. However, with k = 0.05, and h₃ a part of the error is due to the temporal discretization. Thus, if we calculate ${log}_{h_1/h_3}\left(\frac{er{r}_1}{er{r}_3}\right)$ (these values are called Spatial convergence in Tables 1, 2, err₁ being the error with h₁, and err₃ being the error with h₃), we observe numerical rates in the range 1.2–1.7.

Since, part of the error with k = 0.05 is due to the temporal discretization, and the temporal convergence is fourth-order, let us choose a smaller k₄ = 0.025, and repeat the process with this length step in time. In Table 3, errors with both methods (s = 100 and s = 150), and h = Δx = Δy = 0.025, 0.0125, and 0.00625 are shown at both points, p₁ and p₂.

TABLE 3

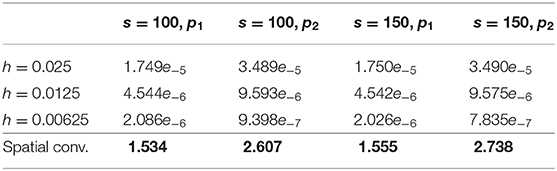
Table 3. Analysis of the numerical convergence at points p₁ = (t, x, y) = (1, 0.15, 0.15), and p₂ = (t, x, y) = (1, 0.5, 0.25) for the ESERK4 algorithm withs = 100 and s = 150 with k = Δt = 0.025, and h = Δx = Δy = 0.025, 0.0125, and 0.00625.

Now, most of the errors are because of the spatial discretization, and we can observe that the numerical spatial convergence rates are in the range 1.5–2.7. They suggest that the numerical convergence rate is 2 as it was expected from the previous theoretical analysis.

In Figure 2, the exact solution and the numerical approximation obtained with ESERK4 with s = 150, k = Δt = 0.025, h = Δx = Δy = 0.00625 are shown. We can check that both plots look identical.

FIGURE 2

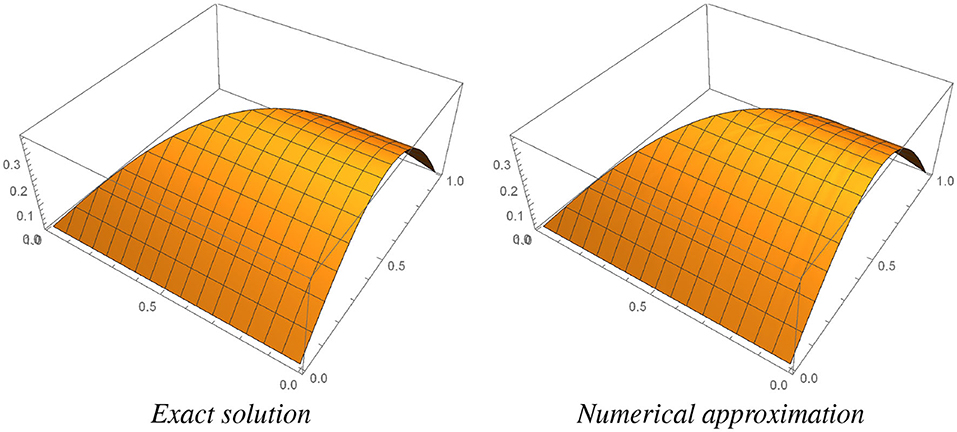
Figure 2. Exact and numerical solutions in the right triangle T_R. Numerical approximation is obtained with ESERK4 with s = 150, k = Δt = 0.025, h = Δx = Δy = 0.00625.

5. Conclusions and Future Goals

In this paper, for the first time, ESERK schemes are proposed to solve nonlinear partial differential equations (PDEs) in right triangles. These codes are explicit, they do not require to solve very large systems of linear nor nonlinear equations at each step. It is demonstrated that such type of codes are able to solve nonlinear PDEs in right triangles. They keep the order of convergence and the absolute stability property under certain conditions. Hence, this paper opens a new line of research, because this new approach will allow, in the future, to solve nonlinear parabolic PDEs with stabilized explicit Runge–Kutta schemes in complex domains, that would be decomposed in rectangles and right triangles.

Additionally, we consider that this procedure can be extended to tetrahedron and other simplixes for the solution of multi-dimensional nonlinear PDEs in complex regions in ℝⁿ.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

The authors acknowledges support from the University of Salamanca through its own Programa Propio I, Modalidad C2 grant 18.KB2B.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Aiken RC. Stiff Computation. New York, NY: Oxford University Press, Inc. (1985).

Google Scholar

2. Cubillos-Moraga MA. General-Domain Compressible Navier-Stokes Solvers Exhibiting Quasi-Unconditional Stability and High-Order Accuracy in Space and Time. PhD thesis. Pasadena, CA: California Institute of Technology (2015). Available online at: https://thesis.library.caltech.edu/8851/

Google Scholar

3. Duarte M, Bonaventura Z, Massot M, Bourdon A, Descombes S, Dumont T. A new numerical strategy with space-time adaptivity and error control for multi-scale streamer discharge simulations. J Comput Phys. (2012) 231:1002–19. doi: 10.1016/j.jcp.2011.07.002

CrossRef Full Text | Google Scholar

4. Duarte M, Descombes S, Tenaud C, Candel S, Massot M. Time-space adaptive numerical methods for the simulation of combustion fronts. Combust Flame. (2013) 160:1083–101. doi: 10.1016/j.combustflame.2013.01.013

CrossRef Full Text | Google Scholar

5. Dumont T, Duarte M, Descombes S, Dronne MA, Massot M, Louvet V. Simulation of human ischemic stroke in realistic 3D geometry. Commun Nonlin Sci Numer Simul. (2013) 18:1539–57. doi: 10.1016/j.cnsns.2012.10.002

CrossRef Full Text | Google Scholar

6. Hairer E, Wanner G. Solving Ordinary Differential Equations. II: Stiff and Differential-Algebraic Problems. Berlin: Springer (1996). doi: 10.1007/978-3-642-05221-7

CrossRef Full Text | Google Scholar

7. Hundsdorfer WH, Verwer JG. Numerical Solution of Time-Dependent Advection-Diffusion-Reaction Equations. Berlin; Heidelberg: Springer (2007).

Google Scholar

8. Martín-Vaquero J, Khaliq AQM, Kleefeld B. Stabilized explicit Runge-Kutta methods for multi-asset American options. Comput Math Appl. (2014) 67:1293–308. doi: 10.1016/j.camwa.2014.01.018

CrossRef Full Text | Google Scholar

9. Zlatev Z. Computer Treatment of Large Air Pollution Models. Dordrecht: Environmental Science and Technology Library; Springer Netherlands (2012). Available online at: https://www.springer.com/gp/book/9780792333289

Google Scholar

10. Abdulle A, Medovikov AA. Second order Chebyshev methods based on orthogonal polynomials. Numer Math. (2001) 90:1–18. doi: 10.1007/s002110100292

CrossRef Full Text | Google Scholar

11. Abdulle A. Fourth order Chebyshev methods with recurrence relation. SIAM J Sci Comput. (2001) 23:2041–54. doi: 10.1137/S1064827500379549

CrossRef Full Text | Google Scholar

12. Kleefeld B, Martín-Vaquero J. SERK2v2: A new second-order stabilized explicit Runge-Kutta method for stiff problems. Numer Methods Part Differ Equat. (2013) 29:170–85. doi: 10.1002/num.21704

CrossRef Full Text | Google Scholar

13. Kleefeld B, Martín-Vaquero J. SERK2v3: solving mildly stiff nonlinear Partial Differential Equations. J Comput Appl Math. (2016) 299:194–206. doi: 10.1016/j.cam.2015.11.045

CrossRef Full Text | Google Scholar

14. Martín-Vaquero J, Janssen B. Second-order stabilized explicit Runge-Kutta methods for stiff problems. Comput Phys Commun. (2009) 180:1802–10. doi: 10.1016/j.cpc.2009.05.006

CrossRef Full Text | Google Scholar

15. Medovikov AA. High order explicit methods for parabolic equations. BIT Numer Math. (1998) 38:372–90. doi: 10.1007/BF02512373

CrossRef Full Text | Google Scholar

16. Sommeijer BP, Shampine LF, Verwer JG. RKC: An explicit solver for parabolic PDEs. J Comput Appl Math. (1997) 88:315–26. doi: 10.1016/S0377-0427(97)00219-7

CrossRef Full Text | Google Scholar

17. Martín-Vaquero J, Kleefeld B. Extrapolated stabilized explicit Runge-Kutta methods. J Comput Phys. (2016) 326:141–155. doi: 10.1016/j.jcp.2016.08.042

CrossRef Full Text | Google Scholar

18. Martín-Vaquero J, Kleefeld A. ESERK5: A fifth-order extrapolated stabilized explicit Runge- Kutta method. J Comput Appl Math. (2019) 356:22–36. doi: 10.1016/j.cam.2019.01.040

CrossRef Full Text | Google Scholar

19. Martín-Vaquero J, Kleefeld A. Solving nonlinear parabolic PDEs in several dimensions: parallelized ESERK codes. J. Comput. Phys. (2020) 109771. doi: 10.1016/j.jcp.2020.109771 Available online at: https://www.sciencedirect.com/science/article/pii/S0021999120305453

CrossRef Full Text | Google Scholar

20. Farago I. Finite element method for solving nonlinear parabolic equations. Comput Math Appl. (1991) 21:59–69. doi: 10.1016/0898-1221(91)90231-R

CrossRef Full Text | Google Scholar

21. Duarte M, Bonaventura Z, Massot M, Bourdon A. A numerical strategy to discretize and solve the Poisson equation on dynamically adapted multiresolution grids for time-dependent streamer discharge simulations. J Comput Phys. (2015) 289:129–48. doi: 10.1016/j.jcp.2015.02.038

CrossRef Full Text | Google Scholar