Stochastic Filtrate of Essential Workers to Reactivate the World Economy Safely

Introduction

Real-time reverse transcription-polymerase chain reaction (RT-PCR) testing is a method commonly employed in molecular biology laboratories. It is one of the most widely used laboratory techniques for detecting the severe acute respiratory syndrome-related coronavirus 2 (SARS-CoV-2). The highly contagious SARS-CoV-2 has resulted in the COVID-19 pandemic, which is affecting the economy in an unprecedented way, despite extensive efforts to use real-time-RT-PCR testing of SARS-CoV-2 to mitigate virus propagation [1]. A possible reason for this failure is that many countries are only administering these tests to patients presenting COVID-19-like symptoms, or to those who were in close contact with such patients, disregarding the asymptomatic SARS-CoV-2 infected population [2]. Given the essential nature of supply chains in meeting society's needs, “focused” strategies of RT-PCR testing should be implemented to test workers needed to maintain those supply chains. Here we propose an approach, termed “stochastic filtrate” with a filtrating agent, which could be employed to timely identify and isolate, under quarantine, essential workers infected with SARS-CoV-2. We propose focused real-time-RT-PCR-testing as an optimal filtrating agent (though other future tests for early detection of SARS-CoV-2 could also be employed). Our method takes advantage of the random nature of stochastic processes, as in randomized controlled trials [3]. Such random sampling has been found to be effective in providing a “quick count” in elections, in which a random sample of polling places is used to identify the “winner” without having to count all the votes. In other words, instead of waiting for the healthcare sector to carry out extensive testing on the whole population, tests would be given to workers employed in essential businesses using a random-sampling based on the stochastic filtrate. Because workers could be infectious several days before showing symptoms, it will be vital to apply the stochastic filtrate to all workers regardless of symptoms. Therefore, we propose that our approach provides a strategy that governments could employ to optimize and speed up testing to protect workers in essential supply chains all over the world. In this article, we present a mathematical framework and simulation to demonstrate that the stochastic filtrate of essential workers could contribute to a safe and productive workforce during the pandemic.

Methods

Stochastic Filtrate

Briefly, to define the concept of “stochastic filtrate,” we first define a “filtrating agent.” It is an abstract mathematical-instrument that removes (isolates) only one particular distinctive element from a set of Z elements:

$\begin{array}{ll}Z={\displaystyle \sum _{j=0}^R}{W}_j^v+{\displaystyle \sum _{j=0}^F}{W}_j& (1)\end{array}$

$\begin{array}{ll}{W}_j^v=W_j=1& (2)\end{array}$

where, $W_j^v$ are elements to be removed and W_j represent elements to be filtrated (Figure 1). Here, R is the number of elements to be removed, and F is the number of elements to be filtrated (Z = R + F, is the total number of elements in the set). Thus, the filtrating agent can be compared with a “sieve,” a device able to remove a distinctive component from a set of elements. In chemistry, the removed element is called the “filtride,” whereas the filtrated element is the “filtrate” (as a noun). In our definition of “stochastic filtrate,” we use “filtrate” as a verb.

FIGURE 1

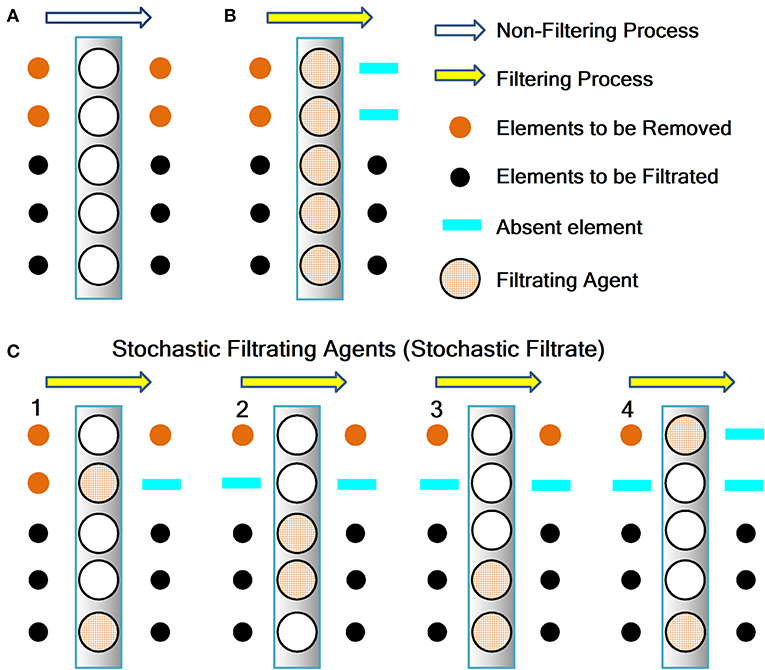
Figure 1. Scheme to explain the mathematical concept of the stochastic filtrate. (A) Absence of filtrating agent. (B) Complete filtrating agent. (C) Stochastic filtrate. We can use the stochastic method illustrated in (C) to obtain the deterministic processes shown in (A,B). Additional explanation is in the text. The elements to be removed are the “filtride” and the elements to be filtered are the “filtrate”.

Specifically, we define “stochastic filtrate” as a process in which a filter of N non-filtrating agents and M filtrating agents, randomly allocated, remove a particular number of distinctive elements $W_j^v$ in a set of size Z, while the rest of the elements $W_j^v$ and W_j from the set pass through such a filter. The following relationships combine the number of elements in the set and the stochastic filter:

$\begin{array}{ll}Z\le N+M& (3)\end{array}$

$\begin{array}{ll}R+F\le N+M& (4)\end{array}$

The stochastic filtrate is a process related to a stochastic filtrating agent. For clarity, in Figure 1, we illustrate the filtrating agent with a sieve symbol, and the non-filtrating agent with white circles, whereas each filtrating instrument is depicted by a vertical gray rectangle.

There are three types of possible filters, depending on values N and M:

1. When N = Z and M = 0, we obtain a filter with the “absence of a filtrating agent.” In this case, there is no filtering process, and the distinct elements (filtrides) remain mixed without separation from the original set (Figure 1A).

2. When N = 0 and M = Z, we obtain a filter with a “complete filtrating agent.” In this case, there is a separation of all distinctive elements (filtrides) from the set in a single trial (Figure 1B).

3. When N ≠ 0 and M ≠ 0, we obtain a filter with a “stochastic filtrating agent” (stochastic filtrate). In this case, M filtrating agents randomly remove one or several distinctive elements (filtrides) from the set. We define M as the “random sampling size” (RSS) of our stochastic filtrate. For instance, if the random sample size is two, then up to two elements from the set can be randomly separated (Figure 1C). A characteristic of this stochastic filtrate is that it requires several trials to remove all distinctive elements from the set. The number of trials needed for the complete extinction of unique elements is inversely proportional to M. Moreover, when M = 0, the number of trials needed for complete removal is indefinite. Additionally, when M is equal to the number of elements in the set, then the number of trials necessary for complete disappearance is one.

Note that the abovementioned stochastic filtrate in the third type of filter is a general class of filtering that reproduces the first and second types of filters, depending on the value of parameter RSS. Thus, it is interesting that these two deterministic filters derive from a stochastic one, with the level of uncertainty in the stochastic filtrate being a function of RSS. Furthermore, if we set RSS to the “random sampling size” M for the stochastic filtrate, then:

$\begin{array}{ll}\text{R}\text{S}\text{S}=\text{M}& (5)\end{array}$

$\begin{array}{ll}RSS\ge {\displaystyle \sum _{j=0}^R}{W}_j^v+{\displaystyle \sum _{j=0}^F}{W}_j-N& (6)\end{array}$

To our knowledge, this is the first time that this formalism and method of “stochastic filtrate” is introduced. In the next section, we will explain how to employ this approach, as a strategy to opportunely identify and isolate, under quarantine, essential workers infected with SARS-CoV-2. For such a purpose, we will suggest the use of the focused real-time-RT-PCR-testing as a filtrating agent.

Results

Stochastic Filtrate of Workers From an Essential Company

We adapted the general conceptual framework illustrated in Figure 1, to SARS-CoV-2-infected and non-infected workers (see Figure 2). Figure 2A shows the scenario in which a focused filtrating agent is lacking for workers from a particular company. Such a scenario is similar to the current world situation of unfocused usage of real-time RT-PCR testing, as these tests are performed only on patients with COVID-19 symptoms, or those persons who were in close contact with such patients. Current testing is not focused on the population sector without COVID-19 symptoms, including essential supply chain workers.

FIGURE 2

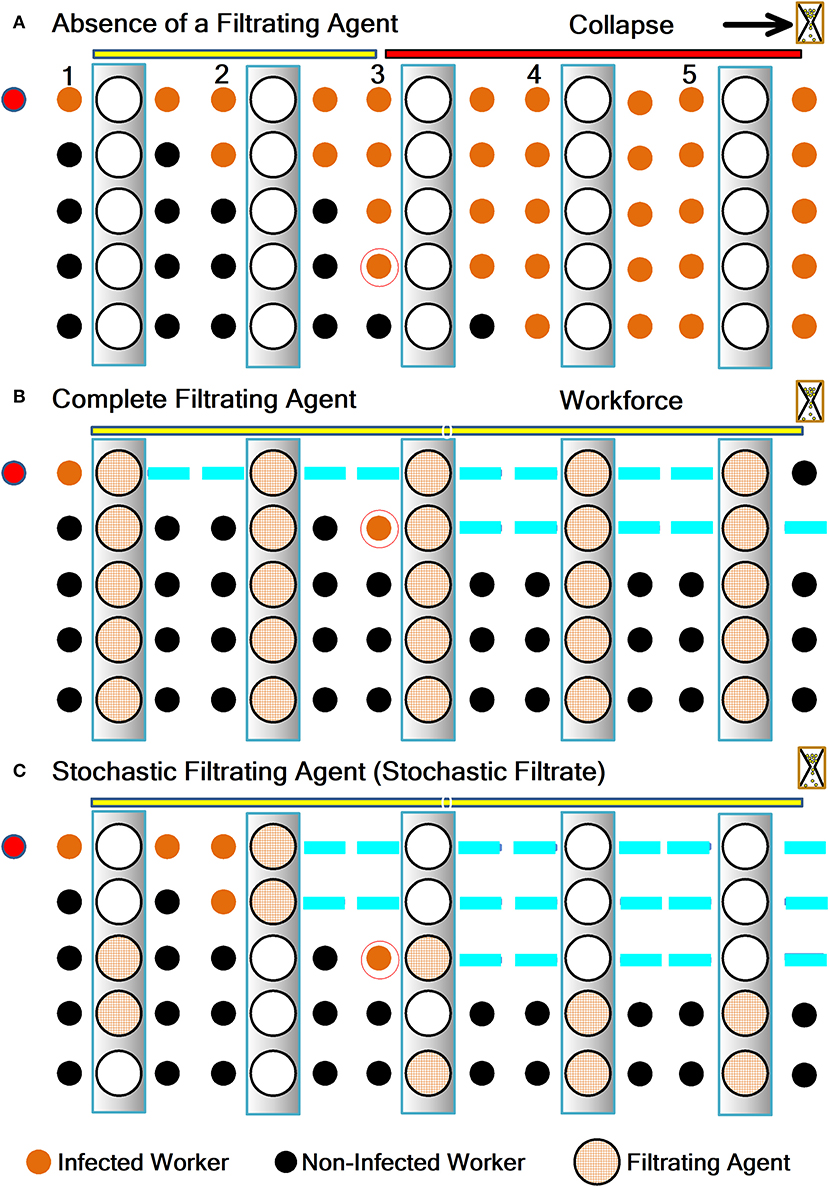
Figure 2. Strategies with real-time-RT-PCR as a filtrating agent, including the stochastic filtrate. (A) There is no filtration process when a filtrating agent is absent. (B) The filtrate is highly effective when there is a complete filtrating agent (real-time-RT-PCR testing for all workers). (C) The case of the stochastic filtrate. Here the infected workers are the “filtride,” and the non-infected workers are the “filtrate.” Note that (C) is similar to Figure 1C, but for infection between workers. The blue line indicates that an infected worker is in quarantine. The filtrating agent randomly selects subjects (see vertical rectangles containing white circles and sieve circles). For this example, the random sampling size (RSS, number of filtrating agents) is two in a population of five complete filtrating agents (i.e., RSS = 40%). Interestingly, when the RSS is equal to the number of complete filtrating agents (100%), then we obtain the scenario illustrated in (B). However, when the RSS is zero %, we get the situation depicted in (A). Thus, our method shown in (C) reproduces the three scenarios. RSS is expressed as percentage of the total number of filtrating agents; i.e., when the filter is in the “complete filtrating agent” condition (N = 0 and M = Z, see Methods).

The scheme in Figure 2A illustrates five consecutive vertical rectangles with white circles, each depicting a lack of filtrating agents. The space around the vertical boxes represents the scenario of contagion between workers each successive day (see numbers) after they come into the company. Note that an infection occurred on day 2 resulting from the close interaction between workers on day 1 (see the new orange circle). On day 3, another contagion occurred and there was the addition of another infected worker outside the company (orange circle highlighted with a ring). Note that in this scenario, there is a collapse of the company on day 4.

In contrast, with the use of a complete filtrating agent from days 1 to 5 (i.e., periodic testing using focused real-time-RT-PCR for all workers; see Figure 2B), the contagion is controlled inside the company, and the workforce is not affected. Although this approach is intuitive, it could be unpractical and expensive for companies with thousands of workers. However, there is a more feasible approach, as illustrated in Figure 2C. With this approach, the filtrating agent (real-time-RT-PCR test) is adequate to mitigate the contagion and maintain the workforce, as expected from the theory of “stochastic filtrate.” In this last scenario, the number of real-time-RT-PCR tests (i.e., RSS) could be empirically adjusted depending on the number of workers. This would save money and the human resources needed to perform such focused and periodical tests. Note that the effectiveness of the strategy described in Figure 2C is between that of the procedures depicted in Figures 2A,B.

It is clear that the filtrating agent randomly changes its position across trials, from days 1 to 5 (see vertical rectangles with circles, and the horizontal yellow line in Figure 2C). When the filtrating agent detects an infected worker (an orange circle), then it “sieves” such an infected worker from the rest of the workers and isolates it under quarantine (horizontal blue lines). The “sieve” (i.e., the filtrating agent) changes its position in each trial according to a stochastic process. In this way, there is a chance that in repeated tests, any infected worker could be identified and timely separated. Note that the filtrating agent does not separate non-infected workers (black circles), who continue working in the company installations. In this example, there are three workers who are infected, but two others continue working (workforce), maintaining the company economically active. This is an advantage compared with the scenario illustrated in Figure 2A, in which all workers quickly become infected, possibly leading to the company's collapse. After quarantine, all workers could return to the company, with the exception of those with potential long-term health problems associated with COVID-19.

It is clear that the cases shown in Figures 2B,C, the complete and the stochastic filtrate, respectively, were useful in avoiding the company's collapse, allowing a safe economic reactivation maintained by non-infected workers. The model introduced in Figure 2 could be generalized to any number of workers and random-sampling size across trials.

Conceptual Model of a Stochastic Process

To validate the proposal that stochastic filtrate is useful in mitigating COVID-19 contagion, we developed a conceptual model of a stochastic process for risky physical interactions between workers in the three scenarios explained in Figure 2. We hypothesize that asymptomatic workers carrying the virus “v” can be timely identified and isolated in focused tests with the complete filtrating agent and stochastic filtrate with real-time-RT-PCR testing.

Briefly, our conceptual model consists of two compartments in Cartesian space: “company” and “street.” We also included a restrictive criterion for entering the company (i.e., when a worker tests positive). With these assumptions, we generated the three scenarios mentioned above for a random walk of infected and non-infected workers:

$\begin{array}{ll}{W}_j^v(x^v,y^v,t),j=1,\dots ,R& (7)\end{array}$

$\begin{array}{ll}{W}_j(x,y,t),j=1,\dots ,F& (8)\end{array}$

These are matricial representations for worker “j” as a function of Cartesian coordinates “xy” and time “t,” where the superscript “v” indicates a “j” worker infected with the virus SARS-CoV-2. Here R is the number of workers put under quarantine and F is the number of non-infected workers to be filtrated and allowed to work at the company building.

We generated a stochastic process by assigning random numbers to the xy coordinates. Then we obtained random walk-like trajectories for each subject, with the possibility of emulating a more realistic walking behavior using filters to smooth such paths. We included the option of persons walking on the street infected with SARS-CoV-2, who are represented by:

$\begin{array}{ll}{P}_j^v(x^v,y^v,t),j=1,\dots ,C& (9)\end{array}$

We assumed that some “C” citizens could potentially infect workers in the street. To simplify, we defined a risky interaction of non-infected workers with infected workers and persons walking on the road as the case when the first crossing between trajectories occurs in proximity, and one of the workers carries the SARS-CoV-2.

$\begin{array}{ll}(x^v,y^v,t)-(x,y,t)=\Delta \mu & (10)\end{array}$

Here, Δμ is a proximity value of social distancing. We employed trajectory crossings to estimate the incidence of infected workers in the three scenarios. We also considered that the trajectory crossing represents infection with a determined probability. This last point is necessary because not all persons who are walking in proximity will be infected; it will depend on various preventive measures (see Discussion section).

Furthermore, RSS is the number of real-time-RT-PCR tests performed during the stochastic filtrate of workers from a particular company, where:

$\begin{array}{ll}RSS=\#of{}^{″}Real\text{\_}Time\text{\_}RT\text{\_}PCR\text{\_}tes{t}^{″}& (11)\end{array}$

$\begin{array}{ll}RSS\ge {\displaystyle \sum _{j=0}^R}{W}_j^v(x^v,y^v,t)+{\displaystyle \sum _{j=0}^F}{W}_j(x,y,t)-N& (12)\end{array}$

$\begin{array}{ll}N=\#ofworkers-RSS& (13)\end{array}$

$\begin{array}{ll}Workforce(D)={\displaystyle \sum _{day=1}^D}[{\displaystyle \sum _{j=0}^F}{W}_j(x,y,t){]}_{day}& (14)\end{array}$

Here the workforce is defined as the number of non-infected workers to testing day D, who are still working after the successive stochastic filtrate. In our model, RSS can be expressed as the percentage of the total number of filtrating agents; i.e., when the filter is in the “complete filtrating agent” condition (N = 0 and M = Z, see Methods).

Python Simulation

To illustrate the viability of the conceptual model, we employed Python to simulate the three scenarios with a different number of workers (infected and non-infected) and infected-persons walking on the street. The software can emulate the number of workers in companies around the world. The simulation was based on the mathematical framework and conceptual model described in the previous section. Figures 3A–C show representative elements of the simulation. Black traces represent the random walk of non-infected workers, and orange and red marks indicate the random walk of infected workers and persons walking on the street, respectively. The green circles indicate the Cartesian coordinates of the occurrence of a contagion, and blue rectangles show those infected workers in quarantine after a positive result of a real-time-RT-PCR test. As an example, Figures 3D–F show simulated trajectories for Z = 49 workers on a working day. The initial conditions are 48 workers not infected (F = 48), one worker infected (R = 1), and one infected person (C = 1) walking on the street. This means that for these simulations, we used the following set of parameters and initial conditions: Z = 49, F = 48, R = 1, and C = 1. In Figures 3D–F, we also considered a random sampling size (RSS) = 40%. In the computer simulation RSS was expressed as a percentage of the total number of filtrating agents, i.e., when the filter is in the “complete filtrating agent” condition (N = 0 and M = Z, see Methods). We also included that the probability of contagion by proximity is = 20% inside and outside the company. In the previous section, we defined the parameters: F, R, C, and RSS.

FIGURE 3

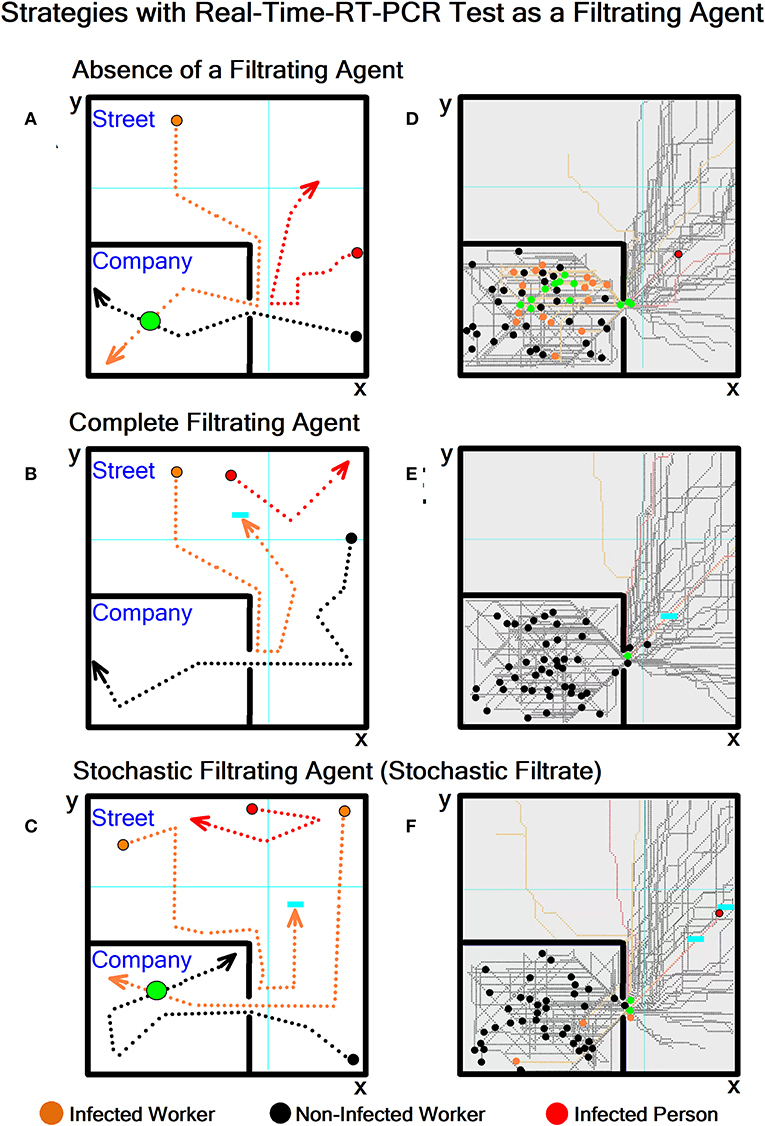
Figure 3. Simulated strategies with real-time-RT-PCR as a filtrating agent. (A–C) Scheme of trajectories for two workers, one infected and another non-infected, and for one infected-person walking on the street. (D–F) The same as (A–C), but for superimposed trajectories of 48 non-infected workers and one infected worker as initial conditions. In this case, there is also one infected-person walking on the street (more explanations in the text). Note that each approach yields different scenarios, with more contagions (orange circles) in situation (D) than in scenarios (E,F). In the Supplementary Material, we included two movies and the Python code with detailed explanations (for purposes of reproducing or extending the analysis). The first movie simulates in sequence the three scenarios during 5 working days in real time: (D) Absence of a filtrating agent with RSS = 0%, (E) Complete filtrating agent RSS = 100%, and (F) Stochastic filtrating agent, where RSS = 40%. The second movie is similar to (D–F), but for RSS = 75%. RSS is expressed as percentage of the total number of filtrating agents; i.e., when the filter is in the “complete filtrating agent” condition (see Figure 2).

To analyze our proposed concept in more detail, we ran the simulation 15 times to compute the infection incidence for 15 different companies with Z = 49 workers. We assigned an RSS = 40% for ten companies and RSS = 75% for another five companies. Then we calculated the cumulative number of cases of infected workers with SARS-CoV-2 for these companies. We obtained a graph of the grand average for the cumulative number of cases (expressed as a percentage of the total number of workers) in the three scenarios for 5 days (Figure 4A). Such a graph shows that the number of infected workers in the first scenario was significantly higher than the number of infected workers in the second and third scenarios. We also calculated the level of uncertainty (95% confidence intervals) in our simulation, utilizing the percentage of infected workers at the end of 5 days vs. four different RSS values (Figure 4B). This graph shows that at intermediate levels of RSS, there is an intermediate uncertainty-level to calculate the number of infected workers. The graph in Figure 4B also illustrates a significant tendency with a low number of infected workers for high values of RSS. Finally, we defined the workforce as the number of non-infected workers, and we obtained the graph of the workforce vs. the number of working days (Figure 5A). In a real context, the periodicity of such “working days” could be defined empirically (see Discussion section). Note that the workforce is 100% for the ideal case of a complete filtrating agent and no contagion from outside the company. This result indicates that both the complete filtrating agent and the stochastic filtrate strategies could help to maintain an active workforce in essential companies. We also found that the mean workforce for the three scenarios was: Absence of a Filtrating Agent = 3.0 ± 0.6%, Complete Filtrating Agent = 74.8 ± 6.7%, Stochastic Filtrate = 32.4 ± 5.6% for RSS = 40% and Stochastic Filtrate = 50.4 ± 9% for RSS = 75% (Mean ± SE). Figure 5B shows this workforce vs. RSS.

FIGURE 4

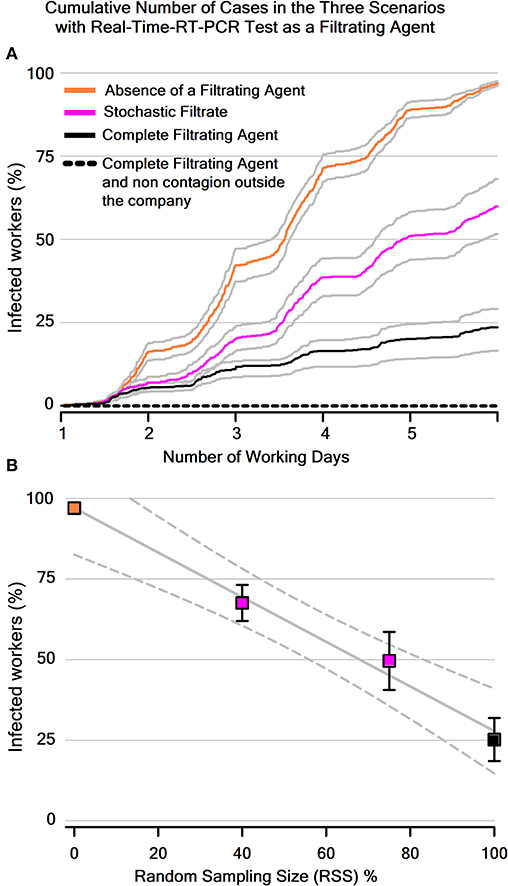
Figure 4. Cumulative mean number of cases of infected workers in the three scenarios: absence of a filtrating agent, complete filtrating, and stochastic filtrate. Quantitative results from the Python simulation for 15 different companies. (A) Superimposed graphs show the number of infected workers (as a percentage of the total number of workers) in the absence of a filtrating agent, complete filtrating, and stochastic filtrate. Note the effectivity of the stochastic filtrate of workers compared with the lack of a filtrating agent. Gray lines indicate the standard error of the mean. In the real situation, the time between “working days” could be defined empirically. These are simulated strategies with real-time-RT-PCR as a filtrating agent, but other filtrate agents detecting SARS-CoV-2 could be employed. (B) Number of infected workers (as a percentage of the total number of workers) vs. random sampling size (RSS in %) employed to generate the three scenarios in the Python simulation. Note that the number of infected workers is inversely proportional to RSS. The graph also shows that the stochastic process is between two deterministic situations: “absence of a filtrate agent” and “complete filtrate agent,” with an uncertainty range to quantify the number of infected workers for intermediate values of RSS (with 95% confidence intervals, dashed lines). Vertical bars represent the standard error.

FIGURE 5

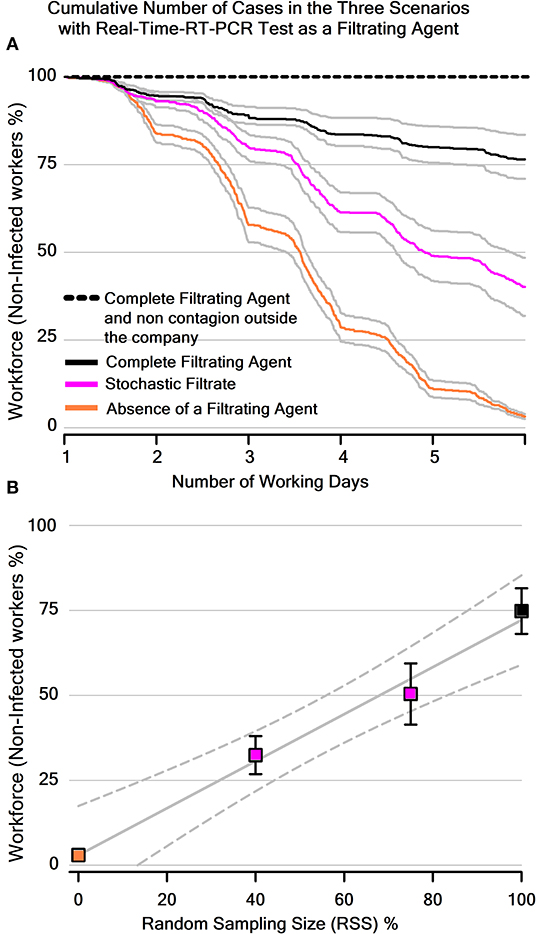
Figure 5. Cumulative mean number of cases of non-infected workers (“workforce”) in the three scenarios: absence of a filtrating agent, complete filtrating, and stochastic filtrate. (A) The same as in Figure 4, but for the workforce (as a percentage of the total number of workers). (B) Workforce vs. random sampling size (RSS in %) employed to generate the three scenarios in the Python simulation. Note that a higher RSS ensures a higher workforce (with 95% confidence intervals, dashed lines). Vertical bars represent the standard error. The graph also shows that the stochastic process is between two deterministic situations: “absence of a filtrate agent” and “complete filtrate agent.” The filtrate agent could be the real-time-RT-PCR.

The results clearly illustrate how the stochastic filtrate strategy could be useful for mitigating the risk of COVID-19 infection in simulated data, thus supporting our proposal. In the Supplementary Material, we included the source code of the simulation software and two movies illustrating the computer simulation in operation.

Discussion

Here, we introduced for the first time the concept of “stochastic filtrate,” in which a mathematical instrument of non-filtrating and filtrating agents, randomly allocated, removes a particular number of distinctive elements in a set. In contrast, the rest of the items from the collection pass through such a filter. We defined “filtrating agent” as an abstract mathematical-instrument that isolates only one particular distinctive element from a group. We extended this mathematical framework to show in a model that the stochastic filtrate of workers could be employed to mitigate SARS-CoV-2 propagation in essential supply chains. For this purpose, we used focused real-time-RT-PCR-testing as an optimal filtrating agent, although other more effective tests or procedures developed in the future could be implemented instead. We compared three scenarios: “absence of a filtrating agent,” “complete filtrating agent,” and “stochastic filtrate.” The first scenario represented the case of “unfocused,” RT-PCR testing to any person in a country, but not specifically targeting workers of essential companies. The second scenario illustrated the case of focused RT-PCR testing for all workers at an essential company. Finally, the third scenario involved random focused-RT-PCR testing. Our results support the hypothesis, and thus our proposed concept that both the “complete filtrating agent” and “stochastic filtrate” could be useful to mitigate the risk of SARS-CoV-2 contagion in simulated data.

Advantages of the Stochastic Filtrate

An advantage of our concept is that it does not require the RT-PCR testing, and it could be implemented with other clinically approved tests for SARS-CoV-2 that will be available after this publication. Another advantage is that governments, companies, and citizens would most certainly benefit from this concept, given the current emergency and the long time before a vaccine for COVID-19 is available [4]. Another advantage is the random nature of the sampling, necessitating only a few RT-PCR assays per day (depending on the RSS). Such a strategy is economically convenient, given that supplies for RT-PCR analyses are scarce and overpriced in some countries. Therefore, it would be ideal if governments could freely provide, as a human right, this type of periodic test to workers involved in essential supply chains during the COVID-19 pandemic. Then, the proposed strategy of random focused-RT-PCR testing, when combined with other preventive measures against COVID-19 [5–7] and future vaccines, could be successfully implemented. Some additional precautionary measures are frequent handwashing, the combined use of medical face shields and masks [8], social distancing, body temperature sensors, and targeted isolation [9]. Because many experts warn that SARS-CoV-2 spreads through the air in respiratory aerosols (see references in the last paragraph of this section), then air-conditioning systems should be temporarily shut down and replaced by natural ventilation through open windows and doors. Another logical preventive measure is the implementation of monitoring stations outside the company doors to detect a quick response (QR) code for every worker.

Such a QR code could contain timely information about the results of RT-PCR testing of each worker, as well as of their possible risky physical interactions with others within company installations. You Only Look Once (YOLO) based human action recognition and localization software [10] combined with a QR code, for instance, could be employed to analyze walking trajectories. Alternative technologies are available from many private companies and universities, such as social distancing software [11] with contact data tracing and a variety of monitoring devices to mitigate the COVID-19 pandemic. Recently entries to the market include wearable badge holders based on proximity sensors with an alarm and contact tracing with mapping software to be used inside the workplace [12]. Also, there has been a proposal to employ prediction methods to forecast the number of COVID-19 cases, which could be useful to government decision-making on the measures to impose [13, 14]. All of these new technological devices and prevention methods could be implemented together with the stochastic filtrate for essential worker populations. We hypothesize that the combined and rigorous implementation of such measures could keep the number of infected workers low in order to maintain a highly productive workforce, as illustrated by the horizontal dashed lines in Figures 4A, 5A. Another significant advantage of our method is that it could allow us to choose, as a filtrating agent, another simpler and quicker testing-technique in the future to detect SARS-CoV-2 with the best precision.

Limitations of the Stochastic Filtering With a Filtrating Agent

The first limitation of our proposal is that empirical research is needed to determine the number of days between the working days illustrated in Figures 4, 5. A possibility could be to employ a 10-4 cyclic strategy, i.e., a cyclic schedule of a 4-day work period and 10-day lockdown, or similar variants, as suggested in recent models [7]. Another limitation is that some workers will not agree to the privacy and data protection policy necessary for QR information, or the complementary use of wearable proximity sensors and video surveillance in offices and other workplace environments. The contributions of psychologists and social scientists would be very helpful in addressing these challenges. Governments could also assist by fostering empathy campaigns during the “new reality” in the COVID-19 pandemic. Another concerning limitation is that some governments may disregard the proposal described here due to political issues or conflicts of interest with the selective distribution of funds to protect essential workers with random focused-RT-PCR testing. However, it would be crucial to highlight that the proportion of resources necessary for such tests would be only a small part of the total funds used for all citizens. This means that the use of random focused-RT-PCR assays for the rest of the population would still be available.

Accuracy of the filtrating agent (real-time-RT-PCR test) is another relevant issue of concern. False-negative cases could affect the valuable utility of RT-PCR assays to correctly identify and isolate infected workers. There is evidence that 29% of patients infected with SARS-CoV-2 could receive an initial RT-PCR false-negative result [15]. Therefore, such findings reinforce the need for repeated testing in persons with suspicion of SARS-CoV-2 [16]. Another alternative is the combined use of other types of available tests to detect SARS-CoV-2, or IgM antibodies against the virus, thus raising the quality of diagnostic accuracy. Importantly, correct sampling procedures with high-quality extraction of viral RNA and the real-time RT-PCR kit performed by experts in biomolecular assays could also improve the efficiency and reduce inaccurate results [16].

Simulation Limitations, Advantages, and Challenges

A limitation of our Python simulation is that it is simple, due to the use of only two compartments and one restriction parameter. However, simplicity in simulation also offers advantages. For example, simple simulations are easy to understand, and they motivate more sophisticated uses. Nevertheless, other simulation studies of our conceptual model and method could include more compartments of different sizes within the company boundaries, a different number of workers in different working spaces, and more detailed probabilities of incorrect use of masks or incomplete handwashing, quantified by YOLO-like approaches. Other more sophisticated parameters could include decision making in emulated workers via artificial intelligence procedures, big data strategies, and 3D avatar-based representations. In this form, walking trajectories and physical interactions among several emulated workers may be more realistic. Inclusion of “decision making” with avatars, based on social networks with positive and negative prevention information, could also be useful to quantify a more realistic epidemic propagation [17]. It would also be interesting to extend our simulation by using epidemiologic models of two-layer multiplex networks, where the upper layer represents the awareness diffusion regarding epidemics, and the lower layer expresses the epidemic propagation [18]. On the other hand, future simulations should consider preventive measures to eliminate respiratory aerosols with SARS-CoV-2, a form of virulent particulate matter (PM) 2.5 in the air [19]. The computer simulation of these respiratory aerosols is relevant, given that essential workers very often share close spaces. It would be convenient to simulate far-UVC light [20] and electrostatic precipitators [21, 22] to eliminate SARS-CoV-2 in virulent PM 2.5 to control the air quality in such spaces. This new realistic computer simulation could help to capture real-world situations and thus examine more effective measures to prevent and control infectious spreading among essential workers during the COVID-19 pandemic.

Conclusion

The stochastic filtrate of essential workers could undoubtedly contribute to protect and efficiently improve each country's economy during the different stages of the “new reality” in the COVID-19 pandemic.

Data Availability Statement

All data is available in the main text or the Supplementary Material. All data, code, and materials used in the analysis are open to any researcher for purposes of reproducing or extending the analysis, and they are available at the Supplementary Material section.

Author Contributions

EM conceived the article, mathematical framework, and conceptual model of stochastic filtrate and wrote the paper. Coauthors RO and HAS-I implemented the Python simulation, and LC provided information about the real-time-RT-PCR test, SARS-CoV-2, and COVID-19. EM supervised all aspects of the work. All the authors revised and approved the manuscript.

Funding

CONACyT Fronteras de la Ciencia #536 (EM), Cátedra Marcos Moshinsky (EM), and VIEP-PIFI-FOMES-PROMEP-BUAP-Puebla (EM), Comité de Internacionalización and VIEP BUAP (HAS-I, EM), México.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Dr. Judith Percino for encouraging the publication of this research and Dr. David Pinto for comments on the manuscript. We thank John Reid and Paul Kretchmer for proofreading the English document.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2020.00371/full#supplementary-material

Supplementary Video 1. Video 1.MP4. Movie of the Python simulation for RSS = 40%. The first stage of this video shows part of a code and starts with simulated action after 4 s. The first five trials reproduce scenarios as illustrated in Figure 3D; whereas the second group of five trials, reproduce the situation of Figure 3E. The last five trials reproduce a scene as illustrated in Figure 3F. Green symbols indicate the moment of occurrence of new infections and orange circles represent the infected workers. The blue rectangles represent the infected workers in quarantine. We considered the same parameters mentioned in the Results section.

Supplementary Video 2. Video 2.MP4. Movie of the Python simulation for RSS = 75%. Note that the stochastic filtrating agent could be most efficient for RSS = 75% than for RSS = 40%.

Simulation Code. SimulationCode-40percentRSS.py (to reproduce random scenarios similar to those illustrated in Video 1.MP4) (Here we used porTest = 40 in the main Python code).
SimulationCode-75percentRSS.py (to reproduce random scenarios similar to those illustrated in Video 2.MP4) (Here we used porTest = 75 in the main Python code). actors.py positions.py. The code is in the Data Sheet 1.ZIP file and is open to any researcher for purposes of reproducing or extending the analysis.

References

1. Liu R, Han H, Liu F, Lv Z, Wu K, Liu Y, et al. Positive rate of RT-PCR detection of SARS-CoV-2 infection in 4880 cases from one hospital in Wuhan, China, from Jan to Feb 2020. Clin Chim Acta. (2020) 505:172–5. doi: 10.1016/j.cca.2020.03.009

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Hellewell J, Abbott S, Gimma A, Bosse NI, Jarvis CI, Russell TW, et al. Feasibility of controlling COVID-19 outbreaks by isolation of cases and contacts. Lancet Glob Health. (2020) 8:e488–96. doi: 10.1016/S2214-109X(20)30074-7

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Haushofer J, Metcalf CJE. Which interventions work best in a pandemic? Science. (2020) 368:1063–5. doi: 10.1126/science.abb6144

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Corey BL, Mascola JR, Fauci AS, Collins FS. A strategic approach to COVID-19 vaccine R&D. Science. (2020) 368:948–50. doi: 10.1126/science.abc5312

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Prem K, Liu Y, Russell TW, Kucharski AJ, Eggo RM, Davies N, et al. The effect of control strategies to reduce social mixing on outcomes of the COVID-19 epidemic in Wuhan, China: a modelling study. Lancet Public Health. (2020) 5:e261–70. doi: 10.1016/S2468-2667(20)30073-6

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Balachandar V, Mahalaxmi I, Kaavya J, Vivekanandhan G, Ajithkumar S, Arul N, et al. COVID-19: emerging protective measures. Eur Rev Med Pharmacol Sci. (2020) 24:3422–5. doi: 10.26355/eurrev_202003_20713

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Karin O, Bar-On YM, Milo T, Katzir I, Mayo A, Korem Y, et al. Adaptive cyclic exit strategies from lockdown to suppress COVID-19 and allow economic activity. medRxiv [Preprint]. (2020) 2020.04.04.20053579.

Google Scholar

8. Eikenberry SE, Mancuso M, Iboi E, Phan T, Eikenberry K, Kuang Y, et al. To mask or not to mask: modeling the potential for face mask use by the general public to curtail the COVID-19 pandemic. Infect Dis Model. (2020) 5:293–308. doi: 10.1016/j.idm.2020.04.001

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Neufeld Z, Khataee H, Czirok A. Targeted adaptive isolation strategy for Covid-19 pandemic. medRxiv [Preprint]. (2020) 2020.03.23.20041897.

PubMed Abstract | Google Scholar

10. Shinde S, Kothari A, Gupta V. YOLO based human action recognition and localization. Proc Comput Sci. (2018) 113:831–8. doi: 10.1016/j.procs.2018.07.112

CrossRef Full Text | Google Scholar

11. Braithwaite I, Callender T, Bullock M, Aldridge R. Automated and semi-automated contact tracing: protocol for a rapid review of available evidence and current challenges to inform the control of COVID-19. medRxiv [Preprint]. (2020) 2020.04.14.20063636.

Google Scholar

12. Nguyen CT, Saputra YM, Huynh NV, Nguyen NT, Khoa TV, Tuan BM, et al. Enabling and emerging technologies for social distancing: a comprehensive survey. arXiv [Preprint]. arXiv:2005.02816 (2020)

Google Scholar

13. Perc M, Gorišek Miksić N, Slavinec M, StoŽer A. Forecasting COVID-19. Front Phys. (2020) 8:127. doi: 10.3389/fphy.2020.00127

CrossRef Full Text | Google Scholar

14. Tsallis C, Tirnakli U. Predicting COVID-19 peaks around the world. Front Phys. (2020) 8:217. doi: 10.3389/fphy.2020.00217

CrossRef Full Text | Google Scholar

15. Arevalo-Rodriguez I, Buitrago-Garcia D, Simancas-Racines D, Zambrano-Achig P, Del Campo R, Ciapponi A, et al. False-negative results of initial RT-PCR assays for COVID-19: a systematic review. medRxiv [Preprint]. (2020) 2020.04.16.20066787.

Google Scholar

16. Tahamtan A, Ardebili A. Real-time RT-PCR in COVID-19 detection: issues affecting the results. Expert Rev.Mol Diagn. (2020) 20:453. doi: 10.1080/14737159.2020.1757437

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Wang ZS, Xia CY, Chen ZQ, Chen GR. Epidemic propagation with positive and negative preventive information in multiplex networks. IEEE Trans Cybern. (2020). doi: 10.1109/TCYB.2019.2960605

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Wang ZS, Guo QT, Sun SW, Xia CY. The impact of awareness diffusion on SIR-like epidemics in multiplex networks. Appl Math Comput. (2019) 349:134–47. doi: 10.1016/j.amc.2018.12.045

CrossRef Full Text | Google Scholar

19. Zhang R, Li Y, Zhang AL, Wang Y, Molina MJ. Identifying airborne transmission as the dominant route for the spread of COVID-19. Proc Natl Acad Sci USA. (2020) 117:14857–63. doi: 10.1073/pnas.2009637117

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Buonanno M, Welch D, Shuryak I, Brenner DJ. Far-UVC light (222 nm) efficiently and safely inactivates airborne human coronaviruses. Sci Rep. (2020) 10:10285. doi: 10.1038/s41598-020-67211-2

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Kettleson EM, Ramaswami B, Hogan CJ, Lee MH, Statyukha GA, Biswas P, et al. Airborne virus capture and inactivation by an electrostatic particle collector. Environ Sci Technol. (2009) 43:5940–6. doi: 10.1021/es803289w

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Kettleson EM, Schriewer JM, Buller RML, Biswas P. Soft-X-ray-enhanced electrostatic precipitation for protection against inhalable allergens, ultrafine particles, and microbial infections. Appl Environ Microbiol. (2013) 79:1333–41. doi: 10.1128/AEM.02897-12

PubMed Abstract | CrossRef Full Text | Google Scholar