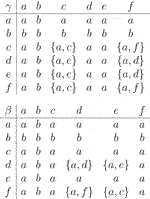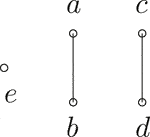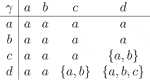1. Introduction
One of the motivations for the study of hyperstructures comes from biological inheritance and physical phenomenon as the nuclear fission. Another motivation for the study of hyperstructures comes from chemical reactions and redox reactions. Dehghan Nezhad et al. [1] provided a physical example of hyperstructures associated with the elementary particle physics: leptons. As we know, the Higgs boson is an elementary particle in the standard model of particle physics. In [2], it is shown that the leptons and gauge bosons along with the interactions between their members construct an -structure. Yaqoob et al. [3] studied some properties of (fuzzy) -hyperideals in involution -semihypergroups. In [4], the concepts of uni-soft -hyperideals and uni-soft interior -hyperideals of ordered -semihypergroups are investigated.
Algebraic hyperstructures are a suitable generalization of classical algebraic structures. In a classical algebraic structure, the composition of two elements is an element, while in an algebraic hyperstructure, the composition of two elements is a set. The concept of hyperstructures was first introduced by Marty [5] at the eighth congress of Scandinavian Mathematicians in 1934. Nowadays, we can easily find well-written books for the introduction to hyperstructures, which include Corsini [6], Corsini and Leoreanu [7], Davvaz [8], Davvaz and Leoreanu-Fotea [9], Davvaz and Vougiouklis [10], and Vougiouklis [11]. For the information about hyper rings, we refer the reader to Ref. 9.
The study of ordered semihypergroups began with the work of Heidari and Davvaz [12]. In 2015, Davvaz et al. [13] discussed the notion of a pseudo-order in an ordered semihypergroup. The focus of the study was to find out if there is a relationship between ordered semihypergroups and ordered semigroups by using pseudo-orders. In 2016, Gu and Tang [14] answered to the open problem given by Davvaz et al. [13]. In [15], Tipachot and Pibaljommee introduced the concept of fuzzy interior hyperideals on ordered semihypergroups. Recently, Mahboob et al. [16] studied the concept of -hyperideals on ordered semihypergroups. Recall, from Ref. 12, that an ordered semihypergroup is a semihypergroup together with a (partial) order relation that is compatible with the hyperoperation , meaning that, for any ,
Here, means that for any , there exists such that , for all nonempty subsets A and B of S.
Good and Hughes [17] introduced the notion of bi-ideals of a semigroup as early as 1952. In 1962, Wallace [18] introduced the notion of relative ideals (-ideals) on semigroups. In 1967, Hrmová [19] generalized the notion of -ideal by introducing the notion of a -ideal of a semigroup S. Recently, Khan and Ali [20] introduced the concept of relative bi-ideals in ordered semigroups. The notion of -semigroup was introduced by Sen and Saha [21] in 1986, which is a generalization of semigroups. In 2011, Anvariyeh et al. [22] introduced the notion of -hyperideal of a -semihypergroup. Later on, Yaqoob and Aslam [23] studied prime bi--hyperideals of -semihypergroups. Omidi et al. [24, 25] discussed some important properties of bi--hyperideals of an ordered -semihypergroup. Bi--hyperideal is a special case of --hyperideal [26]. In 2017, Tang et al. [27] considered and proved some theorems on fuzzy interior -hyperideals in ordered -semihypergroups. Pseudo-orders are the bridge between ordered -semigroups and ordered -semihypergroups, see Ref. 28.
After an introduction, in Section 2, we introduce some notation and terminologies. Section 2 aims for summarizing the fundamental materials on ordered -semihypergroups. Section 3 is devoted to the study of relative -hyperideals (--hyperideals) and relative bi--hyperideals (-bi--hyperideals) of an ordered -semihypergroup. In this section, our main results are stated and proved. -simple ordered -semihypergroups are characterized by using the notions of --hyperideals and -bi--hyperideals. Finally, in Section 4, the notion of -(bi-)int--hyperideals (-(bi-)interior--hyperideals) are studied and their related properties are discussed. It is shown that, in -regular ordered -semihypergroups the --hyperideals and the -int--hyperideals coincide.
2. Preliminaries
Let S and be two nonempty sets. Then, S is called a -semihypergroup [22] if every is a hyperoperation on S, i.e., , for every , , and , we have
If every is an operation, then S is a -semigroup. Let A and B be two nonempty subsets of S. We define
Also,
In the following, we recall the notion of an ordered -semihypergroup, and then we present basic definitions and notations, which we will need in this article. Throughout this article, unless otherwise specified, S is always an ordered -semihypergroup .
Definition 2.1 (see [29]). An algebraic hyperstructure is called an ordered -semihypergroup if is a -semihypergroup and is a partially ordered set such that for any and , implies and . Here, if A and B are two nonempty subsets of S, then we say that if, for every , there exists such that .
Let S be an ordered -semihypergroup. By a sub -semihypergroup of S, we mean a nonempty subset A of S such that for all and . A nonempty subset A of S is called idempotent if .
Example 1. (See Ref. 25.) Let be an ordered semihypergroup and a nonempty set. We define for every and . Then, is an ordered -semihypergroup.
Let be a nonempty subset of an ordered -semihypergroup . If H is a nonempty subset of , then we define
Note that if , then we define
If A and B are nonempty subsets of S, then we have
(1) for all
(2)
(1) If , then
(2)
An element a of an ordered -semihypergroup is regular [25] if there exist and such that . This is equivalent to saying that , for each . An ordered -semihypergroup S is said to be regular if every element of S is a regular element.
Definition 2.2. Let be an ordered -semihypergroup. A nonempty subset A of S is called a left (resp. right) -hyperideal [24] of S if it satisfies the following conditions:
(1) (resp. )
(2) If , , and , then
If A is both a left -hyperideal and a right -hyperideal of S, then it is called a -hyperideal (or two-sided -hyperideal) of S.
3. Basic Properties of Relative Bi--Hyperideals (-Bi--Hyperideals)
Let be an ordered -semihypergroup and and be the nonempty subsets of S. Then, is called a left --hyperideal of S if it satisfies the following conditions:
(1)
(2) When and such that , it implies that
A right --hyperideal of an ordered -semihypergroup S is defined in a similar way. By two-sided --hyperideal or simply --hyperideal, we mean a nonempty subset of S which is both left and right --hyperideal of S.
Definition 3.1. Let and be the nonempty subsets of S. A nonempty subset of S is said to be an --hyperideal of S if it satisfies the following conditions:
(1) and
(2) When and such that , it implies that
Example 2. Let and be the sets of binary hyperoperations defined as follows:
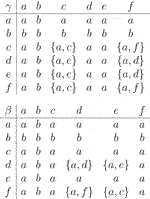
Then, S is a -semihypergroup [23]. We have as an ordered -semihypergroup, where the order relation is defined by
The covering relation and the figure of S are given by
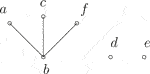
Let , and . One can check that is a --hyperideal of S.Here are some elementary properties of these concepts.
Lemma 3.2. Let be an ordered -semihypergroup. If is a sub -semihypergroup of S, then is a --hyperideal of S for each .
Proof. Let . We show that is a --hyperideal of S. We have
Similarly, we have . Now, let and such that . Then, for some . Hence, and so . Therefore, is a --hyperideal of S.
Theorem 3.3. Let I be a left -hyperideal of an ordered -semihypergroup and such that . If M is an idempotent left --hyperideal of I, then M is a left -hyperideal of S.
Proof. Clearly, I is an ordered sub--semihypergroup of S. We have
If and such that , then we have . Since M is a left --hyperideal of I, it follows that . Hence, M is a left -hyperideal of S. ∎
Theorem 3.4. Let I be a -hyperideal of a regular ordered -semihypergroup and , such that . Then, any --hyperideal of I is a -hyperideal of S.
Proof. Let I be a -hyperideal of S. Then, . So, I is an ordered sub--semihypergroup of S. Let A be a --hyperideal of I. We prove that A is a -hyperideal of S. Let . Then, there exist and such that
Since I is a -hyperideal of S, it follows that
Hence, , for some . This means that . Therefore, I is a regular ordered sub--semihypergroup of S.
Let and . Then, where . Now, suppose that . Then, there exist and such that
Similarly, we have .
If and such that , then we have . Since A is a --hyperideal of I, it follows that . Hence, A is a -hyperideal of S.
Let a be an element of an ordered -semihypergroup . We denote by (resp. , ) the left (resp. right, two-sided) relative -hyperideal of S generated by a. The intersection of all --hyperideals of S containing the element a is denoted by , where .
Lemma 3.5. Let a be an element of an ordered -semihypergroup and and be two sub--semihypergroups of S. Then,
(1)
(2)
(3) , where
Proof. Since and , it follows that . We have
On the contrary, we have . Thus, is a left --hyperideal of S containing a. This means that .
Now, we show that is the smallest left --hyperideal of S containing a. Suppose that A is a left --hyperideal of S containing a. We have
This proves that (1) holds. Conditions (2) and (3) are proved similarly.
Let be an ordered -semihypergroup and and be nonempty subsets of S. Then, S is said to be left -simple if it has no proper left --hyperideal. In the same way, we can define a right -simple ordered -semihypergroup. If S is a left -simple and right -simple) ordered -semihypergroup, then S is a , -simple ordered -semihypergroup.
Lemma 3.6. Let be an ordered -semihypergroup and and be sub--semihypergroups of S such that . Then, the following assertions hold:
(1) S is left -simple if and only if for each
(2) S is right -simple if and only if for each
(3) S is (, )-simple if and only if for each
Proof. The proof is straightforward.
We continue this section with the following definition.
Definition 3.7. Let be an ordered -semihypergroup and a nonempty subset of S. A sub--semihypergroup of S is called a relative bi--hyperideal (-bi--hyperideal) of S if the following conditions hold:
(1)
(2) When and such that , it implies that
Example 3. We come back to Example 2 and consider ordered -semihypergroup . Let and . It is a routine matter to verify that is a -bi--hyperideal of S.
Lemma 3.8. The intersection of any family of -bi--hyperideals of an ordered -semihypergroup is a -bi--hyperideal of S.
Proof. This proof is straightforward.
Let be an ordered -semihypergroup and be any nonempty subset of S. Then, S is said to be -regular if, for each , there exist and such that .
Theorem 3.9. Let be an ordered -semihypergroup and a sub--semihypergroup of S. Then, the following assertions are equivalent:
(1) S is -regular
(2) for every -bi--hyperideal of S
Proof. Assume that (1) holds. Since is a -bi--hyperideal of S, we get . Thus, . Now, let . Since S is -regular, there exist and such that
Hence, and so . Therefore, . Let be a right --hyperideal and a left --hyperideal of S. By routine checking, we can easily verify that and are -bi--hyperideals of S. By Lemma 3.8, is a -bi--hyperideal of S. By hypothesis, we have
Let . Since and , it follows that . By (1) and (2) of Lemma 3.5, we have
Then, , for some . If , then . So, . Therefore, S is -regular. If , then , for some and . Thus, . Therefore, S is -regular.
Definition 3.10. Let be an ordered -semihypergroup and and be the nonempty subsets of S. A sub--semihypergroup of S is said to be a -bi--hyperideal of S if it satisfies the following conditions:
(1)
(2) When and such that , it implies that
Example 4. Let and be the sets of binary hyperoperations defined as follows:

Then, S is a -semihypergroup [23]. We have as an ordered -semihypergroup, where the order relation is defined by
The covering relation and the figure of S are given by
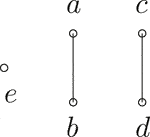
Let , , and . It is easy to see that is a -bi--hyperideal of S.
The concept of -bi--hyperideals of an ordered -semihypergroup is a generalization of the concept of --hyperideals (left --hyperideals and right --hyperideals) of an ordered -semihypergroup. Obviously, every left (right) --hyperideal of an ordered -semihypergroup S is a -bi--hyperideal of S, but the following example shows that the converse is not true in the general case.
Example 5. Consider the ordered -semihypergroup given in Example 2. It is easy to check that is a -bi--hyperideal on S, where , but it is not a right --hyperideal on S. Since and , but which implies that does not hold.
Theorem 3.11. Let be an ordered -semihypergroup and and be two sub--semihypergroups of S. Then, S is left -simple and right -simple if and only if S does not contain proper -bi--hyperideals.
Proof. Let S be a left -simple and right -simple ordered -semihypergroup and B a -bi--hyperideal of S. It is sufficient to prove that . Consider and . Since S is left -simple, we obtain
by Lemma 3.5. We need to consider only two cases:
Case 1. Let . As B is -bi--hyperideal, we have .
Case 2. Let , for some and . By assumption, S is a right -simple ordered -semihypergroup. Therefore,
by Lemma 3.5. Since , we have or for some and . By Lemma 3.6, we have
and so
where . Hence, S is a -regular ordered -semihypergroup. So, there exist and such that . We now turn to the case . From this, we conclude that . So, we obtain
Since , it follows that . This gives . If , then
and so . We thus get .
Conversely, suppose that S does not contain proper -bi--hyperideals. Let M be a left --hyperideal and right --hyperideal of S. We have
Hence, M is a -bi--hyperideal of S. By assumption, we have . Therefore, S is a left -simple and right -simple ordered -semihypergroup.
4. Relative (Bi)-Int--Hyperideals (-(Bi)-Int--Hyperideals)
Definition 4.1. Let be an ordered -semihypergroup and a nonempty subset of S. A sub--semihypergroup of S is called a -int--hyperideal of S if the following conditions hold:
(1)
(2) If , , and , then
It is not difficult to see that every --hyperideal of an ordered -semihypergroup S is a -int--hyperideal of S. The following example shows that the converse is not true in general.
Example 6. Let and . We define
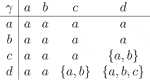
Then, S is a -semihypergroup. We have is an ordered -semihypergroup, where the order relation is defined by
The covering relation and the figure of S are given by
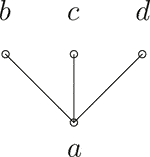
Let and . Here, is a -int--hyperideal of S, but not a --hyperideal of S. Indeed, since , it follows that is not a --hyperideal of S.The following example shows that a -regular ordered -semihypergroup is not regular in general.
Example 7. Consider the -semihypergroup given in Example 6. Let be the relation on S defined as follows:
Then, is an ordered -semihypergroup. The covering relation and the figure of S are given by:
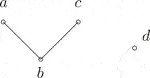
Let . An easy computation shows that S is a -regular ordered -semihypergroup, but it is clearly not regular.
Theorem 4.2. Let be a -regular ordered -semihypergroup, where is a nonempty subset of S. Then, every -int--hyperideal of S is a --hyperideal of S.
Proof. Let be a -int--hyperideal of S. Then, is a sub--semihypergroup of S and . Let . Since S is -regular, there exist and such that . Now, let and . Then,
Thus, . By a similar argument, we have . Hence, the result follows.In the following, we introduce the notion of -bi-int--hyperideals as a generalization of --hyperideals, -bi--hyperideals, and -int--hyperideals of ordered -semihypergroups.
Definition 4.3. Let be an ordered -semihypergroup and a nonempty subset of S. A sub--semihypergroup of S is called a -bi-int--hyperideal of S if the following conditions hold:
(1)
(2) If , , and , then
Lemma 4.4. Let be an ordered -semihypergroup and a nonempty subset of S. Then, the following statements hold:
(1) Every --hyperideal of S is a -bi-int--hyperideal of S
(2) The intersection of -bi-int--hyperideals of S is a -bi-int--hyperideal of S
(3) If B is a -bi--hyperideal and C a -int--hyperideal of S, then is a -bi-int--hyperideal of S
Proof. (1) Let A be a --hyperideal of S. Then, and . We have
and
Therefore, A is a -bi-int--hyperideal of S.
(2) The proof is similar to the proof of Lemma 3.8.
(3) Clearly, is a sub--semihypergroup of S. We have
and
Hence, . Therefore, is a -bi-int--hyperideal of S.
Example 8. Let and . We define

Then, S is a -semihypergroup. We have as an ordered -semihypergroup [29], where the order relation is defined by
The covering relation and the figure of S are given by
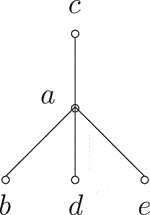
Let and . Then, and , so . Hence, is a -bi-int--hyperideal of S. It is easy to see that () is not a --hyperideal of S.
5. Conclusion
In this article, we studied some properties of -(bi-)-hyperideals of ordered -semihypergroups. In particular, we introduced and studied -int--hyperideals and -bi-int--hyperideals. Furthermore, we proved that -int--hyperideals and --hyperideals coincide in -regular ordered -semihypergroups. When we deal with -(bi-)-hyperideals of ordered -semihypergroups, it is natural to talk about fuzzy -(bi-)-hyperideal. According to the research results, it is suggested to define and investigate some properties of fuzzy -(bi-)-hyperideals, rough prime -bi--hyperideals, fuzzy prime -bi--hyperideals, and uni-soft -int--hyperideals in ordered -semihypergroups. As an application of the results of this article, the corresponding results of ordered semihypergroups can be also obtained by moderate modification.
Data Availability Statement
All datasets presented in this study are included in the article/supplementary material.
Author Contributions
All authors have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This work was supported by the National Key R&D Program of China (Grant no. 2019YFA0706402), the Natural Science Foundation of Guangdong Province (Grant no. 2018A0303130115), and Guangzhou Academician and Expert Workstation (Grant no. 20200115-9).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Dehghan Nezhad, A, Moosavi Nejad, SM, Nadjafikhah, M, and Davvaz, B. A physical example of algebraic hyperstructures: leptons. Indian J Phys. (2012). 86(11):1027–32. doi: 10.1007/s12648-012-0151-x
CrossRef Full Text | Google Scholar
2. Davvaz, B, Nezhad, AD, and Nejad, SMM. Algebraic hyperstructure of observable elementary particles including the Higgs boson. Proc Natl Acad Sci, India, Sect A Phys Sci. (2020). 90:169–76. doi: 10.1007/s40010-018-0553-z
CrossRef Full Text | Google Scholar
3. Yaqoob, N, Tang, J, and Chinram, R. Structures of involution Γ-semihypergroups. Honam Mathematical J (2018). 40(1):109–24. doi: 10.5831/HMJ.2018.40.1.109
Google Scholar
4. Khan, A, Farooq, M, and Yaqoob, N. Uni-soft structures applied to ordered Γ-semihypergroups. Proc Natl Acad Sci, India, Sect A Phys Sci. (2020). 90:457. doi: 10.1007/s40010-019-00602-x
CrossRef Full Text | Google Scholar
5. Marty, F. Sur une generalization de la notion de groupe. In: Proceedings of the 8th Congress Math. Scandinaves, Stockholm, Sweden; Stockholm, Sweden (1934). p. 45–49.
Google Scholar
6. Corsini, P. Prolegomena of hypergroup theory. 2nd ed. Udine, Italy: Aviani Editore (1993).
Google Scholar
7. Corsini, P, and Leoreanu, V. Applications of hyperstructure theory. In: Advances in mathematics. Dordrecht, Netherlands: Kluwer Academic Publishers (2003).
Google Scholar
8. Davvaz, B. Semihypergroup theory. New York, NY: Elsevier (2016).
Google Scholar
9. Davvaz, B, and Leoreanu-Fotea, V. Hyperring theory and applications. Palm Harbor, FL: International Academic Press (2007).
Google Scholar
10. Davvaz, B, and Vougiouklis, T. A walk through weak hyperstructures-Hυ-structures. Hackensack, NJ: World Scientific Publishing Co. Pte. Ltd. (2019).
Google Scholar
11. Vougiouklis, T. Hyperstructures and their representations. Palm Harbor, FL: Hadronic Press Inc. (1994).
Google Scholar
12. Heidari, D, and Davvaz, B. On ordered hyperstructures. Politehn Univ Bucharest Sci Bull Ser A Appl Math Phys. (2011). 73(2):85–96.
Google Scholar
13. Davvaz, B, Corsini, P, and Changphas, T. Relationship between ordered semihypergroups and ordered semigroups by using pseudoorder. Eur J Combinator. (2015). 44:208–17. doi: 10.1016/j.ejc.2014.08.006
CrossRef Full Text | Google Scholar
14. Gu, Z, and Tang, X. Ordered regular equivalence relations on ordered semihypergroups. J Algebra. (2016). 450:384–97. doi: 10.1016/j.jalgebra.2015.11.026
CrossRef Full Text | Google Scholar
15. Tipachot, N, and Pibaljommee, B. Fuzzy interior hyperideals in ordered semihypergroups. Ital J Pure Appl Math. (2016). 36:859–70.
Google Scholar
16. Mahboob, A, Khan, NM, and Davvaz, B. (m, n)-hyperideals in ordered semihypergroups. Categ General Alg Structures Appl. (2020). 12(1):43–67. doi: 10.29252/cgasa.12.1.43
CrossRef Full Text | Google Scholar
17. Good, RA, and Hughes, DR. Associated groups for a semigroup. Bull Am Math Soc. (1952). 58:624–5.
Google Scholar
18. Wallace, A. Relative ideals in semigroups, I (Faucett’s theorem). Colloq Math. (1962). 9:55–61. doi: 10.4064/cm-9-1-55-61.
CrossRef Full Text | Google Scholar
19. Hrmová, R. Relative ideals in semigroups. Matematický časopis (1967). 17(3):206–23.
Google Scholar
20. Khan, NM, and Ali, MF. Relative bi-ideals and relative quasi ideals in ordered semigroups. Hacet J Math Stat (2020). 49(3):950–61. doi: 10.15672/hujms.624046
CrossRef Full Text | Google Scholar
21. Sen, MK, and Saha, NK. On Γ-semigroup I. Bull Calcutta Math Soc. (1986). 78:180–6.
Google Scholar
22. Anvariyeh, SM, Mirvakili, S, and Davvaz, B. On Γ-hyperideals in Γ-semihypergroups. Carpathian J Math. (2010). 26(1):11–23.
Google Scholar
23. Yaqoob, N, and Aslam, M. Prime (m, n) Bi-Γ -hyperideals in Γ-semihypergroups. Appl Math Inf Sci. (2014). 8(5):2243–9. doi: 10.12785/amis/080519
CrossRef Full Text | Google Scholar
24. Omidi, S, and Davvaz, B. Bi-Γ-hyperideals and Green’s relations in ordered Γ-semihypergroups. Eurasian Mathematical J (2017). 8(4):63–73.
Google Scholar
25. Omidi, S, Davvaz, B, and Hila, K. Characterizations of regular and intra-regular ordered Γ-semihypergroups in terms of bi-Γ-hyperideals. Carpathian Math Publ. (2019). 11(1):136–51. doi: 10.15330/cmp.11.1.136-151
CrossRef Full Text | Google Scholar
26. Basar, A, Abbasi, MY, and Bhavanari, S. On generalized Γ-hyperideals in ordered Γ-semihypergroups. Fundam J Math Appl. (2019). 2(1):18–23. doi: 10.33401/fujma.543712
Google Scholar
27. Tang, J, Davvaz, B, Xie, X-Y, and Yaqoob, N. On fuzzy interior Γ-hyperideals in ordered Γ-semihypergroups. J Intell Fuzzy Syst. (2017). 32:2447–60. doi: 10.3233/jifs-16431
CrossRef Full Text | Google Scholar
28. Omidi, S, Davvaz, B, and Abdiogluv, C. Some properties of quasi-Γ-hyperideals and hyperfilters in ordered Γ-semihypergroups. Southeast Asian Bull Math. (2018). 42(2):223–42.
Google Scholar
29. Omidi, S, and Davvaz, B. Convex ordered Gamma-semihypergroups associated to strongly regular relations. Matematika (2017). 33(2):227–40. doi: 10.11113/matematika.v33.n2.838
CrossRef Full Text | Google Scholar
 Yongsheng Rao1
Yongsheng Rao1 Peng Xu
Peng Xu Zehui Shao
Zehui Shao Saeed Kosari
Saeed Kosari