Actively Driven Fluctuations in a Fibrin Network

1 Introduction

The extracellular matrix (ECM) interacts with and provides a variety of mechanical and biochemical cues to cells [1,2]. Experimental systems using naturally derived ECMs more closely mimic in vivo cell-ECM interactions than, for example, plastic [3]. Common naturally derived ECMs such as collagen and fibrin hydrogels exhibit important characteristics such as micron-scale pores and cell adhesion sites [4]. The fibrous nature of these ECMs plays potentially critical roles in cell-cell communication through the ECM, especially in 3-D culture systems [5,6]. For example, cells respond to forces an order-of-magnitude farther away in naturally derived fibrous materials than materials with sub-micron pores, often treated as a continuum at the cellular scale [7–10]. Therefore, understanding force propagation through naturally derived fibrous materials at the cellular scale is of great interest. Fibrin, a major component of hemostasis, is well suited for studying force propagation through fiber networks. Fibrin forms the provisional ECM of a blood clot, is used as tissue glue, and is a substrate for the study of wound healing and in tissue engineering [11–14]. Fibrin hydrogels can be formed by activating soluble fibrinogen with thrombin, which forms a randomly arranged 3-D network of fibrin fibers.

At the fiber scale, experimental observations using optical tweezers and atomic force microscopy (AFM) as well as computational simulations show that individual fibers act as strain stiffening elastic beams [15–20]. While force transmission at the scale of single fibers is well understood, force transmission in assembled networks has not been fully elucidated [21]. At scales much larger than the average pore size, the material can be treated as a continuum, but at the scale of pores, and even cells, it is necessary to consider that forces cannot elastically transmit through the liquid region and are confined to the fibers [9,22]. At this mesoscale, the existence of a preferred pathway for force transmission or a ‘force transmission highway’ has been observed in simulations and inferred in experimental observations [7,9,21,23–25]. Simulations that take into account the fibrous structure of the ECM show that when the matrix is extended, subsets of fibers within the network carry higher tension than would be expected from a continuum model of the material, while other fibers carry less tension or are buckled under compression [22,23]. How and where these high tension pathways form and change may play a role in cell orientation [26], cell migration or invasion [27,28], and capillary sprouting [29]. A method for directly assessing which fibers in a network carry tension can provide insight into force transmission at this mesoscale.

Here, we describe an approach to detect which fibers within a 3-D fibrin hydrogel are involved in force transmission. Optical tweezers are used to apply a low frequency oscillatory force to a bead embedded in a fibrin network. We measure the response of the fibers within the network using confocal microscopy by analyzing the fluctuation of the fluorescence intensity. Both confocal microscopy and optical tweezers are able to access regions deep within a hydrogel without invasive disruption of the structure, unlike AFM. Future studies will aim to extend this method for identifying force transmission pathways around cells and to study how naturally derived ECMs participate in cell-cell and cell-ECM communication.

2 Materials and Methods

2.1 Fibrin Gel

Bovine fibrinogen (Sigma-Aldrich, F8630) was dissolved in Phosphate buffered saline (PBS; ThermoFisher, 14040117) and sterile filtered 0.22 μm. 2 μm beads (Bang Laboratories, SC05000) were added to the fibrin solution (final concentration 1.5 mg/ml clottable protein) and thrombin (final concentration 4 U/mL; Sigma-Aldrich, 605,157) was added immediately before casting the hydrogel in glass bottom dishes (MatTek, P35G-1.5–10-C). After at least 12 h incubation at ${37}^{\circ }$C, the fibrin hydrogel was fluorescently labeled using Atto 488 NHS-ester (Sigma-Aldrich, 41,698) fluorophore and imaged after washing out excess dye with PBS.

2.2 Bead Oscillation

A 1064 nm continuous wave laser (IPG, YLR-5-1064-LP) was used to optically trap a 2 m diameter silica bead embedded approximately 35 μm above the glass in a fibrin network with a 60×1.45 NA oil immersion microscope objective (Olympus). The focused laser beam was steered as a sine wave in the image plane using galvanometer mirrors (Thorlabs, GVS102). Bead displacement was detected by a co-aligned 785 nm (Thorlabs, LP785-SF100) laser-diode beam. The beam was back scattered from the bead and directed onto a quadrant photodetector (Newport, 2,901 and 2,903). Trap stiffness was determined by trapping a bead without oscillation of the trap and measuring the corner frequency of the displacement power spectrum in water [30]. Laser power was adjusted to achieve a trap stiffness of 34 pN/m for all experiments. Schematic of the optical tweezer system can be found in Supplementary Figure S1. Optical tweezers were used to oscillate the bead in the x (horizontal in the image) or y (vertical in the image) directions at the desired frequency (driving frequency, $F_d$). The position of the optical tweezers oscillated as a sine wave with 1 m peak-to-peak amplitude unless otherwise stated.

2.3 Fluorescence Microscopy

Fluorescence microscopy images were recorded using an Olympus Fluoview 1,200 laser scanning confocal microscope. The Atto 488 NHS-ester fluorophore was excited using the 488 nm laser line operating at 0.7% of maximum power as indicated in the Olympus Fluoview software. Images of fibrin were acquired using the rapid-scanning imaging mode to achieved maximum frame rates of 15.4 frames/second. This imaging mode limits image resolution to 256 by 256 pixels to cover a field of view of 21.1 μm by 21.1 μm unless otherwise stated. 400 consecutive images were recorded over 26 s. Z-stacks of at least 10 μm thickness (5 μm above and below the bead) were acquired prior to bead oscillation in order to identify the local fiber network around each bead.

2.4 Image Analysis

Images in the Olympus OIF format were converted to TIFF files using ImageJ [31]. Pixel-by-pixel 1-D Fourier transforms were performed in MATLAB (MathWorks). Figures were generated with MATLAB. Binary image masks were generated by setting a threshold of mean intensity (in time) of each pixel that is 20% greater than mean intensity (in space and time) of all pixels. Pseudo-color 3-D image stacks were generated using the ‘temporal-color code’ function in ImageJ and all figures were arranged in Microsoft PowerPoint. Our custom MATLAB code is made available in Supplementary Materials along with all TIFF images. One must first execute pixelflucatuation.m for image input and fast Fourier transform computation. Next, pixelflucatuationfigures.m should be executed. It operates on the output from pixelflucatuation.m to generate all figures. The code as provided assumes all files are placed in the same folder.

2.5 Quantification of Local Phase Variance

The Orientational Order Parameter (OOP), also known as the nematic order parameter [32,33], was used to determine local organization in phase (θ) images. For OOP, the variance in the orientation of n unit pseudovectors ($\overrightarrow{r}$, which has components $r_x=cos\theta$ and $r_y=sin\theta$) can be quantified [34–36]. Pseudovectors are vector-like objects, which are invariant under inversion ($\overrightarrow{r}=-\overrightarrow{r}$), and are also called “axial vectors” [37]. The OOP ranges from 0 to 1, and will be 0 when the data is uniformly distributed (perfectly isotropic) and will increase as the data becomes more anisotropic toward a value of 1 for perfectly aligned data.

In order to calculate the OOP, the tensor, ${\widehat{\mathbb{T}}}_i$ in Equation 1, is constructed for each $\overrightarrow{r_i}$ ($i=1,\cdots ,n$)

${\widehat{\mathbb{T}}}_i=\left[\begin{array}{cc}{r}_{i,x}{r}_{i,x}& r_{i,x}{r}_{i,y}\\ r_{i,x}{r}_{i,y}& r_{i,y}{r}_{i,y}\end{array}\right](1)$

The orientational order tensor, $\mathbb{T}$ in Equation 2, is constructed by normalizing each tensor ${\widehat{\mathbb{T}}}_i$ (Equation 1), and averaging the normalized tensors. The OOP is the maximum eigenvalue of the orientational order tensor $\mathbb{T}$, shown in Equation 2

$\mathbb{T}=\langle 2\left[\begin{array}{cc}{r}_{i,x}{r}_{i,x}& r_{i,x}{r}_{i,y}\\ r_{i,x}{r}_{i,y}& r_{i,y}{r}_{i,y}\end{array}\right]-\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]\rangle (2)$

In order to quantify local phase organization, the OOP was calculated at each pixel in a 7 × 7 pixel neighborhood. The MATLAB functions calculate_OOP.m and hoodOOP.m, found in the Supplementary Materials, were used for the OOP calculations.

3 Results

Fluorescence confocal microscopy videos were recorded while optical tweezers applied an oscillatory force on a 2 μm bead entangled in a fibrous fibrin network. Supplementary Video S1 shows a bead with no applied oscillation. Supplementary Video S2 shows the same bead oscillated in the horizontal x-direction. The bead and some of the surrounding fibers move noticeably in response to the oscillation of the optical tweezers. For many fibers, motion is difficult to track precisely from frame to frame due to noise. However, a subset of pixels show increased intensity fluctuations at the optical tweezers’ drive frequency ($F_d$) (Figure 1). Intensity, denoted as I, is plotted for several representative pixels overlaying the bead, fibers, or liquid region (Figures 1A,B). Figure 1A shows the mean intensity image, where each pixel is the mean fluorescence intensity over time, denoted by $<I>$. The spectral magnitudes of the 1-D Fourier transform of I in time, denoted by $\left|\widehat{I}\right|$, for the representative pixels are plotted in Figure 1C. $\left|\widehat{I}\right|$ does not show prominent peaks without applied oscillations (Figure 1C orange). However, with applied oscillations, some of the representative pixels show a peak at the driving frequency, denoted by $F_d$ (Figure 1C blue). Pixel i lies on the bead and a strong peak in $\left|\widehat{I}\right|$ occurs at $F_d$. A similar but less prominent peak is present for pixel ii, which lies on a fiber directly attached to the bead. Pixel v does not lie on a fiber and is instead in the liquid region or pore of the fiber network. We found that $\left|\widehat{I}\right|$ in these regions are insensitive to the applied bead oscillation and pixels in these regions also have lower I as well as lower $\left|\widehat{I}\right|$ at all frequencies. Pixels iii and iv lie on fibers farther away from the bead, which are not directly connected to the bead by the in-focus portion of the fiber network (Figure 1A). Determining if these fibers are oscillating with the bead can be difficult based on the spectral plot of individual pixels as presented in Figure 1C, when $\left|\widehat{I}\right|$ at $F_d$ is near to the mean $\left|\widehat{I}\right|$ across all frequencies. We can improve identification of fibers which are mechanically coupled to the bead by taking into account the intensity fluctuations of all the pixels over each fiber. We can visualize these spatial relationships in $\left|\widehat{I}\right|$ images (Figure 2, Supplementary Video S3 bottom). As an example, Supplementary Video S3 shows the $\left|\widehat{I}\right|$ images series for the same bead as in Figure 1 with (bottom right) and without (bottom left) applied oscillation. Even without applied oscillations, fibers are visible in these $\left|\widehat{I}\right|$ images (example: Figure 2A) as regions of increased $\left|\widehat{I}\right|$ relative to the liquid regions that form the pores within the fibrin network. When an oscillation is applied, $\left|\widehat{I}\right|$ images are similar to the no-oscillation condition, except at $F_d$ (Supplementary Video S3 bottom, Figures 2A–D) where regions of elevated $\left|\widehat{I}\right|$ are evident and lie on a subset of fiber pixels. To remove the portion of $\left|\widehat{I}\right|$ which is independent of applied oscillations, we first define a background image $\langle \left|\widehat{I}\right|\rangle$ to be the mean value of $\left|\widehat{I}\right|$ across all frequencies, excluding 0 and $F_d$ (Figure 2E) and then $<\left|\widehat{I}\right|>$ is subtracted from each $\left|\widehat{I}\right|$ image (example: Figures 2F–H). For the remainder of this paper we redefine $\left|\widehat{I}\right|$ as $\left|\widehat{I}\right|-$$<\left|\widehat{I}\right|>$ to simplify notation, unless otherwise noted. The $\left|\widehat{I}\right|$ image at $F_d$ (Figure 2G) highlights oscillating pixels, but cannot identify the fibers that do not oscillate, since fibers not oscillating in Figure 2G are indistinguishable from the liquid region. To identify both oscillating and non-oscillating fibers, image masks can be generated from $<I>$ images (example: Figure 1A) and applied to $\left|\widehat{I}\right|$ images (example: Figures 2I–K). Reexamination of pixels iii and iv from Figure 1 shows that the fiber containing pixel iii is oscillating in response to the bead while pixel iv is not (Figures 2G,K). In summary, an increase in pixel intensity fluctuations can be detected for subsets of pixels when oscillatory forces are applied to the fiber network. Such pixel intensity oscillations preserve the frequency of the applied force and are identifiable after mean-magnitude subtraction.

FIGURE 1

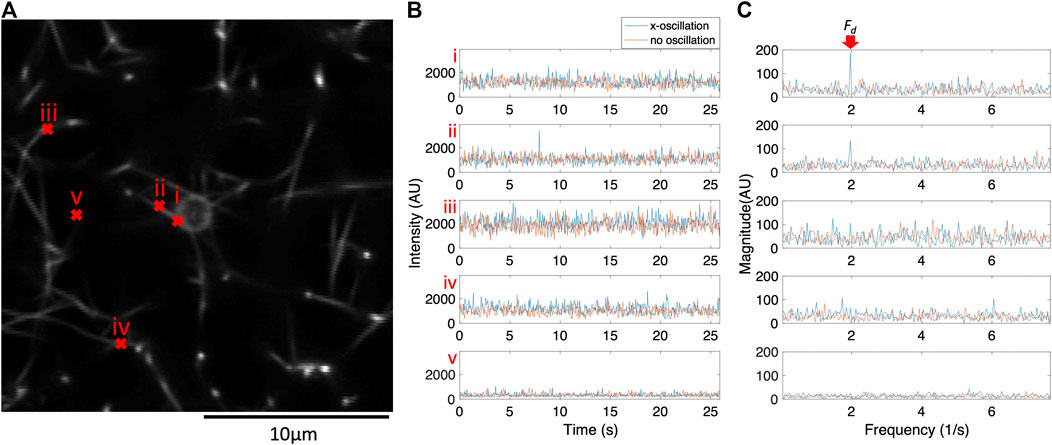
FIGURE 1. The frequency components of pixel intensity fluctuations for a subset of pixels respond to the physical oscillations of the bead. For this subset of pixels, peak intensity fluctuations occur at the same frequency as the optical tweezers oscillation ($F_d$). (A) Time averaged fluorescence intensity image. White regions are fibers labeled with fluorescent dye. The bead is in the center of the image. Red X symbols indicate the position of representative pixels shown in panels (B,C). Point i is on the edge of the bead. Point ii, iii, iv are on fibers. Point v is in the liquid region. (B) Fluorescence intensity of pixels over time with optical tweezers either oscillating in the x-direction (blue) or not oscillating (orange). (C) Magnitude spectra of the 1-D Fourier transformed fluorescence intensity in time with optical tweezers either oscillating in the x-direction (blue) or not oscillating (orange). A red arrow highlights $F_d$.

FIGURE 2

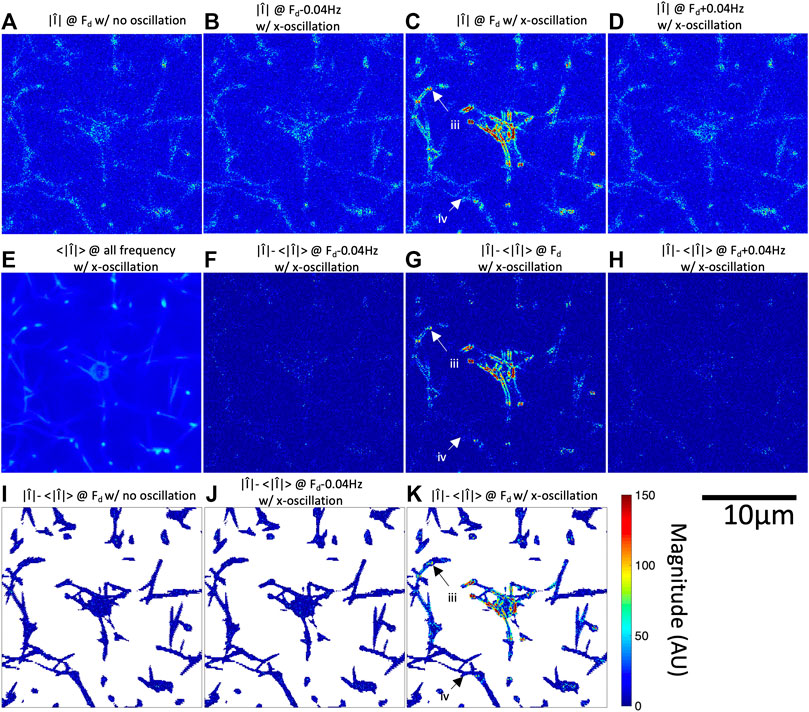
FIGURE 2. Fourier magnitude image at $F_d$ identifies subsets of fibers which oscillate with the optically trapped bead. Identification of these fibers can be improved by mean-magnitude background subtraction and masking of the liquid regions. (A) Fourier magnitude at $F_d$ with no applied bead oscillations. Fourier magnitude at (B)$F_d-0.04$ Hz, (C)$F_d$, and (D)$F_d+0.04$ Hz while the bead is oscillated in the x-direction. (E) Mean magnitude image over all frequencies excluding 0 Hz and $F_d$. Mean-magnitude subtracted images at (F)$F_d-0.04$ Hz, (G)$F_d$, and (H)$F_d+0.04$ Hz while the bead is oscillated in the x-direction. (I) Mean-magnitude subtracted image at $F_d$ while bead is not oscillated displaying only pixels covering the fiber network. (J) Mean-magnitude subtracted image at $F_d-0.04$ Hz displaying only pixels covering the fiber network. (K) Mean-magnitude subtracted image at $F_d$ displaying only pixels covering the fiber network. Arrows in panel (C,G,K) indicate locations of pixels iii and iv in Figure 1.

In addition to $\left|\widehat{I}\right|$, we investigated the corresponding phase of pixel fluctuations, $\angle \widehat{I}$ (Supplementary Video S3 top). In the absence of applied oscillations, $\angle \widehat{I}$ is random and uniformly distributed (Figures 3A,B). When an oscillation is applied to the bead, the $\angle \widehat{I}$ at $F_d$ displays local organization along some of the fibers. These fibers appear as two joined parallel lines shifted in phase by π radians (Figure 3D). The phase distribution of all pixels becomes non-uniform exhibiting modes separated by π (Figures 3D,E). This π shift is an artifact of imaging due to the motion of the fibers relative to the fixed position of pixels, such that as a fiber moves rightwards, the pixels on the right side of the fiber get brighter. At the same time, pixels on the left side of the fiber get dimmer. The relationship reverses as the fiber moves leftwards. This distinct pattern allows for easy identification of the oscillating fibers by eye. We can distinguish the background liquid region and non-oscillating fibers which both have random $\angle \widehat{I}$ distributions by applying the $\langle I\rangle$ mask to exclude the liquid regions just like we did with the $\left|\widehat{I}\right|$ image (Figure 3G). Notably, the fibers which have increased $\angle \widehat{I}$ organization in Figure 3G match the fibers which show increased $\left|\widehat{I}\right|$ in Figures 2K, 3C,F. The organization of the phase of the pixel intensity fluctuations at $F_d$ can be quantified using the Orientational Order Parameter (OOP), which treat the phase vectors as pseudovectors with components equal to $cos\left(\angle \widehat{I}\right)$ and $sin\left(\angle \widehat{I}\right)$ (Figure 3H) ([11, 32, 44]). A locally disordered system will have a local OOP of 0 while a locally ordered (i.e. aligned) system will have a local OOP of 1. In this work, we define “local” to be pixels in a seven by seven pixel neighborhood. In summary, fiber fluctuations resulting from forced bead oscillations are detectable by $\angle \widehat{I}$ and $\left|\widehat{I}\right|$, while local organization of $\angle \widehat{I}$ can be quantified using OOP.

FIGURE 3

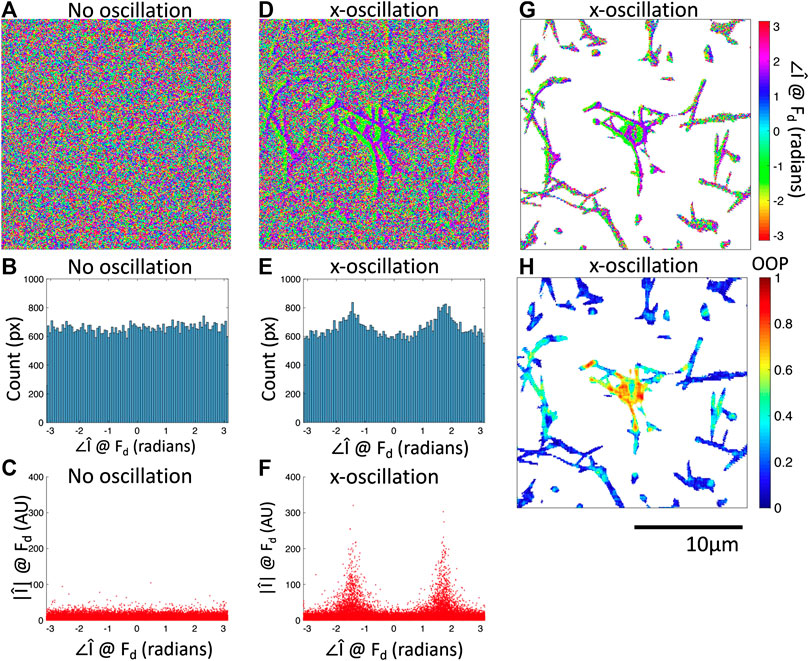
FIGURE 3. Fourier phase images at $F_d$ identify subsets of fibers which oscillate with the bead. (A) Phase image at $F_d$ with no applied oscillation. (B) Histogram of the phase image in panel A showing uniformly distributed phase. (C) Comparison of phase and magnitude for each pixel with no applied oscillation. (D) Phase image at $F_d$ with oscillation applied in the x-direction. The two sides of the bead and some fibers show a distinct pattern. (E) Histogram of the phase image in panel D showing two peaks in the distribution of the phase. (F) Comparison of phase and magnitude for each pixel with oscillation applied in the x-direction. Pixels with increased magnitude tend toward one of the peaks in the phase distribution. (G) Phase image at $F_d$ from panel (D) displaying only pixels covering the fiber network. (H) Local OOP of the phase image from panel (D) displaying only pixels covering the fiber network. Local OOP is computed for each seven by seven pixel region. The organized regions have high OOP and the unorganized regions have low OOP.

We have shown that oscillation of the optical tweezers with an amplitude of 1 m results in a response from the bead and a subset of the fiber network detectable by the $\angle \widehat{I}$, $\left|\widehat{I}\right|$, and OOP. Next, we investigate how $\angle \widehat{I}$, $\left|\widehat{I}\right|$, and OOP change with oscillation amplitude or direction (Figure 4). There is a subtle increase in the $\left|\widehat{I}\right|$ as the amplitude of oscillation was increased from 1 μm to 1.2 μm (Figure 4A). While it is difficult to directly identify differences in the $\angle \widehat{I}$ in response to increasing the amplitude of oscillation, the increased fiber recruitment and phase organization of already oscillating fibers is apparent when looking at the OOP image (Figures 4B,C). Conversely, decreasing the amplitude of oscillation results in decreasing $\left|\widehat{I}\right|$ and OOP (Figure 4). At an oscillation amplitude of 0.2 μm, the $\angle \widehat{I}$, $\left|\widehat{I}\right|$, and OOP are indistinguishable from the no-oscillation control (Figure 4). Subtle differences appear in the $\angle \widehat{I}$ and OOP images with oscillations at or above 0.5 m, but not the $\left|\widehat{I}\right|$ image (Figure 4). This indicates that the $\angle \widehat{I}$ is more sensitive to small oscillations in the fiber network than the $\left|\widehat{I}\right|$. Now that we have shown pixel fluctuations are dependent on the optical tweezers oscillation amplitude, we next investigated if the subset of image pixels that are phase coupled (i.e. on fibers) changes with bead oscillation direction. Experiments are repeated with forced oscillations in the y-direction after oscillations in the x-direction, both with 1 μm oscillation of the optical tweezers. The in-focus fiber network structure can be seen in the $\langle I\rangle$ image for each bead (Figure 5A). It is observed that some subset of the fiber network responds to the oscillation of the bead and this response can been seen in the $\left|\widehat{I}\right|$, $\angle \widehat{I}$, and OOP images (Figures 5B–G). The subset of engaged fibers is dependent on the direction of the bead oscillation (Figure 5 arrows). We can compare the response of the fiber network to the direction of oscillation by looking at the differences in $\left|\widehat{I}\right|$ images between applying oscillation in the x-direction or y-direction. It is apparent that some regions of the fiber network are more responsive to oscillation in the x-direction (blue) or oscillation in the y-direction (red) (Figure 6A). This preference in response suggests fluctuations travel farther through the network along the axis of oscillation. This trend can be visualized by comparing $\left|\widehat{I}\right|$ of pixels located along the oscillation direction of the bead to the pixels located perpendicular to the oscillation direction (Figure 6B). Four regions of the $\left|\widehat{I}\right|$ image from Figures 5B,C, each $\pi /4$ radians wide, are denoted as either parallel (cyan) or perpendicular (magenta) to the axis of oscillation (Figure 6B). Figure 6C shows that $\left|\widehat{I}\right|$ of the fibers decreases with distance from the bead, but to a lesser extent in the direction parallel to the oscillation. The force transmission observed in individual experiments is complex and not easily predicted from the $\langle I\rangle$ image. For example, when bead iv in Figure 5C is oscillated vertically, fibers below the bead exhibit elevated $\left|\widehat{I}\right|$ while fibers above the bead do not. In summary, the response of the fiber network to the oscillation of an embedded bead depends on the fiber network and the direction of oscillation.

FIGURE 4

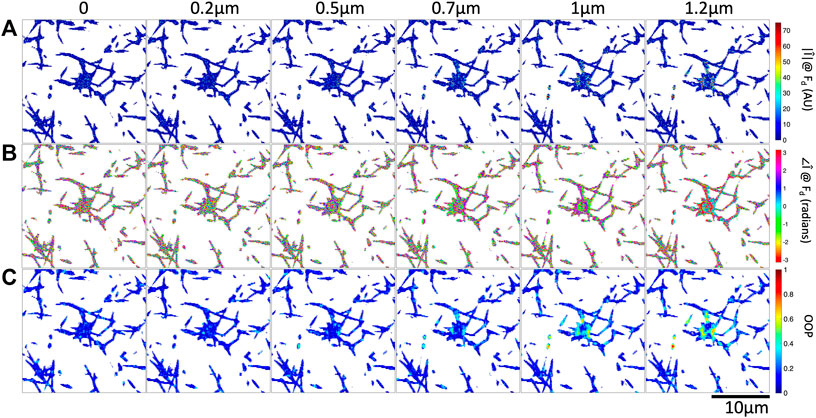
FIGURE 4. Increasing optical tweezers oscillation amplitude results in increased Fourier magnitude and more organized Fourier phase at $F_d$. The amplitude of optical tweezers oscillation is indicated at the top of each column. (A) Fourier magnitude at $F_d$ for a bead within a fibrin fiber network. Corresponding (B) Fourier phase and (C) local OOP at $F_d$ are shown.

FIGURE 5

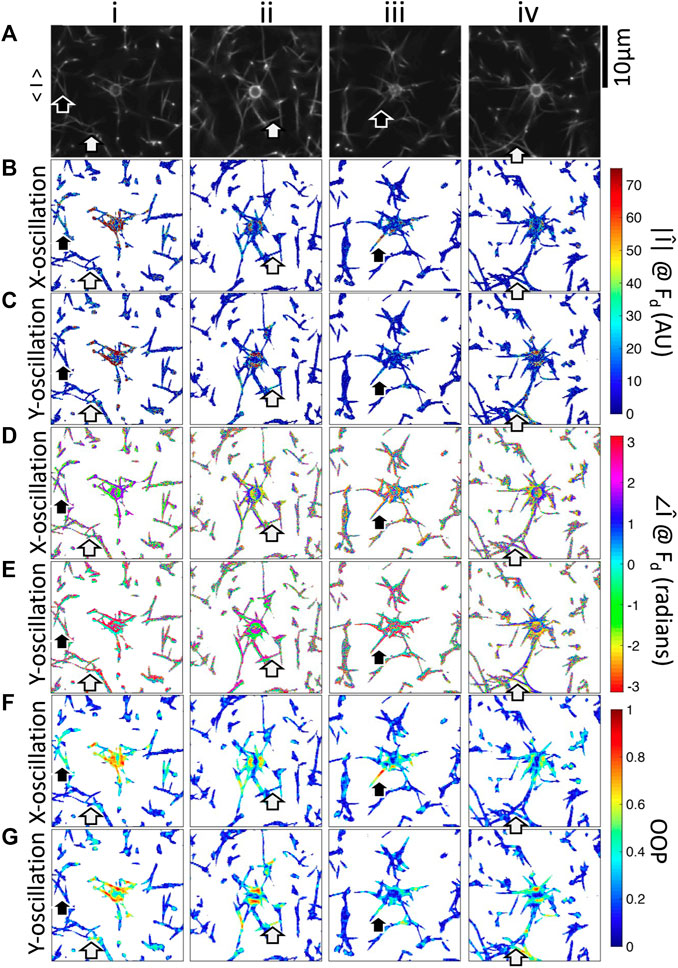
FIGURE 5. Fourier magnitude, phase, and OOP images of four beads embedded in fibrin networks oscillated in the x-direction or y-direction. i–iv are different beads. (A) Fluorescence microscopy images showing the bead and fibers. Mean-magnitude subtracted images at $F_d$ for oscillation in either the (B)x-direction or (C)y-direction. Phase images at $F_d$ with oscillation in either the (D)x-direction or (E)y-direction. OOP images at $F_d$ in either the (F)x-direction or (G)y-direction. Black arrows indicate regions where the network responds more to oscillations in the y-direction while white arrows indicate the opposite.

FIGURE 6

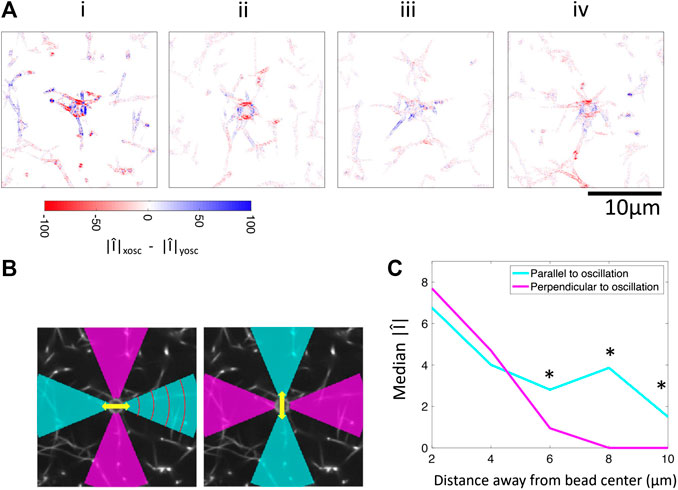
FIGURE 6. Comparison of Fourier magnitudes in response to applied oscillations in the x-direction and y-direction. (A) Difference between Fourier magnitude at $F_d$ in response to x-oscillation and y-oscillation. Blue indicates greater response to x-oscillation while red indicates greater response to y-oscillation. i–iv match the beads shown in Figure 5. (B) Image illustrating binning for panel (C). Yellow arrow indicates the axis of oscillation. $\pi /4$ radian wide regions parallel (cyan) or perpendicular (magenta) to the axis of oscillation are binned according to their distance from the center of the bead with a bin width of 2 μm, indicated by the red arcs. (C) The median of the Fourier magnitude for each bin is plotted (Supplementary Figure S2 presents the distribution of the data as violin plots with quartile ranges). *indicates medians are statistically different as determined by Wilcoxon rank sum test ($p<{10}^{-5}$).

4 Discussion

We have shown a method to identify which fibers within a 3-D fiber network carry tension in response to the application of a localized force. Specifically, the method determines which fibers are oscillating in phase with an actively driven bead embedded within a pore of the network and assumes that pure elastic forces are driving these fiber motions. Here, fiber oscillation is measured by quantifying intensity fluctuations of all pixels in a plane confocal to the bead. As expected, Fourier magnitudes of pixel intensity fluctuations ($\left|\widehat{I}\right|$) at the drive frequency ($F_d$) are sensitive to even sub-pixel fiber oscillations (Figure 1C). By looking at the $\left|\widehat{I}\right|$, we find that displacements are larger along the direction of the bead’s oscillatory displacement (Figure 6), which is also the expected behavior in continuum viscoelastic materials [38]. In our system, however, we do not find quantitative agreement between the continuum-based theory and our data. Unlike in a continuum, we observe displacement propagation along complex paths at the scale of the mesh, likely dependent on the architecture of the local fiber network (Figures 5B,C). In addition to $\left|\widehat{I}\right|$, we find that pixels intensity fluctuations along fibers either have random phase ($\angle \widehat{I}$) or exhibit local pixel neighborhoods of similar $\angle \widehat{I}$ occurring on fibers that $\left|\widehat{I}\right|$ indicate are under tension. In order to quantify and aid in the detection of such neighborhoods we compute the Orientational Order Parameter, or OOP. By use of the OOP, we identified distinctive sets of fibers that are engaged as the direction and amplitude of oscillation of applied force varied (Figures 4C, 5F,G). Importantly, while we are interested in the static, or zero-frequency force map, we opt to use low-frequency oscillation of the bead in order to take advantage of lock-in detection and further to provide resilience to forces beyond those applied by the optical tweezers (e.g., cell-generated forces). The choice of a low frequency ensures our findings are not complicated by nonlinear material properties of the system that emerge at higher frequency oscillations or viscoelastic properties of the local mesh. Our choice of applying small displacements relative to the scale of the pores also ensures that we are measuring the current state of the system and not further complicate the measurement with additional network rearrangement and fiber alignment that emerge with larger applied deformations [21,22,39]. As compared to methods such as fiber tracing and application of static forces, our method may be more suitable for use in the presence of cells or other force centers, which can induce fiber displacements in addition to the actively driven displacements. Also, the lower frequencies and displacements are well within the technical capabilities of our optical tweezers-confocal microscope apparatus.

Force transmission pathways as detected by fiber fluctuation analysis is highly variable from bead to bead due to the different network structure. One consistent observation is that fibers not appearing to be connected to the bead in the confocal $\langle I\rangle$ image still oscillated in phase with that bead (Figures 4, 5). This coordination is most likely due to the fact that not all force transmission pathways are in the plane containing the midpoint of the trapped bead. In order to identify potential out-of-plane force transmitting fibers, we overlay the OOP image on top of confocal z-stacks of the fiber network (Figure 7). We find that there are fibers or a network of fibers which connect all the isolated in-plane high OOP and $\left|\widehat{I}\right|$ regions to the bead. Black arrows in Figure 7 identify local sets of out-of-plane fibers connected on both sides to fibers exhibiting oscillations as detected by the local OOP (Figure 7). It is evident from the data that some fiber chains transmit forces while others do not. Extension of pixel fluctuation intensity analysis to include these out-of-plane fibers is a goal for future method development.

FIGURE 7

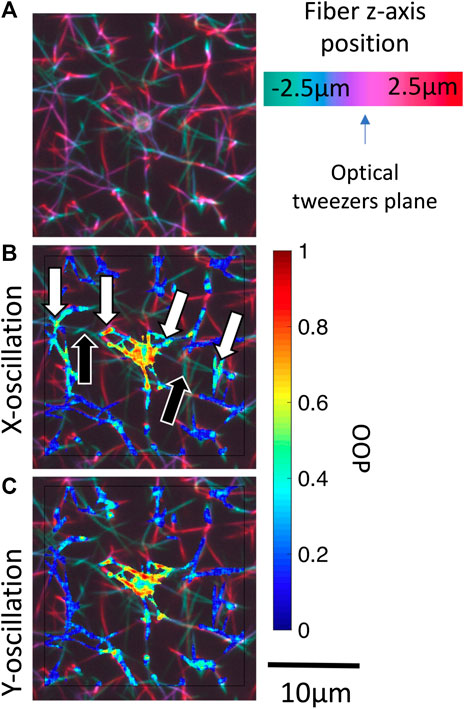
FIGURE 7. Identification of potential out-of-plane force transmission pathways. (A) Pseudo color projection is used to encode depth within a 3-D confocal image stack for bead i (Figure 5). Masked local OOP images are superposed onto the depth images for oscillations in the (B)x-direction and (C)y-direction. Black arrows indicate out-of-plane fibers which may be transmitting forces. White arrows indicate the oscillating fiber network regions on either side of the out-of-plane fiber. Supplementary Figure S3 shows OOP overlaid on 3-D confocal image stack for beads i-iv.

Lastly, we discuss a caveat of this intensity fluctuation analysis. $\left|\widehat{I}\right|$, $\angle \widehat{I}$, and OOP should not be directly compared between fibers, especially fibers of different fluorescence brightness $<I>$. More precisely, a major factor determining the $\left|\widehat{I}\right|$ is the gradient of fluorescence brightness along the direction of oscillation. For example, the gradients of $\langle I\rangle$ the along x (Figure 8A) and y (Figure 8B) axes for bead i in Figure 5 are shown. Magnified regions of Figures 8A,B show that a fiber aligned with the y axis has steep intensity gradients across the fiber in the x-direction and shallow gradient along the fiber in the y-direction (Figures 8C,D). Consequently, detection of oscillation in the y-direction will not be as sensitive as in the x-direction. Of note, punctate bright regions (Figures 8A,B black arrows) have steep intensity gradients along all directions and consequently our method should be equally sensitive to oscillations along any axis at such regions. We show that there are parts of the fiber network which have very shallow or non-existent gradient intensity. This lack of gradient is especially evident along a uniformly fluorescently labeled fiber, which makes it difficult to detect the displacement of that fiber. This observation motivates future work in which texture in fiber fluorescence intensity could be introduced to every fluorescent fiber thus mitigating anisotropic sensitivity to displacement. Such texture could be achieved either through a labeling strategy or the use of structured light illumination. A labeling strategy that introduces bright and high contrast images would enable the use of well-established tracking methods such as optical flow analysis, digital image correlation, or erosion-and-reconstruction methods [40–49].

FIGURE 8

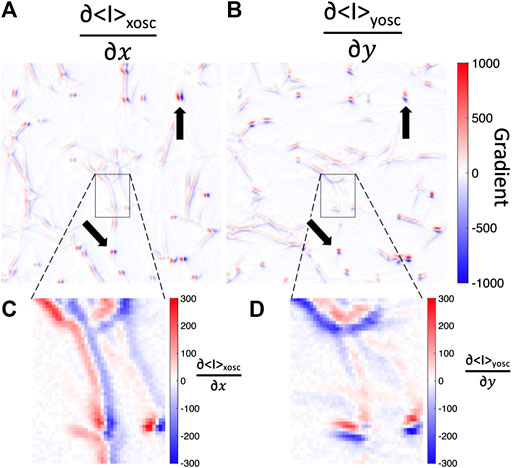
FIGURE 8. Fluorescence image intensity gradients are steep across fibers but not along fibers. Spatial gradients in the (A)x-direction or (B)y-direction of the mean-intensity image while the bead is oscillated in the (A)x-direction (${\langle I\rangle }_x$) or (B)y-direction (${\langle I\rangle }_y$). Black arrows indicate some of the brightly fluorescent points in the fibers network which have steep intensity gradients in both directions. (C,D) Magnified area showing a vertically aligned fiber which has a distinct gradient across in the x-direction but a shallow gradient in the y-direction.

In conclusion, we developed a straightforward approach to quantitatively determine which fibers are participants in force transmission highways. The use of local variations in the phase of intensity fluctuations provides sensitivity to even small displacements in the fiber network, where magnitude of intensity fluctuations were not distinguishable from noise. Ultimately, we aim to observe changes to the force transmission characteristics of biologically derived fiber networks and how these characteristics change as cells interact with the ECM. While we have shown the response of a fiber network in its relaxed state, future application of this technique lies in exploring how the response changes when the network contains cells. For example, cell contractile forces will apply a tensile preload that may change the subset of tensed fibers thus altering the scope of cell-cell force communication. Such observations of how force transmission pathways change in response to cellular contraction and ECM remodeling offers potentially new insights into processes such as growth, wound healing, cancer growth and metastasis.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation. Raw data related to the article can also be found at the following Dryad link: https://doi.org/10.7280/D1ZT21.

Author Contributions

QH was responsible for planning, data acquisition, analysis, and writing for the paper. TM and AG were responsible for analysis and writing for the paper. AL and EB were responsible for planning, analysis, and writing for the paper.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We would like to thank Micah Lim for assisting with data acquisition and editing the manuscript. We would like to thank Dr. Mark Keating and Alicja Jagiełło for their contribution in building the optical tweezers microscopy system. QH and EB acknowledges support from the United States Air Force Office of Scientific Research FA9550-17-1-0,193 and the Office of the President of the University of California. TM and AG acknowledges support from NIH R01 HL129008 and NIH T32 HL116270. AL acknowledges partial support from NSF-DMR-1709785.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2020.568736/full#supplementary-material.

References

1. Janmey PA, Winer JP, Murray ME, Wen Q. The hard life of soft cells. Cell Motil Cytoskeleton (2009) 66:597–605. doi:10.1002/cm.20382

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Falvo PA, Fletcher D, Reinhart-King CA. Stiffness sensing in cells and tissues. Physiol Rev (2019) 100:455–506. doi:10.1007/978-1-4020-9003-5_11

CrossRef Full Text | Google Scholar

3. Edmondson R, Broglie JJ, Adcock AF, Yang L. Three-dimensional cell culture systems and their applications in drug discovery and cell-based biosensors. Assay Drug Dev Technol (2014) 12:207–18. doi:10.1089/adt.2014.573

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Caliari SR, Burdick JA. A practical guide to hydrogels for cell culture. Nat Methods (2016) 13:405–14. doi:10.1038/nmeth.3839

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Pedersen JA, Swartz MA. Mechanobiology in the third dimension. Ann Biomed Eng (2005) 33:1469–90. doi:10.1007/s10439-005-8159-4

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Buxboim A, Rajagopal K, Brown AE, Discher DE. How deeply cells feel: methods for thin gels. J Phys Condens Matter (2010) 22:194116. doi:10.1088/0953-8984/22/19/194116

PubMed Abstract | CrossRef Full Text | Google Scholar

7. FabryMünster C, Pastore JJ, MacKintosh FC, Lubensky TC, Janmey PA. Nonlinear elasticity in biological gels. Nature (2005) 435:191–4. doi:10.1038/nature03521

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Rudnicki MS, Cirka HA, Aghvami M, Sander EA, Wen Q, Billiar KL. Nonlinear strain stiffening is not sufficient to explain how far cells can feel on fibrous protein gels. Biophys J (2013) 105:11–20. doi:10.1016/j.bpj.2013.05.032

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Ma X, Schickel ME, Stevenson MD, Sarang-Sieminski AL, Gooch KJ, Ghadiali SN, et al. Fibers in the extracellular matrix enable long-range stress transmission between cells. Biophys J (2013) 104:1410–8. doi:10.1016/j.bpj.2013.02.017

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Ronceray P, Broedersz CP, Lenz M. Fiber networks amplify active stress. Proc Natl Acad Sci USA (2016) 113:2827–32. doi:10.1073/pnas.1514208113

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Clark RA. Fibrin and wound healing. Ann N Y Acad Sci (2001) 936:355–67. doi:10.1111/j.1749-6632.2001.tb03522.x

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Morin KT, Tranquillo RT. In vitro models of angiogenesis and vasculogenesis in fibrin gel. Exp Cell Res (2013) 319:2409–17. doi:10.1016/j.yexcr.2013.06.006

PubMed Abstract | CrossRef Full Text | Google Scholar

13. de la Puente P, Ludeña D. Cell culture in autologous fibrin scaffolds for applications in tissue engineering. Exp Cell Res (2014) 322:1–11. doi:10.1016/j.yexcr.2013.12.017

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Weisel JW, Litvinov RI. Fibrous proteins: structures and mechanisms formation, structure and properties. Subcell Biochem Springer (2017) 82:405–56. doi:10.1007/978-3-319-49674-0_13

CrossRef Full Text | Google Scholar

15. Collet JP, Shuman H, Ledger RE, Lee S, Weisel JW. The elasticity of an individual fibrin fiber in a clot Proc Natl Acad Sci USA (2005) 102:9133–7. doi:10.1073/pnas.0504120102

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Liu W, Carlisle C, Sparks E, Guthold M. The mechanical properties of single fibrin fibers. J Thromb Haemostasis (2010) 8:1030–6. doi:10.1111/j.1538-7836.2010.03745.x

CrossRef Full Text | Google Scholar

17. Sun OV, Litvinov RI, Weisel JW, Alber MS. Structural basis for the nonlinear mechanics of fibrin networks under compression. Biomaterials (2014) 35:6739–49. doi:10.1016/j.biomaterials.2014.04.056

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Hudson NE, Houser JR, O'Brien ET, Taylor RM, Superfine R, Lord ST, et al. Stiffening of individual fibrin fibers equitably distributes strain and strengthens networks. Biophys J (2010) 98:1632–40. doi:10.1016/j.bpj.2009.12.4312

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Yesudasan S, Averett RD. Multiscale network modeling of fibrin fibers and fibrin clots with protofibril binding mechanics. Polymers (2020) 12:1223. doi:10.3390/polym12061223

CrossRef Full Text | Google Scholar

20. Lim BB, Lee EH, Sotomayor M, Schulten K. Molecular basis of fibrin clot elasticity. Structure (2008) 16:449–59. doi:10.1016/j.str.2007.12.019

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Grill MJ, Kernes J, Slepukhin VM, Wall WA, Levine AJ (2020). Directed force propagation in semiflexible networks. arXiv preprint arXiv:2006.15192.

Google Scholar

22. Wang H, Abhilash A, Chen CS, Wells RG, Shenoy VB. Long-range force transmission in fibrous matrices enabled by tension-driven alignment of fibers. Biophys J (2014) 107:2592–603. doi:10.1016/j.bpj.2014.09.044

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Notbohm J, Lesman A, Rosakis P, Tirrell DA, Ravichandran G. Microbuckling of fibrin provides a mechanism for cell mechanosensing. J R Soc Interface (2015) 12:20150320. doi:10.1098/rsif.2015.0320

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Hart A, Sopher RS, Goren S, Shelah O, Tchaicheeyan O, Lesman A. Force chains in cell–cell mechanical communication. J R Soc Interface (2019) 16:20190348. doi:10.1098/rsif.2019.0348

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Natan S, Koren Y, Shelah O, Goren S, Lesman A. Long-range mechanical coupling of cells in 3d fibrin gels. Mol Biol Cell (2020) 31:1474–85. doi:10.1091/mbc.E20-01-0079

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Vader D, Kabla A, Weitz D, Mahadevan L. Strain-induced alignment in collagen gels. PLoS One (2009) 4:e5902. doi:10.1371/journal.pone.0005902

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Kim J, Feng J, Jones CAR, Mao X, Sander LM, Levine H, et al. Stress-induced plasticity of dynamic collagen networks. Nat Commun (2017) 8:842–7. doi:10.1038/s41467-017-01011-7

PubMed Abstract | CrossRef Full Text | Google Scholar

28. CardonaPreibisch Q, Ghosh RP, Engelke H, Rycroft CH, Cassereau L, Sethian JA, et al. Rapid disorganization of mechanically interacting systems of mammary acini. Proc Natl Acad Sci USA (2014) 111:658–63. doi:10.1073/pnas.1311312110

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Korff T, Augustin HG. Tensional forces in fibrillar extracellular matrices control directional capillary sprouting. J Cell Sci (1999) 112 (Pt 19):3249–58

PubMed AbstractGoogle Scholar

30. Keating M, Kurup A, Alvarez-Elizondo M, Levine A, Botvinick E. Spatial distributions of pericellular stiffness in natural extracellular matrices are dependent on cell-mediated proteolysis and contractility. Acta Biomater (2017) 57:304–12. doi:10.1016/j.actbio.2017.05.008

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Schindelin J, Arganda-Carreras I, Frise E, Kaynig V, Longair M, Pietzsch T, et al. Fiji: an open-source platform for biological-image analysis. Nat Methods (2012) 9:676–82. doi:10.1038/nmeth.2019

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Meier G, Saupe A. Dielectric relaxation in nematic liquid crystals. Mol Cryst Liq Cryst (1966) 1:515–25.

CrossRef Full Text | Google Scholar

33. Chaikin P, Lubensky T. Principles of condensed matter physics. Cambridge: cambridge univ. Press (1995).

CrossRef Full Text

34. Umeno A, Kotani H, Iwasaka M, Ueno S. Quantification of adherent cell orientation and morphology under strong magnetic fields. IEEE Trans Magn (2001) 37:2909–11. doi:10.1109/20.951344

CrossRef Full Text | Google Scholar

35. Grosberg A, Kuo PL, Guo CL, Geisse NA, Bray MA, Adams WJ, et al. Self-organization of muscle cell structure and function. PLoS Comput Biol (2011) 7:e1001088. doi:10.1371/journal.pcbi.1001088

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Morris TA, Naik J, Fibben KS, Kong X, Kiyono T, Yokomori K, et al. Striated myocyte structural integrity: automated analysis of sarcomeric z-discs. PLoS Comput Biol (2020) 16:e1007676. doi:10.1371/journal.pcbi.1007676

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Grosberg PM, Feshbach H. Methods of theoretical Physics. New York: McGraw-Hill Book Campany, Inc (1954). Vol. 1.

Google Scholar

38. Levine AJ, Lubensky T. One- and two-particle microrheology. Phys Rev Lett (2000) 85:1774. doi:10.1103/PhysRevLett.85.1774

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Han YL, Ronceray P, Xu G, Malandrino A, Kamm RD, Lenz M, et al. Cell contraction induces long-ranged stress stiffening in the extracellular matrix. Proc Natl Acad Sci USA (2018) 115:4075–80. doi:10.1073/pnas.1722619115

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Horn BK, Schunck BG. Determining optical flow techniques and applications of image understanding. Int Society Opt Photonics (1981) 281:319–31

Google Scholar

41. Beauchemin SS, Barron JL. The computation of optical flow. ACM Comput Surv (1995) 27:433–66. doi:10.1109/wvm.1989.47101

CrossRef Full Text | Google Scholar

42. Mesbah M. Gradient-based optical flow: a critical review. In: ISSPA’99. Proceedings of the fifth international symposium on signal processing and its applications, 1 (1999). Brisbane, Queensland, Australia, Australia; 22-25 August 1999; p. 467–70. IEEE Cat. No. 99EX359).

Google Scholar

43. Chen JG, Davis A, Wadhwa N, Durand F, Freeman WT, Büyüköztürk O. Video camera–based vibration measurement for civil infrastructure applications. J Infrastruct Syst (2017) 23:B4016013. doi:10.1061/(asce)is.1943-555x.0000348

CrossRef Full Text | Google Scholar

44. Yang J, Bhattacharya K. Augmented lagrangian digital image correlation. Exp Mech (2019) 59:187–205. doi:10.1007/s11340-018-00457-0

CrossRef Full Text | Google Scholar

45. Pan B, Qian K, Xie H, Asundi A. Two-dimensional digital image correlation for in-plane displacement and strain measurement: a review. Meas Sci Technol (2009) 20:062001. doi:10.1088/0957-0233/20/6/062001

CrossRef Full Text | Google Scholar

46. LiphardtWeaver J, Metzner C, Skodzek K, Lang N, Thievessen I, Mark C, et al. Three-dimensional force microscopy of cells in biopolymer networks. Nat Methods (2016) 13:171–6. doi:10.1038/nmeth.3685

PubMed Abstract | CrossRef Full Text | Google Scholar

47. ParkerSheehy E-Y, Chawla N, Jing T, Torquato S, Jiao Y. Accurate modeling and reconstruction of three-dimensional percolating filamentary microstructures from two-dimensional micrographs via dilation-erosion method. Mater Char (2014) 89:33–42. doi:10.1016/j.matchar.2013.12.011

CrossRef Full Text | Google Scholar

48. Liang L, Jones C, Chen S, Sun B, Jiao Y. Heterogeneous force network in 3d cellularized collagen networks. Phys Biol (2016) 13:066001. doi:10.1088/1478-3975/13/6/066001

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Keating M, Lim M, Hu Q, Botvinick E. Selective stiffening of fibrin hydrogels with micron resolution via photocrosslinking. Acta Biomater (2019) 87:88–96. doi:10.1016/j.actbio.2019.01.034

PubMed Abstract | CrossRef Full Text | Google Scholar