Mitigation of the Stopping Power Effect on Proton-Boron11 Nuclear Fusion Chain Reactions

A proton beam with a velocity of the order of 10⁹ cm/s is generated to interact with a charge neutral hydrogen-boron medium such as H₃B. The created charged particles are confined by magnetic fields. This concept was the basis for a novel non-thermal fusion reactor, published recently in Laser and Particle Beams [1]. The fusion is initiated by protons followed by a process of chain reactions in a neutral medium density of the order of 10¹⁹ cm⁻³, heated by the pB¹¹ fusion created alphas up to a temperature of about one electron volt. In this system, the radiation losses by bremsstrahlung are negligible and the plasma thermal pressure is low. The ionization of the gaseous medium is caused by the alpha elastic nuclear collisions with the hydrogen atoms and their thermal heating and it is < 10⁻⁴. An external electric field is applied to avoid the energy losses of the protons particles by friction, due to their interaction with the electrons of the medium, to keep the proton-boron fusion at the maximum cross section of about 600 keV at the center of mass frame of reference. The alphas created in the pB¹¹ fusion undergo nuclear elastic collisions with the hydrogen protons of the medium and causing a pB¹¹ chain reaction. In this paper the equation of motion of these proton and alphas are solved numerically for the one-dimensional (1D) case, and their possible solutions are analyzed and discussed. Specifically, it is shown how the electric field can mitigate the stopping power for the proton11-proton nuclear fusion. Our results show that starting from a bunch of 10¹³ protons in our volume, an alpha number of particles of 6 × 10¹⁶ was accepted after a 5 ms cycle of applying our specially designed electric field. Consequently, the medium temperature was raised to 1.3 eV. The aim of this paper is to present a new concept by addressing only the main physical processes and not to present a complete engineering design. The configuration for mitigating the stopping power and the numerical solution in this paper is novel and promises few applications with a viable proton-boron11 fusion reactions.

Introduction

Two different distinctive schemes for solving the energy problem with fusion have been investigated in the past 60 years: (1) Magnetic confinement fusion (MCF) based on high intensity magnetic fields (several Teslas) confining low-density (~10¹⁴ cm⁻³) and high temperatures (~10 keV) plasmas for long or practically continuous times (2). Inertial confinement fusion (ICF) based on rapid heating and compressing the fusion fuel to very large densities (~10²⁴ cm⁻³) and very high temperatures for a very short time. The main fusion candidate so far has been the interactions of the heavy hydrogen isotopes deuterium and tritium yielding an alpha and a neutron.

In a recent paper [1] a novel concept for a nuclear fusion reactor has been proposed for proton-boron11 yielding 3 alphas,

$\begin{array}{ll}p{+}^{11}B\to 3\alpha +8.9MeV& (1)\end{array}$

In this novel reactor [1] the fusion events are initiated by protons accelerated by a high power laser (or by an accelerator) followed by a process of chain reactions in a medium. This medium (e.g., H₃B) is a charge-neutral gas with a density of the order of 10¹⁹ cm⁻³ that is heated to a maximum one (or few) electron-volt (eV), so that the radiation level and the plasma thermal pressure are very low. Here the alphas collide with the hydrogen-protons of the medium causing a pB¹¹ chain reaction without neutrons. An external electric field keeps the chain reaction process going on, for a pulse long enough to get a chain reaction producing alphas.

The novel scheme described here can be used also for a combination such as helium3-deuterium (He³+D→p + α+18.3 MeV), proton-litium6 (p+⁶Li→He³ + α+4.0 MeV), proton-litium7 (p+⁷Li→2α+17.2 MeV), etc. In this paper we follow the clean (i.e., without neutrons) proton-boron11 fusion yielding 3α. The starting point of this idea is supported by the experimental development in the last decade for proton-boron11 fusions created by high irradiance lasers as described in the next paragraph.

Using lasers, 10³ alphas were derived in pB¹¹ reactions [2] by Belyaev et al. in 2005. In 2013 the lasers produced more than 10⁷ pB¹¹ fusions [3] at LULI laboratory in France. At Prague in 2014 the PALS facility measured [4] 10⁹ alpha particles and recently [5] in 2020 more than 10¹¹ alphas were published per laser shot.

In section The pB¹¹ Chain Reactions and the Stopping Power Problem we describe our chain reaction and the alpha energy losses (stopping power) due to their interaction with the electrons. In section The Equations of Motion of Charge Particles in an External Electric Field the alpha equations of motion are given for a realistic case in the presence of an external electric field and are solved numerically. In section Discussion and Conclusion a discussion of our scheme is analyzed and our numerical results discussed. In an appendix we check the recombination process and using the Saha equation the proton density and the temperature are calculated.

The PB¹¹ Chain Reactions and the Stopping Power Problem

In a classical collision between two particles 1 (an alpha) and 2 (a proton at rest) with masses m₁ and m₂ accordingly at a scattering angle θ₁, one gets the ratio between the alpha velocity after collision v_1f and its velocity before collision v_1i by [6]

$\begin{array}{ll}\frac{v_{1f}}{v_{1i}}=\left(\frac{m_1}{m_1+m_2}\right)\text{cos }{\theta }_1\pm \left(\frac{1}{m_1+m_2}\right)\sqrt{m_2^2-m_1^2{\theta }_1}& (2)\end{array}$

In this collision the maximum scattering angle θ_1,max for the α particle is $\text{sin }{\theta }_{1,\text{max}}=\frac{m_p}{m_{\alpha }}=\pm 1/4$, namely θ₁ ≤ θ_1,max = ±14.5, namely we have forward and backward scattering to a good approximation.

The maximum energy W_2f acquired by particle 2 that is initially at rest (W_2i = 0) is

$\begin{array}{ll}{W}_{2f}=\left(\frac{4m_1{m}_2}{{(m_1+m_2)}^2}\right)W_{1i}& (3)\end{array}$

In this case the final (minimum) energy W_1f of particle 1 and its initial laboratory energy in comparison with the center of mass energy for this collision is given by

$\begin{array}{l}{W}_{1f}=\left(1-\frac{4m_1{m}_2}{{(m_1+m_2)}^2}\right)W_{1i}={\left(\frac{m_1-m_2}{m_1+m_2}\right)}^2{W}_{1i}\\ \begin{array}{l}{W}_{lab}=W_{1i}=\left(\frac{m_1+m_2}{m_2}\right)W_{cm}\end{array}& (4)\end{array}$

The avalanche of proton-boron11 reaction as described before [7] needs 2 elastic collisions before inducing a nuclear fusion creating 3 new alphas. In the first stage (i) an alpha (created in the pB¹¹ fusion) collides with a proton (at rest in the laboratory frame of reference) and in the second stage (ii) this alpha has a second collision with another proton of the medium (at rest). This energetic proton with an energy $W_{p^{\prime }}$ interacts with a B¹¹ of the medium (at rest) (iii) creating 3 new alphas.

In this paper the chain reaction of proton-boron11 requires only one elastic collision, so that our novel scheme is

$\begin{array}{l}p+B^{11}\to {\alpha }_1+{\alpha }_2+{\alpha }_3\\ {\alpha }_1+H\left(rest,lab\right)\to {{\alpha }_1}^{\prime }+p^{\prime }+e\Rightarrow (i)\\ p^{\prime }+B^{11}\left(rest,lab\right)\to {\alpha }_1+{\alpha }_2+{\alpha }_3+11e(ii)& (5)\end{array}$

After a first collision of an alpha with a hydrogen-proton, the proton gets an energy $W_{p^{\prime }}$ and in the center of mass the energy W_cm(pB¹¹) is given by (3) and (4)

$\begin{array}{l}{W}_{{\alpha }^{\prime }}=\left(1-\frac{16}{25}\right)W_{\alpha }=\frac{9}{25}{W}_{\alpha };W_{p^{\prime }}=\frac{16}{25}{W}_{\alpha }\\ \begin{array}{l}{W}_{cm}\left(p{B}^{11}\right)=\frac{11}{12}·\frac{16}{25}{W}_{\alpha }\cong 0.59W_{\alpha }\end{array}& (6)\end{array}$

Ignoring the electronic stopping power in the medium, an alpha with the energy of about 1 MeV would produce W_cm(pB¹¹) = 590 keV where the fusion cross section is maximum.

The rate of the chain reactions (5) are described by

$\begin{array}{l}\frac{d{n}_p}{dt}=n_H{n}_{\alpha }{\sigma }_{el}{v}_{\alpha }-n_p{n}_B{\sigma }_{fus}{v}_p\\ \begin{array}{l}\frac{d{n}_{\alpha }}{dt}=3n_p{n}_B{\sigma }_{fus}{v}_p\end{array}& (7)\end{array}$

In Equation (7) n_p is the proton density created after colliding with an alpha, and destroyed after a fusion event, as described by (i) and (ii) in Equation (5). σ_el and σ_fus are accordingly the elastic and the fusion cross sections in (5) and v_α is the relative velocity of proton-alpha before the elastic collision, while v_p is the relative velocity of proton-boron in the fusion reaction. In principle, Equation (7) should include recombination terms, however, it can be shown that the recombination rate is expected to be very small in our medium conditions (see Appendix A). The proton-alpha elastic total cross section σ_el is of the order of

$\begin{array}{ll}{\sigma }_{el}(\alpha ,p)\cong \pi {\left(\frac{e^2}{\mu v_{\alpha }^2}\right)}^2& (8)\end{array}$

Where $\mu =\frac{4}{5}{m}_p$ (the alpha-proton reduced mass) and $v_{\alpha }={\left(\frac{2W_{\alpha }}{m_{\alpha }}\right)}^{1/2}$ equals the relative alpha-proton velocity since the proton is initially at rest. This estimate is consistent with more accurate calculations [8, 9] where ${\sigma }_{el}~10^{-24}c{m}^2$.

We are interested in the fusion rate of pB11 i.e. σ_fusv_p, where the fusion cross section is σ_fus and given experimentally [10] and v_p is the relative pB11 velocity, as obtained from W_α (non-relativistic)

$\begin{array}{l}{W}_{cm}\left(p{B}^{11}\right)=\frac{1}{2}\left(\frac{m_p{m}_B}{m_p+m_B}\right)v_p^2=\frac{1}{2}\left(\frac{11}{12}\right)m_p{c}^2{\left(\frac{v_p}{c}\right)}^2\\ \begin{array}{l}{v}_p={\left(\frac{W_{cm}\left(p{B}^{11}\right)\left[keV\right]}{4.58·10^5\left[keV\right]}\right)}^{1/2}c\end{array}& (9)\end{array}$

For example, if $W_{cm}(p{B}^{11})=600keV$ then the relative p-B¹¹ velocity v_p is 1.1 × 10⁹ cm/s and σ_fusv_p ~ 10⁻¹⁵ cm³/s.

In our scheme we use a chain reaction process as described in Equation (7). To make the chain reactions a reality and overcome the objections raised by Shmatov [7] and Belloni et al. [11] we use an external electric field acting on the charged particles in the medium with densities of the order of 10¹⁹ cm⁻³ and temperature of the order 1 eV or less. These electromagnetic field prolong the chain reaction process in a reasonable volume [1] (~10⁴ cm³) by overcoming the Bethe-Bloch energy loss [12] of the alphas and protons due to their collisions with the bound electrons in our neutral gas,

$\begin{array}{l}\frac{d{T}_A}{dx}=-\frac{4\pi Z_A^2{Z}_B{e}^4{n}_0}{m_e{c}^2{\beta }^2}\left[\text{ln}\left(\frac{2m_e{c}^2{\beta }^2{\gamma }^2}{Z_{B}I}\right)-{\beta }^2\right]\\ \begin{array}{l}\beta =\frac{v}{c};\gamma =\frac{1}{\sqrt{1-{\beta }^2}}\end{array}& (10)\end{array}$

The projectile (proton or alpha in our case) with a mass M_A and a charge Z_Ae (e is the positive value of the electron charge) dissipates its energy into the medium (H₃B) via interactions with the electrons of the medium. T_A is the kinetic energy of projectile A, βc is the projectile velocity (β < 1/137), index B is the medium where its particles have a charge Z_Be. The medium density is n₀ [atoms/cm³], m_e is the electron mass and I ~ 10 eV is a phenomenological constant describing the binding of the electrons to the medium.

The Equations of Motion of Charge Particles in an External Electric Field

A constant external field E₀ acting on the medium is taken to revoke the stopping power energy loss. We solve numerically the following equation of motion

$\begin{array}{ll}{M}_A\frac{dv}{dt}=Z_{A}e{E}_0-\frac{d{T}_A}{dx}.& (11)\end{array}$

Theoretically, the calculation of the stopping power is given in the literature [13–16] for different states of the medium. The stopping power contributions are calculated for electrons bound to the target atoms and for the free electron in a plasma medium. The mean excitation energy, I, that appears in the Bethe logarithm can be calculated according to the atoms of the medium under consideration.

For our neutral gas, we take the stopping power given experimentally [17]. The figures of this paper are all given for our numerical solutions with the stopping power given in [17] as will be further explained. Before solving numerically, we give some simple analytical solution.

For simplicity, as a zeroth-order estimation, we approximate the stopping force (10) by

$\begin{array}{l}\frac{d{T}_A}{dx}=-\frac{g(v)}{v^2}\cong -\frac{g(v_0)}{v^2}\\ g(v_0)=\frac{4\pi Z_A^2{Z}_B{e}^4{n}_0}{m_e}\left[\text{ln}\left(\frac{2m_e{v}_0^2{\gamma }^2}{Z_{B}I}\right)-\frac{v_0^2}{c^2}\right]\\ \begin{array}{l}\cong \frac{4\pi Z_A^2{Z}_B{e}^4{n}_0}{m_e}\text{ln}\left[2.7·10^{-17}{v}_0^2\right]\end{array}& (12)\end{array}$

where v₀ ≪ c. The 1D equation of motion in this case is

$\begin{array}{ll}{M}_A\frac{dv}{dt}=Z_{A}e{E}_0-\frac{g(v_0)}{v^2}& (13)\end{array}$

And the implicit solution gives

$\begin{array}{l}v=v_0+c_{1}t+\frac{1}{2}{v}_1\text{ln }\left(\frac{(v_0-v_1)(v+v_1)}{(v_0+v_1)(v-v_1)}\right)\\ \begin{array}{l}{c}_1=\frac{Z_{A}e{E}_0}{M_A};c_2=-\frac{g(v_0)}{M_A};v_1=\sqrt{\frac{c_2}{c_1}}\end{array}& (14)\end{array}$

Since even at a constant energy of 0.6 MeV the protons' mean free path for fusion $l={(n_0{\sigma }_{fus})}^{-1}~10^3$ m is extremely large, we assume a magnetic field confinement that will rotate the particles in a periodic track and enable them to achieve a chain reaction in a relatively small confinement, such as in a torus or spiral configuration.

It should be noted that for the alpha-proton elastic collision presented following Equation 2, the proton in principle can be scattered at large angles. However, calculating the protons (at 0.6 MeV) and alphas (at 3 MeV) mean free path from the stopping power of our medium yields 10 and 25 cm, respectively. This short distance (which may be shortened further by increasing the medium density) enables us to disregard the scattering angle and consider our schema as 1D. This point will be clearer when we present our cycle based schema in which all particles come to a complete stop every cycle, and the electric field accelerates all the particles in a single direction.

For the external field to accelerate both alphas and protons the right-hand side of (13) must be positive, hence e.g.,

$\begin{array}{ll}{E}_0\ge \frac{g(v)}{Z_{A}e{v}^2}=\{\begin{array}{c}3.0·10^5\frac{V}{m}\text{ for proton at }1MeV\\ 1.7·10^6\frac{V}{m}\text{ for alpha at }1MeV\\ \end{array}.& (15)\end{array}$

While a constant, sufficiently strong external field as in (15) will accelerate the particles, it will not necessarily improve the fusion rate, since the cross section of p-B11 fusion is quite low for fast protons (>1 MeV). The problem intensifies if we consider the unstable nature of the equation of motion (13) (11). The right-hand side of (11) comprises of a constant (i.e., velocity independent) driving force and an opposing friction force that is inversely proportional to the velocity. When the particle accelerates, the friction force decreases while the driving force is unchanged, hence the total force increases, and the acceleration rate becomes even larger. The result of that instability is that every particle which is infinitesimally faster than the steady-state velocity (dv/dt = 0) will accelerate very rapidly to relativistic speeds, while particles which are infinitesimally slower will come to a complete stop.

To overcome that instability, we will use experimental data [17] for the stopping force, which is more accurate at low energies than the Bethe Equation (10). At low energies, as can be seen in Figure 1, the stopping force has a distinct maximum, which means that at very low speeds (~10 keV) the total force is indeed stable: an increase in speed will lead to a decrease in the acceleration until equilibrium is reached. However, as can be seen in Figure 2, if we wanted to slow down protons at 1 MeV, we would need to use a sufficiently small driving force that will cause the total force at 1 MeV to be negative. At such a small force the acceleration will be negative for all speeds below 1 MeV and the proton will reach a complete stop. On the other hand, to accelerate the proton again to 600 keV (all our calculations were made at the lab frame of reference, and since the boron is assumed at rest, the small difference in the maximum cross section energy was neglected) we have to make sure the total force is positive for all energies below 600 keV, and now it will keep accelerating to higher velocities.

FIGURE 1

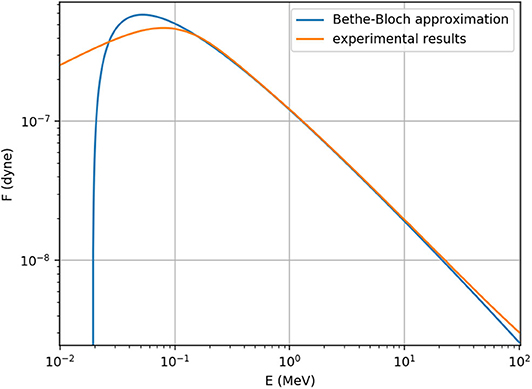
Figure 1. Comparison of Bethe Bloch approximation (10) and experimental data [17] for protons in helium (Z = 2, as the average charge for nucleus in H₃B).

FIGURE 2

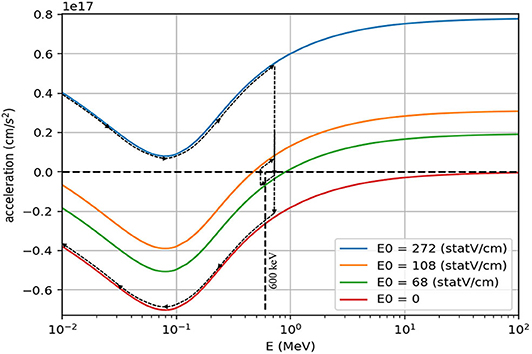
Figure 2. Proton acceleration under different values of the external field E₀. Dashed arrows represent the speed of a proton under the external field described in Figure 3.

We can go around that problem if we use pulsed external field. A single cycle of such scheme would involve turning the external field on and off, so the average proton speed would remain around 600 keV. However, because of the unstable nature of the equation of motion, the speed of the proton after a complete cycle will never be exactly constant, and after a few cycles the speed will either diverge, or decay to zero, just like with the constant field suggested in the last paragraph.

Therefore, we suggest an even more sophisticated scheme, where we first turn off the external field completely, in order to stop all motion of both the alphas and the protons. Then, we accelerate all the charge particles and use pulsed electric field to keep the protons around an average speed of 600 keV for as long as possible, as can be seen in Figure 3. The exact values of the external field in each part of the cycle was chosen with the help of Figure 2, and shown in dashed arrows along the acceleration curves (Figure 2): The initial acceleration is made with external field large enough so that the force on the protons is positive for all speeds; Then, the force is decreased to a point where it is negative for energies on the order of 600 keV; After all protons slowed down to around 550 keV the force is increased again, but only to a value sufficiently large to make those slower protons accelerate again. The last two stages repeat a few times until the speed starts to diverge again, at which time we turn the field off again and start the whole cycle all over again. The long pauses allow all particles to reach the only known and defined speed that we can control (zero), so although the process is still unstable, the predictability of the initial velocity allow us to reach the desired energy for a considerable time.

FIGURE 3

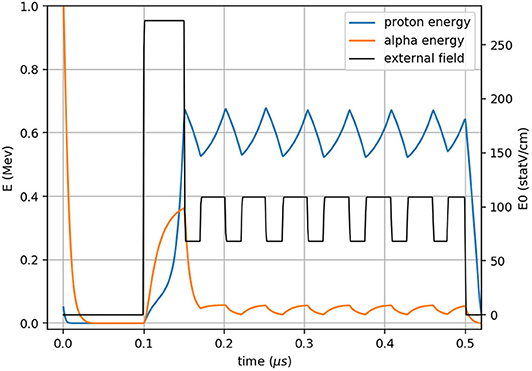
Figure 3. A single cycle of the external field (black), with the resulting speeds of the protons (blue), and alphas (orange).

The above method is quite sensitive, and the exact shape of the external field cycle depends strongly on the medium density. However, owing to the long pause at the beginning of each cycle, it is independent of the initial velocity of neither the protons nor the alphas, and therefore quite robust. By this method we are able to keep the protons for 76% of the time at ~600 KeV where the chance for p-B11 fusion is at its maximum (Figure 3). The medium density n₀ = n_H + n_B is assumed to comprise of hydrogen density $n_H=0.75·10^{19}$ and ¹¹B density $n_B=0.25·10^{19}$.

The fusion rate is found by solving (7) with the above calculated velocities, is shown in Figure 4. An increase in proton density and in alpha density, that indicate fusion events, is apparent during every cycle of the external field. As is evident from Figure 4, during the intervals between cycles, when the external field is turned off, no fusion occurs. At these times the number of protons and alphas is constant as there are no recombination mechanisms in (7). The normalized proton density and hence the fusion rate for longer periods is given in Figure 5, with p-B11 fusion cross section σ_fus is given numerically [10] and the alpha-proton elastic cross section was taken as a constant σ_el = 1b. The initial densities $n_{p0}=10^9$ and $n_{\alpha 0}=0c{m}^{-3}$ were set under the assumption of 10⁹ protons [these days it is typical to obtain proton beams of 10¹³ particles with high power lasers [18], and particle accelerators [19]], produced by either laser-target interaction or an accelerator, evenly dispersed in a 10⁴ cm³ container.

FIGURE 4

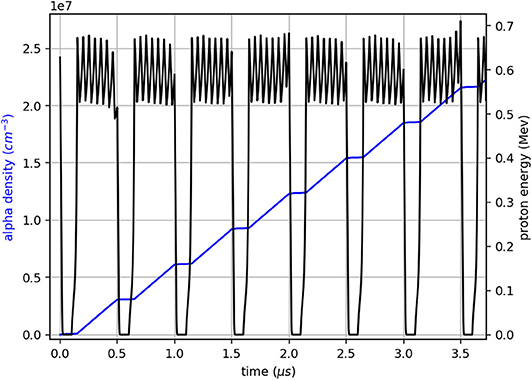
Figure 4. Alpha particle density during the first seven cycles of the external field. Small differences in proton speed in each cycle are explained by infinitesimal fluctuations in initial energy.

FIGURE 5

Figure 5. Normalized proton density ($n_{p0}=10^9$) calculated from (7).

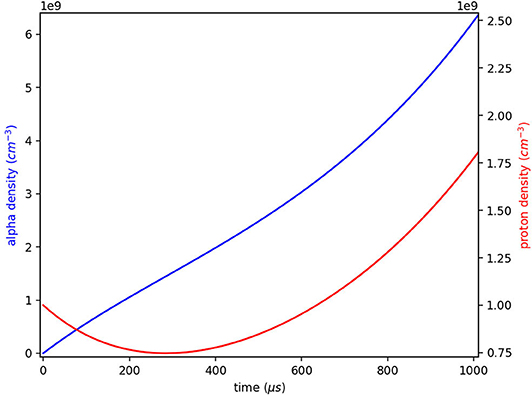
Figure 6 presents a comparison of the proton and alpha densities in a relatively short time after the beginning of the calculation, it can be seen that the proton density decreases initially due to fusion reactions that creates the alpha particles.

FIGURE 6

Figure 6. Proton and alpha densities in the first 1 ms of the calculation.

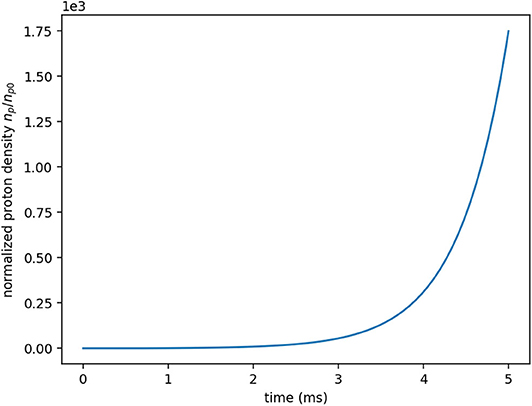
In Figure 7 the proton and alpha densities calculated to the first 5 ms are presented.

FIGURE 7

Figure 7. Proton and alpha densities in the first 5 ms of the calculation.

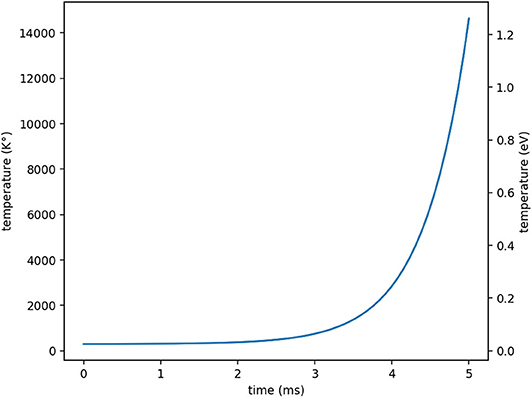
Assuming a constant volume and a complete transfer of the alpha energy to the medium, the medium temperature is calculated from the alpha density:

$\begin{array}{ll}{n}_{\alpha }{E}_{\alpha }=n_{\alpha }(8.9MeV/3)=n_0\left(\frac{3}{2}\right)k_{B}T& (16)\end{array}$

A graph of the temperature for the first 5 ms is presented in Figure 8.

FIGURE 8

Figure 8. The medium temperature calculated from the alpha density.

Discussion and Conclusion

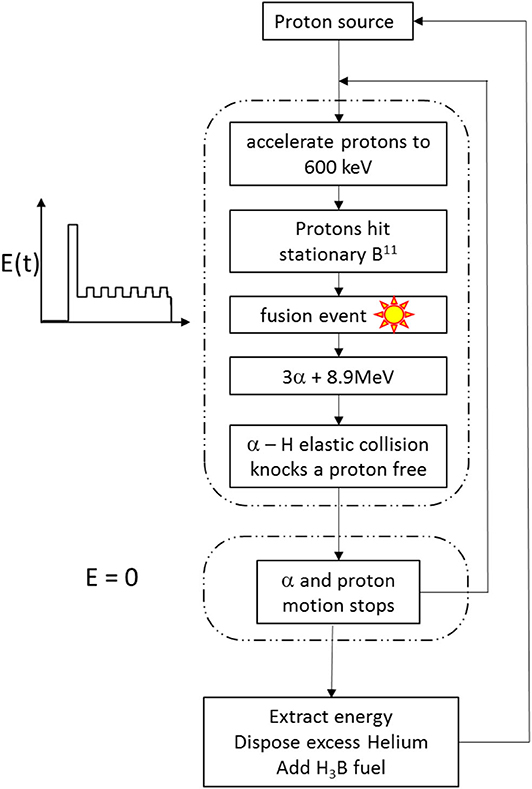
The process described in this paper is schematically shown in Figure 9. Our scheme is initiated by introducing a small amount (relative to the neutral gas concentration) proton (or alpha) particles. These charged particles serve as a starter. It is shown explicitly how to mitigate the stopping power effect in a media for nuclear fusions to occur. The prolonged interaction range is obtained by applying a customized electromagnetic field at a specific temporal shape to apply the right amount of force on the target ions. The applied force design is made to avoid divergence of the ions velocity due to the inherent instability in the equation of motion.

FIGURE 9

Figure 9. A schematic representation of the reaction process.

This novel idea may be used in numerous applications, in this paper we present a rough design for a possible configuration in which an initial proton bunch are accelerated in an H3B gas to the maximum fusion cross section energy of 600 KeV. Those protons create alpha particles by a fusion reaction with the stationary boron atoms. The accelerated alpha particles in turn, elastically collide with the stationary hydrogen atoms to produce new accelerated protons. This chain reaction can continue for several cycles. Due to the nature of the applied force, at each cycle, the force is turned off to allow the protons and alpha particle to reach zero velocity, which allows an accurate control over the ion's velocity at each cycle. In general, this process can continue for long time periods and produce an ongoing increasing alpha densities.

The energy input in the starter is supplied by the initial pulsed laser or accelerator. For our example we took 10⁹ protons per cm³, within a volume of 10⁴ cm³, namely we took as a starter 10¹³ protons. For the laser case, we need few hundred Joules [18]. After the avalanche process, our numerical calculations show an alpha number of particles (see Figure 7 at a time of 5 ms) of 6 × 10¹⁶ having a total energy of 2.8 × 10⁴ J. Thus, one can ignore the startup energy in comparison with the output alpha energy in calculating the energy efficiency of the process. Under the rough assumption that the work done by the external field on the charged particles is counteracted by friction forces (i.e., stopping power) and eventually transforms into heat of the neutral gas, additional energy is not lost. The only external field energy that is not recovered into heat is the electric field energy required to accelerate the protons that undergo fusion. These protons create three alphas with an energy of 8.9 MeV, or alternatively we can use the resonant [10, 11] of the pB11 cross section at 150 keV to achieve an appropriate chain reaction.

The energy estimations are an order of magnitude estimation only since exact calculations of the losses effects is out of the scope of this paper. However, an idea of the radiation losses by bremsstrahlung is

$\begin{array}{l}{P}_{br}\left(\frac{w}{c{m}^3}\right)\approx 1.7\times 10^{-32}{n}_e\left(c{m}^{-3}\right)T_e{(eV)}^{\frac{1}{2}}{Z}_i^2{n}_i;\\ \begin{array}{l}{W}_{br}(J)=P_{br}\left(\frac{w}{c{m}^3}\right)V\left(c{m}^{-3}\right)t(s)\end{array}& (17)\end{array}$

Using our numerical solutions, we have (see Figures A10, 11) $n_e=n_i\approx 10^{17}c{m}^{-3};Z_i=1,T_e=0.5eV,V=10^{4}c{m}^3$, only for 0.1 ms out of our 5 ms. The rest of the time n_e = n_i ≈ 0. We thus get the bremsstrahlung energy losses W_br of about 120 J. This loss is also negligible in comparison with the fusion output energy of 2.8 × 10⁴ J.

The calculations presented in this paper are of course not a fusion reactor design; however, they might indicate the possibility of a viable proton-boron11 fusion reactor for clean energy creation.

Data Availability Statement

All datasets generated for this study are included in the article/Supplementary Material.

Author Contributions

JM and SE conceived the presented idea. YS, SE, and NN developed the theory. YS performed the computations. SE wrote the manuscript with support YS and NN. All authors contributed to the article and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2020.573694/full#supplementary-material

References

1. Eliezer S, Martinez-Val JM. A novel fusion reactor with chain reactions for proton–boron11. Laser Part Beams. (2020) 38:39–44. doi: 10.1017/S0263034619000818

CrossRef Full Text | Google Scholar

2. Belyaev VS, Matafonov AP, Vinogradov VI, Krainov VP, Lisitsa VS, Roussetski AS, et al. Observation of neutronless fusion reactions in picosecond laser plasmas. Phys Rev. (2005) 72:26406 doi: 10.1103/PhysRevE.72.026406

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Labaune C, Baccou C, Depierreux S, Goyon C, Loisel G, Yahia V, et al. Fusion reactions initiated by laser-accelerated particle beams in a laser-produced plasma. Nat Commun. (2013) 4:2506. doi: 10.1038/ncomms3506

CrossRef Full Text | Google Scholar

4. Picciotto A, Margarone D, Velyhan A, Bellutti P, Krasa J, Szydlowsky A, et al. Boron-proton nuclear-fusion enhancement induced in boron-doped silicon targets by low-contrast pulsed laser. Phys Rev. (2014) 4:31030. doi: 10.1103/PhysRevX.4.031030

CrossRef Full Text | Google Scholar

5. Giuffrida L, Belloni F, Margarone D, Petringa G, Milluzzo G, Scuderi V, et al. High-current stream of energetic α particles from laser-driven proton-boron fusion. Phys Rev. (2020) 101:13204 doi: 10.1103/PhysRevE.101.013204

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Landau LD, Lifshitz EM. Course of Theoretical Physics. Oxford: Mechanics (1960).

Google Scholar

7. Eliezer S, Hora H, Korn G, Nissim N, Martinez Val J. Avalanche proton-boron fusion based on elastic nuclear collisions. Phys Plasmas. (2016) 23:50704. doi: 10.1063/1.4950824

CrossRef Full Text | Google Scholar

8. Dodder DC, Gammel JL. Elastic scattering of protons and neutrons by helium. Phys Rev. (1952) 88:520. doi: 10.1103/PhysRev.88.520

CrossRef Full Text | Google Scholar

9. Pusa P, Rauhala E, Gurbich A, Nurmela A. Alpha–proton elastic scattering cross sections for ERDA in the resonance region. Nucl. Instrum. Methods Phys. Res. B. (2004) 222:686–9. doi: 10.1016/j.nimb.2004.02.036

CrossRef Full Text | Google Scholar

10. Nevins WM, Swain R. The thermonuclear fusion rate coefficient for p-11B reactions. Nucl Fusion. (2000) 40:865. doi: 10.1088/0029-5515/40/4/310

CrossRef Full Text | Google Scholar

11. Belloni F, Margarone D, Picciotto A, Schillaci F, Giuffrida L. On the enhancement of p-11B fusion reaction rate in laser-driven plasma by α → p collisional energy transfer. Phys Plasmas. (2018) 25:20701. doi: 10.1063/1.5007923

CrossRef Full Text | Google Scholar

12. Bethe HA, Ashkin J. Passage of radiation through matter. In: E. Segré, editor. 1, Part II 253. New York, NY: John Wiley & Sons, Inc., London: Chapman & Hall, Limited. (1953).

Google Scholar

13. Maynard G, Deutsch C. Born random phase approximation for ion stopping in an arbitrarily degenerate electron fluid. J Phys. (1985) 46:1113. doi: 10.1051/jphys:019850046070111300

CrossRef Full Text | Google Scholar

14. Garbet X, Deutsch C, Maynard G. Mean excitation energies for ions in gases and plasmas. J Appl Phys. (1987) 61:907. doi: 10.1063/1.338141

CrossRef Full Text | Google Scholar

15. Barriga-Carrasco MD, Casas D. Electronic stopping of protons in xenon plasmas due to free and bound electrons. Laser Particle Beams. (2013) 31:105. doi: 10.1017/S0263034612000900

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Casas D, Barriga-Carrasco MD, Rubio J. Evaluation of slowing down of proton and deuteron beams in CH2, LiH, and Al partially ionized plasmas. Phys Rev. (2013) 88:033102. doi: 10.1103/PhysRevE.88.033102

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Berger MJ, Coursey JS, Zucker MA, Chang J. ESTAR J, PSTAR, and ASTAR: Computer Programs for Calculating Stopping-Power and Range Tables for Electrons, Protons, and Helium Ions (version 2.0.1), Gaithersburg, MD. (2005). Available online at: http://physics.nist.gov/Star.

Google Scholar

18. Brenner CM, Robinson APL, Markey K, Scott RHH, Gray RJ, Rosinski M, et al. High energy conversion efficiency in laser-proton acceleration by controlling laser-energy deposition onto thin foil targets. App Phys Lett. (2014) 104:081123. doi: 10.1063/1.4865812

CrossRef Full Text | Google Scholar

19. Weng WT. Ultra-high intensity proton accelaretors and their applications. In: Proceedings of the 1997 Particle Accelerator Conference (Cat. No.97CH36167) (Vancouver, BC).