Quasi-Stationary States in Ionic Liquid-Liquid Crystal Mixtures at the Nematic-Isotropic Phase Transition

An open system is a system driven away from equilibrium by a source that supplies an inflow of energy and a sink to maintain an outflow. A typical example of an open system is a system close to its phase transition temperature under irradiation by a laser. This provides a steady flow of energy through a photon flux. The sink in that case is the environment to which energy is lost in the form of heat dissipation. Creation of such a thermodynamically open state suggests that we can expect generation of exotic spatio-temporal structures length-scale independent correlation maintained under the global dissipative forces provided by the surroundings. Internal long-range forces can bring in additional spatio-temporal correlations, giving rise to states with a very long lifetime, the “quasistationary states” (QSS). In this communication, we report evolution of quasistationary states, in a mixture of the well-known liquid crystal (N-(4-methoxybenzylidene)-4-butylaniline, MBBA) and an iron-based room temperature ionic liquid (RTIL), namely, 1-ethyl-3-methylimidazolium tetrachloroferrate (EMIF) at the Nematic-Isotropic phase transition, when focused radiation with 532 nm wavelength from a Nd:YAG laser (200–300 mW optical power) is incident on the sample. We explain the QSS by invoking a sharp negative thermal gradient due to the laser photon flux and dipolar interactions. In our model, the dipoles are the charge transfer complexes (CTCs) formed in the RTIL by resonant laser pumping, which create an orientational ordering and balance the fluctuating force of the thermal gradient to create the QSS. In the absence of such CTCs in a mixture of MBBA and a Gallium-based RTIL (1-ethyl-3-methylimidazolium tetrachlorogallate, EMIG), the QSS was not observed.

Introduction

When in a phase transition the system transforms from one equilibrium structure to another with a change in symmetry, there is exchange of a fixed amount of energy with the surrounding at a fixed temperature. Both the phases co-exist during this conversion. These are the hallmarks of a first order transition following Arrhenius law of linear dependence of logarithm of the rate of energy transfer on the inverse of the temperature. The slope of this line is the fixed enthalpy of transition or the activation barrier of the transition.

In complex systems, there are departures from these characteristics. An example of this is the Nematic-Isotropic (NI) transition in liquid crystals (LCs), classified as “weakly first order” by de Gennes [1]. Here, while there is a definite change in symmetry in transition from the orientationally ordered nematic to the totally disordered isotropic phase, there is no finite co-existence region of these phases.

This transition in the well-known LC material N-(4-methoxybenzylidene)-4-butylaniline (MBBA) does not follow the Arrhenius law [2]. More interestingly, it is not strictly an equilibrium phase transition [3] in that both the transition enthalpy and temperature are dependent on the rate of energy supply. However, mixing MBBA with polar molecules [4], and in particular with an iron-based room temperature ionic liquid (RTIL), 1-ethyl-3-methylimidazolium tetrachloroferrate ([EMI]⁺[FeCl4]⁻, EMIF), converts this NI transition to a first order equilibrium transition between an Isotropic phase and a phase where the conformational entropy of the MBBA molecule is drastically reduced [5]. These studies were carried out on systems through near-equilibrium processes. Here the interaction between MBBA and EMIF molecules is carried out at the molecular, i.e., sub nm length scale and a time scale covering 100 ps−10 ns, while the orientational ordering giving rise to the phase transition takes place at a macroscopic length scale covering the bulk (mm to cm) and over at least 100 s. Hence, the complex nature of the transition, working at these two spatiotemporal hierarchies, is apparent.

In thermodynamically open systems, on the other hand, an external source supplies an inflow and an external sink provides an outflow of energy and/or material to the system [6]. This “sink” may be the surrounding or the environment itself and these inflow-outflow processes are, in general, irreversible. An open system is thus in a non-equilibrium state, characterized by an inhomogeneous distribution of the variables and non-vanishing values of the fluxes. The inhomogeneities and fluxes give rise to structures with spatiotemporal hierarchies, which are not observed in equilibrium systems. These dissipative structures are dependent on time by definition, implicitly if not explicitly, and they can be changed by changing the inflow-outflow rates [7, 8]. They are also coupled by a length-scale-independent correlation imposed by the fluxes [9]. Internal long-range forces can bring in additional spatiotemporal correlations to such open systems, giving rise to states with a very long lifetime, the so-called “quasistationary states” (QSS) [10–12]. Quasistationary states involving spin chains [13], lattices with infinity of absorbing states [14], and in hydrodynamics on a torus [15] have proved the general character of these states.

Treating the EMIF-MBBA system at around the NI transition under open, non-equilibrium conditions is expected to generate dissipative structures that will highlight this spatiotemporal hierarchy through their dynamics. RTILs are composed of bulky cations (such as imidazolium) and considerably large anions and remain liquid and ionized at ambient temperatures due to the large amount of configurational entropy contained in these ions, as well as the reduced inter-ionic Coulomb forces owing to the charge delocalization within the ions [16]. Their large dipole moments can couple them to LC molecules and transfer this large entropy to the LC system, affecting its phase transitions, viz., taking the nematic-isotropic transition to lower temperatures. RTILs also have the attractive physical properties of having extremely low vapor pressure, thermal stability and a large liquid window (~200°C). LC systems, due to their orientational order, are amenable to studies with non-invasive polarization microscopy and the dipolar coupling between RTILs such as EMIF and EMIG on one hand, and LCs like MBBA on the other, is expected to have a strong effect on the polarization of the latter and cause a commensurate variation in the microscopic images.

A radial pattern of polarization has been observed in EMIF on irradiation by a focused laser [17]. On switching the laser off, the pattern showed a fast (<1 s) change followed by a quasistationary structure for more than 100 s. That this dissipative structure is indeed caused by a resonant pumping by the laser is confirmed from the fact that it is not observed with 1-ethyl-3-methylimidazolium tetrachlorogallate ([EMI]⁺[GaCl4]⁻, EMIG), a Ga-based RTIL with the same laser power.

Thus, we see that an EMIF-MBBA mixture, resonantly pumped by a focused laser may give rise to an open system, where the coupling between the EMIF and MBBA molecules can compete with the thermal dissipation provided by laser heating. Creation of such a thermodynamically open state suggests that we can expect generation of exotic spatiotemporal structures different from the static structures under equilibrium. In particular, the orientational ordering imposed on MBBA by EMIF, as evident from ref 5, can give rise to a QSS consisting the nematic and isotropic phases in co-existence. These considerations and the expected strong variation of images in polarization microscopy due to the change in orientation of MBBA as evidence of presence or otherwise of RTIL-LC coupling motivated us to carry out these studies. To the best of our knowledge, such studies have not been carried out with other LC and RTIL mixtures.

In this communication, we report evolution of QSS under the above conditions. We explain the QSS by invoking a sharp negative thermal gradient due to the laser photon flux and dipolar interactions. In our model, the dipoles are formed in the RTIL by resonant laser pumping, which create an orientational ordering and balance the fluctuating force of the thermal gradient to create the QSS. This allows probing of the transition through polarization microscopy. Hence, we have carried out polarization microscopy experiments to arrive at our results.

Equilibrium Properties of the Mixtures

In all cases, the sample is a dip-coated film on a glass slide. As samples, we used mixtures of MBBA and EMIF, and MBBA and EMIG. The structures of MBBA, EMIF, and EMIG are shown in Figures 1A–C, respectively. MBBA (99% pure) was purchased from Nacalai Tesque, Japan and used without further purification. EMIF and EMIG were synthesized and purified in the lab [18]. The LC was found to be strongly hydrophobic.

FIGURE 1

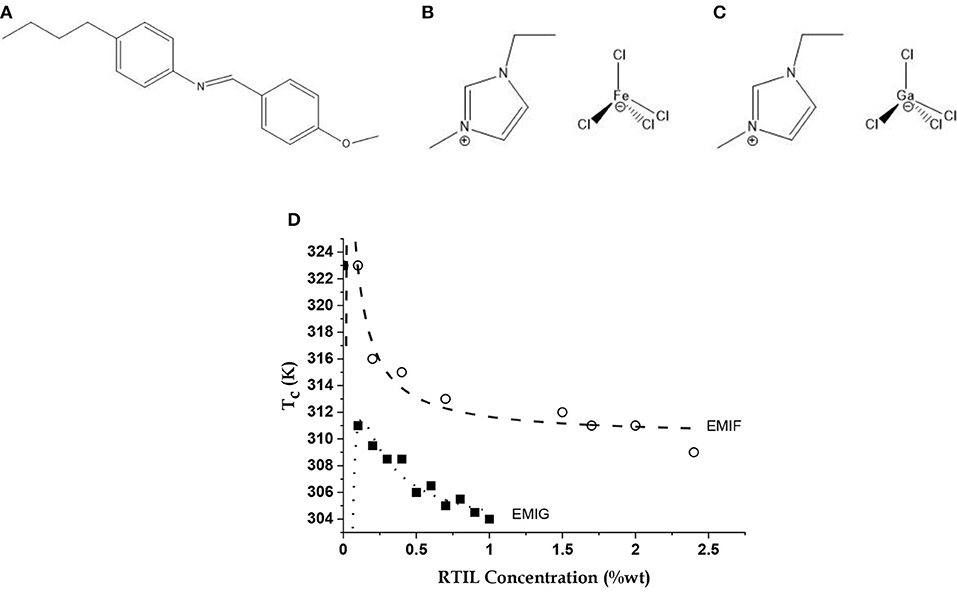
Figure 1. The molecules and their equilibrium property. Molecular structures of the liquid crystal (LC) (A) n-(4-methoxybenzylidene)-4-butylaniline (MBBA), and the room temperature ionic liquids (RTILs) (B) 1-ethyl-3-methylimidazolium tetrachloroferrate (EMIF) and (C) 1-ethyl-3-methylimidazolium tetrachlorogallate (EMIG); (D) Variations of Nematic-Isotropic transition temperature (T_c) of LC-RTIL mixtures with EMIF and EMIG concentrations shown as open circles and filled squares, respectively. Data simulated (dashed and dotted lines, respectively) with a model of the MBBA dipoles screened by RTIL ions taking into account the self-screening of the ions [5] using Equation (1). See text for details.

The LC and the RTILs were mixed to vary the concentration of EMIF at different values from 0.00 and 2.42 wt%. The mixture became turbid on keeping and had to be periodically stirred and heated with warm air to regain its transparency. The NI transition temperature (T_c) was determined for each of these mixtures by varying temperature between 298 and 328 K in 1 K steps using a hotplate stage (accuracy 0.1 K). The phases were detected by a polarization microscope (IX70, Olympus, Japan) equipped with a 20 × objective lens and a CCD camera (640 × 480 pixels). The data is the average over three measurements in each case with insignificant errors.

The EMIF-MBBA and EMIG-MBBA mixtures showed lowering of N-I transition temperature (T_c) with C, the weight percentage of the RTIL in the mixture, until the components segregated (Figure 1D). The data are calculated from a model of interacting MBBA dipoles screened by the free charges of the RTILs, accounting also for the self-screening of the charges. Here we assume that the ions of EMIF are active in both screening the MBBA molecular quadrupoles and in self-screening while other forces (such as, dispersion forces) play no role in the transition. Thus, there is an effective charge q located at each MBBA molecule screened by the counterions of EMIF surrounding charges on the molecular quadrupole. If it is further assumed that addition of a small amount of ionic liquid only changes the value of q keeping the intermolecular separations, unchanged, then increase in C will lead to more screening and hence to a lowering of q (q = k₁/C). However, this process will generate its own self-screening and the final relation between C and q, with all other factors such as intermolecular separation being lumped into two constant terms k1 and k2, is given by C = k₁/q (1 –k₂/q).

The dependence of T_c on C, the wt% concentration of RTIL, is then given by this model as

$\begin{array}{ll}{T}_c=T_c^0+\frac{A_T}{C^2}-\frac{B_T}{C}& (1)\end{array}$

where $T_{\text{c}}^0$ is the transition temperature of pristine MBBA (323 K), and A_T and B_T are the self-screening and screening parameters, respectively [5]. The values of A_T and B_T for EMIF come out to be −0.03 and −1.5 K, respectively, and for EMIG they are −0.14 and −2.25 K, respectively. Thus, EMIG has a considerably stronger screening and self-screening effect, possibly due to the smaller size of Ga and thus the tetrachlorogallate anion.

The Open Systems and Their Dynamics

We have investigated the microscopic N-I transition induced by a continuous wave (cw) at 532 nm, 200 mW optical power focused (spot diameter ~ 1 μm) on samples taken in a 3 cm × 3 cm × 25 μm cell. The linearly polarized laser was assembled from a randomly polarized laser source (JOL-D8PK-Y, JENOPTIK, Germany), and a Ti: Sapphire polarization beam splitter. The laser was made incident on the sample by a dichroic mirror. We have performed polarization microscopy (IX70, Olympus, Japan) to study the NI transition induced by the laser. We recorded the microscopic phase transitions in EMIF-(EMIG-) MBBA through a CCD camera (30 frames/s, 640 × 480 pixels) attached to the eyepiece of the polarization microscope. We took the terminal value of C as the maximum achievable value [C_max, ~ 2.42 (~1.32) wt% for EMIF- (EMIG-) MBBA, from Figure 1D] and carried out the laser-induced transition on these “C_max” mixtures at 33°C, close to but lower than the corresponding T_c.

Upon irradiation, both mixtures generate an isochromic (or black) droplet of diameter ~ 5 μm, centered about the laser beam, of the I-phase to form on the nematic bulk. These are shown for 200 mW of laser power in Supplementary Movies 1, 2, respectively. Supplementary Movie 1 has been truncated in the final portion after the isotropic phase has been achieved, i.e., without any loss of important information, due to the large filesize. We have detected the macroscopically defined orientation of the N-phase by rotating the sample in plane.

We extracted the spatiotemporal maps of the entire events from M1 and M2 using the freeware ImageJ (National Institute of Health, USA) and presented them in the respective Figures 2A,B, where we also show typical frames corresponding to the main stages of the evolution at the bottom of maps. We indicate the macroscopic orientation of the nematic phase by an arrow in the relevant frames. In Figure 2C, we present the evolution of MBBA only, under irradiation by the same laser power. As shown, we could observe no transition to the isotropic phase (isochromic or black droplet) other than an increase in the local orientational disorder. These coarsen into increasingly bigger regions shown in Figure 2Cii and finally cover the field of view, with few isolated domains. This occurred even on increasing optical power to 500 mW without RTIL or with the mixtures at all proportions but with the laser radiation at 1,064 nm.

FIGURE 2

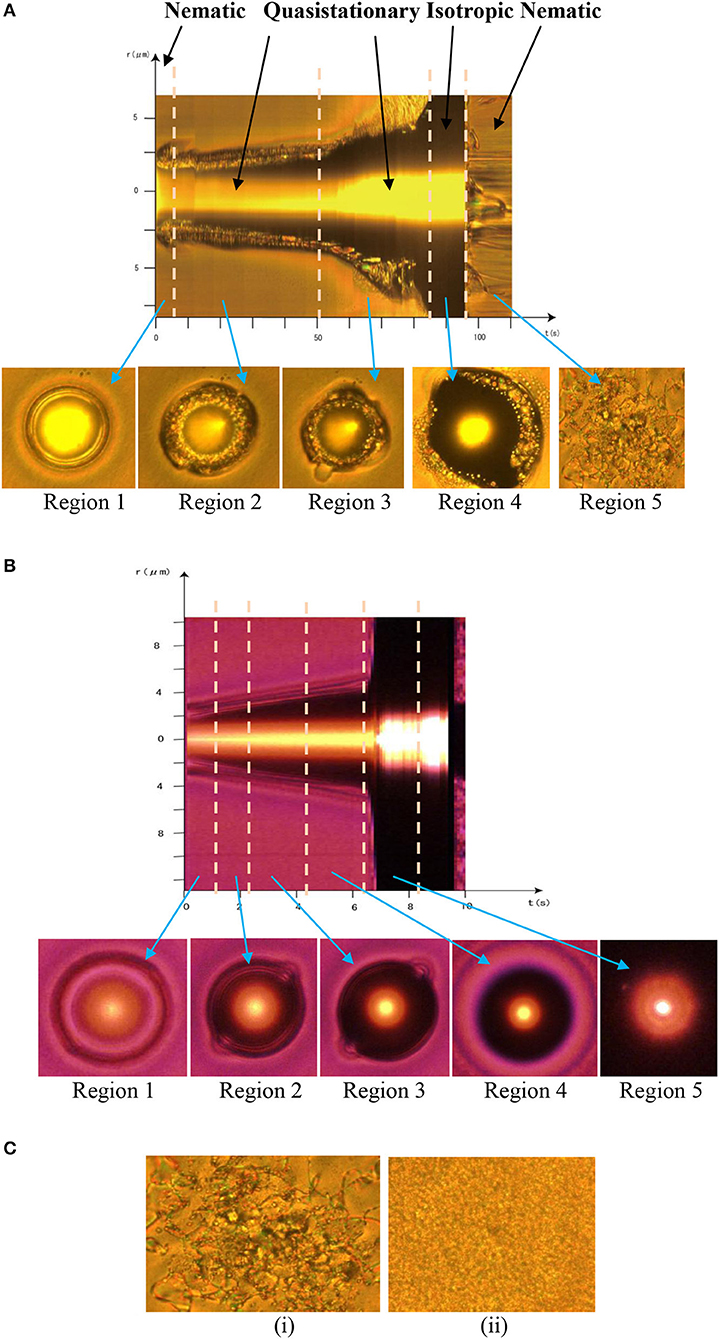
Figure 2. Spatiotemporal evolution of the mixtures. Spatiotemporal maps of (A) EMIF-MBBA (with phases marked) and (B) EMIG-MBBA mixtures (C_max concentration) over the entire evolution at the corresponding T_c, extracted from Supplementary Movies 1, 2, respectively. The different regions in each map are separated by dashed lines and the typical frame of each region is shown below the map, designated by arrows. (C) Frames at (i) 100 μs and (ii) 300 μs of irradiation of MBBA only, by the laser. All data were taken at 200 mW of laser power.

In EMIF-MBBA, the isotropic droplet first appears with a clean and sharp boundary (region 1, Figure 2A). However, within ~100 ms, a number of clusters of different colors (but with no color variation within each cluster), on the average going from red to green outwards, appear in the region located between the isotropic droplet and the nematic bulk (region 2, Figure 2A), producing an “opal-like” texture [19]. Since a particular color corresponds to a particular polarization it is clear that these clusters are individual domains of the nematic or, better, “nematic-like” phase with the size ~ 500 nm whose directors are randomly oriented and M1 shows that, unlike natural or synthetic opals [20], these clusters are in incessant motion. The major types of motion involved are (i) convective motion of domains, and (ii) predominantly two-body coalescence of domains ending in merging of these coalesced domains into the nematic bulk. From region 2 of Figure 2A we see that throughout these motions, for ~50 s, the diameter of the isotropic droplet remains near 5 μm and the width of the interfacial zone that contains the nematic domains remains at ~1.5 μm, which indicates the presence of a QSS.

With EMIG-MBBA, the above interfacial region with its internal dynamics is entirely absent (Figure 2B). Though the system shows slow dynamics at 200 mW, the speed increases monotonically with laser power, and the in data at 500 mW presented in Figure 2B, there is no trace of a QSS. This contrasts sharply with the Fe-based RTIL system where increase in laser power within this range does not affect the QSS formation and stability, nor are there any other changes in the dynamics with laser power from 200 to 500 mW, and similarly the change in the film thickness of the sample made no noticeable difference in behavior. This is consistent with the long range correlations in QSS [10–12].

In the next stage of EMIF-MBBA N-I transition dynamics (region 3, Figure 2A), roughly triangular areas with their bases on the nematic-isotropic boundary open up in the nematic bulk. These patches consist of randomly oriented, nanometer-sized domains similar to those in the interfacial zone. The former domains move inwards while the latter move outwards, whereby they meet and coalesce. The coalesced domains, unlike in the second stage, now shrink and disappear into the isotropic phase. Thus, this process disrupts the quasistationary structure and finally the isotropic region expands to cover the whole field of view, as can be seen in region 4 of the spatiotemporal image. The last stage, region 5, is after switching the laser off, when the reverse transition to the nematic phase takes place without any intermediate QSS but only through coalescence of large nematic domains.

We have investigated the kinematics of the QSS at two levels: for the overall isotropic-interfacial region system and for the clusters or domains within the interfacial region. To quantify the overall kinematics, we have presented the log-log plots of the diameter (D) of isotropic droplet (open circles) and width (w) of the interfacial region (filled circles), vs. elapsed time (t), in Figure 3. Due to the inherent large dynamic range of the data, this average over 10 measurements has to be presented in a log-log scale and error bars are less meaningful. In both plots, the QSS (region 2) and the next state (region 3) in system dynamics show excellent linear fits, which gave reliable values of p and q in the relations: D ~ t^p and w ~ t^q. For the QSS, p = 0.31 ± 0.04, q = −0.32 ± 0.07, showing the characteristic slow dynamics in both the isotropic phase and the interfacial region in this stage, whereas for the next state p = 2.16 ± 0.14, q = 4.54 ± 0.55. Hence, expansion of the interfacial region clearly dominates the expansion in this dynamic state. After 76 s, the interfacial region suddenly vanishes and the isotropic phase covers the field of view in 84 s. Therefore, there is an initial fast growth phase of the interfacial zone covering the first 5 s after the laser is switched on, followed by the QSS that stabilizes this zone for the next 70 s, and finally the 8–9 s of fast decay of the interfacial zone.

FIGURE 3

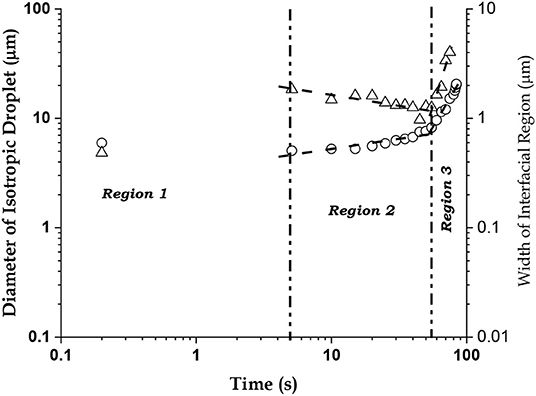
Figure 3. The Quasistationary State (QSS). Log-log plots of the diameter (D, in μm, open circles) of the isotropic phase (dark droplet at the center of the laser beam) and the width (w, in μm, open triangles) of the interfacial region containing nematic clusters, vs. time (in s). The QSS occurs in Region 2.

The interfacial zone in QSS has its own dynamics. We find that there are two co-existing groups of domains separated by size, “small” (D < 500 nm) and “big” (D > 500 nm), and they have quite distinct dynamics. We show these two types of domains in the magnified image of the interfacial region in Figures 4A,B, respectively. The small domains have uniform yellow color that does not change noticeably with time and they show some movement, while big domains show non-uniformity of color and change color from red to yellow to green (sometimes almost black) randomly but stay almost stationary. Thus, small domains change position but not orientation while big domains do not change position but change orientation randomly. What is perhaps more important is that big domains very seldom acquire the color, and hence the molecular orientation, of the small domains. The incident of two adjacent large domains acquiring the same color is also rare. These observations suggest that the small domains may contain a higher fraction of the EMIF that holds the LCs to a state with fixed orientation uniformly within the domain, against thermal fluctuations caused by the laser. Similarly, the big domains may have lower fractions of the RTIL. The LCs within them are fluctuating in orientation randomly with the heat and seldom reaching the highly oriented state of the small domains, or stable enough to induce the orientation in adjacent large domains.

FIGURE 4

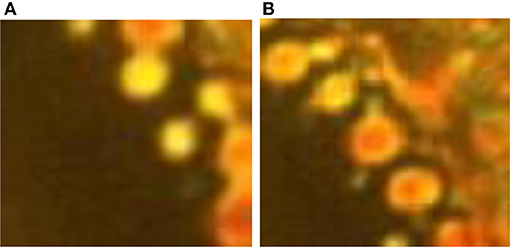
Figure 4. Domains in the interfacial zone. The interfacial zone consists of (A) “small” (D < 500 nm) and (B) “big” (D > 500 nm) domains.

We present log-log graphs of growth in domain size vs. time of two randomly chosen members from each group in Figures 5A,B, respectively, the data being shown by open and filled circles for the two members. From linear fits, in solid and dashed lines for the two members in each group, the growth exponents of the small clusters come out to be 1.71 ± 0.26 and 0.74 ± 0.24, whereas those of the big clusters are 0.11 ± 0.09 and 0.20 ± 0.09. Thus, though both groups show fluctuations in their growth dynamics the small clusters exhibit a general growth trend by coalescence in contrast to the big clusters whose size fluctuates about a mean value. This becomes clearer from Figures 5C,D, showing the size distributions of the clusters. The interesting thing, however, is that the primary maxima of both members in each group are very close: 275 and 285 nm for the small clusters, and 562 and 565 nm for the big clusters. This shows the quasistationary nature of dynamics even at the scale of the clusters or domains.

FIGURE 5

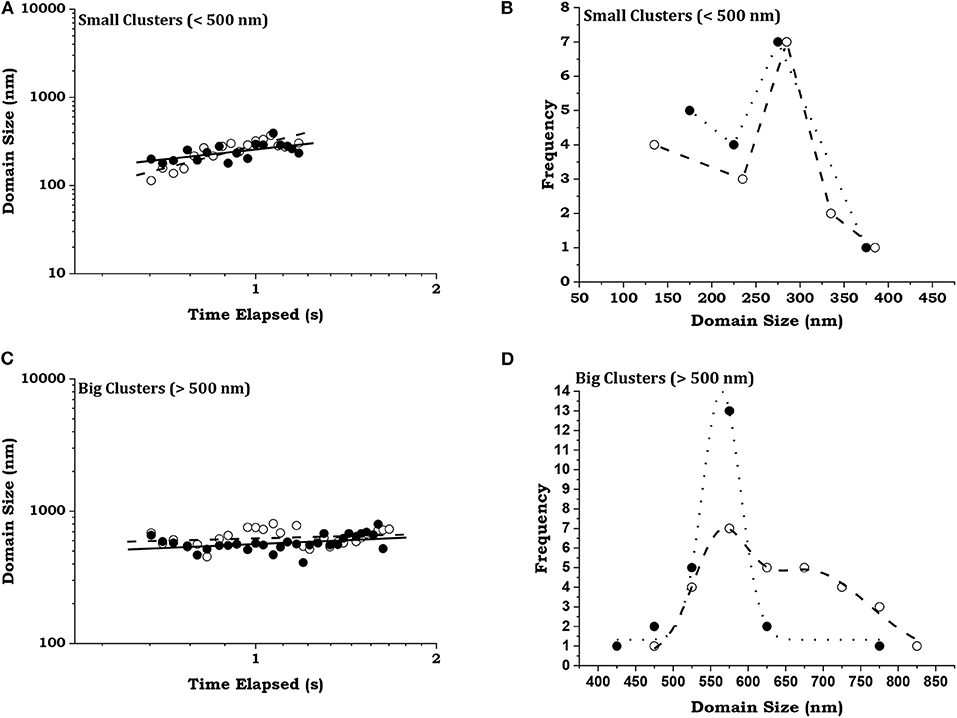
Figure 5. Distribution of domains. Two randomly chosen members are represented by open and filled circles from (A), (C) small (diameter < 500 nm) and (B), (D) big (diameter > 500 nm) domains. The variations of domain size with time are shown as log-log plots in (A,B), with dotted and dashed lines as fits to the data. The distributions of the domain sizes are shown in (C,D) with Gaussian simulations of the data.

Origin of the QSS: a Tentative Explanation

From the equilibrium and non-equilibrium properties of the mixtures described in sections Equilibrium Properties of the Mixtures and The Open Systems and Their Dynamics, respectively, we find that (1) EMIG has a stronger effect on the NI transition than EMIF under equilibrium conditions while (2) it has essentially no effect on the transition under non-equilibrium conditions. This sharp difference between the two conditions is based on the way the RTIL molecules interact with the MBBA in absence and presence of the laser.

In the absence of the laser radiation, RTILs are characterized by free or uncoordinated ions. In an EMIF-MBBA mixture these free charges have been shown to screen the MBBA molecular dipoles, with some degree of self-screening among these charges [5]. This interaction also converts the NI transition from a non-Arrhenius to an Arrhenius transition by suppressing the in-plane and out-of-plane motions of the benzene rings of MBBA. This freezes the intra-molecular motion of the molecular axis which converts the entropic NI activation barrier to an enthalpic or constant inter-molecular barrier. As Figure 1D shows, the same model can very well explain the EMIG-MBBA interaction. Indeed, this interaction is stronger in this case.

With pure EMIF, there is a vibronic, dipole forbidden d–d transition from the ⁶A₁ ground state to the ⁴${\text{A}}_{1,}^4$E (degenerate) excited state of Fe³⁺ in the ${\text{FeCl}}_4^{-}$ molecular anion, at around 536 nm (Figure 6) [21]. It is also seen in this figure, that while the spectrum of MBBA has no band at or near that wavelength, this transition in the EMIF is quenched in the EMIF+MBBA mixture, indicating a strong coupling between the molecules in which this state plays the most important role. While the ground state of the ${\text{FeCl}}_4^{-}$ molecular anion has a tetrahedral structure [22], the excited state has a doubly degenerate vibration mode and is most probably a square planar structure [23]. We propose that, since the imidazolium cation is also a predominantly planar structure, the coordination between the counterions is much enhanced in this state leading to the formation of EMIF dipoles.

FIGURE 6

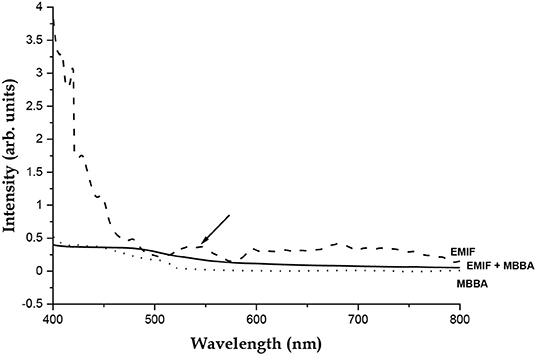
Figure 6. Ultraviolet-Visible Spectrum of EMIF (dashed line), MBBA (dotted line) and the MBBA-EMIF mixture used (solid line). The ${}^6{A}_1{\to }^4{A}_{1,}^4$E transition band at 536.68 nm is marked with an arrow. This transition is seen to be quenched in the mixture.

Due to the weakness of the transition, strong resonant optical pumping by the laser is required to produce a sufficient number of such dipoles to form long range orientational correlation, since the dipole-dipole interaction is orientation dependent, unlike the screened Coulomb interaction obtaining in absence of the laser radiation. On the other hand, the high intensity of the laser also produces a thermal gradient across the laser intensity profile, falling off from the center outwards, which causes a stochastic, dissipative force to disrupt this orientational order. The continuous competition between these ordering and disordering forces stabilizes EMIF into a QSS [17]. The dissipative structure produced lasts after the laser is switched off as the laser induced heating dies down. Pure EMIG cannot form such a QSS since it does not have such a transition in this spectral region

We then explain the dynamics of the EMIF-MBBA open system by proposing that in presence of the laser, the EMIF-MBBA interaction is a dipole-dipole attraction, where the EMIF dipole, generated by the laser through this vibronic transition in a time scale of about 100 ps, interacts with the MBBA molecular dipole. This orientation dependent force creates a long range orientational correlation that competes with the thermal dissipative force and takes the correlated structure to a time scale of seconds. The latter drives the nematic phase to the isotropic phase while the former has a reverse drive and the competition between them stabilizes the interfacial zone into a quasistationary state, creating a “dynamic coexistence region” of the two phases. Again, as EMIG does not have this band resonant with the laser this QSS is not produced.

Here we put forward a qualitative model to explain the formation of the QSS. The major assumptions in our model are: (1) Since RTILs have mostly un-coordinated ions, they behave predominantly as collection of unscreened charges; (2) Optical pumping by the laser at 532 nm combines these charges to form dipoles resonantly for EMIF and not for EMIG. Let dipoles of magnitude μ_R be generated by the laser uniformly within the sample at a steady rate and stochastically, i.e., the dipole moment is either μ_R or 0. The number of these dipoles remains constant within the laser beam diameter of d₀ = 2r₀ (d₀ = 1μm) and the orientation of the dipoles, given by angle θ of the dipole with the nematic or optic axis, remains completely random within this diameter, due to the large thermal fluctuation set up by the laser.

For the EMIF-MBBA mixture, we assume the number of dipoles to fall off exponentially outside the direct influence of the laser beam (r ≥ r₀, where r is the distance from the beam center) while they become exponentially oriented to the optic axis. We base this last assumption on the presence of the orientating force of the molecules in the nematic bulk. We also assume that the orientation of the EMIF dipoles decides the orientation of the LC dipoles and thereby the polarization of the sample. Thus, our model points to a balance between the long-range dipolar orientating force and the thermal fluctuating force, since both are produced by the same source, i.e., the laser. Following our previous discussion, we propose that this balance is vital for the formation of the quasi-stationary state.

This model can be mapped to the Hamiltonian mean-field (HMF) model of globally coupled rotators [11] with the important modification that N, the number of coupled rotators is now a function of r, the distance from the laser center. Here we present a very simple and phenomenological version of the model to explain the profile of the polarization P(r) across the phase boundary, assuming that the laser produces dipoles with a time-averaged number density < n(r)> from the RTIL molecules, where each molecule has the dipole moment of magnitude μ_R and time-averaged orientation with the optic axis given by < cosθ(r)>.

For the LC molecule, the magnitude of the dipole moment is μ_L and orientation is given by the dipoles of RTIL molecules. There is of course a fraction of LC molecules that are not acted on by these dipoles but we can consider that this fraction is basically unaffected by the laser and can be neglected. The total effective polarization of the sample along the optic axis, caused by the laser, is then

$\begin{array}{ll}P(r)=\langle n(r)\rangle ({\mu }_R+{\mu }_L)\langle cos\theta (r)\rangle & (2)\end{array}$

According to our model, for r<r₀, <n(r)> = n₀, <cosθ (r)> ~ 0, hence P(r) ~ 0, while, for r ≥ r₀, <n(r)> = n₀ exp[-k₁ (r₀ – r)], <cosθ (r)> = 1 - exp[k₂ (r₀ – r)]

Hence,

$\begin{array}{ll}P(r)=n_0({\mu }_R+{\mu }_L)exp\left[{-k}_1(r_0-r)\right](1-exp\left[k_2(r_0-r)\right])& (3)\end{array}$

A plot of P(r) calculated from Equation (3) is shown in Figure 7. Though the value of the polarization is completely arbitrary, the functional form captures the essential physical aspects of the QSS, with nearly correct values for D and w, if k₁ and k₂ are set to the values of 2.0 and 0.025 μm⁻¹, respectively. These correspond to a “decay length” ~ 500 nm for the dipoles, which corresponds to the average size of the nematic domains in the interfacial zone and an “effective range” ~40 μm for the force responsible for orientational ordering. This relatively long-range force is responsible for the QSS.

FIGURE 7

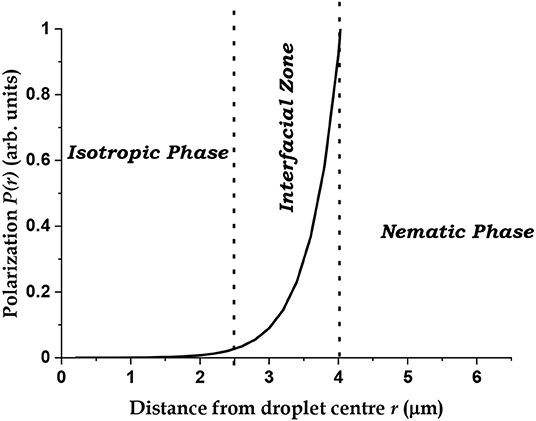
Figure 7. Calculated average polarization profile of the EMIF-MBBA open system based on Equation (3).

The above model in itself, however, is inadequate since it cannot explain the slow dynamics at the nanocluster level. Here, we have to invoke the concept, apparent from the results, that, clusters can coalesce only when they are in the same orientational state. Since the orientational states of the large clusters fluctuate with time, coalescence to the bulk nematic phase has a fractional growth exponent, typical of random events. This mechanism is responsible for the QSS-like situation at the nanometer length scales. For the EMIG-MBBA mixture, our model indicates that the laser cannot produce dipoles but can only create the thermal fluctuation in the un-coordinated charges. Hence, we see a monotonically increasing isotropic domain, where the growth rate of that domain increases with laser power.

This qualitative and tentative model of the RTIL system, besides explaining the quasi-stationary states formed in this particular situation provides the framework for deciding the requirements to generate QSS in this class of materials that are emerging as highly promising for a wide range of application.

Conclusion

We have shown that a quasistationary state is generated at the nematic-isotropic interfacial region of a mixture of a liquid crystalline material and an iron-based room temperature ionic liquid on focused irradiation by a laser. The quasistationary state consists of a coexistence of incessantly moving domains of the nematic phase at different orientational states and the isotropic phase. A mixture of the liquid crystal with a gallium-based analog of the ionic liquid does not produce the quasistationary state, though in absence of the laser both ionic liquids affect the nematic-isotropic phase transition in a similar way by lowering the transition temperature. The iron-based ionic liquid has a vibronic band that resonates with the laser wavelength and it is proposed that the resulting optical pumping produces molecular dipoles in the ionic liquid that interact with the liquid crystal molecular dipoles. This leads to a long range orientational ordering that competes with the dissipative forces of laser heating to generate the quasistationary state.

The iron-based ionic liquid in question has been found to exhibit long range antiferromagnetic order among spin orientations of the iron-containing anion [24] under equilibrium conditions. The long range molecular orientational order in the dissipative structures of the ionic liquid molecules themselves, as found in [17], or of the ionic liquid-liquid crystal mixtures, as found in this work, make these structures fascinating candidates for study of magnetic properties under non-equilibrium in general, and of the coupling between spin orientation and molecular orientation in particular.

Data Availability Statement

All datasets generated for this study are included in the article/Supplementary Material.

Author Contributions

AD carried out the experimental study, analyzed the data, and wrote the manuscript. KY defined the problem, provided the infrastructure, and took part in analysis and manuscript preparation. YY synthesized the samples in collaboration with GS. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the Japan Society for the Promotion of Science (JSPS) KAKENHI Grant Numbers JP20H02708.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

AD would like to thank the Japan Society for Promotion of Science for a Visiting Professorship and the Department of Atomic Energy, Government of India, for a Raja Ramanna Fellowship, as well as Swapnasopan Datta of Jawaharlal Nehru Center for Advanced Scientific Research for Figures 1A–C and for useful discussions regarding the vibronic transition and structural changes of the anions.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2020.583173/full#supplementary-material

References

1. de Gennes PG, Prost J. The Physics of Liquid Crystals Oxford: Oxford University Press (1995).

Google Scholar

2. Dan K, Roy M, Datta A. Convex Arrhenius behaviour in a nematic-isotropic phase transition. Europhys Lett. (2014) 108:36007. doi: 10.1209/0295-5075/108/36007

CrossRef Full Text | Google Scholar

3. Dan K, Roy M, Datta A. Non-equilibrium phase transitions in a liquid crystal. J Chem Phys. (2015) 143:094501. doi: 10.1063/1.4929607

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Dan K, Roy M, Datta A. Entropic screening preserves non-equilibrium nature of nematic phase while enthalpic screening destroys it. J Chem Phys. (2016) 144:064901. doi: 10.1063/1.4941365

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Dan K, Datta A, Yoshida Y, Saito G, Yoshikawa K, Roy M. Screening out the non-arrhenius behaviour of nematic-isotropic transition by room temperature ionic liquid. J Chem Phys. (2016) 144:084904. doi: 10.1063/1.4942521

PubMed Abstract | CrossRef Full Text | Google Scholar

6. de Hemptinne X. Non-Equilibrium Statistical Thermodynamics. Singapore: World Scientific (1992).

Google Scholar

7. Mukai SA, Magome NH, Kitahata H, Yoshikawa K. Liquid/liquid dynamic phase separation induced by a focused laser. Appl Phys Lett. (2003) 83:2557. doi: 10.1063/1.1613795

CrossRef Full Text | Google Scholar

8. Sadakane K, Kitahata H, Seto H, Yoshikawa K. Rhythmic oscillation dynamic instability of micrometer-size phase separation under continuous photon flux by a laser. Phys Rev E Stat Nonlin Soft Matter Phys. (2008) 78:046214. doi: 10.1103/PhysRevE.78.046214

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Toyama H, Yoshikawa K, Kitahata H. Homogenization of a phase-separated droplet in a polymer mixture caused by the dielectric effect of a laser. Phys Rev. (2009) 78:060801. doi: 10.1103/PhysRevE.78.060801

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Latora V, Rapisarda A, Ruffo S. Lyapunov instability finite size effects in a system with long-range forces. Phys Rev Lett. (1998) 80:692. doi: 10.1103/PhysRevLett.80.692

CrossRef Full Text | Google Scholar

11. Campa A, Giansanti A, Morelli G. Long-time behavior of quasistationary states of the Hamiltonian mean-field model. Phys Rev E. (2007) 76:041117. doi: 10.1103/PhysRevE.76.041117

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Barré J, Bouchet F, Dauxois T, Ruffo S. Large deviation techniques applied to systems with long-range interactions. J Stat Phys. (2005) 119:677–713. doi: 10.1007/s10955-005-3768-8

CrossRef Full Text | Google Scholar

13. Fagotti M. Locally quasi-stationary states in noninteracting spin chains. Sci Post Phys. (2020) 8:048. doi: 10.21468/SciPostPhys.8.3.048

CrossRef Full Text | Google Scholar

14. Jara DAC, Alcaraz FC. Quasi-stationary states in nonlocal stochastic growth models with infinitely many absorbing states. J Stat Mech. (2017) 4:043205. doi: 10.1088/1742-5468/aa668c

CrossRef Full Text | Google Scholar

15. Beck M, Cooper E, Lord GJ, Spiliopoulos K. Selection of quasi-stationary states in the stochastically forced navier–stokes equation on the torus. J Nonlin Sci. (2020) 30:1677–702. doi: 10.1007/s00332-020-09621-0

CrossRef Full Text | Google Scholar

16. Welton T. Room-temperature ionic liquids. solvents for synthesis and catalysis. Chem Rev. (1999) 99:2071–84. doi: 10.1021/cr980032t

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Iguchi N, Datta A, Yoshikawa K, Yoshida Y, Saito G. A non-equilibrium quasistationary state in an ionic liquid caused by a focused laser. Chem Phys Lett. (2010) 485:110–13. doi: 10.1016/j.cplett.2009.12.035

CrossRef Full Text | Google Scholar

18. Yoshida Y, Otsuka A, Saito G, Natsume S, Nishibori E, Takata M, et al. Conducting and magnetic properties of 1-ethyl-3-methylimidazolium (EMI) salts containing paramagnetic irons: liquids [EMI][M^IIICl₄] (M = Fe and Fe_0.5Ga_0.5) and solid [EMI]₂[Fe^IICl₄]. Bull Chem Soc Jpn. (2005) 78:1921–8. doi: 10.1246/bcsj.78.1921

CrossRef Full Text | Google Scholar

19. O'Donoghue M. Characterization of crystals with gem applications. Prog Cryst Growth Charact. (1981) 3:193–209. doi: 10.1016/0146-3535(80)90019-2

CrossRef Full Text | Google Scholar

20. van der Beek D, Radstake PB, Petukhov AV, Lekkerkerker HNW. Fast formation of opal-like columnar colloidal crystals. Langmuir. (2007) 23:11343–6. doi: 10.1021/la7012914

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Yoshida Y, Saito G. Influence of structural variations in 1-alkyl-3-methylimidazolium cation and tetrahalogenoferrate(III) anion on the physical properties of the paramagnetic ionic liquids. J Mat Chem. (2006) 16:1254–63. doi: 10.1039/b515391c

CrossRef Full Text | Google Scholar

22. Murata K, Irish DE. Raman studies of the hydrated melt of FeCl₃6H₂O. Spectrochim Acta. (1988) 44:739–43. doi: 10.1016/0584-8539(88)80136-3

CrossRef Full Text | Google Scholar

23. Krzystek K, Telser J. Insight into electronic and magnetic properties through HFEPR studies. In: Holynska M, editor. Single-Molecule Magnets: Molecular Architectures and Building Blocks for Spintronics. John Wiley and Sons (2019). p. 135–72.

PubMed Abstract

24. de Pedro I, Rojas DP, Albo J, Luis P, Irabien A, Blanco JA, et al. Long-range magnetic ordering in magnetic ionic liquid: emim[FeCl₄]. J Phys Condens Matter. (2010) 22:296006. doi: 10.1088/0953-8984/22/29/296006

PubMed Abstract | CrossRef Full Text | Google Scholar