- Terahertz Research Center, Cooperative Innovation Centre of Terahertz Science, School of Electronic Science and Engineering, University of Electronic Science and Technology of China, Chengdu, China
An ultra-high sensitive metamaterials absorption sensor based on centrosymmetric double F-shaped metal resonators (CDFMR) is proposed, and its application in terahertz is analyzed. The sensor achieved perfect narrow-band absorption spectrum at 5.92 THz, with a high Q factor of 49.6. The resonance frequency is sensitive to the refractive index of the surface analyte, ultra-high sensitivity of 1,800 GHz/RIU and Fom value of 15 have been achieved. In addition, with a typical biomedical analyte of n = 1.3, the thickness sensitivity is 134 GHz/μm. It has important application in THz ultrasensitive biomedical sensor and detector.
Introduction
Terahertz (THz) waves is located in the frequency range of 0.1–10 THz [1, 2], which has revealed more and more unique applications in biomedical fields such as image [3] label-free detection [4] and recognition [5]. Metamaterials (MMs) are artificially designed electromagnetic materials composed of periodically arranged sub-wavelength elements [6–17]. Since Veselago defined and analyzed the properties of MMs with negative dielectric constant and negative permeability in 1967 [18], research on MMs biosensors at THz frequency has achieved great progress in recent years for MMs' strong electromagnetic response [19–22]. For example, Dong demonstrated a biosensor with resonators on a silicon substrate, its sensitivity is 85 GHz/RIU [23]. Sam et al. presented a refractive index MMs biosensor with a sensitivity of 300 GHz/RIU and thickness sensitivity of 23.7 GHz/μm [24]. Zhang et al. proposed a high-sensitivity MMs biosensor with a sensitivity of 638 GHz/RIU [25]. Furthermore, a metamaterial based double Corrugated Metal stripe label-free biosensor was modeled with sensitivity of 1,750 GHz/RIU [26]. Niknam et al. have also presented a metamaterial absorber sensor with refractive index sensitivity of 1.966 THz per unit refractive index variation and the thickness sensitivity of 52.5 GHz/μm [27]. Although biosensors based on MMs have been studied extensively, the thickness and refractive index of sensitivity still needs to be improved for practical applications.
In this study, we designed an ultrasensitive MMs sensor composed of centrosymmetric double F-shaped metal resonators (CDFMR) array. The simulation results show that its average absorption rate is 0.95, the Q-factor of the resonant peaks reaches 49.6, display excellent ability on frequency selectivity. Furthermore, the sensor shows ultra-high sensitivity on the variation of refractive index and thickness of analyte. The result will shed light on better application prospect in THz biosensors and detectors.
Structure Design
Figure 1A shows the schematic of the proposed metamaterial sensor. Figure 1B is the unit cell of the presented sensor, which consists of two gold layers on the top and in the bottom of the structure. The top layer is double F-shaped gold resonators layer with a thickness of h1, l1, and w1 are the length and width of the metal strips, respectively, three gaps with width of w2 are formed between the two resonators. While the bottom layer is a continuous gold plate with a thickness of h3, the conductivity of gold is set as σ = 4.09 × 107S/m [24], the dielectric medium between them is polytetrafluoroethylene (Teflon), its dielectric constant is εr + jεj = 2.1 + j0.01 [24] with a thickness of h2. The analysis and design of the structure is based on the Full Vector Finite Element Method [28]. The period of the unit cell are Px = Py = 36 μm in x and y directions, separately, h1 = 0.2 μm, h2 = 5 μm, h3 = 1 μm, l1 = 20 μm, and w1 = w2 = 2.5 μm.
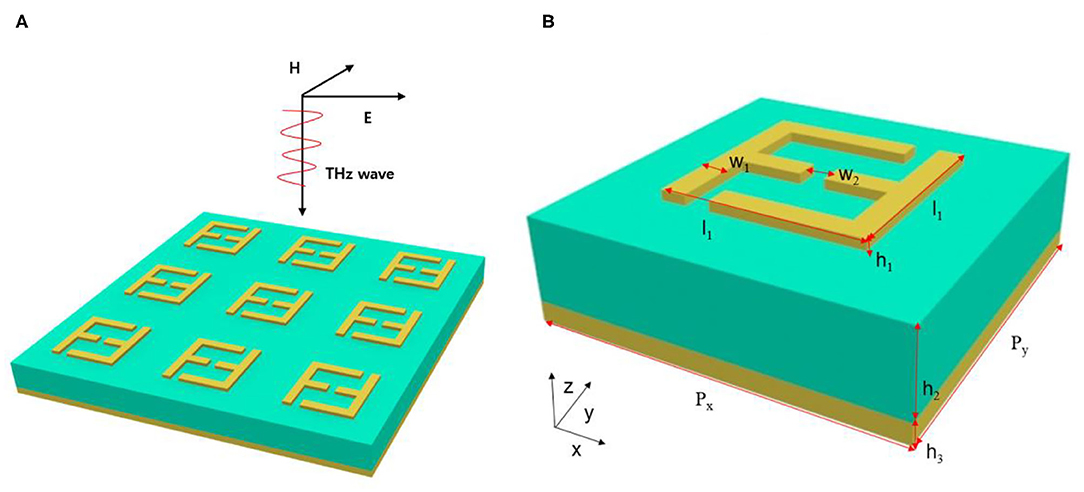
Figure 1. Schematic of the metamaterial sensor (A) array of the sensor; (B) unit cell of the sensor.
Excited by a linearly p-polarized plane incident wave (with electric component along the x direction), the absorption curve of the sensor without analyte is shown in Figure 2A, a perfect absorption peak at 5.95 THz is obtained. The full-width half-maximum value (FWHM) of the absorption peak is 0.12 THz, the quality factor (Q-factor) equal to 49.6 which is defined as Q = f/FWHM, where f = 5.95 THz is the central resonance frequency and FWHM = 0.12 THz is the full-width at half-maximum [29].
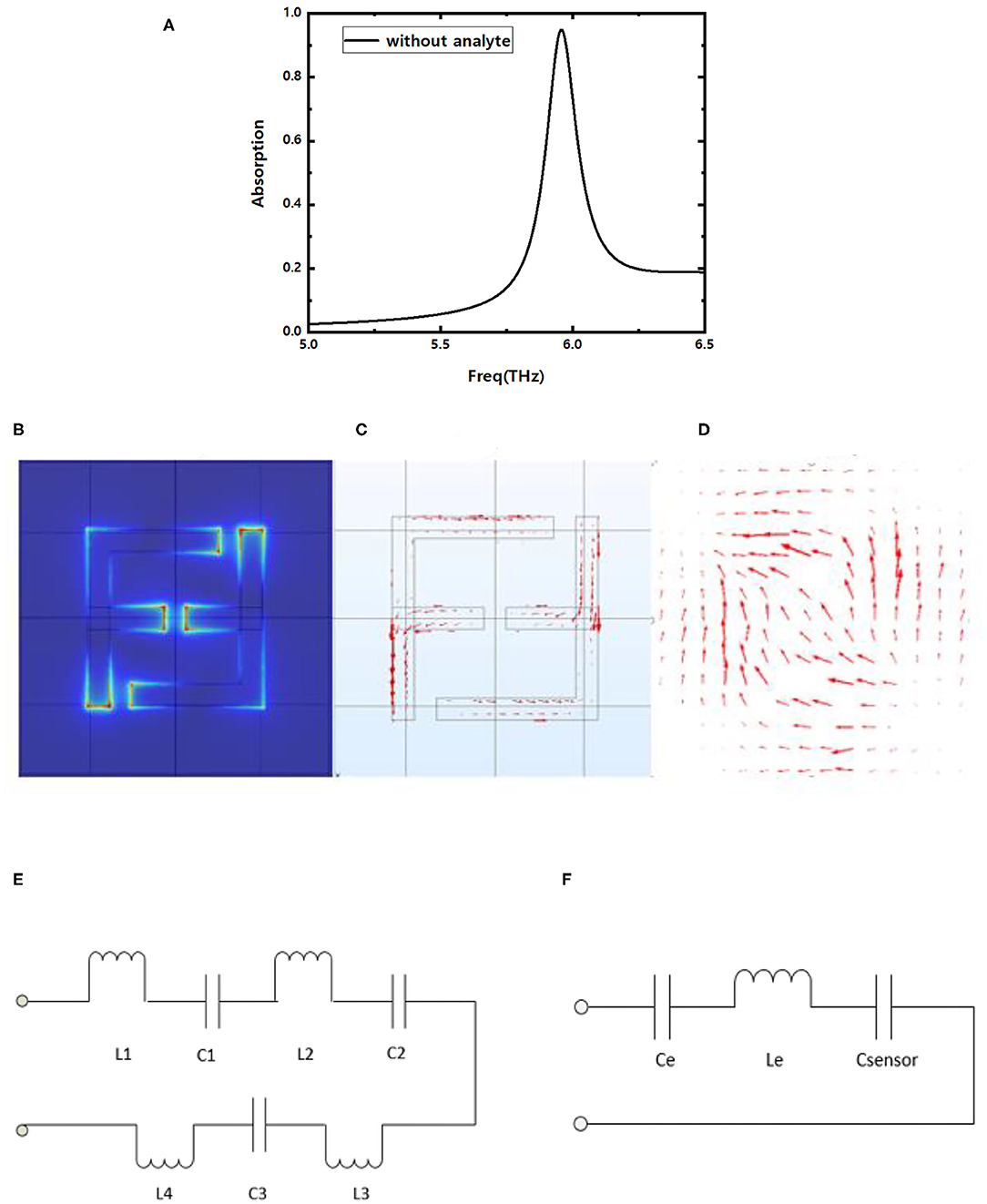
Figure 2. (A) Absorption spectrum of CDFMR at 5.95 THz without analyte; (B) electric field distribution, (C) upper surface current distribution on the resonators and (D) bottom surface current distribution on the metal base plate at 5.95 THz resonance frequency; (E) equivalent circuit model of F-shaped resonators; (F) simplified equivalent circuit model of CDFMR.
The electricfield (E-field) distribution and surface current distribution of the sensor at the resonance frequency of 5.95 THz are simulated and analyzed. Figure 2B demonstrate the E-field are concentrate near the gaps of the resonance. Correspondingly, we can observe from Figure 2C that the current distribute mainly on the metal strips of the double F-shaped resonance, and there are strong induced current distributions on the bottom metal plane due to the magnetic resonance effect in the structure as shown in Figure 2D. According to the equivalent circuit theory, The F-shaped metal strips and the metal base plate form a current loop. The gaps form equivalent capacitances C1, C2, and C3 and the metal strips form equivalent inductances L1, L2, L3, and L4 as shown in Figure 2E.
Effective capacitances of the structure also come from the top analyte and the dielectric layer sandwiched between the two mental layers, and assuming they are defined as Csensor and Cd, separately. So, there are a total inductance Le = L1 + L2 + L3 + L4, a total device capacitance Ce = Cd + C1 + C2 + C3 and a sensing capacitance Csensor. The value of Csensor will vary with the refractive index n and thickness h0 of the surface analyte. Then, equivalent circuit model of CDFMR can be simplified as Figure 2F for convenient analysis of the sensor properties in the following discussion. The resonance frequency of the sensor is expressed as
The equivalent device capacitance Ce can be much smaller than Csensor once the relative dielectric constant of dielectric is small and the gaps between the double F are narrow. So that Csensor will take charge of equivalent capacitance of the sensor, and further brings a prominent shift of resonance frequency when there is a minor variation of analyte refractive index, finally realizes high sensitivity.
Results and Discussion
With a fixed thickness t = 5 μm, the corresponding absorption curves are described in Figure 3A when the surface analyte on the sensor possess different refractive indexes n = 1.0, 1.1, 1.2, 1.3, 1.4, respectively. It can be seen that the resonance frequency of the sensor will red-shift when the refractive index n of the analysis layer increases. The result can be explained by the equivalent circuit theory, the dielectric constant ε is proportional to the refractive index n with εμ = n2 [30]. Therefore, the equivalent capacitance Csensor of the analyte will increase with n, and resonance frequency will increase according to formula (1), the increasing scale is near linearity as shown in Figure 3B. The sensitivity of a sensor is normally defined as S = Δf/Δn, where Δf is the offset of resonance frequency, Δn is the change rate of refractive index n [23], and the ultra-high sensitivity of 1,800 GHz/RIU can be obtained for the presented sensor. Furthermore, the FOM value take absorption bandwidth into account but only offset of resonance frequency, it is a more commonly used parameter for better evaluation of the synthetical performance of a sensor and the calculation formula is defined as Fom = S/FWHM [29], where S is the sensitivity of the sensor. Obviously, for a certain S, the smaller the 3 dB bandwidth FWHM of the resonance frequency band is, the higher the FOM value can be achieved. The FOM value for the proposed sensor is as high as 15. It is worth noting that the refractive index of typical biomedical samples is usually between 1.3 and 1.4. For example, the refractive index of blood for healthy human being is 1.35, and the n of blood samples infected with T-type leukemia (Jurkat) is 1.39 [31]. Remarkable offset of absorption band can be observed in Figure 3A when n varying with a step of 0.1, and the deviation of resonance peaks still keep distinct even though the variation step of n is only 0.02 in the range of 1.3–1.4. Obviously, the device can act as a supersensitive biosensor with high sensitivity and high Q-value.
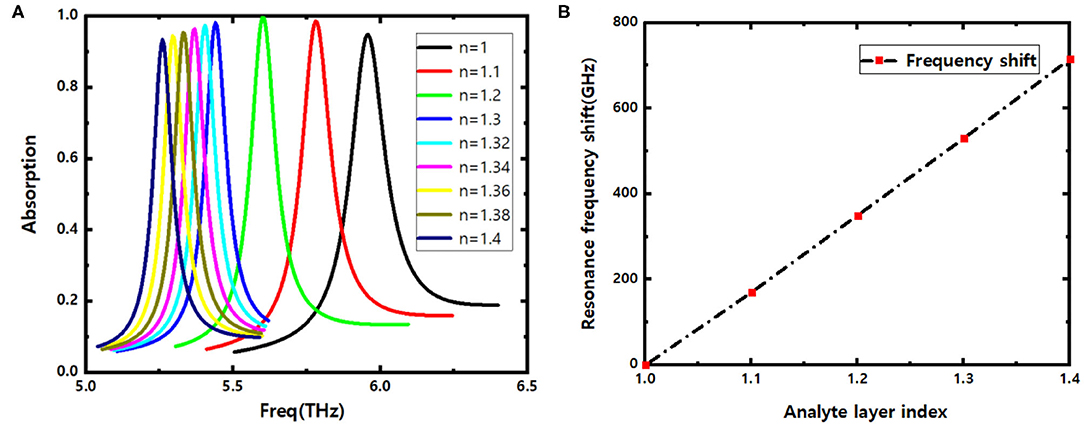
Figure 3. (A) Offset of absorption curves vs. refractive index n of the analyte; (B) resonance frequency shift with the varying index of refraction n.
The influence of the geometrical parameters of the double F-shaped resonator on the sensing performance are analyzed for the gap width w2, the strip width w1 and the strip length L2. As shown in Figure 4A, when w2 increases from 2.25 to 3 μm, the resonance frequency is blue-shifted, and the peak of the absorption spectrum decreases at the same time accompany with an absorption bandwidth broadening. According to formula (1), the increase of w2 will reduce the equivalent capacitances C1, C2, and C3, and the blue shift happens for the resonance frequency. Simultaneously, the reduction of the equivalent capacitances will weaken the absorption ability of the structure to the incident EM wave.
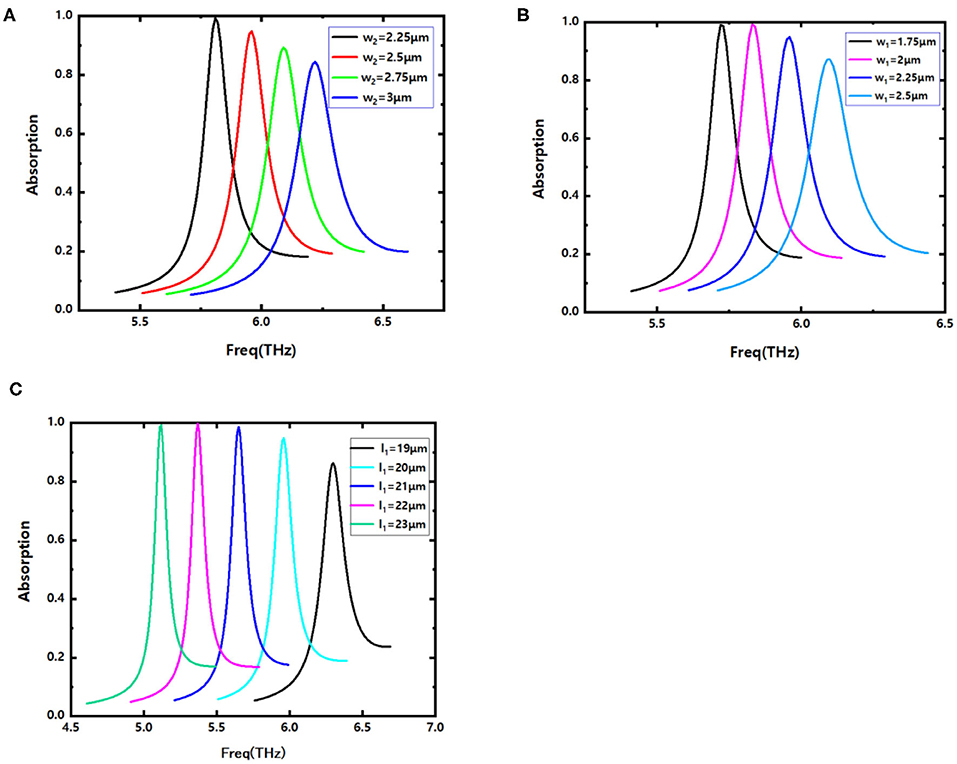
Figure 4. Absorption spectra with (A) different gap widths w2; (B) different metal strip width w1; (C) different metal strip length l1.
Increasing width w1 of the metal strip of the F-shaped resonance will induce larger value of its inductance Le and capacitance C1 + C2 + C3, which bring with a blue shift of the resonant frequency. Obviously, the result is agreement well with the evolution of the absorption curves shown in Figure 4B. Meanwhile, there is a decrease of the absorption peak and the Q-value.
Finally, we discussed the effect of the metal strip length l1 on the resonance frequency. As shown in Figure 4C, red shift of the resonance frequency happens as l1 increases, which is due to the increase of the total inductance Le. It is noteworthy that the absorption rate and the Q-value of the absorption band will increase with increasing l1.
The thickness of the analyte layer will also impact the sensing performance. For a typical biological analyte slice with refractive index of n = 1.3, Figure 5A shows the absorption curves vs. thickness of analyte h0, it hints that the resonance frequency will red shift non-uniformly when h0 increasing from 0 to 6 μm with step of 1 μm, the absorption spectrum band get narrower and more sharp. Furthermore, there is a long span offset for the case of the thickness of surface analyte change from 0 to 1 μm, which represent that of without or with surface analyte on the sensor, evidently, the proposed sensor unfolds a better performance with analyte loaded.
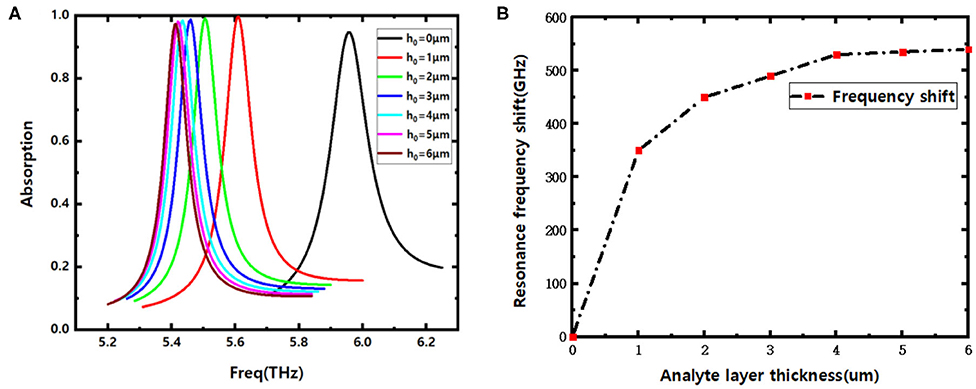
Figure 5. (A) Absorption curves for different analyte thickness h0; (B) resonance frequency shifts with increasing analyte thickness h0.
Figure 5B declares the red shift of resonance frequency with the increase of the analyte thickness. It can be seen that the deviation of the resonance frequency will tend to be gentle on per unit increase of thickness primarily, and become negligible when the thickness of the analyte exceeds 4 μm. Considering the thickness sensing is defined as S = Δf/Δh0 [24], in which Δf is the resonance frequency offset and Δh0 is the thickness variation of analyte slice. When the thickness of the analyte changes from 0 to 4 μm, the sensitivity of the proposed sensor can reach S = 134 GHz/μm.
Conclusion
In summary, a metamaterial biosensor with good performances is designed and proposed, ultrahigh sensitivity and high Fom value are obtained, the sensing characteristics and resonance mechanism are discussed in detail. The results show that the sensor can realize an average absorption rate of 0.95 and a Q factor of 49.6, the sensitivity can reach 1,800 GHz/RIU and the Fom value is 15, which realizes high sensitive and high Q factor refractive index sensing in THz frequency band. At the same time, it shows a high thickness sensitivity of 134 GHz/μm when the thickness of the analyte changes from 0 to 4 μm. The proposed sensor has important application in THz ultrasensitive biomedical sensor and detector.
Data Availability Statement
All datasets generated for this study are included in the article/supplementary material.
Author Contributions
AM and RZ conceived the idea of the research, carried out the whole simulation, performed the acquisition and analysis of data, and they also wrote the manuscript. All authors contributed to the final manuscript.
Funding
This study was supported by the National Key Research and Development Program of China (2018YFF01013001 and 2017YFA0701000) and the Natural Science Foundation of China (61701084 and 61505022).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Williams G. Filling the THz gap—high power sources and applications. Rep Prog Phys. (2006) 69:301–26. doi: 10.1088/0034-4885/69/2/R01
2. Liu H, Liu Y, Zhu D. Chemical doping of graphene. J Mater Civ Eng. (2011) 21:3335–45 doi: 10.1039/C0JM02922J
3. Al-Naib I. Biomedical sensing with conductively coupled terahertz metamaterial resonators. IEEE J Sel Top Quantum Electron. (2017) 23:4700405. doi: 10.1109/JSTQE.2016.2629665
4. Chen X, Fan W, Song C. Multiple plasmonic resonance excitations on graphene metamaterials for ultrasensitive terahertz sensing. Carbon. (2018) 133:416–22. doi: 10.1016/j.carbon.2018.03.051
5. Zhang Z, Ding H, Yan X. Sensitive detection of cancer cell apoptosis based on the non-bianisotropic metamaterials biosensors in terahertz frequency. Opt Mater Express. (2018) 8:659–67. doi: 10.1364/OME.8.000659
6. Chen M, Fan F. Terahertz ultrathin film thickness sensor below λ/90 based on metamaterial. Appl Opt. (2016) 55:6471. doi: 10.1364/AO.55.006471
7. Ferguson B, Zhang XC. Materials for terahertz science and technology. Nat Mater. (2002) 1:26–33. doi: 10.1038/nmat708
8. Mirzaei S, Green NG, Rotaru M, Pu SH. Detecting and identifying DNA via the THz backbone frequency using a metamaterialbased label-free biosensor. In: Proceedings of SPIE. Francisco, CA. (2017). p. 10103. doi: 10.1117/12.2263694
9. Su L, Naqui J, Mata-Contreras J, Martín F. Modeling and applications of metamaterial transmission lines loaded with pairs of coupled complementary split-ring resonators (CSRRs). IEEE Antennas Wirel Propag Lett. (2016) 15:154–7. doi: 10.1109/LAWP.2015.2435656
10. Srivastava YK, Cong LQ, Singh R. Dual-surface flexible THz fano metasensor. Appl Phys Lett. (2017) 111:201101. doi: 10.1063/1.5000428
11. Cai W, Chettiar UK, Kildishev AV, Shalaev VM. Optical cloaking with metamaterials. Nat Photon. (2007) 1:224–7. doi: 10.1038/nphoton.2007.28
12. Chen Q, Zhang H, Shao YJ, Zhong T. Bandwidth and gain improvement of an L-shaped slot antenna with metamaterial loading. IEEE Antennas Wirel Propag Lett. (2018) 17:1411–5. doi: 10.1109/LAWP.2018.2848639
13. Chakyar SP, Simon KS, Bindu C, Andrews J, Joseph VP. Complex permittivity measurement using metamaterial split ring resonators. J Appl Phys. (2017) 121:54101. doi: 10.1063/1.4975111
14. Dincer F, Karaaslan M, Unal E, Akgol O, Sabah C. Design of polarization-and incident angle-independent perfect metamaterial absorber with interference theory. J Electron Mater. (2014) 43:3949–53. doi: 10.1007/s11664-014-3316-x
15. Gu J, Singh R, Liu X, Zhang X, Ma Y, Zhang S, et al. Active control of electromagnetically induced transparency analogue in terahertz metamaterials. Nat Commun. (2012) 3:1151. doi: 10.1038/ncomms2153
16. Cong L, Tan S, Yahiaoui R, Yan F, Zhang W, Singh R. Experimental demonstration of ultrasensitive sensing with terahertz metamaterial absorbers: a comparison with the metasurfaces. Appl Phys Lett. (2015) 106:031107. doi: 10.1063/1.4906109
17. Sabah C, Dincer F, Karaaslan M, Bakir M, Unal E, Akgol O. Biosensor applications of chiral metamaterials for marrowbone temperature sensing. J Electromagn Waves Appl. (2015) 17:2393–403. doi: 10.1080/09205071.2015.1084894
18. Veselago VG. The electrodynamics of substances with simultaneously negative values of ε and μ. Sov Phys Usp. (1968) 10:509. doi: 10.1070/PU1968v010n04ABEH003699
19. Chen L, Xu N, Leenae S, Cui T. Defect-induced fano resonances in corrugated plasmonic metamaterials. Adv Opt Mater. (2017) 5:960. doi: 10.1002/adom.201600960
20. Salim A, Lim S. Recent advances in the metamaterial-inspired biosensors. Biosens Bioelectron. (2018) 117:398–402. doi: 10.1016/j.bios.2018.06.031
21. Yan X, Maosheng Y. The terahertz electromagnetically induced transparencylike metamaterials for sensitive biosensors in the detection of cancer cells. Biosens Bioelectron. (2019) 126:485–92. doi: 10.1016/j.bios.2018.11.014
23. Li D, Lin S, Hu F. Metamaterial terahertz sensor for measuring thermal-induced denaturation temperature of insulin. IEEE Sens J. (2020) 20:1821–8. doi: 10.1109/JSEN.2019.2949617
24. Saadeldin AS, Hameed MFO. Highly sensitive terahertz metamaterial sensor. IEEE Sens J. (2019) 19:7993–9. doi: 10.1109/JSEN.2019.2918214
25. Zhang W, Feng L, Xuan J. Ultrasensitive dual-band terahertz sensing with metamaterial perfect absorber. In: Proceedings of IEEE MTT-S International Microwave Workshop Series on Advanced Materials and Processes for RF and THz Applications Pavia. (2017). p. 1–3. doi: 10.1109/IMWS-AMP.2017.8247404
26. Niknam S, Yazdi M, Behboudi Amlashi S. Enhanced ultra-sensitive metamaterial resonance sensor based on double corrugated metal stripe for terahertz sensing. Sci Rep. (2019) 9:7516. doi: 10.1038/s41598-019-44026-4
27. Chen X, Fan W. Ultrasensitive terahertz metamaterial sensor based on spoof surface plasmon. Sci Rep. (2017) 7:2092. doi: 10.1038/s41598-017-01781-6
28. Zhang Y, Li T, Zeng B, Zhang H, Lv H, Huang X, et al. A graphene based tunable terahertz sensor with double fano resonances. Nanoscale. (2015) 7:12682. doi: 10.1039/C5NR03044G
29. Yan F, Li L, Wang R, Tian H. Ultrasensitive tunable terahertz sensor with graphene plasmonic grating. J Lightw Technol. (2019) 37:1103–12. doi: 10.1109/JLT.2018.2886412
30. Wu XJ, Quan BG, Pan XC. Alkanethiol-functionalized terahertz metamaterial as label-free, highly-sensitive and specific biosensor. Biosens Bioelectron. (2013) 42:626–31. doi: 10.1016/j.bios.2012.10.095
Keywords: metamaterial, THz, biosensor, sensitivity, absorber
Citation: Ma A, Zhong R, Wu Z, Wang Y, Yang L, Liang Z, Fang Z and Liu S (2020) Ultrasensitive THz Sensor Based on Centrosymmetric F-Shaped Metamaterial Resonators. Front. Phys. 8:584639. doi: 10.3389/fphy.2020.584639
Received: 17 July 2020; Accepted: 07 September 2020;
Published: 22 October 2020.
Edited by:
Shuncong Zhong, Fuzhou University, ChinaReviewed by:
Dejun Liu, Shanghai Normal University, ChinaWeiqiang Ding, Harbin Institute of Technology, China
Copyright © 2020 Ma, Zhong, Wu, Wang, Yang, Liang, Fang and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Renbin Zhong, cmJ6aG9uZ0B1ZXN0Yy5lZHUuY24=
 Anchen Ma
Anchen Ma Renbin Zhong
Renbin Zhong Zhenhua Wu
Zhenhua Wu