Parallel Quantum Computation of Vibrational Dynamics

The vibrational dynamics in a linear triatomic molecule is emulated by a quantum information processing device operating in parallel. The quantum device is an ensemble of semiconducting quantum dot dimers addressed and probed by ultrafast laser pulses in the visible frequency range at room temperature. A realistic assessment of the inherent noise due to the inevitable size dispersion of colloidal quantum dots is taken into account and limits the time available for computation. At the short times considered only the electronic states of the quantum dots respond to the excitation. A model for the electronic states quantum dot (QD) dimers is used which retains the eight lowest bands of excitonic dimer states build on the lowest and first excited states of a single QD. We show how up to 8² = 64 quantum logic variables can be realistically measured and used to process information for this QD dimer electronic level structure. This is achieved by addressing the lowest and second excited electronic states of the QD’s. With a narrower laser bandwidth (= longer pulse) only the lower band of excited states can be coherently addressed enabling 4² = 16 logic variables. Already this is sufficient to emulate both energy transfer between the two oscillators and coherent motions in the vibrating molecule.

Introduction

We describe the theoretical background for an experimental setup, an ensemble of quantum dot dimers that can and has been realized in the laboratory. We show explicitly how this device is used to emulate the quantum vibrational dynamics of a linear triatomic molecule and discuss possible extensions. In 1985 Deutsch defined a quantum computer as a device that could simulate effectively an arbitrary physical system [1]. Our aim here is much more modest. We seek to describe a device that can be realized with currently available laboratory techniques. Furthermore, the device needs to provide computational answers only for a limited set of variables of the physical system. The computation is realized by mapping of the dynamics of the physical variables of this limited set using a set of observations of the time-evolution of the device. The set of possible observations of the device is the set of our N² logic variables. The number N is less than or equal to the number of accessible quantum states of the logic device. N² is larger than the number of variables of interest for the physicochemical system that is emulated.

The quantum mechanical device is characterized by a set of observables and that is why we call the logic done by the device “computing by observables” [2, 3]. With such a device one can emulate a physical system that requires up to this number for simulating a closed set of physical variables. Increasing levels of resolution provided by the description of a physicochemical system can be characterized by an increasing numbers of variables. An example used in this paper is that of two coupled harmonic oscillators. For each oscillator there is a denumerable number of bound states. So, in principle, a fully complete characterization of each oscillator can require up to a denumerably infinite number of variables. An opposite extreme is a thermal state of the oscillator. Its complete description requires two physical variables, a normalization of the probabilities and the mean energy. For the coupled oscillators we will describe several physical levels of resolution that are intermediate between these two limits.

The variables that we deal with can be regarded as vectors in a linear space. They can, if so desired, be made orthogonal etc. As vectors, the variables seem to behave like classical variables but they are a quantum mechanical description of the system. In textbooks one is more used to a linear vector space of wave functions, what is sometimes called a Hilbert space. The observables are also defined in a space with a scalar product and a Mathematician may choose to call it a Hilbert space. But if the Hilbert space of the wave functions has N dimensions, the corresponding linear vector space of observables has N² dimensions. If $\left\{|i\rangle \right\}$ is a set of basis vectors in the Hilbert space of wave functions, $i=\mathrm{1,2},\mathrm{.}\mathrm{.},N$, a basis set for the observables can be written as $\left\{X_{ij}=|i\rangle \langle j|\right\},i,j=\mathrm{1,2},\mathrm{.}\mathrm{.},N$. The N² expectation values of these are our variables. We will refer to the expectation values when $i\ne j$ as coherences. The N diagonal elements are populations. By taking linear combinations, e.g., $|i\rangle \langle j|+|j\rangle \langle i|$, we can arrange all the variables to be Hermitian and all the variables to be real.

In this paper we use two distinct linear vector spaces. One is suitable to describe the dynamics of the computing device and one the dynamics of the physical system we aim to emulate. We do not consider the device as providing an analog for the physical system. To emphasize this point we use a device that operates on the dynamics of purely electronic states pumped and read by ultrafast laser pulses. A schematic description of the device and the physical system is shown in Figure 1. The dynamics in the electronic Hilbert space of the quantum dot dimers is mapped to simulate the time evolving physical variables in the nuclear Hilbert space. We will therefore need a separate discussion of the logic variables provided by the computing device and those required to describe the physical system.

FIGURE 1

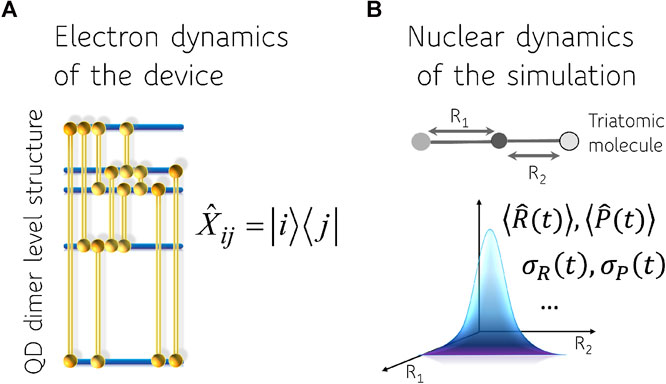
FIGURE 1. Representation of the computing device (A) and the physical system (B). The four bands of excited electronic states of the device that are used are indicated as well as the ten pairs i, j whose twenty corresponding coherences $X_{ij}$ are used as logic variables. The physical system we emulate is a vibrating triatomic molecule in a non-stationary quantum mechanical state. We will simulate the mean position and momentum of each of the two coupled oscillators as well as the respective widths, σ_R and σ_P.

Quantum computing algorithms have been developed for problems of chemical interest. This includes not only electronic structure [4–13] but also quantum enhanced machine learning algorithms [8] and algorithms for dimension reduction including Principal Component Analysis, Canonical Correlation Analysis and other algebraic methods used for dimension reduction such as surprisal analysis [6, 15–17] A preliminary report on our quantum computation has been published [18].

The Computing Device

Our computing device is an array of CdSe quantum dot QD dimers. Addressing the device is by a sequence of laser pulses and read-out is performed simultaneously on many dots [19–24] as in 2D electronic spectroscopy [25, 26]. Measuring over a classical ensemble of dots importantly means that we directly read the mean values and that there is no interference between measuring different observables that individually do not commute. In the short time interval during which the time and probe are performed the primary source of noise is the variability in the size of the quantum dots. This means that the two dots making the dimer are not quite identical so strictly speaking we have heterodimers. We therefore need to average the read-out over the distribution of dimer sizes. The states of different dimers are at slightly different energies so that the coherences between different pairs of states beat at slightly different frequencies. This reduces the frequency resolution or, equivalently, the time available for read-out [13] to faster than the dephasing time of the mixture of not fully identical dimers. So we do not read individual quantum states but bands of closely adjacent states belonging to different dimers. In our computations we use an experimentally realizable size of the dots and their size dispersion.

In this paper we employ rather elementary dynamics of the computing device. Using a sequence of laser pulses we bring each dimer to a multicoherent state. From then on the device is unperturbed and it is the oscillations of different coherences that are used to simulate the time dependence of the physical system. The coherence between the ground state and any electronic excited state oscillates quite fast so it dephases faster then the dephasing of the coherences between the electronically excited states. The very fast beating coherence, few fs’s or less, between the ground state and an electronic excited state cannot therefore be reliably detected. So very fast oscillations cannot be simulated by our device due to the currently available dispersion in sizes of colloidal quantum dots. It is expected that a lower dispersion will be experimentally possible in the near future.

This paragraph is a sketch of the counting of electronically excited states in a CdSe dot of nanometric mean size between 2 and 5 nm in diameter and of a dimer of two dots drawn from an ensemble of dots of the same mean size. The two dots making up the dimer are of about the same but not identical size. The first electronically excited state of a dot is a band of 12 states, as follows. The spin of the hole is coupled to a p (l = 1) orbital of Se to give rise to two spin orbit components, $1/2\text{ and }3/2$. The s orbital on Cd contributes only a spin of $1/2$. The total orbital angular momentum F of the excitonic $3/2$ state has the projections $F_z=\pm 2,\pm \mathrm{1,0}$ and $F_z=\pm \mathrm{1,0}$ for the hole and the electron respectively, eight states all together. There are four states, ($F_z=\pm \mathrm{1,0}$ and 0) for the $1/2$ excitonic state. The two excitonic bands of states, (of eight and four states, respectively), can be experimentally resolved [23]. There are similarly two resolvable bands of states for the second electronically excited state of CdSe. All together, four bands of electronically excited states per dot. In the dimer, or dots with short ligands, the dots are interacting by Coulomb and exchange coupling. Thereby each one of the four bands of states of the monomer is split into two. In the visible range a dimer has eight resolvable bands of states, four bands that correspond primarily to the lower electronic state and four to the higher excited state of a monomer. Since the dimers are made of two dots that are not quite identical, all eight bands are optically active from the common dimer ground state, see Supplementary Materials, section 1.1 for more details.

Using the counting as above the CdSe dots enable a choice of four or eight bands of states in the visible range. Addressing coherently the states of all the eight bands requires shorter laser pulses. Smaller QD have larger energy difference between their two lower excited electronic states and therefore one needs a larger energy bandwidth of the pulse or a higher carrier frequency to simultaneously address them. On the other hand, for larger dots, the energy difference between the two lowest excited states may become smaller or comparable to strength of the spin-orbit coupling, which leads to a loss of resolution between the different bands [23, 24]. Commercially available fast lasers in the visible can easily address coherently all the states of the four lowest bands. The minimal capability of our device is therefore 5² logic variables, the five populations of the ground and four excited states and the 5 × 4 coherences. Four (times two, complex values) coherences of the transitions between the ground state and the four excited states and 12 coherences between the four excited states. After the laser pulses are over, each coherence will oscillate with a fixed frequency determined by the differences in energy of the two states. The highest frequencies are for the transitions up from the ground state. These are rather fast. So in this paper we consider the coherences between pairs of excited states.

To describe the dynamics of the device we take it that initially it is in the ground electronic state. We assume that the addressing lasers are weak enough so that only one photon transitions are possible. The lasers are in the visible so that transitions between the excited states are way out of resonance and so are excluded. Indeed and as we shall discuss, the frequencies of the transitions between the excited states are in the range of molecular vibrational frequencies so that we can use the coherences between excited states to emulate the time scales relevant to the physical systems. The range of timescales is determined by the size of the quantum dot dimers as is discussed above and by the coherence width of the excitation lasers. The bandwidth of a 6 fs pulse is about 2,100 cm⁻¹.

The excitation scheme is that typically used in 2D electronic spectroscopy [25, 26]. The first fast laser pulse generates the absorption from the ground state. Next, with some delay, is a second laser pulse. One frequency axis that we will use is the Fourier transform with respect to this time delay. The system is next allowed to evolve for a time interval that is typically denoted T. After the second pulse, the system can be back in the ground state, in one of the excited states, or in a coherence between two excited states. After the time T the third laser pulse stimulates emission that is monitored in time and the second frequency axis is a Fourier transform with respect to this time. So for each value of the time T we generate a 2D frequency map. In the echo phase matching direction of emission, the populations of the excited states appear on the diagonal of the 2D maps and the coherences are on the off-diagonal at a position determined by the excitation frequency of the two excited states they connect. At different values of the time interval T, the intensities at the off-diagonal positions on the map will vary according to the time-evolution of the respective coherences, and this is how we can simulate the time dependence of the physical variables. As emphasized above, due to the size dispersion the coherence beating frequencies will have a finite spread. The ability to resolve coherences between different pairs of states depends on this spread to be limited enough. From the complementary time-dependent point of view, the coherence contributions decay in time as a Gaussian with a width that is governed by the width of the frequency distribution of the coherence [3]. On the plus side, the finite spread of the frequency of every coherence means that the computing device can simulate finite spans of values, roughly the width of the Gaussian, about different frequencies.

Deterioration of the signal due to dephasing has been an issue for quantum computing from its early beginning [27, 28]. Often it is dephasing due to interaction with the environment. Here too, the limiting factor is dephasing but it is a dephasing due to an inhomogeneous broadening caused by the size dispersion of the QD’s. In the short times that we probe, the electronic states of each dimer practically are not yet perturbed. The dephasing is due to the probe averaging over many dimers, dimers with slightly different frequencies [3]. We pay special care to make the dephasing realistic. The mean diameter of the CdSe QD’s, 4.4 nm, that we use to compute the spectrum and the size dispersion, 5%, have been realized experimentally [23, 29]. We emphasize the considerable improvement in performance that can be achieved by an even modest reduction in the dispersion in sizes. Yet even the already accessible 5% size variability is sufficient to enable a quite powerful device. We also stress that the 2DES measurements that we rely upon are performed at room temperature, in solution [23] or on a solid state device [24].

We can emulate dynamics by measuring 2D coherence maps at a range of values for the time interval T. With current chemical synthetic capabilities the dephasing due to the size dispersion of the dot is the primary limitation on how long T can be. At longer times, say beyond 100 fs, coupling to the phonons also sets in.

For each experiment there will be a sequence of transitions leading to the same coherence between two excited states during the delay time T between the second and the third pulse. For weak pulses so that first order time-dependent theory and the impulsive limit transition applies at each interaction with the pulse, the two coordinates of the 2D maps are the absorption frequency from the ground state (GS) and the emission frequency to GS. When two excited states, i and j, can be reached by one photon transitions from the ground state (GS) there are four positions in the 2D maps, two diagonal ones at $\left({\omega }_{0i},{\omega }_{0i}\right)$ and $\left({\omega }_{0j,}{\omega }_{0j}\right)$ and two off-diagonal ones $\left({\omega }_{0i},{\omega }_{0j}\right)$ and $\left({\omega }_{0j},{\omega }_{0i}\right)$ where ${\omega }_{0i}$ and ${\omega }_{0j}$ are the excitation frequencies of states i and j from the GS. In the rephasing phase matching (echo) direction, eight Liouvillian paths contribute to these four positions. They are spelled out explicitly in Supplementary Figure S3 in the notation of ref. [26], see also refs. [2, 30].

Four paths fall on the diagonal of the 2D map at the excitation frequencies of the two excited states: one ground state bleaching (GSB) path for which the system is the GS during the time interval T and one stimulated emission paths (SE) for which the system is in excited state i during T at $\left({\omega }_{0i},{\omega }_{0i}\right)$ and a GSB and a SE path for which the system is in excited state j at $\left({\omega }_{0j},{\omega }_{0j}\right)$. At the short times below 200 fs considered here, there is no exchange of population between the GS and the two excited states during T and the contribution of these four paths to the 2D response is time-independent. Two time-dependent GSB paths contribute to the two off diagonal positions, $\left({\omega }_{0i},{\omega }_{0j}\right)$ and $\left({\omega }_{0j},{\omega }_{0i}\right)$, respectively. Two paths that are the signature of the electronic coherence between the two excited states also contribute at the same off diagonal positions. The two coherence paths are beating during T with the transition frequency ${\omega }_{ij}$ of the coherence between the excited states i and j.

The eight paths, see Supplementary Figure S3, contribute simultaneously to the time evolution of the density matrix and therefore to the 2D map, hence “parallel” in our title. When the system has more than two excited states, each pair of excited states contributes 8 paths to the time evolution of the density matrix. For example, there are 16 coherences between excited states for the five level system (GS + 4 excited states) discussed above, meaning that 16x8 paths contribute in parallel. Of these, only the 16x2 paths that lead to a distinct off diagonal position on the 2D maps are used to map observables of the system that is emulated. There are also 8 paths per pair of excited states in the non rephasing phase matching direction. So in principle, the larger the number of states in the band that can be accessed by one photon transition from the GS, the larger the number of observables that can be emulated.

As explained above, colloidal QD’s are synthesized with a finite size dispersion which leads to a distribution of transition frequencies for each coherence, both from the GS, the ${\omega }_{0i}$ type and between excited states (the ${\omega }_{ij}$ type). At the level of the ensemble, the inherent size dispersion of the QD’s leads to a Gaussian distribution in energy of the addresses $\left({\omega }_{0i},{\omega }_{0j}\right)$ of coherences between excited states and to their Gaussian dephasing along T and therefore limits the number of coherence positions that can be resolved on the map. When controlled and limited to a few percent in diameter, the size dispersion can also be used to advantage. Scanning positions on the 2D maps around the address corresponding to the mean transition frequencies from the GS gives slightly different periods of the coherence along T which provides flexibility in mapping the periods of the observables of the emulated systems.

Figure 1 shows a scheme where there are four bands of excited states that are accessed by the laser pulses. The four coherences at a relatively high frequency when the ground state is one of the two states are not detected in 2D spectroscopy. There are the twelve lower frequency coherences that, as mentioned, will be used to emulate the vibrational motions of the physical system. Note that there is a spread in the frequencies and the very lower ones will be used to emulate splittings due to coupling of two vibrational modes.

The Physical System: Linear Vibrating Triatomic Molecule

In this paper we track the electronic dynamics in the QD dimers to emulate the vibrational motion in non-stationary states of a triatomic molecule, Figure 2.

FIGURE 2

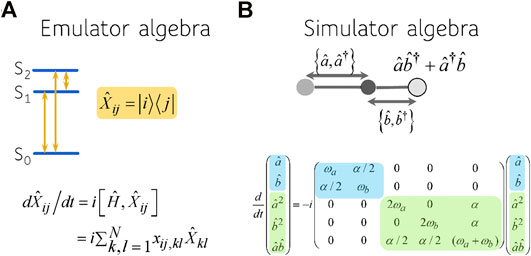
FIGURE 2. The algebra characterizing the device (A) and the physical system (B). The coherences $X_{ij}=|i\rangle \langle j|$ between excited levels i and j of the quantum dot dimer are our logic variables. After the laser pulses are over, the coherences oscillate in time with a frequency that is the difference between the energies of the two states that they connect. We aim to simulate the time dependence of observables of the coupled oscillators system. For example, as shown in Eq. 7, we need the time dependence of $\langle a^2\rangle$ to compute the variance of the bond displacement of the first oscillator.

The system we emulate is two coupled harmonic local vibrations, each representing a bond. The coupling is due to the motion of the central atom and it depends on its mass and its displacement from equilibrium [31]. By expanding the potential of the system and keeping only up to quadratic terms in the deviation of the bond displacements from equilibrium, the Hamiltonian for two harmonically coupled harmonic modes, denoted a and b, is, using $\hslash =1$,

$\widehat{H}={\omega }_a{\widehat{a}}^{†}\widehat{a}+{\omega }_b{\widehat{b}}^{†}\widehat{b}+(\alpha /2)({\widehat{a}}^{†}\widehat{b}+{\widehat{b}}^{†}\widehat{a})(1)$

Here we use the standard notation for the creation and annihilation operators for the two local vibrational modes. The vibrational quantum number mismatch is determined by $\langle {\widehat{a}}^{†}\widehat{a}-{\widehat{b}}^{†}\widehat{b}\rangle$ and the frequency mismatch is $\delta \omega ={\omega }_a-{\omega }_b$. The harmonic coupling is $\widehat{a}{\widehat{b}}^{†}+{\widehat{a}}^{†}\widehat{b}$ and the strength is $\alpha /2$. Due to this coupling, the creation and annihilation operators of the two oscillators are correlated.

We characterize vibrational motion of the local modes by the mean values of the bond distance, momenta and dispersion of both quantities. Computation of the values of the mean bond distance and mean momenta involves description of the evolution of both creation and annihilation operators: $\langle {\widehat{R}}_a\rangle =\langle \widehat{a}+{\widehat{a}}^{†}\rangle /\sqrt{2m_a{\omega }_a}$. A simple application of the Heisenberg equation of motion leads to a set of equations of motion:

$\frac{d}{dt}\left(\begin{array}{c}\widehat{a}\\ \widehat{b}\end{array}\right)=-i\left(\begin{array}{cc}{\omega }_a& \alpha /2\\ \alpha /2& {\omega }_b\end{array}\right)\left(\begin{array}{c}\widehat{a}\\ \widehat{b}\end{array}\right)(2)$

and an adjoint equation:

$\frac{d}{dt}\left(\begin{array}{c}{\widehat{a}}^{†}\\ {\widehat{b}}^{†}\end{array}\right)=i\left(\begin{array}{cc}{\omega }_a& \alpha /2\\ \alpha /2& {\omega }_b\end{array}\right)\left(\begin{array}{c}{\widehat{a}}^{†}\\ {\widehat{b}}^{†}\end{array}\right)(3)$

One can write these as one equation for a vector of four components using a Liouvillian operator $\widehat{L}$: $d\mathbf{v}/dt=i\mathbf{L}\mathbf{v}$, where ${\mathbf{v}}^{+}=\left(\widehat{a},\widehat{b},{\widehat{a}}^{†},{\widehat{b}}^{†}\right)$ and Liouvillian:

$\mathbf{L}=\left(\begin{array}{cccc}-{\omega }_a& -\alpha /2& 0& 0\\ -\alpha /2& -{\omega }_b& 0& 0\\ 0& 0& {\omega }_a& \alpha /2\\ 0& 0& \alpha /2& {\omega }_b\end{array}\right)(4)$

As is well known, one can diagonalize the Hamiltonian leading to an antisymmetric and a symmetric vibrational modes. Here this corresponds to diagonalizing the Liouvillian, Eq. 4, leading to the frequencies:

$(1/2)({\omega }_a+{\omega }_b\pm \Omega )(5)$

where ${\Omega }^2={\alpha }^2+{\left(\delta \omega \right)}^2$.

We use as an example vibrational dynamics in the CS₂ molecule, where ${\omega }_a={\omega }_b=\omega$ and $\Omega =\alpha$. The eigenfrequencies, Eq. 5, become $\omega \pm \alpha /2$ for the $\widehat{a}\pm \widehat{b}$ eigenvectors and similarly for their complex conjugate analogs. Taking expectation values it is useful to note that equations imply that the mean values at the time t can be computed given their initial values, for example:

$\begin{array}{l}\langle \widehat{a}+\widehat{b}\rangle \left(t\right)=\langle \widehat{a}+\widehat{b}\rangle \left(0\right)\exp \left(-i(\omega +\alpha /2)t\right)\\ \langle {\widehat{a}}^{†}+{\widehat{b}}^{†}\rangle \left(t\right)=\langle {\widehat{a}}^{†}+{\widehat{b}}^{†}\rangle \left(0\right)\exp \left(i(\omega +\alpha /2)t\right)\end{array}(6)$

The mean values of the bond displacement, $\left(\langle \widehat{a}\rangle \left(t\right)+\langle {\widehat{a}}^{†}\rangle \left(t\right)\right)/\sqrt{2m\omega }$ or the momentum $i\left(\langle {\widehat{a}}^{†}\rangle \left(t\right)-\langle \widehat{a}\rangle \left(t\right)\right)\cdot \sqrt{m\omega }/\sqrt{2}$ can thereby be computed.

To describe the dispersion of the nuclear wave packets in coordinate space and in momentum space we need to extend our algebra. In the basis of the vibrational states the dispersion in the displacement of a local oscillator can be written as follows:

${\sigma }_R^2\left(t\right)=\langle R^2\rangle \left(t\right)-{(\langle R\rangle \left(t\right))}^2=\frac{1}{2m\omega }\langle {\left(\widehat{a}+{\widehat{a}}^{†}\right)}^2\rangle \left(t\right)-\frac{1}{2m\omega }{\left(\langle \left(\widehat{a}+{\widehat{a}}^{†}\right)\rangle \left(t\right)\right)}^2(7)$

And similar for the dispersion in the momentum space:

${\sigma }_P^2=\langle P^2\rangle -{\langle P\rangle }^2=-\frac{m\omega }{2}\langle {\left({\widehat{a}}^{†}-\widehat{a}\right)}^2\rangle +\frac{m\omega }{2}{\langle \left({\widehat{a}}^{†}-\widehat{a}\right)\rangle }^2(8)$

Therefore we need to describe the dynamics of the $\left\{{\widehat{a}}^2,{\left({\widehat{a}}^{†}\right)}^2,{\widehat{a}}^{†}\widehat{a}\right\}$ and $\left\{{\widehat{b}}^2,{\left({\widehat{b}}^{†}\right)}^2,{\widehat{b}}^{†}\widehat{b}\right\}$ for the dispersion in $R$ and $P$ of the two coupled local bonds. Note connection between the dispersion of the wave packets in different representations to the energy transfer between the two coupled oscillators, $\langle {\widehat{a}}^{†}\widehat{a}\rangle$ or $\langle {\widehat{b}}^{†}\widehat{b}\rangle$ mean values. Therefore we need a hardware computing device that can emulate 10 logic variables. The computing hardware described above can emulate 16 logic variables when only the lowest four exciton bands are addressed and 64 when shorter laser pulses are used.

Results

We use the device as discussed in section above to simulate the time dependence of the physical variables as revealed by the algebras for the coupled vibrations that are discussed in section III. Each coherence of the device is a point on the 2D frequency map generated by the 2D spectroscopy. The size dispersion of the quantum dots means that each point is actually a cloud of points at nearby frequencies. This dispersion in the frequency associated with each coherence is what enables one device to simulate different but similar physical systems. In this section we show how different coherences can simulate the time evolution of different physical variables of the system.

The results for the mean bond displacement $\langle R\rangle \left(t\right)$ and its dispersion ${\sigma }_R^2\left(t\right)$, Eq. 7, are shown in panels (a) and (c) of Figure 3. The computations are for a symmetric system that is not stationary in time because of an asymmetry in the initial conditions. One oscillator starts with low energy and the other, the one shown, is initially energy richer. On the right side of the figure we show relevant segments of 2D frequency maps computed at different values of the time interval T that enable the device to simulate the two functions of time $\langle R\rangle \left(t\right)$ and ${\sigma }_R^2\left(t\right)$. Shown for each are three values of T that correspond to extreme displacement and dispersion. One can, of course, measure at intermediate values as well.

FIGURE 3

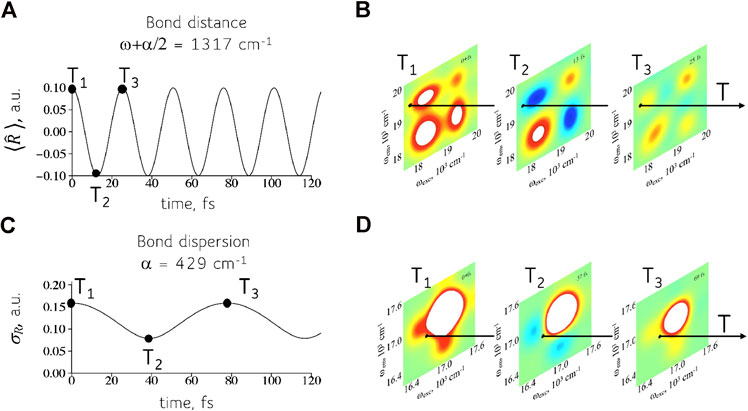
FIGURE 3. Time-evolution of the physical variables (A, C) and their computation (B, D) using 2D frequency maps for the device of the QD dimers. The response of the quantum device, panels (B) and (D), can simulate the time dependent observables of the physical system such as the mean bond displacement, panel (A), and the dispersion in the bond displacement, panel (C). The physical system shown is a symmetric triatomic molecule. Shown are the real part of the 2D maps. See Supplementary Material, Section 1.2, for details about the computation of the 2D maps.

The mean bond displacement of a local oscillator, frequency $\omega$, in a symmetric molecule such as CO₂, Figure 3A, is seen to be faster varying in time than the width, 3(c), of the wavepacket describing the oscillator. This reflects the difference in magnitude between the eigenfrequencies $\omega \pm \alpha /2$ and the coupling parameter $\alpha$. In the absence of coupling between the oscillators, $\alpha =0$ in the Hamiltonian, Eq. 1, the width of a coherent state of the harmonic potential will not vary with time. The coupling induces a slow, frequency $\alpha$, energy transfer between the two oscillators as reflected in the variation of the width of the wavepacket localized on one of the two bonds.

It might seem from Figure 3 that one has to assemble a new device for each different triatomic molecule. This is because for each one of the two frequencies $\omega +\alpha /2$ and $\alpha$ one would need a different electronic level structure in the dimer of the two quantum dots. The same size dispersion of the quantum dots that hitherto limited our abilities is here an advantage. The somewhat different sizes of the monomers means that there is a finite range of frequencies for each coherence. The range should not be too broad as otherwise we will lose resolution in frequency. Moreover, since the distribution of spacings of a particular coherence is, at low dispersions, Gaussian [3], we should not probe too far toward the wings. Complementary, when the range is broad we can only measure at short times before serious dephasing sets in. But the times cannot be too short because we want to measure only after the laser pulses are over. Practical implications of the distribution of spacings can be seen in Figure 4. Shown is a 2D frequency map for both regions used to compute the time-evolution of the bond distance (region A of Figure 4) and its dispersion (region B, Figure 4). Slightly different time-evolution of the coherences for the neighboring positions on the map enables fine-tuning of the period of the oscillations as is shown on the side panels of Figure 4.

FIGURE 4

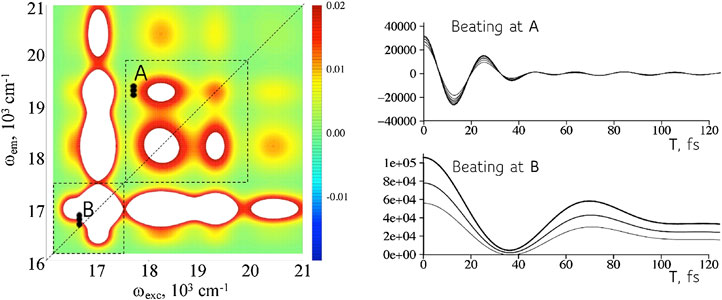
FIGURE 4. The same device can simulate a range of frequencies. Left: A 2D frequency map (real part) for the device at a particular value of the time interval T (computed for the full frequency range of the excited states, Supplementary Figure S4). The dispersion in sizes means that there is a range of frequencies corresponding to each coherence. Point A. A higher frequency coherence, more off the diagonal in the map, used to compute the time-evolution of the bond distance, Figures 3A,B. Shown are the intensities of the coherence vs time T for points in the range shown on the map. Point B. Coherence at a lower frequency for the computation of the bond dispersion, Figures 3C,D. A wider range in the frequency is possible but reading nearer to the diagonal is experimentally more challenging.

A coherence is a complex valued observable so each coherence can describe two conjugate physical variables as shown in Figure 5. Equation 6 shows that the expectation values,$\langle R\rangle \left(t\right)=\left(\langle \widehat{a}\rangle \left(t\right)+\langle {\widehat{a}}^{†}\rangle \left(t\right)\right)/\sqrt{2m\omega }$ and $\langle P\rangle \left(t\right)=i\left(\langle {\widehat{a}}^{†}\rangle \left(t\right)-\langle \widehat{a}\rangle \left(t\right)\right)\cdot \sqrt{m\omega }/\sqrt{2}$ of the bond displacement and of the momentum can both be computed at the same point of the map, by reading the real and imaginary values. The two values are shifted by a phase difference of $\pi /2$ as is to be expected. There is an uncertainty with the momentum, σ_P, and position, σ_R, as shown in Eqs. 7 and 8. Time-evolution of the uncertainty in the position, related to the width of the wavepacket in coordinate representation, is shown in Figures 3C,D. As discussed therein these uncertainties are time-dependent because of the coupling between the two oscillators so that they are more slowly varying and reflect the energy transfer between the two oscillators. The time-evolution of the uncertainty in the momentum representation is following the same time-dependence as σ_R therefore no additional computation is needed.

FIGURE 5

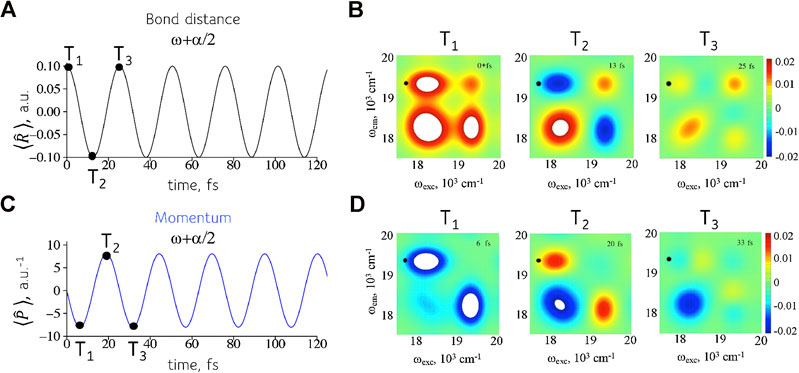
FIGURE 5. Reading two conjugate variables at the same position on the 2D frequency maps. Left entries: mean position (A) and momentum (C) as given by Eq. 6. As expected the displacement is maximal at a turning point of the motion while the momentum is maximal when the wavepacket crosses the equilibrium position of the oscillator. Right entries: real (B) and imaginary (D) values of the intensities in the frequency map in the frequency range of interest. The values shown are reading at different time intervals T.

Concluding Remarks

A versatile quantum mechanical computing device that operates on a laser addressed solid array of quantum dots dimers has been discussed. Experimental data shows that such a device can operate at room temperature [23, 24]. The device was effectively used to simulate the quantal dynamics of non-stationary states of coupled vibrations. We show how the read-out of the coherences engineered in the device following interaction with a sequence of the laser pulses enables parallel computation of the two conjugated variables, mean position and momentum of the local oscillators. Extension to the more detailed dynamics is shown by simulating also the dispersion in coordinate representation of the quantum wave packets of the coupled oscillators. Simulation is provided by matching the beating frequency of the coherence and the oscillation frequency of the physical variable. This mapping is in principle always possible for systems where the algebraic description of the physical variables is closed upon their commutation with Hamiltonian. Diagonalization of the respective Liouvillian operator, Eq. 4, determines eigenfrequencies ${\omega }_k$, for example Eq. 5, and enables transformation to observables $A_k\left(t\right)$ that evolve in time as $A_k\left(0\right)\exp \left(i{\omega }_{k}t\right)$. It is these frequencies that need to be measured by the time evolution of the coherences of the device. The inevitable size dispersion of the quantum dots limits the span of time that is available for emulation but on the other hand allows a fine-tuning of a frequency of interest.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

RDL and FR designed the research; KG, RDL and FR performed the research and wrote the ms, KG, HG and FR carried out the computations.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Prof. Elisabetta Collini for many incisive discussions about the experiments on the device. This work was supported by the FET open EC project COPAC #766563 and the Fonds National de la Recherche Scientifique (F.R.S-FNRS, Belgium), #T.0205.20 and #J.0012.18. Computational resources have been provided by the COPAC project and by the Consortium des Equipements de Calcul Intensif (CECI), funded by the F.R.S.-FNRS under Grant #2.5020.11.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2020.590699/full#supplementary-material

References

1. Deutsch D. Quantum theory, the Church–Turing principle and the universal quantum computer. Proc. R. Soc. A (1985) 400(1818):97–117. doi:10.1098/rspa.1985.0070.

CrossRef Full Text | Google Scholar

2. Fresch B, Hiluf D, Collini E, Levine RD, Remacle F. Molecular decision trees realized by ultrafast electronic spectroscopy. Proc Natl Acad Sci USA (2013) 110(43):17183–8. doi:10.1073/pnas.1314978110.

CrossRef Full Text | Google Scholar

3. Gattuso H, Levine RD, Remacle F. Massively parallel classical logic via coherent dynamics of an ensemble of quantum systems with dispersion in size. Proc Natl Acad Sci USA (2020) 117(35):21022. doi:10.1073/pnas.2008170117.

CrossRef Full Text | Google Scholar

4. Smith A, Kim MS, Pollmann F, Knolle J. Simulating quantum many-body dynamics on a current digital quantum computer. Npj Quantum Inf (2019) 5(1):106. doi:10.1038/s41534-019-0217-0.

CrossRef Full Text | Google Scholar

5. Cao Y, Romero J, Olson JP, Degroote M, Johnson PD, Kieferová M, et al. Quantum chemistry in the age of quantum computing. Chem Rev (2019) 119(19):10856–915. doi:10.1021/acs.chemrev.8b00803.

CrossRef Full Text | Google Scholar

6. Xia R, Kais S. Quantum machine learning for electronic structure calculations. Nat Commun (2018) 9(1):4195. doi:10.1038/s41467-018-06598-z.

CrossRef Full Text | Google Scholar

7. Argüello-Luengo J, González-Tudela A, Shi T, Zoller P, Cirac JI. Analogue quantum chemistry simulation. Nature (2019) 574(7777):215–8. doi:10.1038/s41586-019-1614-4.

CrossRef Full Text | Google Scholar

8. Bian T, Murphy D, Xia R, Daskin A, Kais S. Quantum computing methods for electronic states of the water molecule. Mol Phys (2019) 117(15-16):2069–82. doi:10.1080/00268976.2019.1580392.

CrossRef Full Text | Google Scholar

9. Kandala A, Mezzacapo A, Temme K, Takita M, Brink M, Chow JM, et al. Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature (Lond) (2017) 549(7671):242–6. doi:10.1038/nature23879.

CrossRef Full Text | Google Scholar

10. Hempel C, Maier C, Romero J, McClean J, Monz T, Shen H, et al. Quantum chemistry calculations on a trapped-ion quantum simulator. Phys. Rev. X (2018) 8(3):031022. doi:10.1103/PhysRevX.8.031022.

CrossRef Full Text | Google Scholar

11. Yung MH, Casanova J, Mezzacapo A, McClean J, Lamata L, Aspuru-Guzik A, et al. From transistor to trapped-ion computers for quantum chemistry. Sci Rep (2014) 4(1):3589. doi:10.1038/srep03589.

CrossRef Full Text | Google Scholar

12. Xu K, Chen J-J, Zeng Y, Zhang Y-R, Song C, Liu W, et al. Emulating many-body localization with a superconducting quantum processor. Phys Rev Lett. (2018) 120(5):050507. doi:10.1103/PhysRevLett.120.050507.

CrossRef Full Text | Google Scholar

13.Google. Hartree-Fock on a superconducting qubit quantum computer. Science (2020) 369(6507):1084. doi:10.1126/science.abb9811.

CrossRef Full Text | Google Scholar

14. Ciliberto C, Herbster M, Ialongo Alessandro D, Pontil M, Rocchetto A, Severini S, et al. Quantum machine learning: a classical perspective. Proc R Soc A (2018) 474(2209):20170551. doi:10.1098/rspa.2017.0551.

CrossRef Full Text | Google Scholar

15. Rebentrost P, Steffens A, Marvian I, Lloyd S. Quantum singular-value decomposition of nonsparse low-rank matrices. Phys Rev A (2018) 97(1):012327. doi:10.1103/PhysRevA.97.012327.

CrossRef Full Text | Google Scholar

16. Schuld M, Sinayskiy I, Petruccione F. Prediction by linear regression on a quantum computer. Phys Rev A (2016) 94(2):022342. doi:10.1103/PhysRevA.94.022342.

CrossRef Full Text | Google Scholar

17. Alhassid Y, Levine RD. Connection between the maximal entropy and the scattering theoretic analyses of collision processes. Phys Rev A (1978) 18(1):89–116. doi:10.1103/PhysRevA.18.89.

CrossRef Full Text | Google Scholar

18. Komarova K, Gattuso H, Levine RD, Remacle F. Quantum device emulates the dynamics of two coupled oscillators. J Phys Chem Lett (2020) 11:6990–5. doi:10.1021/acs.jpclett.0c01880.

CrossRef Full Text | Google Scholar

19. Kambhampati P. Unraveling the structure and dynamics of excitons in semiconductor quantum dots. Acc Chem Res (2011) 44(1):1–13. doi:10.1021/ar1000428.

CrossRef Full Text | Google Scholar

20. Caram JR, Zheng H, Dahlberg PD, Rolczynski BS, Griffin GB, Dolzhnikov DS, et al. Exploring size and state dynamics in CdSe quantum dots using two-dimensional electronic spectroscopy. J Chem Phys (2014) 140(8):084701. doi:10.1063/1.4865832.

CrossRef Full Text | Google Scholar

21. Turner DB, Hassan Y, Scholes GD. Exciton superposition states in CdSe nanocrystals measured using broadband two-dimensional electronic spectroscopy. Nano Lett (2012) 12(2):880–6. doi:10.1021/nl2039502.

CrossRef Full Text | Google Scholar

22. Cassette E, Dean JC, Scholes GD. Two-dimensional visible spectroscopy for studying colloidal semiconductor nanocrystals. Small (2016) 12(16):2234–44. doi:10.1002/smll.201502733.

CrossRef Full Text | Google Scholar

23. Collini E, Gattuso H, Bolzonello L, Casotto A, Volpato A, Dibenedetto CN, et al. Quantum phenomena in nanomaterials: coherent superpositions of fine structure states in CdSe nanocrystals at room temperature. J Phys Chem C (2019) 123:31286–93. doi:10.1021/acs.jpcc.9b11153.

CrossRef Full Text | Google Scholar

24. Collini E, Gattuso H, Kolodny Y, Bolzonello L, Volpato A, Fridman HT, et al. Room-temperature inter-dot coherent dynamics in multilayer quantum dot materials. J Phys Chem C (2020). doi:10.1021/acs.jpcc.0c05572.

CrossRef Full Text | Google Scholar

25. Cho M. Two-Dimensional Optical Spectroscopy. Boca Raton: CRC Press (2009).

Google Scholar

26. Mukamel S. Principle of non linear optical spectroscopy. Oxford: Oxford University Press (1995).

Google Scholar

27. Nielsen MA, Chuang IL. Quantum Computation and Quantum Information. Cambridge: Cambridge University Press (2010).

Google Scholar

28. Preskill J. "Fault-Tolerant Quantum Computation," in Introduction to Quantum Computation and Information., eds. H-K Lo, T Spiller, S Popescu. Singapore: World Scientific (1998) 213–69.

Google Scholar

29. Dibenedetto CN, Fanizza E, Brescia R, Kolodny Y, Remennik S, Panniello A, et al. Coupling effects in QD dimers at sub-nanometer interparticle distance. Nano Res (2020) 13(4):1071–80. doi:10.1007/s12274-020-2747-3.

CrossRef Full Text | Google Scholar

30. Fresch B, Cipolloni M, Yan T-M, Collini E, Levine RD, Remacle F. Parallel and multivalued logic by the two-dimensional photon-echo response of a Rhodamine–DNA complex. J Phys Chem Lett (2015) 6:1714–8. doi:10.1021/acs.jpclett.5b00514.

CrossRef Full Text | Google Scholar

31. Steinfeld JI. Molecules and Radiation. Mineola: Dover (2005).

Google Scholar