On Topological Indices of mth Chain Hex-Derived Network of Third Type

Huo, Yuhong; Ali, Haidar; Binyamin, Muhammad Ahsan; Asghar, Syed Sheraz; Babar, Usman; Liu, Jia-Bao

doi:10.3389/fphy.2020.593275

BRIEF RESEARCH REPORT article

Front. Phys., 20 November 2020
Sec. Computational Physics
Volume 8 - 2020 | https://doi.org/10.3389/fphy.2020.593275

On Topological Indices of $m t h$ Chain Hex-Derived Network of Third Type

Yuhong Huo¹

Haidar Ali² www.frontiersin.org

Muhammad Ahsan Binyamin²* www.frontiersin.org

Syed Sheraz Asghar²

Usman Babar³

Jia-Bao Liu⁴

¹School of Finance and Mathematics, Huainan Normal University, Huainan, China
²Department of Mathematics, Government College University, Faisalabad, Pakistan
³Department of Applied Sciences, National Textile University, Faisalabad, Pakistan
⁴School of Mathematics and Physics, Anhui Jianzhu University,Hefei, China

In theoretical chemistry, the numerical parameters that are used to characterize the molecular topology of graphs are called topological indices. Several physical and chemical properties like boiling point, entropy, heat formation, and vaporization enthalpy of chemical compounds can be determined through these topological indices. Graph theory has a considerable use in evaluating the relation of various topological indices of some derived graphs. In this article, we will compute the topological indices like Randić, first Zagreb, harmonic, augmented Zagreb, atom-bond connectivity, and geometric-arithmetic indices for chain hex-derived network of type 3 $C H D N 3 (m, n)$ for different cases of m and n. We will also compute the numerical computation and graphical view to justify our results.

Mathematics Subject Classification: 05C12, 05C90

Introduction and Preliminary Results

A branch of numerical science called graph theory is the one in which we use tools of graph parameters to reveal the compound phenomenon precisely. Graph theory, for instance, when used in the study of molecular structures, characterizes a field among various disciplines of science known as molecular topology or chemical graph theory.

Chemical graph theory has provided a considerable part of study to chemist through which they can execute graph theory to mathematical demonstrating of chemical marvel. We are usually interested in estimating the structural characters to elaborate quantitative structure–activity relationships using techniques taken from graph theory.

Topological description of chemical structures with required properties can be used to categorize the molecules and to model unknown structures. Molecules and molecular compounds are frequently demonstrated by molecular graph. In graph theory, a molecular graph is the illustration of structural formula of chemical compounds. The vertices are expressed by the atoms of molecule while the edges suggest the covalent bonds between the atoms.

Quantitative structure–activity (QSAR) and structure–property (QSPR) relationships that are used to analyze the organic activities and properties of biological compounds can be studied by the help of a new subject known as cheminformatics, which is the composition of mathematics, information science, and chemistry.

At present, the numerical programming of biological structure with topological descriptors is increasing in consequence in invigorating science, bioinformatics, and pharmaceutics.

In QSAR/QSPR study, physicochemical properties of the topological descriptors like Wiener index, Randić index, sieged index, first and second Zagreb index, augmented Zagreb index, harmonic index, and geometric–arithmetic index are useful to classify the bioactivity of the chemical compounds.

A graph can be characterized by a polynomial, a numeric number, and a sequence of numbers or a matrix. A numeric quantity interrelated with a graph that remains invariant under the graph automorphism and differentiate the topology of graph is called molecular descriptor. A graph theoretical characteristic that is sustained by an isomorphism is called topological descriptor.

At present, in the field of computational chemistry, topological indices have a rising interest, which is actually associated to their use in nonempirical quantitative structure–property relationship and quantitative structure–activity relationship.

Topological descriptor, Top (G), may also be defined with the property of isomorphism, that is, for every graph H isomorphic to G, Top (G) = Top (H). The idea of topological indices was first introduced by Weiner [35] during the laboratory work on boiling point of paraffin and named this result as path number, which was later named as Weiner index.

This article takes into account the topological indices of hexagonal networks derived from a hexagonal graph, which contain molecular graphs of unbranched benzene hydrocarbons. Hexagonal structure graphs consist of hexagons that are fused together. Theoretical chemists pay great attention to this class of chemical compounds. Topological index theory has been intensively developed over the past four decades for the individual molecular graphs. Benzene hydrocarbons are not only the major chemical industry raw materials but also harmful pollutants [15, 16, 28].

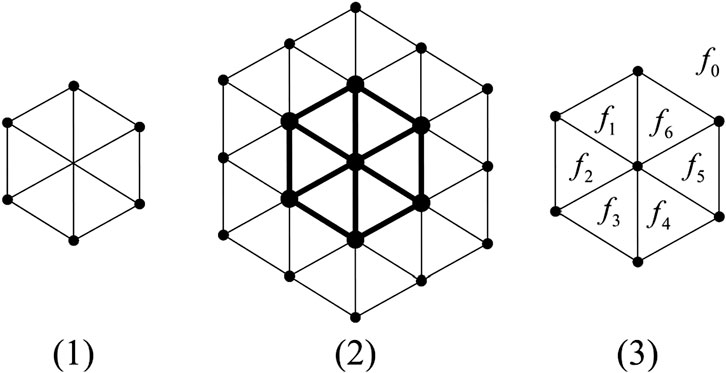
Chen et al. [9] derived a hexagonal mesh. Hexagonal mesh made by a set of triangles is shown in Figure 1. There exists no hexagonal mesh with one dimension. A two dimensional hexagonal mesh $H X (2)$ can be generated from six triangles. A three dimensional hexagonal mesh $H X (3)$ can be obtained by adding a layer of triangles around the each wall of $H X (2)$ . In the similar way, $H X (n)$ can be produced by adding n layers around all the sides of every proceeding hexagonal mesh.

FIGURE 1

FIGURE 1. Hexagonal meshes: (1) HX (2), (2) HX (3), and (3), all facing HX (2).

Drawing algorithm of $H D N 3$ networks.

Step-1: First, we draw a hexagonal network of dimension n.

Step-2: All the $K_{3}$ subgraphs are converted into planar octahedron network $P O H$ and the graph obtained is known as $H D N 3$ [29] [see Figures 1, 2)] network.

Step-3: An mth $C H D N 3 (m, n)$ can be easily formed from the $H D N 3$ network (see Figures 2, 3).

FIGURE 2

FIGURE 2. Chain hex-derived networks $C H D N 3 (m, n)$ for different conditions for m and n like even and odd.

FIGURE 3

FIGURE 3. Chain hex-derived network $C H D N 3 (m, n)$ .

In $C H D N 3 (m, n)$ , m represents the number of rows and n are the number of triangles in each row.

In this article, $G$ is considered a network with a $V (G)$ vertex set and an edge set of $E (G)$ , and $d_{r}$ is the degree of vertex $r \in V (G)$ .

The Randić index [27] is denoted by $R_{\frac{- 1}{2}} (G)$ and makes us aware of Milan $Randić$ and is represented as follows:

R_{\frac{- 1}{2}} (G) = \sum_{r s \in E (G)} \frac{1}{\sqrt{d_{r} d_{s}}} . (1)

The general Randić index is the sum of ${(d_{r} d_{s})}^{α}$ over all edges $e = r s$ $\in$ $E (G)$ , represented as

R_{α} (G) = \sum_{r s \in E (G)} {(d_{r} d_{s})}^{α} f o r α = 1, \frac{1}{2}, - 1, \frac{- 1}{2} . (2)

Trinajstić [31] makes us aware of $T I' s$ , which are the first and second Zagreb indices, denoted by $M_{1} (G)$ and formalized as follows:

M_{1} (G) = \sum_{r s \in E (G)} (d_{r} + d_{s}) . (3)

Furtula et al. [13] introduced the augmented Zagreb index and described it as

A Z I (G) = \sum_{r s \in E (G)} {(\frac{d_{r} d_{s}}{d_{r} + d_{s} - 2})}^{3} . (4)

Zhong [37] introduced the harmonic index and described it as

H (G) = \sum_{r s \in E (G)} (\frac{2}{d_{r} + d_{s}}) . (5)

The index atom–bond connectivity (ABC) is one of the well-known degree-based topological indices, given by Estrada et al. [12] and defined as

A B C (G) = \sum_{r s \in E (G)} \sqrt{\frac{d_{r} + d_{s} - 2}{d_{r} d_{s}}} . (6)

Vukićević and Furtula [33] invented the famous geometric–arithmetic index and represented it as

G A (G) = \sum_{r s \in E (G)} \frac{2 \sqrt{d_{r} d_{s}}}{(d_{r} + d_{s})} . (7)

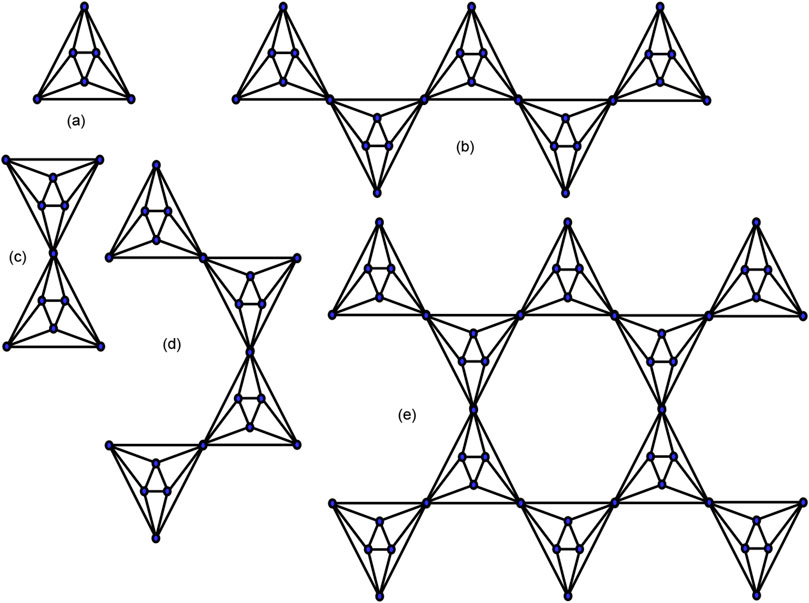
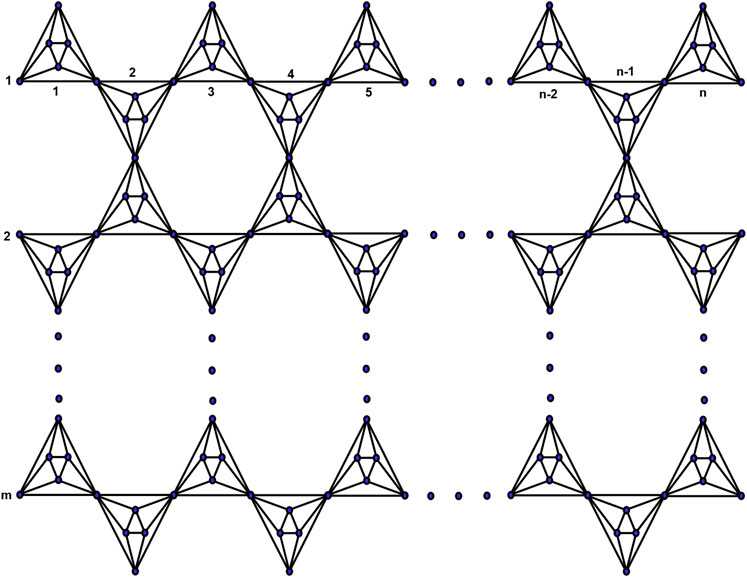
Cases for mth chain hex-derived network of third type. $C H D N 3 (m, n)$

There are three cases for $C H D N 3 (m, n)$ .

Case-1: For $m = n$ , $(m, n) \geq 1$ .

Case-2: For $m < n$ , m is odd and $n \in$ $ℕ$ . For $m > n$ , m is odd and $n \in$ $ℕ$ . For $m < n$ , m and n both are even. For $m > n$ , m and n both are even.

Case-3: For $m < n$ , m is even and n is odd. For $m > n$ , m is even and n is odd.

Main Results

Simonraj et al. [29] discovered hex-derived networks and found the metric dimension of $H D N 3$ . We discuss the newly derived third type of hex-derived networks in this article and calculate the exact results for topological indexes based on degrees. These topological indices and their variants are currently subjected to extensive research activity, see [1–8, 14, 18–25, 30, 32, 34, 36]. For Basic notations and definitions, see [10, 17, 26, 31].

Results for the First Case mth Chain Hex-Derived Network of Third Type CHDN3 (m, n)

In this section, for the very first time, we discuss $C H D N 3 (m, n)$ , which is derived from hex-derived network and compute the exact results for $Randic$ , Zagreb, harmonic, augmented Zagreb, atom–bond connectivity, and geometric–arithmetic indices for case 1.

Theorem 2.1.1. Consider the $m t h$ chain hex-derived network of type 3 $C H D N 3 (m, n)$ , the general Randić index is equal to

R_{α} (G) = {\begin{array}{l} 16 (2 - 9 m + 27 m n - 9 n), & α = 1; \\ 4 (6 - 4 \sqrt{2} - 3 m + (9 + 6 \sqrt{2}) m n - 3 n), & α = \frac{1}{2}; \\ \frac{1}{8} (6 - 4 \sqrt{2} + 3 m + (9 + 6 \sqrt{2}) m n + 3 n), & α = \frac{- 1}{2}; \\ \frac{1}{64} (2 + 9 m + 27 m n + 9 n), & α = - 1. \end{array}

Proof. Let $G ≅ C H D N 3 (m, n)$ . Table 1 shows such an edge partition of $G$ for $m = n$ . Using Equation $(2)$ , we have

R_{α} (G) = \sum_{r s \in E (G)} {(d_{r} d_{s})}^{α} .

TABLE 1

TABLE 1. Degree-Based Edge partition for m = n

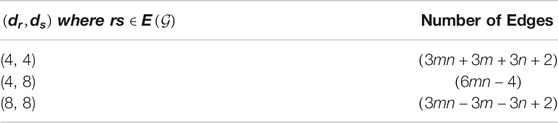
Using edge partitions in Table 1, we get the following.

For $α = 1$ , Eq. 2 becomes

R_{1} (G) = {(16)}^{1} (3 m n + 3 m + 3 n + 2) + {(32)}^{1} (6 m n - 4) + {(64)}^{1} (3 m n - 3 m - 3 n + 2) .

By making some calculations, we get

\Rightarrow R_{1} (G) = 16 (2 - 9 m + 27 m n - 9 n) .

For $α = \frac{1}{2}$ , Eq. 2 becomes

R_{\frac{1}{2}} (G) = {(16)}^{\frac{1}{2}} (3 m n + 3 m + 3 n + 2) + {(32)}^{\frac{1}{2}} (6 m n - 4) + {(64)}^{\frac{1}{2}} (3 m n - 3 m - 3 n + 2) .

By making some calculations, we get

\Rightarrow R_{\frac{1}{2}} (G) = 4 (6 - 4 \sqrt{2} - 3 m + (9 + 6 \sqrt{2}) m n - 3 n) .

For $α = - \frac{1}{2}$ , Eq. 2 becomes

R_{- \frac{1}{2}} (G) = {(16)}^{- \frac{1}{2}} (3 m n + 3 m + 3 n + 2) + {(32)}^{- \frac{1}{2}} (6 m n - 4) + {(64)}^{- \frac{1}{2}} (3 m n - 3 m - 3 n + 2) .

By making some calculations, we get

\Rightarrow R_{- \frac{1}{2}} (G) = \frac{1}{8} (6 - 4 \sqrt{2} + 3 m + (9 + 6 \sqrt{2}) m n + 3 n) .

For $α = - 1$ , Eq. 2 becomes

R_{- 1} (G) = {(16)}^{- 1} (3 m n + 3 m + 3 n + 2) + {(32)}^{- 1} (6 m n - 4) + {(64)}^{- 1} (3 m n - 3 m - 3 n + 2) .

By making some calculations, we get

\Rightarrow R_{- 1} (G) = \frac{1}{64} (2 + 9 m + 27 m n + 9 n) .

Theorem 2.1.2. Consider the $m t h$ chain hex-derived network of type 3 $C H D N 3 (m, n)$ , the first Zagreb index is equal to

M_{1} (G) = - 24 (m - 6 m n + n) .

Proof. Let $G ≅ C H D N 3 (m, n)$ . In Table 1, there is an edge partition of $G$ for $m = n$ . Using Eq. 3, we have

M_{1} (G) = \sum_{r s \in E (G)} (d_{r} + d_{s}) .

Using edge partitions in Table 1, we get

M_{1} (G) = (4 + 4) (3 m n + 3 m + 3 n + 2) + (4 + 8) (6 m n - 4) + (8 + 8) (3 m n - 3 m - 3 n + 2),

= (8) (3 m n + 3 m + 3 n + 2) + (12) (6 m n - 4) + (16) (3 m n - 3 m - 3 n + 2),

By making some calculations, we get

\Rightarrow M_{1} (G) = - 24 (m - 6 m n + n) .

Theorem 2.1.3. Consider the $m t h$ chain hex-derived network of type 3 $C H D N 3 (m, n)$ , the augmented Zagreb index and harmonic index are equal to

A Z I (G) = \frac{512}{1157625} (221398 - 519375 m + 1221153 m n - 519375 n) .

H (G) = \frac{1}{24} (2 + 9 m + 51 m n + 9 n) .

Proof. Let $G ≅ C H D N 3 (m, n)$ . Using Eq. 4, we have

A Z I (G) = \sum_{r s \in E (G)} {(\frac{d_{r} d_{s}}{d_{r} + d_{s} - 2})}^{3} .

From Table 1, using the edge partition, the outcome can be obtained as

A Z I (G) = {(\frac{4 \times 4}{4 + 4 - 2})}^{3} (3 m n + 3 m + 3 n + 2) + {(\frac{4 \times 8}{4 + 8 - 2})}^{3} (6 m n - 4)

+ {(\frac{8 \times 8}{8 + 8 - 2})}^{3} (3 m n - 3 m - 3 n + 2),

= {(\frac{8}{3})}^{3} (3 m n + 3 m + 3 n + 2) + {(\frac{16}{5})}^{3} (6 m n - 4) + {(\frac{32}{7})}^{3} (3 m n - 3 m - 3 n + 2) .

By making some calculations, we get

\Rightarrow A Z I (G) = \frac{512}{1157625} (221398 - 519375 m + 1221153 m n - 519375 n) .

Using Eq. 5, we have

H (G) = \sum_{r s \in E (G)} (\frac{2}{d_{r} + d_{s}}) .

From Table 1, using the edge partition, the outcome can be obtained as

H (G) = (\frac{2}{4 + 4}) (3 m n + 3 m + 3 n + 2) + (\frac{2}{4 + 8}) (6 m n - 4) + (\frac{2}{8 + 8}) (3 m n - 3 m - 3 n + 2),

= (\frac{1}{8}) (3 m n + 3 m + 3 n + 2) + (\frac{1}{6}) (6 m n - 4) + (\frac{1}{8}) (3 m n - 3 m - 3 n + 2) .

By making some calculations, we get

\Rightarrow H (G) = \frac{1}{24} (2 + 9 m + 51 m n + 9 n) .

Theorem 2.1.4. Let $G$ be the $m t h$ chain hex-derived network of third type $C H D N 3 (m, n)$ , then atom–bond connectivity index and geometric–arithematic index are equal to

A B C (G) = \frac{1}{8} (4 \sqrt{5} (3 m n - 2) + \sqrt{14} (2 - 3 m + 3 m n - 3 n) + 2 \sqrt{6} (2 + 3 m + 3 m n + 3 n)) .

G A (G) = 4 + 6 m n + \frac{4 \sqrt{2}}{3} (3 m n - 2) .

Proof. Let $G ≅ C H D N 3 (m, n)$ . Using Eq. 6, we have

A B C (G) = \sum_{r s \in E (G)} \sqrt{\frac{d_{r} + d_{s} - 2}{d_{r} d_{s}}} .

From Table 1, using the edge partition, the outcome can be obtained as

A B C (G) = \sqrt{\frac{4 + 4 - 2}{4 \times 4}} (3 m n + 3 m + 3 n + 2) + \sqrt{\frac{4 + 8 - 2}{4 \times 8}} (6 m n - 4)

+ \sqrt{\frac{8 + 8 - 2}{8 \times 8}} (3 m n - 3 m - 3 n + 2),

= \sqrt{\frac{3}{8}} (3 m n + 3 m + 3 n + 2) + \sqrt{\frac{14}{64}} (6 m n - 4) + \sqrt{\frac{7}{32}} (3 m n - 3 m - 3 n + 2),

By making some calculations, we get

\Rightarrow A B C (G) = \frac{1}{8} (4 \sqrt{5} (3 m n - 2) + \sqrt{14} (2 - 3 m + 3 m n - 3 n) + 2 \sqrt{6} (2 + 3 m + 3 m n + 3 n)) .

Using Eq. 7,

G A (G) = \sum_{r s \in E (G)} \frac{2 \sqrt{d_{r} d_{s}}}{d_{r} + d_{s}} .

From Table 1, using the edge partition, we get the outcome as,

G A (G) = \frac{2 \sqrt{4 \times 4}}{(4 + 4)} (3 m n + 3 m + 3 n + 2) + \frac{2 \sqrt{4 \times 8}}{(4 + 8)} (6 m n - 4) + \frac{2 \sqrt{8 \times 8}}{(8 + 8)},

(3 m n - 3 m - 3 n + 2)

= (1) (3 m n + 3 m + 3 n + 2) + \frac{2 \sqrt{2}}{3} (6 m n - 4) + (1) (3 m n - 3 m - 3 n + 2) .

By making some calculations, we get

\Rightarrow G A (G) = 4 + 6 m n + \frac{4 \sqrt{2}}{3} (3 m n - 2) .

Results for the Second Case of Chain Hex-Derived Networks of Third Type CHDN3 (m, n)

In this section, for the very first time, we discuss $C H D N 3 (m, n)$ derived from of hex-derived network and compute the exact results forRandic, Zagreb, harmonic, augmented Zagreb, atom–bond connectivity, and geometric–arithmetic indices for case 2.

Theorem 2.2.1. Consider the $m t h$ chain hex-derived network of type 3 $C H D N 3 (m, n)$ , the general Randic index for second case is equal to

R_{α} (G) = {\begin{array}{l} 16 (2 - 12 m + 27 m n - 6 n), & α = 1; \\ 4 (6 - 4 \sqrt{2} - 4 m + (9 + 6 \sqrt{2}) m n - 2 n), & α = \frac{1}{2}; \\ \frac{1}{8} (6 - 4 \sqrt{2} + 4 m + (9 + 6 \sqrt{2}) m n + 2 n,) & α = \frac{- 1}{2}; \\ \frac{1}{64} (2 + 12 m + 27 m n + 6 n), & α = - 1. \end{array}

Proof. Let $G ≅ C H D N 3 (m, n)$ . Table 2 shows such an edge partition of $G$ for second case.

TABLE 2

TABLE 2. Degree-Based Edge partition for Case 2.

Using Eq. 2, we get

R_{α} (G) = \sum_{r s \in E (G)} {(d_{r} d_{s})}^{α} .

Using edge partitions in Table 2, we get, for $α = 1$ ,

R_{1} (G) = {(16)}^{1} (3 m n + 4 m + 2 n + 2) + {(32)}^{1} (6 m n - 4) + {(64)}^{1} (3 m n - 4 m - 2 n + 2),

By making some calculations, we get

\Rightarrow R_{1} (G) = 16 (2 - 12 m + 27 m n - 6 n) .

For $α = \frac{1}{2}$ ,

R_{\frac{1}{2}} (G) = {(16)}^{\frac{1}{2}} (3 m n + 4 m + 2 n + 2) + {(32)}^{\frac{1}{2}} (6 m n - 4) + {(64)}^{\frac{1}{2}} (3 m n - 4 m - 2 n + 2),

By making some calculations, we get

\Rightarrow R_{\frac{1}{2}} (G) = 4 (6 - 4 \sqrt{2} - 4 m + (9 + 6 \sqrt{2}) m n - 2 n) .

For $α = - \frac{1}{2}$ ,

R_{- \frac{1}{2}} (G) = {(16)}^{- \frac{1}{2}} (3 m n + 4 m + 2 n + 2) + {(32)}^{- \frac{1}{2}} (6 m n - 4) + {(64)}^{- \frac{1}{2}} (3 m n - 4 m - 2 n + 2) .

By making some calculations, we get

\Rightarrow R_{\frac{- 1}{2}} (G) = \frac{1}{8} (6 - 4 \sqrt{2} + 4 m + (9 + 6 \sqrt{2}) m n + 2 n) .

For $α = - 1$ ,

R_{- 1} (G) = {(16)}^{- 1} (3 m n + 4 m + 2 n + 2) + {(32)}^{- 1} (6 m n - 4) + {(64)}^{- 1} (3 m n - 4 m - 2 n + 2) .

By making some calculations, we get

\Rightarrow R_{- 1} (G) = \frac{1}{64} (2 + 12 m + 27 m n + 6 n) .

Theorem 2.2.2. Consider the $m t h$ chain hex-derived network of type 3 $C H D N 3 (m, n)$ , the first Zagreb index is equal to

M_{1} (G) = - 16 (2 m - 9 m n + n) .

Proof. Let $G ≅ C H D N 3 (m, n)$ . Table 2 shows such an edge partition of $G$ for second case.

Using Eq. 3,

M_{1} (G) = \sum_{r s \in E (G)} (d_{r} + d_{s}) .

Using edge partitions in Table 2, we get

M_{1} (G) = (4 + 4) (3 m n + 4 m + 2 n + 2) + (4 + 8) (6 m n - 4) + (8 + 8) (3 m n - 4 m - 2 n + 2),

= (8) (3 m n + 4 m + 2 n + 2) + (12) (6 m n - 4) + (16) (3 m n - 4 m - 2 n + 2) .

By making some calculations, we get

\Rightarrow M_{1} (G) = - 16 (2 m - 9 m n + n) .

Theorem 2.2.3. Let $G$ be the $C H D N 3 (m, n)$ $m t h$ chain hex-derived network of third type, the augmented Zagreb index and harmonic index are equal to

A Z I (G) = \frac{512}{1157625} (221398 - 692500 m + 1221153 m n - 346250 n) .

H (G) = \frac{1}{24} (2 + 12 m + 51 m n + 6 n) .

Proof. Consider $G$ be the $C H D N 3 (m, n)$ $m t h$ chain hex-derived network of third type. Using Eq. 4, we get

A Z I (G) = \sum_{r s \in E (G)} {(\frac{d_{r} d_{s}}{d_{r} + d_{s} - 2})}^{3} .

From Table 1, using the edge partition, the outcome can be obtained as

A Z I (G) = {(\frac{4 \times 4}{4 + 4 - 2})}^{3} (3 m n + 4 m + 2 n + 2) + {(\frac{4 \times 8}{4 + 8 - 2})}^{3} (6 m n - 4)

{+ (\frac{8 \times 8}{8 + 8 - 2})}^{3} (3 m n - 4 m - 2 n + 2),

= ({(\frac{8}{3})}^{3}) (3 m n + 4 m + 2 n + 2) + {(\frac{16}{5})}^{3} (6 m n - 4) + {(\frac{32}{7})}^{3} (3 m n - 4 m - 2 n + 2) .

By making some calculations, we get

\Rightarrow A Z I (G) = \frac{512}{1157625} (221398 - 692500 m + 1221153 m n - 346250 n) .

By using Eq. 5, we have

H (G) = \sum_{r s \in E (G)} (\frac{2}{d_{r} + d_{s}}) .

From Table 1, using the edge partition, the outcome can be obtained as

H (G) = (\frac{2}{4 + 4}) (3 m n + 4 m + 2 n + 2) + (\frac{2}{4 + 8}) (6 m n - 4) + (\frac{2}{8 + 8}) (3 m n - 4 m - 2 n + 2),

= (\frac{1}{8}) (3 m n + 4 m + 2 n + 2) + (\frac{1}{6}) (6 m n - 4) + (\frac{1}{8}) (3 m n - 4 m - 2 n + 2) .

By making some calculations, we get

\Rightarrow H (G) = \frac{1}{24} (2 + 12 m + 51 m n + 6 n) .

Theorem 2.2.4. Let $G$ be the $C H D N 3 (m, n)$ $m t h$ chain hex-derived network of third type, then atom–bond connectivity and geometric–arithematic index are equal to

A B C (G) = \frac{1}{8} (4 \sqrt{5} (3 m n - 2) + \sqrt{14} (2 - 4 m + 3 m n - 2 n) + 2 \sqrt{6} (2 + 4 m + 3 m n + 2 n)) .

G A (G) = 4 + 6 m n + \frac{4 \sqrt{2}}{3} (3 m n - 2) .

Proof. Consider $G ≅ C H D N 3 (m, n)$ . By using Eq. 6, we have

A B C (G) = \sum_{r s \in E (G)} \sqrt{\frac{d_{r} + d_{s} - 2}{d_{r} d_{s}}} .

From Table 2, by using the edge partition, we get the outcome as,

A B C (G) = \sqrt{\frac{4 + 4 - 2}{4 \times 4}} (3 m n + 4 m + 2 n + 2) + \sqrt{\frac{4 + 8 - 2}{4 \times 8}} (6 m n - 4)

+ \sqrt{\frac{8 + 8 - 2}{8 \times 8}} (3 m n - 4 m - 2 n + 2),

= \sqrt{\frac{3}{8}} (3 m n + 4 m + 2 n + 2) + \sqrt{\frac{14}{64}} (6 m n - 4) + \sqrt{\frac{7}{32}} (3 m n - 4 m - 2 n + 2) .

By making some calculations, we get

\Rightarrow A B C (G) = \frac{1}{8} (4 \sqrt{5} (3 m n - 2) + \sqrt{14} (2 - 4 m + 3 m n - 2 n) + 2 \sqrt{6} (2 + 4 m + 3 m n + 2 n)) .

Using Eq. 7, we have

G A (G) = \sum_{r s \in E (G)} \frac{2 \sqrt{d_{r} d_{s}}}{(d_{r} + d_{s})} .

From Table 2, using the edge partition, we get the outcome as,

G A (G) = \frac{2 \sqrt{4 \times 4}}{(4 + 4)} (3 m n + 4 m + 2 n + 2) + \frac{2 \sqrt{4 \times 8}}{(4 + 8)} (6 m n - 4) + \frac{2 \sqrt{8 \times 8}}{(8 + 8)} (3 m n - 4 m - 2 n + 2),

= (1) (3 m n + 4 m + 2 n + 2) + \frac{2 \sqrt{2}}{3} (6 m n - 4) + (1) (3 m n - 4 m - 2 n + 2) .

By making some calculations, we get

\Rightarrow G A (G) = 4 + 6 m n + \frac{4 \sqrt{2}}{3} (3 m n - 2) .

Results for the Third Case of $C H D N 3 (m, n)$ Chain Hex Derived Networks of Third Type

In this section, for the very first time, we discuss $C H D N 3 (m, n)$ –derived hex-derived network and compute the exact results forRandic, Zagreb, harmonic, augmented Zagreb, atom–bond connectivity, and geometric–arithmetic indices for case 3.

Theorem 2.3.1. Consider the $m t h$ chain hex-derived network of type 3 $C H D N 3 (m, n)$ , the general $R a n d \overset{´}{i} c$ index for third case is equal to

R_{α} (G) = {\begin{array}{l} - 16 (2 + 12 m - 27 m n + 6 n), & α = 1; \\ 4 (- 4 m + (9 + 6 \sqrt{2}) m n - 2 (- 5 + 4 \sqrt{2} + n)), & α = \frac{1}{2}; \\ \frac{1}{8} (4 m + (9 + 6 \sqrt{2}) m n + 2 (7 - 4 \sqrt{2} + n)), & α = \frac{- 1}{2}; \\ \frac{1}{64} (10 + 12 m + 27 m n + 6 n), & α = - 1. \end{array}

Proof. Let $G ≅ C H D N 3 (m, n)$ . Using Eq. 2, we get

R_{α} (G) = \sum_{r s \in E (G)} {(d_{r} d_{s})}^{α} .

Using edge partitions in Table 3, we get, for $α = 1$

R_{1} (G) = {(16)}^{1} (3 m n + 4 m + 2 n + 6) + {(32)}^{1} (6 m n - 8) + {(64)}^{1} (3 m n - 4 m - 2 n + 2) .

TABLE 3

TABLE 3. Degree-Based Edge partition for Case 3.

By making some calculations, we get

\Rightarrow R_{1} (G) = - 16 (2 + 12 m + 27 m n + 6 n) .

For $α = \frac{1}{2}$ ,

R_{\frac{1}{2}} (G) = {(16)}^{\frac{1}{2}} (3 m n + 4 m + 2 n + 6) + {(32)}^{\frac{1}{2}} (6 m n - 8) + {(64)}^{\frac{1}{2}} (3 m n - 4 m - 2 n + 2) .

By making some calculations, we get

\Rightarrow R_{\frac{1}{2}} (G) = 4 (- 4 m + (9 + 6 \sqrt{2}) m n - 2 (- 5 + 4 \sqrt{2} + n)) .

For $α = - \frac{1}{2}$ ,

R_{- \frac{1}{2}} (G) = {(16)}^{- \frac{1}{2}} (3 m n + 4 m + 2 n + 6) + {(32)}^{- \frac{1}{2}} (6 m n - 8) + {(64)}^{- \frac{1}{2}} (3 m n - 4 m - 2 n + 2) .

By making some calculations, we get

\Rightarrow R_{- \frac{1}{2}} (G) = \frac{1}{8} (4 m + (9 + 6 \sqrt{2}) m n + 2 (7 - 4 \sqrt{2} + n)) .

For $α = - 1$ ,

R_{- 1} (G) = {(16)}^{- 1} (3 m n + 4 m + 2 n + 6) + {(32)}^{- 1} (6 m n - 8) + {(64)}^{- 1} (3 m n - 4 m - 2 n + 2) .

By making some calculations, we get

\Rightarrow R_{- 1} (G) = \frac{1}{64} (10 + 12 m + 27 m n + 6 n) .

Theorem 2.3.2. Consider the $m t h$ chain hex-derived network of type 3 $C H D N 3 (m, n)$ , the first Zagreb index is equal to

M_{1} (G) = - 16 (1 + 2 m - 9 m n + n) .

Proof. Let $G ≅ C H D N 3 (m, n)$ . Table 3 shows such an edge partition of $G$ for third case. Using Eq. 3, we get

M_{1} (G) = \sum_{r s \in E (G)} (d_{r} + d_{s}) .

Using edge partitions in Table 3, we get

M_{1} (G) = (4 + 4) (3 m n + 4 m + 2 n + 6) + (4 + 8) (6 m n - 8) + (8 + 8) (3 m n - 4 m - 2 n + 2),

= (8) (3 m n + 4 m + 2 n + 6) + (12) (6 m n - 8) + (16) (3 m n - 4 m - 2 n + 2) .

By making some calculations, we get

\Rightarrow M_{1} (G) = - 16 (1 + 2 m - 9 m n + n) .

Theorem 2.3.3. Consider the $m t h$ chain hex-derived network of type 3 $C H D N 3 (m, n)$ , the augmented Zagreb index and Harmonic Zagreb index are equal to

A Z I (G) = \frac{512}{1157625} (96546 - 692500 m + 1221153 m n - 346250 n) .

H (G) = \frac{1}{24} (10 + 12 m + 51 m n + 6 n) .

Proof. Let $G ≅ C H D N 3 (m, n)$ . Using Eq. 4,

A Z I (G) = \sum_{r s \in E (G)} {(\frac{d_{r} d_{s}}{d_{r} + d_{s} - 2})}^{3} .

From Table 3, using the edge partition, the outcome can be obtained as

A Z I (G) = {(\frac{4 \times 4}{4 + 4 - 2})}^{3} (3 m n + 4 m + 2 n + 6) + {(\frac{4 \times 8}{4 + 8 - 2})}^{3} (6 m n - 8)

+ {(\frac{8 \times 8}{8 + 8 - 2})}^{3} (3 m n - 4 m - 2 n + 2),

= ({(\frac{8}{3})}^{3}) (3 m n + 4 m + 2 n + 6) + {(\frac{16}{5})}^{3} (6 m n - 8) + {(\frac{32}{7})}^{3} (3 m n - 4 m - 2 n + 2) .

By making some calculations, we get

\Rightarrow A Z I (G) = \frac{512}{1157625} (96546 - 692500 m + 1221153 m n - 346250 n) .

Using Eq. 5,

H (G) = \sum_{r s \in E (G)} (\frac{2}{d_{r} + d_{s}}) .

From Table 3, using the edge partition, the outcome can be obtained as

H (G) = = (\frac{2}{4 + 4}) (3 m n + 4 m + 2 n + 2) + (\frac{2}{4 + 8}) (6 m n - 8) + (\frac{2}{8 + 8}) (3 m n - 4 m - 2 n + 2),

= (\frac{1}{8}) (3 m n + 4 m + 2 n + 6) + (\frac{1}{6}) (6 m n - 8) + (\frac{1}{8}) (3 m n - 4 m - 2 n + 2) .

By making some calculations, we get

\Rightarrow H (G) = \frac{1}{24} (10 + 12 m + 51 m n + 6 n) .

Theorem 2.3.4. Let $G$ be the $C H D N 3 (m, n)$ $m t h$ chain hex-derived network of third type, then atom–bond connectivity index is equal to

A B C (G) = \frac{1}{8} (4 \sqrt{5} (3 m n - 4) + \sqrt{14} (2 - 4 m + 3 m n - 2 n) + 2 \sqrt{6} (6 + 4 m + 3 m n + 2 n)) .

G A (G) = 8 + 6 m n + \frac{4 \sqrt{2}}{3} (3 m n - 4) .

Proof. Let $G ≅ C H D N 3 (m, n)$ . Using Eq. 6, we get

A B C (G) = \sum_{r s \in E (G)} \sqrt{\frac{d_{r} + d_{s} - 2}{d_{r} d_{s}}} .

From Table 3, by using the edge partition, the outcome can be obtained as

A B C (G) = \sqrt{\frac{4 + 4 - 2}{4 \times 4}} (3 m n + 4 m + 2 n + 6) + \sqrt{\frac{4 + 8 - 2}{4 \times 8}} (6 m n - 8)

+ \sqrt{\frac{8 + 8 - 2}{8 \times 8}} (3 m n - 4 m - 2 n + 2),

= \sqrt{\frac{3}{8}} (3 m n + 4 m + 2 n + 6) + \sqrt{\frac{14}{64}} (6 m n - 8) + \sqrt{\frac{7}{32}} (3 m n - 4 m - 2 n + 2) .

By making some calculations, we get

\Rightarrow A B C (G) = \frac{1}{8} (4 \sqrt{5} (3 m n - 4) + \sqrt{14} (2 - 4 m + 3 m n - 2 n) + 2 \sqrt{6} (6 + 4 m + 3 m n + 2 n)) .

Using Eq. 7, we have

G A (G) = \sum_{r s \in E (G)} \frac{2 \sqrt{d_{r} d_{s}}}{d_{r} + d_{s}} .

From Table 3, using the edge partition, the outcome can be obtained as

G A (G) = \frac{2 \sqrt{4 \times 4}}{(4 + 4)} (3 m n + 4 m + 2 n + 6) + \frac{2 \sqrt{4 \times 8}}{(4 + 8)} (6 m n - 8) + \frac{2 \sqrt{8 \times 8}}{(8 + 8)} (3 m n - 4 m - 2 n + 2),

= (1) (3 m n + 4 m + 2 n + 6) + \frac{2 \sqrt{2}}{3} (6 m n - 8) + (1) (3 m n - 4 m - 2 n + 2) .

By making some calculations, we get

\Rightarrow G A (G) = 8 + 6 m n + \frac{4 \sqrt{2}}{3} (3 m n - 4) .

$•$ For the comparison of First Zagreb, harmonic, atom–bond connectivity, and geometric–arithmetic indices of $C H D N 3 (m, n)$ for $m = n$ , we computed the indices for different values of m and n. By increasing the values of m and n, we can clearly check from the following Table 4, the order of indices is also increasing, and their graphical structure is shown in Figure 4.

$•$ For the comparison of first Zagreb, harmonic, atom–bond connectivity, and geometric–arithmetic indices of $C H D N 3 (m, n)$ for $m < n$ , where m is odd and n is natural number. By increasing the values of m and n, we can clearly check from the following Table 5, the order of indices is also increasing, and their graphical structure is shown in Figure 5.

$•$ For the comparison of first Zagreb, harmonic, atom–bond connectivity, and geometric–arithmetic indices of $C H D N 3 (m, n)$ for $m < n$ , where m and n both are even. By increasing the values of m and n, we can clearly check from the following Table 6, the order of indices is also increasing, and their graphical structure is shown in Figure 6.

$•$ For the comparison of first Zagreb, harmonic, atom–bond connectivity, and geometric–arithmetic indices of $C H D N 3 (m, n)$ for $m < n$ , where m is even and n is odd. By increasing the values of m and n, we can clearly check from the following Table 7, the order of indices is also increasing, and their graphical structure is shown in Figure 7.

TABLE 4

TABLE 4. Numerical computation of $C H D N 3 (m, n)$ for $m = n$ .

FIGURE 4

FIGURE 4. Graphical representation of $C H D N 3 (m, n)$ for different values of $m = n$ .

TABLE 5

TABLE 5. Numerical computation of $C H D N 3 (m, n)$ network for $m < n$ , where m is odd and n is natural number.

FIGURE 5

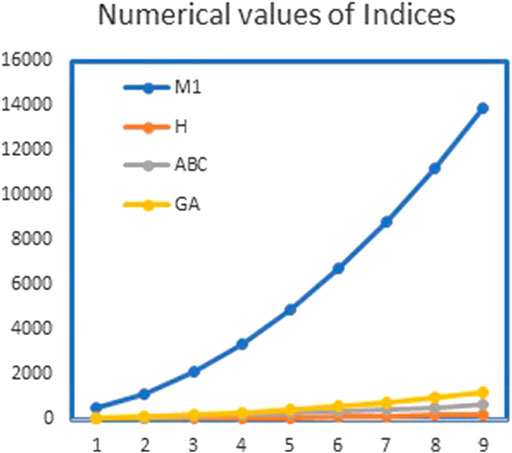
FIGURE 5. Graphical representation of $C H D N 3 (m, n)$ for different values of $m < n$ , where m is odd and n is natural number.

TABLE 6

TABLE 6. Numerical computation of $C H D N 3 (m, n)$ network for $m < n$ , where m and n both are even.

FIGURE 6

FIGURE 6. Graphical representation of $C H D N 3 (m, n)$ for different values of $m < n$ , where m and n both are even.

TABLE 7

TABLE 7. Numerical computation of $C H D N 3 (m, n)$ network for $m < n$ , where m is even and n is odd.

FIGURE 7

FIGURE 7. Graphical representation of $C H D N 3 (m, n)$ for different values of $m < n$ , where m is even and n is odd.

Conclusion

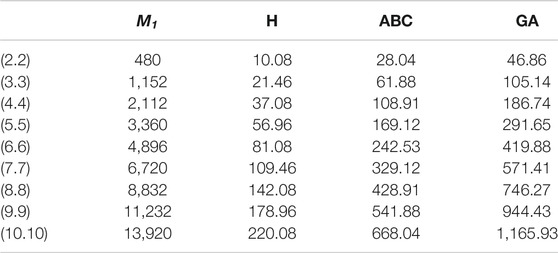
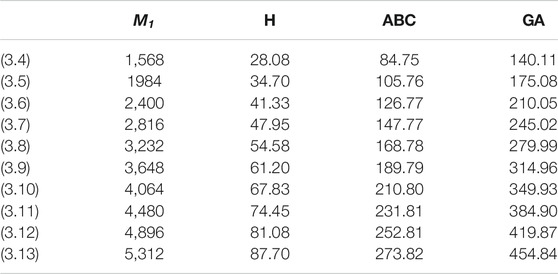
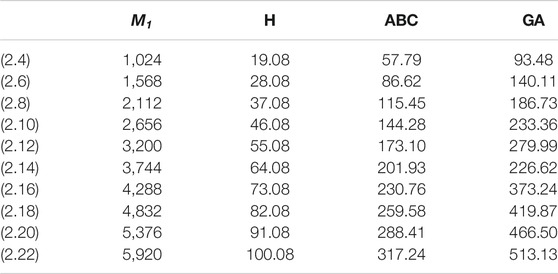
In this article, we have calculated the exact solutions for degree-based indices for mth-hex-derived networks of third type. Hex-derived network has a variety of useful applications in pharmacy, electronics, and networking. We obtained the degree-based indices such as Randić, first Zagreb, augmented Zagreb, harmonic, atom–bond connectivity index, and geometric–arithmetic index for hex derived networks. For this network, we have also given the tabular and graphical comparison between indices. We came to know that by increasing the values of m and n, there is also increase in the indices, which shows the correctness of our results. These results may be helpful for people working in computer science and chemistry who encounter hex-derived networks.

Data Availability Statement

All datasets presented in this study are included in the article/Supplementary Material.

Author Contributions

All the authors participated in the preparation and presenting of the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2020.593275/full#supplementary-material

References

1. Ali A, Nazeer W, Munir M, Min Kang S. M-polynomials and topological indices of zigzag and rhombic benzenoid systems. Open Chem (2018). 16(1):73–8. doi:10.1515/chem-2018-0010

CrossRef Full Text | Google Scholar

2. Ali H, Sajjad A, Sajjad A. On further results of hex derived networks. Open J Discret Appl Math (2019). 2(1):32–40. doi:10.30538/psrp-odam2019.0009

CrossRef Full Text | Google Scholar

3. Ali H, Binyamin MA, Shafiq MK, Gao W. On the degree-based topological indices of some derived networks. Mathematics (2019). 7:612. doi:10.3390/math7070612

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Asif F, Zahid Z, Zafar S. Leap Zagreb and leap hyper-Zagreb indices of Jahangir and Jahangir derived graphs. Eng Appl Sci Lett (2020). 3(2):1–8. doi:10.30538/psrp-easl2020.0036

CrossRef Full Text | Google Scholar

5. Aslam F, Zahid Z, Zahid Z, Zafar S. 3-total edge mean cordial labeling of some standard graphs. Open J Math Sci (2019). 3(1):129–38. doi:10.30538/oms2019.0056

CrossRef Full Text | Google Scholar

6. Bača M, Horváthová J, Mokrišová M, Semaničová-Feňovxcxíkovxax A, Suhányiovǎ A. On topological indices of carbon nanotube network. Can J Chem (2015). 93:1–4. doi:10.1139/cjc-2015-0175

CrossRef Full Text | Google Scholar

7. Baig AQ, Imran M, Ali H. On topological indices of poly oxide, poly silicate, DOX and DSL networks. Can J Chem (2015). 93:730739. doi:10.1139/cjc-2014-0490

CrossRef Full Text | Google Scholar

8. Baig AQ, Imran M, Ali H, Rehman SU. Computing topological polynomials of certain nanostructures. J Optoelectron Adv Mater (2015). 17(5–6):877–83.

Google Scholar

9. Chen M-S, Shin KG, Kandlur DD. Addressing, routing, and broadcasting in hexagonal mesh multiprocessors. IEEE Trans Comput (1990). 39(1):10–8. doi:10.1109/12.46277

CrossRef Full Text | Google Scholar

10. Diudea MV, Gutman I, Lorentz J Molecular topology. Huntington, NY: Nova Science Publishers (2001).

Google Scholar

11. Eliasi M, Iranmanesh A, Gutman I. Multiplicative versions of first Zagreb index. Match-Communi Math Compu Chem (2012). 68(1):217.

Google Scholar

12. Estrada E, Torres L, Rodrigueza L, Gutman I. An atom-bond connectivity index: modelling the enthalpy of formation of alkanes. Indian J Chem (1998). 37A:849–55.

Google Scholar

13. Furtula B, Graovac A, Vukičević D. Augmented Zagreb index. J Math Chem (2010). 48:370–80. doi:10.1007/s10910-010-9677-3

CrossRef Full Text | Google Scholar

14. Gao W, Siddiqui MK, Naeem M, Imran M. Computing multiple ABC index and multiple GA index of some grid graphs. Open Phys (2018). 16(1):588–98. doi:10.1515/phys-2018-0077

CrossRef Full Text | Google Scholar

15. Gutman I. Topological properties of benzenoid systems. Top Curr Chem (1992). 162:2128.

PubMed Abstract | Google Scholar

16. Gutman I, Cyvin SJ. Introduction to the theory of benzenoid hydrocarbons. Berlin, Germany: Springer (1989).

CrossRef Full Text | Google Scholar

17. Gutman I, Rusić B, Trinajsti N, Wilcox CF. Graph theory and molecular orbitals. XII. Acyclic polyenes. J Chem Phys (1975). 62(9):3399–405. doi:10.1063/1.430994

CrossRef Full Text | Google Scholar

18. Imran M, Baig AQ, Siddiqui HMA, Sarwar R. On molecular topological properties of diamond-like networks. Can J Chem (2017). 95:758–70. doi:10.1139/cjc-2017-0206

CrossRef Full Text | Google Scholar

19. Liu J-B, Wang C, Wang S, Wei B. Zagreb indices and multiplicative Zagreb indices of Eulerian graphs. Bull Malays Math Sci Soc (2019). 42(1):67–78. doi:10.1007/s40840-017-0463-2

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Liu J-B, Zhao J, He H, Shao Z. Valency-based topological descriptors and structural property of the generalized sierpiński networks. J Stat Phys (2019). 177(6):1131–47. doi:10.1007/s10955-019-02412-2

CrossRef Full Text | Google Scholar

21. Liu J-B, Zhao J, Min J, Cao J. The hosoya index of graphs formed by a fractal graph. Fractals (2019). 27(8):1950135. doi:10.1142/s0218348x19501354

CrossRef Full Text | Google Scholar

22. Liu J-B, Shi Z-Y, Pan Y-H, Cao J, Abdel-Aty M, Al-Juboori U. Computing the Laplacian spectrum of linear octagonal-quadrilateral networks and its applications, Polycycl Aromat Comp (2020). 40: 1–12. doi:10.1080/10406638.2020.1748666

CrossRef Full Text | Google Scholar

23. Liu JB, Jing Z, Zheng QC. On the generalized adjacency, Laplacian and signless Laplacian spectra of the weighted edge corona networks. Physica A: Stat Mech Appl (2020). 540:123073. doi:10.1016/j.physa.2019.123073

CrossRef Full Text | Google Scholar

24. Liu JB, Zhao J, Zhu Z. On the number of spanning trees and normalized Laplacian of linear octagonal‐quadrilateral networks. Int J Quant Chem (2019). 119(17):e25971. doi:10.1002/qua.25971

CrossRef Full Text | Google Scholar

25. Munir M, Nazeer W, Rafique S, Kang S. M-polynomial and degree-based topological indices of polyhex nanotubes. Symmetry (2016). 8(12):149. doi:10.3390/sym8120149

CrossRef Full Text | Google Scholar

26. Nayak A, Stojmenovic I. Hand book of applied algorithms: solving scientific, engineering, and practical problems. John Wiley & Sons (2007). 560 p.

Google Scholar

27. Randic M. Characterization of molecular branching. J Am Chem Soc (1975). 97:6609–15. doi:10.1021/ja00856a001

CrossRef Full Text | Google Scholar

28. Salema K, Klavzarc S, Gutman I. On the role of hypercubes in the resonance graphs of benzenoid graphs. Discret Math (2006). 306:699704. doi:10.1016/j.disc.2005.11.017

CrossRef Full Text | Google Scholar

29. Simonraj F, George A. On the metric dimension of HDN3 and PHDN3. In: Proceedings of the IEEE international conference on power, control, signals and instrumentation engineering (ICPCSI); Chennai, India, 2017 September 21--22 (2017). p 1333–6.

CrossRef Full Text | Google Scholar

30. Tabassum A, Umar MA, Umar MA, Perveen M, Raheem A. Antimagicness of subdivided fans. Open J Math Sci (2020). 4(1):18–22. doi:10.30538/oms2020.0089

CrossRef Full Text | Google Scholar

31. Trinajstic N. Chemical graph theory. London, United Kingdom: Routledge (1992).

Google Scholar

32. Umar MA, Ali N, Ali N, Tabassum A, Ali BR. Book graphs are cycle antimagic. Open J Math Sci (2019). 3(1):184–90. doi:10.30538/oms2019.0061

CrossRef Full Text | Google Scholar

33. Vukićevic D, Furtula B. Topological index based on the ratios of geometrical and arithmetical means of end-vertex degrees of edges. J Math Chem (2009). 46:1369–76.

Google Scholar

34. Wang D, Ahmad H, Nazeer W. Hosoya and Harary polynomials of TUC 4 nanotube. Math Methods Appl Sci (2020). 1–17. doi:10.1002/mma.6487

Google Scholar

35. Wiener H. Structural determination of paraffin boiling points. J Am Chem Soc (1947). 69:17–20. doi:10.1021/ja01193a005

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Wei C-C, Ali H, Binyamin MA, Naeem MN, Liu J-B. Computing degree based topological properties of third type of hex-derived networks. Mathematics (2019). 7:368. doi:10.3390/math7040368

CrossRef Full Text | Google Scholar

37. Zhong L. The harmonic index for graphs. Appl Math Lett (2012). 25:561–6. doi:10.1016/j.aml.2011.09.059

CrossRef Full Text | Google Scholar

Keywords: Randić, index, first and second Zagreb index, augmented Zagreb index, harmonic index, atom–bond connectivity and geometric–arithmetic index

Citation: Huo Y, Ali H, Binyamin MA, Asghar SS, Babar U and Liu J-B (2020) On Topological Indices of $m t h$ Chain Hex-Derived Network of Third Type. Front. Phys. 8:593275. doi: 10.3389/fphy.2020.593275

Received: 24 August 2020; Accepted: 23 September 2020;
Published: 20 November 2020.

Edited by:

Jinjin Li, Shanghai Jiao Tong University, China

Reviewed by:

Waqas Nazeer, University of Education, Winneba, Ghana
Mohammad Reza Farahani, Iran University of Science and Technology, Iran

Copyright © 2020 Huo, Ali, Binyamin, Asghar, Babar and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.

*Correspondence: Muhammad Ahsan Binyamin, ahsanbanyamin@gmail.com

BRIEF RESEARCH REPORT article

On Topological Indices of mth Chain Hex-Derived Network of Third Type

Introduction and Preliminary Results

Main Results

Results for the First Case mth Chain Hex-Derived Network of Third Type CHDN3 (m, n)

Results for the Second Case of Chain Hex-Derived Networks of Third Type CHDN3 (m, n)

Results for the Third Case of CHDN3(m,n) Chain Hex Derived Networks of Third Type

Conclusion

Data Availability Statement

Author Contributions

Conflict of Interest

Supplementary Material

References

People also looked at

On Topological Indices of $m t h$ Chain Hex-Derived Network of Third Type

Results for the Third Case of $C H D N 3 (m, n)$ Chain Hex Derived Networks of Third Type