- 1School of Finance and Mathematics, Huainan Normal University, Huainan, China
- 2Department of Mathematics, Government College University, Faisalabad, Pakistan
- 3Department of Applied Sciences, National Textile University, Faisalabad, Pakistan
- 4School of Mathematics and Physics, Anhui Jianzhu University,Hefei, China
In theoretical chemistry, the numerical parameters that are used to characterize the molecular topology of graphs are called topological indices. Several physical and chemical properties like boiling point, entropy, heat formation, and vaporization enthalpy of chemical compounds can be determined through these topological indices. Graph theory has a considerable use in evaluating the relation of various topological indices of some derived graphs. In this article, we will compute the topological indices like Randić, first Zagreb, harmonic, augmented Zagreb, atom-bond connectivity, and geometric-arithmetic indices for chain hex-derived network of type 3
Mathematics Subject Classification: 05C12, 05C90
Introduction and Preliminary Results
A branch of numerical science called graph theory is the one in which we use tools of graph parameters to reveal the compound phenomenon precisely. Graph theory, for instance, when used in the study of molecular structures, characterizes a field among various disciplines of science known as molecular topology or chemical graph theory.
Chemical graph theory has provided a considerable part of study to chemist through which they can execute graph theory to mathematical demonstrating of chemical marvel. We are usually interested in estimating the structural characters to elaborate quantitative structure–activity relationships using techniques taken from graph theory.
Topological description of chemical structures with required properties can be used to categorize the molecules and to model unknown structures. Molecules and molecular compounds are frequently demonstrated by molecular graph. In graph theory, a molecular graph is the illustration of structural formula of chemical compounds. The vertices are expressed by the atoms of molecule while the edges suggest the covalent bonds between the atoms.
Quantitative structure–activity (QSAR) and structure–property (QSPR) relationships that are used to analyze the organic activities and properties of biological compounds can be studied by the help of a new subject known as cheminformatics, which is the composition of mathematics, information science, and chemistry.
At present, the numerical programming of biological structure with topological descriptors is increasing in consequence in invigorating science, bioinformatics, and pharmaceutics.
In QSAR/QSPR study, physicochemical properties of the topological descriptors like Wiener index, Randić index, sieged index, first and second Zagreb index, augmented Zagreb index, harmonic index, and geometric–arithmetic index are useful to classify the bioactivity of the chemical compounds.
A graph can be characterized by a polynomial, a numeric number, and a sequence of numbers or a matrix. A numeric quantity interrelated with a graph that remains invariant under the graph automorphism and differentiate the topology of graph is called molecular descriptor. A graph theoretical characteristic that is sustained by an isomorphism is called topological descriptor.
At present, in the field of computational chemistry, topological indices have a rising interest, which is actually associated to their use in nonempirical quantitative structure–property relationship and quantitative structure–activity relationship.
Topological descriptor, Top (G), may also be defined with the property of isomorphism, that is, for every graph H isomorphic to G, Top (G) = Top (H). The idea of topological indices was first introduced by Weiner [35] during the laboratory work on boiling point of paraffin and named this result as path number, which was later named as Weiner index.
This article takes into account the topological indices of hexagonal networks derived from a hexagonal graph, which contain molecular graphs of unbranched benzene hydrocarbons. Hexagonal structure graphs consist of hexagons that are fused together. Theoretical chemists pay great attention to this class of chemical compounds. Topological index theory has been intensively developed over the past four decades for the individual molecular graphs. Benzene hydrocarbons are not only the major chemical industry raw materials but also harmful pollutants [15, 16, 28].
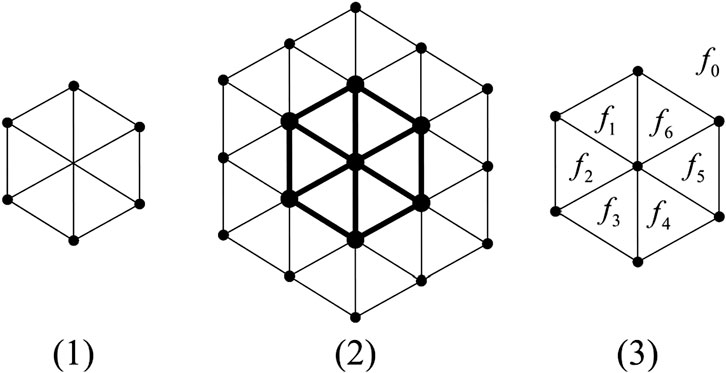
Chen et al. [9] derived a hexagonal mesh. Hexagonal mesh made by a set of triangles is shown in Figure 1. There exists no hexagonal mesh with one dimension. A two dimensional hexagonal mesh
Drawing algorithm of
Step-1: First, we draw a hexagonal network of dimension n.
Step-2: All the
Step-3: An mth
In
In this article,
The Randić index [27] is denoted by
The general Randić index is the sum of
Trinajstić [31] makes us aware of
Furtula et al. [13] introduced the augmented Zagreb index and described it as
Zhong [37] introduced the harmonic index and described it as
The index atom–bond connectivity (ABC) is one of the well-known degree-based topological indices, given by Estrada et al. [12] and defined as
Vukićević and Furtula [33] invented the famous geometric–arithmetic index and represented it as
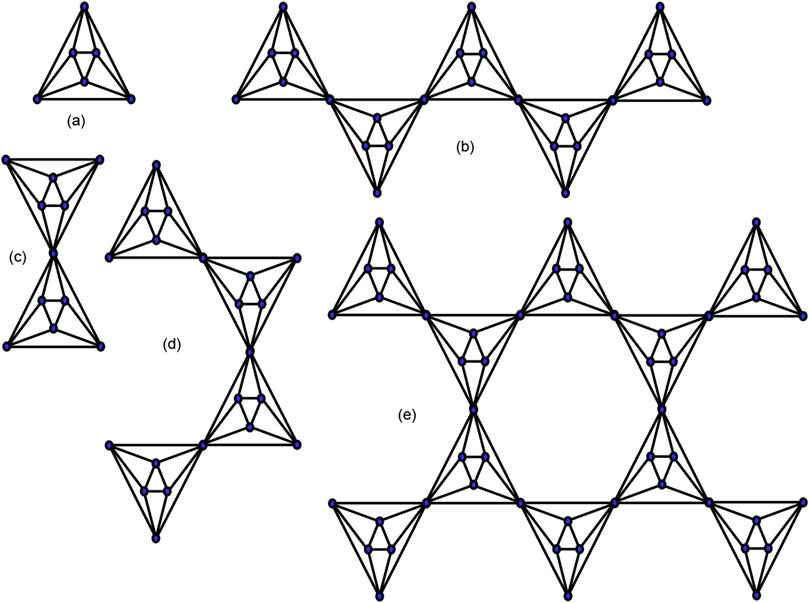
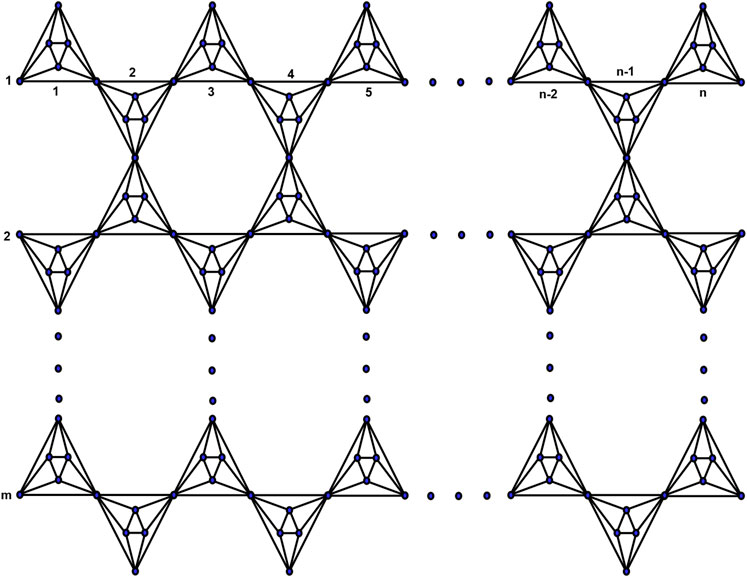
Cases for mth chain hex-derived network of third type.
There are three cases for
Case-1: For
Case-2: For
Case-3: For
Main Results
Simonraj et al. [29] discovered hex-derived networks and found the metric dimension of
Results for the First Case mth Chain Hex-Derived Network of Third Type CHDN3 (m, n)
In this section, for the very first time, we discuss
Theorem 2.1.1. Consider the
Proof. Let
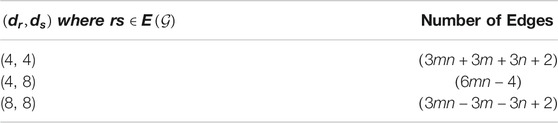
Using edge partitions in Table 1, we get the following.
For
By making some calculations, we get
For
By making some calculations, we get
For
By making some calculations, we get
For
By making some calculations, we get
Theorem 2.1.2. Consider the
Proof. Let
Using edge partitions in Table 1, we get
By making some calculations, we get
Theorem 2.1.3. Consider the
Proof. Let
From Table 1, using the edge partition, the outcome can be obtained as
By making some calculations, we get
Using Eq. 5, we have
From Table 1, using the edge partition, the outcome can be obtained as
By making some calculations, we get
Theorem 2.1.4. Let
Proof. Let
From Table 1, using the edge partition, the outcome can be obtained as
By making some calculations, we get
Using Eq. 7,
From Table 1, using the edge partition, we get the outcome as,
By making some calculations, we get
Results for the Second Case of Chain Hex-Derived Networks of Third Type CHDN3 (m, n)
In this section, for the very first time, we discuss
Theorem 2.2.1. Consider the
Proof. Let
Using Eq. 2, we get
Using edge partitions in Table 2, we get, for
By making some calculations, we get
For
By making some calculations, we get
For
By making some calculations, we get
For
By making some calculations, we get
Theorem 2.2.2. Consider the
Proof. Let
Using Eq. 3,
Using edge partitions in Table 2, we get
By making some calculations, we get
Theorem 2.2.3. Let
Proof. Consider
From Table 1, using the edge partition, the outcome can be obtained as
By making some calculations, we get
By using Eq. 5, we have
From Table 1, using the edge partition, the outcome can be obtained as
By making some calculations, we get
Theorem 2.2.4. Let
Proof. Consider
From Table 2, by using the edge partition, we get the outcome as,
By making some calculations, we get
Using Eq. 7, we have
From Table 2, using the edge partition, we get the outcome as,
By making some calculations, we get
Results for the Third Case of
In this section, for the very first time, we discuss
Theorem 2.3.1. Consider the
Proof. Let
Using edge partitions in Table 3, we get, for
By making some calculations, we get
For
By making some calculations, we get
For
By making some calculations, we get
For
By making some calculations, we get
Theorem 2.3.2. Consider the
Proof. Let
Using edge partitions in Table 3, we get
By making some calculations, we get
Theorem 2.3.3. Consider the
Proof. Let
From Table 3, using the edge partition, the outcome can be obtained as
By making some calculations, we get
Using Eq. 5,
From Table 3, using the edge partition, the outcome can be obtained as
By making some calculations, we get
Theorem 2.3.4. Let
Proof. Let
From Table 3, by using the edge partition, the outcome can be obtained as
By making some calculations, we get
Using Eq. 7, we have
From Table 3, using the edge partition, the outcome can be obtained as
By making some calculations, we get
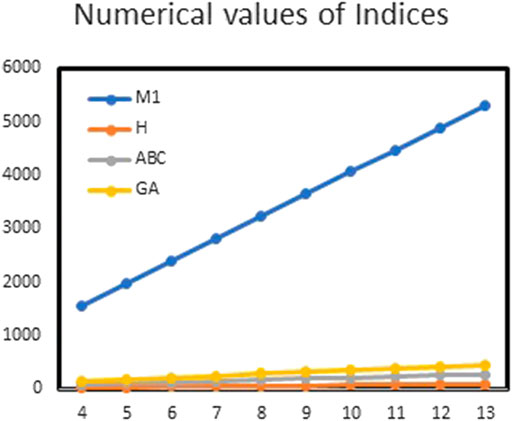
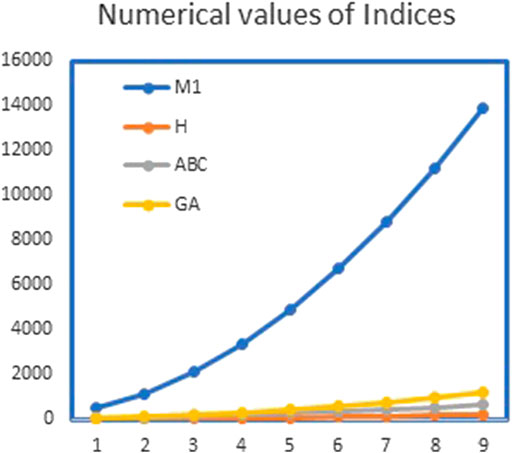
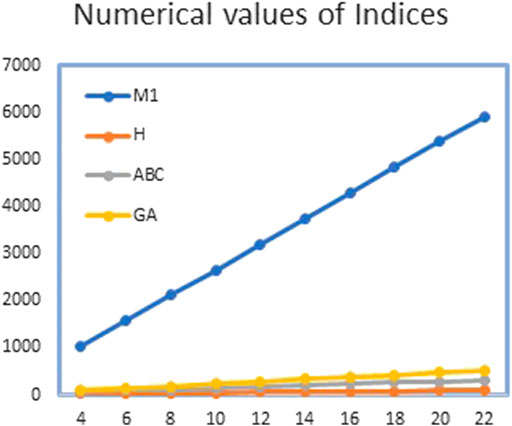
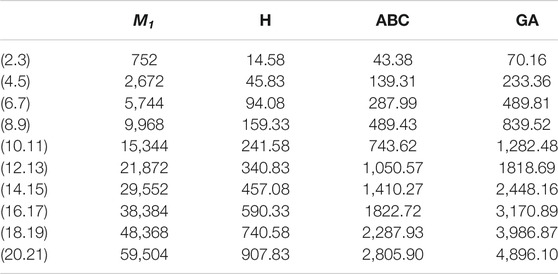
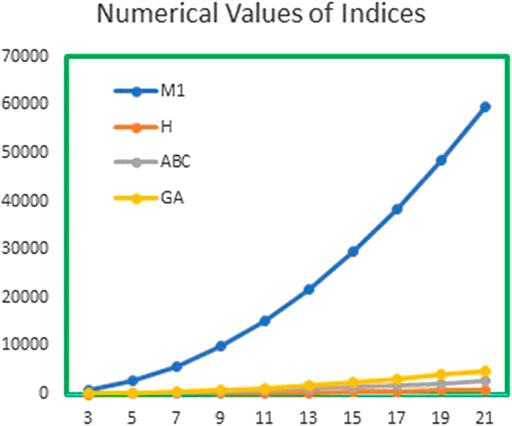
FIGURE 5. Graphical representation of
Conclusion
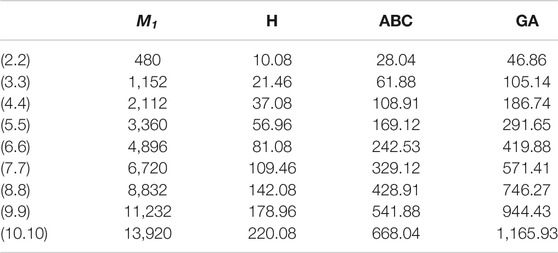
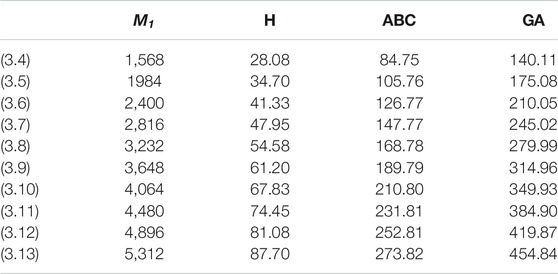
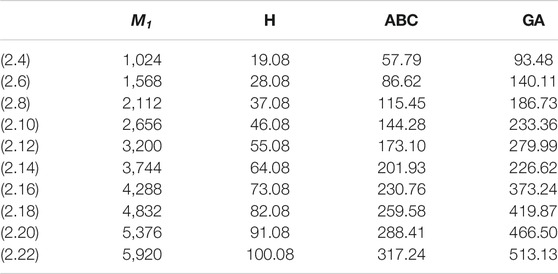
In this article, we have calculated the exact solutions for degree-based indices for mth-hex-derived networks of third type. Hex-derived network has a variety of useful applications in pharmacy, electronics, and networking. We obtained the degree-based indices such as Randić, first Zagreb, augmented Zagreb, harmonic, atom–bond connectivity index, and geometric–arithmetic index for hex derived networks. For this network, we have also given the tabular and graphical comparison between indices. We came to know that by increasing the values of m and n, there is also increase in the indices, which shows the correctness of our results. These results may be helpful for people working in computer science and chemistry who encounter hex-derived networks.
Data Availability Statement
All datasets presented in this study are included in the article/Supplementary Material.
Author Contributions
All the authors participated in the preparation and presenting of the manuscript.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2020.593275/full#supplementary-material
References
1. Ali A, Nazeer W, Munir M, Min Kang S. M-polynomials and topological indices of zigzag and rhombic benzenoid systems. Open Chem (2018). 16(1):73–8. doi:10.1515/chem-2018-0010
2. Ali H, Sajjad A, Sajjad A. On further results of hex derived networks. Open J Discret Appl Math (2019). 2(1):32–40. doi:10.30538/psrp-odam2019.0009
3. Ali H, Binyamin MA, Shafiq MK, Gao W. On the degree-based topological indices of some derived networks. Mathematics (2019). 7:612. doi:10.3390/math7070612
4. Asif F, Zahid Z, Zafar S. Leap Zagreb and leap hyper-Zagreb indices of Jahangir and Jahangir derived graphs. Eng Appl Sci Lett (2020). 3(2):1–8. doi:10.30538/psrp-easl2020.0036
5. Aslam F, Zahid Z, Zahid Z, Zafar S. 3-total edge mean cordial labeling of some standard graphs. Open J Math Sci (2019). 3(1):129–38. doi:10.30538/oms2019.0056
6. Bača M, Horváthová J, Mokrišová M, Semaničová-Feňovxcxíkovxax A, Suhányiovǎ A. On topological indices of carbon nanotube network. Can J Chem (2015). 93:1–4. doi:10.1139/cjc-2015-0175
7. Baig AQ, Imran M, Ali H. On topological indices of poly oxide, poly silicate, DOX and DSL networks. Can J Chem (2015). 93:730739. doi:10.1139/cjc-2014-0490
8. Baig AQ, Imran M, Ali H, Rehman SU. Computing topological polynomials of certain nanostructures. J Optoelectron Adv Mater (2015). 17(5–6):877–83.
9. Chen M-S, Shin KG, Kandlur DD. Addressing, routing, and broadcasting in hexagonal mesh multiprocessors. IEEE Trans Comput (1990). 39(1):10–8. doi:10.1109/12.46277
10. Diudea MV, Gutman I, Lorentz J Molecular topology. Huntington, NY: Nova Science Publishers (2001).
11. Eliasi M, Iranmanesh A, Gutman I. Multiplicative versions of first Zagreb index. Match-Communi Math Compu Chem (2012). 68(1):217.
12. Estrada E, Torres L, Rodrigueza L, Gutman I. An atom-bond connectivity index: modelling the enthalpy of formation of alkanes. Indian J Chem (1998). 37A:849–55.
13. Furtula B, Graovac A, Vukičević D. Augmented Zagreb index. J Math Chem (2010). 48:370–80. doi:10.1007/s10910-010-9677-3
14. Gao W, Siddiqui MK, Naeem M, Imran M. Computing multiple ABC index and multiple GA index of some grid graphs. Open Phys (2018). 16(1):588–98. doi:10.1515/phys-2018-0077
16. Gutman I, Cyvin SJ. Introduction to the theory of benzenoid hydrocarbons. Berlin, Germany: Springer (1989).
17. Gutman I, Rusić B, Trinajsti N, Wilcox CF. Graph theory and molecular orbitals. XII. Acyclic polyenes. J Chem Phys (1975). 62(9):3399–405. doi:10.1063/1.430994
18. Imran M, Baig AQ, Siddiqui HMA, Sarwar R. On molecular topological properties of diamond-like networks. Can J Chem (2017). 95:758–70. doi:10.1139/cjc-2017-0206
19. Liu J-B, Wang C, Wang S, Wei B. Zagreb indices and multiplicative Zagreb indices of Eulerian graphs. Bull Malays Math Sci Soc (2019). 42(1):67–78. doi:10.1007/s40840-017-0463-2
20. Liu J-B, Zhao J, He H, Shao Z. Valency-based topological descriptors and structural property of the generalized sierpiński networks. J Stat Phys (2019). 177(6):1131–47. doi:10.1007/s10955-019-02412-2
21. Liu J-B, Zhao J, Min J, Cao J. The hosoya index of graphs formed by a fractal graph. Fractals (2019). 27(8):1950135. doi:10.1142/s0218348x19501354
22. Liu J-B, Shi Z-Y, Pan Y-H, Cao J, Abdel-Aty M, Al-Juboori U. Computing the Laplacian spectrum of linear octagonal-quadrilateral networks and its applications, Polycycl Aromat Comp (2020). 40: 1–12. doi:10.1080/10406638.2020.1748666
23. Liu JB, Jing Z, Zheng QC. On the generalized adjacency, Laplacian and signless Laplacian spectra of the weighted edge corona networks. Physica A: Stat Mech Appl (2020). 540:123073. doi:10.1016/j.physa.2019.123073
24. Liu JB, Zhao J, Zhu Z. On the number of spanning trees and normalized Laplacian of linear octagonal‐quadrilateral networks. Int J Quant Chem (2019). 119(17):e25971. doi:10.1002/qua.25971
25. Munir M, Nazeer W, Rafique S, Kang S. M-polynomial and degree-based topological indices of polyhex nanotubes. Symmetry (2016). 8(12):149. doi:10.3390/sym8120149
26. Nayak A, Stojmenovic I. Hand book of applied algorithms: solving scientific, engineering, and practical problems. John Wiley & Sons (2007). 560 p.
27. Randic M. Characterization of molecular branching. J Am Chem Soc (1975). 97:6609–15. doi:10.1021/ja00856a001
28. Salema K, Klavzarc S, Gutman I. On the role of hypercubes in the resonance graphs of benzenoid graphs. Discret Math (2006). 306:699704. doi:10.1016/j.disc.2005.11.017
29. Simonraj F, George A. On the metric dimension of HDN3 and PHDN3. In: Proceedings of the IEEE international conference on power, control, signals and instrumentation engineering (ICPCSI); Chennai, India, 2017 September 21--22 (2017). p 1333–6.
30. Tabassum A, Umar MA, Umar MA, Perveen M, Raheem A. Antimagicness of subdivided fans. Open J Math Sci (2020). 4(1):18–22. doi:10.30538/oms2020.0089
32. Umar MA, Ali N, Ali N, Tabassum A, Ali BR. Book graphs are cycle antimagic. Open J Math Sci (2019). 3(1):184–90. doi:10.30538/oms2019.0061
33. Vukićevic D, Furtula B. Topological index based on the ratios of geometrical and arithmetical means of end-vertex degrees of edges. J Math Chem (2009). 46:1369–76.
34. Wang D, Ahmad H, Nazeer W. Hosoya and Harary polynomials of TUC 4 nanotube. Math Methods Appl Sci (2020). 1–17. doi:10.1002/mma.6487
35. Wiener H. Structural determination of paraffin boiling points. J Am Chem Soc (1947). 69:17–20. doi:10.1021/ja01193a005
36. Wei C-C, Ali H, Binyamin MA, Naeem MN, Liu J-B. Computing degree based topological properties of third type of hex-derived networks. Mathematics (2019). 7:368. doi:10.3390/math7040368
Keywords: Randić, index, first and second Zagreb index, augmented Zagreb index, harmonic index, atom–bond connectivity and geometric–arithmetic index
Citation: Huo Y, Ali H, Binyamin MA, Asghar SS, Babar U and Liu J-B (2020) On Topological Indices of
Received: 24 August 2020; Accepted: 23 September 2020;
Published: 20 November 2020.
Edited by:
Jinjin Li, Shanghai Jiao Tong University, ChinaReviewed by:
Waqas Nazeer, University of Education, Winneba, GhanaMohammad Reza Farahani, Iran University of Science and Technology, Iran
Copyright © 2020 Huo, Ali, Binyamin, Asghar, Babar and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Muhammad Ahsan Binyamin, YWhzYW5iYW55YW1pbkBnbWFpbC5jb20=
 Yuhong Huo
Yuhong Huo Haidar Ali
Haidar Ali Muhammad Ahsan Binyamin2*
Muhammad Ahsan Binyamin2* Usman Babar
Usman Babar Jia-Bao Liu
Jia-Bao Liu