Non-Trivial Transport Interface in a Hybrid Topological Material With Hexagonal Lattice Arrangement

In this paper, a hybrid topological material with hexagonal lattice arrangement is proposed, consisting of six metal cylindrical resonators and a dielectric slab. As a unit cell, the six metal cylindrical resonators satisfying the C₆ symmetry are selected, and the cylindrical resonators are inserted in the dielectric slab. It is demonstrated that a double Dirac cone is created at the $\Gamma$ point in the proposed topological material. Since the topological effects of the proposed system can be invoked merely by varying the geometric parameters of the unit cell, two band gaps with different topological characteristics can be easily achieved. It is further demonstrated that the topologically protected edge states can be obtained by connecting the two types of lattices with different topological characteristics. Finally, we implement a sharp bend waveguide by using these two types of the topological lattices. It is demonstrated that electromagnetic waves can propagate robustly along the sharp bend interface.

Introduction

Topological insulator is a kind of new phase of matter state about electron conductivity proposed by condensed-matter physicists. It soon becomes a hot topic in condensed matter physics and quantum materials [1, 2]. Topological insulator is realized firstly by electrons. The interior of a topological insulator is insulated, but there is always a conductive edge state on its boundary or surface. The edge state of the topological insulators is stable, and the motion direction of conducting electrons with different spins is opposite. Therefore, the transmission can be controlled by the spin of the electron, rather than transmitted by electric charge as traditional materials, and this process does not involve dissipation.

Recently, topological insulators have been extended to further areas of photonics [3–7], mechanics [8–13] and acoustics [14–21]. Topological insulators are different from conventional insulators in that the spin-orbit coupling effect of topological insulators is relatively significant. Based on the spin-orbit coupling effect, some researchers proposed a new topological crystalline insulators state [22–27]. For instance, Yang et al. proposed a chiral hyperbolic photonic metamaterial with broken inversion symmetry [26]. Ma et al. proposed a photonic topological insulator with complete topological band gap, which can emulate spin-orbit interaction through bianisotropy [27]. The quantum spin Hall effect is one of the most unique effects of topological insulators [28–31]. Wu et al. presented quantum spin Hall effect in photonic crystals [30]. Yang et al. investigated the pseudo-spin edge states for flexural waves in a honeycomb perforated phononic plate, which behaves an elastic analogue of the quantum spin Hall effect [31].

Besides the quantum spin Hall effect, topological edge state has also set off a research boom. Tzuhsuan et al. proposed a photonic structure consisting of metal rods arranged as a hexagonal array lattice, and demonstrated scattering-free edge states [32]. Huo et al. proposed two-dimensional solid phononic crystal structures, which simultaneously supported the topologically protected edge states for out-of-plane and in-plane bulk elastic waves [33]. Besides metal-based topological materials, dielectric-based topological materials have also been investigated in recent years. Xu et al. proposed a triangle photonic crystal by using core-shell dielectric materials, and demonstrated a helical edge states [34]. Xie et al. proposed a second-order topological insulator in dielectric photonic crystals and visualized one-dimensional topological edge states [35]. The topologically protected edge state has excellent characteristics of robustness, back-scattering suppression and defect immunity [36–40], which have potential applications for manufacturing new computer chips and other components in the future. In addition, topological insulators can also have been widely applied to the fields of transport in photonic crystals [41], phonon crystals [42] and even circuits composed of classical electronic components [43].

Different from the dielectric-based topological materials or metal-based topological materials presented in the previous references, in this paper, we propose a hybrid topological model consisting of metal and dielectric materials. It provides a new method to realize the topological edge state. The hybrid topological material consists of six metal cylindrical resonators and a dielectric slab. The six cylindrical resonators are inserted into the dielectric slab. The zone-folding technique [44] (using a larger unit cell instead of an irreducible one in a hexagonal crystal lattice) is applied to this present system, so that the double Dirac cone can be generated easily at the $\Gamma$ point. We demonstrate that the topologically non-trivial and trivial band gaps can be opened near the double Dirac cone by varying the parameter R. Therefore, the topologically protected edge states can be realized easily by combining two types of lattices with different topological characteristics in the proposed system. Finally, we construct a directional sharp bend waveguide, which shows the robustness propagation of electromagnetic waves is observed in the sharp bend waveguide interface.

Theoretical Model and Band Structure of the Hybrid Topological Material

A hexagonal arrangement of the metal cylindrical resonators is shown in Figure 1A. The six cylindrical resonators are inserted into a dielectric slab as presented in Figure 1B. We choose rhombus-shaped unit cell, where the relevant parameters are shown as follows: the lattice length of unit cell is a, and the distance between the center of each resonator to the center of rhombus-shaped unit cell is R. Each rhombus-shaped unit cell includes six cylindrical resonators in a hexagonal arrangement, showing the C₆ symmetry.

FIGURE 1

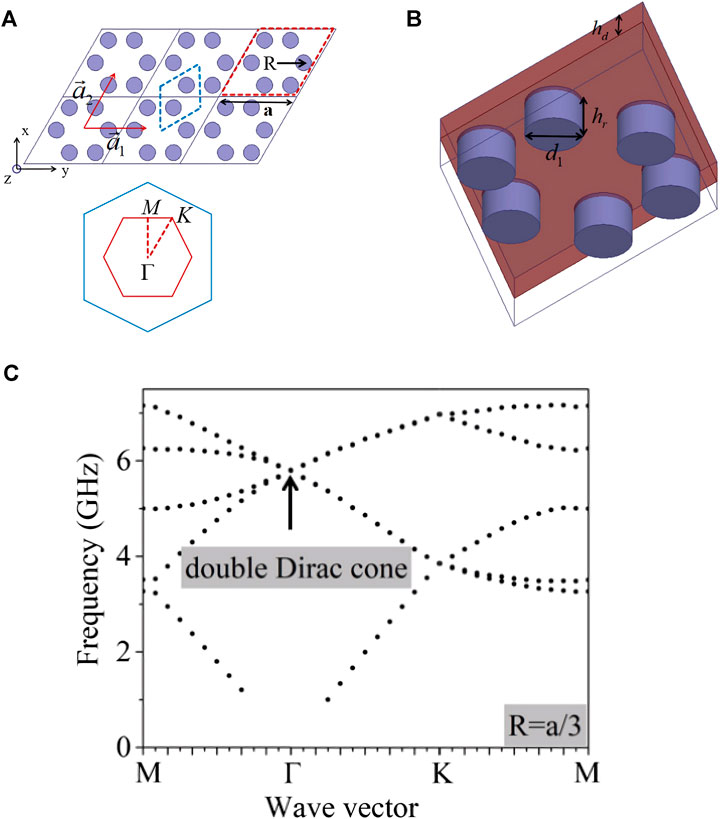
FIGURE 1. (A) Hexagonal arrangement of the metal cylindrical resonators. The red dotted box indicates six cylindrical resonators. ${\overrightarrow{a}}_1$ and ${\overrightarrow{a}}_2$ are lattice vectors and $a$ is the lattice length of unit cell. The blue dotted box represents the irreducible unit cell in the hexagonal arrangement. The lattice length of the irreducible unit cell is $a/\sqrt{3}$. According to the zone-folding technique, we choose a larger unit cell consisting of six resonators (red dotted box). The below panel is the corresponding Brillouin zones. (B) Detailed view of a hybrid unit cell consisting of six metal cylindrical resonators and a dielectric slab. The six metal cylindrical resonators are inserted into the dielectric slab. (C) Dispersion diagram of the proposed structure with $R=a/3$. It shows that a double Dirac cone is created at the $\Gamma$ point.

Numerical simulations are performed by using a commercial simulation software High Frequency Structure Simulation Software (HFSS) based on three-dimensional finite element numerical analysis. The metal cylindrical resonators are defined as PEC, and the dielectric slab is Teflon with the relative permittivity of 2.1 and the thickness of $h_d=2.5\text{mm}$. The size of the unit cell is $a=17\sqrt{3}mm$, and $R=a/3$. The diameter and the height of the cylindrical resonator are both 6 mm (i.e., $d_1=h_r=6mm$). The periodic boundary conditions are introduced in the direction of the two lattice vectors. Based on the zone-folding technique, as shown in Figure 1A, we select a unit cell composed of six resonators instead of two resonators. Figure 1C presents the band structure, which shows a double Dirac cone is created at the $\Gamma$ point ($f_d=5.55GHz$).

As shown in Figure 2, it is demonstrated that the band structure can be changed by varying the parameters R. The band inversion can be realized by different values of R. When R is shrunk (Figure 2A) or expanded (Figure 2B), it can be seen that a complete band gap appears, and simultaneously, the double Dirac cone becomes two double-degenerate modes. The emergence of band gap is due to the change in translational periodicity of the resonators. Keeping the C₆ symmetry, these double-degenerate modes are located above and below the Dirac frequency, respectively. Analogy to electronic orbital shapes, as $R=0.91a/3$, the lower frequency modes are p-type (p₁ and p₂ as shown in the bottom of Figure 2A), and the higher frequency modes are d-type (d₁ and d₂, upper in Figure 2A). However, as $R=1.06a/3$, the topological characteristic of the band gap is completely different from the case of $R=0.91a/3$. As shown in Figure 2B, the degenerate modes are flipped, p-type modes are at the higher frequency and d-type are at the lower frequency. That is to say, band inversion is realized as R varies.

FIGURE 2

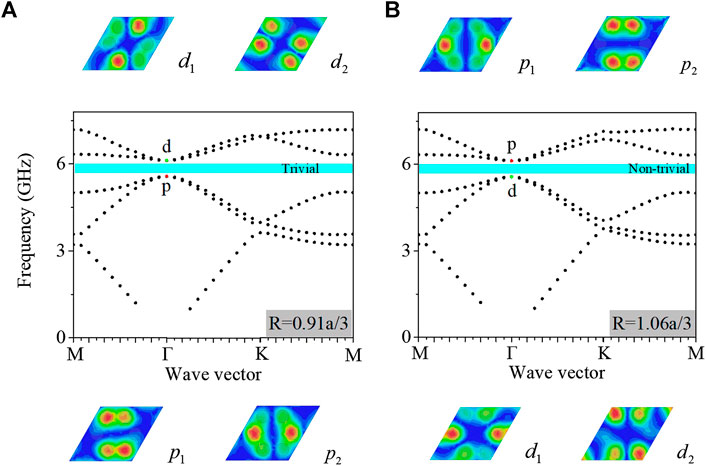
FIGURE 2. Band structure for different R. The band gap is opened at the $\Gamma$ point as R varies. (A) As $R=0.91a/3(R<a/3)$, band gap is topologically trivial. d-type modes are at the higher frequency and p-type modes are at the lower frequency, which the electric field distributions are shown in the upper and lower illustrations of the band structure diagram, respectively. (B) As $R=1.06a/3$($R>a/3$), the band gap is topologically non-trivial. The p-type modes and d-type modes are reversed.

We use the method proposed by Takahiro Fukui et al. [45] to calculate the spin Chern number of the proposed topological material. As $R=0.91a/3$, the spin Chern number is zero, indicating topologically trivial. In contrast, as $R=1.06a/3$, the bands have non-zero spin Chern number, which shows the topologically non-trivial. The change of spin Chern number indicates the topological phase transition. Combined Figure 1C and Figure 2, it can be seen that there is a band gap near the Dirac frequency. As R is shrunk, the double Dirac cone is opened and a complete band gap occurs. In contrast, as R is expanded, the double Dirac cone can also be opened and a band inversion occurs with the topological phase transition. These results indicate the proposed topological material can possess the characteristics from topologically trivial to topologically non-trivial.

Topological Edge States

In this section, we combine topologically non-trivial ($R=1.06a/3$) and topologically trivial ($R=0.91a/3$) lattices to form multi-cell configurations, and study wave guiding characteristics. As shown in Figure 3A, the multi-cell configuration consists of two parts, with 10 topologically non-trivial lattices on the left and 10 topologically trivial lattices on the right. In the simulations, the periodic boundary conditions are introduced in the direction of the two lattice vectors. The band structure of the multi-cell configuration is shown in Figure 3B, where the blue and red lines represent edge states. It can be seen that there are two points A and B corresponding to the same eigen-frequency (5.57 GHz). Figure 3C presents the electric field distribution of the points A and B, which shows the electromagnetic wave is well confined at the interface between the topologically non-trivial and trivial lattices both for A and B. However, for the point A, the clockwise pseudo-spin mode is realized at the interface, and anticlockwise pseudo-spin mode is observed for the point B. The direction of the two pseudo-spin modes at the interface is opposite.

FIGURE 3

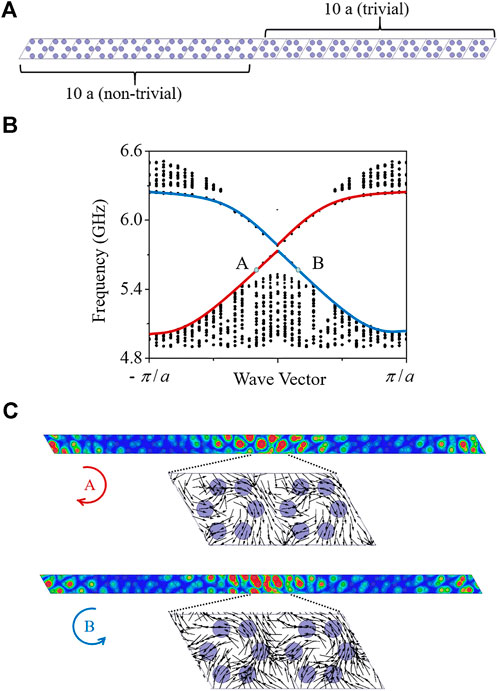
FIGURE 3. (A) Multi-cell configuration consists of two parts with 10 topologically non-trivial lattices on the left and 10 topologically trivial lattices on the right. (B) Band structure of the multi-cell configuration, where the blue and red lines represent the edge states. It can be seen that there are two different pseudo-spin modes at the interface. Red indicates clockwise and blue is anticlockwise. (C) Electric field distributions of the multi-cell configuration. The direction of pseudo-spin modes corresponding to A and B in Figure 3B. The color represents the electric field intensity, and the arrows represent the direction of the time-averaged energy flux.

As shown in Figure 3B, there are two different pseudo-spin modes at the interface of topologically non-trivial and trivial lattices at the same frequency. As shown in Figure 3C, opposite spins of these modes can be verified. In general, each frequency of the topological band gap corresponds to two edge states, and the pseudo-spin directions of the two edge states are different. Electromagnetic waves with a certain pseudo-spin direction can only propagate in a fixed direction, which is consistent with the characteristics of the quantum Hall effect.

Sharp Bend Waveguides

Since the proposed structure can support topological edge states, it is expected that new devices can be implemented by using this unique property. We construct a sharp bend interface by using two types of lattices ($R=1.06a/3$ and $R=0.91a/3$), which can operate as a directional waveguide. As shown in Figure 4A, we combine topologically non-trivial and topologically trivial lattices to form a two-dimensional sharp bend structure. The upper part of the red line is the topologically non-trivial lattices, and the lower part of the red line is the topologically trivial lattices. In this case, the interface of the two lattices has sharp angles.

FIGURE 4

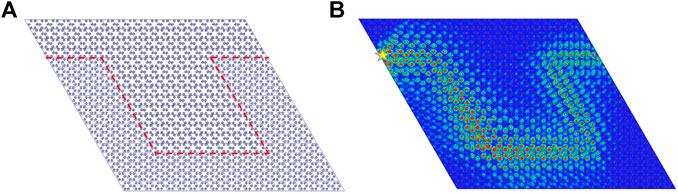
FIGURE 4. (A) Two-dimensional sharp bend structure consists of topologically non-trivial and trivial lattices. The upper part of the red line is the topologically non-trivial lattices, and the lower part of the red line is the topologically trivial lattices. (B) Electric field distribution of the sharp bend structure at 5.7 GHz. The yellow star indicates the excitation source, and the color indicates the electric field intensity.

In the simulation, the excitation source (denoted by a yellow star in Figure 4B) is set at the left side of the junction of the topologically non-trivial and trivial lattices. Radiation boundary conditions are introduced around the two-dimensional sharp bend structure. Simulation results show that the electromagnetic waves can propagate along the sharp bend interface in the frequency range of 5.54–5.8 GHz without obvious backscattering. Figure 4B presents the electric field distribution of the structure at 5.7 GHz, which shows electromagnetic waves can propagate along the sharp angles interface without back-scattering. The interface of the non-trivial transport operates like a waveguide.

In order to further verify the robustness of electromagnetic wave propagation along the sharp bend interface, as shown in Figure 5, two types of defects are introduced. For the defect 1 as presented in Figure 5A, six metal cylindrical resonators are removed from the topologically trivial lattices. The simulated electric field distribution shows there is no back-scattering and electromagnetic waves can transmit completely in this sharp bend interface. For the defect 2 as presented in Figure 5B, we remove the four resonators in the same topologically trivial lattices. As expected, the similar result is observed. Therefore, it can be seen that this non-trivial edge state transmission is robust.

FIGURE 5

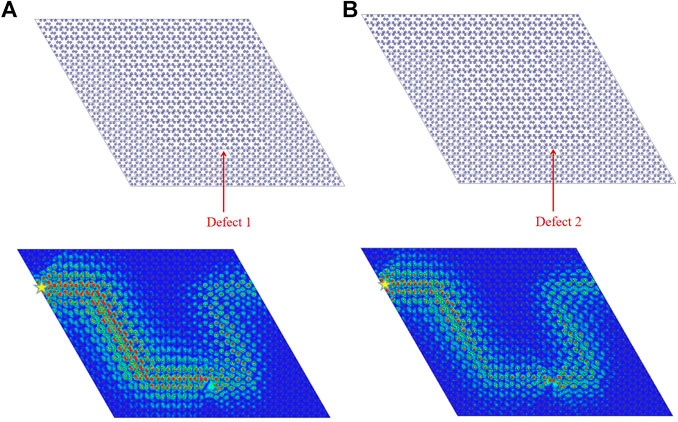
FIGURE 5. Two types of the defects and the corresponding electric field distributions at 5.7 GHz. (A) Defect 1, and (B) Defect 2.

Conclusion

To conclude, we present a design scheme for a topological material, consisting of six metal cylindrical resonators and a dielectric slab. The topological properties of the system are studied numerically. Different topologically band gaps are achieved by via changing the geometric parameter R. It is demonstrated that the multi-cell configuration composed of two types of lattices with distinct topologies can generate topologically protected edge states. Moreover, the topologically protected edge states can be used to design a sharp bend waveguide, and it exhibits great robustness with immunity to imperfections. It can be expected that this edge state of back-scattering suppression can have potential applications in optical transport and photonic integrated circuits.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

YL conceived the idea and supervised the project. LD and ML performed the numerical simulations. KS and XZ did the theoretical analysis. LD and YL co-wrote the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work is supported by the National Natural Science Foundation of China (Grant Nos. 11874301, and 61601375), the Natural Science Basic Research Plan in Shaanxi Province of China (Grant No. 2020JM-094), and the Fundamental Research Funds for the Central Universities (Grant No. 310201911cx030).

References

1. Qi, XL, and Zhang, SC. Topological insulators and superconductors. Rev. Mod. Phys (2011). 83:1057. doi:10.1103/revmodphys.83.1057

CrossRef Full Text | Google Scholar

2. Hasan, MZ, and Kane, CL. Colloquium: topological insulators. Rev. Mod. Phys (2010). 82:3045. doi:10.1103/revmodphys.82.3045

CrossRef Full Text | Google Scholar

3. Wang, Z, Chong, Y, Joannopoulos, JD, and Soljačić, M. Observation of unidirectional backscattering-immune topological electromagnetic states. Nature (2009). 461(7265):772–5. doi:10.1038/nature08293

CrossRef Full Text | Google Scholar

4. Khanikaev, AB, Mousavi, SH, Tse, WK, Kargarian, M, MacDonald, AH, and Shvets, G. Photonic topological insulators. Nature Mater (2013). 12:233–9. doi:10.1038/nmat3520

CrossRef Full Text | Google Scholar

5. Liang, GQ, and Chong, YD. Optical resonator analog of a two-dimensional topological insulator. Phys Rev Lett (2013). 110:203904. doi:10.1103/physrevlett.110.203904

CrossRef Full Text | Google Scholar

6. Hafezi, M, Mittal, S, Fan, J, Migdall, A, and Taylor, JM. Imaging topological edge states in silicon photonics. Nature Photon (2013). 7:1001–5. doi:10.1038/nphoton.2013.274

CrossRef Full Text | Google Scholar

7. He, C, Sun, XC, Liu, XP, Lu, MH, Chen, Y, Feng, L, et al. Photonic topological insulator with broken time-reversal symmetry. Proc Natl Acad Sci USA (2016). 113(18):4924–8. doi:10.1073/pnas.1525502113

CrossRef Full Text | Google Scholar

8. Chen, BGg, Upadhyaya, N, and Vitelli, V. Nonlinear conduction via solitons in a topological mechanical insulator. Proc Natl Acad Sci USA (2014). 111(36):13004–9. doi:10.1073/pnas.1405969111

CrossRef Full Text | Google Scholar

9. Paulose, J, Chen, BGg, and Vitelli, V. Topological modes bound to dislocations in mechanical metamaterials, Nature Phys (2015). 11:153–6. doi:10.1038/nphys3185CrossRef Full Text

Google Scholar

10. Meeussen, AS, Paulose, J, and Vitelli, J. Geared topological metamaterials with tunable mechanical stability. Phys Rev X (2016). 6:041029. doi:10.1103/physrevx.6.041029CrossRef Full Text

Google Scholar

11. Nash, LM, Kleckner, D, Read, A, Vitelli, V, Turner, AM, and Irvine, WTM. Topological mechanics of gyroscopic metamaterials. Proc Natl Acad Sci USA (2015). 112(47):14495–500. doi:10.1073/pnas.1507413112CrossRef Full Text

Google Scholar

12. Süsstrunk, R, and Huber, SD. Observation of phononic helical edge states in a mechanical topological insulator. Science (2015). 349(6243):47–50. doi:10.1126/science.aab0239CrossRef Full Text

Google Scholar

13. Vila, J, Pal, RK, and Ruzzene, M. Observation of topological valley modes in an elastic hexagonal lattice. Phys Rev B (2017). 96:134307. doi:10.1103/physrevb.96.134307CrossRef Full Text

Google Scholar

14. Xiao, M, Ma, G, Yang, Z, Sheng, P, Zhang, ZQ, and Chan, CT. Geometric phase and band inversion in periodic acoustic systems. Nature Phys (2015). 11:240–4. doi:10.1038/nphys3228CrossRef Full Text

Google Scholar

15. Khanikaev, AB, Fleury, R, Mousavi, SH, and Alu, A. Topologically robust sound propagation in an angular-momentum-biased graphene-like resonator lattice. Nat Commun (2015). 6:8260. doi:10.1038/ncomms9260CrossRef Full Text

Google Scholar

16. Mousavi, SH, Khanikaev, AB, and Wang, Z. Topologically protected elastic waves in phononic metamaterials. Nat Commun (2015). 6:8682. doi:10.1038/ncomms9682CrossRef Full Text

Google Scholar

17. Fleury, R, Khanikaev, AB, and Alu, A. Floquet topological insulators for sound. Nat Commun (2016). 7:11744. doi:10.1038/ncomms11744CrossRef Full Text

Google Scholar

18. He, C, Ni, X, Ge, H, Sun, XC, Chen, YB, Lu, MH, et al. Acoustic topological insulator and robust one-way sound transport. Nature Phys (2016). 12:1124–9. doi:10.1038/nphys3867CrossRef Full Text

Google Scholar

19. Peng, YG, Qin, CZ, Zhao, DG, Shen, YX, Xu, XY, Bao, M, et al. Experimental demonstration of anomalous floquet topological insulator for sound. Nat Commun (2016). 7:13368. doi:10.1038/ncomms13368CrossRef Full Text

Google Scholar

20. Liu, TW, and Semperlotti, F. Tunable acoustic valley-hall edge states in reconfigurable phononic elastic waveguides. Phys. Rev. Appl (2018). 9:014001. doi:10.1103/physrevapplied.9.014001CrossRef Full Text

Google Scholar

21. Geng, ZG, Peng, YG, Li, PQ, Shen, YX, Zhao, DG, and Zhu, XF. Mirror-symmetry induced topological valley transport along programmable boundaries in a hexagonal sonic crystal. J Phys Condens Matter (2019). 31(24):245403. doi:10.1088/1361-648x/ab0fcc

Google Scholar

22. Fang, C, and Fu, L. Rotation anomaly and topological crystalline insulators. arXiv:1709.01929 (2017).

Google Scholar

23. Song, ZD, Fang, Z, and Fang, C. (d-2)-dimensional edge states of rotation symmetry protected topological states. Phys Rev Lett (2017). 119:246402. doi:10.1103/physrevlett.119.246402CrossRef Full Text

Google Scholar

24. Schindler, F, Cook, AM, Vergniory, MG, Wang, Z, Parkin, SSP, Bernevig, BA, et al. Higher-order topological insulators. Sci Adv (2018). 4:eaat0346. doi:10.1126/sciadv.aat0346CrossRef Full Text

Google Scholar

25. Liu, YH, Guo, QH, Liu, HC, Liu, CC, Song, K, Yang, K, et al. Circular-polarization-selective transmission induced by spin-orbit coupling in a helical tape waveguide. Phys Rev Applied (2018). 9:054033. doi:10.1103/physrevapplied.9.054033CrossRef Full Text

CrossRef Full Text | Google Scholar

26. Yang, B, Guo, QH, Tremain, B, Barr, LE, Gao, WL, Liu, HC, et al. Direct observation of topological surface-state arcs in photonic metamaterials. Nat Commun (2017). 8:97. doi:10.1038/s41467-017-00134-1. CrossRef Full Text

Google Scholar

27. Ma, T, Khanikaev, AB, Mousavi, SH, and Shvets, G. Guiding electromagnetic waves around sharp corners: topologically protected photonic transport in metawaveguides. Phys Rev Lett(2015). 114:127401. doi:10.1103/physrevlett.114.127401CrossRef Full Text

Google Scholar

28. Kane, CL, and Mele, EJ. Quantum spin hall effect in graphene. Phys Rev Lett (2005). 95:226801. doi:10.1103/physrevlett.95.226801CrossRef Full Text

Google Scholar

29. Bernevig, BA, Hughes, TL, and Zhang, SC. Quantum spin hall effect and topological phase transition in HgTe quantum wells. Science (2006). 314(5806):1757–61. doi:10.1126/science.1133734CrossRef Full Text

Google Scholar

30. Wu, LH, and Hu, X. Scheme for achieving a topological photonic crystal by using dielectric material. Phys Rev Lett (2015). 114:223901. doi:10.1103/physrevlett.114.223901CrossRef Full Text

Google Scholar

31. Yang, L, Yu, K, Wu, Y, Zhao, R, and Liu, S. Topological spin-hall edge states of flexural wave in perforated metamaterial plates. J Phys D Appl Phys (2018). 51(32):325302. doi:10.1088/1361-6463/aace49

CrossRef Full Text | Google Scholar

32. Tzuhsuan, M, and Shvets, G. Scattering-free edge states between heterogeneous photonic topological insulators. Phys Rev B (2017). 95:165102. doi:10.1103/physrevb.95.165102

CrossRef Full Text | Google Scholar

33. Huo, SY, Chen, JJ, and Huang, HB. Topologically protected edge states for out-of-plane and in-plane bulk elastic waves. J Phys Condens Matter (2018). 30:145403. doi:10.1088/1361-648x/aab22a.

CrossRef Full Text | Google Scholar

34. Xu, L, Wang, HX, Xu, YD, Chen, HY, and Jiang, JH. Accidental degeneracy in photonic bands and topological phase transitions in two-dimensional core-shell dielectric photonic crystals. Opt Express (2016). 24:18059. doi:10.1364/oe.24.018059CrossRef Full Text

Google Scholar

35. Xie, BY, Su, GX, Wang, HF, Wang, HF, Su, H, Shen, XP, et al. Visualization of higher-order topological insulating phases in two-dimensional dielectric photonic crystals. Phys Rev Lett (2019). 122:233903. doi:10.1103/physrevlett.122.233903CrossRef Full Text

Google Scholar

36. Lu, L, Joannopoulos, JD, and Soljačić, M. Topological photonics. Nat Photon (2014). 8:821–29. doi:10.1038/nphoton.2014.248CrossRef Full Text

Google Scholar

37. Sun, XC, He, C, Liu, XP, Lu, MH, Zhu, SN, and Chen, YF. Two-dimensional topological photonic systems. Prog Quantum Electron (2017). 55:52–73. doi:10.1016/j.pquantelec.2017.07.004CrossRef Full Text

Google Scholar

38. Wu, Y, Li, C, Hu, XY, Ao, YT, Zhao, YF, and Gong, QH. Applications of topological photonics in integrated photonic devices. Adv Opt Mater (2017). 5(8):1700357. doi:10.1002/adom.201700357CrossRef Full Text

Google Scholar

39. Khanikaev, AB, and Shvets, G. Two-dimensional topological photonics. Nature Photon (2017). 11:763–73. doi:10.1038/s41566-017-0048-5CrossRef Full Text

Google Scholar

40. Ozawa, T, Price, HM, Amo, A, Goldman, N, Hafezi, M, Lu, L, et al. Topological photonics. Rev Mod Phys (2019). 91:015006. doi:10.1103/RevModPhys.91.015006

CrossRef Full Text | Google Scholar

41. Haldane, FDM, and Raghu, S. Possible realization of directional optical waveguides in photonic crystals with broken time-reversal symmetry. Phys Rev Lett (2008). 100:013904. doi:10.1103/physrevlett.100.013904CrossRef Full Text

Google Scholar

42. Zhang, Z, Tian, Y, Wang, Y, Gao, S, Cheng, Y, Liu, X, et al. Directional acoustic antennas based on valley-hall topological insulators. Adv Mater (2018). 30(36):1803229. doi:10.1002/adma.201803229CrossRef Full Text

Google Scholar

43. Wei, F, Liu, CW, Li, D, Wang, CY, Zhang, HR, Sun, JR, et al. Broken mirror symmetry tuned topological transport in PbTe/SnTe heterostructures. Phys Rev B (2018). 98:161301. doi:10.1103/physrevb.98.161301CrossRef Full Text

Google Scholar

44. Chaunsali, R, Chen, CW, and Yang, J. Subwavelength and directional control of flexural waves in zone-folding induced topological plates. Phys Rev B (2018). 97:054307. doi:10.1103/physrevb.97.054307CrossRef Full Text

Google Scholar

45. Fukui, T, Hatsugai, Y, and Suzuki, H. Chern numbers in discretized brillouin zone: Efficient method of computing (spin) hall conductances. J Phys Soc Jpn (2005). 74(6):1674–77. doi:10.1143/jpsj.74.1674CrossRef Full Text

Google Scholar