Frontiers in Physics

1 Introduction

Within the framework of a fully nonlinear two-dimensional potential solver [4], computed the temporal evolution of a Stokes wavetrain with a small modulation. They found that the energy becomes focused, at the maximum of modulation, into a short wave packet of large amplitude they called a steep wave event (SWE). They showed that the Peregrine breather, which is an exact solution of the self-focusing nonlinear Schrödinger equation, was the most convenient approximation of the envelope of the SWE. Note that the Peregrine breather can be derived from the Kuznetsov-Ma breather and the Akhmediev breather in the limit of infinite temporal and spatial period (see [7]) [3]. suggested that the Peregrine breather may provide a useful and simple model for rogue wave events [1]. presented the first experimental observation of the Peregrine breather in a water wave tank. More recently [2], presented the first ever observation in a wave tank of dark solitons on the surface of water, so demonstrating the probable existence at the sea surface of dark solitons in finite depth for $kh<1.363$ where k is the carrier wavenumber and h the water depth. They found a good agreement between the experimental soliton and the dark soliton solution of the defocusing nonlinear Schrödinger equation. Dark solitons occur as envelope holes. Rogue waves are large-amplitude waves which occurs at the sea surface suddenly without warning. Such waves are accompanied by deep holes before and/or after the largest crest. Another possible mechanism of these holes in the ocean could be dark or gray soliton generation. There is an abundant literature on the interaction between surface water waves and spatially uniform currents. In the real ocean, currents are never uniform. Spatially varying currents may affect strongly the water wave behavior. Herein, we paid attention to the evolution of a Peregrine breather propagating at the surface of a vertically sheared current. In this Brief Research Report we propose, based on the NLS equation in infinite depth, a physical mechanism of gray soliton generation from a Peregrine breather evolving on slowly varying underlying water vorticity. Section 2 is devoted to the presentation of the vor-NLS equation in the presence of constant vorticity derived by [8]. The vor-NLS equation is self-focusing or defocusing according to the magnitude of the vorticity. Vorticity effect on the soliton solutions of the vor-NLS of self-focusing and defocusing types is displayed. A numerical simulation of the transformation of the Peregrine breather propagating at the free surface of a water flow of slowly varying vorticity is presented in section 3. A conclusion is given in section 4.

2 The VOR-NLS

We choose an Eulerian frame $\left(Oxyz\right)$ with unit vectors $\left(e_x,e_y,e_z\right)$. The vector $e_z$ is oriented upwards so that the acceleration due to gravity is $g=-g{e}_z$ with $g>0$. The equation of the undisturbed free surface is $z=0$. The water waves are traveling at the surface of an underlying vertically sheared current of constant vorticity given by $U\left(z\right)=\Omega z$. The study is restricted to modulated wave trains propagating with positive phase velocities so long as both negative and positive values of $\Omega$ are considered. [8], have shown that the spatio-temporal evolution of the complex envelope $a\left(\xi ,\tau \right)$ of the surface elevation of a two-dimensional weakly nonlinear modulated wave train propagating in the presence of constant water vorticity is governed by the nonlinear Schrödinger equation (NLS equation)

$i{a}_{\tau }+\alpha a_{\xi \xi }+\gamma {\left|a\right|}^{2}a=0(1)$

In the case of a wave train propagating at the surface of a deep water flow of constant vorticity $\zeta =-\Omega$, the dispersive and nonlinear coefficients of the vor-NLS Eq.1 are

$\alpha =-\frac{\omega {\left(1+\overline{\Omega }\right)}^2}{k^2{\left(2+\overline{\Omega }\right)}^3},\gamma =-\frac{\omega k^2}{8}\frac{\left(\overline{\Omega }+2/3\right)\left(3{\overline{\Omega }}^2+6\overline{\Omega }+6\right)}{1+\overline{\Omega }},$

with $\overline{\Omega }=\Omega /\omega$. We consider a carrier wave traveling from left to right in deep water whose intrinsic frequency, intrinsic phase velocity and intrinsic group velocity are

$\begin{array}{l}\omega =-\frac{\Omega }{2}+\sqrt{\frac{{\Omega }^2}{4}+gk},\\ c_p=-\frac{\Omega }{2k}+\sqrt{\frac{{\Omega }^2}{4k^2}+\frac{g}{k}},\\ c_g=\frac{\Omega +\sqrt{{\Omega }^2+4gk}}{2\sqrt{{\Omega }^2+4gk}}{c}_p,\end{array}$

with k the carrier wavenumber and g the gravitational acceleration.

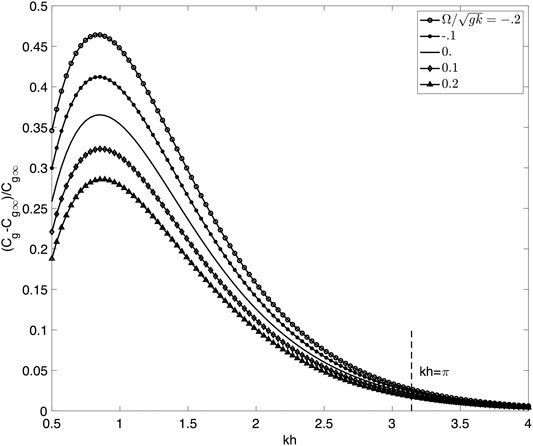
[5] have compared both the linear intrinsic phase velocities and total energies of gravity waves in the presence of constant vorticity in finite depth and deep water and came to the conclusion that linear gravity waves in finite depth propagating at the surface of a water flow of constant vorticity behave like waves in infinite depth if $kh>\pi$. We can conclude that the unbounded water flow at $z=-\infty$ does not influence the kinematics and dynamics of the surface waves. In addition to the results of [5], Figure 1 shows the dimensionless intrinsic group velocity deviation between finite and infinite depths for different values of the vorticity. As we can see the difference between the group velocities in finite and infinite depth becomes very weak as $kh$ increases beyond the value π. Equation 1 is focusing for $\overline{\Omega }>-2/3$ and defocusing for $\overline{\Omega }<-2/3$. Note that $\overline{\Omega }>-1$, $\forall \Omega$.

FIGURE 1

FIGURE 1. Dimensionless group velocity deviation between finite and infinite depths as a function of the dispersive parameter for several values of the dimensionless vorticity. In dimensionless terms, the units of acceleration and length are the acceleration of gravity g and $2\pi$ ($g=1$ and $k=1$).

2.1 Effect of Vorticity on the Peregrine Breather and Gray Soliton

The focusing vor-NLS equation admits the Peregrine breather as solution

$a_P\left(\xi ,\tau \right)=a_{0}k\sqrt{-\frac{\omega }{2\gamma }}\left(1-\frac{4\left(1-i{a}_0^2{k}^2\omega \tau \right)}{1-\omega a_0^2{k}^2{\xi }^2/\alpha +a_0^4{k}^4{\omega }^2{\tau }^2}\right)\exp \left(-i{a}_0^2{k}^2\omega \tau /2\right).(2)$

Note that $\alpha <0$ and $\gamma <0$, $\forall \overline{\Omega }>-2/3$. The defocusing vor-NLS equation admits the dark, $a_D$, and the gray, $a_G$, solitons as solutions.

$a_D=a_0\tanh \left(\sqrt{-\frac{\gamma }{2\alpha }}{a}_0\xi \right)\exp \left(i\gamma a_0^2\tau \right)(3)$

$a_G=a_0\frac{\exp \left(2im\right)+\exp \left(2a_0\sin \left(m\right)\left(\sqrt{-\frac{\gamma }{2\alpha }}\xi +a_0\gamma \tau \cos \left(m\right)\right)\right)}{1+\exp \left(2a_0\sin \left(m\right)\left(\sqrt{-\frac{\gamma }{2\alpha }}\xi +a_0\gamma \tau \cos \left(m\right)\right)\right)}{e}^{i{a}_0^2\gamma \tau }(4)$

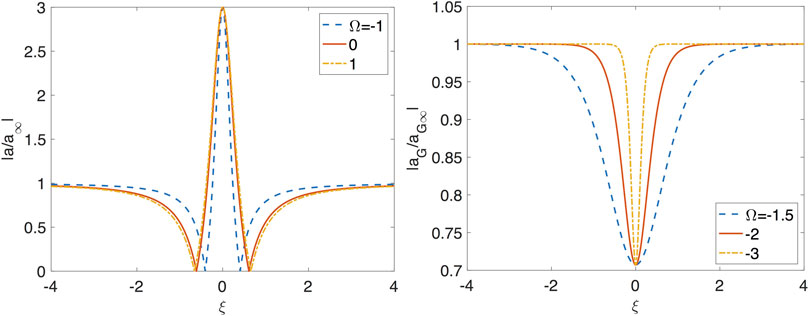
where $a_0$ is the envelope amplitude of the background carrier wave. The parameter m fixes the minimum of amplitude at the center of the soliton. For $m=\pi /2$ this minimum is zero, with a phase shift, that corresponds to the dark soliton. Note that $\alpha <0$ and $\gamma >0$, $\forall -1<\overline{\Omega }<-2/3$ ($\overline{\Omega }>-1$ whatever the value of $\Omega$). Equation 3 can be derived from Eq. 4 when $m=\pi /2$. In Figure 2 are plotted several dimensionless profiles of the Peregrine breather and the gray soliton for different values of the vorticity $\zeta =-\Omega$. The vorticity does not modify the amplification factor $\left|a_P\right|/\left|a_{P\infty }\right|$. The envelope amplitude of the background carrier wave is $\left|a_{P\infty }\right|=a_{0}k\sqrt{-\omega /\left(2\gamma \right)}$ whereas the maximum amplitude of the envelope is $3a_{0}k\sqrt{-\omega /\left(2\gamma \right)}$. Consequently, the normalized maximum of the modulation envelope does not depend on the vorticity. The Peregrine breather is narrower (wider) for positive (negative) vorticity. The width of the breather decreases as the vorticity increases. The minimal amplitude at the center of the gray soliton is not modified by the presence of the vortical flow. The gray solitons becomes narrower as the positive vorticity increases.

FIGURE 2

FIGURE 2. Dimensionless profiles of the Peregrine breather (left) and the gray soliton (right) for several values of the vorticity with $g=1$ and $k=1$.

3 Evolution of the Peregrine Breather on Slowly Varying Vortical Flow

Within the framework of Eq. 1, we have performed a numerical simulation of the transformation of a Peregrine breather traveling at the free surface of a vortical water flow whose vorticity varies very slowly. $\overline{\Omega }$ varies from zero to a value less than $-2/3$. For $\overline{\Omega }=0$Eq. 1 is focusing whereas for $\overline{\Omega }<-2/3$ this equation is defocusing. Consequently, the slow variation of the vorticity transforms the focusing vor-NLS equation into defocusing. We consider a Peregrine breather that meets progressively a vortical water flow whose temporal variation is

$\begin{array}{l}\Omega \left(\tau \right)=\sin \left(\sigma \tau +\pi /2\right)-1,0\le \sigma \tau \le \pi \\ \Omega \left(\tau \right)=-2,\sigma \tau >\pi .\end{array}$

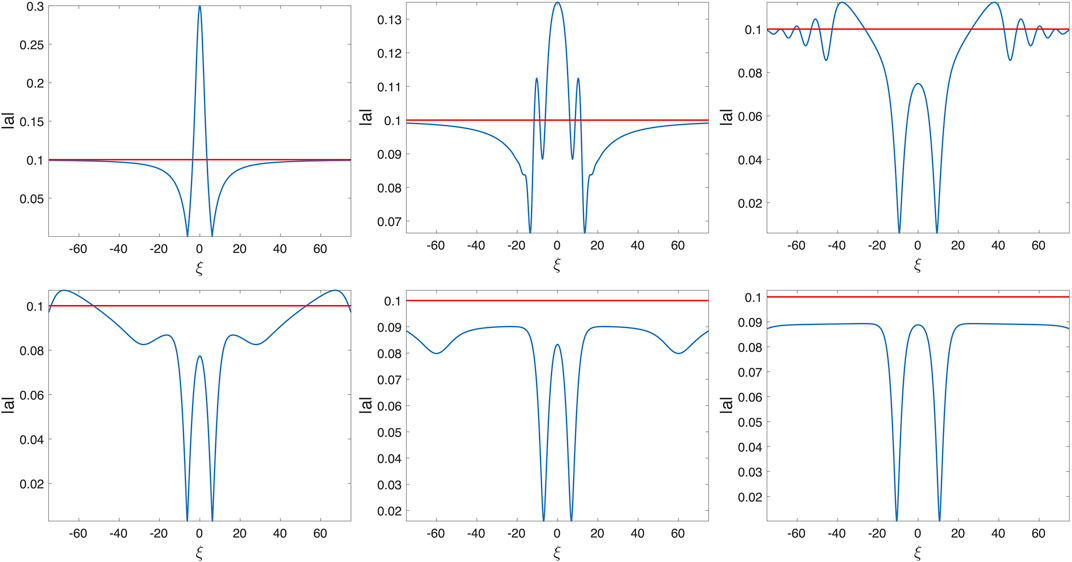
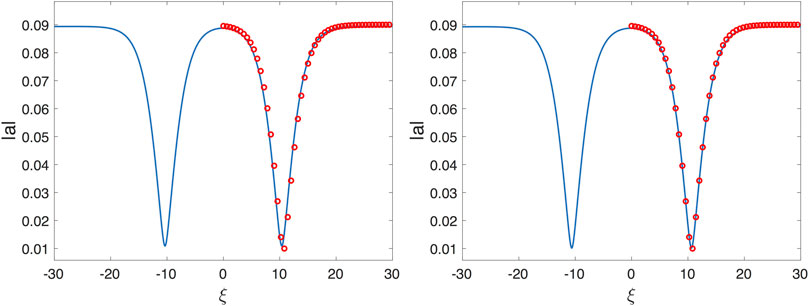
The parameter σ is chosen such that the average temporal variation of the vorticity along the ramp is of $\mathrm{}\left(a_0^2{k}^2\right)$. The vorticity remains constant when $\sigma \tau >\pi$. Note that $\overline{\Omega }\left(0\right)=0$ and $\overline{\Omega }(\sigma \tau =\pi )\approx -0.828$. The vor-NLS equation is solved numerically using a pseudo-spectral Fourier method. The periodicity length of the spatial domain is $L=160\pi$. The number of grid points is $N=6000$. Dealiasing is used. Time integration is carried out with a second order time-splitting method and a fourth order Runge Kutta scheme as well. The numerical code is checked using comparisons with the exact breather solutions and by the self consistency of the results of the two time integration schemes also. We have used a spatial filter similar to that of [6] to avoid numerical instabilities. The filter does not modify the envelope evolution because it cancels the highest modes that do not participate in the global dynamic of the envelope. The transfer function of the filter is $\exp \left(-\nu {\kappa }^2\right)$, where κ is a wavenumber in the Fourier space and $\nu ={10}^{-5}$ is used. With this value of ν the loss of the energy of the carrier wave is of the order of 1% over approximately 1,000 periods of time evolution of the carrier. The numerical simulation has been run in dimensionless units with $k=1$ and $g=1$. The initial condition at $\tau =0$ is the Peregrine breather with $a_0=0.10$ and $\Omega =0$. Figure 3 shows the evolution of the envelope at several times. The vorticity $\zeta =-\Omega$ varies slowly along the ramp from $\zeta (\tau =0)=0$ to $\zeta (\tau \approx 10T)=2$. At $\tau \approx 6T$ the vor-NLS equation becomes defocusing. T is the period of the background of the Peregrine breather. During its propagation along the ramp the width of the breather increases whereas its amplitude decreases. At $\tau \approx 20T$, on both sides of the crest of the envelope two small local troughs occur that then deepen during the propagation of the envelope to give rise to the formation of two gray solitons whose profiles are close to that of a dark soliton. Figure 4 shows the profiles of the two gray solitons at two different times. An excellent agreement is obtained between the numerical and analytical profiles.

FIGURE 3

FIGURE 3. Time evolution of the tranformation of the Peregrine breather into a two-grey soliton with $g=1$ and $k=1$. Top panels from left to right: $\tau =0,23T,145T$. Bottom panels from left to right: $\tau =298T,596T,901T$. T is the period of the Peregrine breather background.

FIGURE 4

FIGURE 4. Gray soliton profiles at $t=867T$(left) and $t=900T$(right). The solid lines correspond to the numerical simulation whereas the circles correspond the analytical solution of Eq. 4 for $a_0=0.09$ and $m=\pi /2-1/10$.

4 Conclusion

Within the framework of the vor-NLS equation in infinite depth we have shown numerically that a Peregrine breather propagating at the free surface of a slowly varying vortical flow may generate gray solitons. The present simulation confirms in a different context the result of [2] on the existence of dark solitons on the surface of shallow water ($kh<1.363$) in the absence of vorticity. Our approach presents two limitations. The vor-NLS equation which was derived for constant vorticity has been used with a slowly varying vorticity to transform the focusing NLS equation into defocusing during a limited time. Nevertheless, the very slow variation of the vorticity on a small number of periods lead us to believe that our results are physically relevant. The time to obtain the formation of the gray solitons is beyond the time range of validity of the NLS equation. However, it is well known that approximate models can be valid beyond their validity domain [4]. found, from their numerical simulations of the NLS equation over several thousands of periods, that their computations were in qualitative good agreement over a much longer time scale than expected, namely when the wave steepness of the carrier wave is not too steep. Despite these limitations we conjecture the existence of gray solitons on deep water in the presence of varying water shear flows. Our numerical simulation provides only preliminary results on this transition which has to be confirmed by using models free of these two limitations.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

HH, Conceptualization of the project, Methodology, and formal analysis checking. MA, Formal analysis checking; Software design; Numerical simulations; Validation; Investigation; Visualization. YC, Conceptualization of the project and formal analysis checking. CK, Conceptualization; Methodology; Formal analysis; Investigation; Writing.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Chabchoub A, Hoffmann N, Akhmediev N. Rogue wave observation in a water wave tank. Phys Rev Lett (2011) 106:204502. doi:10.1103/PhysRevLett.106.204502

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Chabchoub A, Kimmoun O, Branger H, Hoffmann N, Proment D, Onorato M, et al. Experimental observation of dark solitons on the surface of water. Phys Rev Lett (2013) 110:124101. doi:10.1103/PhysRevLett.110.124101

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Dysthe KB, Trulsen K. Note on breather type solutions of the NLS as models for freak-waves. Physica Scripta (1999) T82:48–52. doi:10.1238/physica.topical.082a00048

CrossRef Full Text | Google Scholar

4. Henderson KL, Peregrine DH, Dold JW. Unsteady water wave modulations: fully nonlinear solutions and comparison with the nonlinear schrödinger equation. Wave Motion (1999) 29:341–61. doi:10.1016/s0165-2125(98)00045-6

CrossRef Full Text | Google Scholar

5. Kharif C, Abid M. Miles theory revisited with constant vorticity in water of infinite depth. Jmse (2020) 8(8):623. doi:10.3390/jmse8080623

CrossRef Full Text | Google Scholar

6. Lo E, Mei CC. A numerical study of water-wave modulation based on a higher-order nonlinear schrödinger equation. J Fluid Mech (1985) 150:395–416. doi:10.1017/s0022112085000180

CrossRef Full Text | Google Scholar

7. Peregrine DH. Water waves, nonlinear schrödinger equations and their solutions. J Aust Math Soc Ser B, Appl. Math (1983) 25:16–43. doi:10.1017/s0334270000003891

CrossRef Full Text | Google Scholar

8. Thomas R, Kharif C, Manna M. A nonlinear schrödinger equation for water waves on finite depth with constant vorticity. Phys Fluids (2012) 24:127102. doi:10.1063/1.4768530

CrossRef Full Text | Google Scholar