New and More Solitary Wave Solutions for the Klein-Gordon-Schrödinger Model Arising in Nucleon-Meson Interaction

This paper considers methods to extract exact, explicit, and new single soliton solutions related to the nonlinear Klein-Gordon-Schrödinger model that is utilized in the study of neutral scalar mesons associated with conserved scalar nucleons coupled through the Yukawa interaction. Three state of the art integration schemes, namely, the e^−Φ(ξ)-expansion method, Kudryashov's method, and the tanh-coth expansion method are employed to extract bright soliton, dark soliton, periodic soliton, combo soliton, kink soliton, and singular soliton solutions. All the constructed solutions satisfy their existence criteria. It is shown that these methods are concise, straightforward, promising, and reliable mathematical tools to untangle the physical features of mathematical physics equations.

1. Introduction

Many of the problems arising in mathematically-oriented scientific fields such as physics and engineering are described by partial differential equations (PDEs). PDEs are used to depict an ample variety of phenomena such as dislocations in crystals, superconductivity, laser pulses in two-phase [1, 2], waves in ferromagnetic materials, and many more [3–6]. Many theories such as electromagnetism, diffusion, fluid flow, etc. are presented to understand the dynamics of PDEs [7, 8]. Therefore, exploring exact solutions for PDEs plays an important role in such fields. These solutions might be essential and important for exploring some physical phenomena. The majority of PDEs are not exactly solvable with existing mathematical techniques. Especially for higher order nonlinear PDEs, existing methods are not able to find exact solutions. However, due to the invention of algebraic system solvers such as Mathematica and Maple, many integrating schemes have been proposed, such as the e^−Φ(ξ)-expansion method, Hirota's bilinear method, the homogeneous balance reduction of the PDE to a quadrature problem, the truncated Painlevé expansion, etc. [9–13].

Solitons are formed because of an interplay between nonlinear and dispersive effects. The importance of such waves lies in their roles in telecommunication systems as well as other physical sciences such as nonlinear optics, acoustics, convictive fluids, condensed matter, and solid-state and plasma physics [14–19].

The main successes of quantum mechanics in the quantitative description of non-relativistic systems are connected with the Schrödinger equation. Schrödinger used the Klein-Gordon equation (KGE) to model a system of motion of massive spinless particles in a quantum field hypothesis [20, 21]. The quantum wave model is thought of as the non-relativistic limitation of the KGE. The KGE is a second order differential equation in both spatial and temporal coordinates, reduced to two coupled first order differential equations. To obtain explicit exact solutions, various techniques have been implemented such as the Jacobi elliptic expansion method, the mapping method, and the F-expansion method but these methods produce very complex solution expressions [22–24].

The nonlinear Klein-Gordon-Schrödinger (KGS) framework depicts the association of neutral scalar mesons connecting with scalar nucleons. This model depicts complex processes and has attracted the consideration of researchers from different fields. Many authors examined the behavior of solutions by employing numerical and analytical techniques. Solitary wave solutions are studied in [20], the behavior of the equations is evaluated by a modified decomposition method in [25], Biswas and Triki [26] scrutinize the KGS model alongside power law nonlinearity to attain the solution in the form of solitons, the Chebyshev pseudo spectral multidomain strategy was taken into consideration for the mathematical solution of the given system in [27], Yumak et al. analyzed the exact periodic and solitary wave polynomial solutions of nonlinear KGS equations in [28], a high-order compact finite difference technique is examined for a governing model in [29]. In addition, various techniques are applied in [30, 31].

The aim of this paper is to establish some novel and widely applicable traveling wave solutions of the non-linear KGS equation through effective methods such as the tanh-coth expansion method, e^−Φ(ξ)-expansion method, and Kudryashov's method. This model depicts the scalar nucleons associating with neutral scalar mesons linked by the Yukawa potential in quantum field theory [32, 33]. These methods are used to obtain a new explicit solution of the KGS system which can be useful to study the physical nature of many nonlinear phenomena in a number of fields such as modern physics, fluid dynamics, quantum mechanics, and plasma physics.

This paper is arranged as follows: In section 2, we proposed the model. In section 3, solutions of the KGS system are formulated through integration schemes and graphical interpretation. Section 4 contains the results and discussion. In section 5, concluding points are expressed.

2. Proposed Model

The proposed model [20] has the form

$\begin{array}{ll}i{W}_t+W_{xx}+NW=0,& (1)\end{array}$

$\begin{array}{ll}{N}_{tt}-c^2{N}_{xx}+N+|W{|}^2=0.& (2)\end{array}$

This coupled system describes the interplay of a meson field with a nucleon field and is significant in modern physics. Here N = N(x, t) is a meson field, W = W(x, t) is a complex scalar nucleon field, and c is a real constant.

3. Soliton Solutions of (1+1)-Dimensional KGS Equations

In this section, three state of the art integration schemes, Raza et al. [34], Asokan and Vinodh [35], and Ullah et al. [36] are employed to extract bright soliton, dark soliton, dipole and combo soliton, kink soliton, and singular soliton solutions.

The following wave transformation

$\begin{array}{ll}W(x,t)=w(\xi )e^{i(-kx+\omega t)},N(x,t)=n(\xi ),& (3)\end{array}$

is applied, where ξ = x − αt, to obtain traveling wave solutions for the proposed model given by Equations (1) and (2). In the above transformation the wave number is ω, k is the frequency, and α is the velocity of the soliton.

Plugging Equation (3) into Equations (1) and (2), then equating the real parts gives

$\begin{array}{ll}{(w(\xi ))}^{″}+w(\xi )n(\xi )-(k^2+\omega )w(\xi )=0,& (4)\end{array}$

$\begin{array}{ll}({\alpha }^2-c^2){(n(\xi ))}^{″}+n(\xi )+{(w(\xi ))}^2=0.& (5)\end{array}$

The imaginary part of Equation (1) gives the velocity of soliton, i.e., α = −2k.

Solving Equation (4) for n(ξ), we get

$\begin{array}{ll}n(\xi )=\frac{(k^2+\omega )w(\xi )-{(w(\xi ))}^{″}}{w(\xi )}.& (6)\end{array}$

After plugging the value of n(ξ) in Equation (5), we obtain the following ODE as

$\begin{array}{ll}({\alpha }^2-c^2){\left(\frac{(k^2+\omega )w-w^{″}}{w}\right)}^{″}+\left(\frac{(k^2+\omega )w-w^{″}}{w}\right)+w^2=0.& (7)\end{array}$

In accordance with the e^−Φ(ξ)-expansion scheme [34], the solution of Equation (7) has the form

$\begin{array}{ll}w(\xi )={\displaystyle \sum _{i=0}^N}{a}_i{(e^{-\Phi (\xi )})}^i.& (8)\end{array}$

The homogenous balance method gives N = 1. For N = 1, Equation (8) becomes

$\begin{array}{ll}w(\xi )=a_0+a_1{e}^{-\Phi (\xi )},& (9)\end{array}$

here Φ(ξ) is the solution of the following ODE

$\begin{array}{ll}{\Phi }^{\prime }(\xi )=e^{-\Phi (\xi )}+m{e}^{-\Phi (\xi )}+l.& (10)\end{array}$

By substituting Equation (9) into Equation (7) a system of equations for a₀ and a₁ is retrieved by comparing the coefficients of e^−Φ(ξ) equal to zero. By finding unknowns a₀ and a₁ from the obtained system and inserting them into Equation (9), solutions of the coupled KGS Equations (1) and (2) are obtained.

The obtained results are summarized in the following sets.

SET 1

$\begin{array}{l}{a}_0=-\frac{l}{\sqrt{2}},a_1=-\sqrt{2},\\ \omega =-k^2-\frac{l^2}{2}+2m,c=-\alpha .\end{array}$

SET 2

$\begin{array}{l}{a}_0=0,a_1=\pm \sqrt{2},l=0,\\ \omega =-k^2+2m,c=-\alpha .\end{array}$

Soliton solutions for Set 1 are calculated.

When s > 0 and m ≠ 0, then

$\begin{array}{l}W(x,t)=-e^{i(-kx+\omega t)}[\frac{l}{\sqrt{2}}\\ +\frac{2\sqrt{2}m}{-l-\sqrt{s}tanh\left[\frac{1}{2}\sqrt{s}(C+\xi )\right]}]& (11)\end{array}$

and

$\begin{array}{l}N(x,t)=\\ -\left[\frac{s\left(-2m+(s+2m)cosh[\sqrt{s}(C+\xi )]+l\sqrt{s}sinh[\sqrt{s}(C+\xi )]\right)}{2{\left(lcosh[\frac{1}{2}\sqrt{s}(C+\xi )]+\sqrt{s}sinh[\frac{1}{2}\sqrt{s}(C+\xi )]\right)}^2}\right]& (12)\end{array}$

The Figure 1, depicts the graphical representation of the absolute values of the obtained soliton solutions given in Equation (11) and Equation (12). In Figure 1A represents the kink soliton and Figure 1B represents the bright soliton.

FIGURE 1

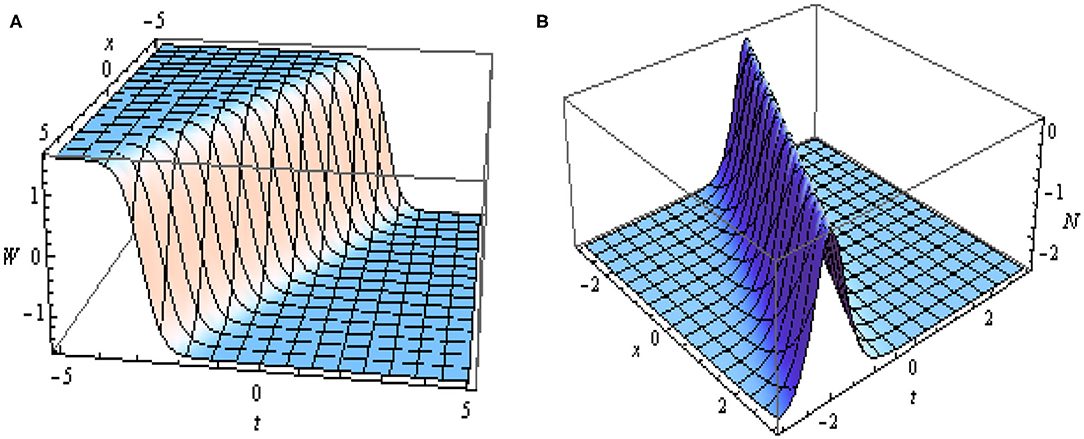
Figure 1. 3D plots of |W(x, t)| and |N(x, t)| given in Equations (11) and (12) with suitable choose of values of parameters as l = 3, s = 1, m = 2, k = 1, ξ = x + 2t and C = 0.

When s < 0 and m ≠ 0, then

$\begin{array}{l}W(x,t)=\pm e^{i(-kx+\omega t)}[\frac{l}{\sqrt{2}}\\ +\frac{2\sqrt{2}m}{-l-\sqrt{-s}tan[\frac{1}{2}\sqrt{-s}(C+\xi )]}]& (13)\end{array}$

and

$\begin{array}{l}N(x,t)=-\frac{s}{2}\\ +\frac{2sm}{{\left(lcos[\frac{1}{2}\sqrt{-s}(C+\xi )]-\sqrt{-s}sin[\frac{1}{2}\sqrt{-s}(C+\xi )]\right)}^2}& (14)\end{array}$

The Figure 2, depicts the graphical representation of the absolute values of the obtained soliton solutions given in Equation (13) and Equation (14). In Figure 2A represents the periodic soliton and Figure 2B represents the singular soliton.

FIGURE 2

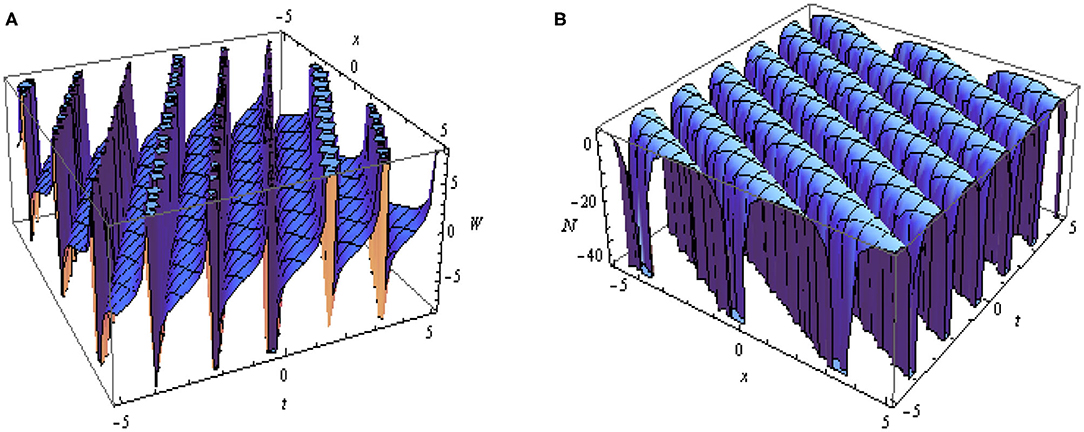
Figure 2. 3D plots of |W(x, t)| and |N(x, t)| given in Equations (13) and (14) with values of parameters as l = 1, s = −3, m = 1, k = 1, ξ = x + 2t and C = 0.

When s > 0 and m = 0 and l ≠ 0 then

$\begin{array}{ll}W(x,t)=-e^{i(-kx+\omega t)}\frac{lcoth[\frac{1}{2}l(C+\xi )]}{\sqrt{2}}& (15)\end{array}$

and

$\begin{array}{ll}N(x,t)=2m-\frac{1}{2}{l}^2{coth}^2[\frac{1}{2}l(C+\xi )]& (16)\end{array}$

When s = 0 and m ≠ 0 and l ≠ 0, then

$\begin{array}{ll}W(x,t)=\pm e^{i(-kx+\omega t)}\frac{l}{\sqrt{2}(-1+l(C+\xi ))}& (17)\end{array}$

and

$\begin{array}{ll}N(x,t)=2m+l^2\left(-\frac{1}{2}-\frac{2}{{(-1+l(C+\xi ))}^2}\right)& (18)\end{array}$

When s = 0 and m = 0 and l = 0, then

$\begin{array}{ll}W(x,t)=\pm e^{i(-kx+\omega t)}\frac{\sqrt{2}}{C+\xi }& (19)\end{array}$

and

$\begin{array}{ll}N(x,t)=-\frac{{\lambda }^2}{2}+2\mu -\frac{2}{{(C+\xi )}^2},& (20)\end{array}$

where C is the constant of integration and s = l² − 4m.

Soliton solutions for Set 2 are calculated.

When s > 0 and m ≠ 0, then

$\begin{array}{ll}W(x,t)=\mp e^{i(-kx+\omega t)}\frac{\sqrt{2}mcoth[\sqrt{-m}(C+\xi )]}{\sqrt{-m}},& (21)\end{array}$

provided that m < 0.

$\begin{array}{ll}N(x,t)=2m({\text{coth}}^2[\sqrt{-m}(C+\xi )]),& (22)\end{array}$

provided that m < 0.

When s < 0 and m ≠ 0, then

$\begin{array}{ll}W(x,t)=\pm e^{i(-kx+\omega t)}\sqrt{2m}\text{\hspace{0.17em}cot}[\sqrt{m}(C+\xi ),& (23)\end{array}$

provided that m > 0.

$\begin{array}{ll}N(x,t)=-2m({\text{cot}}^2[\sqrt{m}(C+\xi )]),& (24)\end{array}$

provided that m > 0, where C is the constant of integration and s = l² − 4m.

According to the the tanh-coth method [35], the estimated solution of Equation (7) has the form

$\begin{array}{ll}w(\xi )={\displaystyle \sum _{i=0}^N}{a}_i{tanh}^i(m\xi )+{\displaystyle \sum _{i=1}^N}{b}_i{tanh}^{-i}(m\xi ).& (25)\end{array}$

The homogenous balance method, gives N = 1. For N = 1, the above equation takes the form

$\begin{array}{ll}w(\xi )=a_0+a_1\text{ tanh}(m\xi )+b_1\text{ coth}(m\xi ).& (26)\end{array}$

Substituting Equation (26) into Equation (7), a system of nonlinear equations for a₀, a₁, and b₁ is obtained by the comparison of the coefficients of tanh(mξ) to zero. Upon solving the obtained system for a₀, a₁, and b₁ and plugging them in Equation (26), the solutions of the coupled KGS Equations (1) and (2) are obtained.

The obtained results are summarized in the following sets.

SET 1

$\begin{array}{l}{a}_0=0=a_1,b_1=\pm \sqrt{2}m,\\ \omega =-k^2-2m^2,\alpha =-c& (27)\end{array}$

SET 2

$\begin{array}{l}{a}_0=0,a_1=\pm \sqrt{2}m,b_1=\pm \sqrt{2}m,\\ \omega =-k^2-8m^2,\alpha =-c& (28)\end{array}$

SET 3

$\begin{array}{l}{a}_0=0=b_1,a_1=\pm \sqrt{2}m,\\ \omega =-k^2-2m^2,\alpha =-c& (29)\end{array}$

Singular soliton solutions relative to SET 1 are obtained as

$\begin{array}{ll}W(x,t)=\pm e^{i(-kx+\omega t)}\sqrt{2}m\text{ coth}\left[m\xi \right],& (30)\end{array}$

and

$\begin{array}{ll}N(x,t)=-2m^2{\text{ coth}}^2\left[m\xi \right]& (31)\end{array}$

A dark-singular combo soliton solution relative to SET 2 is attained as

$\begin{array}{ll}W(x,t)=\pm e^{i(-kx+\omega t)}\sqrt{2}m\left(\text{coth}[m\xi ]+\text{tanh}[m\xi ]\right),& (32)\end{array}$

and a singular soliton is calculated as

$\begin{array}{ll}N(x,t)=-8m^2{\text{ coth}}^2\left[2m\xi \right]& (33)\end{array}$

The Figure 3, depicts the graphical representation of the absolute values of the obtained soliton solutions given in Equation (32) and Equation (33). In Figure 3A represents the dark-singular combo soliton and Figure 3B represents the singular soliton.

FIGURE 3

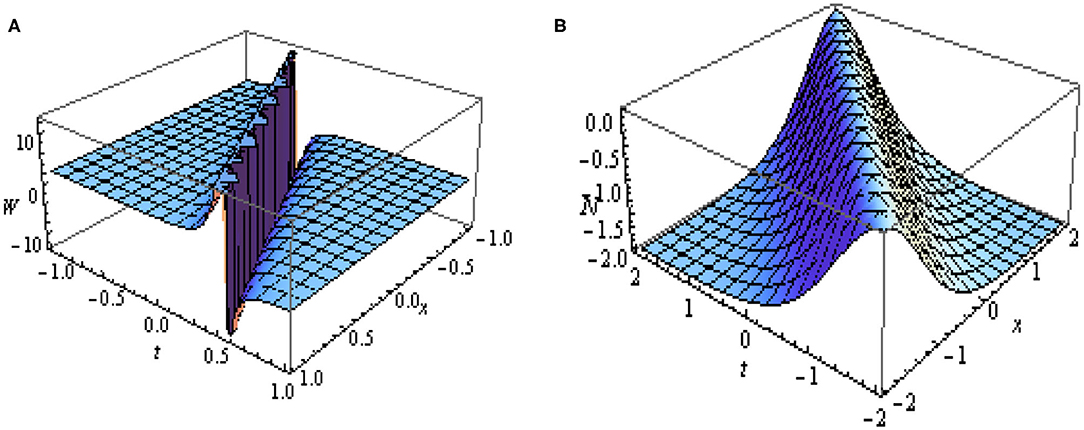
Figure 3. 3D plots of |W(x, t)| and |N(x, t)| given in Equations (32) and (33) with values of parameters as m = 1, k = 1 and ξ = x + 2t.

A dark soliton solution relative to SET 3 is attained as

$\begin{array}{ll}W(x,t)=\pm e^{i(-kx+\omega t)}\sqrt{2}m\text{ tanh}\left[m\xi \right],& (34)\end{array}$

and bright soliton is calculated as

$\begin{array}{ll}N(x,t)=-2m^2(1-{sech}^2\left[m\xi \right])& (35)\end{array}$

According to Kudryashov's method [36], the predicted solution of Equation (7) has the following form

$\begin{array}{ll}w(\xi )={\displaystyle \sum _{i=0}^N}{a}_i{\left(\frac{1}{1+d(\text{cosh}(\xi )+\text{sinh}(\xi ))}\right)}^i.& (36)\end{array}$

The homogenous balance method gives N = 1. For N = 1, Equation (36) becomes

$\begin{array}{ll}w(\xi )=a_0+\frac{a_1}{1+d(\text{sinh}(\xi )+\text{cosh}(\xi ))}.& (37)\end{array}$

Inserting Equation (37) into ODE Equation (7), an algebraic system of equations for a₀ and a₁ is obtained by equating every coefficient of different powers of $\frac{1}{1+d(\text{cosh}(\xi )+\text{sinh}(\xi ))}$ to zero. The obtained system is solved for a₀ and a₁, and replacing these values in Equation (37) gives solutions of the coupled KGS Equations (1) and (2).

The following solution set arises

SET 1

$\begin{array}{l}{a}_0=\pm \frac{1}{\sqrt{2}},a_1=\mp \sqrt{2},c=-\alpha ,\\ \omega =\frac{1}{2}(-1-2k^2)\end{array}$

A kink soliton solution is given as

$\begin{array}{ll}W(x,t)=e^{i(-kx+\omega t)}\sqrt{2}m\left(\pm \frac{1}{\sqrt{2}}\mp \frac{\sqrt{2}}{1+d(\text{cosh}\left[\xi \right]+\text{sinh}\left[\xi \right])}\right)& (38)\end{array}$

and a bright soliton solution is obtained as

$\begin{array}{ll}N(x,t)=-\frac{{(-1+d(\text{sinh}\left[\xi \right]+\text{cosh}\left[\xi \right]))}^2}{2{(1+d(\text{sinh}\left[\xi \right]+\text{cosh}\left[\xi \right]))}^2}.& (39)\end{array}$

The Figure 4, depicts the graphical representation of the absolute values of the obtained soliton solutions given in Equation (38) and Equation (39). In Figure 4A represents the kink soliton and Figure 4B represents the bright soliton.

FIGURE 4

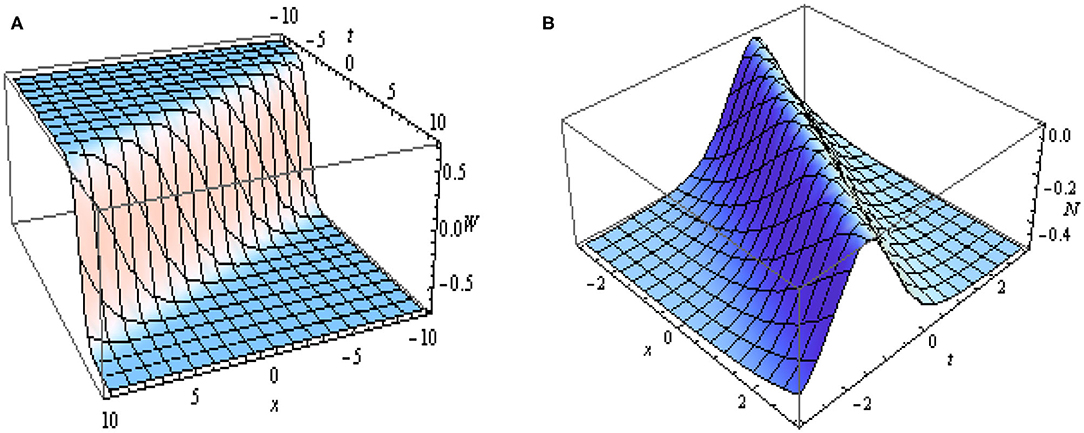
Figure 4. 3D plots of |W(x, t)| and |N(x, t)| given in Equations (38) and (39) with values of parameters as m = 1, d = 1, k = 1 and ξ = x + 2t.

3.1. Novelty of the Results

It is worth mentioning here that the proposed model has been solved for the first time by the e^−Φ(ξ)-expansion method, tanh-coth expansion technique, and Kudryashov's method to extract solitonic structures. The results presented in this piece of research could be very useful in discussing the physical properties of the different nonlinear evolution equations emerging in quantum mechanics, fluid dynamics, and plasma physics. The solitonic structures obtained in this study could attract the attention of researchers working in the field of optical fiber communication systems. The comparison of our results, with the outcomes of [20, 21], show that bright and dark solitons as well as dipole soliton, singular soliton, and kink soliton solutions have been found for the first time in this article.

4. Results and Discussion

It is important to clarify that the analytical methods utilized in this article are truly state of the art techniques for extracting the soliton solution of the non-linear Klein-Gordon-Schrödinger model. It is important to note here that each integration method has its own benefits and disadvantages compared to other accessible strategies. For example, the inverse scattering method is not useful for log-law, power law, and dual-power law nonlinearities. Only bright solitons are recovered by the semi-inverse variational algorithm. Likewise, here, the e^−Φ(ξ)-expansion technique gives bright soliton, kink soliton, periodic soliton, and singular soliton solutions. The second method applied in this research extracts dark soliton, dark-singular combo soliton, and singular soliton solutions. The third method employed here obtains bright soliton and kink soliton solutions.

5. Conclusion

In this article, new soliton solutions have been obtained by utilizing three well-known integration architectures namely, the tanh-coth expansion strategy, Kudryashov's strategy, and the e^−Φ(ξ)-expansion strategy. To the best of our knowledge, these fresh examples of soliton solutions have been obtained for the first time for the KGS model. Since the invention of symbolic computation tools, the solution procedures have been simplified, and therefore the described methods are becoming more efficient in solving many physical problems. The outcomes of this paper consist of dispersive solitons incorporating CQS and cubic nonlinearities. Kudryashov's method along with the generalized tanh method extract singular, bright, singular periodic, and a combo type of solitons for the given model. The advantage of these techniques is quite evident as they have no limitations in finding such wave profiles.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.

Author Contributions

All authors contributed equally to the writing of this paper and read and approved the final version of the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Hiki Y, Kogure Y, Itoh A. Effect of crystal dislocation on superconductivity of aluminum. Jpn J Appl Phys. (1987) 26:3. doi: 10.7567/JJAPS.26S3.929

CrossRef Full Text | Google Scholar

2. Mustafa H, Matthews DTA, Ramer GRBE. Investigation of the ultrashort pulsed laser processing of zinc at 515 nm, morphology, crystallography and ablation threshold. Mater Design. (2019) 169:103922. doi: 10.1016/j.matdes.2019.107675

CrossRef Full Text | Google Scholar

3. Raza N, Jhangeer A, Rezazadeh H, Bekir A. Explicit solutions of the (2+ 1)-dimensional Hirota–Maccari system arising in nonlinear optics. Int J Modern Phys B. (2019) 33:1950360. doi: 10.1142/S0217979219503600

CrossRef Full Text | Google Scholar

4. Raza N, Javid A. Optical dark and singular solitons to the Biswas-Milovic equation in nonlinear optics with spatio-temporal dispersion. Optik. (2018) 158:1049–57. doi: 10.1016/j.ijleo.2017.12.186

CrossRef Full Text | Google Scholar

5. Gao W, Rezazadeh H, Pinar Z, Baskonus HM, Sarwar S, Yel G. Novel explicit solutions for the nonlinear Zoomeron equation by using newly extended direct algebraic technique. Opt Quant Electron. (2020) 52:1–13. doi: 10.1007/s11082-019-2162-8

CrossRef Full Text | Google Scholar

6. Rezazadeh H, Korkmaz A, Eslami M, Mirhosseini-Alizamini SM. A large family of optical solutions to Kundu–Eckhaus model by a new auxiliary equation method. Opt Quant Electron. (2019) 51:84. doi: 10.1007/s11082-019-1801-4

CrossRef Full Text | Google Scholar

7. Birbil S, Fang SC. An electromagnetism-like mechanism for global optimization. J Glob Optimiz. (2003) 25:263–82. doi: 10.1023/A:1022452626305

CrossRef Full Text | Google Scholar

8. Aronovitz JA, Nelson DR. Anomalous diffusion in steady fluid flow through a porous medium. Phys Rev A. (1984) 30:1948. doi: 10.1103/PhysRevA.30.1948

CrossRef Full Text | Google Scholar

9. Gardner CS, Greene JM, Kruskal MD, Miura RM. Method for solving the Korteweg-Devries equation. Phys Rev Lett. (1967) 19:1095. doi: 10.1103/PhysRevLett.19.1095

CrossRef Full Text | Google Scholar

10. Hirota R. Exact N-soliton solutions of the wave equation of long waves in shallow-water and in nonlinear lattices. J Math Phys. (2003) 14:810. doi: 10.1063/1.1666400

CrossRef Full Text | Google Scholar

11. Weiss J, Tabor M, Carnevale G. The painleve property for partial differential equations. J Math Phys. (1998) 24:522. doi: 10.1063/1.525721

CrossRef Full Text | Google Scholar

12. Cariello F, Tabor M. Similarity reductions from extended Painleve expansions for non-integrable evolution equations. Phys D. (1991) 53:59–70. doi: 10.1016/0167-2789(91)90164-5

CrossRef Full Text | Google Scholar

13. Otwinowski N, Paul R, Laidlaw RG. Exact travelling wave solutions of a class of nonlinear diffusion equations by reduction to a quadrature. Phys Lett A. (1988) 128:483–7. doi: 10.1016/0375-9601(88)90880-8

CrossRef Full Text | Google Scholar

14. Jhangeer A, Raza N, Rezazadeh H, Seadawy A. Nonlinear self-adjointness, conserved quantities, bifurcation analysis and travelling wave solutions of a family of long-wave unstable lubrication model. Pramana. (2020) 94:1–9. doi: 10.1007/s12043-020-01961-6

CrossRef Full Text | Google Scholar

15. Wazwaz AM. Gaussian solitary wave solutions for nonlinear evolution equations with logarithmic nonlinearities. Nonlin Dyn. (2016) 83:591–6. doi: 10.1007/s11071-015-2349-x

CrossRef Full Text | Google Scholar

16. Ghanbari B, Raza N. An analytical method for soliton solutions of perturbed Schrödinger equation with quadratic-cubic nonlinearity. Modern Phys Lett B. (2019) 33:1950018. doi: 10.1142/S0217984919500180

CrossRef Full Text | Google Scholar

17. Wazwaz AM. Multiple soliton solutions and multiple complex soliton solutions for two distinct Boussinesq equations. Nonlin Dyn. (2016) 85:731–7. doi: 10.1007/s11071-016-2718-0

CrossRef Full Text | Google Scholar

18. Ali KK, Wazwaz AM, Osman MS. Optical soliton solutions to the generalized nonautonomous nonlinear Schrödinger equations in optical fibers via the sine-Gordon expansion method. Optik. (2020) 208:164132. doi: 10.1016/j.ijleo.2019.164132

CrossRef Full Text | Google Scholar

19. Raza N, Sial S, Kaplan M. Exact periodic and explicit solutions of higher dimensional equations with fractional temporal evolution. Optik. (2018) 156:628–34. doi: 10.1016/j.ijleo.2017.11.107

CrossRef Full Text | Google Scholar

20. Wang YP, Xia DF. Generalized solitary wave solutions for the Klein-Gordon-Schrödinger equations. Comput Math Appl. (2009) 58:2300–6. doi: 10.1016/j.camwa.2009.03.012

CrossRef Full Text | Google Scholar

21. Kumar D, Singh J, Kumar S, Sushila. Numerical computation of Klein-Gordon equations arising in quantum field theory by using homotopy analysis transform method. Alexand Eng J. (2014) 53:469–74. doi: 10.1016/j.aej.2014.02.001

CrossRef Full Text | Google Scholar

22. Petrovic NZ, Bohra M. General Jacobi elliptic function expansion method applied to the generalized (3 + 1)-dimensional nonlinear Schrödinger equation. Opt Quant Electron. (2016) 48:4. doi: 10.1007/s11082-016-0522-1

CrossRef Full Text

23. Abdou MA. The extended F-expansion method and its application for a class of nonlinear evolution equations. Chaos Solitons Fract. (2007) 31:95–104. doi: 10.1016/j.chaos.2005.09.030

CrossRef Full Text | Google Scholar

24. Hsu CS, Chiu HM. A cell mapping method for nonlinear deterministic and stochastic systems-Part II. J Appl Mech. (1986) 53:702–10. doi: 10.1115/1.3171834

CrossRef Full Text | Google Scholar

25. Ray SS. An application of the modified decomposition method for the solution of the coupled Klein-Gordon-Schrödinger equation. Commun Nonlin Sci Numer Simul. (2008) 13:1311–7. doi: 10.1016/j.cnsns.2006.12.010

CrossRef Full Text | Google Scholar

26. Biswas A, Triki H. 1-Soliton solution of the Klein-Gordon-Schrödinger's equation with power law nonlinearity. Appl Math Comput. (2010) 217:3869–74. doi: 10.1016/j.amc.2010.09.046

CrossRef Full Text | Google Scholar

27. Dehghan M, Taleei A. Numerical solution of the Yukawa-coupled Klein-Gordon-Schrödinger equations via a Chebyshev pseudo spectral multi domain method. Appl Math Model. (2012) 36:2340–9. doi: 10.1016/j.apm.2011.08.030

CrossRef Full Text | Google Scholar

28. Yumak A, Boubaker K, Petkova P. An attempt to give exact solitary and periodic wave polynomial solutions to the nonlinear Klein-Gordon-Schrödinger equations. Chaos Solitons Fract. (2015) 81:299–302. doi: 10.1016/j.chaos.2015.09.031

CrossRef Full Text | Google Scholar

29. Wang J, Liang D, Wang Y. Analysis of a conservative high-order compact finite difference scheme for the Klein-Gordon-Schrödinger equation. J Comput Appl Math. (2019) 358:84–96. doi: 10.1016/j.cam.2019.02.018

CrossRef Full Text | Google Scholar

30. Kong L, Chen M, Yin X. A novel kind of efficient symplectic scheme for Klein-Gordon-Schrödinger equation. Appl Numer Math. (2019) 135:481–96. doi: 10.1016/j.apnum.2018.09.005

CrossRef Full Text | Google Scholar

31. Liang H. Linearly implicit conservative schemes for long-term numerical simulation of Klein-Gordon-Schrödinger equations. Appl Math Comput. (2014) 238:475–84. doi: 10.1016/j.amc.2014.04.032

CrossRef Full Text | Google Scholar

32. Fukuda M, Tsutsumi M. On the Yukawa-coupled Klein-Gordon Schrödinger equations in three space dimensions. Proc Jpn Acad. (1975) 51:402–5. doi: 10.3792/pja/1195518563

CrossRef Full Text | Google Scholar

33. Fukuda M, Tsutsumi M. On coupled Klein-Gordon-Schrdinger equations II. J Math Anal Appl. (1978) 66:358–78. doi: 10.1016/0022-247X(78)90239-1

CrossRef Full Text | Google Scholar

34. Raza N, Arshed S, Sial S. Optical solitons for coupled Fokas-Lenells equation in birefringence fibers. Modern Phys Lett B. (2019) 33:1950317. doi: 10.1142/S0217984919503172

CrossRef Full Text | Google Scholar

35. Asokan R, Vinodh D. The tanh-coth Method for Soliton and Exact Solutions of the Sawada-Kotera Equation. Int J Pure Appl Math. (2017) 117:19–27. Available online at: https://acadpubl.eu/jsi/2017-117-11-14/articles/13/3.pdf

Google Scholar

36. Ullah N, Rehman H, Imran MA, Abdeljawad T. Highly dispersive optical solitons with cubic law and cubic-quintic-septic law nonlinearities. Results Phys. (2020) 17:103021. doi: 10.1016/j.rinp.2020.103021

CrossRef Full Text | Google Scholar