Spatiotemporal Complexity Mediated by Higher-Order Peregrine-Like Extreme Events

The Peregrine soliton is the famous coherent solution of the non-linear Schrödinger equation, which presents many of the characteristics of rogue waves. Usually studied in conservative systems, when dissipative effects of injection and loss of energy are included, these intrigued waves can disappear. If they are preserved, their role in the dynamics is unknown. Here, we consider this solution in the framework of dissipative systems. Using the paradigmatic model of the driven and damped non-linear Schrödinger equation, the profile of a stationary Peregrine-type solution has been found. Hence, the Peregrine soliton waves are persistent in systems outside of the equilibrium. In the weak dissipative limit, analytical description has a good agreement with the numerical simulations. The stability has been studied numerically. The large bursts that emerge from the instability are analyzed by means of the local largest Lyapunov exponent. The observed spatiotemporal complexity is ruled by the unstable second-order Peregrine-type soliton.

1. Introduction

Among a large number of the exact solutions of the Non-linear Schrödinger equation, Over the past decade, the Peregine soliton (PS) [1] has become one of the most attractive ones within the non-linear science community. So far, PS is the best-known coherent structure that has been successfully proposed as a prototype solution for rogues waves in conservative systems, and it aims its localization in both temporal and spatial directions. The interest in PS has also been reinforced by the experimental observation in an optical fiber [2], with a suitable pulse sent through the fiber. The Peregrine soliton has been reported to spontaneously emerge from a saturated state of modulational instability displayed by any continuous-wave solution of the non-linear Schrödinger equation [3, 4]. The common feature of all the aforementioned works is that they are considered in the conservative limit. An open question is the persistence and role of Peregrine waves in the complex spatiotemporal dynamic observed in the dissipative system. Indeed, when losses are added into the equation of a conservative dynamical system, solutions of a family generally reduce to a single one [5]. A classic example is how the solitons form a family in the non-linear Schrödinger equations (NLS) equation due to infinite conserved quantities for the same set of parameters. From these families, only one persists in the dissipative regime due to the additional balance between losses and energy injection. Many dissipative systems are described by the NLS equation alongside driving and energy loss. Examples include the driven-damped [6–8] and, parametrically, the driven-damped [9] non-linear Schrödinger equations. In the case of the driven and damped [7] non-linear Schrödinger equation, the equation becomes non-integrable. Hence, emerges the question of the persistence of the NLS Peregrine soliton. Another open question is the following: if the PSs persist, do they play the same role here also as some coherent rogue wave-like solutions? Indeed, rogue wave and extremes events were also reported in dissipative systems. In those systems, a new mechanism has been found to induce extreme events or rogue waves: the chaos in purely temporal systems and the spatiotemporal chaos in large degree of freedom systems [10–13]. To infer the existence of chaos, it is mandatory to prove the largest Lyapunov exponent is positive [14]. For large degree of freedom, such as systems with a transport or coupling mechanism (diffraction, diffusion, dispersion, etc.), there exists a continuous set of exponents: the Lyapunov spectrum [15]. Spatiotemporal chaos is characterized by that must have a positive range. In this work, we address the problem of the persistence of the NLS Peregrine Soliton and study the link with some of the rogue waves reported in the dissipative regime.

For this purpose, we consider the paradigmatic optical dissipative system, which consists of the synchronous injection of a light wave in ring-type Kerr medium waveguides such as optical fiber or microresonators. The envelope of the temporal profile of the light inside the waveguide is well-described by the driven and damped non-linear Schrödinger equation [6–8]. This model was derived initially from the context of forced plasmas with oscillatory fields [6, 7] and dipole excitations in condensed matter. In the optics, this envelope equation is also known as the Lugiato-Lefever equation (LLE) [16–18]. The LLE is a non-integrable equation and, to our knowledge, no closed-form solution has been reported, yet. However, neglecting only the dissipation may allow us to find some solutions [9, 19] in the form of rational periodic or localized solutions. Even in this limit, intriguingly, no rational solution of Peregrine-type was reported. Likewise to the conservative systems, rogue waves have been reported in the LLE [18, 20, 21]. For one of the operating modes, the bistable regime–three possible outputs for a same value of the driving–the rogue waves emerge in the dynamics where the spatiotemporal chaos is seeded by a breathing cavity solitons [18, 20]. However, the analytical profile itself and the features of these spatiotemporal chaotic rogue waves are not well-known. The purpose of this report is an attempt to open up a discussion about this point. Therefore, we use the dissipationless limit to write a closed-form rational polynomial solution of the LLE. This analytical result is then compared to the numerically integrated solution. Next, we consider the persistence of this ideal case solution in the full LLE, and it can be linked to the dissipative rogue wave previously reported. In particular, we will show that the complexity in the LLE is mediated by rogue waves approximated by second-order Peregrine-like solitons.

2. The Peregrine-Type Solution

As mention in the introduction, the propagation of light in the optical fiber loop is modeled without loss of generality by the non-linear Schrödinger equation augmented with boundary conditions or an Ikeda map [17, 22, 23]:

$\begin{array}{ll}{\partial }_{z}A(z,T)=-i\frac{{\beta }_2}{2}{\partial }_T^{2}A(z,T)+i\gamma A(z,T)|A(z,T){|}^2,& (1)\end{array}$

$\begin{array}{ll}A(0,T+T_R)=\sqrt{\theta }{E}_i(T)+\sqrt{\rho }A(L,T)e^{-i{\Phi }_0},& (2)\end{array}$

where T_R stands for the round-trip time, which is the time taken by the pulse to propagate along the cavity with the group velocity, Φ₀ is the linear phase shift, θ (ρ) is the mirror transmission (reflection) coefficient, and L is the geometrical cavity length. The complex amplitude of the electric field inside the cavity is A. Each of the coefficients β₂ is responsible for the second order dispersion, and γ is the non-linear coefficient of the fiber. The independent variable z refers to the longitudinal coordinate while T is the time in a reference frame moving with the group velocity of the light and E_i(T) is the amplitude of the pump field. For large enough cavity finesse ${F}=\pi /\alpha$, with α the effective losses of the cavity, the evolution of the electric field inside the loop is well-described by the Lugiato-Lefever equation [16, 17]:

$\begin{array}{ll}\frac{\partial \psi }{\partial t}=S-(\alpha +i\delta )\psi -i\eta \frac{{\partial }^2\psi }{\partial {\tau }^2}+i|\psi {|}^2\psi ,& (3)\end{array}$

where α = θ/2, $S=2E_i\sqrt{\gamma L}$, $\psi =A\sqrt{\gamma L}$, t = αT/T_R t = αm, and τ = T/T_n with $T_n=\sqrt{\left|{\beta }_{2}L\right|/2}$. δ = (2kπ−Φ₀) is the detuning with respect to the nearest cavity resonance k. The integer m gives the roundtrip number and the coefficient η = ±1 is the sign of the group velocity dispersion term (β₂). In the following, we will consider η = −1 as corresponding to an anomalous group velocity dispersion. Despite its apparent simplicity this equation is non-integrable and closed form solution have been found only for α = 0 [9, 19], which corresponds to a Hamiltonian equation. Numerically and experimentally, almost all the solutions obtained in this limit of α = 0 have been observed [24]. Among these solutions, the localized structure and cavity solution have been the most studied but have never been described by a Peregrine-like profile. This is the purpose of the following. Considering α = 0, assuming a constant phase, and introducing u(t, τ) = ψ(τ)exp(iπ/2), the equation for the steady solution of the LLE reads as follows:

$\begin{array}{ll}{u}_{\tau \tau }-\delta u+u^3=-S.& (4)\end{array}$

Multiplying Equation (4) by u_τ, integrating over τ and introducing f = u + a, its follows

$\begin{array}{ll}{f}_{\tau }=f\sqrt{f^2/2+2af+(\delta -3a^2)},& (5)\end{array}$

where a is solution of the cubic equation

$\begin{array}{ll}{a}^3-\delta a-S=0.& (6)\end{array}$

Namely, a accounts for a uniform solution of the driven dissipative non-linear Schrödinger Equation (3). Hence, for δ−a² > 0 we can recover the solution founded in [9, 25]. Then, for the special case of a² = δ/3 the solution is as follows:

$\begin{array}{ll}{u}_P(\tau )=\frac{\delta }{\sqrt{3}}\left[-1+\frac{12}{{(\tau /{\tau }_0)}^2+3}\right],& (7)\end{array}$

where τ₀ = 2δ. Note that this function corresponds to a decent Lorentzian, that is, a Lorentzian supported on a negative value. Then $u_P^2(\tau )$ has the shape of a Mexican hat as illustrated in Figure 1. u_P(τ) has the same profile as the maximally compressed Peregrine soliton.

FIGURE 1

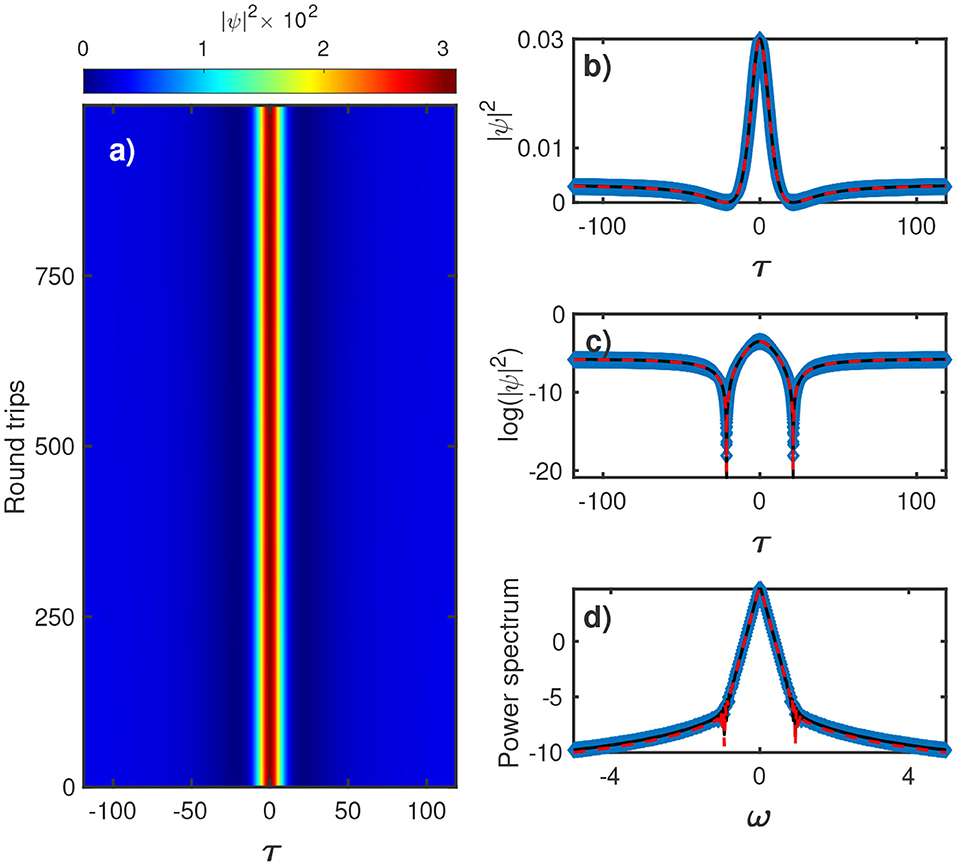
Figure 1. Localized structure of the driven dissipative non-linear Schrödinger Equation (3). (a) Evolution of the driven dissipative non-linear Schrödinger obtained by integration of Equation (3) with α = 10⁻⁵, δ = 10⁻², and S = 4 × 10⁻⁴. In the right panel, (b–d), the black dashed lines correspond to the initial condition given by the stationary Peregine profile (7), blue diamonds correspond to the numerical profile at T = 1, 000 and the red dash line to the solution from [19], respectively.

The result of the numerical integration of the LLE (3) for α = 10⁻⁵, δ = 10⁻², and S = 4 × 10⁻³ starting with u_P(τ) (Equation 7) is shown in Figure 1. These parameters are chooses for the purpose to numerically test the stability of the solution of Equation (7). As can be seen from the left panel this figure, the solution remains stable. The right panel of Figure 1 gives the instantaneous profiles in linear (b) and logarithmic (c) scales, respectively. This chart reveals that u_P(τ) (black dashed line) is a good approximation of the numerical solution (blue diamonds). The red dashed line corresponding to the solution provided by [25] is plotted for comparison. The spectra profiles Figure 1c are also in a good agreement.

Increasing, the detuning parameter, the solution u_P(τ) develops an instability and shows a breathing dynamical behaviors [26]. By increasing the detuning or forcing strength further, the localized structure gives rise to a complex spatiotemporal dynamic, as illustrated in Figure 2, characterized by two counter-propagating fronts between the homogeneous and the complex spatiotemporal states [20, 24]. The inserts of Figure 2 account for the profile of the highest peak in the spatiotemporal map. Hence, the destabilization of the localized solution corresponds to a process of self-replication [27]. In turn, the complex spatiotemporal dynamical behavior observed is a consequence of the interaction of these localized structures that self-replicate. For comparison, we have also plotted in the same figure the profile of u_P(τ) (dash line). It clear that u_P fails to describe this local profile. However, using the expression of the maximally compressed second-order Peregrine soliton given by

$\begin{array}{ll}{u}_{SP}(\tau )={\left[a_0+\frac{{\tau }^4+a_1{\tau }^2+a_2}{{\tau }^6+a_3{\tau }^4+a_4{\tau }^2+a_5}\right]}^2.& (8)\end{array}$

the best fit profile corresponds to the red solid lines in the bottom panel of Figure 2. This suggests that the complex behavior observed may be mediated by a higher-order Peregrine soliton. The current instability scenario of the stationary non-dissipative solution u_P(τ) qualitatively preserve in the dissipative regime [18, 20, 24]. In this limit, the dynamics have been demonstrated to be of spatiotemporal chaos [20], and statistics on the bursts emitted have revealed rogue waves [18]. In the following, we investigate the local dynamics in the dissipative case to see how the emerging rogues waves relate to the undamped solutions.

FIGURE 2

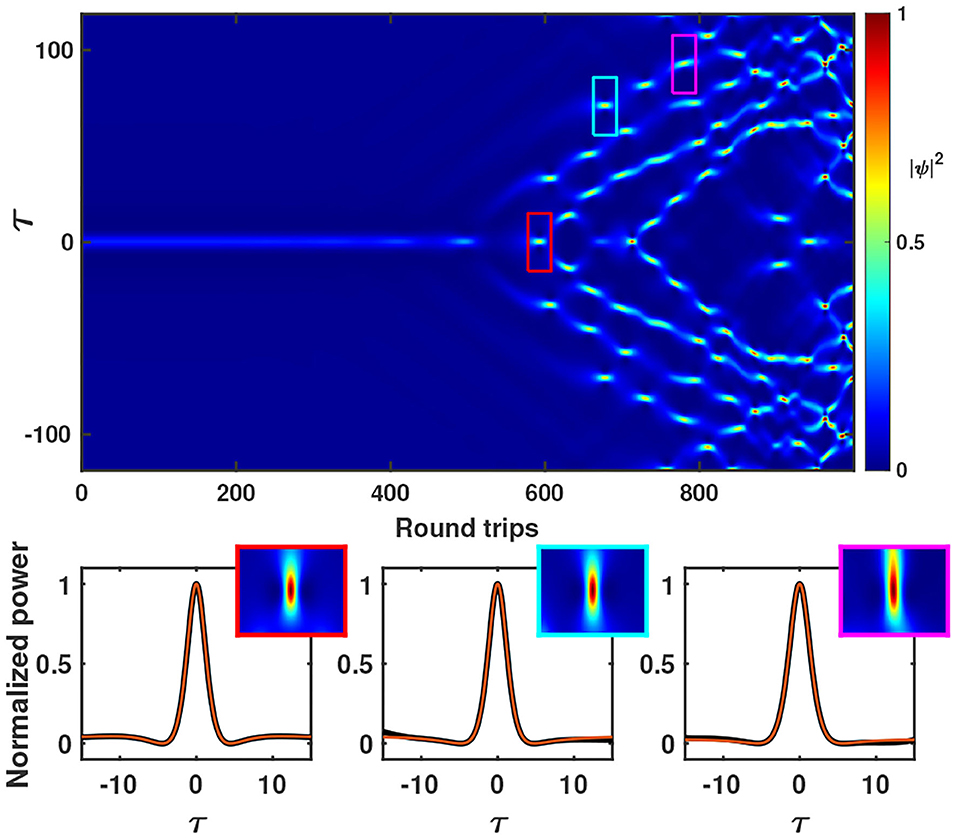
Figure 2. Evolution of the LLE obtained by integration of Equation (3) with α = 10⁻⁵, δ = 5 × 10⁻², and S = 4.3 × 10⁻³. The bottom panels show the instantaneous profile of the highest peak obtained in the red, cyan, and magenta box and the red line correspond to the best fit using the maximally compressed second order Peregrine soliton (8), respectively.

3. Peregrine-Type Solitons in the Spatiotemporal Chaos of the LLE

Strictly speaking, to prove a spatiotemporal chaotic dynamic one may have to compute several quantities. In particular, it is mandatory to compute the Lyapunov spectrum. Next, this spectrum must have a positive part and a continuous region that has an area to linearly increase along with the size of the system. The computation of the Lyapunov spectrum itself is very well-documented [28] and is not the purpose here. Let us recall the main steps.

From the state of the system at a given time, the linear evolution of any small perturbation δX can be described by ∂_tδX = JδX, where J is the respective Jacobian. In the present case, we introduce ψ = ψ_r + iψ_i, with ψ_r and ψ_i being the real and imaginary part of ψ respectively. At a time t = t₀, introducing ψ = ψ₀ + δψ, with δψ≪ψ(t = t₀) = ψ₀ the matrix J reads as follows:

$\begin{array}{ll}J=\left[\begin{array}{cc}-(\alpha +2{\psi }_0{}_r{\psi }_0{}_i)& \delta -{\psi }_0{}_r^2-3{\psi }_0{}_i^2-{\partial }_{\tau }^2\\ -\delta +{\psi }_0{}_i^2+3{\psi }_0{}_r^2)+{\partial }_{\tau }^2& -(\alpha -2{\psi }_0{}_r{\psi }_0{}_i)\end{array}\right]& (9)\end{array}$

and $\delta \mathbf{\text{X}}={(\delta {\psi }_r,\delta {\psi }_r)}^t$. Suppose that we want to compute the n-th first dominant exponents of the spectrum, we introduce the matrix L, which contains n orthonormal vectors v_i to be used as initial conditions when solving ∂_tδX = JδX:

$\begin{array}{ll}L\left(t=t_0\right)\equiv \left[v_1{v}_2...v_n\right]=\left[\begin{array}{l}{x}_{11}{x}_{12}{x}_{13}...x_{1n}\\ x_{21}{x}_{22}{x}_{23}...x_{2n}\\ ..........\\ x_{d1}{x}_{d2}{x}_{d3}...x_{dn}\end{array}\right],& (10)\end{array}$

where d is the dimension of the system. After a time increment dt, the matrix L evolves to $\mathbf{\text{L}}(t_0+dt)=\widehat{\mathbf{\text{U}}}\mathbf{\text{L}}(t_0)$ where $\widehat{\mathbf{\text{U}}}=e^{\mathbf{\text{J}}*dt}$. Using the modified Gram-Schmidt QR decomposition on L(t₀ + dt), the diagonal elements of R account for the Lyapunov exponents ${\tilde{\lambda }}_i(i=1,\dots ,n)$ at time t₀ + dt, that is

$\begin{array}{ll}{\tilde{\lambda }}_i(t_0+dt)=\frac{1}{dt}ln({\text{R}}_{ii}(t_0+dt)).& (11)\end{array}$

Repeating this procedure several time, after a large number of iterations N, the Lyapunov exponents can be approximated by

$\begin{array}{ll}{\lambda }_i\equiv \langle {\tilde{\lambda }}_i\rangle =\frac{1}{Ndt}{\displaystyle \sum _{k=1}^N}ln({\text{R}}_{ii}(t_0+kdt)).& (12)\end{array}$

From the spectrum {λ_i} an estimator of the dimension of the chaotic attractor is given by the York-Kaplan dimension $D_{kY}=p+\sum _{i=1}^p{\lambda }_i/\left|{\lambda }_{p+1}\right|$ where p is such that $\sum _{i=1}^p{\lambda }_i>0$ and $\sum _{i=1}^{p+1}{\lambda }_i<0$ [29]. For a one-dimensional system of size L, a spatiotemporal chaos implies that D_KY increase linearly with L. The spatiotemporal chaotic nature of the current dynamic has already been proven [20] and is not the purpose here. Our purpose now is to go inside the local dynamics. Indeed, from the whole process of computing the Lyapunov spectrum, only average quantities are used to make conclusion. However, looking at the spatiotemporal evolution such as that shown in Figure 3 (bottom panel) it is obvious that local bursts may impact the average value. To verify this point, we have also plotted the evolution of the largest Lyapunov exponent. The local maxima of this exponent, marked by gray lines, always correspond to a spatiotemporal local maximum. This shows that local bursts are those with the largest contribution to the average of the first Lyapunov exponent. After all, this also means that the spatiotemporal local maxima are the highest unstable structures that can appear in the dynamics. We can now extract from the temporal local maxima the profile of the local maximally compressed spatiotemporal bursts. As expected in the parameters used [18], a fraction of the peak values represent extreme events, as can be seen from Figure 4A. The mean profiles of the five highest peaks have been used with the Equation (8) to find the best-fit parameters. The result is given in Figure 4B and shows a good agreement between the two profiles. This confirms that the persistent of the behavior observed in the non-dissipative limit comes also with the fact that the spatiotemporal chaos observed in the dissipative limit is mediated by second-order Peregrine-type solitons.

FIGURE 3

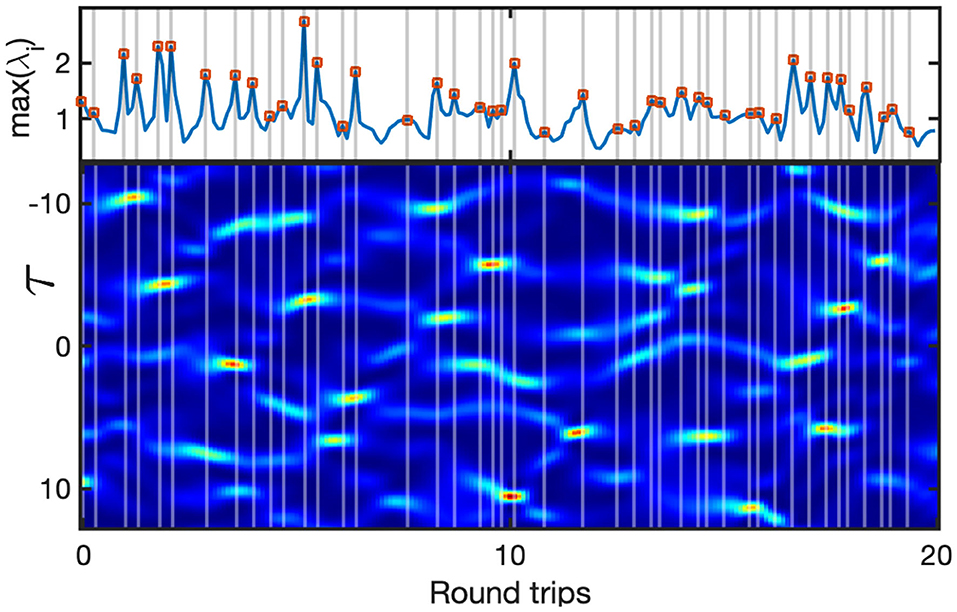
Figure 3. Evolution of the driven dissipative non-linear Schrödinger obtained by integration of Equation (3) for α = 0.2, δ = 1, and S = 0.43. The blue line correspond to the local largest Lyapunov exponent, while the red circles are the local maxima detected. The gray bars mark the location of these local maxima.

FIGURE 4

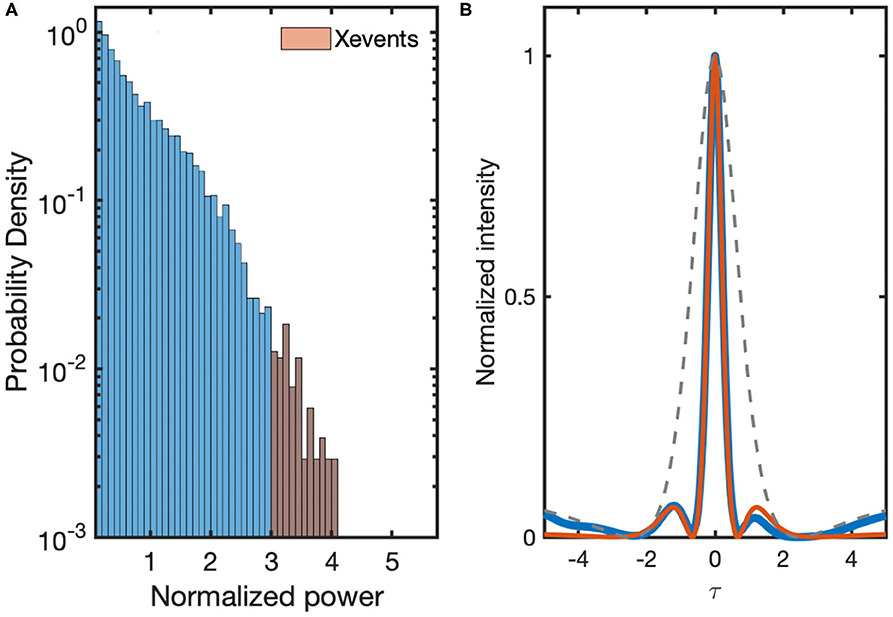
Figure 4. Probability density function (A) of intensity bursts observed in the spatiotemporal chaos of Equation (3) for α = 0.2, δ = 1, and S = 0.43. Light red bars correspond to the values above the characteristic wave height. (B) Mean intensity profile from the five larger pulses and the result of the best fit of this profile with Equation (8). Xevents in (A) correspond to the bursts with peak values above twice the significant wave height. This height is defined as the average value of the largest 1/3 burst.

4. Discussion

The Peregrine soliton is the famous coherent solution of the nonlinear Schrödinger equation that presents many of the characteristics of rogue waves. As a result, it became one of the most studied localized solution of the Non-linear Schrödinger equation. Despite the great interest around this solution, the studies in dissipative systems are few relatively compared to those in conservative systems. In this work, we have considered the emergence of the Peregrine solitons in the paradigmatic dissipative system and the driven and damped Non-linear Schrödinger equation. Using the dissipationless limit, we were able to obtain a Peregrine-like solution of this system. Even in this limit, such a rational polynomial solution was not reported up to now. The comparison of our solution to the result of the numerical simulation is in quite good agreement (cf. Figure 1). With the dissipation as no closed-form solution can be found, we have performed numerical integration. The stationary Peregrine soliton bifurcates to a breathing state. The local maximally compressed state was successfully interpolated by the profile of a second-order Peregrine soliton (see Figure 2). Unfortunately, as a result of a bifurcation, the derivation of the corresponding closed-form solution can not be done from the dissipationless limit. The instability that can develop this intrigued solution leads to the emergence of the second-order type Peregrine soliton. In the dissipative limit, the complex behavior observed in the conservative case persevere. Indeed, using the tools of the theory of chaos, we were able to follow the local dynamics (see Figure 3). In this spatiotemporal complexity shown to be extensive chaos, we have shown that the dynamics are ruled by the same profile of the second-order Peregrine-type soliton. Indeed, we show that burst in local metric entropy occurs at the same time as the emergence of a maximally compressed second-order Peregrine soliton. Despite the effort made to find configurations of the Non-linear Schrödinger equation, such as variable parameters, the fact is that losses and dissipation are the rules instead of the exceptions in real-world systems. Hence, we believe that as with dissipative solitons, dissipative systems are the opportunity to investigate new dynamics for the Peregrine soliton. This work attempts to that this is possible, and we are convinced that many other works will follow this one.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

All authors equally contributed to the theoretical work and the preparation to the manuscript.

Funding

MC was thankful for financial support from the ANID–Millennium Science Initiative Program–ICN17_012 and Fondecyt 1180903 project. SC acknowledges the LABEX CEMPI (ANR-11-LABX-0007) as well as the Ministry of Higher Education and Research, Hauts de France council, and the European Regional Development Fund (ERDF) through the Contract de Projets Etat-Region (CPER Photonics for Society P4S).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Peregrine DH. Water waves, nonlinear Schrödinger equations and their solutions. ANZIAM J. (1983) 25:16–43. doi: 10.1017/S0334270000003891

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Kibler B, Fatome J, Finot C, Millot G, Dias F, Genty G, et al. The Peregrine soliton in nonlinear fibre optics. Nat Phys. (2010) 6:790–5. doi: 10.1038/nphys1740

CrossRef Full Text | Google Scholar

3. Toenger S, Godin T, Billet C, Dias F, Erkintalo M, Genty G, et al. Emergent rogue wave structures and statistics in spontaneous modulation instability. Sci Rep. (2015) 5:10380. doi: 10.1038/srep10380

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Agafontsev DS, Zakharov VE. Integrable turbulence and formation of rogue waves. Nonlinearity. (2015) 28:2791–821. doi: 10.1088/0951-7715/28/8/2791

CrossRef Full Text | Google Scholar

5. Akhmediev N, Ankiewicz A. Dissipative Solitons: From Optics to Biology and Medicine. Vol. 751. Verlag Berlin; Heidelberg: Springer Science & Business Media; 2008.

Google Scholar

6. Morales G, Lee Y. Ponderomotive-force effects in a nonuniform plasma. Phys Rev Lett. (1974) 33:1016. doi: 10.1103/PhysRevLett.33.1016

CrossRef Full Text | Google Scholar

7. Kaup DJ, Newell AC. Theory of nonlinear oscillating dipolar excitations in one-dimensional condensates. Phys Rev B. (1978) 18:5162. doi: 10.1103/PhysRevB.18.5162

CrossRef Full Text | Google Scholar

8. Nozaki K, Bekki N. Solitons as attractors of a forced dissipative nonlinear Schrödinger equation. Phys Lett A. (1984) 102:383–6. doi: 10.1016/0375-9601(84)91060-0

CrossRef Full Text | Google Scholar

9. Barashenkov I, Smirnov YS. Existence and stability chart for the ac-driven, damped nonlinear Schrödinger solitons. Phys Rev E. (1996) 54:5707. doi: 10.1103/PhysRevE.54.5707

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Bonatto C, Feyereisen M, Barland S, Giudici M, Masoller C, Leite JRR, et al. Deterministic optical rogue waves. Phys Rev Lett. (2011) 107:053901. doi: 10.1103/PhysRevLett.107.053901

CrossRef Full Text | Google Scholar

11. Pisarchik AN, Jaimes-Reátegui R, Sevilla-Escoboza R, Huerta-Cuellar G, Taki M. Rogue waves in a multistable system. Phys Rev Lett. (2011) 107:274101. doi: 10.1103/PhysRevLett.107.274101

CrossRef Full Text | Google Scholar

12. Selmi F, Coulibaly S, Loghmari Z, Sagnes I, Beaudoin G, Clerc MG, et al. Spatiotemporal chaos induces extreme events in an extended microcavity laser. Phys Rev Lett. (2016) 116:013901. doi: 10.1103/PhysRevLett.116.013901

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Coulibaly S, Clerc M, Selmi F, Barbay S. Extreme events following bifurcation to spatiotemporal chaos in a spatially extended microcavity laser. Physi Rev A. (2017) 95:023816. doi: 10.1103/PhysRevA.95.023816

CrossRef Full Text | Google Scholar

14. Pikovsky A, Politi A. Lyapunov Exponents: A Tool to Explore Complex Dynamics. Cambridge: Cambridge University Press (2016).

Google Scholar

15. Ruelle D. Large volume limit of the distribution of characteristic exponents in turbulence. Commun Math Phys. (1982) 87:287–302. doi: 10.1007/BF01218566

CrossRef Full Text | Google Scholar

16. Lugiato LA, Lefever R. Spatial dissipative structures in passive optical systems. Phys Rev Lett. (1987) 58:2209. doi: 10.1103/PhysRevLett.58.2209

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Haelterman M, Trillo S, Wabnitz S. Dissipative modulation instability in a nonlinear dispersive ring cavity. Optics Commun. (1992) 91:401–7. doi: 10.1016/0030-4018(92)90367-Z

CrossRef Full Text | Google Scholar

18. Coillet A, Dudley J, Genty G, Larger L, Chembo YK. Optical rogue waves in whispering-gallery-mode resonators. Phys Rev A. (2014) 89:13835. doi: 10.1103/PhysRevA.89.013835

CrossRef Full Text | Google Scholar

19. Renninger WH, Rakich PT. Closed-form solutions and scaling laws for Kerr frequency combs. Sci Rep. (2016) 6:24742. doi: 10.1038/srep24742

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Liu Z, Ouali M, Coulibaly S, Clerc M, Taki M, Tlidi M. Characterization of spatiotemporal chaos in a Kerr optical frequency comb and in all fiber cavities. Optics Lett. (2017) 42:1063–6. doi: 10.1364/OL.42.001063

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Coulibaly S, Taki M, Bendahmane A, Millot G, Kibler B, Clerc MG. Turbulence-induced rogue waves in Kerr resonators. Phys Rev X. (2019) 9:11054. doi: 10.1103/PhysRevX.9.011054

CrossRef Full Text | Google Scholar

22. Ikeda K. Multiple-valued stationary state and its instability of the transmitted light by a ring cavity system. Optics Commun. (1979) 30:257–61. doi: 10.1016/0030-4018(79)90090-7

CrossRef Full Text | Google Scholar

23. Coen S, Haelterman M. Modulational instability induced by cavity boundary conditions in a normally dispersive optical fiber. Phys Rev Lett. (1997) 79:4139. doi: 10.1103/PhysRevLett.79.4139

CrossRef Full Text | Google Scholar

24. Leo F, Gelens L, Emplit P, Haelterman M, Coen S. Dynamics of one-dimensional Kerr cavity solitons. Optics Express. (2013) 21:9180–91. doi: 10.1364/OE.21.009180

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Gradshteyn IS, Ryzhik IM. Table of Integrals, Series, and Products, (see 2.266, pp. 97). Amsterdam: Academic Press (2014).

Google Scholar

26. Taki M, Spatschek K, Fernandez J, Grauer R, Reinisch G. Breather dynamics in the nonlinear Schrödinger regime of perturbed sine-Gordon systems. Physica D. (1989) 40:65–82. doi: 10.1016/0167-2789(89)90027-4

CrossRef Full Text | Google Scholar

27. Bordeu I, Clerc MG, Couteron P, Lefever R, Tlidi M. Self-replication of localized vegetation patches in scarce environments. Sci Rep. (2016) 6:33703. doi: 10.1038/srep33703

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Skokos C. The Lyapunov Characteristic Exponents and Their Computation. Berlin; Heidelberg: Springer (2010). p. 63–135.

Google Scholar

29. Ott E. Chaos in Dynamical Systems. Cambridge: Cambridge University Press (2002).

Google Scholar