Superoscillations in Finite-Energy Airy Beams

Superoscillations naturally arise in optical fields with dense packing of nodal points of amplitude. Airy wave packets are highly oscillatory and rich of phase singularities. We study to the best of our knowledge, for the first time, the superoscillatory behavior in a band-limited Airy beam whose spectrum is sharply truncated. Our results show that not as expected, the superoscillations occur outside of the Airy-like region, but in regions above a defining line where the beam stops being Airy-like. The degree of superoscillation can be very high there.

1 Introduction

The phenomenon that a band-limited signal can oscillate faster, although locally somewhere in its domain, than its largest frequency is called superoscillation. The discovery of this phenomenon dates back to the studies in quantum mechanics by Aharonov et al. [1]. This topic stimulates recent interest in optics [2-4] because of its close connection to, in particular, super-resolution imaging. The latter is usually achieved in the scheme of recovering evanescent waves. More interestingly, the desired large local frequency, or local wave number in optical case, naturally occurs near phase singularities, where it diverges. This connection leads to a recent method of achieving superoscillation using optical vortexed waves [5].

In fact, the superoscillatory behavior is ubiquitous in optics. Dennis et al. [4] showed that for certain speckle patterns, the area of the superoscillating region can be of 1/3 in fraction. Makris et al. [6] constructed diffraction-less beams that can transport subwavelength features into the far field. These studies stimulate us to study the superoscillations embedded in optical Airy beams. Our motivation comes from the facts that Airy beams are oscillatory and rich in optical singularities, hinting that super large local wave numbers may occur even though the beam is inherently paraxial. First discovered by Berry and Balazs [7] as a set of solutions to the Schrodinger equation, Airy wave packets raise great interest [8, 9] in the context of beam optics due to their peculiar features as diffraction-less propagation, self-acceleration, and self-healing. However, a complete Airy beam is of unlimited spectrum. To facilitate our current task, after briefly reviewing the theory of and the criterion for superoscillation in Section 2, we introduce in Section 3 the method of sharply truncating the Airy beam spectrum; in Section 4, we give the method to compute the local wave number through its relation to optical currents, and then study the superoscillatory area in both a longisection and a transverse section; finally, we give a conclusion of the study.

2 Superoscillations in Light Fields

Suppose we have a general optical wave field, denoted by ϕ(r), propagating in free space, then the vector r denotes the position in three-dimensional space. We write ϕ(r) in terms of its amplitude ρ(r) and phase φ(r):

$\varphi \left(\mathbf{r}\right)=\rho \left(\mathbf{r}\right)\text{exp}\left[i\phi \left(\mathbf{r}\right)\right].(1)$

If ϕ is a plane wave, that is, the eigenfunction of momentum, associated with ϕ, then there is a unique and global wavenumber k, with corresponding spatial frequency v = k/2π. However, for general waves that have complicated distribution of φ(r), no such global wave number can be designated. What we have instead is the local wave vector k, defined as the gradient of the phase function:

$\mathbf{k}=\nabla \phi \left(\mathbf{r}\right),(2)$

where $\nabla$ stands for gradient operation whose form depends on the dimensionality and coordinate chosen. For a band-limited optical signal with maximum wave number k_max, we define the criterion of superoscillation as:

$\left|\nabla \phi \left(\mathbf{r}\right)\right|>k_{\max }.(3)$

For most complex fields, even φ itself cannot be explicitly given. For such cases, one can use a relationship between the phase gradient and the optical current [11] J,

$\mathbf{J}=\mathrm{\Im }\left[{\varphi }^{\text{*}}\left(\mathbf{r}\right)\nabla \varphi \left(\mathbf{r}\right)\right]={\rho }^2\left(\mathbf{r}\right)\nabla \phi \left(\mathbf{r}\right),(4)$

where the symbol $\mathrm{\Im }[\cdot ]$ denotes the imaginary part. We will use Eq. (4) to calculate the phase gradient of Airy beams.

3 Optical Incomplete Airy Beams

In this article, we will formulate the propagation problem in the 2 D scenario, that is, one transverse plus one longitudinal dimension. We will assign the x coordinate to be the transverse position and ξ coordinate to be the longitudinal one. A full 3 D formulation can be obtained by incorporating another transverse dimension (the y coordinate), which is formally identical to x. Let ϕ(x,ξ) be the amplitude of a light wave, satisfying the normalized paraxial wave

$i\frac{\partial \varphi \left(x,\xi \right)}{\partial \xi }+\frac{1}{2}\frac{{\partial }^2\varphi \left(x,\xi \right)}{\partial x^2}=0.(5)$

One way to construct the Airy beam is to conceive that the wave is propagated from an initial, say ξ = 0 plane, with its distribution ϕ(x,0) being the Airy function Ai(x):

$\text{Ai}\left(x\right)={\displaystyle {\int }_{-\infty }^{\infty }ds\text{exp}\left[i\left(\frac{1}{3}{s}^3+sx\right)\right]}.(6)$

This equation indicates that the spatial spectrum of the Airy function is given by the unimodular cubic phase factor exp(is³/3). To obtain the beam profile at any longitudinal position Ai(x,ξ), we model the paraxial propagation through the method of angular spectrum. The wave number along ξ, denoted as k_ξ, can be computed under the Fresnel approximation:

$k_{\xi }=\sqrt{1-s^2}\approx 1-\frac{1}{2}{s}^2.(7)$

Thus, we have

$\text{Ai}\left(x,\xi \right)={\displaystyle {\int }_{-\infty }^{\infty }ds\text{exp}\left(i\frac{1}{3}{s}^3\right)\text{exp}\left[i\left(1-\frac{1}{2}{s}^2\right)\xi \right]\text{exp}\left(isx\right)},$

$\propto \text{exp}\left(i\xi \right){\displaystyle {\int }_{-\infty }^{\infty }ds\text{exp}\left\{i\left[\frac{1}{3}{\left(s+a\right)}^3+\left(s+a\right)\left(x+b\right)\right]\right\}}.(8)$

The second line of Eq. (8) shows that the beam is propagation invariant up to translation, as long as we set the parameters a and b in the integration to be

$a=-\frac{\xi }{2},b=-a^2=-\frac{{\xi }^2}{4}.(9)$

When exp(iξ) is decreased, we finally have the complex envelope of the Airy beam.

$\text{Ai}\left(x,\xi \right)=\text{exp}\left[i\left(\frac{x\xi }{2}-\frac{{\xi }^3}{12}\right)\right]\text{Ai}\left(x-\frac{{\xi }^2}{4}\right).(10)$

From Eq. (10), we can readily see that the point of peak intensity of the wave packet moves from x = 0 in the initial plane to the point x = ξ²/4 for a particular ξ. This phenomenon is the so-called self-acceleration of Airy beams. The path of the peak intensity in the x−ξ plane is evidently a parabola.

So far what we obtain from Eq. (10) is an Airy beam with unlimited spectrum. However, for the purpose of tracking the superoscillatory behavior, we are in need of a band-limited light field with a sharp spectrum limit. There are different ways of truncating the beam, leading to different modulations of the spectrum. The exponential truncation introduced in [9] will introduce a long-tailed Gaussian filter to the spectrum. A sharp limiting spectrum can be achieved by imposing a rectangular window, as was done in [11]. We choose the maximum spectrum to be S and use (11), and now the Airy beam changes to the incomplete one:

${\text{Ai}}_S\left(x,\xi \right)=\text{exp}\left[i\left(\frac{x\xi }{2}-\frac{{\xi }^3}{12}\right)\right]\underset{-S-\xi /2}{\overset{S-\xi /2}{{\displaystyle \int }}}ds\text{exp}\left[i\left(\frac{1}{3}{s}^3-\frac{1}{4}s{\xi }^2+sx\right)\right].(11)$

For the sake of clarity, we omit the integration limits of Eq. (11) and rewrite it into a compact form:

${\text{Ai}}_S\left(x,\xi \right)=U\left(x,\xi \right){\displaystyle \int V\left(s,x,\xi \right)ds}.(12)$

We use the subscript _S to denote the maximum transverse wave number. Note that due to the truncation, the second term in Eq. (12) is generally no longer a real function of x and ξ, as is the complete Airy function.

4 Superoscillations in Incomplete Airy Beams

4.1 Superoscillations in a Longisection

Now our task is to compute the phase gradient of the incomplete Airy beam given by (12). As the second term of (12) is complex, the overall phase φ(x,ξ) of the beam is not explicit, and we invoke formula 4:

$\nabla \phi \left(x,\xi \right)=\frac{\mathrm{\Im }\left({\text{Ai}}_S^{\text{*}}\nabla {\text{Ai}}_S\right)}{I\left(x,\xi \right)},(13)$

where I(x,ξ) = |Ai_s|² is the beam intensity. Using Eqs. (11) and (12), we expand the gradient in the numerator as:

$\begin{array}{l}{\partial }_x{\text{Ai}}_S\left(x,\xi \right)=\left(\frac{i}{2}\xi \right)U{{\displaystyle \int }}^{\text{}}Vds+U{{\displaystyle \int }}^{\text{}}isVds,\\ {\partial }_{\xi }{\text{Ai}}_S\left(x,\xi \right)=i\left(\frac{x}{2}-\frac{{\xi }^2}{4}\right)U{{\displaystyle \int }}^{\text{}}Vds+U{{\displaystyle \int }}^{\text{}}\left(-\frac{i}{2}s\xi \right)Vds.\end{array}(14)$

Substituting Eq. (14) into Eq. (13), we obtain:

${\partial }_x\phi \left(x,\xi \right)=\frac{\xi }{2}+\frac{\mathrm{\Im }\left\{{\displaystyle \int Vds}{\displaystyle \int i{s}^{\prime }Vd{s}^{\prime }}\right\}}{I},$

${\partial }_{\xi }\phi \left(x,\xi \right)=\frac{x}{2}-\frac{{\xi }^2}{4}+\frac{\mathrm{\Im }\left\{{\displaystyle \int Vds}{\displaystyle \int \left(-i{s}^{\prime }\xi /2\right)Vd{s}^{\prime }}\right\}}{I}.(15)$

We have numerically solved Eqs. (11) and (15) for an incomplete Airy beam truncated at S = 10, with x being in the range of 2π[−12.8,12.8] and the propagation range $\xi \in \left[\mathrm{0,15}\right]$. Figure 1 shows the beam intensity distribution normalized with respect to its maximum.

FIGURE 1

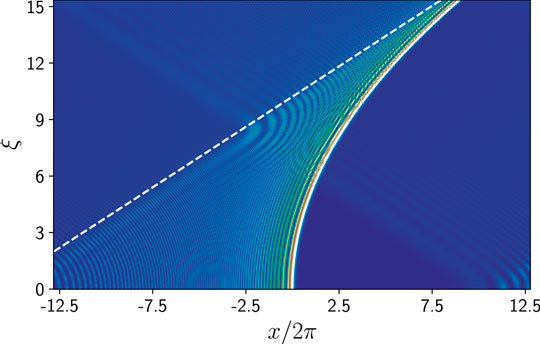
FIGURE 1. Density plot of the normalized beam intensity of the incomplete Airy beam, Ai_s=10(x,ξ). The white dashed line is the defining line x = Sξ−S², separating Airy-like and non–Airy-like regions. The beam retains Airy features to the right of the line. The white solid line is the main lobe parabola, x = ξ²/4.

According to [10], regions satisfying x > Sξ−S², that is, fields above the dashed white line, lost Airy-like features.

Both the total and the x₋ component phase gradients are computed and shown in Figure 2. Please note that for the total gradient $\nabla \phi \left(\text{r}\right)$, we plot the function ${\text{log}}_{10}\left(|\nabla \phi |-1\right)$ because the overall wave number is 1. We use the log function because negative arguments are automatically identified as invalid and rendered in white. It is interesting that superoscillations appear excluding the non–Airy-like regions for the transverse local wave number. However, for the total gradient, the entire beam region is superoscillatory. This means that the z− component of the gradient compensates that of the x− component. But this is clearly not due to evanescent waves (for which s > 1), as it is readily seen that as ξ increases, $|\nabla \phi |$ is getting larger, while the contribution from evanescent waves diminishes. The physics of such phenomena can be ascribed to the wave contents demonstrated by Eq. (11). For different longitudinal positions, the wave is a sum of different spectra because the limits of the integral are controlled by a window sliding with ξ; this induces the rapid change along ξ direction. From the integrand, we know that the integral can be approximated by contributions from the two saddle points, given by $s=\pm \sqrt{{\xi }^2/4-x}$. As the window slides, the window edges eventually cross the saddle points and leave only contributions from oscillatory regions, marked by the defining line x = Sξ−S².

FIGURE 2

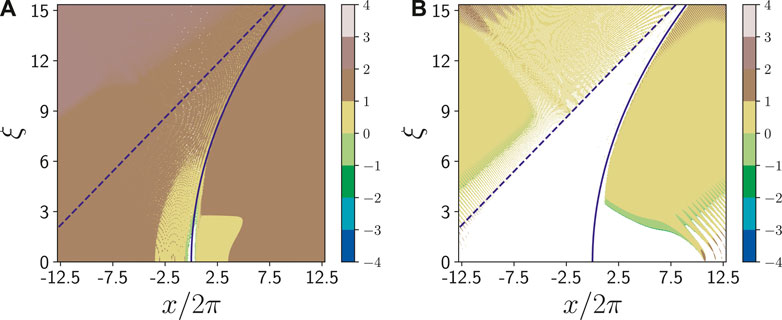
FIGURE 2. Density plots of the local phase gradients: a, ${\text{log}}_{10}\left(|\nabla \phi |-1\right)$ and b, ${\text{log}}_{10}\left(\left|{\partial }_x\phi \right|-S\right)$. In colored regions, the fields superoscillate, while in regions in white, the local wave number is smaller than the corresponding wave number. The defining line and the parabola are plotted in blue.

4.2 Superoscillations in Transverse Cross Sections

Now, we turn to the superoscillations in cross sections of a three-dimensional Airy beam. Without loss of generality, we concentrate on the x–y symmetric beam, that is, the beam is just the simple product of two incomplete one-dimensional Airy beams, one along each of the two transverse coordinates. The two-factor beams have the same truncations and other parameters. We denote the three-dimensional beam as Ai₃, and it is given in the simple separable form:

${\text{Ai}}_3\left(x,y,\xi \right)={\text{Ai}}_S\left(x,\xi \right)\times {\text{Ai}}_S\left(y,\xi \right).(16)$

We denote the overall phase function of Ai₃ by Ѱ(x,y) in a transverse cross section specified by ξ = ξ₀. Simple calculations give the following relation:

$\frac{{\text{Ai}}_3^{\text{*}}\left(x,y,{\xi }_0\right){\partial }_x{\text{Ai}}_3\left(x,y,{\xi }_0\right)}{\left|{\text{Ai}}_3\left(x,y,{\xi }_0\right)\right|{ }^2}=\frac{{\text{Ai}}_S^{\text{*}}\left(x,{\xi }_0\right){\partial }_x{\text{Ai}}_S\left(x,{\xi }_0\right)}{|{\text{Ai}}_S\left(x,{\xi }_0\right){|}^2},$

$\frac{{\text{Ai}}_3^{\text{*}}\left(x,y,{\xi }_0\right){\partial }_y{\text{Ai}}_3\left(x,y,{\xi }_0\right)}{\left|{\text{Ai}}_3\left(x,y,{\xi }_0\right)\right|{ }^2}=\frac{{\text{Ai}}_S^{\text{*}}\left(y,{\xi }_0\right){\partial }_y{\text{Ai}}_S\left(y,{\xi }_0\right)}{|{\text{Ai}}_S\left(y,{\xi }_0\right){|}^2}.(17)$

This means

${\partial }_x\text{Ψ}\left(x,y,{\xi }_0\right)={\partial }_x\phi \left(x,{\xi }_0\right),{\partial }_y\text{Ψ}\left(x,y,{\xi }_0\right)={\partial }_y\phi \left(y,{\xi }_0\right),(18)$

and we can use the computational results in the longisection to construct the local phase gradients in the transverse plane.

We used the same parameter set as in the 2 D case, for both the x and y directions. As shown in Figure 3, the main lobe position in each sub-figures is the intersection point of the two white solid line, which is computed using the parabola equation for a specified ξ₀ position. The dashed black lines are the defining lines separating different regions. Regions to the right of and above the horizontal black lines are Airy-like. As shown in Figure 1, the dashed and solid lines get tangent to each other at a particular value of ξ.

FIGURE 3

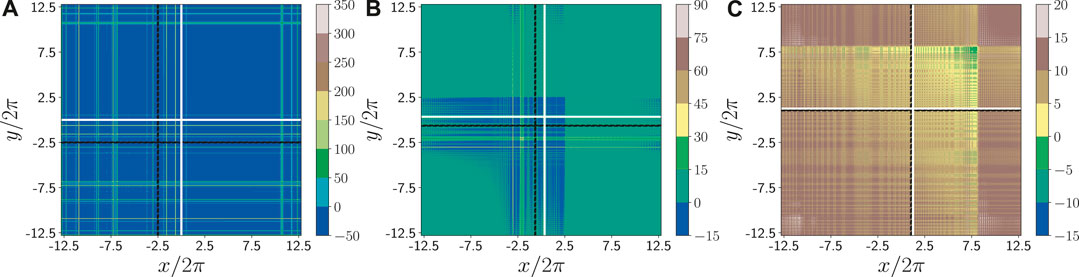
FIGURE 3. Shaded contour plots of the transverse phase gradient $|\nabla \text{Ψ}\left(x,y,{\xi }_0\right)|-/\sqrt{2}\text{\hspace{0.17em}S}$ for three different propagation distances: a, ξ₀ = 0.176; b, ξ₀ = 7.5; and c, ξ₀ = 14.063. Positive regions are superoscillatory, while negative ones are not. Solid white and dashed black lines are, respectively, the projections of the parabola and defining lines.

It is obvious that as the beam propagates, the Airy-like region (squares circumscribed by the white and black lines) gets increasingly smaller, while the superoscillating region gets increasingly larger. For small distance, ξ = 0.176, part of the lower left corner enclosed by the parabola is Airy-like, and part is not, while superoscillations occur only on discrete lines. For moderate distance, the beam region becomes totally non–Airy-like, but continuous area emerges as superoscillatory. For all the three cases, the Airy-like regions are always non-superoscillatory, agreeing with cases in the longisection.

5 Conclusion

In conclusion, we studied the superoscillatory behavior in an incomplete Airy beam in both a longisection and transverse cross sections. Sharply truncating the beam spectrum leads to the emergence of non–Airy-like regions in the beam area which gradually enlarge during propagation. However, in such regions, the fields can oscillate much faster than those in both the largest frequency and the Airy-like region. No finite area in the Airy-like region is found to support superoscillations.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author/s.

Author Contributions

YH conceived the research and derived equations about the incomplete Airy beams and the phase gradients, and XC and LN wrote the computational codes, computed the numerical results, and made the figure plots; the three authors wrote the manuscript.

Funding

The research presented in this article is financially supported by the Natural Science Foundation of Guangdong Province, China (Grant No. 2016A030307026).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors thank Tianle Li and Weiling Zhu in our department for their helpful discussions.

References

1. Aharonov Y, Bergmann PG, Lebowitz JL. Time symmetry in the quantum process of measurement. Phys Rev (1964) 134:B1410–B1416. doi:10.1103/PhysRev.134.B1410

CrossRef Full Text | Google Scholar

2. Berry MV, Popescu S. Evolution of quantum superoscillations and optical superresolution without evanescent waves. J Phys A: Math Gen (2006) 39:6965–77. doi:10.1088/0305-4470/39/22/011

CrossRef Full Text | Google Scholar

3. Huang FM, Chen Y, de Abajo FJG, Zheludev NI. Optical super-resolution through super-oscillations. J Opt A: Pure Appl Opt (2007) 9:S285–S288. doi:10.1088/1464-4258/9/9/s01

CrossRef Full Text | Google Scholar

4. Dennis MR, Hamilton AC, Courtial J. Superoscillation in speckle patterns. Opt Lett (2008) 33:2976–8. doi:10.1364/OL.33.002976

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Smith MK, Gbur GJ. Construction of arbitrary vortex and superoscillatory fields. Opt Lett (2016) 41:4979–82. doi:10.1364/OL.41.004979

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Makris KG, Psaltis D. Superoscillatory diffraction-free beams. Opt Lett (2011) 36:4335–7. doi:10.1364/OL.36.004335

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Berry MV, Balazs NL. Nonspreading wave packets. Am J Phys (1979) 47:264–7. doi:10.1119/1.11855

CrossRef Full Text | Google Scholar

8. Siviloglou GA, Broky J, Dogariu A, Christodoulides DN. Observation of accelerating airy beams. Phys Rev Lett (2007) 99:213901. doi:10.1103/PhysRevLett.99.213901

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Siviloglou GA, Christodoulides DN. Accelerating finite energy airy beams. Opt Lett (2007) 32:979–81. doi:10.1364/OL.32.000979

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Berry MV. Optical currents. J Opt A: Pure Appl Opt (2009) 11:094001. doi:10.1088/1464-4258/11/9/094001

CrossRef Full Text | Google Scholar

11. Ring JD, Howls CJ, Dennis MR. Incomplete airy beams: finite energy from a sharp spectral cutoff. Opt Lett (2013) 38:1639–41. doi:10.1364/OL.38.001639

PubMed Abstract | CrossRef Full Text | Google Scholar