A Three-Dimensional Dual-Band Terahertz Perfect Absorber as a Highly Sensitive Sensor

Terahertz (THz) absorbers are highly desirable in sensing and detection devices. Herein, we have proposed a 3D dual-band near-perfect absorber that works in the THz regime for sensing applications. The theoretical calculation shows that the absorption efficiency of the absorber can reach 99.0 and 97.0% at 1.125 and 1.626 THz, respectively. Double absorption peaks can be tuned independently by alternating the geometric parameters of unit resonators. The underlying physical mechanism of the absorber matches well with the well-known impedance matching theory. Compared with its planar counterpart, our proposed absorber exhibits a figure of merit enhancement of at least two times due to its out-of-plane induced large interfacial area. Additionally, the absorber can work robustly at a wide range of incident angles and keep insensitive to polarization states, which renders it great for highly sensitive sensing.

Introduction

Terahertz (THz) waves, ranging from 0.1 to 10 THz, have drawn enormous attention to a broad variety of applications such as THz imaging [1–3], communication [4–6], energy harvesting [7–9], and nano-trapping [10]. As a novel tool for controlling and manipulating electromagnetic waves, THz metamaterials, the artificial structures with periodic sub-wavelength patterns in the micrometer scale, can significantly improve light–matter interactions and show significant advantages in THz sensing and detection. The metamaterial-based THz absorber, especially the absorber with multiple frequency selectivity [11–13] or extremely narrow bandwidth [14], is one of the most notable devices in THz sensing and detection, which is typically configured with three layers, namely a metamaterial layer, a dielectric spacer, and a ground plane [15] and can perfectly characterize the refractive index (RI) of analytes by feature extraction from the absorption spectra.

In recent years, a massive number of efforts have been devoted to exploring meta-absorber-based high sensitivity THz sensors [16–20]. For example, Shin et al. have developed the metamaterial to detect the 4-Methylimidazole by a planar metal array using an electric-field-coupled inductor-capacitor (ELC) resonator structure [18]. It can be observed that the metamaterial layer remains constrained to the two-dimensional plane, which hinders the precise sensitivity of the metamaterial for the sensing purpose. Wang et al. have presented several THz sensors with a rather narrow bandwidth excited from the interaction of neighboring unit cells [21, 22] or the combined effect of localized resonance and surface lattice resonance [23], resulting in the enhancement of sensing performance. To overcome the in-plane limit of the traditional metamaterial, Wang et al. [24] have proposed a 3D split-ring resonator-based THz sensor with enhanced sensing sensitivity by eliminating the bianisotropy to induce an LC resonance of high-quality factor and reducing the dielectric loss of the substrate. Zhou et al. [25] proposed an out-of-plane THz biosensor that consists of a cross-shaped, plate-hole structure-based absorber, which can significantly improve the sensing sensitivity by enlarging the spatial overlap between the analyte and the locally enhanced electromagnetic field (hot-spots). Therefore, the 3D metamaterial can improve the sensitivity by tuning the interfacial interaction with the analyte. In addition, Chen et al. [20] have proposed a graphene-based metamaterial that can excite multiple plasmonic resonant modes and achieve high sensing sensitivity due to its unique 3D meta-structure. However, some of these THz sensors might face the paradox of simple fabrication and multiband resonant peaks with high sensitivity simultaneously.

In this paper, we have proposed a 3D dual-band and easily fabricated THz absorber utilized to detect the RI of analytes. The electric field and the current distributions are used to explain the near-unity absorption phenomenon. The absorption spectra at different incident angles and polarization angles as well as the geometric parameters are systematically analyzed. The proposed absorber exhibits great sensing performance and might have great potential in highly sensitive sensing.

Structure and Design

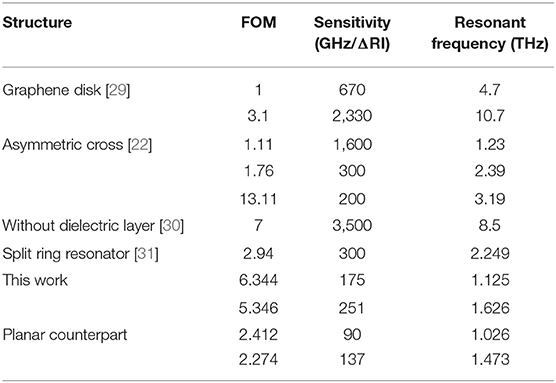
Figure 1A shows that the THz metamaterial absorber (meta-absorber) consists of three independent layers including two layers of gold with a conductivity of σ = 4.561 × 10⁷ S/m as the ground and resonator and a middle layer of polyimide (PI) with a dielectric constant of ε = 3.5(1+0.0027i). Differing from traditional planar designs by embedding the metal into the dielectric plane [26] or depositing the metal on the plane, the unit cell has a 3D structure by building the dielectric layer out of the middle dielectric plane. The unit cell of the proposed absorber involves a square ring and four triangles. The period (p) of the unit cell is set as 120 μm. The side length (w₁) and the metal width (h) of the square ring are set as 60 and 14 μm, respectively. The length of the right triangles (w₂) is set as 35 μm. The thicknesses of the gold (t₁) and dielectric (t) are 200 nm and 4 μm, respectively. To evaluate the performance of the proposed 3D meta-absorber, a corresponding planar absorber is also modeled with the same geometrical parameters as shown in Figure 1B. All numerical simulations and analyses are carried out by using the CST Microwave Studio full-wave simulator (2019). Unit cell boundary conditions are incorporated for the transverse boundaries of the unit cell, while open (add space) boundary conditions are applied along the z-axis. Unless otherwise stated, the incident wave illuminates along the negative z-axis with zero polarization angle.

FIGURE 1

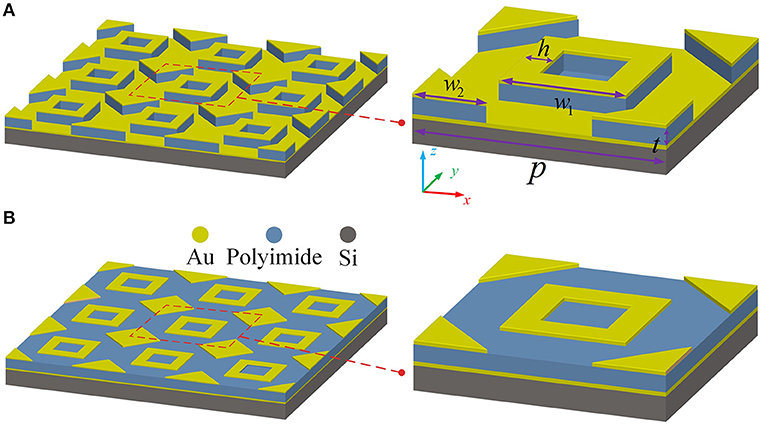
Figure 1. (A) The 3D schematic view of the meta-absorber and its enlarged unit cell with geometric parameters: period p = 120 μm, the width of the square ring w₁ = 60 μm, h = 14 μm, the side length of right triangles w₂ = 35 μm, the thickness of polyimide t = 4 μm, and the thickness of Au is 200 nm. (B) The 3D view of the planar absorber and the enlarged view of its unit cell with the same dimensions as the meta-absorber, except the polyimide layer becomes a complete plane.

Numeral Simulation and Discussion

Basic Characteristics

To investigate the absorption performance of the proposed meta-absorber, its reflection and absorption spectra under the normal THz incidence are shown in Figure 2A. The absorption can be simplified as $A=1-R=1-S_{11}^2$, where R represents the reflection and S₁₁ represents the reflection coefficient extracted from the CST simulation. It can be evidently observed that the absorption spectrum of meta-absorber has a dual-band feature due to the combined rectangular and triangle resonators when interacting with the incident waves. Two absorption peaks reach as high as 99.0 and 97.0% at 1.125 THz (f₁) and 1.626 THz (f₂), respectively. The transmission of the incident THz waves through the meta-absorber can be ignored due to the existence of metal ground with thickness beyond the skin depth (200 nm) at the frequency of interest. Similarly, the traditional planar absorber also has two absorption peaks with amplitudes around 96.6 and 97.9% at 1.026 and 1.473 THz, respectively. Quality factor (Q), defined as Q = f_i/FWHM, is utilized to quantify the resonant performance of two absorbers, where f_i(i = 1, 2) is the resonant frequency and FWHM refers to the full width at a half maximum of the absorption. As a result, the Q values of the two resonant frequencies are 27.2 and 24.4 for the planar absorber, while they are 26.4 and 25.4 for the meta-absorber. In general, metamaterial absorbers with high absorption (or Q value) and high sensitivity are highly desirable in the research community; nonetheless, for most cases, it is truly demanding to augment the absorption and high sensitivity simultaneously. For our proposed 3D absorber, the sensitivity can be enhanced almost two times as discussed in the later section, while the absorption (at f₂) and Q value (at f₁) of the meta-absorber are less than that of the planar absorber, demonstrating that the difference of absorption Q value between two absorbers is trivial and does not affect the sensing performance.

FIGURE 2

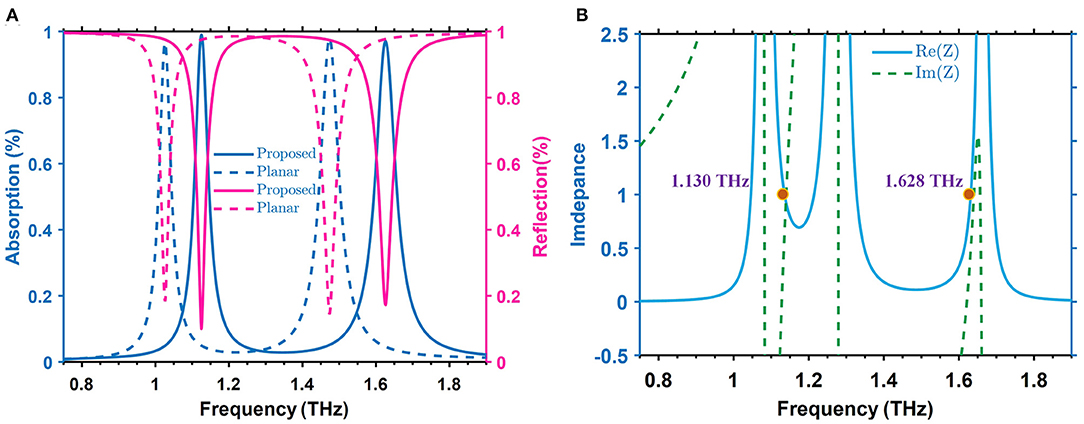
Figure 2. (A) The absorption (blue solid line) and reflection (red solid line) spectrum of the meta-absorber and the absorption (blue dashed line) and reflection (red dashed line) spectrum of the planar absorber. (B) The real part Re(Z(ω)) and imaginary part Im(Z(ω)) of impedance Z(ω) retrieved from S-parameters.

Physical Mechanism and Theory Analysis

The impedance matching theory has been widely utilized to interpret the near-perfect absorption mechanism [27]. Here, the effective impedance of meta-absorber is described as $Z_1=\sqrt{\mu (\omega )/\epsilon (\omega )}$, where ε(ω) refers to the complex electric permittivity and μ(ω) refers to the magnetic permeability of the absorber. Then, the relative impedance Z(ω) can be written as

$\begin{array}{ll}Z(\omega )=\frac{Z_1}{Z_0}=\sqrt{\frac{{(1+S_{11})}^2-S_{21}^2}{{(1-S_{11})}^2-S_{21}^2}},& (1)\end{array}$

where Z₀ is the impedance of the free space and S₁₁, S₂₁ are the S-parameters extracted from the CST simulation. Figure 2B shows the real and imaginary parts of Z(ω). It can be found that the real part and imaginary part are close to 1 and 0 at the near-unity absorption peaks, respectively, which indicates that the effective impedance of the meta-absorber at resonant frequencies matches well with that of free space. From the impedance matching theory, the proposed unit cell might intrigue the dual-band feature based on the independent design of the unit cell of meta-absorber.

To better understand the underlying physical mechanism of the meta-absorber, the distributions of electric field and surface current are rigorously calculated under the transverse electric (TE) mode. Figure 3A shows that the electric field at f₁=1.125 THz is highly confined at the top and bottom arm of the square ring, which can be ascribed to the excitation of an electric dipole and agrees well with the surface current distributions in Figure 3C. At f₂=1.626 THz in Figure 3B, the electric field concentrates at all edges of the four triangles by introducing an electric quadrupole. The surface current distribution of f₂ shown in Figure 3D indicates that the y-component of surface current is consistent with the direction of the TE waves. From the electric field and surface current distribution, it is suggested that the dual-band absorption spectra are individually excited from the two divergent resonators and there is no straightforward cross-coupling between the two resonators in the unit cell, which makes it possible to control the two absorption peaks independently.

FIGURE 3

Figure 3. The average electric field distributions of different resonators at (A) f₁=1.125 THz and (B) f₂ = 1.626 THz under normal incidence. The corresponding current distributions on the top surface at (C) f₁ and (D) f₂.

To explore the effects of the geometric parameters on the absorption spectra, w₁, h, w₂, and t are systematically screened. As depicted in Figure 4A, when w₁ changes from 50 to 70 μm every 5 μm, f₁ experiences an apparent redshift while f₂ stays relatively stable, which indicates that the square ring accounts for the dynamic change of band f₁during the geometrical design. On the contrary, when increasing w₂ from 20 to 47 μm every 3 μm, f₁ remains unchanged while f₂ has a distinct redshift, which is shown in Figure 4B. Interestingly, by further expanding the triangles, the absorption peaks of double bands will first coincide and finally separate again. In other words, each resonant mode is independently excited and tuned from the optimal structural design of a square ring and triangles. When the distance between the square ring and triangles is shortened gradually, f₁ and f₂ begin to interact with each other. Once the distance reaches the critical limit, the original resonant modes will be destroyed and a new resonant mode will be excited. Figure 4C shows the evolution of the absorption spectra under different h. Similar to Figure 4A, f₂ remains unchanged while f₁ varies drastically, in both frequency and absorption amplitude. This unchanged f₂ mode further proves the independent tuning abilities of the square ring for the incident waves. Figure 4D shows the variations of the different thicknesses of the insulator layer on the absorption spectra. It can be observed that f₁ exhibits the frequency blueshift and uncontrollable amplitude change. f₂ sticks to the initial resonant mode but experiences significant decrement (close to one-half) of the absorption amplitude. This phenomenon can be well-explained by using the interference theory [28]. Based on this theory, a partial incidence wave reflects directly from the top layer of the absorber while the remaining part transmits into the dielectric layer until it reaches the ground. Under multiple reflections, it will propagate back to the top surface again, which indicates that the overall reflection is attributed to the superposition of the direct reflection and multiple reflections. The thickness of the dielectric layer plays an important role in the phase delay, which results in constructive/destructive interference and further modulates the absorption spectra. It is worth noting that reflection can always reach zero by optimizing the dielectric thickness.

FIGURE 4

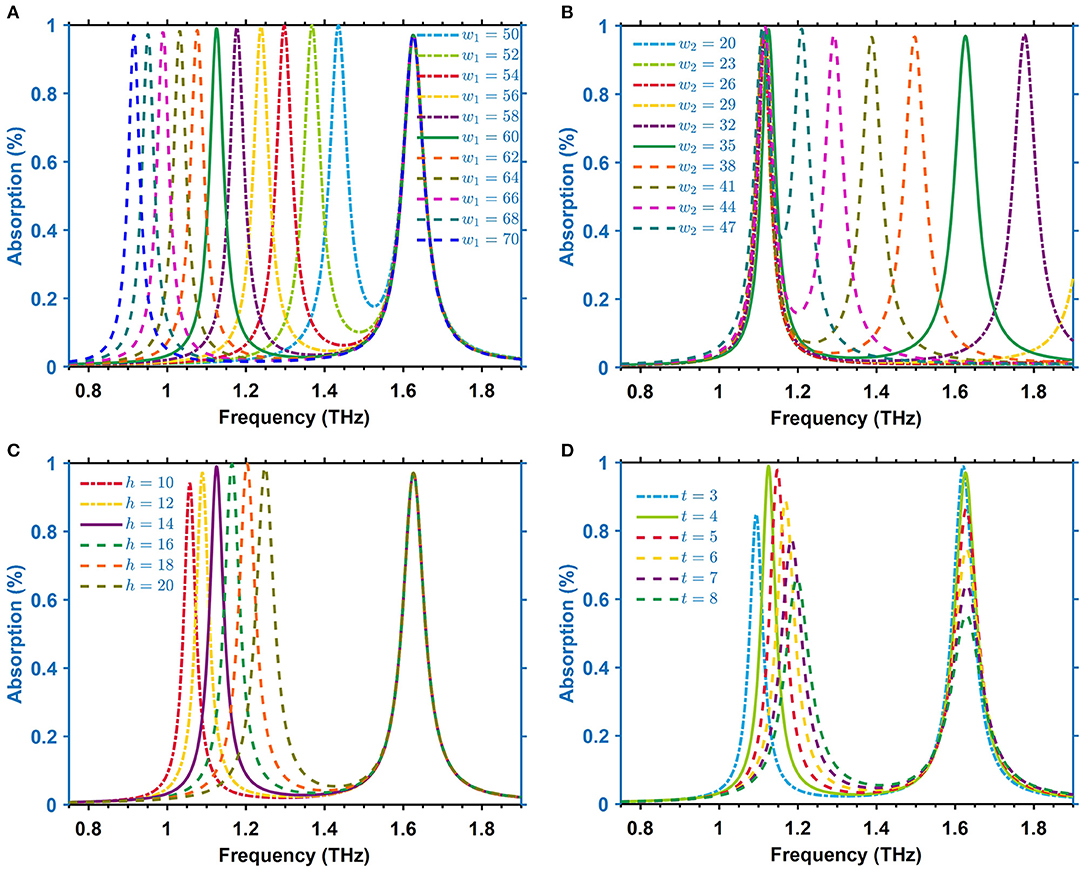
Figure 4. The shifts of absorption peak with different geometric parameters; (A,C) the width of the square ring w₁, h, respectively (B), the length of the right triangles w₂, and (D) the thickness of dielectric layer t.

Figure 5A shows the schematic diagram of the polarization and incident angles of THz waves. Figure 5B shows the convolution between polarization angles and absorption spectra under TE mode along the y-axis. The double band absorption spectra remain consistent, while polarization angles change from 0 to 90° under the normal incidence. In other words, the meta-absorber stays insensitive to the polarization states, which can be attributed to the symmetrical structure. In the above studies, the absorption characteristics of the meta-absorber are investigated with the normal incident angles; however, an absorber with high absorption efficiency at an oblique incident angle is highly desirable for practical applications. In Figure 5C, the peak amplitude of double band absorption spectra under TE mode keeps over 80% until the angle of incidence passes through 70°. Starting from an incident angle of 40°, a redshift occurs on f₂ and a new absorption peak is generated. When the incident angle changes from 40 to 70°, the bandwidths become narrower and the figure of merit (FOM) can be largely enhanced. Under the transverse magnetic (TM) mode in Figure 5D, not only the intensity but also the bandwidth of f₁ remains unchanged until the angle passes over 85°. f₂ shows a similar tendency as that under TM mode. For both TE and TM modes, the insensitivity when the incident angle is <35° will be beneficial to the sensing performance under crucial testing conditions. Moreover, it is evident that f₂ shifts drastically than f₁ for both TE and TM modes, which is resulted from the fact that f₂ is electrically induced by the triangle edges, and the effective component acting on those edges would decrease with the increment of incident angles. It is worth noting that the sensitivity of the planar absorber to polarization states and incident angles (Supplementary Figure 1) shows a slight difference in the absorption amplitudes and the frequency shift (FS).

FIGURE 5

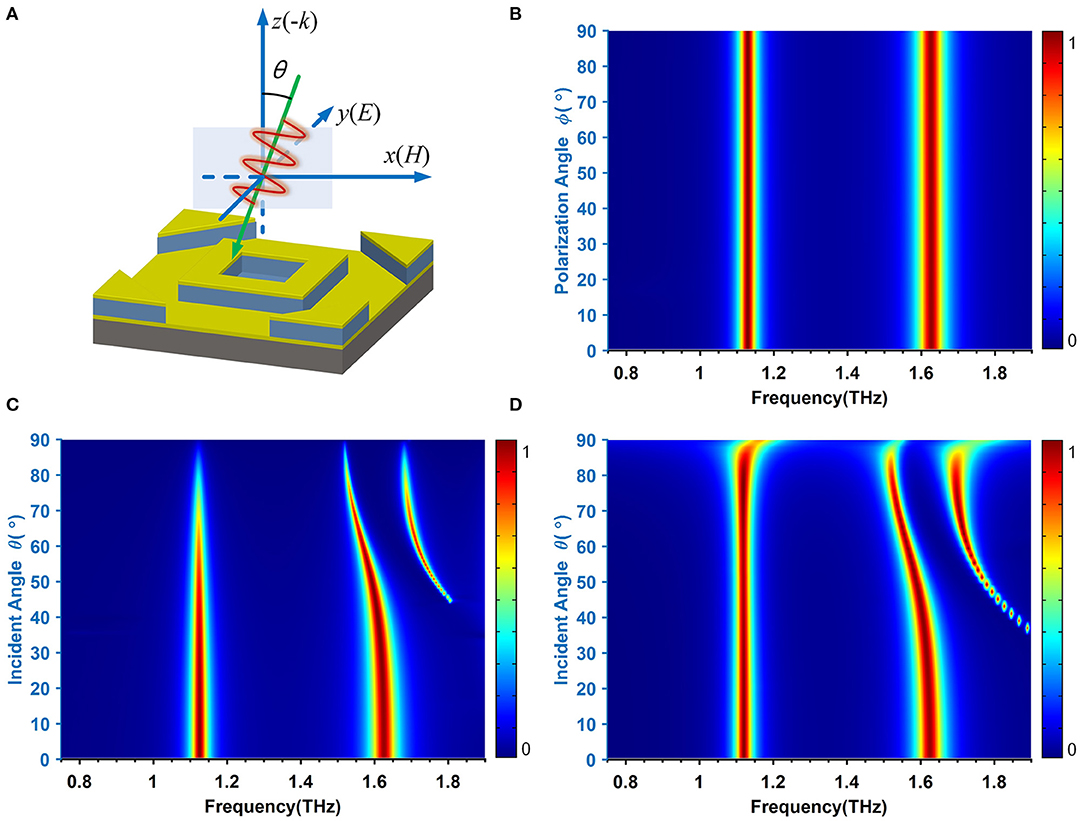
Figure 5. (A) The schematic diagram of the incident angle of THz waves. (B) Absorption spectra with different polarization angles ϕ under normal incidence. Absorption spectra under different incident angles θ under (C) TE mode and (D) TM mode.

To unveil the underlying mechanism of the occurrence of the new peak from an incident angle of 40°, we have extracted the electric field at 1.7 THz with an incident angle of 60°. It can be observed that the electric field mainly localizes at the corners of the triangle surface under TE and TM modes shown in Figures 6A,B, respectively. The difference in the distribution of the electric field from that at 1.125 and 1.626 THz indicates that the new absorption peak results from the electric quadrupole resonant mode under the oblique incidence.

FIGURE 6

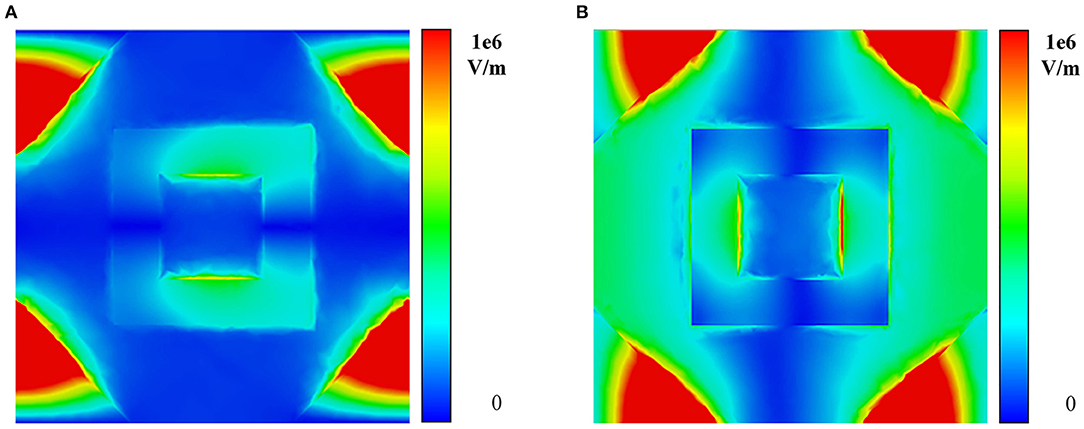
Figure 6. The average electric field distribution at 1.7 THz with an incident angle of 60° under (A) TE mode and (B) TM mode.

Sensing Performance

The sensing behavior of the meta-absorber is examined by analyzing the absorption spectra when a layer of the analyte with the thickness fixed as 8 μm covers the sensor surface. Figure 7A shows that both f₁ and f₂ of the meta-absorber experience the redshift as the RI of the analyte increases from 1.0 to 2.0. Two resonant frequencies of the planar absorber as portrayed in Figure 7B follow a similar trend but are less pronounced than that of meta-absorber. To quantificationally estimate the performance of two absorbers, the sensitivity (S) is introduced as S = FS/ΔRI to assess their performance. The FS is defined as FS = f−f₀, where f₀ is the frequency when the RI equals 1 and ΔRI refers to the change of RI. S at f₁ and f₂ for the meta-absorber can achieve 175 GHz/ΔRI and 251 GHz/ΔRI. In contrast, S for the planar absorber is limited up to 90 GHz/ΔRI and 137 GHz/ΔRI. The near-half cutoff of the sensitivity demonstrates that the sensor sensitivity can be enhanced almost two times by transforming the planar resonator into the proposed 3D resonator. It is apparent that S at f₂ for both absorbers is highly sensitive to the changes of the RI.

FIGURE 7

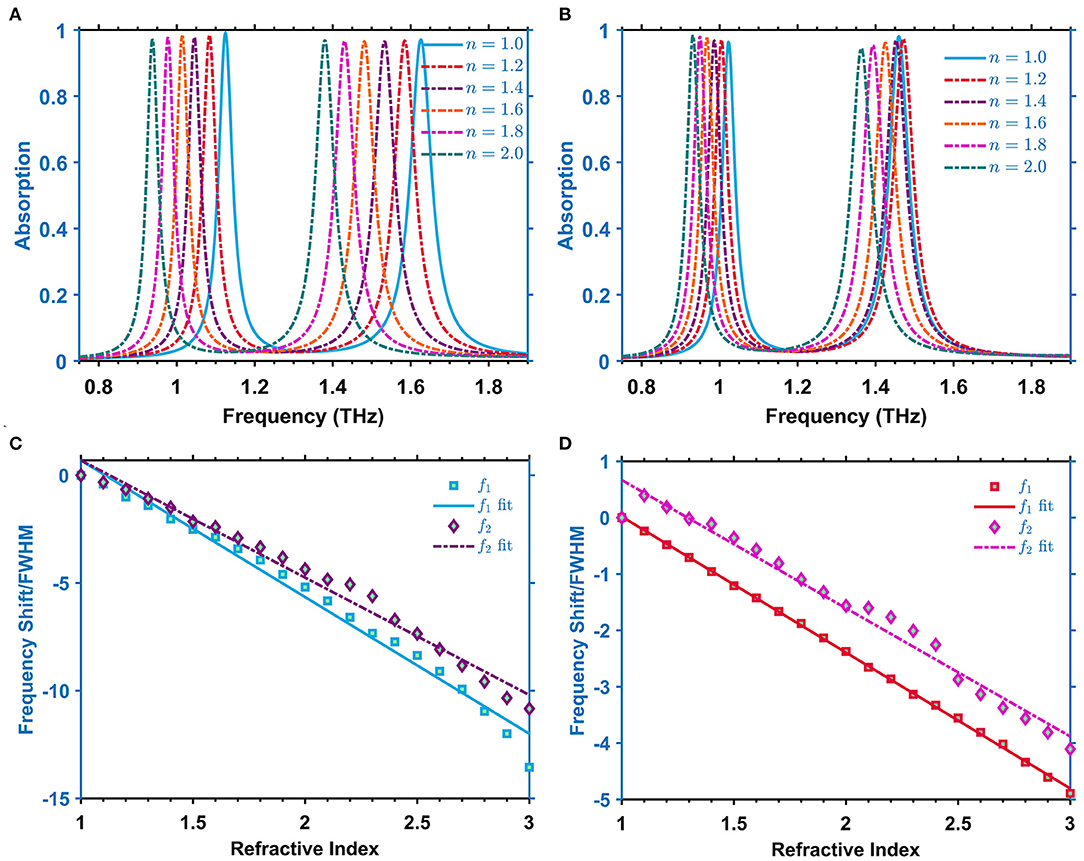
Figure 7. The shifts of the absorption spectra of analytes with different refractive indices of (A) the meta-absorber and (B) the planar absorber. Frequency shift/FWHM as a function of the refractive index of (C) the meta-absorber and (D) the planar absorber. The analyte thickness h here is set as 8 μm.

By involving the impact of the resonant frequency on the absorption spectra, the FOM is introduced to evaluate the capability more practically, which can be written as [26]

$\begin{array}{ll}\text{FOM}=\frac{\text{FS}}{\text{FWHM}}·\frac{1}{\Delta RI}.& (2)\end{array}$

As shown in Figure 7C, the fitted line at f₁ of the meta-absorber inclines more obliquely than that at f₂, which indicates that f₁ has a higher FOM (6.344) than f₂ (5.446). The smaller FOM at f₂ can be attributed to the fact that the bandwidths of the absorption spectra are broadened when resonant frequencies experience the blueshift. For the planar absorber shown in Figure 7D, f₁ and f₂ are almost parallel to each other with close FOMs, namely 2.412 and 2.274, respectively, which indicates that the influence of the resonant frequency on the absorption spectra can be ignored. The change in FOM suggests that the sensing FOM of the meta-absorber has been effectively enhanced 2.6 times when compared to the planar absorber.

In order to investigate the advantages of the meta-absorber, the comparison of the sensing performances between the meta-absorber and the planar counterpart, together with some previous work, is listed in Table 1. As shown in Table 1, the suggested meta-absorber shows considerable FOM among its competitors; however, one can also notice that the sensitivity of this work shows insufficient superiority, which can be attributed that a more remarkable frequency shift will be easily attained if the resonant frequency is higher. The resonant frequencies of the meta-absorber are obviously lower, thus resulting in less sensitivity; nevertheless, the sensitivity improvement by a factor of almost two can be still realized as compared with its planar counterpart, indicating that the meta-absorber achieves effective enhancement in FOM as well as sensitivity.

TABLE 1

Table 1. Comparison of sensing performance.

To further explore the impact of the analyte thicknesses on the FOM, t_A in Figure 8 is swept from 5 μm to 17 μm. For both absorbers, FOM at f₁ and f₂ will be enhanced when t_A increases from 5 μm to 11 μm. However, as shown in Figures 8B,D, the singularities of FOM at f₂ indicate that the absorption spectra at f₁ might be more suitable in providing valuable sensing data. The disorder of FOM at f₂ is highly suppressed in the meta-absorber; therefore, it shows a better FOM than that of the planar structure. Thus, the absorption spectra at f₁ for the meta-absorber are more favorable in estimating the sensing performance of the analyte.

FIGURE 8

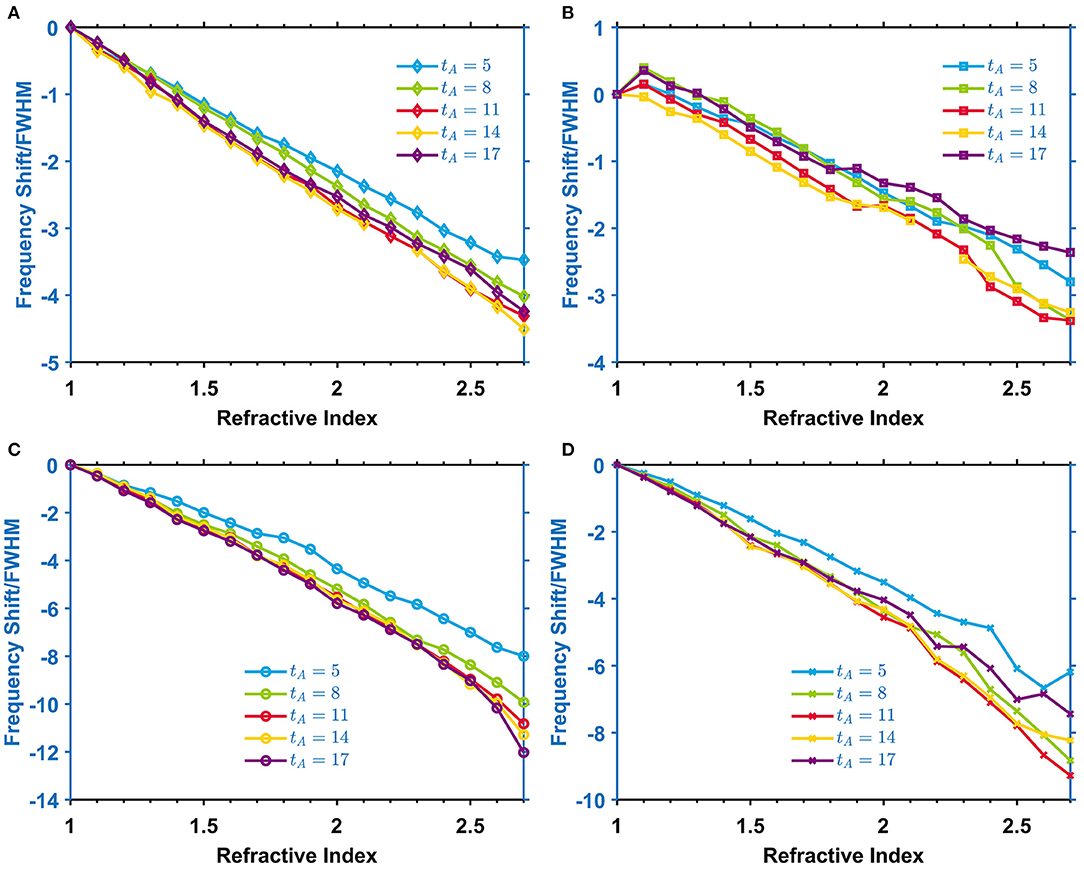
Figure 8. The frequency shift/FWHM as a function of refractive index at f₁ (A) and f₂ (B) of the planar absorber, and (C,D) of meta-absorber, as analyte thickness t_A changes from 5 to 17 μm with an increment of 3 μm.

It was found from testing the analyte with different RI and thickness that the proposed meta-absorber exhibits a large enhancement of FOM that can be explained by the following reasons. Firstly, the shape of the dielectric layer plays a crucial role in energy dissipation loss. Figures 3A,B show that the electromagnetic field is principally confined around the areas between the dielectric and the metal at the resonant frequency, which agrees well with previous research [32]. Once the planar dielectric is broken into pieces, the interfacial contact area is largely increased, which will result in a significant enhancement in the interaction between the analytes and the absorber. In other words, more incident energy confined at the internal side of the absorber will leak out and transfer to the analytes. Therefore, the absorption spectra will be significantly affected by the 3D structure which is inaccessible through the traditional planar absorber. Secondly, it can be seen from Figure 7 that larger a RI will result in the redshift of the resonant peak, and, in turn, a small RI will result in the blueshift of the resonant peak. As for the meta-absorber without any analytes, the equivalent RI can be regarded as the combination of the RI of the air and the absorber. Since there is a lesser filling ratio of the dielectric but more air in the meta-absorber, its RI is lower than that of the planar absorber, which can further explain why the resonant frequencies of the meta-absorber are higher than that of the planar absorber, as depicted in Figure 2A. Furthermore, when the analyte fully covers the meta-absorber by replacing the existing air, the RI will increase significantly and exhibit high sensitivity to the change in RI.

Conclusion

In conclusion, we have proposed a dual-band near-perfect THz absorber with the unit cell consisting of an out-of-plane square ring and four out-of-plane triangles. The absorption amplitudes can reach up to 99.0 and 97.0% at 1.125 and 1.626 THz, respectively. The resonant frequencies of the meta-absorber enable independent modulation by adjusting the geometrical parameters for different resonators. Additionally, the absorber is insensitive to the polarization and functions normally with a wide range of incident angles up to 40°. Compared with the traditional planar absorber, the sensitivity and the FOM of the proposed meta-sensor to analyte sensing are strongly enhanced by a factor of two due to the increased contact area between the analytes and the absorber. It can be estimated that the proposed meta-absorber in the THz regime will promote significant prospects in highly sensitive sensing and shed light on novel functional THz devices.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

WY performed the numerical calculation and wrote the manuscript. ZS and SL performed the data analysis and provided constructive discussions. LZ and XC are the main supervisors, and they provided supervision and feedback and reviewed the research.

Funding

This work was supported by the Science and Technology Innovation Committee of Shenzhen Municipality (Grant no. JCYJ20180306170652664 to LZ), the National Natural Science Foundation of China (Grant no. 51805414), and the Zhejiang Provincial Natural Science Foundation of China (Grant no. LZ19A020002).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.665280/full#supplementary-material

References

1. Hu BB, Nuss MC. Imaging with terahertz waves. Optics Letters. (1995) 20:1716–8. doi: 10.1364/OL.20.001716

CrossRef Full Text | Google Scholar

2. Li B, Wang R, Ma JJ, Xu WH. Research on crop water status monitoring and diagnosis by terahertz imaging. Front. Phys. (2020) 8:571628. doi: 10.3389/fphy.2020.571628

CrossRef Full Text | Google Scholar

3. Li JT, Li J, Zheng CL, Wang SL, Li MY, Zhao HL, et al. Dynamic control of reflective chiral terahertz metasurface with a new application developing in full grayscale near field imaging. Carbon. (2021) 172:189–99. doi: 10.1016/j.carbon.2020.09.090

CrossRef Full Text | Google Scholar

4. Jornet JM, Akyildiz IF. Graphene-based plasmonic nano-antenna for terahertz band communication in nanonetworks. IEEE J Sel Area Commun. (2013) 31:685–94. doi: 10.1109/JSAC.2013.SUP2.1213001

CrossRef Full Text | Google Scholar

5. Nagatsuma T, Horiguchi S, Minamikata Y, Yoshimizu Y, Hisatake S, Kuwano S, et al. Terahertz wireless communications based on photonics technologies. Opt Express. (2013) 21:23736–47. doi: 10.1364/OE.21.023736

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Dash S, Liaskos C, Akyildiz IF, Pitsillides A. Nanoantennas design for THz communication: material selection and performance enhancement. In: Proceedings of the 7th ACM International Conference on Nanoscale Computing and Communication. (Catania) (2020). doi: 10.1145/3411295.3411312

CrossRef Full Text | Google Scholar

7. Dragoman M, Aldrigo M. Graphene rectenna for efficient energy harvesting at terahertz frequencies. Appl Phys Lett. (2016) 109:113105. doi: 10.1063/1.4962642

CrossRef Full Text | Google Scholar

8. Pierobon M, Jornet JM, Akkari N, Almasri S, Akyildiz IF. A routing framework for energy harvesting wireless nanosensor networks in the terahertz band. Wirel Netw. (2014) 20:1169–83. doi: 10.1007/s11276-013-0665-y

CrossRef Full Text | Google Scholar

9. Shih E, Cho SH, Ickes N, Min R, Sinha A, Wang A, et al. Physical layer driven protocol and algorithm design for energy-efficient wireless sensor networks. In:Proceedings of the 7th Annual International Conference on Mobile Computing and Networking. (Rome) (2001). doi: 10.1145/381677.381703

CrossRef Full Text | Google Scholar

10. Shen ZL, Becton M, Han DH, Fang XD, Wang XQ, Zhang LY, et al. Terahertz plasmonic nanotrapping with graphene coaxial apertures. Phys Rev A. (2020) 102:053507. doi: 10.1103/PhysRevA.102.053507

CrossRef Full Text | Google Scholar

11. Wang BX. Quad-band terahertz metamaterial absorber based on the combining of the dipole and quadrupole resonances of two SRRs. IEEE J Sel Top Quantum Electr. (2017) 23:1–7. doi: 10.1109/JSTQE.2016.2547325

CrossRef Full Text | Google Scholar

12. Wang BX, He YH, Lou PC, Zhu HX. Multi-band terahertz superabsorbers based on perforated square-patch metamaterials. Nanoscale Adv. (2021) 3:455–62. doi: 10.1039/D0NA00903B

CrossRef Full Text | Google Scholar

13. Wang BX, He YH, Lou PC, Huang WQ, Pi FW. Penta-band terahertz light absorber using five localized resonance responses of three patterned resonators. Results Phys. (2020) 16:102930. doi: 10.1016/j.rinp.2020.102930

CrossRef Full Text | Google Scholar

14. Wang BX, Tang C, Niu Q, He Y, Chen T. Design of narrow discrete distances of dual-/triple-band terahertz metamaterial absorbers. Nanoscale Res Lett. (2019) 14:64. doi: 10.1186/s11671-019-2876-3

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Duan GW, Schalch J, Zhao XG, Li AB, Chen CX, Averitt RD, et al. A survey of theoretical models for terahertz electromagnetic metamaterial absorbers. Sensor Actuator A Phys. (2019) 287:21–8. doi: 10.1016/j.sna.2018.12.039

CrossRef Full Text | Google Scholar

16. Xu W, Xie L, Zhu J, Wang W, Ye Z, Ma Y, et al. Terahertz sensing of chlorpyrifos-methyl using metamaterials. Food Chem. (2017) 218:330–4. doi: 10.1016/j.foodchem.2016.09.032

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Meng L, Zhao D, Ruan Z, Li Q, Yang Y, Qiu M. Optimized grating as an ultra-narrow band absorber or plasmonic sensor. Opt Lett. (2014) 39:1137–40. doi: 10.1364/OL.39.001137

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Shin HJ, Jang HW, Ok G. Highly sensitive detection of 4-methylimidazole using a terahertz metamaterial. Sensors. (2018) 18:4304. doi: 10.3390/s18124304

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Xu WD, Xie LJ, Zhu JF, Tang LH, Singh R, Wang C, et al. Terahertz biosensing with a graphene-metamaterial heterostructure platform. Carbon. (2019) 141:247–52. doi: 10.1016/j.carbon.2018.09.050

CrossRef Full Text | Google Scholar

20. Chen X, Fan WH, Song C. Multiple plasmonic resonance excitations on graphene metamaterials for ultrasensitive terahertz sensing. Carbon. (2018) 133:416–22. doi: 10.1016/j.carbon.2018.03.051

CrossRef Full Text | Google Scholar

21. Wang BX, Zhai X, Wang GZ, Huang WQ, Wang LL. A novel dual-band terahertz metamaterial absorber for a sensor application. J Appl Phys. (2015) 117:014504. doi: 10.1063/1.4905261

CrossRef Full Text | Google Scholar

22. Wang BX, Wang GZ, Sang T. Simple design of novel triple-band terahertz metamaterial absorber for sensing application. J Phys D Appl Phys. (2016) 49:7. doi: 10.1088/0022-3727/49/16/165307

CrossRef Full Text | Google Scholar

23. Wang BX, He YH, Lou PC, Xing WH. Design of a dual-band terahertz metamaterial absorber using two identical square patches for sensing application. Nanoscale Adv. (2020) 2:763–9. doi: 10.1039/C9NA00770A

CrossRef Full Text | Google Scholar

24. Wang W, Yan FP, Tan SY, Zhou H, Hou YF. Ultrasensitive terahertz metamaterial sensor based on vertical split ring resonators. Photonics Res. (2017) 5:571–7. doi: 10.1364/PRJ.5.000571

CrossRef Full Text | Google Scholar

25. Zhou H, Yang C, Hu DL, Li DX, Hui XD, Zhang F, et al. Terahertz biosensing based on bi-layer metamaterial absorbers toward ultra-high sensitivity and simple fabrication. Appl Phys Lett. (2019) 115:143507. doi: 10.1063/1.5111584

CrossRef Full Text | Google Scholar

26. Kang M, Zhang HF, Zhang XQ, Yang QL, Zhang WL, Han JG. Interferometric control of dual-band terahertz perfect absorption using a designed metasurface. Phys Rev Appl. (2018) 9:054018. doi: 10.1103/PhysRevApplied.9.054018

CrossRef Full Text | Google Scholar

27. Smith DR, Vier DC, Koschny T, Soukoulis CM. Electromagnetic parameter retrieval from inhomogeneous metamaterials. Phys Rev E Stat Nonlin Soft Matter Phys. (2005) 71:036617. doi: 10.1103/PhysRevE.71.036617

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Chen HT. Interference theory of metamaterial perfect absorbers. Opt Express. (2012) 20:7165–72. doi: 10.1364/OE.20.007165

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Li J, Liao QH, Li HM, Liu WX, Yu TB, Wang TB. Tunable dual-band perfect metamaterial absorber based on monolayer graphene arrays as refractive index sensor. Jpn J Appl Phys. (2020) 59:095002. doi: 10.35848/1347-4065/aba9a5

CrossRef Full Text | Google Scholar

30. Hu X, Xu GQ, Wen L, Wang HC, Zhao YC, Zhang YX, et al. Metamaterial absorber integrated microfluidic terahertz sensors. Laser Photonics Rev. (2016) 10:962–9. doi: 10.1002/lpor.201600064

CrossRef Full Text | Google Scholar

31. Saadeldin AS, Hameed MFO, Elkaramany EMA, Obayya SSA. Highly sensitive terahertz metamaterial sensor. IEEE Sens J. (2019) 19:7993–9. doi: 10.1109/JSEN.2019.2918214

CrossRef Full Text | Google Scholar

32. Wang W, Yan FP, Tan SY, Li HS, Du XM, Zhang LN, et al. Enhancing sensing capacity of terahertz metamaterial absorbers with a surface-relief design. Photonics Res. (2020) 8:519–27. doi: 10.1364/PRJ.386040

CrossRef Full Text | Google Scholar