- Molecular Nanophotonics Group, Peter Debye Institute for Soft Matter Physics, Leipzig University, Leipzig, Germany
The Maxwell–Boltzmann distribution is a hallmark of statistical physics in thermodynamic equilibrium linking the probability density of a particle’s kinetic energies to the temperature of the system that also determines its configurational fluctuations. This unique relation is lost for Hot Brownian Motion, e.g., when the Brownian particle is constantly heated to create an inhomogeneous temperature in the surrounding liquid. While the fluctuations of the particle in this case can be described with an effective temperature, it is not unique for all degrees of freedom and suggested to be different at different timescales. In this work, we report on our progress to measure the effective temperature of Hot Brownian Motion in the ballistic regime. We have constructed an optical setup to measure the displacement of a heated Brownian particle with a temporal resolution of 10 ns giving a corresponding spatial resolution of about 23 pm for a 0.92
1 Introduction
Brownian motion provides a window to microscopic dynamics. Observing the erratic motion of a colloid in a fluid delivers information on the strong interconnection of fluctuation and dissipation summarized, for example, by the simple Stokes–Einstein relation for the diffusion coefficient that is determined by temperature and viscous friction in thermal equilibrium. Breaking this equilibrium by introducing, for example, a single laser-heated particle to the solution [1–6] also breaks the fundamental assumption of equipartition and new physical descriptions are required. However, Hot Brownian Motion can be still mapped onto the well known fluctuation–dissipation relation when introducing effective quantities for temperature and viscosity [7]. Recent theoretical studies have shown that the effective temperatures are not unique for all degrees of freedom (i.e., rotation [8] and translation of colloids) due to their coupling to the generated hydrodynamic flow fields [9]. As these flow fields due to the translation and rotation of colloids in liquids also depend on the timescale of observation, the corresponding effective temperatures shall also reveal a frequency dependence as suggested in recent theoretical work [9]. The effective configurational temperature of Hot Brownian Motion governing the diffusion coefficient at long times shall, therefore, also differ from the effective kinetic temperature that would enter a Maxwell–Boltzmann like description. Here we explore in a sophisticated experiment the short time dynamics of a heated Brownian particle. We have constructed an optical tweezers to trap and heat colloidal particles in water. We demonstrate on isothermal particles the spatial resolution of about 23 pm at a time resolution of 10 ns, which allows us to approach the ballistic regime of Brownian motion. Introducing an additional heating of the particle we explore the capabilities of the setup to provide information on the hot ballistic motion of particles for the first time.
The one-dimensional Maxwell–Boltzmann distribution (Eq. 1) was originally used to describe the velocity distribution of atoms and molecules in an ideal gas where it is assumed that there is no interaction or potential between any pair of arbitrary particles except brief collisions,
Here the mass of the particle M and the temperature of the system T control the distribution. While this is true for gases with elastic collisions [10], the Maxwell–Boltzmann distribution has also been shown to hold experimentally in condensed matter with complex intermolecular interactions [11, 12]. Yet, in liquids additional hydrodynamic effects play an important role on intermediate timescales. Liquid flows that are induced by the displacement of the colloid particle lead to long living perturbations that travel a distance of the particle radius on timescales of several microseconds [13–15]. This hydrodynamic memory has to be included in the Langevin equation [16, 17] to yield the equation of motion of a colloidal particle in an incompressible liquid,
The effective mass
Finally, the last term in Eq. 2 contains the trapping force with the spring constant k.
This already complex dynamics of a Brownian particle in a dense liquid is for Hot Brownian Motion altered by a stationary inhomogeneous temperature profile taking the shape
where
in the long-time limit, which we can use to verify our experiments on long timescales. The effective quantities
with
2 Experimental Setup
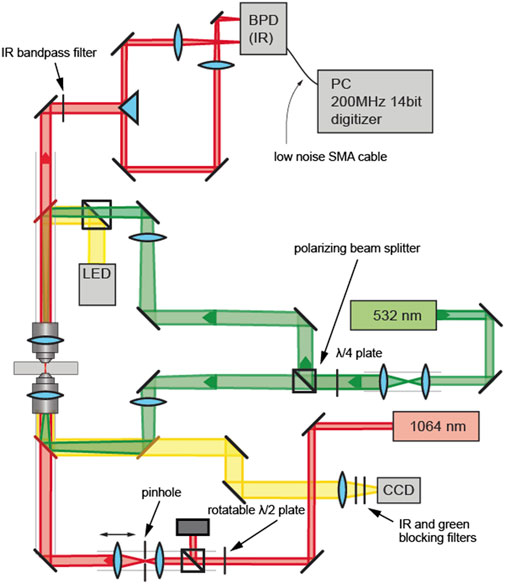
Our experimental setup is shown in Figure 1 and mainly consists of three parts. The primary part of the measurement system is for particle trapping and tracking. Light of a 1,064 nm laser (Mephisto, Coherent) is sent through a rotatable half-wave plate to adjust the IR power in the sample without modifying the driving current of the laser. A beam expander is further used to overfill the first objective (Olympus ×100/1.3NA) lens. The beam is tightly focused by this objective lens to generate a stable trapping potential [20–23] for the Brownian particles in three dimensions. A second objective is used to collect light from the trapping region that is split by a knife-edge prism and sent to a 350 MHz bandwidth balanced photodetector (Thorlabs) with a damage threshold of 20 mW. Our setup, therefore, detects the particle motion only in one dimension (e.g., the x-direction), while other dimensions may show different trapping stiffness [24]. The analog signal is converted by a 200 MHz digitizer card and saved on the computer. The second part of the setup comprises the beam path for heating the gold nanoparticles on the polymer colloid surface at 532 nm wavelength (Sapphire, Coherent). The laser beam is passing a quarter wave plate and a polarizing beam splitter to obtain two equal-power beams with orthogonal polarization to avoid interference in the sample region. Both 532 nm beams are focused to the sample region by two lenses and two Olympus 100x/1.3NA objective lenses (where one is also used by the IR beam). The additional lenses ensure a homogeneous heating of the particles. The remaining third part (yellow) including an LED illumination and a CCD is used to check the particle trapping and particle quality.
In our experiments we use PMMA (Poly (methyl methacrylate)) polymer particles (
3 Results and Discussion
We analyze the mean squared displacement (MSD), power spectral density (PSD) and velocity distribution of the Brownian particle trapped in the optical tweezers. To decrease the statistical noise, we take 20 trajectories for each type of particle with a sampling rate of 200 MHz (10 MHz for Hot Brownian Motion) and obtain the averaged results for MSD and PSD analyses [25–27].
We first address the general performance of the setup to detect spatial displacements under isothermal conditions. In Figure 2, we show the PSD curve of the diameter
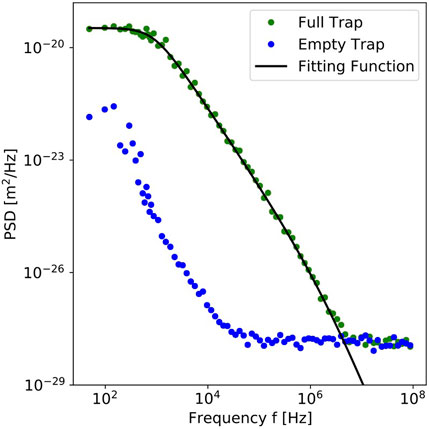
FIGURE 2. Power spectral density (PSD, green dots) of a
We further calculate from the data the mean squared displacement. For the calculation of the MSD we take the average of every two adjacent data points to bin the position data of the balanced photodetector and subtract from the particle’s MSD the MSD calculated for the empty trap. Figure 3 displays the result of the MSD calculation together with a fit using Eq. A1, which nicely represents the measured data. The figure also displays as guides the power laws corresponding to a diffusive
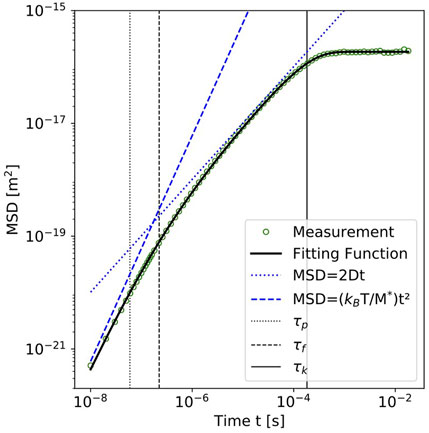
FIGURE 3. Mean squared displacement determined for the
Based on this performance, we now explore the dynamics of a gold-covered polystyrene particle with a diameter
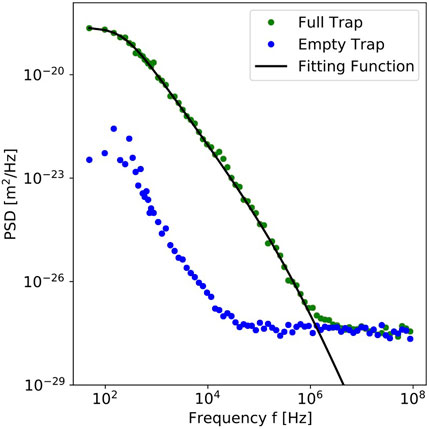
FIGURE 4. Experimental power spectral density for a
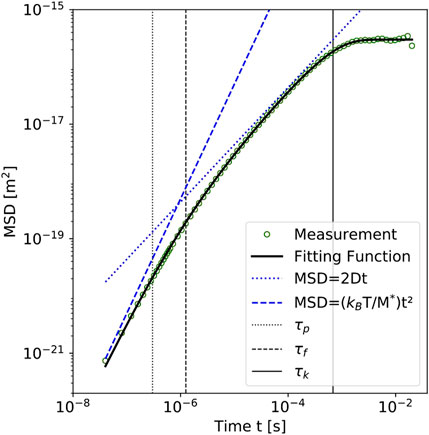
FIGURE 5. Mean squared displacement for the
Since the theoretical momentum relaxation time equals
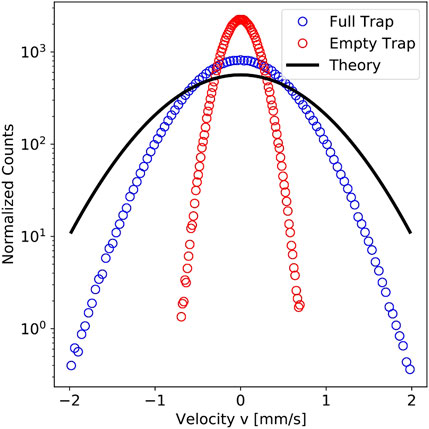
FIGURE 6. Normalized velocity distribution (refer to Eq. 1 with M replaced by
To carry out measurements with a heated Brownian particle, we first measure the temperature increase near the surface of the heated AuPS particle in a separate experiment. For this purpose, we exploit the phase transition of a liquid crystal (5CB, see [31] for more details). The inset in Figure 7 displays the results of the measured surface temperature increases converted for when the AuPS particle is immersed in water with an incident laser at 532 nm wavelength under heating powers of 9.34, 12.66, 16.12 and 19.12 mW. The temperature increase
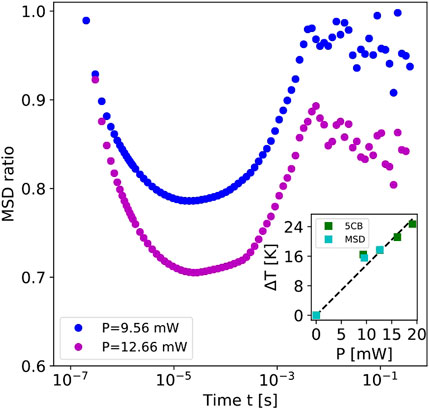
FIGURE 7. Calculated ratio of the mean squared displacement for the 2.15 µm diameter AuPS particle at different heating powers with a 532 nm laser (see legend). The inset displays the surface temperature increment of the colloids as determined from a separate measurement in a liquid crystal (5CB, see text) as well as from the effective temperature of Hot Brownian Motion (
Figure 7 shows the resulting MSD ratios for a single AuPS particle trapped with 12 mW laser power (1,064 nm) at a temperature of 23.8 °C. A 532 nm laser as mentioned above with a power of 9.56 and 12.66 mW is split into two equal but perpendicularly polarized beams that are focused to a beam waist of
4 Conclusion
In summary, we have constructed an experimental setup to explore the short time dynamics of heated Brownian particles known as Hot Brownian Motion. With the help of isothermal liquid environments and Poly (methyl methacrylate) (PMMA) particles, we have demonstrated a spatial resolution of 23 pm with a time resolution of 10 ns with our setup. With this time resolution we are close to resolving the ballistic motion of the PMMA particle. We have further used gold-nanoparticle covered polystyrene particles to allow an optical heating of the particle surface in the trap. We observe direct indication for Hot Brownian Motion at long timescales as well as strong effects of the increased surface temperature on the hydrodynamic long-time-tails in the mean squared displacement. Our experiments demonstrate for the first time that with the help of such a setup and particles the ballistic regime of a single heated particle in a dense liquid could become accessible to studies exploring new regimes of non-equilibrium physics, for example the Maxwell–Boltzmann temperature of a heated Brownian particle.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
FC conceived the experiment. XS and AF carried out the experiments and data analysis. FC, XS and AF wrote the manuscript.
Funding
The authors acknowledge financial support by the German Research Foundation (Deutsche Forschungsgemeinschaft, DFG) through project number 336492136. We acknowledge support from Leipzig University for Open Access Publishing.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank A. Kramer for helping to revise the manuscript. We thank M. Selmke for his help constructing the setup.
References
1. Radünz R, Rings D, Kroy K, Cichos F. Hot Brownian Particles and Photothermal Correlation Spectroscopy. J Phys Chem A (2009) 113:1674–7. doi:10.1021/jp810466y
2. Rings D, Schachoff R, Selmke M, Cichos F, Kroy K. Hot Brownian Motion. Phys Rev Lett (2010) 105:090604. doi:10.1103/PhysRevLett.105.090604
3. Ruijgrok PV, Verhart NR, Zijlstra P, Tchebotareva AL, Orrit M. Brownian Fluctuations and Heating of an Optically Aligned Gold Nanorod. Phys Rev Lett (2011) 107:037401. doi:10.1103/PhysRevLett.107.037401
4. Català F, Marsà F, Montes-Usategui M, Farré A, Martín-Badosa E. Influence of Experimental Parameters on the Laser Heating of an Optical Trap. Sci Rep (2017) 7:16052. doi:10.1038/s41598-017-15904-6
5. Sevilla PR, Arita Y, Liu X, Jaque D, Dholakia K. The Temperature of an Optically Trapped, Rotating Microparticle. ACS Photon (2018) 5. doi:10.1021/acsphotonics.8b00822
6. Rodríguez-Rodríguez H, Salas G, Arias-Gonzalez JR. Heat Generation in Single Magnetic Nanoparticles under Near-Infrared Irradiation. J Phys Chem Lett (2020) 11:2182–7. doi:10.1021/acs.jpclett.0c00143
7. Chakraborty D, Gnann MV, Rings D, Glaser J, Otto F, Cichos F, et al. Generalised Einstein Relation for Hot Brownian Motion. Epl (2011) 96. doi:10.1209/0295-5075/96/60009
8. Rings D, Chakraborty D, Kroy K. Rotational Hot Brownian Motion. New J Phys (2012) 14:053012. doi:10.1088/1367-2630/14/5/053012
9. Falasco G, Gnann MV, Rings D, Kroy K. Effective Temperatures of Hot Brownian Motion. Phys Rev E Stat Nonlin Soft Matter Phys (2014) 90:032131. doi:10.1103/PhysRevE.90.032131
10. Li T, Kheifets S, Medellin D, Raizen MG. Measurement of the Instantaneous Velocity of a Brownian Particle. Science (2010) 328:1673–5. doi:10.1126/science.1189403
11. Kheifets S, Simha A, Melin K, Li T, Raizen MG. Observation of Brownian Motion in Liquids at Short Times: Instantaneous Velocity and Memory Loss. Science (2014) 343:1493–6. doi:10.1126/science.1248091
12. Mo J, Simha A, Kheifets S, Raizen MG. Testing the Maxwell-Boltzmann Distribution Using Brownian Particles. Opt Express (2015) 23:1888–93. doi:10.1364/OE.23.001888
13. Henderson S, Mitchell S, Bartlett P. Propagation of Hydrodynamic Interactions in Colloidal Suspensions. Phys Rev Lett (2002) 88:088302. doi:10.1103/PhysRevLett.88.088302
14. Lukic B, Jeney S, Tischer C, Kulik AJ, Forro L, Florin EL. Direct Observation of Nondiffusive Motion of a Brownian Particle. Phys Rev Lett (2005) 95:160601. doi:10.1103/PhysRevLett.95.160601
15. Franosch T, Grimm M, Belushkin M, Mor FM, Foffi G, Forró L, et al. Resonances Arising from Hydrodynamic Memory in Brownian Motion. Nature (2011) 478:85–8. doi:10.1038/nature10498
17. Uhlenbeck GE, Ornstein LS. On the Theory of the Brownian Motion. Phys Rev (1930) 36. doi:10.1103/physrev.36.823
19. Rings D, Selmke M, Cichos F, Kroy K. Theory of Hot Brownian Motion. Soft Matter (2011) 7:3441-3452. doi:10.1039/c0sm00854k
20. Ashkin A. Forces of a Single-Beam Gradient Laser Trap on a Dielectric Sphere in the ray Optics Regime. Biophys J (1992) 61:569–82. doi:10.1016/S0006-3495(92)81860-X
21. Rohrbach A, Stelzer EH. Trapping Forces, Force Constants, and Potential Depths for Dielectric Spheres in the Presence of Spherical Aberrations. Appl Opt (2002) 41:2494–507. doi:10.1364/ao.41.002494
22. Grier DG. A Revolution in Optical Manipulation. Nature (2003) 424:810–816. doi:10.1038/nature01935
23. Magazzu A, Spadaro D, Donato MG, Sayed R, Messina E, D’Andrea C, et al. Optical Tweezers: a Non-destructive Tool for Soft and Biomaterial Investigations. Rend Fis Acc Lincei (2015) 26:203–218. doi:10.1007/s12210-015-0395-4
24. Rohrbach A. Stiffness of Optical Traps: Quantitative Agreement between Experiment and Electromagnetic Theory. Phys Rev Lett (2005) 95:168102. doi:10.1103/PhysRevLett.95.168102
25. Jones PH, Maragò OM, Volpe G. Optical Tweezers - Principles and Applications. Cambridge University Press (2015).
26. Flyvbjerg H, Berg-Sorensen K. Power Spectrum Analysis for Optical Tweezers. Rev Scientific Instr (2004) 75.
27. Nørrelykke SF, Flyvbjerg H. Harmonic Oscillator in Heat bath: Exact Simulation of Time-Lapse-Recorded Data and Exact Analytical Benchmark Statistics. Phys Rev E (2011) 83:041103. doi:10.1103/PhysRevE.83.041103
28. Huang R, Chavez I, Taute KM, Luki B, Jeney S, Raizen MG, et al. Direct observation of the full transition from ballistic to di_usive Brownian motion in a liquild. Nat Phys (2011) 7:576–580. doi:10.1038/nphys1953
29. Kumar S, Kumar A, Gunaseelan M, Vaippully R, Chakraborty D, Senthilselvan J, et al. Trapped in Out-Of-Equilibrium Stationary State: Hot Brownian Motion in Optically Trapped Upconverting Nanoparticles. Front Phys (2020) 8:429. doi:10.3389/fphy.2020.570842
30. Schmidt F, Magazzù A, Callegari A, Biancofiore L, Cichos F, Volpe G. Microscopic Engine Powered by Critical Demixing. Phys Rev Lett (2018) 120:068004. doi:10.1103/PhysRevLett.120.068004
31. Fränzl M, Muios-Landin S, Holubec V, Cichos F. Fully Steerable Symmetric Thermoplasmonic Microswimmers. ACS Nano (2021) 15:3434-3440. doi:10.1021/acsnano.0c10598
Appendix
We use the following mean squared displacement of the particle for fitting, where
The power spectral density (the squared modulus of the position signal’s Fourier transform) in Eq. A3, which is normalized by the measurement time of one trajectory, is fitted with the following equation
Here D is the diffusion coefficient and
Keywords: Brownian motion, non-equilibrium model, frequency-dependent temperature, optical tweezers, Maxwell-Boltzmann distribution
Citation: Su X, Fischer A and Cichos F (2021) Towards Measuring the Maxwell–Boltzmann Distribution of a Single Heated Particle. Front. Phys. 9:669459. doi: 10.3389/fphy.2021.669459
Received: 18 February 2021; Accepted: 01 June 2021;
Published: 24 June 2021.
Edited by:
Ayan Banerjee, Indian Institute of Science Education and Research Kolkata, IndiaReviewed by:
Basudev Roy, Indian Institute of Technology Madras, IndiaRaúl A. Rica, University of Granada, Spain
Copyright © 2021 Su, Fischer and Cichos. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Frank Cichos, Y2ljaG9zQHBoeXNpay51bmktbGVpcHppZy5kZQ==
 Xiaoya Su
Xiaoya Su Alexander Fischer
Alexander Fischer Frank Cichos
Frank Cichos