Remarks on Wiener Index of Bipolar Fuzzy Incidence Graphs

Introduction

The reason why the mathematical theory and application technology of fuzzy systems can be focused by researchers and has been rapidly developed in the past 60 years is mainly due to the extensive and profound application background in human society and production practice [1–6]. The development of the mathematical theory of fuzzy systems largely depends on the development of fuzzy engineering technology and application. Fuzzy engineering technology is not only the driving force for the development of fuzzy mathematics theory, but also the core of fuzzy mathematics serving the social production practice. With the continuous maturity of the mathematical theory and application technology of fuzzy systems, the application of fuzzy mathematics methods in the engineering field has received more and more attention, and the fields of application have become more and more extensive. The main aspects include general fuzzy controller [7–9], fuzzy knowledge representation [10–12], fuzzy information theory [13, 14] and fuzzy information coding [15–17], fuzzy prediction technology [18], fuzzy decision and evaluation technology [19, 20], fuzzy statistical theory and application [21], fuzzy operational research [including fuzzy optimization [22], fuzzy random service system, fuzzy linear programming [23], fuzzy countermeasures, etc.] and its applications.

As one of the earliest topological indexes, Wiener index plays a key role in the history of chemical topological indices. Its definition is related to accidental discoveries in chemical experiments and can be used to predict some basic properties of compounds. As a result, people realize that the physical and chemical properties of a compound are also closely related to its molecular structure. The formulation of Wiener index is denoted by the sum of the distances of each pair of vertices on the graph. With the deepening of the research, various related distance-based topological indexes are introduced. So far, variants of Wiener index have been studied and applied in a large number of engineering applications.

In recent years, fuzzy topological indices on fuzzy graphs have gradually attracted the attention of researchers. These indices have played valuable roles in fuzzy decision-making systems and fuzzy reasoning. Poulik and Ghorai [24] introduced the Wiener index of bipolar fuzzy graphs, and later, Gong and Hua [25] defined the Wiener index in bipolar fuzzy incidence graph. Although some results about Wiener index of bipolar fuzzy incidence graph were obtained in Gong and Hua [25], more features need to be explored further. For this reason, we continue to study the fuzzy distance measure in this paper. The contributions of this remark can be summarized into three aspects:

• Introduce bipolar Wiener absolute index for bipolar fuzzy incidence graph;

• Determine the extreme values of Wiener index and bipolar Wiener absolute index for bipolar fuzzy incidence graph in some special settings;

• Discuss the relationship of values of these bipolar fuzzy index, for example, the bipolar fuzzy incidence graph and its subgraph, or two isomorphic bipolar fuzzy incidence graphs.

The following contents are organized as follows: first we introduce the concepts which will be used in the paper, and then the main results are obtained based on fuzzy distance computing.

Bipolar Fuzzy Incidence Graph

An incidence graph of graph G = (V, E) is denoted by G = (V, E, I) with I ⊆ V × E. If (v, vv′) in incidence graph, then (v, vv′) is an incidence pair or shortly pair. A sequence v₀, (v₀, v₀v₁),v₀v₁, (v₁, v₀v₁), v₁,…, v_n−1, (v_n−1, v_n−1v_n),v_n−1v_n,(v_n, v_n−1v_n), v_n is a walk in incidence graph. If v₀ = v_n, then it said to be closed. A walk is a path if all vertices are different, and an incidence graph is connected if all pair of vertices are connected by a path. The following concepts from Gong and Hua [25].

Definition 1. [Gong and Hua [25]] Let G = (V, E) be a graph, η^P : V → [0, 1], η^N : V → [−1, 0], θ^P : E → [0, 1], θ^N : E → [−1, 0], Ψ^P : V × E → [0, 1], Ψ^N : V × E → [−1, 0]. If Ψ^P(v, e) ≤ η^P(v)∧θ^P(e) and Ψ^N(v, e) ≥ η^N(v) ∨ θ^N(e) for any v ∈ V and e ∈ E, then (Ψ^P, Ψ^N) is called a bipolar fuzzy incidence of G.

Definition 2. [Gong and Hua [25]] Let G = (V, E) be a graph, and (η^P, η^N, θ^P, θ^N) be a bipolar fuzzy subgraph of G. If (Ψ^P, Ψ^N) is a bipolar fuzzy incidence of G, then G = (η^P, η^N, θ^P, θ^N, Ψ^P, Ψ^N) is called a bipolar fuzzy incidence graph of G.

Definition 3. [Gong and Hua [25]] Let G = (η^P, η^N, θ^P, θ^N, Ψ^P, Ψ^N) be a bipolar fuzzy incidence graph. Then H = (κ^P, κ^N, ϕ^P, ϕ^N, Ω^P, Ω^N) is a bipolar fuzzy incidence subgraph of G if κ^P(v) ≤ η^P(v), κ^N(v) ≥ η^N(v) for any v ∈ V, ϕ^P(e) ≤ θ^P(e), ϕ^N(e) ≥ θ^N(e) for any e ∈ E, and Ω^P(v, e) ≤ Ψ^P(v, e), Ω^N(v, e) ≥ Ψ^N(v, e) for any (v, e) ∈ V × E.

Definition 4. [Gong and Hua [25]] Let G = (η^P, η^N, θ^P, θ^N, Ψ^P, Ψ^N) be a bipolar fuzzy incidence graph. Set η^*, θ^*, and Ψ^* as the vertex set, edge set and incidence set (set of V × E) of G (these three sets represent the specific component elements of bipolar fuzzy incidence graph G). A fuzzy incidence path λ from v to v' (vv′ ∈ η^*∪θ^*) is a sequence of elements η^*, θ^*, and Ψ^*. The minimum value of Ψ^P(v, vv′) is called positive incidence strength and the maximum value of Ψ^N(v, vv′) is called negative incidence strength, where (v, v′) ∈ λ.

Definition 5. [Gong and Hua [25]] Let G be a bipolar fuzzy incidence graph. An incidence pair (v, vv′) is strong if ${\text{Ψ}}^P(v,v{v}^{\prime })\ge ICON{N}_{G-(v,v{v}^{\prime })}^P(v,v{v}^{\prime })$, ${\text{Ψ}}^N(v,v{v}^{\prime })\le ICON{N}_{G-(v,v{v}^{\prime })}^N(v,v{v}^{\prime })$ where $ICON{N}_{G-(v,v{v}^{\prime })}^P(v,v{v}^{\prime })$ is the maximum positive incidence strength of a − ab and $ICON{N}_{G-(v,v{v}^{\prime })}^N(v,v{v}^{\prime })$ is the minimum negative incidence strength of a − ab. If ${\text{Ψ}}^P(v,v{v}^{\prime })>ICON{N}_{G-(v,v{v}^{\prime })}^P(v,v{v}^{\prime })$ and ${\text{Ψ}}^N(v,v{v}^{\prime })<ICON{N}_{G-(v,v{v}^{\prime })}^N(v,v{v}^{\prime })$, then the pair (v, vv′) is called α -strong. If ${\text{Ψ}}^P(v,v{v}^{\prime })=ICON{N}_{G-(v,v{v}^{\prime })}^P(v,v{v}^{\prime })$ and ${\text{Ψ}}^N(v,v{v}^{\prime })=ICON{N}_{G-(v,v{v}^{\prime })}^N(v,v{v}^{\prime })$, then the pair (v, vv′) is called β -strong.

Definition 6. [Gong and Hua [25]] Let G be a bipolar fuzzy incidence graph. If all pair of λ are strong, then an incidence path λ in G is called strong incidence path.

Definition 7. [Gong and Hua [25]] Let G = (η^P, η^N, θ^P, θ^N, Ψ^P, Ψ^N) be a bipolar fuzzy incidence graph. Then H = (κ^P, κ^N, ϕ^P, ϕ^N, Ω^P, Ω^N) is a subgraph of G if κ^P(v) = η^P(v), κ^N(v) = η^N(v) for any v ∈ κ^*, ϕ^P(e) = θ^P(e), ϕ^N(e) = θ^N(e) for any e ∈ ϕ^*, and Ω^P(v, e) = Ψ^P(v, e), Ω^N(v, e) = Ψ^N(v, e) for any (v, e) ∈ Ω^*.

Definition 8. [Gong and Hua [25]] A bipolar fuzzy incidence graph G = (η^P, η^N, θ^P, θ^N, Ψ^P, Ψ^N) is said to be complete if Ψ^P(v, vv′) = η^P(v)∧θ^P(vv′) and Ψ^N(v, vv′) = η^N(v) ∨ θ^N(vv′) for any (v, vv′) ∈ ψ^*.

Definition 9. [Gong and Hua [25]] Let G = (η^P, η^N, θ^P, θ^N, Ψ^P, Ψ^N) be a bipolar fuzzy incidence graph. The connectivity index of G is formulated by:

$\begin{array}{l}C{I}_{BFI}(G)=(C{I}_{BFI}^P(G),C{I}_{BFI}^N(G))\\ =({\displaystyle \sum _{x,y\in {\eta }^{*}}}{\eta }^P(x){\eta }^P(y)ICON{N}_G^P(x,y),\\ {\displaystyle \sum _{x,y\in {\eta }^{*}}}{\eta }^N(x){\eta }^N(y)ICON{N}_G^N(x,y)),\end{array}$

where $C{I}_{BFI}^P(G)$ and $C{I}_{BFI}^N(G)$ are positive connectivity index and negative connectivity index of G, $ICON{N}_G^P(x,y)$ is the maximum value of positive incidence strength for all the possible incidence paths between x and y, and $ICON{N}_G^N(x,y)$ is the minimum value of negative incidence strength for all the possible incidence paths between x and y.

Definition 10. [Gong and Hua [25]] Let $G_1=({\eta }_1^P,{\eta }_1^N,{\theta }_1^P,{\theta }_1^N,{\text{Ψ}}_1^P,{\text{Ψ}}_1^N)$ and $G_2=({\eta }_2^P,{\eta }_2^N,{\theta }_2^P,{\theta }_2^N,{\text{Ψ}}_2^P,{\text{Ψ}}_2^N)$ be two bipolar fuzzy incidence graphs. If there is a bijective mapping f : V(G₁) → V(G₂) with ${\eta }_1^P(v)={\eta }_2^P(f(v))$, ${\eta }_1^N(v)={\eta }_2^N(f(v))$ for all $v\in G_1({\eta }^{*})$, ${\theta }_1^P(v{v}^{\prime })={\theta }_2^P(f(v)f(v^{\prime }))$, ${\theta }_1^N(v{v}^{\prime })={\theta }_2^N(f(v)f(v^{\prime }))$ for all $v{v}^{\prime }\in G_1({\theta }^{*})$, and ${\text{Ψ}}_1^P(v,v{v}^{\prime })={\text{Ψ}}_2^P(f(v),f(v)f(v^{\prime }))$, ${\text{Ψ}}_1^N(v,v{v}^{\prime })={\text{Ψ}}_2^N(f(v),f(v)f(v^{\prime }))$ for any pair $(v,v{v}^{\prime })\in G_1({\text{Ψ}}^{*})$. Then the mapping f is called an isomorphism and we denote G₁≅G₂.

Definition 11. [Gong and Hua [25]] The Wiener index of a bipolar fuzzy incidence graph G = (η^P, η^N, θ^P, θ^N, Ψ^P, Ψ^N) is denoted by:

$\begin{array}{l}W{I}_{BFI}(G)=(W{I}_{BFI}^P(G),W{I}_{BFI}^N(G))\\ =({\displaystyle \sum _{x,y\in {\eta }^{*}}}{\eta }^P(x){\eta }^P(y)d_s^P(x,y),{\displaystyle \sum _{x,y\in {\eta }^{*}}}{\eta }^N(x){\eta }^N(y)d_s^N(x,y)).\end{array}$

Main Results and Proofs

In this section, we present the main conclusions and their proofs which mainly follows from Poulik and Ghorai [24] and Gong and Hua [25].

Our first result gives the bound of Wiener index of fuzzy bipolar incidence graphs.

Theorem 1. Let G = (η^P, η^N, θ^P, θ^N, Ψ^P, Ψ^N) be a bipolar fuzzy incidence graph with η^P(v) = 1 and η^N(v) = −1 for all v ∈ η^*. Set:

$\begin{array}{l}{r}_1=min\left\{{\text{Ψ}}^P(v,v{v}^{\prime })|v{v}^{\prime }\in {\theta }^{*},{\text{Ψ}}^P(v,v{v}^{\prime })\ge ICON{N}_G^P(v,v{v}^{\prime })\right\},\\ r_2=max\left\{{\text{Ψ}}^N(v,v{v}^{\prime })|v{v}^{\prime }\in {\theta }^{*},{\text{Ψ}}^N(v,v{v}^{\prime })\le ICON{N}_G^N(v,v{v}^{\prime })\right\}.\end{array}$

Then, $W{I}_{BFI}^P(G)\ge 2r_1(\left|{\eta }^{*}\right|(\left|{\eta }^{*}\right|-1)-\left|{\theta }^{*}\right|)$ and $W{I}_{BFI}^N(G)\le 2r_2(\left|{\eta }^{*}\right|(\left|{\eta }^{*}\right|-1)-\left|{\theta }^{*}\right|)$.

Proof. Let (x, y) be any pair of η^*. If xy ∈ θ^*, then we have $d_s^P(x,y)\ge 2r_1$ and $d_s^N(x,y)\le 2r_2$. For the rest $\left(\begin{array}{c}|{\eta }^{*}|\\ 2\\ \end{array}\right)-|{\theta }^{*}|=\frac{|{\eta }^{*}|(|{\eta }^{*}|-1)}{2}-|{\theta }^{*}|$ pairs, we get $d_s^P(x,y)\ge 2r_1+2r_1=4r_1$ and $d_s^N(x,y)\le 2r_2+2r_2=4r_2$. Thus, ${\displaystyle \sum _{x,y\in {\eta }^{*}}}{\eta }^P(x){\eta }^P(y)d_s^P(x,y)\ge 2|{\theta }^{*}|r_1+4r_1(\frac{|{\eta }^{*}|(|{\eta }^{*}|-1)}{2}-|{\theta }^{*}|)$ which implies $W{I}_{BFI}^P(G)\ge 2r_1(|{\eta }^{*}|(|{\eta }^{*}|-1)-|{\theta }^{*}|)$ and ${\displaystyle \sum _{x,y\in {\eta }^{*}}}{\eta }^N(x){\eta }^N(y)d_s^N(x,y)\le 2|{\theta }^{*}|r_2+4r_2(\frac{|{\eta }^{*}|(|{\eta }^{*}|-1)}{2}-|{\theta }^{*}|)$ which implies $W{I}_{BFI}^N(G)\le 2r_2(|{\eta }^{*}|(|{\eta }^{*}|-1)-|{\theta }^{*}|)$.

In Gong and Hua [25], it is stated that after removing an incidence pair in Ψ^*, the positive Wiener index may decrease and the negative Wiener index may increase. The next result shows the changes of bipolar Wiener index of bipolar fuzzy incidence graph after deleting a vertex, and we skip the detailed proofs.

Theorem 2. Let H = (κ^P, κ^N, ϕ^P, ϕ^N, Ω^P, Ω^N) be a subgraph of bipolar fuzzy incidence graph G = (η^P, η^N, θ^P, θ^N, Ψ^P, Ψ^N) such that ϕ^* = θ^* − {v} with v ∈ η^*. Then $W{I}_{BFI}^P(H)\le W{I}_{BFI}^P(G)$ and $W{I}_{BFI}^N(H)\ge W{I}_{BFI}^N(G)$.

Next, we introduce the bipolar Wiener absolute index for bipolar fuzzy incidence graphs.

Definition 12. The absolute value of the sum of $W{I}_{BFI}^P(G)$ and $W{I}_{BFI}^N(G)$ of bipolar fuzzy incidence graph is called the Wiener absolute index of G which is denoted by:

$\begin{array}{l}WA{I}_{BFI}(G)=|W{I}_{BFI}^P(G)+W{I}_{BFI}^N(G)|.\end{array}$

According to this definition, we get the following result immediately.

Theorem 3. Let $G_1=({\eta }_1^P,{\eta }_1^N,{\theta }_1^P,{\theta }_1^N,{\text{Ψ}}_1^P,{\text{Ψ}}_1^N)$ and $G_2=({\eta }_2^P,{\eta }_2^N,{\theta }_2^P,{\theta }_2^N,{\text{Ψ}}_2^P,{\text{Ψ}}_2^N)$ be two bipolar fuzzy incidence graphs. If WI_BFI(G₁) = WI_BFI(G₂), then WAI_BFI(G₁) = WAI_BFI(G₂).

However, the converse of Theorem 3 is not hold in general.

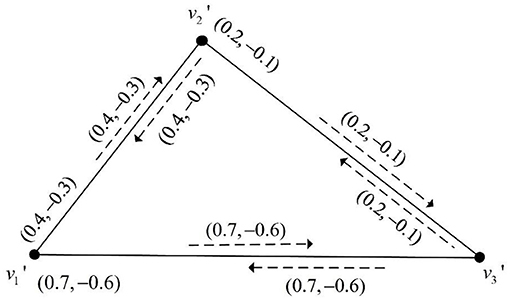
Example 1. A bipolar fuzzy incidence graph G is depicted in Figure 1, we confirm that η* = {v₁, v₂, v₃}, ${\eta }^P(v_1)={\eta }^P(v_2)={\eta }^P(v_3)=1$, ${\eta }^N(v_1)={\eta }^N(v_2)={\eta }^N(v_3)=-1$, ${\theta }^P(v_1{v}_2)=0.8$, ${\theta }^N(v_1{v}_2)=-0.9$, ${\theta }^P(v_1{v}_3)=0.5$, ${\theta }^N(v_1{v}_3)=-0.6$, ${\theta }^P(v_2{v}_3)=0.3$, ${\theta }^N(v_2{v}_3)=-0.4$, ${\text{Ψ}}^P(v_1,v_1{v}_2)=0.8$, ${\text{Ψ}}^N(v_1,v_1{v}_2)=-0.9$, ${\text{Ψ}}^P(v_2,v_2{v}_1)=0.8$, ${\text{Ψ}}^N(v_2,v_2{v}_1)=-0.9$, ${\text{Ψ}}^P(v_2,v_2{v}_3)=0.5$, ${\text{Ψ}}^N(v_2,v_2{v}_3)=-0.6$, ${\text{Ψ}}^P(v_3,v_3{v}_2)=0.5$, ${\text{Ψ}}^N(v_3,v_3{v}_2)=-0.6$, ${\text{Ψ}}^P(v_1,v_1{v}_3)=0.3$, ${\text{Ψ}}^N(v_1,v_1{v}_3)=-0.4$, ${\text{Ψ}}^P(v_3,v_3{v}_1)=0.3$, ${\text{Ψ}}^N(v_3,v_3{v}_1)=-0.4$, $W{I}_{BFI}(G)=(W{I}_{BFI}^P(G),W{I}_{BFI}^N(G))=(5.2,-6)$.

FIGURE 1

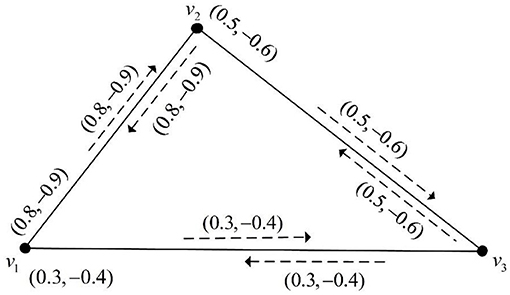
Figure 1. A bipolar fuzzy incidence graph G with $W{I}_{BFI}(G)=(W{I}_{BFI}^P(G),W{I}_{BFI}^N(G))=(5.2,-6)$ and WAI_BFI(G) = 0.8. A bipolar fuzzy incidence graph G′ is depicted in Figure 2, we confirm that ${\eta }^{*}=\left\{v_1^{\prime },v_2^{\prime },v_3^{\prime }\right\}$, ${\eta }^P(v_1^{\prime })={\eta }^P(v_2^{\prime })={\eta }^P(v_3^{\prime })=1$, ${\eta }^N(v_1^{\prime })={\eta }^N(v_2^{\prime })={\eta }^N(v_3^{\prime })=-1$, ${\theta }^P(v_1^{\prime }{v}_2^{\prime })=0.4$, ${\theta }^N(v_1^{\prime }{v}_2^{\prime })=-0.3$, ${\theta }^P(v_1^{\prime }{v}_3^{\prime })=0.2$, ${\theta }^N(v_1^{\prime }{v}_3^{\prime })=-0.1$, ${\theta }^P(v_2^{\prime }{v}_3^{\prime })=0.7$, ${\theta }^N(v_2^{\prime }{v}_3^{\prime })=-0.6$, ${\text{Ψ}}^P(v_1^{\prime },v_1^{\prime }{v}_2^{\prime })=0.4$, ${\text{Ψ}}^N(v_1^{\prime },v_1^{\prime }{v}_2^{\prime })=-0.3$, ${\text{Ψ}}^P(v_2^{\prime },v_2^{\prime }{v}_1^{\prime })=0.4$, ${\text{Ψ}}^N(v_2^{\prime },v_2^{\prime }{v}_1^{\prime })=-0.3$, ${\text{Ψ}}^P(v_2^{\prime },v_2^{\prime }{v}_3^{\prime })=0.2$, ${\text{Ψ}}^N(v_2^{\prime },v_2^{\prime }{v}_3^{\prime })=-0.1$, ${\text{Ψ}}^P(v_3^{\prime },v_3^{\prime }{v}_2^{\prime })=0.2$, ${\text{Ψ}}^N(v_3^{\prime },v_3^{\prime }{v}_2^{\prime })=-0.1$, ${\text{Ψ}}^P(v_1^{\prime },v_1^{\prime }{v}_3^{\prime })=0.7$, ${\text{Ψ}}^N(v_1^{\prime },v_1^{\prime }{v}_3^{\prime })=-0.6$, ${\text{Ψ}}^P(v_3^{\prime },v_3^{\prime }{v}_1^{\prime })=0.7$, ${\text{Ψ}}^N(v_3^{\prime },v_3^{\prime }{v}_1^{\prime })=-0.6$, $W{I}_{BFI}(G^{\prime })=(W{I}_{BFI}^P(G^{\prime }),W{I}_{BFI}^N(G^{\prime }))=(4.4,-3.6)$. Furthermore, by simple computing, we get $WA{I}_{BFI}(G)=WA{I}_{BFI}(G^{\prime })=0.8$.

FIGURE 2

Figure 2. A bipolar fuzzy incidence graph G′ with $W{I}_{BFI}(G^{\prime })=(W{I}_{BFI}^P(G^{\prime }),W{I}_{BFI}^N(G^{\prime }))=(4.4,-3.6)$ and $WA{I}_{BFI}(G^{\prime })=0.8$.

Theorem 4. Let G = (η^P, η^N, θ^P, θ^N, Ψ^P, Ψ^N) be a bipolar fuzzy incidence graph with η^P(v) = a and η^N(v) = b for all v ∈ η^* and Ψ^P(v, vv′) = c, Ψ^N(v, vv′) = d for any pair v, v′ ∈ η^*. We have:

$\begin{array}{l}WA{I}_{BFI}(G)=\left|{\eta }^{*}\right|(\left|{\eta }^{*}\right|-1)|a^{2}c+b^{2}d|.\end{array}$

Proof. Let G = (η^P, η^N, θ^P, θ^N, Ψ^P, Ψ^N) be a bipolar fuzzy incidence graph that satisfies assumptions of Theorem 4. Hence, $(ICON{N}_G^P(v,v^{\prime }),ICON{N}_G^N(v,v^{\prime }))$ are equal for all the pairs of (v, v′) in η^*. Since the positive and negative membership values of all the edges of G are equal, we confirm that $(ICON{N}_G^P(v,v^{\prime }),ICON{N}_G^N(v,v^{\prime }))$ lie on all the edge vv′ ∈ θ^*, and thus

$\begin{array}{r}(d_s^P(v,v^{\prime }),d_s^N(v,v^{\prime }))=(2ICON{N}_G^P(v,v^{\prime }),2ICON{N}_G^N(v,v^{\prime }))\\ =(2{\text{Ψ}}^P(v,v{v}^{\prime }),2{\text{Ψ}}^N(v,v{v}^{\prime }))=(2c,2d).\end{array}$

Note that there are $\left(\begin{array}{c}\left|{\eta }^{*}\right|\\ 2\\ \end{array}\right)=\frac{\left|{\eta }^{*}\right|(\left|{\eta }^{*}\right|-1)}{2}$ edges, and hence

$\begin{array}{l}W{I}_{BFI}^P(G)=\left|{\eta }^{*}\right|(\left|{\eta }^{*}\right|-1)a^{2}c,\end{array}$

and

$\begin{array}{l}{WI}_{BFI}^N(G))=\left|{\eta }^{*}\right|(\left|{\eta }^{*}\right|-1)b^{2}d.\end{array}$

Finally, the result follows from the definition of Wiener absolute index.

Theorem 5. Let G = (η^P, η^N, θ^P, θ^N, Ψ^P, Ψ^N) be a bipolar fuzzy incidence graph. We have:

$\begin{array}{l}WA{I}_{BFI}(G)\le max\left\{{\displaystyle {WI}_{BFI}^P}(G),\left|W{I}_{BFI}^N(G)\right|\right\}.\end{array}$

Brief Proof. First, we note that $W{I}_{BFI}^P(G)\ge 0$ and $W{I}_{BFI}^N(G)\le 0$. Therefore, by the definition of $WA{I}_{BFI}(G)=|W{I}_{BFI}^P(G)+W{I}_{BFI}^N(G)|$, we get the conclusion.

Our last result shows that two isomorphic graphs have the same Winer index and Wiener absolute index.

Theorem 6. Let $G_1=({\eta }_1^P,{\eta }_1^N,{\theta }_1^P,{\theta }_1^N,{\text{Ψ}}_1^P,{\text{Ψ}}_1^N)$ and $G_2=({\eta }_2^P,{\eta }_2^N,{\theta }_2^P,{\theta }_2^N,{\text{Ψ}}_2^P,{\text{Ψ}}_2^N)$ be two bipolar fuzzy incidence graphs with G₁≅G₂. Then, WI_BFI(G₁) = WI_BFI(G₂) and WAI_BFI(G₁) = WAI_BFI(G₂).

Proof. Suppose that $G_1=({\eta }_1^P,{\eta }_1^N,{\theta }_1^P,{\theta }_1^N,{\text{Ψ}}_1^P,{\text{Ψ}}_1^N)$ and $G_2=({\eta }_2^P,{\eta }_2^N,{\theta }_2^P,{\theta }_2^N,{\text{Ψ}}_2^P,{\text{Ψ}}_2^N)$ are two isomorphic bipolar fuzzy incidence graphs. Hence, in light of the definition of the isomorphic between two bipolar fuzzy incidence graphs, there is a bijective mapping f : V(G₁) → V(G₂) with f : V(G₁) → V(G₂) with ${\eta }_1^P(v)={\eta }_2^P(f(v))$, ${\eta }_1^N(v)={\eta }_2^N(f(v))$ for all $v\in G_1({\eta }^{*})$, ${\theta }_1^P(v{v}^{\prime })={\theta }_2^P(f(v)f(v^{\prime }))$, ${\theta }_1^N(v{v}^{\prime })={\theta }_2^N(f(v)f(v^{\prime }))$ for all $v{v}^{\prime }\in G_1({\theta }^{*})$, and ${\text{Ψ}}_1^P(v,v{v}^{\prime })={\text{Ψ}}_2^P(f(v),f(v)f(v^{\prime }))$, ${\text{Ψ}}_1^N(v,v{v}^{\prime })={\text{Ψ}}_2^N(f(v),f(v)f(v^{\prime }))$ for any pair $(v,v{v}^{\prime })\in G_1({\text{Ψ}}^{*})$.

Thus, for each path P_xy : x = x₀, x₁, ⋯ , x_n−1, x_n = y in G₁, we can found a path $P_{x^{\prime }{y}^{\prime }}:x^{\prime }=x_0^{\prime },x_1^{\prime },\cdots ,x_{n-1}^{\prime },x_n^{\prime }=y^{\prime }$ in G₂ such that x = f(x′), $x_1=f(x_1^{\prime })$, …, $x_{n-1}=f(x_{n-1}^{\prime })$, y = f(y′), and the elements in P_xy and $P_{x^{\prime }{y}^{\prime }}$ meet the following relationship in view of the bijective mapping characteristic (for i = 0, 1, ⋯ , n − 1):

$\begin{array}{l}{\theta }_1^P(x_i,x_{i+1})={\theta }_2^P(f(x_i^{\prime }),f(x_{i+1}^{\prime })),\\ {\theta }_1^N(x_i,x_{i+1})={\theta }_2^N(f(x_i^{\prime }),f(x_{i+1}^{\prime })),\\ {\text{Ψ}}_1^P(x_i,x_i{x}_{i+1})={\text{Ψ}}_2^P(f(x_i^{\prime }),f(x_i^{\prime })f(x_{i+1}^{\prime })),\\ {\text{Ψ}}_1^P(x_{i+1},x_{i+1}{x}_i)={\text{Ψ}}_2^P(f(x_{i+1}^{\prime }),f(x_{i+1}^{\prime })f(x_i^{\prime })),\\ {\text{Ψ}}_1^N(x_i,x_i{x}_{i+1})={\text{Ψ}}_2^N(f(x_i^{\prime }),f(x_i^{\prime })f(x_{i+1}^{\prime })),\\ {\text{Ψ}}_1^N(x_{i+1},x_{i+1}{x}_i)={\text{Ψ}}_2^N(f(x_{i+1}^{\prime }),f(x_{i+1}^{\prime })f(x_i^{\prime })).\end{array}$

Therefore, the distance between x and y along P_xy, and the distance between x′ and y′ along $P_{x^{\prime }{y}^{\prime }}$ satisfy

$\begin{array}{l}{d}_{G_1(s)}^P(x,y)=d_{G_2(s)}^P(f(x^{\prime }),f(y^{\prime }))\end{array}$

and

$\begin{array}{l}{d}_{G_1(s)}^N(x,y)=d_{G_2(s)}^N(f(x^{\prime }),f(y^{\prime })).\end{array}$

Furthermore, for i = 0, 1, ⋯ , n, we infer

$\begin{array}{l}{\eta }_1^P(x_i)={\eta }_2^P(f(x_i^{\prime })),\\ {\eta }_1^N(x_i)={\eta }_2^N(f(x_i^{\prime })).\end{array}$

Combing the above facts together, we yield:

$\begin{array}{l}{\displaystyle \sum _{x,y\in G_1(\eta *)}}{\eta }^P(x){\eta }^P(y)d_{G_1(s)}^P(x,y)={\displaystyle \sum _{x^{\prime },y^{\prime }\in G_2(\eta *)}}{\eta }^P(f(x^{\prime })){\eta }^P(f(y^{\prime }))\\ d_{G_2(s)}^P(f(x^{\prime }),f(y^{\prime }))\end{array}$

and

$\begin{array}{l}{\displaystyle \sum _{x,y\in G_1(\eta *)}}{\eta }^N(x){\eta }^N(y)d_{G_1(s)}^N(x,y)={\displaystyle \sum _{x^{\prime },y^{\prime }\in G_2(\eta *)}}{\eta }^N(f(x^{\prime })){\eta }^N(f(y^{\prime }))\\ d_{G_2(s)}^N(f(x^{\prime }),f(y^{\prime })).\end{array}$

It implies that $W{I}_{BFI}^P(G_1)=W{I}_{BFI}^P(G_2)$, $W{I}_{BFI}^N(G_1)=W{I}_{BFI}^N(G_2),W{I}_{BFI}(G_1)=W{I}_{BFI}(G_2),WA{I}_{BFI}(G_1)=WA{I}_{BFI}(G_2)$.□

Intuitively speaking, two isomorphic bipolar fuzzy incidence graphs have a bijective correspondence between their same elements and membership functions. These two graphs can be regarded as one graph without any qualitative difference, so their Wiener index and Wiener absolute index are identical, respectively.

Discussion

In this work, we study the Wiener index of bipolar fuzzy incidence graphs and several conclusions are obtained. The obtained theorems have a positive effect on the development of artificial intelligence, pattern recognition, and fuzzy machine learning related fields. Due to the extremely wide range of applications of fuzzy graph data, this research will improve the practical application capabilities of fuzzy structured data in various disciplines. The results provide tools, methods and application methods in various fields such as big data, Internet of Things, blockchain, cloud services, industrial and mining automation, chemistry, biology, medicine, materials science and social science.

In the chemical experiments in 1960s and 1970s, scientists realized that there was an inevitable connection between the physico-chemical properties of a compound and its molecular structure. That is, what kind of molecular structure possesses what kind of chemical properties. This discovery was gradually confirmed in later experimental science, and a new field was born from this point of view, which uses chemical structure to infer the properties of compounds. According to this idea, scientists use graphs to represent molecular structures: vertices represent atoms, and edges between vertices represent chemical bonds between atoms. The graph is regarded a molecular graph, and the properties of chemicals are studied by defining the topological index on the graph. Early topological indexes include Wiener index, PI index, Szeged index, etc., which can well reflect simple physical properties such as the melting point and boiling point of compounds.

So far, more than 3,000 topological indices have been defined. However, as far as we know, only connectivity index and Wiener index have the corresponding versions in fuzzy graph, bipolar fuzzy graph and bipolar fuzzy incidence graph (see Definitions 9 and 11). Most topological indices have no corresponding definitions on fuzzy graphs and bipolar fuzzy graphs, including some very famous topological indexes, such as Harary index, atom bond connectivity index, PI index, Szeged index, Gutman index, Shultz index, eccentric index, Zagreb index, etc. Studying the expansion of these important indices in fuzzy graphs and bipolar fuzzy graphs can be used as future research work.

Specifically, the following topics can be considered as the future research directions:

• Various distance based topological indices should be introduced in fuzzy graphs, and the definition of distance should be considered in distinct settings (for example, Hamming distance, pseudo Hamming distance, etc.).

• The definition of topological indices should be extended to different fuzzy graphs or fuzzy system, for instance, interval-valued fuzzy systems, or neutrosophic fuzzy systems.

• These fuzzy topology indices should be applied in decision-making settings, such as MCGDM (conjoint decision making with a collection of alternatives), and the corresponding algorithm and analysis should be investigated in the future.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Funding

This work was supported by Natural Science Foundation of Guangdong Province of China (No. 2020A1515010784), Guangdong University of Science and Technology University Major Scientific Research Achievement Cultivation Program Project 2020, and Provincial key platforms and major scientific research projects in Guangdong universities in 2018 (No. 2018KTSCX261).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Abouchabana N, Haddadi M, Rabhi A, Grasso AD, Tina GM. Power efficiency improvement of a boost converter using a coupled inductor with a fuzzylogic controller: application to a photovoltaic system. Appl. Sci. (2021) 11:980. doi: 10.3390/app11030980

CrossRef Full Text | Google Scholar

2. Shanmugam L, Joo YH. Design of interval type-2 fuzzy-based sampled-data controller for nonlinear systems using novel fuzzy Lyapunov functional and its application to PMSM. IEEE Trans Syst Man Cybernet Syst. (2021). 51:542–51. doi: 10.1109/TSMC.2018.2875098

CrossRef Full Text | Google Scholar

3. Gao W, Guirao JLG, Wu H. Nordhaus-Gaddum type inequalities for some distance-based indices of bipartite molecular graphs. J Math Chem. (2020). 58:1345–52. doi: 10.1007/s10910-020-01139-w

CrossRef Full Text | Google Scholar

4. Simsek B, Ic YT. Fuzzy failure mode and effect analysis application to reduce risk level in a ready-mixed concrete plant: a fuzzy rule based system modelling approach. Math Comput Simul. (2020) 178:549–87. doi: 10.1016/j.matcom.2020.06.024

CrossRef Full Text | Google Scholar

5. Kharrat D, Gassara H, El Hajjaji A, Chaabane M. Adaptive observer-based H-infinity FTC for T-S fuzzy systems. Application to cart motion model. J Franklin Inst Eng Appl Math. (2020) 357:12062–84. doi: 10.1016/j.jfranklin.2020.06.024

CrossRef Full Text | Google Scholar

6. Alhevaz A, Baghipur M, Shang Y. On generalized distance Gaussian Estrada index of graphs. Symmetry. (2019) 11:1276. doi: 10.3390/sym11101276

CrossRef Full Text | Google Scholar

7. Pirzada S, Ganie HA, Rather BA, Shaban RU. On generalized distance energy of graphs. Linear Algebra Appl. (2020) 603:1–19. doi: 10.1016/j.laa.2020.05.022

CrossRef Full Text | Google Scholar

8. Gao W, Wu H, Siddiqui MK, Baig AQ. Study of biological networks using graph theory. Saudi J Biol Sci. (2018) 25:1212–9. doi: 10.1016/j.sjbs.2017.11.022

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Azizi M, Ghasemi SAM, Ejlali RG, Talatahari S. Optimization of fuzzy controller for nonlinear buildings with improved charged system search. Struct Eng Mech. (2020) 76:781–97. doi: 10.12989/sem.2020.76.6.781

CrossRef Full Text | Google Scholar

10. Hadrani A, Guennoun K, Saadane R, Wahbe M. Fuzzy rough sets: survey and proposal of an enhanced knowledge representation model based on automatic noisy sample detection. Cogn Syst Res. (2020) 64:37–56. doi: 10.1016/j.cogsys.2020.05.001

CrossRef Full Text | Google Scholar

11. Gellert A, Florea A, Fiore U, Zanetti P, Vintan L. Performance and energy optimisation in CPUs through fuzzy knowledge representation. Inf Sci. (2019) 476:375–91. doi: 10.1016/j.ins.2018.03.029

CrossRef Full Text | Google Scholar

12. Gao W, Wang W, Dimitrov D, Wang Y. Nano properties analysis via fourth multiplicative ABC indicator calculating. Arab J Chem. (2018) 11:793–801. doi: 10.1016/j.arabjc.2017.12.024

CrossRef Full Text | Google Scholar

13. Gamliel E, Kreiner H. Applying fuzzy-trace theory to attribute-framing bias: gist and verbatim representations of quantitative information. J Exp Psychol Learn Mem Cogn. (2020) 46:497–506. doi: 10.1037/xlm0000741

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Calderaro V, Lamberti F, Galdi V, Piccolo A. Power flow problems with nested information: an approach based on fuzzy numbers and possibility theory. Electric Power Syst Res. (2018) 158:275–83. doi: 10.1016/j.epsr.2018.01.008

CrossRef Full Text | Google Scholar

15. Gao W, Siddiqui MK, Rehman NA, Muhammad MH. Topological characterization of dendrimer, benzenoid, and nanocone. J Biosci. (2019). 74:35–43. doi: 10.1515/znc-2018-0153

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Koptyra K, Ogiela MR. Multiply information coding and hiding using fuzzy vault. Soft Comput. (2019) 23:4357–66. doi: 10.1007/s00500-018-3089-x

CrossRef Full Text | Google Scholar

17. Kumar T, Bajaj RK, Maheshwari P. Credibility distribution based R-norm fuzzy information measures in noiseless coding theorems. Int J Gen Syst. (2019) 48:302–20. doi: 10.1080/03081079.2018.1552686

CrossRef Full Text | Google Scholar

18. Basakin EE, Ozger M. Monthly river discharge prediction by wavelet fuzzy time series method. Int J Uncertain Fuzziness Knowl Based Syst. (2021) 29:17–35. doi: 10.1142/S0218488521500021

CrossRef Full Text | Google Scholar

19. Sanchez-Lozano JM, Fernandez-Martinez M, Saucedo-Fernandez AA, Trigo-Rodriguez JM. Evaluation of NEA deflection techniques. A fuzzy Multi-Criteria Decision Making analysis for planetary defense. ACTA Astronaut. (2020) 176:383–97. doi: 10.1016/j.actaastro.2020.06.043

CrossRef Full Text | Google Scholar

20. Coban V. Solar energy plant project selection with AHP decision-making method based on hesitant fuzzy linguistic evaluation. Complex Intell Syst. (2020) 6:507–29. doi: 10.1007/s40747-020-00152-5

CrossRef Full Text | Google Scholar

21. Gao W, Iqbal Z, Ishaq M, Aslam A, Aamir M, Binyamin MA. Bounds on topological descriptors of the corona product of F-sum of connected graphs. IEEE Access. (2019) 7:26788–96. doi: 10.1109/ACCESS.2019.2900061

CrossRef Full Text | Google Scholar

22. Diniz MM, Gomes LT, Bassanezi RC. Optimization of fuzzy-valued functions using Zadeh's extension principle. Fuzzy Sets Syst. (2021) 404:23–37. doi: 10.1016/j.fss.2020.07.007

CrossRef Full Text | Google Scholar

23. Hosseinzadeh E, Hassanpour H. Estimating the parameters of fuzzy linear regression model with crisp inputs and Gaussian fuzzy outputs: a goal programming approach. Soft Comput. (2021) 25:2719–28. doi: 10.1007/s00500-020-05331-7

CrossRef Full Text | Google Scholar

24. Poulik S, Ghorai G. Determination of journeys order based on graph's Wiener absolute index with bipolar fuzzy information. Inf Sci. (2021) 545:608–19. doi: 10.1016/j.ins.2020.09.050

CrossRef Full Text | Google Scholar

25. Gong S, Hua G. Topological indices of bipolar fuzzy incidence graph. (Under review).