Confined Monolayer Ice Between CaF2 (111) and Graphene: Structure and Stability

Water monolayer can form in layered confined systems. Here, CaF₂ (111) and graphene are chosen as modeling systems to explore the structure and stability of confined monolayer water. First, water molecules tend to intercalate into a confined space between graphene and CaF₂, rather than on a bare surface of graphene. Water molecules can move fast in the confined space due to a low diffusion barrier. These water molecules are likely to aggregate together, forming monolayer ice. Four ice phases including ice II, ice III, ice IV, and ice Ih are compared in this confined system. Intriguingly, all the ice phases undergo very small deformation, indicating the 2D monolayer ice can be stable in the CaF₂–graphene–confined system. Beyond, projected band structures are also plotted to understand the electronic behavior of these confined ice phases. Nearly all the bands originated from confined ices are flat and locate about 2–3 eV below the Fermi level. Binding energy calculations suggest that the stability sequence in this confined system as follows: Ih-up ≈ Ih-down ≈ II < IV < III. Our results bring new insights into the formation of water monolayer production in such a confined condition.

Introduction

The behavior of water at surfaces and a nanoconfined space [1] in two, three, or one dimensions is significantly different from that in bulk ice [2–4]. Understanding the structural tendencies of nanoconfined water is of great interest in biology [5], material science [6–8], nanofluidics [9], tribology, and, most recently, electronics [10, 11]. Because of various possible hydrogen bond networks, the structure of water is notoriously perplexed [12], rising as one of the most challenging issues in the 21st century [13]. The subtle interplay between the water–substrate and water–water interactions brings about many new distinctive ice configurations on different substrates [14–18]. In vacuum and on weakly interacting substrates, Xu et al. [14] found a helical ice monolayer with every six water molecules helically arranged along the normal of the basal plane by performing an intensive structural search based on ab initio calculations. On Au(111), a two-dimensional (2D) interlocked ice consisting of two flat hexagonal water layers in which the hexagons in two sheets are in registry is imaged by non-contact atomic force microscopy and identified by density functional calculations [15].

Except for various types of monolayer ice formed on surfaces, 2D monolayer-confined ice also has drawn much attention due to its relevance to a series of processes in nature and industry [19]. Nevertheless, the structures of 2D monolayer ice under distinct confinements are still under debate. Recently, by performing scanning probe microscopy (SPM), graphene ultrathin coatings are utilized to assist the visualization of interfacial water adlayers. This made remarkable progress on interfacial water. Xu et al. [20] observed water adlayers on mica coated by monolayer graphene at room temperature by using atomic force microscopy. The graphene coating can stably “fix” the water adlayer structures, thus permitting the detection of the structure of the first water adlayers under ambient conditions [21]. Therefore, the presence of ambient water adlayers between graphene [19] and various substrates, including mica [11, 21–24], SiO₂ [25, 26], BaF₂ [27], SiC [28], sapphire [29], Ni [30], Ru, Cu [31], and Si [32], has been widely studied by experimental probing techniques. Taking mica as an example, the structure of the first wetting adlayer confined between graphene and mica is unique, quite different from ice Ih, due to strong mica–water interaction [21]. The structural characteristics of intercalated water adlayers between graphene and mica under a thermal treatment were also investigated by Ochedowski et al [22]. They showed that the intercalated water adlayers are partially removed under mild heating (200°C), and the defect density increases, leading to “nanoblister” formation at a temperature of 600°C, causing a transition from the p-type to n-type for graphene layers [22].

CaF₂ (111)/graphene is an excellent platform to trap water molecules and generate confined ice layers. Recently, the formation of a several monolayer thick hydration layer on a graphene-coated hydrophilic substrate CaF₂ (111) was revealed [33]. The first layer is so stable that it cannot be removed upon heating. After this, hydration layers confined between graphene and the CaF₂ substrate were found to electronically modify graphene as the material’s electron density transfers from graphene to the hydration layer [34]. However, the structure and stability of monolayer ice confined between CaF₂ (111) and graphene remain unclear. In an experiment, many factors can influence the hydration layers and properties of graphene [35], such as the types of adhesive tapes [23], other adsorbents [22], and additives. So a theoretical study on structural information and stability of water confined between graphene and CaF₂ at the atomic level is urgently needed.

In this study, the structure and stability of monolayer ice confined between CaF₂ (111) and graphene are investigated systematically based on first-principles calculations. Water molecules tend to aggregate together to form monolayer ice. A water molecule will automatically move to the “edge” of the top surface of the ice layer, promoting monolayer ice growth and prohibiting multilayer nucleation. Beyond, the energy barrier for water diffusion between CaF₂ (111) and graphene is very low. Thus, water molecule can move freely and connect with each other into a monolayer ice between CaF₂ (111) and graphene. Four probable ice phase structures including ice II, ice III, ice IV, and ice Ih are studied in our confined system. All the ice phases are maintained with only small deformations in the CaF₂–graphene–confined system. Binding energy suggests that the most stable monolayer ice confined between CaF₂ (111) and graphene is phase-III. Confined ice III is thermodynamically stable under a wide temperature and pressure span according to the calculated phase diagram. Furthermore, the band structures of these systems are plotted to explore the electronic properties of confined ice phases. The bands originated from confined ice are flat and locate about 2–3 eV below the Fermi level.

Methods

All the first-principles calculations are based on the DFT, which is implanted in the Vienna ab initio simulation package code (VASP) [36]. The Perdew–Burke–Ernzerhof version of the generalized gradient approximation (GGA-PBE) was chosen as the exchange-correlation functional [37] along with the dispersion correction introduced by Grimme (PBE + D3) [38]. In this work, all atoms were fully relaxed using DFT with vdW correction to obtain the equilibrium distance. The electron wave functions are solved with plane wave basis set in conjunction with pseudo potentials by the projector augmented wave (PAW) method [39]. The K points in the first Brillouin zone (BZ) are generated in the form of a Monkhorst–Pack 4 × 4 × 1 grid [40]. A 500 eV kinetic cutoff energy was used for the plane wave basis. The structure of water confined between CaF₂ (111) and graphene were optimized using standard local optimization algorithms with convergence criteria of 10⁻⁴ eV for both electronic and ionic relaxation. In our CaF₂ surface slab, there is a net dipole along the Z direction, which will introduce an artificial electric field in calculations with periodic boundary conditions (PBC), and the dipole correction scheme introduced by Neugebauer and Scheffler is applied in all calculations [41, 42]. To avoid spurious interactions between neighboring structures in the tetragonal supercell, a vacuum layer of 25 Å was included in all non-periodic directions.

The surface lattice of CaF₂ (111) is 3.86 Å, which is in good agreement with prior studies, and the CaF₂ (111) surface slab is terminated with fluorine atoms and composed by two F-Ca-F triple layers. The lattice of graphene is 2.46 Å. All the ice structures including ice II, ice III, and ice IV are from MD simulations [43], which will be intercalated between CaF₂ (111) and graphene. We choose 4 × 4 CaF₂ (111)/3 × 3 ice II/6 × 6 graphene, 3 × 3 CaF₂ (111)/2 × 2 ice III/5 × 5 graphene, 4 × 4 CaF₂ (111)/1 × $\sqrt{3}$ ice IV/6 × 6 graphene, and 4 × 4 CaF₂ (111)/3 × 3 ice Ih/6 × 6 graphene to construct the confined systems. The lattice mismatch of these supercells is 4.4, 5.9, 8.1, and 8.1% for CaF₂ (111)/ice II/graphene, CaF₂ (111)/ice III/graphene, CaF₂ (111)/ice IV/graphene, and CaF₂ (111)/ice Ih/graphene, respectively.

Water molecule diffusion barriers are calculated via the climbing image–nudged elastic band (CI-NEB) [44] method. This technique can efficiently map the minimum energy path and find the saddle points between two given local minima for the system. Six intermediate images are used in CI-NEB calculations. Each image was relaxed until the forces on the atom were less than 0.02 eV/Å.

The binding energies of monolayer ice phases between the CaF₂ and the graphene system are calculated as follows:

$E_b\mathrm{=}\left[\mathrm{E}\left(\mathrm{Total}\right)\mathrm{-E}\left(\mathrm{Ca}{F}_{\mathit{2}}\right)\mathrm{-E}\left(\mathrm{Graphene}\right)\mathrm{-N}\left(H_2\mathrm{O}\right)*\mathrm{E}\left({\mathit{H}}_{\mathit{2}}\mathrm{O}\right)\right]\mathrm{/N}\left({\mathit{H}}_{\mathit{2}}\mathrm{O}\right),(1)$

where E(Total), E(CaF₂), E(Graphene), and E(H₂O) is total energy of the CaF₂/H₂O/graphene system, a clean CaF₂(111), graphene sheet, and an isolated water molecule, respectively.

Results and Discussion

Stratification Test and NEB Calculations

CaF₂ (111)–graphene is an excellent platform to trap water [33, 34]. These water molecules are likely to aggregate together forming monolayer connecting with each other by hydrogen bonding. We perform stratification test to make certain the confined ice is monolayer or not. As shown in Figure 1A, we put a water molecule on top of the monolayer water structure confined between CaF₂ (111) and graphene. After optimization, the water molecule move to the edge of the existing water structure forming a new monolayer (Figure 1B). This process is barrierless, during which the binding energy decrease by 0.73 eV/H₂O. Therefore, the confined ice between CaF₂ (111) and graphene must be monolayer.

FIGURE 1

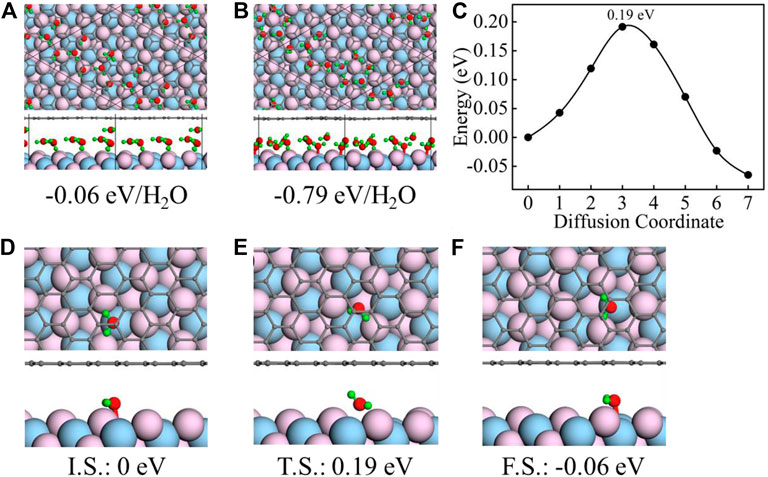
FIGURE 1. Initial (A) and final (B) geometric structures for the stratification test along with their corresponding binding energies. (C) Calculated energy barriers for water molecule diffusion between CaF₂ (111) and graphene. (D–F) Top- and side-view geometric structures of the initial state (I.S.) (D), transition state (T.S.) (E), and final state (F.S.) (F) of water molecule diffusion between CaF₂ (111) and graphene. The total energies for I.S., T.S., and F.S. are all denoted in the bottom as a reference of I.S. In all panels, the black, red, green, flesh pink, and light blue spheres represent the C, O, H, F, and Ca atoms, respectively.

Furthermore, the water molecule diffusion between CaF₂ (111) and graphene is investigated using the CI-NEB method. As shown in Figure 1C, the water diffusion energy barrier is 0.19 eV from initial adsorption local minima (I.S., Figure 1D) to final adsorption local minima (F.S., Figure 1F). During this process, the water molecule is first locates on the top of Ca atom (Figure 1D), then moves to the hollow site (Figure 1E), and finally locates on the top of the neighboring Ca atom (Figure 1F). Choosing the total energy of the I.S. system as a reference, the energy of F.S. and T.S. are all listed in the Figures 1E,F (0.19 eV and −0.06 eV). The speed of water diffusion can be characterized by the water diffusion coefficient $D_{H_{2}O}$ which can be estimated from the diffusion barriers by the following formula:

$D_{H_{2}O}=a^2\nu exp\left(\frac{-\Delta E}{K_{B}T}\right),(2)$

where $a$ is the distance of the hop along the diffusion pathway and $\nu$ is the attempt frequency, about 10¹³ Hz, which is generally in the range of phonon frequencies [45, 46]. $\mathrm{\Delta E}$ is the diffusion energy barrier [45]. $K_B$ is the Boltzmann constant and T represents the temperature. According to the diffusion results, at room temperature (T = 300 K), the water diffusion coefficient $D_{H_{2}O}$ is calculated as 8.35 × 10⁻⁶ cm²/s. The low diffusion energy barrier and high diffusion speed of water molecule provide strong evidence for monolayer ice formation between CaF₂ (111) and graphene.

Structure and Stability of Confined Ice

Four monolayer ice phases including Ice II [43], III [43], IV [43], and Ih are intercalated between CaF₂ (111) and graphene. All the free-standing structures of the four ice phases are depicted in the Supplementary Figure S1 in Supporting Information. For ice I_h, two cases in which H atoms pointing to CaF₂ (Ih-down) or graphene (Ih-up) are all considered. The optimized results are shown in the Figures 2A–E.

FIGURE 2

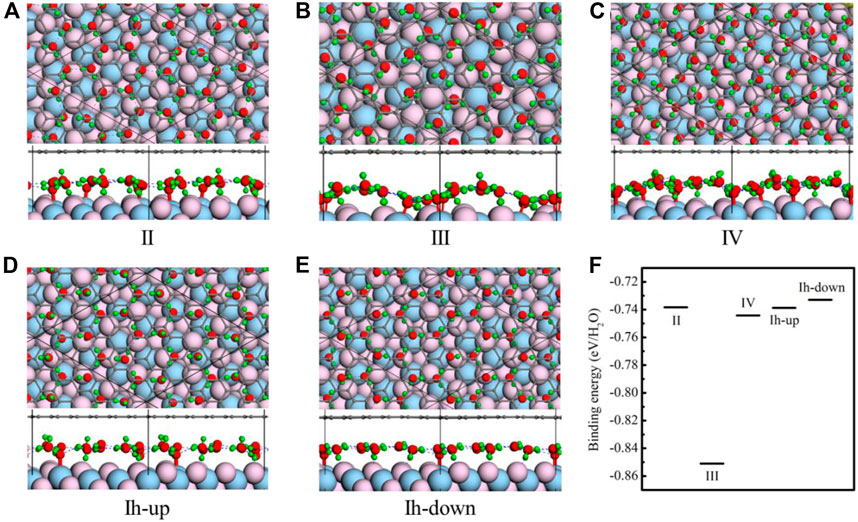
FIGURE 2. Structures of five ice phases including ice II (A), III (B), IV (C), and Ih (D,E) confined between CaF₂(111) and graphene. According to the different orientations of OH, ice Ih can be classified into two kinds. In all panels, the black, red, green, flesh pink, and light blue spheres represent the C, O, H, F, and Ca atoms, respectively. (F) The binding energies of monolayer ice phases between the CaF₂ and the graphene system. Light blue spheres represent the C, O, H, F, and Ca atoms, respectively.

The monolayer ice II has a planar hexagonal morphology, and it is made up of two kinds of water molecules with different orientations. The plane of every water molecule is perpendicular to the planes of three nearest-neighbor molecules. Besides, the monolayer ice II displays considerable net polarization because all the dipole vectors of water molecules are parallel to the longest diagonal of a hexagon. As shown in Figure 2A, under confinement of graphene and CaF₂ (111), the structural motifs of ice II change slightly. The location and orientation of water molecule whose plane is parallel with the CaF₂ (111) is nearly unchanged. Nevertheless, those water molecules whose plane is vertical with CaF₂ (111) rotates slightly to form hydrogen bonds with F atoms. The unit cell is still the six-numbered planar ring, and the hydrogen bond network is the same with ice II which satisfy the ice rule.

Different from ice II, monolayer ice III is composed of planar rhombic rings and all the water molecules tilt with respect to the plane of oxygen. When intercalated into CaF₂ (111) and graphene, it distorts slightly. The four-membered unit cell almost remains unchanged, but the orientations of water molecules become disorganized and delamination appears. Unlike ice II-III, oxygen atoms of ice IV are in alternative ridges with different height in the normal direction. Under confinement, the unit cell of ice IV also changes from rhombic to four-and five-membered rings (Figure 2C).

Ice Ih is also intercalated into the CaF₂ (111) and graphene. Two cases of ice Ih are tried as shown in Figures 2D,E. In the Figure 2D, all the hydrogen atoms are pointing to the graphene coating, while in the Figure 2E, all the hydrogen atoms are pointing to the CaF₂(111). These two ice configurations are called “Ih-up” and “Ih-down,” respectively. In the two cases, the ice structure nearly remains unchanged. The hydrogen atoms tend to point to the CaF₂ (111), so in the structure of “Ih-up,” some water molecules rotate to point to the CaF₂ (111).

To further determine the stability of these monolayer ice phases when they are confined between CaF₂ (111) and the graphene system, the binding energies of monolayer ice phases between the CaF₂ and the graphene system are calculated viaEq. 1. The results are shown in Figure 2F. Clearly, the stability sequence is: III (−0.851 eV/H₂O) > IV (−0.744 eV/H₂O) > II (−0.738 eV/H₂O) ≈ Ih-up (−0.739 eV/H₂O) ≈ Ih-down (−0.733 eV/H₂O). Intriguingly, ice III possesses largest binding energy (−0.85 eV/H₂O), demonstrating its high stability confined between CaF₂ (111) and graphene. Moreover, we have also tried several amorphous water structures in this confined system by random distributing the water molecules. As shown in Supplementary Figure S2, the amorphous water layers retain a monolayer character. But these two amorphous structures are less stable than ordered ice phases. The stability sequence is: III (−0.851 eV/H₂O) > IV (−0.744 eV/H₂O) > II (−0.738 eV/H₂O) ≈ Ih-up (−0.739 eV/H₂O) ≈ Ih-down (−0.733 eV/H₂O) > Amor-1 (Supplementary Figure S2A) (−0.65 eV/H₂O) > Amor-2 (Supplementary Figure S2B) (−0.55 eV/H₂O).

To understand the stability and structural properties through electronic properties, the band structures of the CaF₂/graphene system and five ice phases confined between CaF₂ (111) and graphene are presented in Figures 3A–F, respectively. Due to the different size of the graphene’s supercell, the location of Dirac cone is distinct. The contribution from graphene and CaF₂ (111) is plotted in Figure 3A. Before ice intercalation, the gap of CaF₂ (111) bands is about 6.35 eV; while in the ice confined systems, the gap changes slightly, in the range of (5.5, 6.18) eV. Additionally, in CaF₂ (111)/II/graphene and CaF₂ (111)/Ih-down/graphene, the CaF₂ (111) bands both move downward probably because most H atoms point to the CaF₂ (111) surface. The contribution to each band from ice phases are all depicted in Figures 3B–F. For these five ice phases, band dispersion is very flat along the high symmetry directions in the Brillouin zone. Besides, the ice bands are all located at the deep energy level at least 2–3 eV lower than the Fermi level. Similarly, due to the orientation of H atoms, the locations of bands originated from ice II and ice Ih-down are the deepest among these five ice phases [(−3.79, −2.93) (−5.36, −3.02) eV].

FIGURE 3

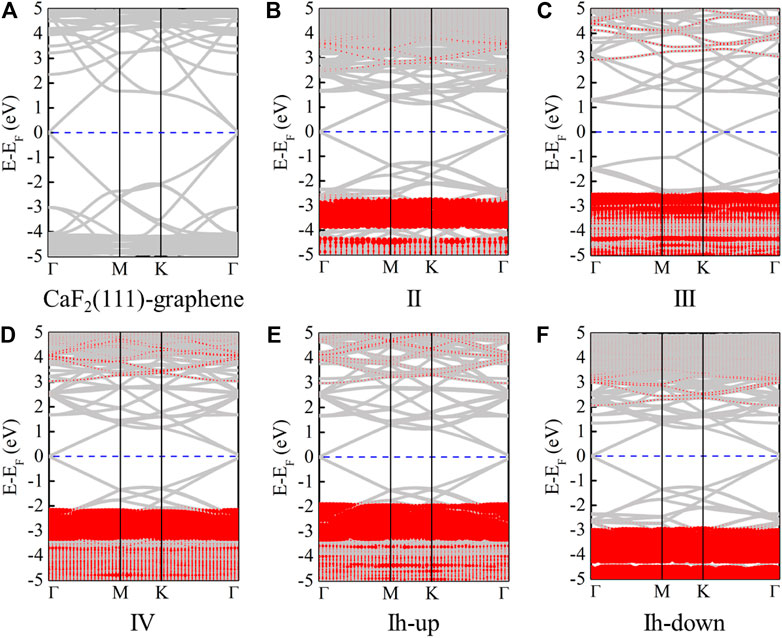
FIGURE 3. Band structures of CaF₂ (111)/graphene (A), CaF₂ (111)/II/graphene (B), CaF₂ (111)/III/graphene (C), CaF₂ (111)/IV/graphene (D), CaF₂ (111)/Ih-up/graphene (E), and CaF₂ (111)/Ih-down/graphene (F), respectively. Here, the red parts represent the contribution from monolayer ice. The Fermi levels are set to zero and indicated by the blue line.

Phase Diagram

Binding energy results demonstrate the highly kinetic stability of ice III; nevertheless, under real environment, the water pressure and temperature must be considered. Based on first-principles thermodynamic calculations [47–50], the free Gibbs energy change ∆G of the CaF₂ (111)/ice III/graphene confined system is defined as:

$\mathrm{\Delta }\mathrm{G}=\left[\mathrm{E}\left(\mathrm{Total}\right)\mathrm{-E}\left(\mathrm{Ca}{\mathit{F}}_{\mathit{2}}\right)\mathrm{-E}\left(\mathrm{Graphene}\right)\mathrm{-N}\left({\mathit{H}}_{\mathit{2}}\mathrm{O}\right)*\mathrm{\Delta \mu }\left({\mathit{H}}_{\mathit{2}}\mathrm{O}\right)\right]\mathrm{/A,}(3)$

where $\mathrm{E}\left(\mathrm{Total}\right)$, $\mathrm{E}\left(\mathrm{Ca}{\mathit{F}}_{\mathrm{2}}\right)$, $\mathrm{E}\left(\mathrm{Graphene}\right)$, and $\mathrm{E}\left({\mathit{H}}_{\mathrm{2}}\mathrm{O}\right)$ is total energy of the CaF₂/H₂O/graphene system, clean CaF₂ (111), graphene sheet, and isolated water molecule, respectively. A is the surface area and $\mathrm{N}\left({\mathit{H}}_{\mathrm{2}}\mathrm{O}\right)$ is the number of the water molecules included in the ice phases. $\mathrm{\Delta \mu }\left({\mathit{H}}_{\mathrm{2}}\mathrm{O}\right)$ is the chemical potentials of water in gas phase, which can be associated with the DFT results and experimental thermodynamic data, as follows:

$\mathrm{\Delta \mu }\left(H_{\mathit{2}}\mathrm{O}\right)\mathrm{=E}\left({\mathit{H}}_{\mathit{2}}\mathrm{O}\right)\mathrm{+}{\mathit{\mu }}_{\mathrm{g}}\left({\mathit{P}}^{\mathit{0}}\mathrm{,T}\right)\mathrm{-}{\mathit{K}}_{\mathit{b}}\mathit{Tln}\left[{\mathit{P}}_{\mathit{g}}\left({\mathit{H}}_{\mathit{2}}\mathit{O}\right)\mathit{/}{\mathit{P}}^{\mathit{0}}\right],(4)$

where $P^0$ = 1 bar and the ${\mu }_g\left(P_0,T\right)$ represents the standard chemical potential of gas water, which can be obtained from standard thermodynamic tables [51].

The free Gibbs energy change ∆G of freestanding ice III [III(free)] and the CaF₂(111)/ice III/graphene [III(confined)] system is depicted in Figure 4A using Eq. 3. When Δμ(H₂O) is lower than −15.07 eV, ice III is not likely to be confined between CaF₂(111) and graphene. On the contrary, the confined system will be more favorable. According to Eq. 4 and the phase transition value of Δμ(H₂O) obtained from Figure 4B, a two-dimensional (T, P) phase diagram is further plotted. Ice III tends to be confined between CaF₂ (111) and graphene under a wide T and P span. For example, at room temperature, confined ice III is more thermodynamically favorable when the water pressure is larger than 10⁻¹⁰ mTorr. However, the condition for freestanding ice III is harsh, often under ultra-high vacuum. Noted that all our configurations were obtained without compression, applying the compression to reduce the layer distance between graphene and CaF₂ could further tune the structure and stability of water layer, which deserves comprehensive study in the future.

FIGURE 4

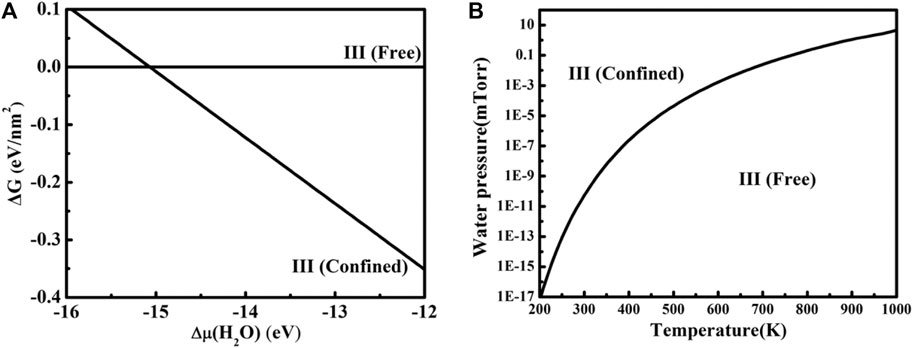
FIGURE 4. (A) Gibbs free energy change ∆G for freestanding ice III and the CaF₂ (111)/ice III/graphene system versus the chemical potential change of the gas water molecule. (B) The phase diagram for free standing ice III and the CaF₂ (111)/ice III/graphene system under different P and T.

Conclusion

In conclusion, we have theoretically studied the structure and stability of monolayer ice phases confined between CaF₂ (111) and graphene. The stratification test and CI-NEB calculations demonstrate the possibility of monolayer ice formation in the CaF₂ (111) and graphene system. Therefore, five systems including monolayer ice II, III, IV, I_h-up, and I_h-down confined between CaF₂(111) and graphene are considered. After optimization, all the ice phases undergo very small deformation, indicating that the 2D monolayer ice can be stable in the CaF₂–graphene–confined system. The electronic properties of these five systems are calculated. Nearly all the bands originated from confined ice are flat and locate about 2–3 eV below the Fermi level. By comparing the binding energy of five systems, the stability sequence is identified as: III > IV > II ≈ Ih-up ≈ Ih-down. Beyond, based on first-principles thermodynamic calculations, a two-dimensional (T, P) phase diagram for III(free) and III(confined) is further plotted. Ice III tends to be confined between CaF₂ (111) and graphene under a wide T and P range.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

JG and S-QL proposed this study. S-QL and SQ performed simulation. JG, HL, and MC conducted the studies and discussed the result. All authors wrote and revised this paper.

Funding

This work was financially supported by the National Natural Science Foundation of China (Nos. 12074053, 91961204, and 11664028) and by Xin Liao Ying Cai Project of the Liaoning Province, China (XLYC1907163). JG thanks the Start-Up grant of DUT (DUT20RC(5)026).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We also acknowledge the computers supporting from the Shanghai Supercomputer Center, the DUT supercomputing Center, and Tianhe supercomputer of Tianjin Center.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.740627/full#supplementary-material

References

1. Soper AK. THERMODYNAMICS: Enhanced: Water and Ice. Science (2002) 297:1288–9. doi:10.1126/science.297.5585.1288

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Zangi R, Mark AE. Monolayer Ice. Phys Rev Lett (2003) 91:025502. doi:10.1103/PhysRevLett.91.025502

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Qiu H, Guo W. Electromelting of Confined Monolayer Ice. Phys Rev Lett (2013) 110:195701. doi:10.1103/physrevlett.110.195701

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Chen J, Schusteritsch G, Pickard CJ, Salzmann CG, Michaelides A. Two Dimensional Ice from First Principles: Structures and Phase Transitions. Phys Rev Lett (2016) 116:025501. doi:10.1103/PhysRevLett.116.025501

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Rasaiah JC, Garde S, Hummer G. Water in Nonpolar Confinement: from Nanotubes to Proteins and beyond. Annu Rev Phys Chem (2008) 59:713–40. doi:10.1146/annurev.physchem.59.032607.093815

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Asay DB, Kim SH. Evolution of the Adsorbed Water Layer Structure on Silicon Oxide at Room Temperature. J Phys Chem B (2005) 109(35):16760–3. doi:10.1021/jp053042o

CrossRef Full Text | Google Scholar

7. Zhang Y, Nappini S, Sankar R, Bondino F, Gao J, Politano A. Assessing the Stability of Cd3As2 Dirac Semimetal in Humid Environments: the Influence of Defects, Steps and Surface Oxidation. J Mater Chem C (2021) 9:1235–44. doi:10.1039/d0tc04883f

CrossRef Full Text | Google Scholar

8. Centi G. Smart Catalytic Materials for Energy Transition. SmartMat (2020) 1:e1005. doi:10.1002/smm2.1005

CrossRef Full Text | Google Scholar

9. Giovambattista N, Rossky PJ, Debenedetti PG. Effect of Pressure on the Phase Behavior and Structure of Water Confined between Nanoscale Hydrophobic and Hydrophilic Plates. Phys Rev E Stat Nonlin Soft Matter Phys (2006) 73:041604. doi:10.1103/PhysRevE.73.041604

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Jang C, Adam S, Chen J-H, Williams ED, Das Sarma S, Fuhrer MS. Tuning the Effective fine Structure Constant in Graphene: Opposing Effects of Dielectric Screening on Short- and Long-Range Potential Scattering. Phys Rev Lett (2008) 101:146805. doi:10.1103/physrevlett.101.146805

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Shim J, Lui CH, Ko TY, Yu Y-J, Kim P, Heinz TF, et al. Water-gated Charge Doping of Graphene Induced by Mica Substrates. Nano Lett (2012) 12:648–54. doi:10.1021/nl2034317

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Li S-Q, Chang Y, Zhang Z, Liu H, Chen M, Han Y, et al. Evolution of Water Layer Adsorption on the GaN(0001) Surface and its Influence on Electronic Properties. J Phys Chem C (2021) 125:667–74. doi:10.1021/acs.jpcc.0c10256

CrossRef Full Text | Google Scholar

13.So Much More to Know. Science. (2005) 309: 78–102. doi:10.1126/science.309.5731.78b

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Xu Y, Xuan X, Zhang Z, Guo W. A Helical Monolayer Ice. J Phys Chem Lett (2020) 11:3860–5. doi:10.1021/acs.jpclett.0c01129

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Ma R, Cao D, Zhu C, Tian Y, Peng J, Guo J, et al. Atomic Imaging of the Edge Structure and Growth of a Two-Dimensional Hexagonal Ice. Nature (2020) 577:60–3. doi:10.1038/s41586-019-1853-4

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Chen J, Guo J, Meng X, Peng J, Sheng J, Xu L, et al. An Unconventional Bilayer Ice Structure on a NaCl(001) Film. Nat Commun (2014) 5:4056. doi:10.1038/ncomms5056

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Nie S, Feibelman PJ, Bartelt NC, Thürmer K. Pentagons and Heptagons in the First Water Layer on Pt(111). Phys Rev Lett (2010) 105:026102. doi:10.1103/PhysRevLett.105.026102

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Yang J, Meng S, Xu LF, Wang EG. Ice Tessellation on a Hydroxylated Silica Surface. Phys Rev Lett (2004) 92:146102. doi:10.1103/physrevlett.92.146102

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Algara-Siller G, Lehtinen O, Wang FC, Nair RR, Kaiser U, Wu HA, et al. Square Ice in Graphene Nanocapillaries. Nature (2015) 519:443–5. doi:10.1038/nature14295

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Xu K, Cao P, Heath JR. Graphene Visualizes the First Water Adlayers on Mica at Ambient Conditions. Science (2010) 329:1188–91. doi:10.1126/science.1192907

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Matheswaran P, Gokul B, Abhirami KM, Sathyamoorthy R. Thickness Dependent Structural and Optical Properties of In/Te Bilayer Thin Films. Mater Sci Semiconductor Process (2012) 15:486–91. doi:10.1016/j.mssp.2012.03.006

CrossRef Full Text | Google Scholar

22. Ochedowski O, Bussmann BK, Schleberger M. Graphene on Mica - Intercalated Water Trapped for Life. Sci Rep (2014) 4:6003. doi:10.1038/srep06003

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Rezania B, Dorn M, Severin N, Rabe JP. Influence of Graphene Exfoliation on the Properties of Water-Containing Adlayers Visualized by Graphenes and Scanning Force Microscopy. J Colloid Interf Sci (2013) 407:500–4. doi:10.1016/j.jcis.2013.06.034

CrossRef Full Text | Google Scholar

24. Severin N, Lange P, Sokolov IM, Rabe JP. Reversible Dewetting of a Molecularly Thin Fluid Water Film in a Soft Graphene-Mica Slit Pore. Nano Lett (2012) 12:774–9. doi:10.1021/nl2037358

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Lee D, Ahn G, Ryu S. Two-Dimensional Water Diffusion at a Graphene-Silica Interface. J Am Chem Soc (2014) 136:6634–42. doi:10.1021/ja4121988

CrossRef Full Text | Google Scholar

26. Lee MJ, Choi JS, Kim J-S, Byun I-S, Lee DH, Ryu S, et al. Characteristics and Effects of Diffused Water between Graphene and a SiO2 Substrate. Nano Res (2012) 5:710–7. doi:10.1007/s12274-012-0255-9

CrossRef Full Text | Google Scholar

27. Verdaguer A, Segura JJ, López-Mir L, Sauthier G, Fraxedas J. Communication: Growing Room Temperature Ice with Graphene. J Chem Phys (2013) 138:121101. doi:10.1063/1.4798941

CrossRef Full Text | Google Scholar

28. Kazakova O, Panchal V, Burnett T. Epitaxial Graphene and Graphene-Based Devices Studied by Electrical Scanning Probe Microscopy. Crystals (2013) 3:191–233. doi:10.3390/cryst3010191

CrossRef Full Text | Google Scholar

29. Komurasaki H, Tsukamoto T, Yamazaki K, Ogino T. Layered Structures of Interfacial Water and Their Effects on Raman Spectra in Graphene-On-Sapphire Systems. J Phys Chem C (2012) 116:10084–9. doi:10.1021/jp301402u

CrossRef Full Text | Google Scholar

30. Xu Z, Ao Z, Chu D, Younis A, Li CM, Li S. Reversible Hydrophobic to Hydrophilic Transition in Graphene via Water Splitting Induced by UV Irradiation. Sci Rep (2014) 4:6450. doi:10.1038/srep06450

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Feng X, Maier S, Salmeron M. Water Splits Epitaxial Graphene and Intercalates. J Am Chem Soc (2012) 134:5662–8. doi:10.1021/ja3003809

CrossRef Full Text | Google Scholar

32. Ochedowski O, Begall G, Scheuschner N, El Kharrazi M, Maultzsch J, Schleberger M. Graphene on Si(111)7×7. Nanotechnology (2012) 23:405708. doi:10.1088/0957-4484/23/40/405708

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Temmen M, Ochedowski O, Schleberger M, Reichling M, Bollmann TRJ. Hydration Layers Trapped between Graphene and a Hydrophilic Substrate. New J Phys (2014) 16:053039. doi:10.1088/1367-2630/16/5/053039

CrossRef Full Text | Google Scholar

34. Bollmann TRJ, Antipina LY, Temmen M, Reichling M, Sorokin PB. Hole-doping of Mechanically Exfoliated Graphene by Confined Hydration Layers. Nano Res (2015) 8:3020–6. doi:10.1007/s12274-015-0807-x

CrossRef Full Text | Google Scholar

35. Xu J, Cui X, Liu N, Chen Y, Wang HW. Structural Engineering of Graphene for High‐resolution Cryo‐electron Microscopy. SmartMat (2021) 2:202–12. doi:10.1002/smm2.1045

CrossRef Full Text | Google Scholar

36. Kresse G, Furthmüller J. Efficient Iterative Schemes Forab Initiototal-Energy Calculations Using a Plane-Wave Basis Set. Phys Rev B (1996) 54:11169–86. doi:10.1103/physrevb.54.11169

CrossRef Full Text | Google Scholar

37. Perdew JP, Burke K, Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys Rev Lett (1996) 77:3865–8. doi:10.1103/PhysRevLett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Grimme S, Antony J, Ehrlich S, Krieg H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J Chem Phys (2010) 132:154104. doi:10.1063/1.3382344

CrossRef Full Text | Google Scholar

39. Kresse G, Joubert D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys Rev B (1999) 59:1758–75. doi:10.1103/physrevb.59.1758

CrossRef Full Text | Google Scholar

40. Monkhorst HJ, Pack JD. Special Points for Brillouin-Zone Integrations. Phys Rev B (1976) 13:5188–92. doi:10.1103/physrevb.13.5188

CrossRef Full Text | Google Scholar

41. Neugebauer J, Scheffler M. Adsorbate-substrate and Adsorbate-Adsorbate Interactions of Na and K Adlayers on Al(111). Phys Rev B (1992) 46:16067–80. doi:10.1103/physrevb.46.16067

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Krukowski S, Kempisty P, Strąk P. Electrostatic Condition for the Termination of the Opposite Face of the Slab in Density Functional Theory Simulations of Semiconductor Surfaces. J Appl Phys (2009) 105:113701. doi:10.1063/1.3130156

CrossRef Full Text | Google Scholar

43. Zhao W-H, Wang L, Bai J, Yuan L-F, Yang J, Zeng XC. Highly Confined Water: Two-Dimensional Ice, Amorphous Ice, and Clathrate Hydrates. Acc Chem Res (2014) 47:2505–13. doi:10.1021/ar5001549

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Henkelman G, Uberuaga BP, Jónsson H. A Climbing Image Nudged Elastic Band Method for Finding Saddle Points and Minimum Energy Paths. J Chem Phys (2000) 113:9901–4. doi:10.1063/1.1329672

CrossRef Full Text | Google Scholar

45. Kang K, Morgan D, Ceder G. First Principles Study of Li Diffusion in I-Li₂NiO₂ Structure. Phys Rev B (2009) 79:014305. doi:10.1103/physrevb.79.014305

CrossRef Full Text | Google Scholar

46. Morgan D, Van der Ven A, Ceder G. Li Conductivity in Li[sub x]MPO[sub 4] (M = Mn, Fe, Co, Ni) Olivine Materials. Electrochem Solid-state Lett (2004) 7:A30. doi:10.1149/1.1633511

CrossRef Full Text | Google Scholar

47. Kowalski PM, Meyer B, Marx D. Composition, Structure, and Stability of the rutileTiO2(110)surface: Oxygen Depletion, Hydroxylation, Hydrogen Migration, and Water Adsorption. Phys Rev B (2009) 79:115410. doi:10.1103/physrevb.79.115410

CrossRef Full Text | Google Scholar

48. Li W, Zhao J, Zhu Q, Wang D. Insight into the Initial Oxidation of 4H-SiC from First-Principles Thermodynamics. Phy Rev B (2013) 87:085320. doi:10.1103/physrevb.87.085320

CrossRef Full Text | Google Scholar

49. Reuter K, Scheffler M. First-principles Atomistic Thermodynamics for Oxidation Catalysis: Surface Phase Diagrams and Catalytically Interesting Regions. Phys Rev Lett (2003) 90:046103. doi:10.1103/PhysRevLett.90.046103

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Zhang W, Wu P, Li Z, Yang J. First-principles Thermodynamics of Graphene Growth on Cu Surfaces. J Phys Chem C (2011) 115:17782–7. doi:10.1021/jp2006827

CrossRef Full Text | Google Scholar

51. Chase JMW. NIST-JANAF Thermochemical Tables. 4th ed. New York: American Institute of Physics (1998).

Google Scholar