Estimating Precipitating Energy Flux, Average Energy, and Hall Auroral Conductance From THEMIS All-Sky-Imagers With Focus on Mesoscales

Recent attention has been given to mesoscale phenomena across geospace (∼10 s km to 500 km in the ionosphere or ∼0.5 R_E to several R_E in the magnetosphere), as their contributions to the system global response are important yet remain uncharacterized mostly due to limitations in data resolution and coverage as well as in computational power. As data and models improve, it becomes increasingly valuable to advance understanding of the role of mesoscale phenomena contributions—specifically, in magnetosphere-ionosphere coupling. This paper describes a new method that utilizes the 2D array of Time History of Events and Macroscale Interactions during Substorms (THEMIS) white-light all-sky-imagers (ASI), in conjunction with meridian scanning photometers, to estimate the auroral scale sizes of intense precipitating energy fluxes and the associated Hall conductances. As an example of the technique, we investigated the role of precipitated energy flux and average energy on mesoscales as contrasted to large-scales for two back-to-back substorms, finding that mesoscale aurora contributes up to ∼80% (∼60%) of the total energy flux immediately after onset during the early expansion phase of the first (second) substorm, and continues to contribute ∼30–55% throughout the remainder of the substorm. The average energy estimated from the ASI mosaic field of view also peaked during the initial expansion phase. Using the measured energy flux and tables produced from the Boltzmann Three Constituent (B3C) auroral transport code (Strickland et al., 1976; 1993), we also estimated the 2D Hall conductance and compared it to Poker Flat Incoherent Scatter Radar conductance values, finding good agreement for both discrete and diffuse aurora.

Introduction

A fundamental question at the heart of the dynamics and coupling of Earth’s magnetosphere-ionosphere system is, “How is energy deposited into the ionosphere from the magnetosphere?” That itself has a complex answer comprised of multiple parts such as electromagnetic energy, particle precipitation, and waves. Great strides have been made in characterizing the global energy input due to precipitation; for example, Newell et al. [1] built an empirical precipitation model using Defense Meteorological Satellite Program (DMSP) statistics to determine the auroral power from diffuse, monoenergetic discrete, and broadband discrete aurora as a function of solar wind coupling. Results were binned by magnetic local time (MLT) and latitude. Their work has been useful for describing auroral power at large spatial scales, but does not explain contribution of specific scale sizes or provide event-based numbers that could be used in global climate models to investigate the ionosphere-thermosphere response to an intense, mesoscale (∼10 s–500 km) auroral form. DMSP statistics-based modeling has been improved over the years, leading to the construction of the Oval Variation, Assessment, Tracking, Intensity, and Online Nowcasting (OVATION) models [2–4] to the current state-of-the art version, OVATION Prime, all of which still excel at the more global precipitation response without capturing the spatially and temporally dynamic aurora that occur on mesoscales.

In a newly developed empirical model, Auroral Spectrum and High-Latitude Electric field and variability (ASHLEY) [5], there is no assumed spectra distribution for the precipitating particles, and the DMSP observed energetic particles in 19-energy channels have been directly binned according to the geomagnetic local time, latitude, and solar wind conditions. ASHLEY has shown some advantage to specify the soft electron precipitation, but is still limited to the large-scale phenomena. Another very recent DMSP statistics-based modeling work employed machine learning techniques to build a new total electron energy flux particle precipitation nowcast model called PrecipNet [6]. PrecipNet better captures the dynamic changes of the auroral flux than OVATION Prime, improving capabilities to reconstruct mesoscale phenomena and making great progress towards nowcasting and forecasting auroral response to solar wind driving.

Though these and other works make great strides towards resolving the role of mesoscale auroral precipitation, the field still lacks a rigorous understanding and characterization of the contribution of the dynamic and energetic mesoscale auroral forms that are embedded within the large-scale system. These are important to resolve, as studies such as Deng et al. [7] and Sheng et al. [8] have illustrated with the Global Ionosphere-Thermosphere model (GITM) how mesoscale phenomena in the ionosphere can vastly alter the ionospheric and mesospheric response.

A major reason for the continued deficiency in mesoscale characterization has been inadequate data sources to fully resolve spatial and temporal ambiguities. The DMSP examples above are perhaps one of the best-suited datasets because they provide in situ measurements of the particle flux and energy, as well as 2D views of the aurora from above as the satellite flies overhead. However, statistics must be employed, since orbiting spacecraft measurements lack continuous coverage over a given 2D area. It is not possible to investigate auroral evolution over a short time in the region of interest. DMSP orbits are also not often optimized for covering the nightside auroral oval, as most of their measurements are made near the dawn-dusk meridian.

In contrast, ground-based observations consistently observe the same geographic location over time, allowing for the temporal changes to be recorded. However, most datasets do not have sufficiently high resolution for observing the aurora’s spatial evolution with a wide spatial coverage in the nightside auroral oval. For example, meridian scanning photometers (MSPs), which observe multiple wavelengths (such as blue, green, and redline aurora), are limited to a line of constant longitude. Incoherent Scatter Radar (ISR) can measure electron densities to determine the precipitated energy, energy flux, and resulting changes in conductance in 1D or 2D (e.g., [9,10]), but the measurement area is limited to ∼100 s km in horizontal spatial extent at 100 km altitude.

All-sky-imagers (ASIs) provide auroral intensity evolution in 2D space as well as over time. ASIs have been used to resolve auroral arcs and to obtain local 2D precipitation information such as energy flux (e.g., [11–16]), Pedersen conductance (e.g., [17]), and arc occurrence and distribution information (e.g., [18]). For example, Lam et al. [17] used the THEMIS ASI at Fort Yukon to demonstrate a relationship between the Pedersen conductance (as determined from Poker Flat Incoherent Scatter Radar (PFISR) data) to white light intensity within 3 mho or 40%. They assumed that the Pedersen conductance is proportional to the square root of the white light intensity, based on Kosch et al. (1998) who argued for this relationship after making the approximations that auroral optical intensity is proportional to ion production rate and that electron production is approximately equal to the electron loss.

Since 2006, NASA’s THEMIS mission has provided an array of white-light ASIs across Canada and Alaska that monitor the majority of the nightside auroral oval at a 3 s cadence and up to 1 km resolution, providing a global view at temporal and spatial resolutions required to study the aurora on mesoscales [19]. This allows us to expand upon previous demonstrations of ASI capabilities to estimate precipitated energy flux and average energy in 2D, but on a continental scale. Our recent work has shown that the THEMIS ASI array can observe evolution of precipitating energy flux over the whole size of a substorm and that it is possible to estimate contributions of mesoscale precipitation over large-scale precipitation [20].

In this paper, we describe the technique that utilizes the white-light ASI array that was not detailed in Nishimura et al. [20], including important upgrades made through the present work, supplemented by MSPs and auroral transport code calculations, to estimate precipitating energy flux, average energy, and Hall conductance, as well as what percent of the energy flux is contributed by mesoscale auroral forms during two back-to-back substorms.

Methodology

Background and Overview

One method to estimate the precipitating energy flux and average energy utilizes the ratio of auroral intensities at different wavelengths (colors). When electrons precipitate into the upper atmosphere, the more energetic ones reach lower altitudes before encountering high enough atmospheric densities to thermalize, whereas the less energetic electrons are stopped and thermalize at higher altitudes. Therefore, the red aurora occurring at higher altitudes are produced by less energetic populations colliding with atomic oxygen, whereas the green and blue aurora occurring at lower altitudes are caused by more energetic populations colliding with oxygen and molecular nitrogen, respectively. Methodologies that utilize the intensity ratios between the different auroral color wavelengths have been developed to determine the integrated energy flux and the average energy of the precipitating particle distribution (e.g., [21–25]); for example, more red than blue light indicates a less energetic population, whereas more blue than red light indicates the opposite.

Janhunen [13] used the figures that plotted intensity ratios from Rees and Luckey [21] and Strickland et al. [22] to develop an inversion method that determines precipitating energy flux from multiwavelength ASIs. They found that the energy flux reconstructed from only the green images was very good, almost indistinguishable from the reconstructions that included the red images. When comparing the reconstructed arc energy flux with energy flux measured by the FAST satellite, they found a good agreement (12 mW m⁻² vs. 10 mW m⁻², respectively). Kauristie et al. [14] used the methods laid out by Janhunen [13] to estimate the energy flux measured by the All-Sky Camera in Kilpisjärvi and compared those values against those measured by the incoherent scatter radar EISCAT, finding a correlation of r = 0.72 between datasets. Partamies et al. [15] further tested the technique by comparing 100 All-Sky Camera images at Longyearbyen with EISCAT energy fluxes, finding that in 35% of all of the blue and green image inversions the relative errors were less than 50%, and in 90% of the blue and green image inversions relative errors were less than 100%. Dahlgren et al. [16] also developed an inversion technique to determine both energy flux and average energy from ASIs combined with EISCAT data. Instead of relying on Rees and Luckey [21], which assumes all secondary, etc., electrons dissipate their energy locally, they determined the average energies of the precipitating electrons from Auroral Structure and Kinetics narrow angle camera emission ratios modelled with the Southampton ion chemistry and electron transport model (described in [11,26]), using atmospheric parameters for the conditions during their case study.

Hecht et al. [24,25] also presented relationships between different auroral wavelength ratios and the average energy of the precipitation using the B3C auroral electron transport code [27,28]. Strickland et al. [22,27,28] made a detailed attempt to investigate dependencies of red line emission on key parameters, unlike Rees and Luckey [21] who did not incorporate knowledge of O abundance relative to N2, which is necessary when using the red line emission. We rely upon and slightly update the methodologies developed by Strickland et al. [22] and Hecht et al. [23–25], which are described in Determining Energy Flux and Average Energy From Aurora Color Ratios. These methodologies, which utilize a model atmosphere to incorporate the appropriate physics and chemistry, improve calculations of the emissions and conductance as functions of the incident energy flux and average energy as compared to Rees and Luckey [21], which Nishimura et al. [20] used. We note that our techniques additionally include more physics and chemistry than the techniques employed by Kosch et al. (1998) and Lam et al. [17], who did not calculate emissions, energy flux, or average energy, but deduced the Pedersen conductance assuming that it is proportional to the square root of the white light intensity.

In order to employ the network of THEMIS ASIs, we developed log-log linear analytical functions to convert from white light counts to red (630.0 nm), green (557.7 nm), and blue (427.8 nm) intensities using overlapping meridian scanning photometer (MSP) data to calibrate. The steps we took are detailed in Converting White Light Intensities to Color Intensities. After obtaining the ratios, we estimated the precipitating electron energy flux and average energy. Using the 2D capabilities of the ASI mosaic, we determined what percentage of the energy flux is contributed by various mesoscales (Results).

From the energy flux and average energy, we estimated the Hall conductance in 2D over time (Determining the Hall Conductance) and compared to Poker Flat Incoherent Scatter Radar (PFISR) data (Results). Because the white light can be related to the OI (557.7 nm) greenline and (427.8 nm) blueline (shown in Converting White Light Intensities to Color Intensities), it does well estimating energy flux (Q). At higher average electron energies that are associated with intense aurora (>5 keV), the Hall conductivity scales very well with Q with little dependence on average electron energy (see Figure 16.5fig165 of [29] and Supplementary Figure S1). At lower energies, there is an energy dependence; but within a factor of two, the major dependent variable is still Q. Since this paper is focused on mesoscales associated with the more intense precipitation events, the Hall conductivities become a byproduct of a measurement of Q.

Instrumentation

THEMIS All-Sky-Imagers

The THEMIS all-sky-imager (ASI) array consists of about 20 unfiltered (white light) fish-eye cameras at any given time spanning Canada and Alaska, covering a large section of the auroral oval with up to 1 km resolution near zenith, 3 km at a 40° elevation angle, 10 km at a 20° elevation angle, and 25 km at a 10° elevation angle (see Figure 6 from [19]). The ASIs are time synchronized with a 3 s cadence. During northern winter, continuous coverage is available from about 00:00–15:00 UT covering approximately 17-07 MLT for each individual site. Data collection began in 2006 and continues to present day [19]. For this study, because ASIs do not differentiate between particle species, we assume the visible light is due to precipitating electrons. Hecht et al. [30] discuss that the electron flux Q can be derived from the blue intensity, and that the proton flux is a small fraction of the electron flux. As we will show, the white light and blueline are well-correlated, so this assumption carries through.

Before we continue, we highlight the caution one needs to take with ASI data at low elevation angles. For studies that require low error in energy flux, energy, or conductance magnitudes, elevation angles above ∼70° will be more trustworthy as they look approximately up the magnetic field line local to the station. The farther from zenith in the ASI field of view (low elevation angles), the more flux tubes the line-of-sight observation cuts through. Because the image is 2D, aurora at different heights may not be observed integrally, but are spread out over several latitudes (and/or longitudes) in the image. This is because all white light is mapped to 110 km altitude and then projected onto the 2D plane. To address the question of mesoscale contribution to auroral precipitation, however, we require a larger field of view; otherwise, the ASIs do not contribute additional perspectives to what we can surmise from, say, ISRs. The uncertainty in mapping can be mitigated in cases where multiple ASI field of views (FOVs) overlap by validating and/or adjusting the mapping altitude to match aurora locations viewed from different imagers. For this study, as will be shown in Results, the arcs were well-aligned between different imagers. Lastly, a future work could be to try further calibrating ASI data to DMSP data, which does not have the low elevation angle error.

NORSTAR Meridian Scanning Photometer

The NORSTAR Meridian Scanning Photometer (MSP) array consists of four ground-based photometers designed to simultaneously measure luminosity in four key auroral bands (470.9, 486.1, 557.7, and 630.0 nm). To use the color ratio relationships discussed in Determining Energy Flux and Average Energy From Aurora Color Ratios, we converted the 470.9 nm intensity to 427.8 nm by multiplying the former by 4.5 [31]. As Omholt [32] showed, the ratio is constant between these auroral emissions. Each MSP utilizes a high speed, 8-channel filter wheel (to observe auroral plus background channels), coupled to a highly sensitive photo-multiplier tube (PMT) which mechanically scans from near horizon-to-horizon in the North-South direction. Each scan consists of approximately 544 elevation steps, taking 30 s to complete a full horizon to horizon scan in high resolution mode. PMT counts from these scans are then background subtracted and converted into units of Rayleighs (R). The green 557.7 nm, blue 470.9 nm, and 486.1 nm emissions are projected to an altitude of 110 km and the red 630.0 nm emission is typically projected to 230 km. We plotted the Fort Smith (FSMI) MSP line of sight (LOS) on top of the FSMI THEMIS ASI field of view (FOV) in Figure 1A, mapped to 110 km.

FIGURE 1

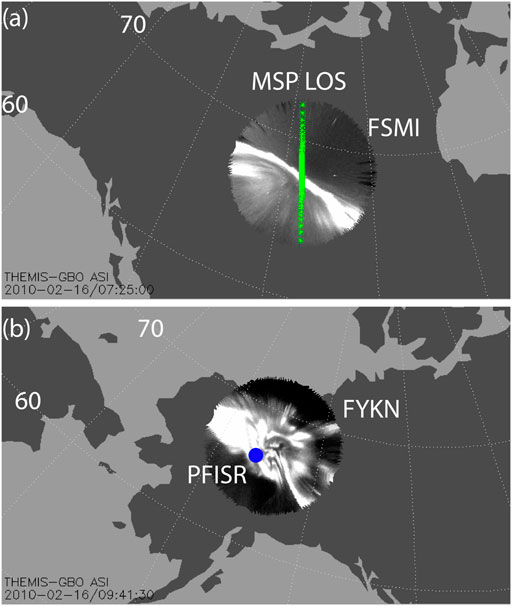
FIGURE 1. (A) Green line depicts the NORSTAR MSP line of sight (LOS) superimposed on top of the THEMIS ASI at Fort Smith, Canada on 2010-02-16 at 07:25 UT. The locations were mapped to 110 km altitude. The white within the ASI FOV is the aurora. Some treetops are visible on the edges of the FOV as black spikes. The stars seen as single white dots are removed in our methodology. (B) The blue dot depicts the PFISR location within the Fort Yukon (FYKN), Canada FOV on 2010-02-16 at 09:41:30 UT. Both panels label the 60° and 70° magnetic latitude lines.

Poker Flat Incoherent Scatter Radar

In order to test how well our optical methods are able to determine the Hall conductance, we compared to the conductance determined from the Poker Flat Incoherent Scatter Radar (PFISR) altitude resolved electron density data. From this perspective the PFISR observations are considered a “truth” dataset, at least for the calculation of the Hall conductance. We plotted the PFISR location on top of the Fort Yukon (FYKN) THEMIS ASI FOV in Figure 1B. The PFISR electron density observations used in this study were estimated from received power measured using the Barker Coded pulses in the 121-beam “Grid11x11_11” mode on 16 February 2010. In this mode, the radar transmitted long-pulses and Barker codes, which are optimize for F region and lower E region observations, respectively, but it did not include alternating code pulses that are optimized for the whole E-region. This 121-beam mode uses a 130 µs, 13 baud Barker Code sampled at 5 µs, which provides electron density observations every 0.75 km with a range resolution of 1.5 km and achieves 48 samples per beam in 14.157 s. The electron density data was post-integrated to achieve ∼30 s integration time. This mode does not provide a vertical beam, so the highest elevation angle beam, 89°, was used to compute conductance.

The Barker code is a pulse-compression code that only decodes properly when the correlation time of the target is longer than the time length of the pulse (e.g., [33]). ISR theory (e.g., [34]) predicts that the correlation time of ionospheric plasma depends strongly on the ion temperature resulting in a decrease of the correlation time as the ion temperature increases. For a 130 µs pulse and given the ion temperature observed by PFISR during the event under study, we expect the performance of the Barker code to significantly decrease for the top of the E region, e.g., above ∼120 km. Above this altitude, the Barker code electron density observations will underestimate the electron density, but the Barker code observations should well-cover the electron densities contributing to the Hall conductance. However, it can be shown that the Pedersen conductivity has a peak at the location where the ratio of the ion cyclotron frequency to ion neutral collision frequency equals one; this altitude typically occurs at ∼120 km (e.g., Sangalli et al., 2009; Burchill et al., 2011; Oyama et al., 2012). Therefore, for this event in particular, a significant portion of the Pedersen conductivity is not well-resolved with the ISR observations, and the Barker code observations from PFISR would underestimate the Pedersen conductivities. Preliminary analysis (not shown) of the PFISR long pulse data shows that there is in fact greater density at altitudes above ∼120 km that contribute to the Pedersen conductance. Unfortunately, the long pulse data has low range resolution (∼72 km) and would require deconvolution (e.g., [35]) to be more useful for conductance calculations. We therefore focus only on the Hall conductance. This works to the strength of the ASI method, since the Hall conductance is essentially a function of Q when average energies exceed 5 keV [29]. Q is essentially a function of the blueline emission [22], which we show later is well-resolved with white light data.

We calculated the Hall conductivity using Eq. 10 from [36],

${\sigma }_H\left(z\right)\approx \frac{e{n}_e\left(z\right)}{B \left[1+ \frac{{\text{Ω}}_i^2}{{\nu }_{in}^2}\right]}(1)$

where ${\text{Ω}}_i$corresponds to the ion cyclotron frequency, $B$ corresponds to the magnetic field, $e$ corresponds to the elementary charge, and z represents the altitude. The altitude resolved electron density, $n_e\left(z\right),$ is obtained using PFISR. The ion neutral collision frequency, ${\nu }_{in}$, is calculated using equation 4.88 from Schunk and Nagy [37] for the non-resonant ion neutral collision frequencies and expressions in Table 4.5tbl45 of Schunk and Nagy [37] for the resonant ion-neutral collision frequencies. This formula has been implemented in the “flipchem” Python package. Eq. 8 is approximately valid above 80 km altitude [36]. To obtain conductance, we perform an altitude integration of conductivity using a Simpson method integration routine. These formulas have been validated with previous results presented in Kaeppler et al. [9]. Results are discussed in Results.

Determining Energy Flux and Average Energy From Aurora Color Ratios

Following Hecht et al. [24,25], we used the B3C auroral electron transport code [27,28] to calculate lookup tables that allow the integrated energy flux (Q; erg cm⁻² s⁻¹), the average energy ($\overline{\text{E}}$; keV), and the oxygen scaling factor (fO) to be derived from measurements of the green, red, and blue emissions (see Figure 2). Since the publication of Hecht et al. [24], the transport code has been updated especially with respect to the green line emission. Hence, the table reproduced below in Figure 2 differs somewhat from the corresponding Figure 8 in the earlier publication. The B3C code solves the coupled set of linear Boltzmann equations for electrons, H⁺, and H atom fluxes with full collisional processes [38] for a given set of cross sections and neutral densities for altitudes from 500 km down to 90 km. The B3C calculations are made with atmospheric neutral densities provided by the empirical MSIS90 model [39] that is parameterized by the geomagnetic Ap and solar flux F10.7 indices. (MSIS90 describes the neutral temperature and densities in Earth’s atmosphere from ground to thermospheric heights.) The code accepts a choice of either a Maxwellian or a Gaussian incident precipitating electron flux spectrum and the associated Q and $\overline{\text{E}}$ for each geographic latitude and longitude of interest. We ran B3C for Gaussian and Maxwellian distributions to provide values for both discrete (Gaussian) and diffuse (Maxwellian) aurora. Figure 2A depicts the Gaussian distribution’s average energies as a function of green to blue and red to blue ratios; Figure 2B depicts the Maxwellian version. A more complete discussion of the MSIS model is given in Background and Overview and Determining Energy Flux and Average Energy From Aurora Color Ratios of Hecht et al. [25].

FIGURE 2

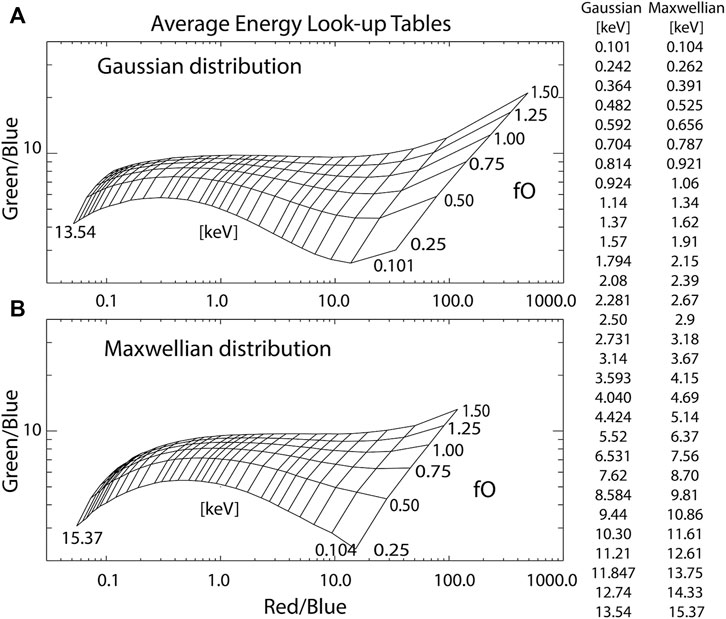
FIGURE 2. Plots of $\overline{\text{E}}$ and fO as a function of the green/blue vs. red/blue ratios for a MSIS90 atmosphere (daily Ap of 22, F10.7 of 85.5 and average F10.7 of 84.7 over Fort Smith, Canada) for electron precipitation characterized by (A) a Gaussian energy distribution with high and low energy tails [28] and (B) a Maxwellian energy distribution. Average energies ($\overline{\text{E}}$) are represented by the semi-vertical lines and are listed on the right for both distributions. The fO value is listed at the end of each semi-horizontal line.

The specific attributes of the model in this work are as follows. MSIS90 was run for 16 February 2010, the date of our event study. The location was chosen as Fort Smith, Canada at 60.0°N, 248.2°E, which is where our primary instrumentation were located. The F10.7 was 85.5, F10.7 average was 84.7, and the daily Ap was 22 (we also incorporated the other six Ap values for 16 February 2010). The reference O/N2 (an fO of 1) for a column density of 10¹⁷ (cm⁻²) of N2, following Strickland et al. [40], is 0.53. This reference value allows a comparison of fO values for different model runs. This is a disturbed atmosphere for higher latitudes as would be suggested by comparing the reference O/N2 (0.53) with the quiet (0.91) and disturbed (0.45) values used in Hecht et al. [30]. Figure 1 of Hecht et al. [30] suggests that uncertainties in the chosen model atmosphere will affect the derived $\overline{\text{E}}$ values. However, for the $\overline{\text{E}}$ values of interest here we would expect the derived values of $\overline{\text{E}}$ might be lower by 10–20% if the actual atmosphere were somewhat more disturbed than the chosen reference model. The exact bias on the derived $\overline{\text{E}}$ and fO values depends upon the area on the plot in Figure 1 being considered.

To determine the average energies more precisely from the non-uniformly gridded look-up table, we first interpolated the 6 × 30 [fO × $\overline{\text{E}}$] look-up table values across log-log space to a 50 × 50 array, allowing for 50 red/blue values and 50 green/blue values, each with a corresponding $\overline{\text{E}}$ and fO value. Q was determined by dividing the 427.8 nm intensity (in Rayleighs) by the yield (Rayleigh/erg cm⁻² s⁻¹), which is a function of $\overline{\text{E}}$ and fO [22] and is another output from the B3C run.

Converting White Light Intensities to Color Intensities

In order to use the methods described in Determining Energy Flux and Average Energy From Aurora Color Ratios, we had to first convert the ASI white light counts to red (630.0 nm), green (557.7 nm), and blue (427.8 nm) intensities. We accomplished this by fitting log-log linear functions via ordinary least-squares linear regression [41] to scatter plots of white light counts vs. green light intensity at the longitude line where the ASI data overlaps the NORSTAR MSP data at Fort Smith, NWT. We then fit scatter plots of the MSP blue light vs. green light, and the MSP red light vs. green light. We fit the data points from 07:00–10:00 UT on 16 February 2010.

Before developing the fits, we processed the ASI data by removing background light by subtracting a quiet-time snapshot from each station. The snapshot was chosen from a dark period immediately preceding any aurora observed in the ASI field of view, prior to the substorm. Starlight was removed by applying a median filter, since the starlight moves over time from the original dark sky snapshot. We ignored MSP data with <50 Rayleighs to avoid color ratio spikes that can occur when the denominator is near zero.

We performed the fitting in log-log space. In fitting the green to the white, we performed an ordinary least squares fit bisector (minimizing the sum of the squares of both white and green residuals [41]) to the median line over the white light range of 600–20,000 counts, to put the weight in the brighter aurora and because count levels below 600 show increased scatter and signal-to-noise ratio (see Figure 3A). (Above 20,000 counts had too few data points per bin.) Figure 3A plots the median and quartiles in yellow (using a white count bin size of 50 counts) and the fitted line in green. The quartiles (dashed yellow lines) are included to demonstrate the spread (uncertainty) in the data. We slightly altered the fit line below 600 counts so it would lay at or above the lower quartile, which still weights the higher counts but doesn’t ignore the shift in median slope below 600 counts completely. When we tried shifting the fit below 600 counts so that it matched the median line, the result was that we frequently over-estimated the green light at low emissions, making it impossible to model low energies (since the green light median does not approach zero when the white light approaches zero).

FIGURE 3

FIGURE 3. (A) Scatter plot of green light intensity vs. white light counts from 07:00–10:00 UT. Solid yellow line shows median whereas dashed yellow lines show quartiles of green intensity for a given white light bin 50 counts wide. The green line represents the functional fit. (B) Scatter plot of blue light intensity vs. green light intensity. Solid yellow line shows median whereas dashed yellow lines show quartiles of blue intensity for a given green light bin 50 R wide. Blue line represents the functional fit. (C) Scatter plot of red light intensity vs. green light intensity. Solid yellow line shows median whereas dashed yellow lines show quartiles of red intensity for a given green light bin 50 R wide. Red line represents the functional fit.

Instead of fitting the white light counts to blue and red, we fit the blue and red intensities to the green intensity to calibrate colors using the same instrument (the MSP) at the exact same location (removing cross-instrument related errors). Figure 3B plots the blue vs. green fit in blue, and the median and quartiles in yellow (using a bin size of 50 R to calculate the medians and quartiles). We applied the three main methods for OLS described in Isobe et al. [41] that minimizes the sum of the squares of the green residuals, the blue residuals, and both green and blue, finding that minimizing the green residuals resulted in the smallest variance in both the slope and the y-intercept. There is no blue light below 225 R in the fitting because, as mentioned above, we did not include MSP data under 50 R and we converted the 470.9 nm intensity to 427.8 nm by multiplying the former by 4.5.

We next show the red vs. green fitting (Figure 3C). We split the fitting into three functions, described in Eq. 5–7. The largest deviation in the fit from the median is between the green line intensities 10³–10⁴ R, where the redline scatter is greatest. We initially tried fitting to the median line within 10³–10⁴ R by splitting the fitting even further, but discovered that because the slope is approximately zero in this range, the red light did not vary according to what was seen in the MSPs during the active events. We therefore fit to the overall median line of the red vs. green scatterplot, which connected the two fits at lower and higher green light intensities (Eq. 5, 7) with Eq. 6. The large scatter of the data points may be because different types or time of aurora had somewhat different color ratios. It is our future work to examine dependence of fitting on auroral types or time.

The conversion functions are as follows:

$\text{Green }557.7 \text{nm} \left[R\right] (\text{where white}>600\text{ cts})={10}^{\left(1.20+0.93lo{g}_{10}\left(white light cts\right)\right)}(2)$

$\text{Green }557.7 \text{nm} \left[R\right] (\text{where white}<600\text{ cts})={10}^{\left(1.54+0.81lo{g}_{10}\left(white light cts\right)\right)}(3)$

$\text{Blue }427.8 \text{nm} \left[R\right]={10}^{\left(-0.61+0.98lo{g}_{10}\left(green intensity\right)\right)}(4)$

$\text{Red }630.0 \text{nm} \left[R\right] \text{where green}>4.e4 \left[R\right]={10}^{\left(2.50+0.20lo{g}_{10}\left(green intensity\right)\right)}(5)$

$\text{Red }630.0 \text{nm} \left[R\right] \text{where} (\text{green}<4.e4 \left[R\right] and green>200)={10}^{\left(1.40+0.44lo{g}_{10}\left(green intensity\right)\right)}(6)$

$\text{Red }630.0 \text{nm} \left[R\right] \text{where green}<200 \left[R\right]={10}^{\left(0.98+0.62lo{g}_{10}\left(green intensity\right)\right)}(7)$

The variances in the slope and the y-intercept [41], respectively, in the log-log space are as follows:

Eq. 2: 0.000336 and 0.00589.

Eq. 3: 0.018 and 0.071 (when compared to the median line below 400 cts).

Eq. 4: 5.5e-6 and 7.6e-5.

Eq. 5: 0.0020 and 0.0521.

Eq. 6: 9.40e-5 and 0.0008.

Eq. 7: 0.0040 and 0.0185.

We note that in early iterations of our fitting process, we discovered that the red and green aurorae—especially at the time of the bright auroral arc seen in Figure 4 from ∼07:18–07:25 UT—were morphologically offset from one another, with the red mapping to lower latitudes than the green (see Supplementary Figure S1). The result was an unphysical situation in which the green overtook the red at a higher latitude and the red overtook the green at a lower latitude, and the artificial result was much higher average energies where the green arc mapped and much lower average energies where the red arc mapped. To align the 630.0 and 557.7 nm emissions, the effective altitude was found to be 160 km. This is below the expected emission altitude close to 200 km (e.g., Solomon, 1988; [42]). This effective altitude may appear lower than expected due to horizontal winds which are known to blow the redline emission (e.g., [43]). Ultimately, because the point of comparing red to green was to obtain an analytical relationship between intensities, we mapped the red to 160 km to match auroral morphologies and to build the scatterplot in Figure 3C.

FIGURE 4

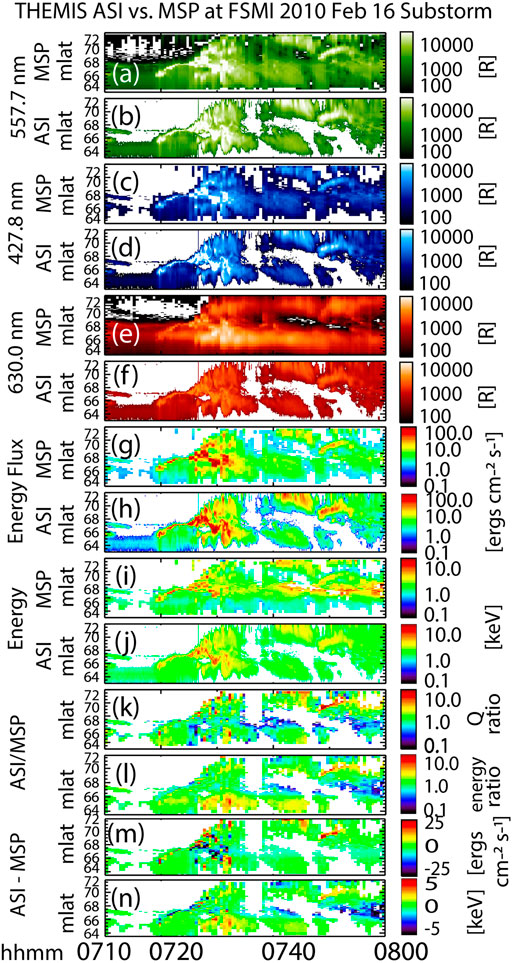
FIGURE 4. Comparison between MSP data and THEMIS ASI data. Plots are keograms, which display magnetic latitude on the y-axis and time on the x-axis. The visual is therefore the auroral evolution along a single line of longitude over time. (A) MSP 557.7 nm intensity [R]. (B) ASI 557.7 nm intensity [R]. (C) MSP 427.8 nm intensity [R]. (D) ASI 427.8 nm intensity [R]. (E) MSP 630.0 nm intensity [R]. (F) ASI 630.0 nm intensity [R]. (G) MSP determined energy flux using color ratios as input to the B3C-generated look-up table described in Background and Overview. (H) ASI determined energy flux using color ratios as input to the B3C-generated look-up table described in Background and Overview. (I) MSP-determined energy using color ratios as input to the B3C-generated look-up table described in section 2.1. (J) ASI-determined energy using color ratios as input to the B3C-generated look-up table described in Background and Overview. (K) The ratio between ASI (interpolated) and MSP energy fluxes, or panel h divided by panel g. (L) The ratio between ASI (interpolated) and MSP average energies, or panel j divided by panel i. (M) The difference between ASI (interpolated) and MSP energy fluxes, or panel h minus panel g. (N) The difference between ASI (interpolated) and MSP average energies, or panel j minus panel i.

The scatterplot in Figure 3C shows that the red and the green intensities are fairly uncorrelated, which may be due to several factors. First, the red to green ratio depends on both the average energy of the precipitating electron distribution and the energy flux. For Gaussian electron distributions that follow the Knight relation [44,45], Q and $\overline{\text{E}}$ should be broadly correlated; but for Maxwellians they are not [30,46,47]. Furthermore, the redline and greenline chemistries have different dependences on atomic oxygen density, which also decreases the correlation. This uncertainty in the average energy estimation could be explored further in future studies by defining when and where discrete aurora occur in order to build a functional relationship between green and red only during discrete auroral times. Figure 4, discussed below, as well as Supplementary Figures S3, S4 do however show the energy comparison between MSP and ASI datasets to be relatively consistent. See also Table 1 and Supplementary Tables S1, S2 which quantify the differences between ASI and MSP derived average energies, along with other parameters.

TABLE 1

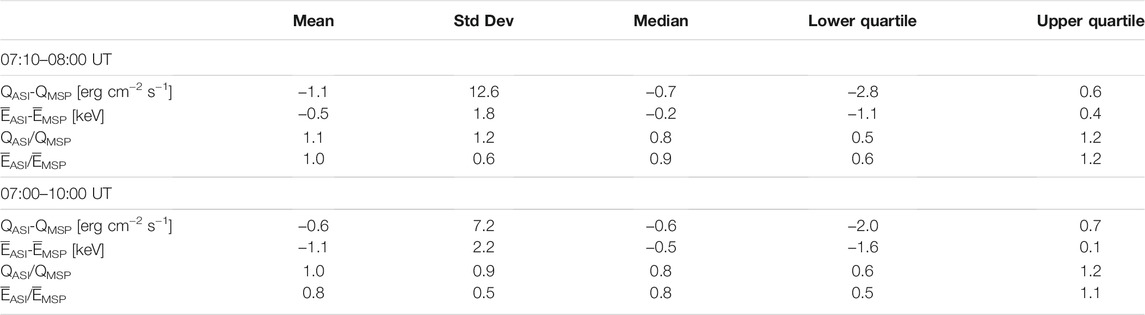
TABLE 1. The mean, standard deviation, median, and upper and lower quartiles of the ratios and the differences between ASI- and MSP-determined energy flux (Q) and average energy ($\overline{\text{E}}$). The first four lines are for the Figure 4 time window (07:10–08:00 UT). The bottom four lines are for the full time window used for the calibration (07:00–10:00 UT).

Figure 4 plots the MSP data (Figures 4A,C,E) next to the THEMIS ASI-derived auroral colors (Figures 4B,D,F) for comparison and validation. Additionally, we determined the energy flux and average energy using the methods described in Background and Overview with the MSP color ratios as input (Figures 4G,I) and the ASI color ratios as input (Figures 3H,J). Visually the comparison is good, but to quantify the differences we interpolated the THEMIS-derived products to match the MSP location and cadence and calculated the ratio and the difference. The mean, standard deviation, median, and upper and lower quartiles of the ratios and the differences are compiled in Table 1 for both the Figure 4 time window (07:10–08:00 UT) and the full time window used for the calibration (07:00–10:00 UT). We present the ratios, the differences, and a similar table that compares the ASI and MSP color intensities in the supplemental materials (Supplementary Figure S3 and Supplementary Table S1). Finally, we also present the percent differences between the ASI and MSP measured and derived quantities in Supplementary Figure S4 and Supplementary Figure S2.

Table 1 tells us, for example, that on average, the ASI energy flux underestimates the MSP energy flux by 1.1 erg cm⁻² s⁻¹ with a standard deviation of 12.6 erg cm⁻² s⁻¹ for the Figure 4 timeframe (07:10–08:00). For the entire calibration time (07:00–10:00), the ASI energy flux underestimates the MSP energy flux by only 0.6 erg cm⁻² s⁻¹ on average with a standard deviation of 7.2 erg cm⁻² s⁻¹. Table 1 also tells us that the average of the ratio of average energies is 1.0, with a median of 0.9 and upper and lower quartiles of 1.2 and 0.6, respectively, for the Figure 4 timeframe. These and the rest of Table 1 indicate the level of uncertainty assuming the MSP data as “truth”. The very slight underestimation in the differences may be due to the fact we did not remove the <600 R greenline data points from the comparison which were not heavily weighted in Figure 3 for the calibrations. As is shown in Supplementary Figure S2, for the full calibration time (07:00–10:00 UT), the percent differences are: for Q, 47.5 $\pm$36.1% with median 39.6% and quartiles 18.4 and 68.6%; for $\overline{\text{E}}$, 46.0 $\pm$ 38.2% with median 35.3% and quartiles 15.8 and 67.6%. We also present the green, blue, and red percent differences in the Supplementary Material.

With these relationships to estimate the color ratios, we determined the energy flux and average energy for all pixels that comprise the ASI mosaic. The energy flux and average energy were then interpolated to a 400 × 400 uniform geographic grid with 0.1° latitude and 0.4° longitude resolution (see Figure 5 for an example). Any points at elevation angles lower than 10° were dropped

FIGURE 5

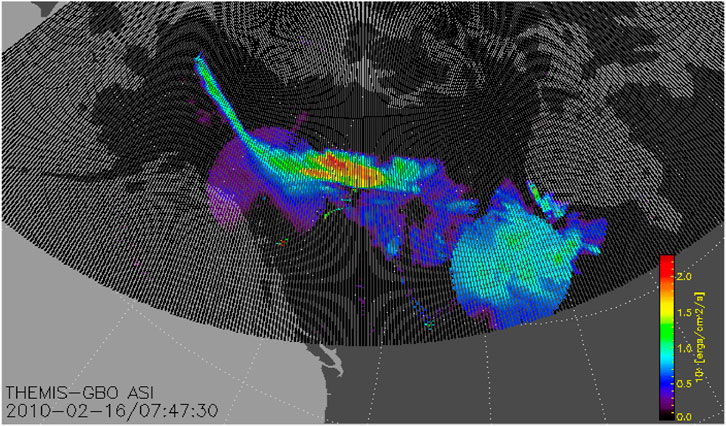
FIGURE 5. Example of the energy flux saved into the 400 × 400 grid. Note that the plot energy flux (color) is in log space, with energy fluxes ranging from 1–200 ergs cm⁻² s⁻¹).

We first applied 2D median filtering with a window size of 3 pixels in both directions. Where more than one ASI fields of view overlap, the pixel with the brightest value usually comes from the imager with better viewing conditions (e.g., higher elevation angle and clearer sky conditions), which are more reliable. We therefore assigned each of the 400 × 400 grid points the maximum energy flux (or maximum energy) value found in any pixel that fell within $\pm$0.05° latitude and $\pm$0.2° longitude of the grid point. The uniform grid system is much simpler than the imager-dependent coordinates that overlap with surrounding imagers.

The data in the uniform grid system is used to calculate total energy flux and average energy across the imager coverage (see Results). Conductance maps are also obtained. Data in this coordinate system are also used to provide data to users. (Note that this grid could be altered to a different desired resolution, e.g., 500 × 500 or 300 × 300.)

Determining the Hall Conductance

We calculated the height-integrated Hall conductance from the incident precipitating electron flux energy spectrum using the B3C auroral transport code for the same F10.7 and Ap values used in Determining Energy Flux and Average Energy From Aurora Color Ratios. The code was run for either a Maxwellian or a Gaussian incident precipitating electron flux spectrum with an associated integrated energy flux and an average energy for each geographic latitude and longitude of interest. A Maxwellian distribution is representative of diffuse auroral electron precipitation whereas a Gaussian distribution is descriptive of an accelerated distribution associated with discrete auroral precipitation [48].

Similar to our methods to obtain energy flux and energy in Determining Energy Flux and Average Energy From Aurora Color Ratios, we used B3C to create a look-up table of conductances given various inputs. The B3C height-integrated Hall conductance was calculated for an incident precipitating electron Maxwellian distribution with combinations of average energies of 0.173, 0.875, 1.81, 3.49, 8.27, 15.7 and 21.9 keV and integrated electron energy flux of 1, 10, and 100 erg cm⁻² s⁻¹. Similarly, the B3C height-integrated conductances are calculated for an incident precipitating electron Gaussian distribution with combinations of average energies of 0.101, 0.477, 0.924, 1.79, 4.42, 8.58, and 16.7 keV and integrated electron energy flux of 1, 10, and 100 erg cm⁻² s⁻¹. The model was run for these various energy fluxes and energies at four different locations across Canada and Alaska: (56.2428°, 280.429°), (55.4554°, 255.580°), (61.3852°, 232.96°), and (65.2333°, 211.044°) in geographic latitude and longitude, respectively.

The Hall conductance was then determined across the 400 × 400 ASI grid by interpolating the look-up table to the given parameters. The energy flux and energies in the B3C look-up table that correspond to a conductance value were treated as a uniform 2D grid that could be interpolated to each observed energy flux and energy stored in the ASI grid. Next, the geographic location in the look-up table closest to the given ASI point (found using the haversine between two geographic points) was used.

Although conductance is computed rigorously with the B3C auroral transport code, for contextual purposes we also calculated the Hall (${\text{Σ}}_H)$conductance with the widely-used Robinson et al. (1987) formulae, where ${\text{Σ}}_P$ is the Pedersen conductance:

${\text{Σ}}_P=\frac{40\overline{E}}{16+{\overline{E}}^2}{\text{Q}}_E^{\frac{1}{2}}(8)$

$\frac{{\text{Σ}}_H}{{\text{Σ}}_P}=0.45{\overline{E}}^{0.85}(9)$

In this case, we simply used the energy flux and average energy value at each of the 400 × 400 grid points as inputs to the formulae. We did this for both the Gaussian and Maxwellian versions, but recognize that the Robinson formulae were intended to provide simple approximations of the conductance.

Results

Figure 6 displays snapshots of the energy flux and average energies determined by the THEMIS ASIs throughout the first substorm lasting from ∼07:18–09:30 UT. The values are from the Gaussian distribution; we include the Maxwellian version in the supplemental material as Supplementary Figure S5. Movies of the substorm are also included in the supplemental material (Supplementary Movies S1–S4). The ASIs capture the substorm onset, expansion, and westward-traveling surge as the vortical auroral form that has elevated energy flux and propagated westward. Note the relatively good agreement in arc location, energy flux, and energy across different ASI FOVs, suggesting overall the mapping is good. We also note that the strongest energy fluxes and average energies come in mesoscales during the expansion phase (e.g., 07:28:30 UT).

FIGURE 6

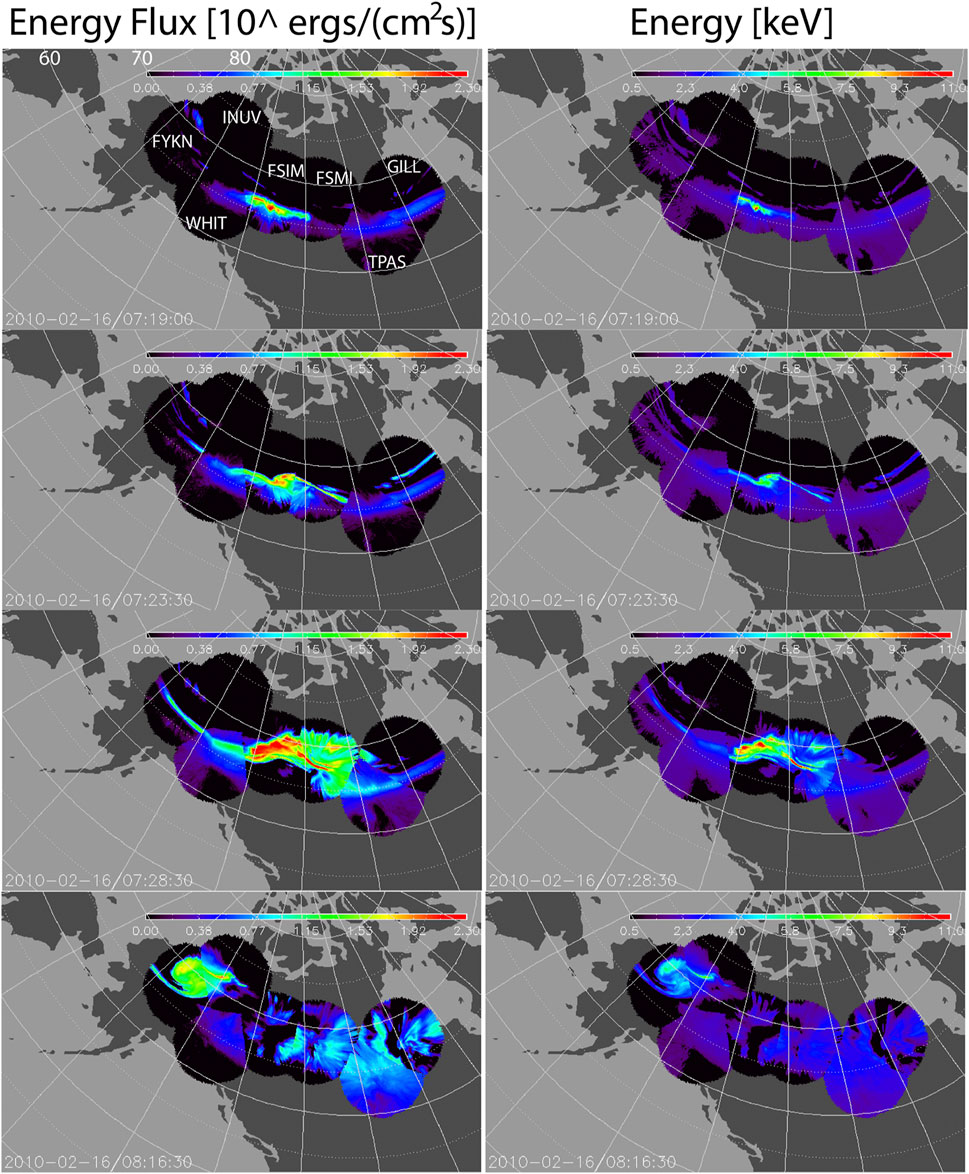
FIGURE 6. Snapshots in time shortly after substorm onset through substorm poleward expansion and westward traveling surge. Left column: Energy flux (plotted logarithmically) from 1–200 erg cm⁻² s⁻¹. Right column: Average energy (plotted linearly) from 0.5–11 keV. Magnetic latitudes and station names are marked in the first panel.

We next interpolated the data onto the 400 × 400 pixel grid to determine the total energy flux deposited in the ASI FOV (above 10° elevation) as well as the average of the average energy. The total energy flux at any given point in time was found by integrating the grid points over the 2D area:

$Q_{Total}={\displaystyle \sum }_{pixe{l}_1}^{pixe{l}_n}((Q_n)(Are{a}_n))(10)$

We ran the ASI grid through a 2D median filter to determine what amount of the total energy flux was deposited as mesoscale auroral forms. For example, to determine the amount of energy flux contributed by scale sizes 500 km and less, for each pixel we found the median across 500 km in 2D (both latitude and longitude directions). We then found the total for that scale size by applying Eq. 10 to the median filtered data, and subtracted that total from the total energy flux:

$Q_{Total}(<500 km)= {\displaystyle \sum }_{pixe{l}_1}^{pixe{l}_n}((Q_n)(Are{a}_n))-{\displaystyle \sum }_{pixe{l}_1}^{pixe{l}_n}{((Q_n)(Are{a}_n))}_{median 500km}(11)$

We weighted the average energies by the energy flux to perform a weighted average of the average energies:

$\overline{E_{avg}}={{\displaystyle \sum }}_{pixe{l}_1}^{pixe{l}_n}((Q_n)(energ{y}_n)){{\displaystyle \sum }}_{pixe{l}_1}^{pixe{l}_n}{Q}_n(12)$

This puts emphasis on the energies that comprise the aurora.

Figure 7 displays these results alongside the magnetograms (Figures 7B,C) and keograms (Figures 7D,E) from the two selected stations that saw the substorm onsets: FSMI and FYKN. Figure 7A displays the SML index [49], which is a measure of the global substorm evolution and strength. The first substorm starts at ∼07:18 UT as a bright, narrow arc that propagates poleward across FSMI’s field of view until the westward traveling surge moves over the keogram longitude (at ∼7:30 UT), showing auroral expansion both poleward and equatorward. The tertiary expansion is seen in Figure 7E as the westward traveling surge brightens and travels over FYKN after 08:00 UT. A bright, latitudinally narrow arc forms at ∼66° magnetic latitude (mlat) during the recovery phase and moves equatorward (seen in Figure 7D from ∼08:45–09:33 UT) until the second substorm onset at ∼09:33 UT, seen in Figure 7E. Figure 7F displays the total energy flux deposited within all available THEMIS ASIs in black, the total energy flux from scale sizes under 500 km, 300 km, and 100 km in red, green, and blue, respectively. Figure 7G displays the percentage of the total energy flux that is contributed by those three scale sizes. Figure 7H displays the average of the average energy.

FIGURE 7

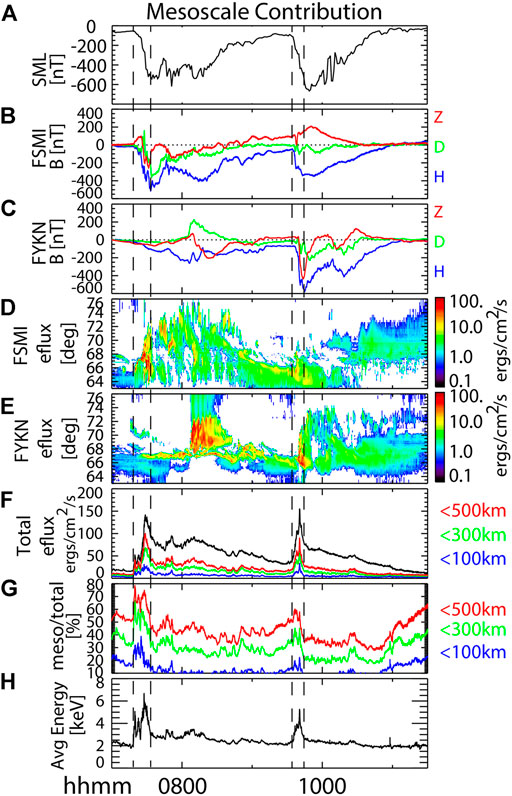
FIGURE 7. (A) SML index. (B) Magnetometer data from Fort Smith, near the first substorm onset. (C) Magnetometer data from Fort Yukon, which was closer to the second substorm’s onset. (D) Keogram of Fort Smith energy flux. (E) Keogram of Fort Yukon energy flux. (F) Total energy flux observed by the ASI mosaic plotted in black. Total energy flux contributed by scale sizes under 500 km, 300 and 100 km plotted in red, green, and blue, respectively. (G) Percent of the total energy flux contributed by scale sizes under 500 km, 300 km, and 100 km plotted in red, green, and blue, respectively. (H) Average of the average energy observed over the ASI mosaic. The vertical dashed lines mark the start of the sharp increase in total energy flux and the end of the sharp decrease in total energy flux that occurs during the substorm expansion phase for each substorm (07:18 and 07:33:20 for the first, 09:34:52 and 09:45 UT for the second).

The main take-aways from Figure 7 are that the mesoscales (<500 km scale sizes) are important in the deposition of energy flux to the ionosphere, particularly so immediately after substorm onset during the rapid expansion phase where they contribute up to ∼80 and ∼60% of the total energy flux in substorms 1 and 2, respectively (Figure 7G, at 07:20 UT and 09:36–09:38). Even the <100 km scale sizes, which only contribute ∼10% of the energy flux throughout the substorm on average, contribute >30% of the energy flux during the rapid expansion phase. Because the difference between the <500 km and <300 km total energy flux is roughly 10%, whereas the difference between the <100 km and <300 km total energy flux is roughly 20%, we can also surmise that more of the energy flux is deposited between 100–300 km scale sizes than 300–500 km scale sizes. The rapid expansion phase is also the most energetic, as the average of the average energy spikes then for both substorms at ∼6.75 and ∼5 keV, respectively (Figure 7H). The maximum average energy is of course, higher. The mesoscale contribution begins to decrease towards the end of the expansion phase, dropping significantly by the beginning of the recovery phase. From Figure 7 and Movies 1-2mmc1-2, we see this is a combination of the mesoscale auroral forms evolving into larger-scale auroras as well as becoming less intense.

These results are related to those presented by Partamies et al. [18], who studied the substorm evolution of auroral arc structures. They found that auroral arcs occur in all conditions as the main element of the aurora, leading to the expectation that mesoscale auroral forms should play an important role in the total precipitating energy flux. They also found that auroral arcs occupy 8.7% of the total growth phase duration, 13.2% of the total expansion phase duration, and 9.2% of the total recovery phase duration. These percentages indicate the prevalence of arcs during the expansion phase—which is when we found the most contribution from mesoscales to the total energy flux. Partamies et al. [50] showed that the average auroral emission intensity is lower during the growth phases of substorms than the bright arcs during the expansion phases, which also aligns with our results showing the total energy flux is lower during the growth phase than the expansion phase.

Auroral arcs in the form of longitudinally localized poleward boundary intensifications and streamers have been correlated to mesoscale plasma sheet fast flows (on the scale of a few R_E) (e.g., [51]; [52-53]; [54–56]). These mesoscale fast flows were shown to play a large role in magnetotail magnetic flux transport [57,58], and now look to also play an important role in providing the precipitated energy flux during substorms. Further analysis to determine the nature of the mesoscale auroral forms—whether or not they are streamers—could be done to investigate how much of the mesoscale contribution to precipitated energy flux is due to these mesoscale plasma sheet fast flows.

We also see that the peak total energy flux of each substorm occurs in the middle of the rapid expansion phase, immediately after the peak in mesoscale contribution (Figure 7F). The vertical dashed lines mark the start of the sharp increase in total energy flux and the end of the sharp decrease in total energy flux that occurs during the substorm expansion phase for each substorm (07:18 and 07:33:20 for the first, 09:34:52 and 09:45 UT for the second). Note that these are coincident with the sharp increase and decrease of the mesoscale contribution. They are also approximately coincident with the substorm onset and the end of the substorm expansion phase, defined by the SML index. The SML index also shows that the first substorm had two more expansions before the final recovery, during each of which there was an increase in total energy flux as well as an increase in mesoscale contribution.

Analyzing the Supplementary Movie S1, the increased mesoscale contribution at the end of the first substorm (∼09:18–09:34:42 UT) appears to be due to the latitudinally narrow, pre-onset arc that formed and moved equatorward prior to the second substorm. The increased mesoscale contribution at the end of the second substorm (∼10:51 UT onward) appears to be from the aurora breaking up and the formation of pulsating aurora (e.g., [59]), a common occurrence after substorms due to whistler mode chorus waves in the magnetosphere.

Figure 8 plots the Hall conductance as determined by PFISR, B3C with ASI inputs, and Robinson formula with ASI inputs (methods described in Poker Flat Incoherent Scatter Radarand Determining the Hall Conductance). We used the FYKN ASI to determine when a discrete auroral arc was over PFISR, during which times we used the Gaussian distribution to determine average energy and energy flux. For other times, we used the Maxwellian distribution. Figure 8A plots the FYKN ASI keogram at the PFISR longitude. The horizontal line represents the PFISR latitude. Mapping the aurora to 110 km, the PFISR measurements lie somewhere between a 31–35° elevation angle in the FYKN field of view. Note that there were gaps in the PFISR data, which is when the black line in Figures 8B,C disappears. Figures 8D–G illustrates the Hall conductance from B3C plotted in the 400 × 400 grid with the PFISR location marked. Figure 8D (09:36:30 UT) is a 2D snapshot of the Hall conductance assuming a Maxwellian distribution, during the time prior to the large increase in conductance due to the bright discrete auroral arc seen in Figure 8F. Figures 8F,G (09:40 and 09:41:30 UT) plot the Hall conductance assuming a Gaussian distribution while the discrete auroral arc is overhead. We see a decrease in conductance when the arc moves slightly away from PFISR in Figure 8G. Figure 8H (10:30:30 UT) again plots the Hall conductance assuming a Maxwellian distribution after the diffuse aurora has returned.

FIGURE 8

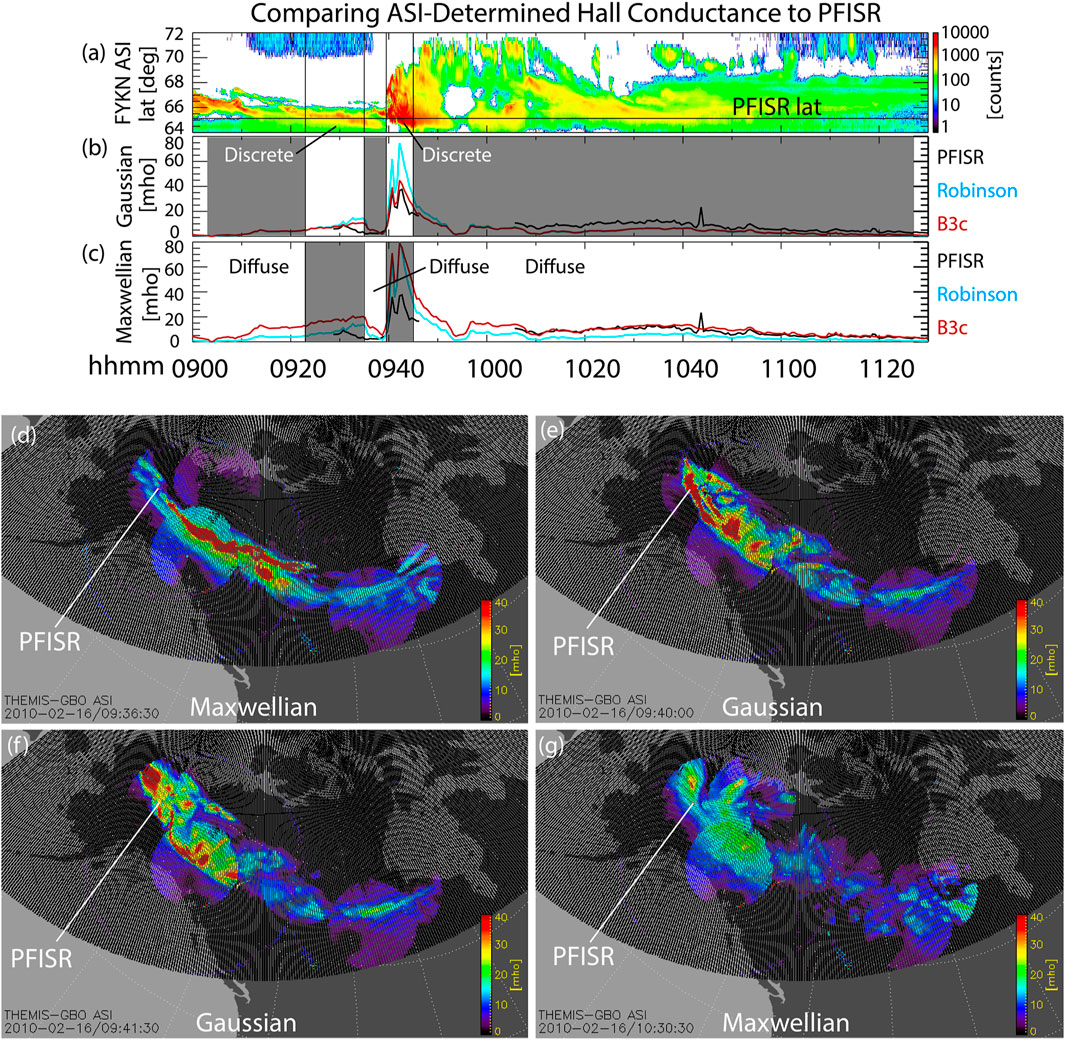
FIGURE 8. Comparing the ASI-determined Hall conductance to PFISR-determined Hall conductance. The discrete and diffuse aurora are marked in panels a–c. The Gaussian distribution was used to determine the conductance related to discrete aurora, and the Maxwellian distribution was used for the diffuse aurora. (A) The FYKN white light intensity keogram at the PFISR longitude. The PFISR latitude line is drawn horizontally. (B) Hall conductance using the Gaussian energy fluxes and average energies from the ASI as input to B3C (red) and Robinson formula (blue) alongside the PFISR-determined result (black). (C) Hall conductance using the Maxwellian energy fluxes and average energies from the ASI as input to B3C (red) and Robinson formula (blue) alongside the PFISR-determined result (black). (D) 2D snapshot of Hall conductance assuming a Maxwellian distribution at 09:36:30 UT. (E) 2D snapshot of Hall conductance assuming a Gaussian distribution at 09:40:00. (F) 2D snapshot of Hall conductance assuming a Gaussian distribution at 09:41:30. (G) 2D snapshot of Hall conductance assuming a Maxwellian distribution at 10:30:30 UT.

Because PFISR measurements are at a lower elevation angle within the FYKN ASI FOV, there is a greater likelihood of introducing error. First, it is possible that an arc maps to a higher or lower altitude than 110 km, in which case a narrow arc above PFISR could be incorrectly mapped in latitude. However, comparing the ASI-informed conductance with the PFISR-determined conductance, we see that the ASIs reproduce relative variations in conductance that is derived from PFISR very well. The fact that the conductances vary at the same time for both the ASI- and PFISR-informed values suggests the mapping is not a primary issue in this case.

Additionally, the ASI is not looking up the magnetic field line at that latitude, whereas PFISR and B3C are integrating along the field line. The result is that not all of the auroral intensity that is actually above PFISR will be mapped to the PFISR latitude and some intensity that is not above PFISR could be mapped to the PFISR latitude, which can result in an under- or over-estimation of the average energy and/or energy flux by the ASI. However, we see that the B3C model informed by the ASIs does exceptionally well at supplying the Hall conductance magnitudes, as it closely follows the PFISR Hall conductance during both discrete and diffuse aurora. Therefore, although the above cautions remain, in this case the methods do well. In contrast, the ASI-informed Robinson formula overestimated the Hall conductance during discrete aurora and underestimated during diffuse aurora. This highlights the improvements physics-based atmospheric modeling provides.

We list the mean and standard deviations, median and quartiles of the differences, ratios, and percent differences between the various B3C informed by ASI (ASI_B3C) and PFISR results in Table 2. Plots of the percent differences over time are included in Supplementary Figure S6. The diffuse aurora (Maxwellian) has a better match than the discrete, which is expected because discrete aurora is more variable and comes on smaller scale sizes, which are more likely to be mapped less precisely for the purposes of exact comparison between datasets. For the discrete aurora, the median percent difference is 24.2% whereas for the diffuse aurora the median percent difference is 18.1%.

TABLE 2

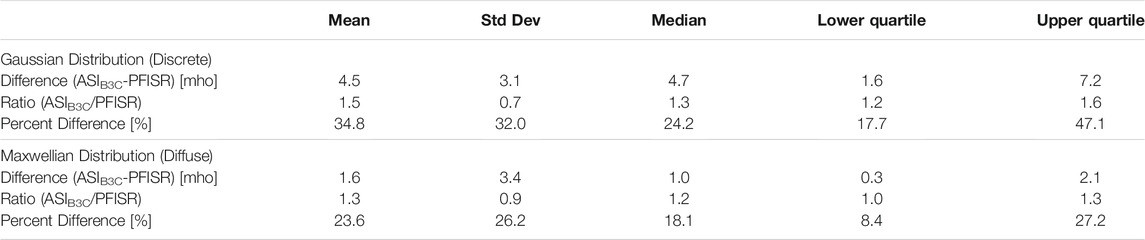
TABLE 2. The mean and standard deviations, median and quartiles of the differences, ratios, and percent differences between the various B3C informed by ASI (ASIB3C) and PFISR results.

Summary

This paper presented a new methodology to utilize the mosaic of THEMIS all-sky-imagers to study auroral precipitation in 2D over time, estimating parameters such as energy flux, average energy, and Hall conductance. Using two consecutive substorms for a case study, results demonstrated the importance of mesoscale auroral forms (10 s km to 500 km scale sizes) to the overall energy flux deposition to the ionosphere, particularly during the initial expansion phase immediately after onset. Roughly 60–80% of the total energy flux immediately after onset, and ∼30–55% thereafter, is from mesoscale auroral forms. These results confirm what we may have hypothesized from the Partamies et al. [18,50] observations, since they had found that auroral arcs occupy the greatest percentage of the substorm expansion phase duration (contrasted with the growth and recovery phases) and are brighter than during the growth phase.

Because prior work highly relied upon statistics or single ASIs, the mesoscale contribution has not been so well-resolved before over a continental scale, especially for specific case studies. The results indicate the importance of including mesoscale auroral forms in global models to appropriately capture the related physics. Additionally, the paper demonstrated the 2D time series data product that can be provided to modelers when ASI data are available, allowing for case-specific data-informed modeling.

The methods showed a good comparison between the calibrated ASI data and the MSP data, as were quantified in Table 1 and Supplementary Tables S1, S2. As expected, the greatest scatter is in 630.0 nm wavelength. As a future work, the redline ASI cameras that are currently coming online as part of the TREx array of ASIs could be used to specify the 630.0 nm wavelength more accurately (https://www.ucalgary.ca/aurora/projects/trex). Comparing and/or calibrating to DMSP energy fluxes and average energies would also provide additional information on the uncertainties and/or improve our estimates. We do point out as mentioned above that the inversion method in Janhunen [13] found little difference in the energy flux results when the red aurora was included, since the energy flux is mostly related to the blue intensity [22,30], which is a close function of the green intensity (Figure 3).

The Hall conductance was well-captured by the B3C auroral transport code, informed by ASI energy fluxes and average energies, when compared to PFISR-determined Hall conductance. The ASI-informed Robinson formula overestimated the Hall conductance during discrete aurora and underestimated during diffuse aurora. As expected, the conductance increased during the intense discrete aurora. These values are not well-constrained in current models that rely on global, diffuse aurora as precipitation input only. These data could therefore be useful to modelers who want to include the larger conductance values that result from mesoscale, discrete aurora. As a future work, a date should be selected when PFISR can provide alternating code observations of the whole E region for a better comparison, and also to include the Pedersen conductance.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: THEMIS ASI: themis.ssl.berkeley.edu. NORSTAR MSP: https://data-portal.phys.ucalgary.ca/msp/summary_plots; http://data.phys.ucalgary.ca/sort_by_project/other/publication_datasets/Gabrielse2021/. PFISR: http://isr.sri.com/madrigal/. SML index: supermag.jhuapl.edu.

Author Contributions

CG led the work, updated techniques developed by TN, performed the analyses, and wrote the paper. TN devised the original ASI-MSP techniques and advised CG on the details. MC ran the B3C code to provide the conductance look-up table for CG to use with ASI inputs, and described the methods in the text. JHH ran the B3C code to provide Figure 1 and the look-up table to determine energy fluxes and average energies from color ratios, as well as the associated text in the manuscript. SK calculated the conductance from the PFISR data and contributed to writing the PFISR section. DMG provided processed MSP data and text describing the instruments. AR provided processed PFISR data and text describing the instrument and dataset. LL contributed discussions about mesoscale auroral phenomena. YD contributed discussions about mesoscale phenomena in the ionosphere and insights on what parameters are important to specify. ED runs THEMIS-ASI in Canada, and contributed discussions on our methodology and use of the MSP data. JE manages the B3C code and gives permission and guidance for its use. All co-authors contributed comments, edits, and text to the manuscript.

Funding

The work in this paper was gratefully funded by NASA grants 80NSSC20K0725, 80NSSC18K0657, 80NSSC20K0604, 80NSSC20K0195, and 80NSSC20K1786, AFOSR Grant FA9559-16-1-0364, and NSF grants AGS 1602862 and AGS-1907698. The THEMIS mission is supported by NASA contract NAS5-02099, NSF grant AGS-1004736, and CSA contract 9F007-046101. This material is based upon work supported by the Poker Flat Incoherent Scatter Radar which is a major facility funded by the National Science Foundation through cooperative agreement AGS-1840962 to SRI International.

Conflict of Interest

JE was employed by the company Computational Physics, Inc.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We gratefully acknowledge the SuperMAG collaborators (https://supermag.jhuapl.edu/info/?page=acknowledgement). The ASI, PFISR and SuperMAG data are available at themis.ssl.berkeley.edu, isr.sri.com/madrigal, and supermag.jhuapl.edu.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.744298/full#supplementary-material

References

1. Newell PT, Sotirelis T, Wing S. Diffuse, Monoenergetic, and Broadband aurora: The Global Precipitation Budget. J Geophys Res (2009) 114:a–n. doi:10.1029/2009JA014326

CrossRef Full Text | Google Scholar

2. Newell PT, Sotirelis T, Wing S. Seasonal Variations in Diffuse, Monoenergetic, and Broadband aurora. J Geophys Res (2010) 115:a–n. doi:10.1029/2009ja014805

CrossRef Full Text | Google Scholar

3. Newell PT, Sotirelis T, Liou K, Lee AR, Wing S, Green J, et al. Predictive Ability of Four Auroral Precipitation Models as Evaluated Using Polar UVI Global Images. Space Weather (2010) 8:a–n. doi:10.1029/2010sw000604

CrossRef Full Text | Google Scholar

4. Newell PT, Lee AR, Liou K, Ohtani S-I, Sotirelis T, Wing S. Substorm Cycle Dependence of Various Types of aurora. J Geophys Res (2010) 115:a–n. doi:10.1029/2010ja015331

CrossRef Full Text | Google Scholar

5. Zhu Q, Deng Y, Maute A, Kilcommons LM, Knipp DJ, Hairston M. ASHLEY: A New Empirical Model for the High‐Latitude Electron Precipitation and Electric Field. Space Weather (2021) 19:e2020SW002671. doi:10.1029/2020SW002671

CrossRef Full Text | Google Scholar

6. McGranaghan RM, Ziegler J, Bloch T, Hatch S, Camporeale E, Lynch K, et al. Toward a Next Generation Particle Precipitation Model: Mesoscale Prediction through Machine Learning (A Case Study and Framework for Progress). Space Weather (2021) 19:e2020SW002684. doi:10.1029/2020SW00268

CrossRef Full Text | Google Scholar

7. Deng Y, Heelis R, Lyons LR, Nishimura Y, Gabrielse C. Impact of Flow Bursts in the Auroral Zone on the Ionosphere and Thermosphere. J Geophys Res Space Phys (2019) 124:10459–67. doi:10.1029/2019JA026755

CrossRef Full Text | Google Scholar

8. Sheng C, Deng Y, Gabrielse C, Lyons LR, Nishimura Y, Heelis RA, et al. Sensitivity of Upper Atmosphere to Different Characteristics of Flow Bursts in the Auroral Zone, Submitted to. J Geophys Res ().

Google Scholar

9. Kaeppler SR, Hampton DL, Nicolls MJ, Strømme A, Solomon SC, Hecht JH, et al. An Investigation Comparing Ground‐based Techniques that Quantify Auroral Electron Flux and Conductanceflux and Conductance. J Geophys Res Space Phys (2015) 120:9038–56. doi:10.1002/2015JA021396

CrossRef Full Text | Google Scholar

10. Sivadas N, Semeter J, Nishimura Y, Mrak S. Optical Signatures of the Outer Radiation belt Boundary. Geophys Res Lett (2019) 46:8588–96. doi:10.1029/2019GL083908

CrossRef Full Text | Google Scholar

11. Lanchester BS, Palmer JR, Rees MH, Lummerzheim D, Kaila K, Turunen T. Energy Flux and Characteristic Energy of an Elemental Auroral Structure. Geophys Res Lett (1994) 21:2789–92.

CrossRef Full Text | Google Scholar

12. Gustavsson B, Steen A, Sergienko T, Brändström BUE. ¨Estimate of Auroral Electron Spectra, the Power of Ground-Based Multi-Station Optical Measurements. Phys Chem Earth (2001) 26:189–94. doi:10.1016/S1464-1917(00)00106-9

CrossRef Full Text | Google Scholar

13. Janhunen P. Reconstruction of Electron Precipitation Characteristics from a Set of Multiwavelength Digital All-Sky Auroral Images. J Geophys Res (2001) 106:18505–16. doi:10.1029/2000JA000263

CrossRef Full Text | Google Scholar

14. Kauristie K, Partamies N, Makinen S, Kuula R, Strømme A. Energy Flux of Electron Precipitation as Monitored by an All-Sky Camera. Int Conf Substorms (2006) 8:123–6.

Google Scholar

15. Partamies N, Janhunen P, Kauristie K, Mäkinen S, Sergienko T. Testing an Inversion Method for Estimating Electron Energy Fluxes from All-Sky Camera Images. Ann Geophys (2004) 22:1961–71. doi:10.5194/angeo-22-1961-2004

CrossRef Full Text | Google Scholar

16. Dahlgren H, Gustavsson B, Lanchester BS, Ivchenko N, Brändström U, Whiter DK, et al. Energy and Flux Variations across Thin Auroral Arcs. Ann Geophys (2011) 29:1699–712. doi:10.5194/angeo-29-1699-2011

CrossRef Full Text | Google Scholar

17. Lam MM, Freeman MP, Jackman CM, Rae IJ, Kalmoni NME, Sandhu JK, et al. How Well Can We Estimate Pedersen Conductance from the THEMIS White‐Light All‐Sky Cameras. J Geophys Res Space Phys (2019) 124:2920–34. doi:10.1029/2018JA026067

CrossRef Full Text | Google Scholar

18. Partamies N, Juusola L, Whiter D, Kauristie K. Substorm Evolution of Auroral Structures. J Geophys Res Space Phys (2015) 120:5958–72. doi:10.1002/2015JA021217

CrossRef Full Text | Google Scholar

19. Mende SB, Harris SE, Frey HU, Angelopoulos V, Russell CT, Donovan E, et al. The THEMIS Array of Ground-Based Observatories for the Study of Auroral Substorms. Space Sci Rev (2008) 141:357–87. doi:10.1007/s11214-008-9380-x

CrossRef Full Text | Google Scholar

20. Nishimura Y, Deng Y, Lyons LR, McGranaghan RM, Zettergren MD. Multiscale Dynamics in the High‐Latitude Ionosphere. In: C Huang, G Lu, Y Zhang, and LJ Paxton, editors. Ionosphere Dynamics and Applications (2021) p. 49–65. doi:10.1002/9781119815617.ch3

CrossRef Full Text | Google Scholar

21. Rees MH, Luckey D. Auroral Electron Energy Derived from Ratio of Spectroscopic Emissions 1. Model Computations. J Geophys Res (1974) 79(NO. 34):5181–6. doi:10.1029/JA079i034p05181

CrossRef Full Text | Google Scholar

22. Strickland DJ, Meier RR, Hecht JH, Christensen AB. Deducing Composition and Incident Electron Spectra from Ground-Based Auroral Optical Measurements: Theory and Model Results. J Geophys Res (1989) 94(13):13527–13539. doi:10.1029/JA094iA10p13527

CrossRef Full Text | Google Scholar

23. Hecht JH, Christensen AB, Strickland DJ, Meier RR. Deducing Composition and Incident Electron Spectra from Ground-Based Auroral Optical Measurements: Variations in Oxygen Density. J Geophys Res (1989) 94:13553–13563. doi:10.1029/JA094iA10p13553

CrossRef Full Text | Google Scholar

24. Hecht JH, Strickland DJ, Conde MG. The Application of Ground-Based Optical Techniques for Inferring Electron Energy Deposition and Composition Change during Auroral Precipitation Events. J Atmos Solar-Terrestrial Phys (2006) 68(13):1502–19. doi:10.1016/j.jastp.2005.06.022

CrossRef Full Text | Google Scholar

25. Hecht JH, Mulligan T, Correira JT, Clemmons JH, Strickland DJ, Walterscheid RL, et al. A Multiyear (2002-2006) Climatology of O/N2in the Lower Thermosphere from TIMED GUVI and Ground-Based Photometer Observations. J Geophys Res (2012) 117:a–n. doi:10.1029/2011JA017146

CrossRef Full Text | Google Scholar

26. Lanchester BS, Rees MH, Lummerzheim D, Otto A, Frey HU, Kaila KU. Large Fluxes of Auroral Electrons in Filaments of 100 M Width. J Geophys Res (1997) 102:9741–8. doi:10.1029/97ja00231

CrossRef Full Text | Google Scholar

27. Strickland DJ, Book DL, Coffey TP, Fedder JA. Transport Equation Techniques for the Deposition of Auroral Electrons. J Geophys Res (1976) 81(16):2755–64. doi:10.1029/ja081i016p02755

CrossRef Full Text | Google Scholar

28. Strickland DJ, Daniell RE, Jasperse JR, Basu B. Transport-Theoretic Model for the Electron-Proton-Hydrogen Atom Aurora, 2. Model Results. J Geophys Res (1993) 98(A12):21533–48. doi:10.1029/93JA01645

CrossRef Full Text | Google Scholar

29. Khazanov GV, Sibeck DG, Chu M. Magnetosphere-Ionosphere Coupling of Precipitating Electrons and Ionospheric Conductance. Magnetospheres in the Solar System. American Geophysical Union (2021) p. 229–42. doi:10.1002/9781119815624.ch16

CrossRef Full Text | Google Scholar

30. Hecht JH, Mulligan T, Strickland DJ, Kochenash AJ, Murayama Y, Tanaka Y-M, et al. Satellite and Ground-Based Observations of Auroral Energy Deposition and the Effects on Thermospheric Composition during Large Geomagnetic Storms: 1. Great Geomagnetic Storm of 20 November 2003. J Geophys Res (2008) 113:a–n. doi:10.1029/2007JA012365

CrossRef Full Text | Google Scholar

31. Xu B-L, Samson JC, Liu WW. Observations of Optical Aurora Modulated by Resonant Alfvén Waves. J Geophys Res (1993) 98:11531–11541. doi:10.1029/93ja00435

CrossRef Full Text | Google Scholar

32. Omholt A. The Optical Aurora. chap. 4. New York: Springer-Veriag (1971). p. 96.

Google Scholar

33. Richards MA, James AS, Jim S, William AH. Principles of Modern Radar: Basic Principles, Vol. 1. Savoy Place, London: Institution of Engineering and Technology (2010). ISBN 1613532016, 9781613532010.

Google Scholar

34. Kudeki E, Milla MA. Incoherent Scatter Spectral Theories-Part I: A General Framework and Results for Small Magnetic Aspect Angles. IEEE Trans Geosci Remote Sensing (2011) 49(1):315–28. doi:10.1109/TGRS.2010.2057252

CrossRef Full Text | Google Scholar

35. Vadas SL, Nicolls MJ. Temporal Evolution of Neutral, Thermospheric Winds and Plasma Response Using PFISR Measurements of Gravity Waves. J Atmos Solar-Terrestrial Phys (2009) 71(Issues 6–7):744–70. doi:10.1016/j.jastp.2009.01.011

CrossRef Full Text | Google Scholar

36. Boström R. A Model of the Auroral Electrojets. J Geophys Res (1964) 69:4983–99. doi:10.1029/JZ069i023p04983

CrossRef Full Text | Google Scholar

37. Schunk RW, Nagy AF. Ionospheres: Physics, Plasma Physics and Chemistry. 2nd ed. Cambridge, U. K: Cambridge Univ. Press (2009).

Google Scholar

38. Basu B, Jasperse JR, Strickland DJ, Daniell RE. Transport-Theoretic Model for the Electron-Proton-Hydrogen Atom Aurora, 1. Theory. J Geophys Res (1993) 98(A12):21517–32. doi:10.1029/93JA01646

CrossRef Full Text | Google Scholar

39. Hedin AE. Extension of the MSIS Thermosphere Model into the Middle and Lower Atmosphere. J Geophys Res (1991) 96(A2):1159–72. doi:10.1029/90JA02125

CrossRef Full Text | Google Scholar

40. Strickland DJ, Evans JS, Paxton LJ. Satellite Remote Sensing of Thermospheric O/N2 and Solar EUV: 1. Theory, J Geophys Res (1995) 100:12217–12226. doi:10.1029/95ja00574

CrossRef Full Text | Google Scholar

41. Isobe T, Feigelson ED, Akritas MG, Babu GJ. Linear Regression in Astronomy. ApJ (1990) 364(1):104–13. doi:10.1086/169390

CrossRef Full Text | Google Scholar

42. Megan Gillies D, Donovan DE, Jackel B, Gillies R, Spanswick E. Identifying the 630 Nm Auroral Arc Emission Height: A Comparison of the Triangulation, FAC Profile, and Electron Density Methodsle, and Electron Density Methods. J Geophys Res Space Phys (2017) 122:8181–97. doi:10.1002/2016JA023758

CrossRef Full Text | Google Scholar

43. Gustavsson B, Kosch M, Wong A, Pedersen T, Heinselman C, Mutiso C, et al. First Estimates of Volume Distribution of HF-Pump Enhanced Emissions at 6300 and 5577 Å: a Comparison between Observations and Theory. Ann Geophys (2008) 26:3999–4012. doi:10.5194/angeo-26-3999-2008

CrossRef Full Text | Google Scholar

44. Knight S. Parallel Electric fields. Planet Space Sci (1973) 21:741–50. doi:10.1016/0032-0633(73)90093-7

CrossRef Full Text | Google Scholar

45. Lyons LR. Generation of Large-Scale Regions of Auroral Currents, Electric Potentials, and Precipitation by the Divergence of the Convection Electric Field. J Geophys Res (1980) 85(A1):17–24. doi:10.1029/JA085iA01p00017

CrossRef Full Text | Google Scholar

46. Christensen AB, Lyons LR, Hecht JH, Sivjee GG, Meier RR, Strickland DG. Magnetic Field-Aligned Electric Field Acceleration and the Characteristics of the Optical aurora. J Geophys Res (1987) 92:6163–7. doi:10.1029/ja092ia06p06163

CrossRef Full Text | Google Scholar

47. Strickland DJ, Hecht JH, Christensen AB, Kelly J. Relationship between Energy Flux Q and the Mean Energy ⟨E⟩ of Auroral Energy Spectra Based on Radar Data from the 1987 CEDAR Campaign at Sondre Stromfjord, Greenland, Disturbance. J Geophys Res (1994) 99:19467–19473. doi:10.1029/94ja01901

CrossRef Full Text | Google Scholar

48. McIntosh RC, Anderson PC. Maps of Precipitating Electron Spectra Characterized by Maxwellian and Kappa Distributions. J Geophys Res Space Phys (2014) 119(12):10116–10132. doi:10.1002/2014JA020080

CrossRef Full Text | Google Scholar

49. Gjerloev JW. The SuperMAG Data Processing Technique. J Geophys Res (2012) 117:a–n. doi:10.1029/2012JA017683

CrossRef Full Text | Google Scholar

50. Partamies N, Juusola L, Tanskanen E, Kauristie K, Weygand JM, Ogawa Y. Substorms during Different Storm Phases. Ann Geophys (2011) 29:2031–43. doi:10.5194/angeo-29-2031-2011

CrossRef Full Text | Google Scholar

51. Henderson MG, Reeves GD, Murphree JS. Are north-south Aligned Auroral Structures an Ionospheric Manifestation of Bursty Bulk Flows. Geophys Res Lett (1998) 25:3737–40. doi:10.1029/98gl02692

CrossRef Full Text | Google Scholar

52. Sergeev VA, Liou K, Newell PT, Ohtani S-I, Hairston MR, Rich F. Auroral Streamers: Characteristics of Associated Precipitation,convection and Field-Aligned Currents. Ann Geophys (2004) 22:537–48. doi:10.5194/angeo-22-537-2004

CrossRef Full Text | Google Scholar

53. Sergeev VA, Sauvaud J-A, Popescu D, Kovrazhkin RA, Liou K, Newell PT, et al. Multiple-spacecraft Observation of a Narrow Transient Plasma Jet in the Earth's Plasma Sheet. Geophys Res Lett (2000) 27(6):851–4. doi:10.1029/1999gl010729

CrossRef Full Text | Google Scholar

54. Lyons LR, Nagai T, Blanchard GT, Samson JC, Yamamoto T, Mukai T, et al. Association between Geotail Plasma Flows and Auroral Poleward Boundary Intensifications Observed by CANOPUS Photometers. J Geophys Res (1999) 104:4485–500. doi:10.1029/1998ja900140

CrossRef Full Text | Google Scholar

55. Lyons LR, Zesta E, Xu Y, Sanchez ER, Samson JC, Reeves GD, et al. Auroral Poleward Boundary Intensifications and Tail Bursty Flows: A Manifestation of a Large-Scale ULF Oscillation. J Geophys Res (2002) 107(A11):1352. doi:10.1029/2001JA000242

CrossRef Full Text | Google Scholar

56. Kauristie K, Sergeev VA, Kubyshkina M, Pulkkinen TI, Angelopoulos V, Phan T, et al. Ionospheric Current Signatures of Transient Plasma Sheet Flows. J Geophys Res (2000) 105:10677–10688. doi:10.1029/1999ja900487

CrossRef Full Text | Google Scholar

57. Angelopoulos V, Kennel CF, Coroniti FV, Pellat R, Kivelson MG, Walker RJ, et al. Statistical Characteristics of Bursty Bulk Flow Events. J Geophys Res (1994) 99(A11):21257–5721. doi:10.1029/94JA01263

CrossRef Full Text | Google Scholar

58. Angelopoulos V, Phan TD, Larson DE, Mozer FS, Lin RP, Tsuruda K, et al. Magnetotail Flow Bursts: Association to Global Magnetospheric Circulation, Relationship to Ionospheric Activity and Direct Evidence for Localization. Geophys Res Lett (1994) 24:2271–4. doi:10.1029/97GL02355

CrossRef Full Text | Google Scholar

59. Li W, Bortnik J, Nishimura Y, Thorne RM, Angelopoulos V. The Origin of Pulsating Aurora: Modulated Whistler Mode Chorus Waves. Washington DC American Geophysical Union Geophysical Monograph Series (2012). p. 197.

Google Scholar