Generalized Su-Schrieffer-Heeger Model in One Dimensional Optomechanical Arrays

1 Introduction

In the past decades, rapid progress has been made in the field ofcavity optomechanical systems, in which a cavity mode is coupled to a mechanical mode via radiation pressure or optical gradient force (for reviews, see Refs. [1–6]). With the advance in technology and the requirement for providing new functionality, the focus has been changed from the simplest optomechanical systems, based on a single mechanical mode coupled to a single optical mode, to more complex setups, including many optical or mechanical modes, such as optomechanical arrays, which are designed as a periodic arrangement of optomechanical systems. Based on the current condition of experiments and technology, optomechanical arrays might be realized in coupled optical microdisks [7–10], on-chip superconducting electromechanical cavity arrays [11–14], and optomechanical crystals [15, 16].

In the past few years, quantum many-body effect in optomechanical arrays has attracted considerable attentions [17–32]. Optomechanical arrays with parametric coupling between the mechanical mode and optical mode provide us a controllable platform to simulate quantum many-body systems and manipulate photons and phonons. Many interesting phenomena have been studied, such as controllable photon propagation [17, 18], synchronization [19–21], artificial magnetic fields for photons [22], optically tunable Dirac-type band structure [23, 24], Anderson localization of hybrid photon-phonon excitations [25, 26], and Kuznetsov-Ma soliton [27]. Besides these, the optomechanical arrays can also be used to engineer topological phase for both photons and phonons [28–32].

Most of the optomechanical arrays, which are used to demonstrate different topological phases and Chern insulators, are implemented in two-dimensional optomechanical crystals. However, two dimension is not a necessary condition for engineering topological phase. The topological properties of photons and phonons can also be realized in a one-dimensional chain of optomechanical cavities. For example, in the recent works, Z₂ topological insulators [33] and Kitaev model [34] were simulated via one-dimensional optomechanical arrays.

The Su-Schrieffer-Heeger (SSH) model, introduced from polyacetylene [35], is well known as one of the simplest models to demonstrate topological character in one dimension. It has been proposed theoretically and demonstrated experimentally in many different setups, such as cold atoms and ions [36–46], optical systems [47–51], mechanical systems [52–54], heterostructure [55], graphene nanoribbons [56], plasmonic systems [57–63], and superconducting circuits [64–71]. In addition, ladder systems, which consist of two or more coupled SSH chains, have been used to demonstrate richer topological quantum phases [72–77].

In this paper, we study the topological properties of a one-dimensional optomechanical array, which can be mapped to a generalized SSH model [78–85] including three complex hopping amplitudes. Different from the standard SSH model, we find that there are three phases in this generalized SSH model, among which, one is trivial and the other two are distinct. It is worth mentioning that a SSH model consisting of three hopping amplitudes with real numbers was discussed in a recent Ref. [77]. Besides the system in our paper is different from that in Ref. [77], we further show that the topological properties of the generalized SSH model depend on both the strengths and the phases of the hopping amplitudes, and topological phase transitions can be demonstrated by tuning the strengths and phases of the effective optomechanical interactions via adjusting the external driving fields. Moreover, we show that four types of edge states can be found in generalized SSH model of an open chain under single-particle excitation, and the dynamical behaviors of the excitation in the open chain are related to the topological properties under the periodic boundary condition. We also show that the edge states can be pumped adiabatically along the optomechanical arrays by periodically modulating the amplitudes and frequencies of the driving fields.

It is worth mentioning that, after the submission of the first version of this manuscript to arXiv [86], there are many new advances have been made in the field of topological phases in optomechanical arrays based on SSH model, such as topological state transfer and topological beam splitter [87], photon-phonon conversion [88], etc. Moreover, topological insulator in two synthetic dimensions was proposed based on an optomechanical resonator [89], and phononic edge modes with unidirectional propagation was simulated in a two-dimensional optomechanical nanobeam lattice [90].

The remainder of this paper is organized as follows. In Section 2, we show the theoretical model of a generalized SSH model based on optomechanical arrays. In Section 3, we study the topological properties of the generalized SSH model and show that there are three phases, one is trivial and two are distinct. Moreover, we show that phase transitions can be observed by tuning the strengths of the optomechanical interactions. In Section 4, four types of edge states are introduced and the relation between the dynamical behaviors of singleparticle excitation in the open chain and the topological properties under the periodic boundary condition are discussed. In Section 5, we demonstrate that the edge states can be pumped adiabatically along the optomechanical arrays by modulating the amplitudes and frequencies of the driving fields periodically. Finally, the results are summarized in Section 6.

2 Theoretical Model

We propose to implement a generalized SSH model by an optomechanical array with N cavity modes and N mechanical modes, which are coupled only by optomechanical interactions, without hopping of photons between neighboring cavity modes (or hopping of phonons between mechanical modes). The Hamiltonian of the optomechanical array is (ℏ = 1)

$H_0=\sum _{j=1}^N\left({\omega }_{c,j}{a}_j^{†}{a}_j+{\omega }_{m,j}{b}_j^{†}{b}_j+H_j\right),(1)$

with

$\begin{array}{ccc}\hfill H_1& =\hfill & \left[\left({\mathit{g}}_{\mathrm{1,0}}{b}_1^{†}+{\mathit{g}}_{1,+}{b}_2^{†}\right)a_1^{†}{a}_1\right.\hfill \\ \hfill & \hfill & \left.+\left({\mathrm{\Omega }}_{\mathrm{1,0}}{e}^{i{\omega }_{\mathrm{1,0}}t}+{\mathrm{\Omega }}_{1,+}{e}^{i{\omega }_{1,+}t}\right)a_1\right]+\mathrm{H}.\mathrm{c}.,\hfill \end{array}(2)$

for the first cavity mode,

$\begin{array}{ccc}\hfill H_N& =\hfill & \left[\left({\mathit{g}}_{N,0}{b}_N^{†}+{\mathit{g}}_{N,-}{b}_{N-1}^{†}\right)a_N^{†}{a}_N\right.\hfill \\ \hfill & \hfill & \left.+\left({\mathrm{\Omega }}_{N,0}{e}^{i{\omega }_{N,0}t}+{\mathrm{\Omega }}_{N,-}{e}^{i{\omega }_{N,-}t}\right)a_N\right]+\mathrm{H}.\mathrm{c}.,\hfill \end{array}(3)$

for the last cavity mode, and

$\begin{array}{ccc}\hfill H_j& =\hfill & \left[\left({\mathit{g}}_{j,0}{b}_j^{†}+{\mathit{g}}_{j,+}{b}_{j+1}^{†}+{\mathit{g}}_{j,-}{b}_{j-1}^{†}\right)a_j^{†}{a}_j\right.\hfill \\ \hfill & \hfill & \left.+\left({\mathrm{\Omega }}_{j,0}{e}^{i{\omega }_{j,0}t}+{\mathrm{\Omega }}_{j,+}{e}^{i{\omega }_{j,+}t}+{\mathrm{\Omega }}_{j,-}{e}^{i{\omega }_{j,-}t}\right)a_j\right]\hfill \\ \hfill & \hfill & +\mathrm{H}.\mathrm{c}.,\hfill \end{array}(4)$

for the jth cavity mode (1 < j < N), where a_j ($a_j^{†}$) is the bosonic annihilation (creation) operator of the jth cavity mode (j = 1, 2, … , N) with resonant frequency ω_c,j, b_j ($b_j^{†}$) is the bosonic annihilation (creation) operator of the jth mechanical mode with resonant frequency ω_m,j, and g_j,0 (g_j,±) is the optomechanical coupling strength between the jth cavity mode and the jth mechanical mode (the (j ± 1)th mechanical mode). The jth cavity mode is driven by a three-tone laser at frequencies ω_j,0 = ω_c,j − ω_m,j and ω_j,± = ω_c,j − ω_m,j±1 with amplitudes Ω_j,0 and Ω_j,± in the well resolved sidebands regime (ω_m,j ≫{κ_j, γ_j}, where κ_j is the decay rate of the jth cavity mode, and γ_j is the damping rate of the jth mechanical mode).

To deal with the Hamiltonians in Eqs 2–4, we will employ the linearization approach widely used for optomechanics [91–96] in the weak single-photon optomechanical coupling regime and under strong driving condition g_j,σ ≪ κ_j ≪Ω_j,σ (σ = 0, ±). The operator for each cavity modes is written as the sum of its classical mean value α_j(t) and quantum fluctuation operator δa_j as a_j → α_j(t) + δa_j. For convenience of the presentation, we rename δa_j → a_j. The classical mean value α_j(t) can be given approximately as ${\alpha }_j(t)\approx {\alpha }_{j,0}{e}^{i{\omega }_{j,0}t}+{\alpha }_{j,+}{e}^{i{\omega }_{j,+}t}+{\alpha }_{j,-}{e}^{i{\omega }_{j,-}t}$, where the classical amplitude α_j,0 ≈ − i2Ω_j,0/(κ_j + 2iΔ_j,0) [α_j,± ≈ − i2Ω_j,±/(κ_j + 2iΔ_j,±)] is given approximately by solving the classical equation of motion with amplitude Ω_j,0 (Ω_j,±) and detuning Δ_j,0 ≡ ω_c,j − ω_j,0 (Δ_j,± ≡ ω_c,j − ω_j,±). In the interaction picture with respect to $H_{\mathrm{r}\mathrm{o}\mathrm{t}}={\sum }_{j=1}^N[{\omega }_{c,j}{a}_j^{†}{a}_j+{\omega }_{m,j}{b}_j^{†}{b}_j]$, the linearized operator a_j is given by

$a_j\to a_j{e}^{i{\omega }_{c,j}t}+\sum _{\sigma =0,\pm }{\alpha }_{j,\sigma }{e}^{i{\omega }_{j,\sigma }t}.(5)$

We assume: 1) min$\left[\left|{\alpha }_{j,0}\right|,|{\alpha }_{j,\pm }|\right]\gg 1$ and max{g_j,0, g_j,±}≪ κ_j, so that we can only keep the first-order terms in the small quantum fluctuation operators a_j and $a_j^{†}$ as

$a_j^{†}{a}_j\to a_j^{†}\sum _{\sigma =0,\pm }{\alpha }_{j,\sigma }{e}^{i{\mathrm{\Delta }}_{j,\sigma }t}+\mathrm{H}.\mathrm{c}..(6)$

2) min{ω_m,j, |ω_m,j − ω_m,j′|_j′=j±1}≫max{|g_j,0α_j,0|, |g_j,±α_j,±|}, and ω_m,j = ω_c,j − ω_j,0 and ω_m,j±1 = ω_c,j − ω_j,±, such that the rotating terms can be neglected safely, and the linearized Hamiltonian with resonant interactions is obtained as

$H_j\approx J{e}^{i\varphi }{a}_j^{†}{b}_j+z{a}_j^{†}{b}_{j+1}+v{a}_j^{†}{b}_{j-1}+\mathrm{H}.\mathrm{c}.,(7)$

where Je^iϕ ≡ g_j,0α_j,0, v ≡ g_j,−α_j,−, and z ≡ g_j,+α_j,+. We assume that the strengths (Ω_j,0, Ω_j,±) and detunings (Δ_j,0, Δ_j,±) of the driving fields are constant (or change slowly in the Section for adiabatic particle pumping), so the classical amplitudes (α_j,0, α_j,±) are constant in the steady state (or change slowly for adiabatic particle pumping). In this case, the classical mean value can be used as a parameter to define J, ϕ, v and z in the Hamiltonians. Without loss of generality, we assume that J, ϕ, v and z are real numbers and the global phase factor ϕ can be tuned by adjusting the relative phase of the driving fields. It should be noted that all these assumptions given above are widely used in the theories for optomechanical systems [4], including in one- and two-dimensional optomechanical lattices [28–34, 87–90].

By substituting Eq. 7 into Eq. 1, the linearized Hamiltonian for the optomechanical array in the interaction picture with respect to $H_{\text{rot}}={\sum }_{j=1}^N[{\omega }_{c,j}{a}_j^{†}{a}_j+{\omega }_{m,j}{b}_j^{†}{b}_j]$ is given by

$H=\sum _{j=1}^{N}J{e}^{i\varphi }{a}_j^{†}{b}_j+\sum _{j=1}^{N-1}\left(v{a}_{j+1}^{†}{b}_j+z{b}_{j+1}^{†}{a}_j\right)+\mathrm{H}.\mathrm{c}.,(8)$

as schematically shown in Figure 1. The linearized Hamiltonian for the optomechanical array shows a generalized SSH model with hopping amplitude z ≠ 0 between the jth cavity mode and (j + 1)th mechanical mode. When the coupling strength z = 0, the Hamiltonian for the optomechanical array becomes the well-known SSH model [78]. It can also be dealt with as a Bogoliubov Hamiltonian if the counter-rotating terms, ζa_j+1b_j + ζ′a_jb_j+1 + H. c. with coupling strengths ζ and ζ′, are taken into account [41, 42].

FIGURE 1

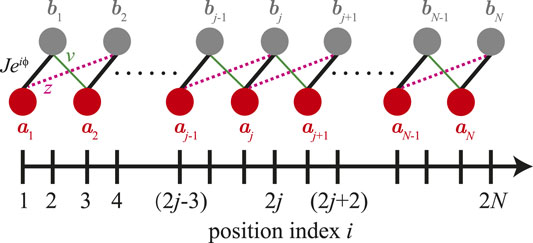
FIGURE 1. (Color online) Schematic diagram of a generalized SSH model based on an optomechanical array. a_j and b_j denote the cavity and mechanical modes respectively, and they are coupled with three different hopping amplitudes Je^iϕ (bold black lines), v (thin green lines) and z (red dashed lines). The optomechanical array can be implemented by an array of coupled optical microdisks [7–10], on-chip superconducting circuit electromechanical cavities [11–14], and optomechanical crystals [15, 16].

3 Topological Phase Transition

To study the topological phase transition in the generalized SSH model, we set a periodic boundary condition, so the linearized Hamiltonian for one-dimensional optomechanical array can be redefined as

$H^{\prime }=\sum _{j=1}^N\left(J{e}^{i\varphi }{a}_j^{†}{b}_j+v{a}_{\left(jmodN\right)+1}^{†}{b}_j+z{b}_{\left(j\mathrm{mod}N\right)+1}^{†}{a}_j\right)+\mathrm{H}.\mathrm{c}.,(9)$

where “mod” stands for the modular calculation. By using the discrete Fourier transform for a_j and b_j as

$\left(\begin{array}{c}\hfill a_j\hfill \\ \hfill b_j\hfill \end{array}\right)=\sum _k{e}^{-ikj}\left(\begin{array}{c}\hfill a_k\hfill \\ \hfill b_k\hfill \end{array}\right),(10)$

then the Hamiltonian in Eq. 9 can be rewritten as

$H^{\prime }=\sum _k\left(\begin{array}{cc}\hfill a_k^{†}\hfill & \hfill b_k^{†}\hfill \end{array}\right)H^{\prime }\left(k\right)\left(\begin{array}{c}\hfill a_k\hfill \\ \hfill b_k\hfill \end{array}\right)(11)$

with

$H^{\prime }\left(k\right)=\left(\begin{array}{cc}\hfill 0\hfill & \hfill h\left(k\right)\hfill \\ \hfill h^{*}\left(k\right)\hfill & \hfill 0\hfill \end{array}\right)(12)$

and

$h\left(k\right)=J{e}^{i\varphi }+v{e}^{-ik}+z{e}^{ik},(13)$

where k is the wavenumber in the first Brillouin zone. The dispersion relation of the generalized SSH model with periodic boundary conditions is given by

$E=\pm \left|J{e}^{i\varphi }+v{e}^{-ik}+z{e}^{ik}\right|.(14)$

The topological invariant of an insulating Hamiltonian can be characterized by the dispersion relation and the winding numbers W defined by [77, 78].

$W=\frac{1}{2\pi i}{\int }_{-\pi }^{\pi }dk\frac{d\ln h\left(k\right)}{dk}.(15)$

For the generalized SSH model with $h\left(k\right)$ given by Eq. 13, the winding number is either 0 or ±1, depending on the parameters J, ϕ, z and v. The phase diagram is shown in Figure 2. When the phase factor ϕ = 0, the winding number is: 1) W = 1 if z > v and z + v > J; 2) W = −1 if z < v and z + v > J; 3) W = 0 if z + v < J.

FIGURE 2

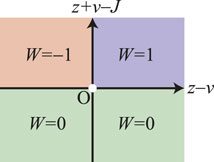
FIGURE 2. (Color online) Phase diagram of the generalized SSH model with ϕ = 0. The winding number is: W = 1 if z > v and z + v > J; W = − 1 if z < v and z + v > J; or W = 0 if z + v < J.

The Hamiltonian for the generalized SSH model in the momentum space can be written in an alternative form as

$\begin{array}{ccc}\hfill H^{\prime }\left(k\right)& =\hfill & \mathbf{d}\left(k\right)\cdot \widehat{\sigma }\hfill \\ \hfill & =\hfill & d_x\left(k\right){\widehat{\sigma }}_x+d_y\left(k\right){\widehat{\sigma }}_y+d_z\left(k\right){\widehat{\sigma }}_z,\hfill \end{array}(16)$

where ${\widehat{\sigma }}_x$, ${\widehat{\sigma }}_y$, and ${\widehat{\sigma }}_z$ are the Pauli matrices, and

$d_x\left(k\right)=J\cos \varphi +v\cos k+z\cos k,(17)$

$d_y\left(k\right)=J\sin \varphi -v\sin k+z\sin k,(18)$

$d_z\left(k\right)=0.(19)$

The winding number can also be obtained graphically by counting the number of times the loop winds around the origin of the d_x, d_y plane.

We show the dispersion relation and the path that the endpoint of the vector $\mathbf{d}\left(k\right)$ traces out in Figure 3 for v > z. As the wavenumber runs through the Brillouin zone, k = 0 → 2π, the path that the endpoint of the vector $\mathbf{d}\left(k\right)$ is a closed ellipse of long axis v + z and short axis |v − z| on the d_x, d_y plane, centered at $\left(J,0\right)$, and the endpoint rotates around the origin clockwise. It is clear that the winding number is W = −1 when z + v > J for z < v, and the winding number is W = 0 when z + v < J.

FIGURE 3

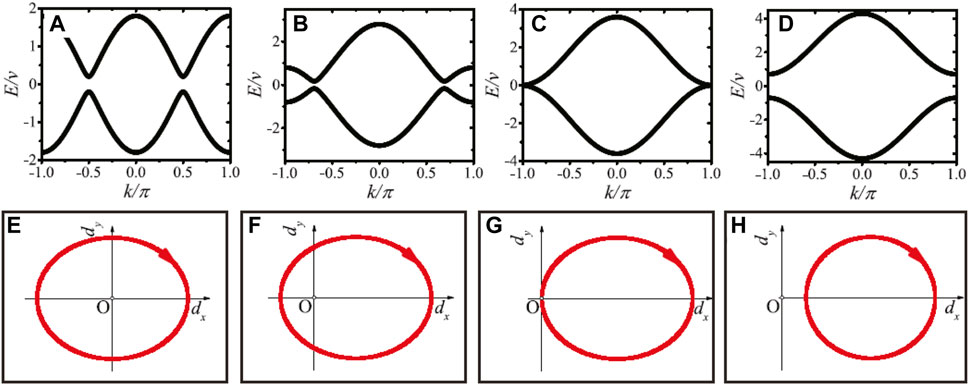
FIGURE 3. (Color online) Dispersion relations of the generalized SSH model with different hopping amplitude J: (A) J = 0; (B) J/v = 1; (C) J/v = 1.8; (D) J/v = 2.5. (E–H) The paths of the endpoint of the vector d(k) corresponding to (A–D) are shown on the d_x, d_y plane as the wavenumber is sweeped across the Brillouin zone, k = 0 → 2π. The other parameters are z/v = 0.8 and ϕ = 0.

Two more figures about the dispersion relation and the path that the endpoint of the vector $\mathbf{d}\left(k\right)$ traces are shown in Supplementary Figures S1, S2 in the supplementary material [97]. As v = z, the path of the endpoint of the vector $\mathbf{d}\left(k\right)$ becomes a straight line on the d_x-axis. As v < z, similarly to the case for v > z, the path of the endpoint of the vector $\mathbf{d}\left(k\right)$ is also a closed ellipse of long axis v + z and short axis |v − z| on the d_x, d_y plane, centered at $\left(J,0\right)$. However, the endpoint rotates around the origin counterclockwise for v < z. So we can conclude that the winding number is 1) W = 1 when z + v > J and v < z; 2) W = −1 when z + v > J and v > z; 3) W = 0 when z + v < J. These consist with the results shown in Figure 2.

The above results are obtained under the condition for ϕ = 0. In Figure 4, we show that the topological phase transition can be induced by tuning the phase ϕ. For ϕ ≠ 0, the path that the endpoint of the vector $\mathbf{d}\left(k\right)$ is centered at $\left(J\cos \varphi ,J\sin \varphi \right)$, so the symmetry of the path about the d_x-axis is broken. The topological phase transition appears when E = 0, as shown in Figure 4B, which gives the critical phase ϕ_c as

$\tan {\varphi }_c=\frac{z-v}{z+v}\tan k,(20)$

where

${\cos }^{2}k=\frac{J^2-{\left(z-v\right)}^2}{{\left(z+v\right)}^2-{\left(z-v\right)}^2}.(21)$

FIGURE 4

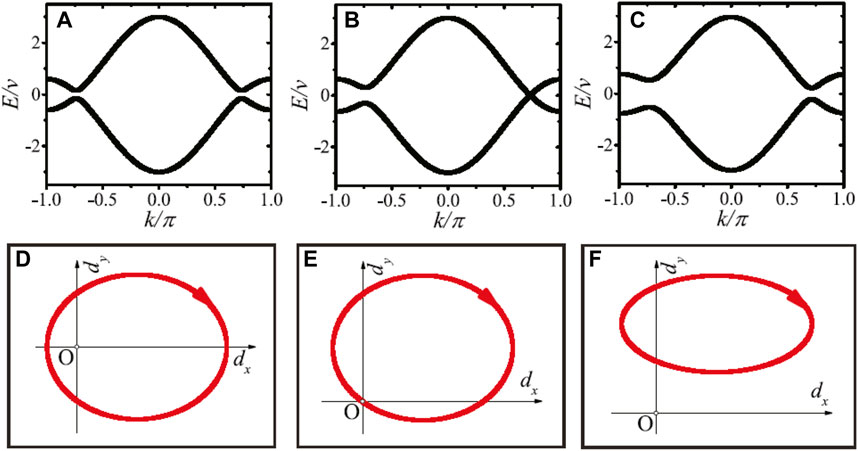
FIGURE 4. (Color online) Dispersion relations of the generalized SSH model for hopping amplitude J/v = 1.2 with different phase: (A) ϕ = 0; (B) ϕ = ϕ_c ≈ 0.04; (C) ϕ = 0.1. (D–F) The paths of the endpoint of the vector d(k), corresponding to (A–C), are shown on the d_x, d_y plane as the wavenumber is sweeped across the Brillouin zone, k = 0 → 2π. The other parameter is z/v = 0.8.

As v > z, we have W = −1 for ϕ = 0 in Figure 4A; we have W = 0 for ϕ = 0.1 in Figure 4C; the winding number is not well-defined at the critical point for ϕ = ϕ_c ≈ 0.04 as shown in Figure 4B. On the contrary, see Supplementary Figure S3 in the supplementary material [97], if v < z, we have W = 1 for ϕ = 0; we have W = 0 for ϕ = 0.3; there is no well-defined winding number at the critical point ϕ = ϕ_c ≈ 0.12. The paths [see Figures 4D–F and Supplementary Figures S3D,F] that the endpoint of the vector $\mathbf{d}\left(k\right)$ traces, corresponding to dispersion relation [see Figures 4A–C and Supplementary Figures S3A,C], show the phase transition from W = ±1 to W = 0 by tuning ϕ.

4 Edge States

We now study how to demonstrate topologically protected edge states in the optomechanical array of an open chain under single-particle excitation. To be specific, we propose an optomechanical array of an open chain for N = 8, then the wave function for the Hamiltanion in Eq. 8 under single-particle excitation can be defined as

$\left|\mathrm{\Psi }\left(t\right)\right.⟩=\sum _{j=1}^N\left[c_{2j-1}\left(t\right)\left|a_j\right.⟩+c_{2j}\left(t\right)\left|b_j\right.⟩\right],(22)$

where $P_{2j-1}\left(t\right)={\left|c_{2j-1}\left(t\right)\right|}^2$ and $P_{2j}\left(t\right)={\left|c_{2j}\left(t\right)\right|}^2$ denote the occupying probabilities in the jth cavity mode and jth mechanical mode, respectively. For simplicity, we define $P_i\left(t\right)={\left|c_i\left(t\right)\right|}^2$ with the position index i, shown in Figure 1.

The energy spectrum of a generalized SSH model for N = 8 is shown in Figure 5. Under the conditions z ≪ v or z ≫ v, see Figures 5A,D, the energy spectrum of a generalized SSH model is similar to that of the standard SSH model. However, due to the level crossings for the nearest neighbor eigenmodes and avoided level crossings for the next-nearest neighbor eigenmodes, there are four (N/2) degenerate points of the zero-energy modes within the interval 0 < J < z + v, as shown in Figures 6A,B, which are the local enlarged drawings of the boxes with red dashed-line in Figures 5A,D. When z = 0.8v, as shown Figure 5B, there are degenerate points for the nearest neighbor eigenmodes and avoided level crossings for the next-nearest neighbor eigenmodes. But when z = v, as shown Figure 5C, all the avoided level crossings for the next-nearest neighbor eigenmodes disappear.

FIGURE 5

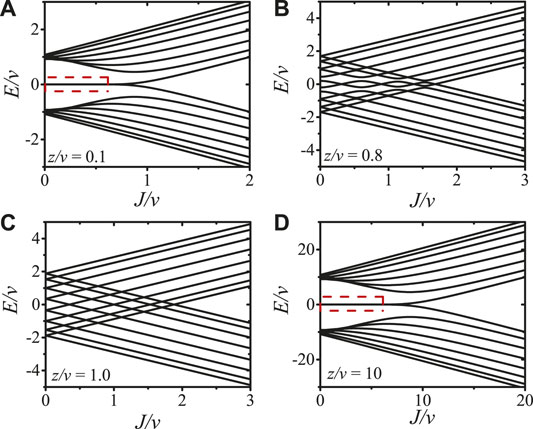
FIGURE 5. (Color online) Energy spectrum of the open chain optomechanical array for N = 8 as a function the intracell hopping amplitude J for different intercell hopping amplitude z: (A) z/v = 0.1; (B) z/v = 0.8; (C) z/v = 1.0; (D) z/v = 10. The phase factor is ϕ = 0.

FIGURE 6

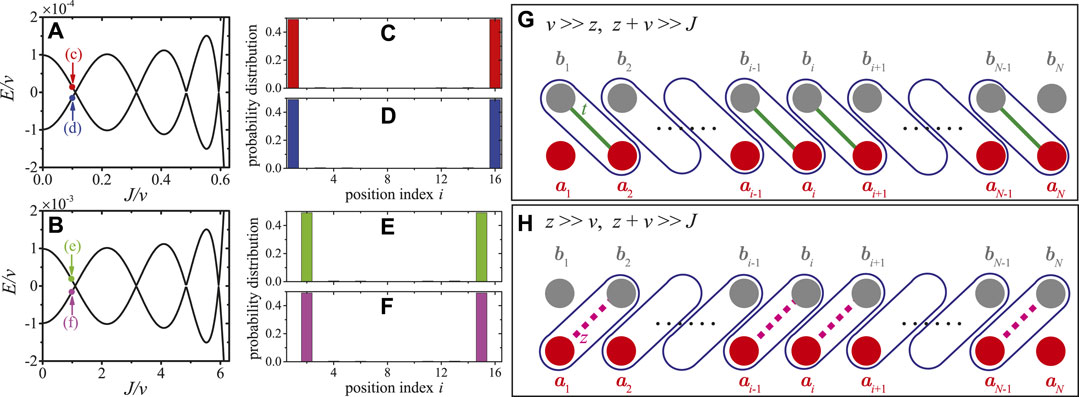
FIGURE 6. (Color online) (A, b) are the local enlarged drawings of (Figures 5A, D). (C–F) show the probability distributions of the eigenfunctions corresponding to the points shown in (A, B). (G) Edge states appear at a₁ and b_N corresponding to (C, D) for v ≫ z and J ≪ v + z. (H) Edge states appear at b₁ and a_N corresponding to (E, F) for z ≫ v and J ≪ v + z.

The probability distributions of the eigenstates, corresponding to the points marked in Figures 6A,B, are shown in Figures 6C–F. It is obvious that the probability distributions of the eigenstates are localized. We define four edge states, i.e., left cavity (LC), left mechniacal (LM), right cavity (RC), right mechniacal (RM) edge states, as

$\left|LC\right.⟩=\sum _{j=1}^N{c}_1{e}^{-2\left(j-1\right)/\xi }\left|a_j\right.⟩,(23)$

$\left|LM\right.⟩=\sum _{j=1}^N{c}_2{e}^{-2\left(j-1\right)/\xi }\left|b_j\right.⟩,(24)$

$\left|RC\right.⟩=\sum _{j=1}^N{c}_{2N-1}{e}^{2\left(j-N\right)/\xi }\left|a_j\right.⟩,(25)$

$\left|RM\right.⟩=\sum _{j=1}^N{c}_{2N}{e}^{2\left(j-N\right)/\xi }\left|b_j\right.⟩,(26)$

where ξ > 0 is the localization length determined by the amplitudes of v, z, and J. When v ≫ z and J ≪ v + z (corresponding to the winding number W = − 1 under the periodic boundary condition), as shown in Figures 6C,D, the edge states are the hybridized states of the LC edge state and RM edge state. A concise physical picture for the edge states with v ≫ z and J ≪ v + z is shown in Figure 6G, where dimers are formed between b_j and a_j+1, and a₁ and b_N are isolated from the others. Similarly, when v ≪ z and J ≪ v + z (corresponding to the winding number W = 1 under the periodic boundary condition), the edge states are the hybridized states of the LM edge state and RC edge state, as shown in Figures 6E,F. The physical picture for the edge states with v ≪ z and J ≪ v + z is shown in Figure 6H, where dimers are formed between a_j and b_j+1, and b₁ and a_N are isolated from the others. When J > v + z (corresponding to the winding number W = 0 under the periodic boundary condition), dimers are formed between a_j and b_j, and no modes are isolated from the others (the physical picture is not shown in the text). Thus, there is no edge state when J > v + z.

Figure 7 shows the time evolution of the probability distribution for the generalized SSH model with the open boundary condition (i.e., an open chain for N = 8). In Figures 7A–E, an excitation is injected at the first cavity mode P₁(0) = 1 for z = v/10, and in Figures 7F–J, an excitation is injected at the first mechanical mode P₂(0) = 1 for z = 10v. From these figures, we can find that: 1) When J = z ≪ v or J = v ≪ z, as shown in Figures 7A,F, the excitation almost localizes in the injected cavity or mechanical mode like a soliton for a long time. With a larger value of J (still with J < z + v), as shown in Figures 7B,G, the excitation spreads to the nearest neighbor modes and the localization of the excitation becomes weaker. 2) When J = z + v (i.e., the topological phase transition point), as shown in Figures 7D,I, the excitation, oscillating like a soliton, travels in the open chain and reflects back at the ends. The traveling speed (the period of oscillation) depends the hopping amplitudes: the excitation travels much faster in Figure 7I with z/v = 10 and J/v = 11 than in Figure 7D with z/v = 0.1 and J/v = 1.1. As J is away from the topological phase transition point (J ≠ z + v), as shown in Figures 7C,E [or Figures 7H,J], the distribution of the traveling excitation disperses much faster than the case with J = z + v. That is, the excitation travels like a soliton with less dispersion in the open chain when the system works at the critical point J = z + v.

FIGURE 7

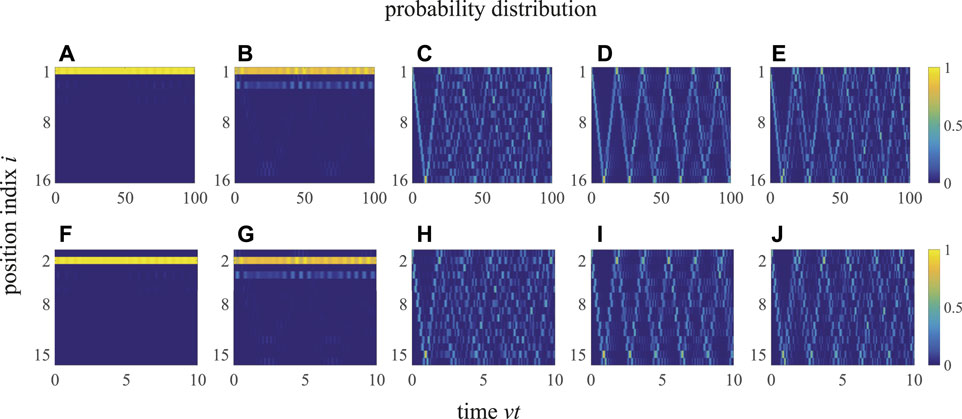
FIGURE 7. (Color online) Time evolution of the probability distribution of an open chain for N = 8: (A–E) z/v = 0.1 and P₁(0) = 1, with (A) J/v = 0.1, (B) J/v = 0.3, (C) J/v = 1.0, (D) J/v = 1.1, (E) J/v = 1.2; (F–J) z/v = 10 and P₂(0) = 1, with (F) J/v = 1, (G) J/v = 3, (H) J/v = 10, (I) J/v = 11, (J) J/v = 12. The phase factor is ϕ = 0.

5 Adiabatic Particle Pumping

As discussed in the previous section, when the driving strengths Ω_j,σ and detunings Δ_j,σ (σ = 0, ±) of the external lasers are constant, and as a result the parameters J, ϕ, z and v are time independent in the steady state, then an excitation injected at one edge will stay there like a stationary state for long. However, we will show that it is possible to transfer the edge states from one to another by adiabatic pumping with periodically modulated optomechanical array. The periodically modulated optomechanical array can be realized by modulating the strengths Ω_j,σ and detunings Δ_j,σ of the driving fields, so that the detuning between the cavity modes and mechanical modes $u\left(t\right)$ and the classical amplitude α_j,σ become time dependent. By solving the classical equation of motion under the condition that the modulation frequency ω is much lower than the mechanical resonant frequency ω_m,j, the classical amplitude α_j,σ can be expressed approximately as

${\alpha }_{j,\sigma }\left(t\right)=-i{\int }_0^t{\mathrm{\Omega }}_{j,\sigma }\left(\tau \right)e^{\left[\frac{{\kappa }_j}{2}+i\left({\omega }_{c,j}-{\omega }_{j,\sigma }\right)\right]\left(\tau -t\right)}d\tau .(27)$

Following the same approach used in Section 2, the linearized Hamiltonian of the periodically modulated optomechanical array is given by

$\begin{array}{ccc}\hfill H& =\hfill & \sum _{j=1}^N\left[\frac{u_a\left(t\right)}{2}{a}_j^{†}{a}_j+\frac{u_b\left(t\right)}{2}{b}_j^{†}{b}_j+J\left(t\right)a_j^{†}{b}_j\right]\hfill \\ \hfill & \hfill & +\sum _{j=1}^{N-1}\left[v\left(t\right)a_{j+1}^{†}{b}_j+z\left(t\right)b_{j+1}^{†}{a}_j\right]+\mathrm{H}.\mathrm{c}.,\hfill \end{array}(28)$

where J(t)e^iϕ ≡ g_j,0α_j,0(t), v(t) ≡ g_j,−α_j,−(t), and z(t) ≡ g_j,+α_j,+(t). To detect the robustness of the adiabatic pumping, we will consider the disorder effect by adding normally distributed random fluctuations ϵ with zero mean value to u_a(t), u_b(t), J(t), v(t), and z(t) in the numerical calculations.

First, we consider a smooth modulation sequence as

$\left\{\begin{array}{c}{u}_a\left(t\right)=\frac{A}{2}\sin \left(\omega t\right),\hfill \\ u_b\left(t\right)=0,\hfill \\ J\left(t\right)=A\left[1-\cos \left(\omega t\right)\right],\hfill \\ v\left(t\right)=\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}.,\hfill \\ z\left(t\right)=\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}.,\hfill \end{array}\right.(29)$

where, u(t) and J(t) are modulated periodically with amplitudes A/2 and A, and frequency ω; u_b(t), v(t), and z(t) are constant.

The instantaneous spectrum of the Hamiltonian in Eq. 28 with time dependent pump sequence defined in Eq. 29 is shown in Figures 8A,B. In Figures 8C–F, the probability distributions of eigenstates corresponding to the points shown in Figures 8A,B, are approximately the edge states defined in Eqs 23–26 as: Figure 8C, LC edge state; Figure 8D, RM edge state; Figure 8E, RC edge state; Figure 8F, LM edge state. When the adiabatic approximation holds, the system will stay in the same eigenstate. Figure 8A shows how a LC edge state is adiabatically pumped to the RM edge state during a pumping cycle, in the mean while Figure 8B shows how a RC edge state is adiabatically pumped to the LM edge state within a pumping cycle.

FIGURE 8

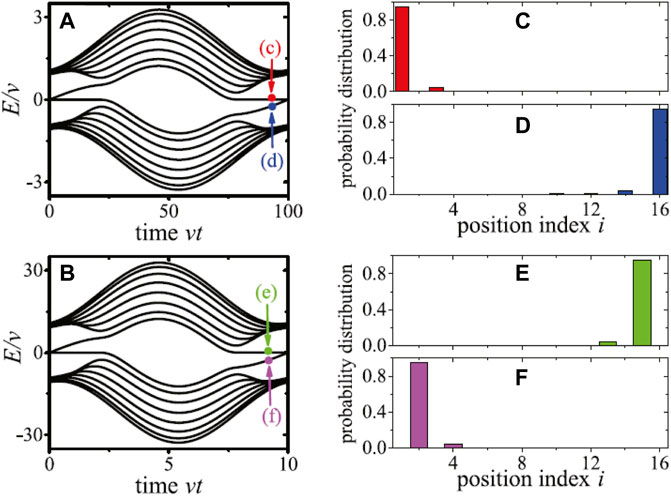
FIGURE 8. (Color online) Instantaneous spectrum of the open chain optomechanical array for N = 8. The time dependent pump sequence is defined in Eq. 29, with (A) z/v = 0.1, A/v = 1.1, and ω/v = 2π/100; (B) z/v = 10, A/v = 11, and ω/v = 2π/10. (C–F) show the probability distributions of the edge states corresponding to the points shown in (A, B). The phase factor is ϕ = 0.

The dynamics of the probability distributions of an open chain with a time dependent pump sequence defined in Eq. 29 is obtained numerically. As shown in Figure 9A, the excitation at the first cavity mode (LC edge state) quickly expands into the bulk, and then the probability distribution is concentrated around the Nth mechanical mode (RM edge state) at the end of the first pumping cycle. In the second pumping cycle, the excitation expands into the bulk again and concentrates on the first cavity mode (LC edge state) at the end of the second pumping cycle. Similarly, as shown in Figure 9B, the excitation at the first mechanical mode (LM edge state) expands into the bulk and concentrates on the Nth cavity mode (RC edge state) at the end of the first pumping cycle, and then the excitation expands into the bulk again and concentrates on the first mechanical mode (LM edge state) at the end of the second pumping cycle. These results are consistent with the instantaneous spectrum in the adiabatic limit, as shown in Figure 8. However, due to the Landau Zener transition, which occurs at the degenerate points ωt = 2nπ (n is positive integer), the periodical behavior of the probability distribution becomes less well-resolved in the following cycles. To prove that the adiabatically pumping is immune to small disorders, we re-plot Figures 9A,B in Figures 9C,D by adding the normally distributed disorder ϵ with a standard deviation 3) 0.05v and 4) 0.5v. It is clear that Figures 9C,D are essentially identical to those in Figures 9A,B, i.e., the adiabatically pumping is robust against small disorders.

FIGURE 9

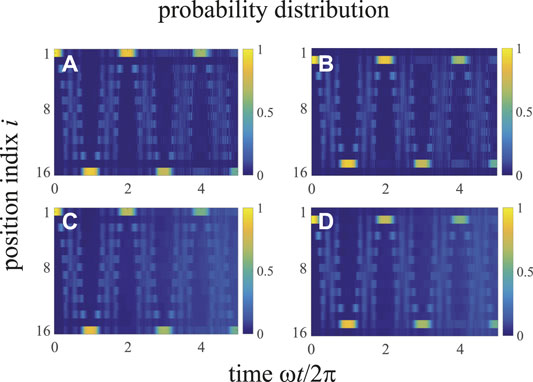
FIGURE 9. (Color online) Time evolution of the probability distribution of an open chain for N = 8. The time dependent pump sequence is defined in Eq. 29, with (A, C) z/v = 0.1, A/v = 1.1, ω/v = 2π/100, and P₁(0) = 1; (B, D) z/v = 10, A/v = 11, ω/v = 2π/10, and P₂(0) = 1. (A, B) are plotted without disorder; (C) is plotted for the normally distributed disorder ϵ with a standard deviation 0.05v; (D) is plotted for the normally distributed disorder ϵ with a standard deviation 0.5v. The phase factor is ϕ = 0.

As shown in Figures 8, 9, with time dependent pump sequence defined in Eq. 29, the LC edge state can be pumped adiabatically to the RM edge state, and the LM edge state can be pumped adiabatically to the RC edge state, and vice versa. However, the LC edge state cannot be pumped adiabatically to the RC edge state, and the LM edge state cannot be pumped adiabatically to the RM edge state. Now, we consider another smooth modulation sequence to realize the adiabatical pumping between the LC (LM) edge state and the RC (RM) edge state. The smooth modulation sequence is defined by

$\left\{\begin{array}{c}{u}_a\left(t\right)=\frac{A}{2}\sin \left(\omega t\right),\hfill \\ u_b\left(t\right)=0,\hfill \\ J\left(t\right)=\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}.,\hfill \\ v\left(t\right)=A\left[1+\cos \left(\omega t\right)\right],\hfill \\ z\left(t\right)=A\left[1-\cos \left(\omega t\right)\right].\hfill \end{array}\right.(30)$

Here, u(t), v(t) and z(t) are modulated periodically with amplitudes A/2 and A, and frequency ω, while u_b(t) = 0 and J(t) is constant.

The instantaneous spectrum of the Hamiltonian in Eq. 28 with time dependent pump sequence defined in Eq. 30 is shown in Figure 10A. In Figures 10B–E, the probability distributions of eigenstates corresponding to the points shown in Figure 10A, are approximately the edge states defined in Eqs 23–26 as: Figure 10B LC edge state; Figure 10C RM edge state; Figure 10D LM edge state; Figure 10E RC edge state. When the adiabatic approximation holds, the system will stay in the same eigenstate. Figure 10A shows how a LC edge state is adiabatically pumped to the RC edge state during a pumping cycle, in the mean while, a LM edge state is adiabatically pumped to the RM edge state within a pumping half-cycle.

FIGURE 10

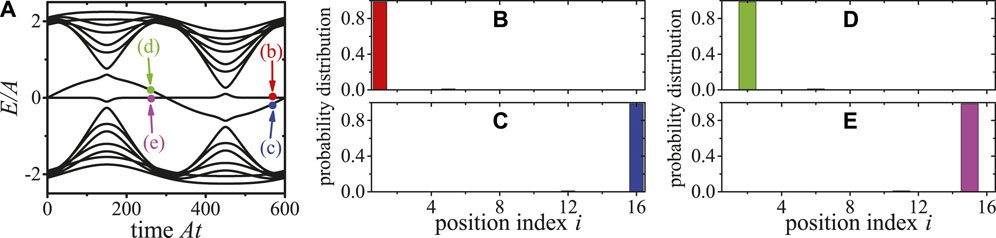
FIGURE 10. (Color online) Instantaneous spectrum of the open chain optomechanical array for N = 8, J/A = 0.1, and ϕ = 0. The time dependent pump sequence is defined in Eq. 30 with ω/A = 2π/600. (B–E) show the probability distributions of the edge states corresponding to the points shown in (A).

The adiabatically pumping can also be studied directly by the dynamics of the probability distribution for an open chain with a time dependent pump sequence defined in Eq. 30. In Figure 11A, the excitation at the first cavity mode (LC edge state) quickly expands into the bulk, and then concentrates on the Nth cavity mode (RC edge state) at the end of the first pumping half-cycle. In the second pumping half-cycle, the excitation expands into the bulk again and concentrates on the first cavity mode (LC edge state) at the end of the first pumping cycle. Similarly, as shown in Figure 11B, the excitation at the first mechanical mode (LM edge state) expands into the bulk and concentrates on the Nth mechanical mode (RM edge state) at the end of the first pumping half-cycle, and then the excitation expands into the bulk again and concentrates on the first mechanical mode (LM edge state) at the end of the first pumping cycle. However, the periodical behavior of the probability distribution becomes less well-resolved in the following cycles, which is induced by the Landau Zener transition at the degenerate points ωt = nπ (n is positive integer). Figures 11A,B are re-plotted in Figures 9C,D for the normally distributed disorder ϵ with a standard deviation 0.01A. Clearly, the adiabatically pumping is immune to the small disorders.

FIGURE 11

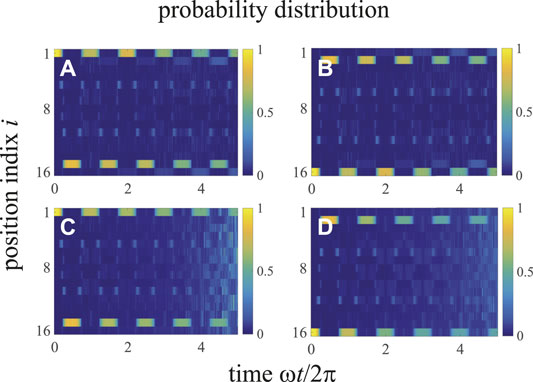
FIGURE 11. (Color online) Time evolution of the probability distribution for an open chain of N = 8. The time dependent pump sequence is defined in Eq. (30) with ω/A = 2π/600, (A, C) P₁(0) = 1; (B, D) P₁₆(0) = 1. (A, B) are plotted without disorder; (C, D) are plotted for the normally distributed disorder ϵ with a standard deviation 0.01A. The other parameters are J/A = 0.1 and ϕ = 0.

Overall, with time dependent pump sequence defined in Eq. 29, the LC edge state can be pumped adiabatically to the RM edge state, and the LM edge state can be pumped adiabatically to the RC edge state; with time dependent pump sequence defined in Eq. 30, the LC edge state can be pumped adiabatically to the RC edge state, and the LM edge state can be pumped adiabatically to the RM edge state. Therefore, the four edge states can be pumped from one to another adiabatically with smooth modulation sequence.

6 Conclusion

In summary, we have proposed to implement a generalized SSH model based on optomechanical arrays. This generalized SSH model supports two distinct nontrivial topological phases, and the transitions between different phases can be observed by tuning the strengths and phases of the effective optomechanical interactions. Dynamical control of the effective optomechanical interactions can be realized by tuning the strengths and phases of driving fields slowly, which allow for dynamical control of the topological phase transitions. Moreover, four types of edge states can be generated in the generalized SSH model of an open chain under single-particle excitation, and the dynamical behaviors of the excitation in the open chain depend on the topological properties under the periodic boundary condition. We show that the edge states can be pumped adiabatically along the optomechanical arrays by periodically modulating the amplitudes and frequencies of the driving fields, and the adiabatically pumping is immune to small disorders. Our results can be applied to control the transport of photons and phonons, and the generalized SSH model based on the optomechanical arrays provides us a tunable platform to engineer topological phases for photons and phonons.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

X-WX, Y-JZ, and HW conceived the idea and X-WX carried out the calculation. X-WX, A-XC, and Y-XL supervised the work. All authors contributed to the interpretation of the work and the preparation of the manuscript.

Funding

National Natural Science Foundation of China (12064010, 11904013, 11847165, 12175199); Natural Science Foundation of Hunan Province (2021JJ20036); Natural Science Foundation of Jiangxi Province (20192ACB21002); National Basic Research Program of China (973 Program) (2014CB921401); Tsinghua University Initiative Scientific Research Program; Tsinghua National Laboratory for Information Science and Technology (TNList) Crossdiscipline Foundation.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.813801/full#supplementary-material

Supplementary Figure S1 | (Color online) Dispersion relations of the generalized SSH model with different hopping amplitude J: (A) J = 0; (B) J/v = 1; (C) J/v = 2; (D) J/v = 2.5. (E–H) The paths of the endpoint of the vector d(k) corresponding to (A–D) are shown on the dx, dy plane as the wavenumber is sweeped across the Brillouin zone, k = 0 → 2π. The other parameters are z/v = 1 and ϕ = 0.

Supplementary Figure S2 | (Color online) Dispersion relations of the generalized SSH model with different hopping amplitude J: (A) J = 0; (B) J/v = 1; (C) J/v = 2.2; (D) J/v = 2.7. (E–H) The paths of the endpoint of the vector d(k) corresponding to (A–D) are shown on the dx, dy plane as the wavenumber is sweeped across the Brillouin zone, k = 0 → 2π. The other parameters are z/v = 1.2 and ϕ = 0.

Supplementary Figure S3 | (Color online) Dispersion relations of the generalized SSH model for hopping amplitude J/v = 1.2 with different phase: (A) ϕ = 0; (B) ϕ = ϕc ≈ 0.12; (C) ϕ = 0.3. (D–F) The paths of the endpoint of the vector d(k) corresponding to (A–C) are shown on the dx, dy plane as the wavenumber is sweeped across the Brillouin zone, k = 0 → 2π. The other parameter is z/v = 1.5.

References

1. Kippenberg TJ, Vahala KJ. Cavity Optomechanics: Back-Action at the Mesoscale. Science (2008) 321:1172–6. doi:10.1126/science.1156032

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Marquardt F, Girvin S. Optomechanics. Physics (2009) 2:40. doi:10.1103/physics.2.40

CrossRef Full Text | Google Scholar

3. Aspelmeyer M, Meystre P, Schwab K. Quantum Optomechanics. Phys Today (2012) 65(7):29–35. doi:10.1063/pt.3.1640

CrossRef Full Text | Google Scholar

4. Aspelmeyer M, Kippenberg TJ, Marquardt F. Cavity Optomechanics. Rev Mod Phys (2014) 86:1391–452. doi:10.1103/revmodphys.86.1391

CrossRef Full Text | Google Scholar

5. Metcalfe M. Applications of Cavity Optomechanics. Appl Phys Rev (2014) 1:031105. doi:10.1063/1.4896029

CrossRef Full Text | Google Scholar

6. Liu Y-l., Wang C, Zhang J, Liu Y-x., Cavity Optomechanics: Manipulating Photons and Phonons towards the Single-Photon strong Coupling. Chin Phys. B (2018) 27:024204. doi:10.1088/1674-1056/27/2/024204

CrossRef Full Text | Google Scholar

7. Lin Q, Rosenberg J, Jiang X, Vahala KJ, Painter O. Mechanical Oscillation and Cooling Actuated by the Optical Gradient Force. Phys Rev Lett (2009) 103:103601. doi:10.1103/physrevlett.103.103601

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Li M, Pernice WHP, Tang HX. Tunable Bipolar Optical Interactions between Guided Lightwaves. Nat Photon (2009) 3:464–8. doi:10.1038/nphoton.2009.116

CrossRef Full Text | Google Scholar

9. Weis S, Rivière R, Deléglise S, Gavartin E, Arcizet O, Schliesser A, et al. Optomechanically Induced Transparency. Science (2010) 330:1520–3. doi:10.1126/science.1195596

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Zhang M, Shah S, Cardenas J, Lipson M. Synchronization and Phase Noise Reduction in Micromechanical Oscillator Arrays Coupled through Light. Phys Rev Lett (2015) 115:163902. doi:10.1103/physrevlett.115.163902

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Teufel JD, Li D, Allman MS, Cicak K, Sirois AJ, Whittaker JD, et al. Circuit Cavity Electromechanics in the strong-coupling Regime. Nature (2011) 471:204–8. doi:10.1038/nature09898

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Massel F, Cho SU, Pirkkalainen J-M, Hakonen PJ, Heikkilä TT, Sillanpää MA. Multimode Circuit Optomechanics Near the Quantum Limit. Nat Commun (2012) 3:987. doi:10.1038/ncomms1993

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Palomaki TA, Teufel JD, Simmonds RW, Lehnert KW. Entangling Mechanical Motion with Microwave Fields. Science (2013) 342:710–3. doi:10.1126/science.1244563

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Suh J, Weinstein AJ, Lei CU, Wollman EE, Steinke SK, Meystre P, et al. Mechanically Detecting and Avoiding the Quantum Fluctuations of a Microwave Field. Science (2014) 344:1262–5. doi:10.1126/science.1253258

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Eichenfield M, Chan J, Camacho RM, Vahala KJ, Painter O. Optomechanical Crystals. Nature (2009) 462:78–82. doi:10.1038/nature08524

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Safavi-Naeini AH, Hill JT, Meenehan S, Chan J, Gröblacher S, Painter O. Two-Dimensional Phononic-Photonic Band Gap Optomechanical Crystal Cavity. Phys Rev Lett (2014) 112:153603. doi:10.1103/physrevlett.112.153603

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Chang DE, Safavi-Naeini AH, Hafezi M, Painter O. Slowing and Stopping Light Using an Optomechanical crystal Array. New J Phys (2011) 13:23003. doi:10.1088/1367-2630/13/2/023003

CrossRef Full Text | Google Scholar

18. Chen W, Clerk AA. Photon Propagation in a One-Dimensional Optomechanical Lattice. Phys Rev A (2014) 89:033854. doi:10.1103/physreva.89.033854

CrossRef Full Text | Google Scholar

19. Heinrich G, Ludwig M, Qian J, Kubala B, Marquardt F. Collective Dynamics in Optomechanical Arrays. Phys Rev Lett (2011) 107:043603. doi:10.1103/PhysRevLett.107.043603

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Ludwig M, Marquardt F. Quantum Many-Body Dynamics in Optomechanical Arrays. Phys Rev Lett (2013) 111:073603. doi:10.1103/PhysRevLett.111.073603

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Lauter R, Mitra A, Marquardt F. From Kardar-Parisi-Zhang Scaling to Explosive Desynchronization in Arrays of Limit-Cycle Oscillators. Phys Rev E (2017) 96:012220. doi:10.1103/PhysRevE.96.012220

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Schmidt M, Kessler S, Peano V, Painter O, Marquardt F. Optomechanical Creation of Magnetic fields for Photons on a Lattice. Optica (2015) 2:635. doi:10.1364/optica.2.000635

CrossRef Full Text | Google Scholar

23. Schmidt M, Peano V, Marquardt F. (2013) Optomechanical Metamaterials: Dirac Polaritons, Gauge fields, and Instabilities. arXiv:1311.7095 [physics.optics].

Google Scholar

24. Schmidt M, Peano V, Marquardt F. Optomechanical Dirac Physics. New J Phys (2015) 17:023025. doi:10.1088/1367-2630/17/2/023025

CrossRef Full Text | Google Scholar

25. Roque TF, Peano V, Yevtushenko OM, Marquardt F. Anderson Localization of Composite Excitations in Disordered Optomechanical Arrays. New J Phys (2017) 19:013006. doi:10.1088/1367-2630/aa52e2

CrossRef Full Text | Google Scholar

26. Wan L-L, Lü X-Y, Gao J-H, Wu Y. Controllable Photon and Phonon Localization in Optomechanical Lieb Lattices. Opt Express (2017) 25:17364. doi:10.1364/oe.25.017364

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Xiong H, Gan J, Wu Y. Kuznetsov-Ma Soliton Dynamics Based on the Mechanical Effect of Light. Phys Rev Lett (2017) 119:153901. doi:10.1103/physrevlett.119.153901

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Peano V, Brendel C, Schmidt M, Marquardt F. Topological Phases of Sound and Light. Phys Rev X (2015) 5:031011. doi:10.1103/physrevx.5.031011

CrossRef Full Text | Google Scholar

29. Peano V, Houde M, Marquardt F, Clerk AA. Topological Quantum Fluctuations and Traveling Wave Amplifiers. Phys Rev X (2016) 6:041026. doi:10.1103/physrevx.6.041026

CrossRef Full Text | Google Scholar

30. Peano V, Houde M, Brendel C, Marquardt F, Clerk AA. Topological Phase Transitions and Chiral Inelastic Transport Induced by the Squeezing of Light. Nat Commun (2016) 7:10779. doi:10.1038/ncomms10779

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Minkov M, Savona V. Haldane Quantum Hall Effect for Light in a Dynamically Modulated Array of Resonators. Optica (2016) 3:200. doi:10.1364/optica.3.000200

CrossRef Full Text | Google Scholar

32. Brendel C, Peano V, Painter O, Marquardt F. Snowflake Phononic Topological Insulator at the Nanoscale. Phys Rev B (2018) 97:020102(R). doi:10.1103/physrevb.97.020102

CrossRef Full Text | Google Scholar

33. Qi L, Xing Y, Wang H-F, Zhu A-D, Zhang S. Simulating Z_2 Topological Insulators via a One-Dimensional Cavity Optomechanical Cells Array. Opt Express (2017) 25:17948. doi:10.1364/oe.25.017948

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Xing Y, Qi L, Cao J, Wang D-Y, Bai C-H, Cui W-X, et al. Controllable Photonic and Phononic Edge Localization via Optomechanically Induced Kitaev Phase. Opt Express (2018) 26:16250. doi:10.1364/oe.26.016250

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Heeger AJ, Kivelson S, Schrieffer JR, Su W-P. Solitons in Conducting Polymers. Rev Mod Phys (1988) 60:781–850. doi:10.1103/revmodphys.60.781

CrossRef Full Text | Google Scholar

36. Bermudez A, Schaetz T, Porras D. Photon-Assisted-Tunneling Toolbox for Quantum Simulations in Ion Traps. New J Phys (2012) 14:053049. doi:10.1088/1367-2630/14/5/053049

CrossRef Full Text | Google Scholar

37. Atala M, Aidelsburger M, Barreiro JT, Abanin D, Kitagawa T, Demler E, et al. Direct Measurement of the Zak Phase in Topological Bloch Bands. Nat Phys (2013) 9:795–800. doi:10.1038/nphys2790

CrossRef Full Text | Google Scholar

38. Goldman N, Juzeliūnas G, Öhberg P, Spielman IB. Light-Induced Gauge Fields for Ultracold Atoms. Rep Prog Phys (2014) 77:126401. doi:10.1088/0034-4885/77/12/126401

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Jotzu G, Messer M, Desbuquois R, Lebrat M, Uehlinger T, Greif D, et al. Experimental Realization of the Topological Haldane Model with Ultracold Fermions. Nature (2014) 515:237–40. doi:10.1038/nature13915

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Duca L, Li T, Reitter M, Bloch I, Schleier-Smith M, Schneider U. An Aharonov-Bohm Interferometer for Determining Bloch Band Topology. Science (2015) 347:288–92. doi:10.1126/science.1259052

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Engelhardt G, Brandes T. Topological Bogoliubov Excitations in Inversion-Symmetric Systems of Interacting Bosons. Phys Rev A (2015) 91:053621. doi:10.1103/physreva.91.053621

CrossRef Full Text | Google Scholar

42. Engelhardt G, Benito M, Platero G, Brandes T. Topological Instabilities in Ac-Driven Bosonic Systems. Phys Rev Lett (2016) 117:045302. doi:10.1103/PhysRevLett.117.045302

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Nakajima S, Tomita T, Taie S, Ichinose T, Ozawa H, Wang L, et al. Topological Thouless Pumping of Ultracold Fermions. Nat Phys (2016) 12:296–300. doi:10.1038/nphys3622

CrossRef Full Text | Google Scholar

44. Lohse M, Schweizer C, Zilberberg O, Aidelsburger M, Bloch I. A Thouless Quantum Pump with Ultracold Bosonic Atoms in an Optical Superlattice. Nat Phys (2016) 12:350–4. doi:10.1038/nphys3584

CrossRef Full Text | Google Scholar

45. Meier EJ, An FA, Gadway B. Observation of the Topological Soliton State in the Su-Schrieffer-Heeger Model. Nat Commun (2016) 7:13986. doi:10.1038/ncomms13986

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Song B, Zhang L, He C, Poon TFJ, Hajiyev E, Zhang S, et al. Observation of Symmetry-Protected Topological Band with Ultracold Fermions. Sci Adv (2018) 4:eaao4748. doi:10.1126/sciadv.aao4748

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Lu L, Joannopoulos JD, Soljačić M. Topological Photonics. Nat Photon (2014) 8:821–9. doi:10.1038/nphoton.2014.248

CrossRef Full Text | Google Scholar

48. Lu L, Joannopoulos JD, Soljačić M. Topological States in Photonic Systems. Nat Phys (2016) 12:626–9. doi:10.1038/nphys3796

CrossRef Full Text | Google Scholar

49. Khanikaev AB, Shvets G. Two-dimensional Topological Photonics. Nat Photon (2017) 11:763–73. doi:10.1038/s41566-017-0048-5

CrossRef Full Text | Google Scholar

50. Sun X-C, He C, Liu X-P, Lu M-H, Zhu S-N, Chen Y-F. Two-dimensional Topological Photonic Systems. Prog Quan Electron (2017) 55:52–73. doi:10.1016/j.pquantelec.2017.07.004

CrossRef Full Text | Google Scholar

51. Ozawa T, Price HM, Amo A, Goldman N, Hafezi M, Lu L, et al. 2018 Topological Photonics. arXiv:1802.04173 [physics.optics].

Google Scholar

52. Fleury R, Sounas D, R Haberman M, Alù A. Nonreciprocal actoustics, Acoust Today (2015) 11:14.

53. Huber SD. Topological Mechanics. Nat Phys (2016) 12:621–3. doi:10.1038/nphys3801

CrossRef Full Text | Google Scholar

54. Xiao M, Ma G, Yang Z, Sheng P, Zhang ZQ, Chan CT. Geometric Phase and Band Inversion in Periodic Acoustic Systems. Nat Phys (2015) 11:240–4. doi:10.1038/nphys3228

CrossRef Full Text | Google Scholar

55. Belopolski I, Xu SY, Koirala N, Liu C, Bian G, Strocov VN, et al. A Novel Artificial Condensed Matter Lattice and a New Platform for One-Dimensional Topological Phases. Sci Adv (2017) 3:e1501692. doi:10.1126/sciadv.1501692

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Gröning O, Wang S, Yao X, Pignedoli CA, Borin Barin G, Daniels C, et al. Engineering of Robust Topological Quantum Phases in Graphene Nanoribbons. Nature (2018) 560:209–13. doi:10.1038/s41586-018-0375-9

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Poddubny A, Miroshnichenko A, Slobozhanyuk A, Kivshar Y. Topological Majorana States in Zigzag Chains of Plasmonic Nanoparticles. ACS Photon (2014) 1:101–5. doi:10.1021/ph4000949

CrossRef Full Text | Google Scholar

58. Cheng Q, Pan Y, Wang Q, Li T, Zhu S. Topologically Protected Interface Mode in Plasmonic Waveguide Arrays. Laser Photon Rev (2015) 9:392–8. doi:10.1002/lpor.201400462

CrossRef Full Text | Google Scholar

59. Ge L, Wang L, Xiao M, Wen W, Chan CT, Han D. Topological Edge Modes in Multilayer Graphene Systems. Opt Express (2015) 23:21585. doi:10.1364/oe.23.021585

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Ling CW, Xiao M, Chan CT, Yu SF, Fung KH. Topological Edge Plasmon Modes between Diatomic Chains of Plasmonic Nanoparticles. Opt Express (2015) 23:2021. doi:10.1364/oe.23.002021

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Liu C, Gurudev Dutt MV, Pekker D. Robust Manipulation of Light Using Topologically Protected Plasmonic Modes. Opt Express (2018) 26:2857–72. doi:10.1364/OE.26.002857

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Downing CA, Weick G. Topological Collective Plasmons in Bipartite Chains of Metallic Nanoparticles. Phys Rev B (2017) 95:125426. doi:10.1103/physrevb.95.125426

CrossRef Full Text | Google Scholar

63. Downing CA, Weick G. (2018) Topological Plasmons in Dimerized Chains of Nanoparticles: Robustness against Long-Range Quasistatic Interactions and Retardation Effects. arXiv:1803.08872 [cond-mat.mes-hall].

Google Scholar

64. Koch J, Houck AA, Hur KL, Girvin SM. Time-reversal-symmetry Breaking in Circuit-QED-Based Photon Lattices. Phys Rev A (2010) 82:043811. doi:10.1103/physreva.82.043811

CrossRef Full Text | Google Scholar

65. Nunnenkamp A, Koch J, Girvin SM. Synthetic Gauge fields and Homodyne Transmission in Jaynes-Cummings Lattices. New J Phys (2011) 13:095008. doi:10.1088/1367-2630/13/9/095008

CrossRef Full Text | Google Scholar

66. Mei F, You JB, Nie W, Fazio R, Zhu SL, Kwek LC. Simulation and Detection of Photonic Chern Insulators in a One-Dimensional Circuit-QED Lattice. Phys Rev A (2015) 92:041805(R). doi:10.1103/physreva.92.041805

CrossRef Full Text | Google Scholar

67. Mei F, Xue Z-Y, Zhang D-W, Tian L, Lee C, Zhu S-L. Witnessing Topological Weyl Semimetal Phase in a Minimal Circuit-QED Lattice. Quan Sci. Technol. (2016) 1:015006. doi:10.1088/2058-9565/1/1/015006

CrossRef Full Text | Google Scholar

68. Yang ZH, Wang YP, Xue ZY, Yang WL, Hu Y, Gao JH, et al. Circuit Quantum Electrodynamics Simulator of at Band Physics in a Lieb Lattice. Phys Rev A (2016) 93:062319. doi:10.1103/physreva.93.062319

CrossRef Full Text | Google Scholar

69. Engelhardt G, Benito M, Platero G, Brandes T. Topologically Enforced Bifurcations in Superconducting Circuits. Phys Rev Lett (2017) 118:197702. doi:10.1103/physrevlett.118.197702

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Tangpanitanon J, Bastidas VM, Al-Assam S, Roushan P, Jaksch D, Angelakis DG. Topological Pumping of Photons in Nonlinear Resonator Arrays. Phys Rev Lett (2016) 117:213603. doi:10.1103/physrevlett.117.213603

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Gu X, Chen S, Liu YX, (2017) Topological Edge States and Pumping in a Chain of Coupled Superconducting Qubits. arXiv:1711.06829v1 [quant-ph].

Google Scholar

72. Clay RT, Mazumdar S. Cooperative Density Wave and Giant Spin Gap in the Quarter-Filled Zigzag Electron Ladder. Phys Rev Lett (2005) 94:207206. doi:10.1103/physrevlett.94.207206

PubMed Abstract | CrossRef Full Text | Google Scholar

73. Li X, Zhao E, Vincent Liu W. Topological States in a Ladder-like Optical Lattice Containing Ultracold Atoms in Higher Orbital Bands. Nat Commun (2013) 4:1523. doi:10.1038/ncomms2523

PubMed Abstract | CrossRef Full Text | Google Scholar

74. Shimizu Y, Aoyama S, Jinno T, Itoh M, Ueda Y. Site-Selective Mott Transition in a Quasi-One-Dimensional VanadateV6O13. Phys Rev Lett (2015) 114:166403. doi:10.1103/physrevlett.114.166403

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Cheon S, Kim T-H, Lee S-H, Yeom HW. Chiral Solitons in a Coupled Double Peierls Chain. Science (2015) 350:182–5. doi:10.1126/science.aaa7055

PubMed Abstract | CrossRef Full Text | Google Scholar

76. Zhang T, Jo G-B. One-dimensional Sawtooth and Zigzag Lattices for Ultracold Atoms. Sci Rep (2015) 5:16044. doi:10.1038/srep16044

PubMed Abstract | CrossRef Full Text | Google Scholar

77. Li C, Lin S, Zhang G, Song Z. Topological Nodal Points in Two Coupled Su-Schrieffer-Heeger Chains. Phys Rev B (2017) 96:125418. doi:10.1103/physrevb.96.125418

CrossRef Full Text | Google Scholar

78. Asbóth JK, Oroszlány L, Pályi A. A Short Course on Topological Insulators. In: Lecture Notes in Physics, 919. Cham: Springer International Publishing (2016). doi:10.1007/978-3-319-25607-8

CrossRef Full Text | Google Scholar

79. Znojil M. Novel Recurrent Approach to the Generalized Su-Schrieffer-Heeger Hamiltonians. Phys Rev B (1989) 40:12468–75. doi:10.1103/physrevb.40.12468

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Li L, Xu Z, Chen S. Topological Phases of Generalized Su-Schrieffer-Heeger Models. Phys Rev B (2014) 89:085111. doi:10.1103/physrevb.89.085111

CrossRef Full Text | Google Scholar

81. Zeng Q-B, Chen S, Lü R. Generalized Aubry-André-Harper Model Withp-Wave Superconducting Pairing. Phys Rev B (2016) 94:125408. doi:10.1103/physrevb.94.125408

CrossRef Full Text | Google Scholar

82. Longhi S. Topological Pumping of Edge States via Adiabatic Passage. Phys Rev B (2019) 99:155150. doi:10.1103/physrevb.99.155150

CrossRef Full Text | Google Scholar

83. Du L, Wu JH, Artoni M, La Rocca GC. Phase-dependent Topological Interface State and Spatial Adiabatic Passage in a Generalized Su-Schrieffer-Heeger Model. Phys Rev A (2019) 100:012112. doi:10.1103/physreva.100.012112

CrossRef Full Text | Google Scholar

84. Du L, Wu JH, Artoni M, La Rocca GC. Fractional Quantum Transport and Staggered Topological Transition in a Lossy Trimerized Lattice. Phys Rev A (2019) 100:052102. doi:10.1103/physreva.100.052102

CrossRef Full Text | Google Scholar

85. Ahmadi N, Abouie J, Baeriswyl D. Topological and Nontopological Features of Generalized Su-Schrieffer-Heeger Models. Phys Rev B (2020) 101:195117. doi:10.1103/physrevb.101.195117

CrossRef Full Text | Google Scholar

86. Xu XW, Zhao YJ, Wang H, Chen AX, Liu YX. (2018) Generalized Su-Schrieffer-Heeger Model in One Dimensional Optomechanical Arrays. arXiv:1807.07880.

Google Scholar

87. Qi L, Wang G-L, Liu S, Zhang S, Wang H-F. Engineering the Topological State Transfer and Topological Beam Splitter in an Even-Sized Su-Schrieffer-Heeger Chain. Phys Rev A (2020) 102:022404. doi:10.1103/physreva.102.022404

CrossRef Full Text | Google Scholar

88. Cao J, Cui W-X, Yi XX, Wang H-F. Controllable Photon-Phonon Conversion via the Topologically Protected Edge Channel in an Optomechanical Lattice. Phys Rev A (2021) 103:023504. doi:10.1103/physreva.103.023504

CrossRef Full Text | Google Scholar

89. Ni X, Kim S, Alù A. Topological Insulator in Two Synthetic Dimensions Based on an Optomechanical Resonator. Optica (2021) 8:1024. doi:10.1364/optica.430821

CrossRef Full Text | Google Scholar

90. Mathew JP, Pino Jd., Verhagen E. Synthetic Gauge fields for Phonon Transport in a Nano-Optomechanical System. Nat Nanotechnol (2020) 15:198–202. doi:10.1038/s41565-019-0630-8

PubMed Abstract | CrossRef Full Text | Google Scholar

91. Safavi-Naeini AH, Chan J, Hill JT, Gröblacher S, Miao H, Chen Y, et al. Laser Noise in Cavity-Optomechanical Cooling and Thermometry. New J Phys (2013) 15:035007. doi:10.1088/1367-2630/15/3/035007

CrossRef Full Text | Google Scholar

92. Kronwald A, Marquardt F, Clerk AA. Arbitrarily Large Steady-State Bosonic Squeezing via Dissipation. Phys Rev A (2013) 88:063833. doi:10.1103/physreva.88.063833

CrossRef Full Text | Google Scholar

93. Xu XW, Li Y, Chen AX, Liu YX. Nonreciprocal Conversion between Microwave and Optical Photons in Electro-Optomechanical Systems. Phys Rev A (2016) 93:023827. doi:10.1103/physreva.93.023827

CrossRef Full Text | Google Scholar

94. Peterson GA, Lecocq F, Cicak K, Simmonds RW, Aumentado J, Teufel JD. Demonstration of Efficient Nonreciprocity in a Microwave Optomechanical Circuit. Phys Rev X (2017) 7:031001. doi:10.1103/physrevx.7.031001

CrossRef Full Text | Google Scholar

95. Bernier NR, Tóth LD, Koottandavida A, Ioannou MA, Malz D, Nunnenkamp A, et al. Nonreciprocal Reconfigurable Microwave Optomechanical Circuit. Nat Commun (2017) 8:604. doi:10.1038/s41467-017-00447-1

PubMed Abstract | CrossRef Full Text | Google Scholar

96. Barzanjeh S, Wulf M, Peruzzo M, Kalaee M, Dieterle PB, Painter O, et al. Mechanical On-Chip Microwave Circulator. Nat Commun (2017) 8:953. doi:10.1038/s41467-017-01304-x

PubMed Abstract | CrossRef Full Text | Google Scholar