Exciton dynamics in conjugated polymer systems

1 Introduction

The theoretical study of exciton dynamics in conjugated polymer systems is both a fascinating and complicated subject. In part this is because characterizing excitonic states themselves is a challenging task: conjugated polymers exhibit strong electron-electron interactions and electron-nuclear coupling, and are subject to spatial and temporal disorder. Another reason for its fascinating complexity is that exciton dynamics is characterised by multiple (and often overlapping) time scales; it is determined by both intrinsic processes (e.g., coupling to nuclear degrees of freedom and electrostatic interactions) and extrinsic processes (e.g., polymer-solvent interactions); and it is both an intrachain and interchain process. Consequently, to make progress in both characterizing exciton states and correctly describing their dynamics, simplified, but realistic models are needed. Moreover, as even these simplified models describe many quantized degrees of freedom, sophisticated numerical techniques are required to solve them. Luckily, fundamental theoretical progress in developing numerical techniques means that simplified one-dimensional models of conjugated polymers are now solvable to a high degree of accuracy.

In addition to the application of various theoretical techniques to understand exciton dynamics, a wide range of time-resolved spectroscopic techniques have also been deployed. These include fluorescence depolarization [1–4], three-pulse photon-echo [5–8] and coherent electronic two-dimensional spectroscopy [9]. Some of the timescales extracted from these experiments are listed in Table 1; the purpose of this review is to describe their associated physical processes.

TABLE 1

TABLE 1. Some of the dynamical timescales observed in conjugated polymers whose associated physical processes are summarized in Table 2. Reproduced from J. Phys. Chem. Lett. 12, 5344 (2021) with the permission of ACS publishing.

As well as being of intrinsic interest, the experimental and theoretical activities to understand exciton dynamics in conjugated polymer systems are also motivated by the importance of this process in determining the efficiency of polymer electronic devices. In photovoltaic devices, large exciton diffusion lengths are necessary so that excitons can migrate efficiently to regions where charge separation can occur. However, precisely the opposite is required in light emitting devices, since diffusion can lead to nonradiative quenching of the exciton.

Perhaps one of the reasons for the failure to fully exploit polymer electronic devices has been the difficulty in establishing the structure-function relationships which allow the development of rational design strategies. An understanding of the principles of exciton dynamics, relating this to multiscale polymer structures, and interpreting the associated spectroscopic signatures are all key ingredients to developing structure-function relationships. An earlier review explored the connection between structure and spectroscopy [14]. In this review we describe our current understanding of the important dynamical processes in conjugated polymers, beginning with photoexcitation and intrachain relaxation on ultrafast timescales ($\sim 10$ fs) and concluding with sub-ns interchain exciton transfer and diffusion. These key processes are summarized in Table 2.

TABLE 2

TABLE 2. The life and times of an exciton: Some of the key exciton dynamical processes, encompassing over four-orders of magnitude in time that occur in conjugated polymer systems.

The contents of this review are the following. We begin by briefly describing some theoretical techniques for simulating exciton dynamics and we emphasize the failures of simple methods. As already mentioned, excitons themselves are fascinating quasiparticles, so before describing their dynamics, in Section 3 we start by describing their stationary states. We stress the role of low-dimensionality, disorder and electron-phonon coupling, and we discuss the fundamental concept of a chromophore. Next, in Section 4, we describe the sub-ps processes of intrachain exciton decoherence, relaxation and localization, which—starting from an arbitrary photoexcited state - results in an exciton forming a chromophore. We next turn to describe the exciton (and energy) transfer processes occurring on post-ps timescales. First, in Section 5, we describe intrachain motion of excitons caused by dynamical disorder arising from stochastic torsional fluctuations. At low temperatures this causes quasiadiabatic exciton-polaron diffusion, while at higher temperatures it additionally causes transient exciton delocalization via extended exciton states. Second, in Section 6, we describe nonadiabatic interchain exciton transfer, both by FRET and transient delocalization. We conclude and address outstanding questions in Section 7.

This review focusses on exciton dynamics in conjugated polymers. For reviews and books on, excitons in conjugated polymers in general, see refs [15–17]; the spectroscopy of conjugated polymers, see Ref. [14]; exciton dynamics and spectroscopy in molecular systems, see Ref. [18]; and for a complementary review, see Ref. [19].

2 A brief critique of theoretical techniques

A theoretical description of exciton dynamics in conjugated polymers poses considerable challenges, as it requires a rigorous treatment of electronic excited states and their coupling to the nuclear degrees of freedom. Furthermore, conjugated polymers consist of thousands of atoms and tens of thousands of electrons. Thus, as the Hilbert space grows exponentially with the number of degrees of freedom, approximate treatments of excitonic dynamics are therefore inevitable. There are two broad approaches to a theoretical treatment. One approach is to construct ab initio Hamiltonians, with an exact as possible representation of the degrees of freedom, and then to solve these Hamiltonians with various degrees of accuracy. Another approach (albeit less common in theoretical chemistry) is to construct effective Hamiltonians with fewer degrees of freedom, such as the Frenkel-Holstein model described in Section 4. These effective Hamiltonians might be parameterized via a direct mapping from ab initio Hamiltonians (e.g., see Appendix H in Ref. [15], Appendix A in Ref. [20] and various papers by Burghardt and co-workers [21]) or else semiempirically [22]. A significant advantage of effective Hamiltonians over their ab initio counterparts is that they can be solved for larger systems over longer timescales and to a higher level of accuracy.

As the Ehrenfest method is a widely used approximation to study charge and exciton dynamics in conjugated polymers, we briefly explain this method and describe the important ways in which it fails. (For a fuller treatment, see [23, 24].) The Ehrenfest method makes two key approximations. The first approximation is to treat the nuclei classically. This means that nuclear quantum tunneling and zero-point energies are neglected, and that exciton-polarons are not correctly described (see Section 3.3). The second assumption is that the total wavefunction is a product of the electronic and nuclear wavefunctions. This means that there is no entanglement between the electrons and nuclei, and so the nuclei cannot cause decoherence of the electronic degrees of freedom (see Section 4.1). A simple product wavefunction also implies that the nuclei move in a mean potential determined by the electrons. This means that a splitting of the nuclear wave packet when passing through a conical intersection or an avoided crossing does not occur (see Section 4.2), and that there is an incorrect description of energy transfer between the electronic and nuclear degrees of freedom (see Section 5.4). As will be discussed in the course of this review, these failures mean that in general the Ehrenfest method is not a reliable one to treat excitonic dynamics in conjugated polymers.

Various theoretical techniques have been proposed to rectify the failures of the Ehrenfest method; for example, the surface-hopping technique [25, 26], while still keeping the nuclei classical, partially rectifies the failures at conical interactions. More sophisticated approaches, for example the MC-TDHF and TEBD methods, quantize the nuclear degrees of freedom and do not assume a product wavefunction.

For a given electronic potential energy surface (PES), the multiconfigurational-time dependent Hartree-Fock (MC-TDHF) method [27] is an (in principle) exact treatment of nuclear wavepacket propagation, although in practice exponential scaling of the Hilbert space means that a truncation is required. In addition, this method is only as reliable as the representation of the PES.

In the time-evolving block decimation (TEBD) method [28, 29] a quantum state, |Ψ⟩, is represented by a matrix product state (MPS) [30]. Its time evolution is determined via

$|\mathrm{\Psi }\left(t+\delta t\right.)\rangle =\exp \left(-\mathrm{i}\widehat{H}\delta t/\hslash \right)|\mathrm{\Psi }\left(t\right)\rangle ,(1)$

where $\widehat{H}$ is the system Hamiltonian and the action of the evolution operator is performed via a Trotter decomposition. Since the action of the evolution operator expands the Hilbert space, |Ψ⟩ is subsequently compressed via a singular value decomposition (SVD).¹ Importantly, this approach is ‘numerically exact’ as long as the truncation parameter exceeds 2^S, where S is the entanglement entropy, defined by S = −∑_αω_α ln₂ω_α and {ω} are the singular values obtained at the SVD. The TEBD method permits the electronic and nuclear degrees of freedom to be treated as quantum variables on an equal footing. It thus rectifies all of the failures of the Ehrenfest method described above and, unlike the MC-TDHF method, it is not limited by the representation of the PES. It can, however, only be applied to quantum systems described by one-dimensional lattice Hamiltonians [31]. Luckily, as described in Section 4, such model Hamiltonians are readily constructed to describe exciton dynamics in conjugated polymers.

3 Excitons in conjugated polymers

Before discussing the dynamics of excitons, we begin by describing exciton stationary states in static conjugated polymers.

3.1 Two-particle model

An exciton is a Coulombically bound electron-hole pair formed by the linear combination of electron-hole excitations across a band gap (for further details see [15, 17, 32]). In a one-dimensional conjugated polymer an exciton is described by the two-particle wavefunction, Φ_mj (r, R) = ψ_m(r)Ψ_j(R).

Ψ_j(R) is the center-of-mass wavefunction, which will be discussed shortly. Before doing that, we first discuss the relative wavefunction, ψ_m(r), which describes a particle bound to a screened Coulomb potential, where r is the electron-hole separation and m is the principal quantum number. The electron and hole of an exciton in a one-dimensional semiconducting polymer are more strongly bound than in a three-dimensional inorganic semiconductor for two key reasons [15, 17]. First, because of the low dielectric constant and relatively large electronic effective mass in π-conjugated systems the effective Rydberg is typically 50 times larger than for inorganic systems. Second, dimensionality plays a role: in particular, the one-dimensional Schrödinger equation for the relative particle [33, 34] predicts a strongly bound state split-off from the Rydberg series. This state is the m = 1 Frenkel (“1B_u”) exciton, with a binding energy of $\sim 1$ eV and an electron-hole wavefunction confined to a single monomer. The first exciton in the Rydberg series is the m = 2 charge-transfer (“2A_g”) exciton.

With the exception of donor-acceptor copolymers, conjugated polymers are generally non-polar, which means that each p-orbital has an average occupancy of one electron. This implies an approximate electron-hole symmetry. Electron-hole symmetry has a number of consequences for the character and properties of excitons. First, it means that the relative wavefunction exhibits electron-hole parity, i.e., ψ_m(r) = +ψ_m(−r) when m is odd and ψ_m(r) = −ψ_m(−r) when m is even. Second, the transition density, $⟨\mathrm{E}\mathrm{X}|{\widehat{N}}_i|\mathrm{G}\mathrm{S}⟩$, vanishes for odd-parity (i.e., even m) excitons. This means that such excitons are not optically active, and importantly for dynamical processes, their Förster exciton transfer rate (defined in Section 6.1) vanishes.

Since Frenkel excitons are the primary photoexcited states of conjugated polymers, their dynamics is the subject of this review. Their delocalization along the polymer chain of N monomers is described by the Frenkel exciton Hamiltonian,

${\widehat{H}}_F=\sum _{n=1}^N{ϵ}_n{\widehat{N}}_n+\sum _{n=1}^{N-1}{J}_n{\widehat{T}}_{n,n+1},(2)$

where n = (R/d) labels a monomer and d is the intermonomer separation. The energy to excite a Frenkel exciton on monomer n is ϵ_n, where ${\widehat{N}}_n=|n\rangle \langle n|$ is the Frenkel exciton number operator.

In principle, excitons delocalize along the chain via two mechanisms [17, 35]. First, for even-parity (odd m) singlet excitons there is a Coulomb-induced (or through space) mechanism. This is the familiar mechanism of Förster resonant energy transfer. The exciton transfer integral for this process is

$J_{DA}=\sum _{\begin{array}{c}i\in D\\ j\in A\end{array}}{V}_{ij}\left[{}_D\langle \mathrm{G}\mathrm{S}|{\widehat{N}}_i|\mathrm{E}\mathrm{X}\rangle _D\right]\left[{}_A\langle \mathrm{E}\mathrm{X}|{\widehat{N}}_j|\mathrm{G}\mathrm{S}\rangle _A\right].(3)$

The sum is over sites i in the donor monomer and j in the acceptor monomer, and V_ij is the Coulomb interaction between these sites. In the point-dipole approximation Eq. 3 becomes

$J_{DA}=\frac{{\kappa }_{mn}{\mu }_0^2}{4\pi {\epsilon }_r{\epsilon }_0{R}_{mn}^3},(4)$

where μ₀ is the transition dipole moment of a single monomer and R_mn is the distance between the monomers m and n. κ_mn is the orientational factor,

${\kappa }_{mn}={\widehat{\mathit{r}}}_{\mathit{m}}\cdot {\widehat{\mathit{r}}}_{\mathit{n}}-3\left({\widehat{\mathit{R}}}_{\mathit{m}\mathit{n}}\cdot {\widehat{\mathit{r}}}_{\mathit{m}}\right)\left({\widehat{\mathit{R}}}_{\mathit{m}\mathit{n}}\cdot {\widehat{\mathit{r}}}_{\mathit{n}}\right),(5)$

where ${\widehat{\mathit{r}}}_{\mathit{m}}$ is a unit vector parallel to the dipole on monomer m and ${\widehat{\mathit{R}}}_{\mathit{m}\mathit{n}}$ is a unit vector parallel to the vector joining monomers m and n. For colinear monomers, the nearest neighbor through space transfer integral is

$J_{DA}=-\frac{2{\mu }_0^2}{4\pi {\epsilon }_r{\epsilon }_0{d}^3}.(6)$

Second, for all excitons there is a superexchange (or through bond) mechanism, caused by a virtual fluctuation from a Frenkel exciton on a single monomer to a charge-transfer exciton spanning two monomers back to a Frenkel exciton on a neighboring monomer. The energy scale for this process, obtained from second order perturbation theory [15], is

$J_{\mathit{SE}}\left(\theta \right)\propto -\frac{\tilde{t}{\left(\theta \right)}^2}{\mathrm{\Delta }E},(7)$

where $\tilde{t}\left(\theta \right)$ (defined in Eq. 12) is proportional to the overlap of p-orbitals neighboring a bridging bond, i.e., $\tilde{t}\left(\theta \right)$ ∝ cos θ and θ is the torsional (or dihedral) angle between neighboring monomers. ΔE is the difference in energy between a charge-transfer and Frenkel exciton.

The total exciton transfer integral is thus

$J_n=J_{\text{DA}}+J_{\text{SE}}^0{\cos }^2{\theta }_n.(8)$

The bond-order operator,

${\widehat{T}}_{n,n+1}=\left(|n\rangle \langle n+1|+|n+1\rangle \langle n|\right),(9)$

represents the hopping of the Frenkel exciton between monomers n and n + 1. Evidently, J_SE vanishes when θ = 0, but J_DA will not. Therefore, even if J_SE vanishes because of negligible p-orbital overlap between neighboring monomers, singlet even-parity excitons can still retain phase coherence over the “conjugation break” [37]. This observation has important implications for the definition of chromophores, as discussed in Section 3.2.

Eq. 2 represents a “coarse-graining” of the exciton degrees of freedom. The key assumption is that we can replace the atomist detail of each monomer (or moiety) and replace it by a “coarse-grained” site, as illustrated in Figure 1. All that remains is to describe how the Frenkel exciton delocalises along the chain, which is controlled by the two sets of parameters, {ϵ} and {J}. Since J is negative, a conjugated polymer is equivalent to a molecular J-aggregate.

FIGURE 1

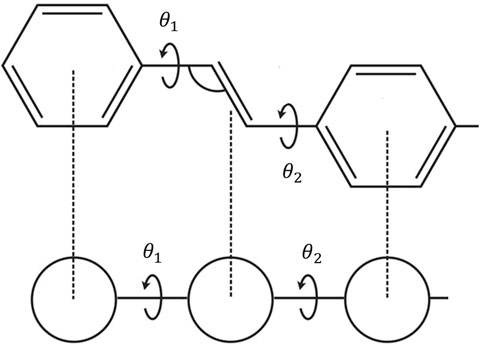
FIGURE 1. The mapping of a polymer chain conformation to a coarse-grained linear site model. Each site corresponds to a moiety along the polymer chain, with the connection between sites characterised by the torsional (or dihedral) angle, θ.

The eigenfunctions of ${\widehat{H}}_F$ are the center-of-mass wavefunctions, Ψ_j(n), where j is the associated quantum number. For a linear, uniform polymer (i.e., ϵ_n ≡ ϵ₀ and J_n ≡ J₀)

${\mathrm{\Psi }}_j\left(n\right)={\left(\frac{2}{N+1}\right)}^{1/2}\sum _{n=1}^N\sin \left(\frac{\pi jn}{N+1}\right),(10)$

forming a band of states with energy

$E_j={ϵ}_0+2J_0\cos \left(\frac{\pi j}{N+1}\right).(11)$

The family of excitons with different j values corresponds to the Frenkel exciton band with different center-of-mass momenta. In emissive polymers the j = 1 Frenkel exciton is generally labeled the 1¹B_u state.

3.2 Role of static disorder: Local exciton ground states and quasiextended exciton states

Polymers are rarely free from some kind of disorder and thus the form of Eq. 10 is not valid for the center-of-mass wavefunction in realistic systems. Polymers in solution are necessarily conformationally disordered as a consequence of thermal fluctuations (as described in Section 5). Polymers in the condensed phase usually exhibit glassy, disordered conformations as consequence of being quenched from solution. Conformational disorder implies that the dihedral angles, {θ} are disordered, which by virtue of Eq. 8 implies that the exciton transfer integrals are also disordered.

As well as conformational disorder, polymers are also subject to chemical and environmental disorder (arising, for example, from density fluctuations). This type of disorder affects the energy to excite a Frenkel exciton on a monomer (or coarse-grained site). As first realized by Anderson [38], disorder localizes a quantum particle (in our case, the exciton center-of-mass particle), and determines their energetic and spatial distributions. The origin of this localization is the wave-like nature of a quantum particle and the constructive and destructive interference it experiences as it scatters off a random potential. Malyshev and Malyshev [39, 40] further observed that in one-dimensional systems there are a class of states in the low energy tail of the density of states that are superlocalized, named local exciton ground states (LEGSs [39–41]). LEGSs are essentially nodeless, non-overlapping wavefunctions that together spatially span the entire chain. They are local ground states, because for the individual parts of the chain that they span there are no lower energy states. A consequence of the essentially nodeless quality of LEGSs is that the square of their transition dipole moment scales as their size [41]. Thus, LEGSs define chromophores (or spectroscopic segments), namely the irreducible parts of a polymer chain that absorb and emit light. Figure 2A illustrates the three LEGSs for a particular conformation of PPV with 50 monomers.

FIGURE 2

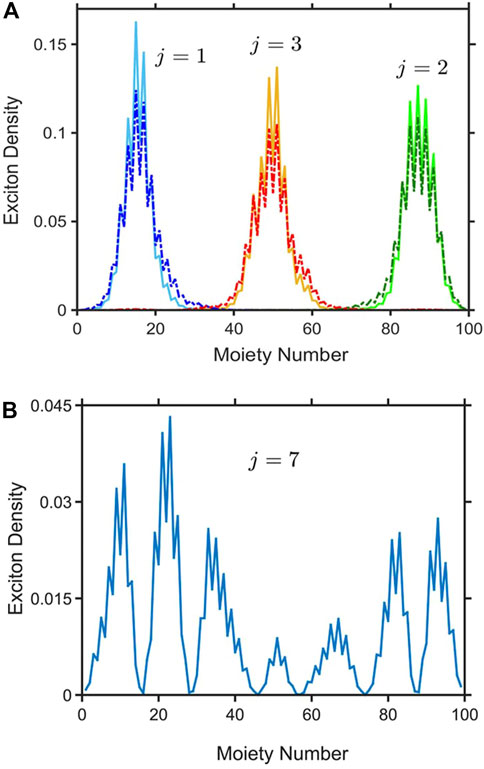
FIGURE 2. (A) The density of three local exciton ground states (LEGSs, dotted curves) and the three vibrationally relaxed states (VRSs, solid curves) for one particular static conformation of a PPV polymer chain made up of 50 monomers. The exciton center-of-mass quantum number, j, for each state is also shown. (B) The exciton density of a quasiextended exciton state (QEES), with quantum number j = 7. Reproduced from J. Chem. Phys. 148, 034901 (2018) with the permission of AIP publishing.

Some researchers claim that “conjugation-breaks” (or more correctly, minimum thresholds in the p_z-orbital overlap) define the boundaries of chromophores [42]. In contrast, we suggest that it is the disorder that determines the average chromophore size, but “conjugation-breaks” can “pin” the chromophore boundaries. Thus, if the average distance between conjugation breaks is smaller than the chromophore size, chromophores will span conjugation breaks but they may also be separated by them. Conversely, if average distance between conjugation breaks is larger than the chromophore size the chromophore boundaries are largely unaffected by the breaks. The former scenario occurs in polymers with shallow torsional potentials, e.g., polythiophene [37].

Higher lying states are also localized, but are nodeful and generally spatially overlap a number of low-lying LEGSs. These states are named quasiextended exciton states (QEESs) and an example is illustrated in Figure 2B.

When the disorder is Gaussian distributed with a standard deviation σ, single parameter scaling theory [43] provides some exact results about the spatial and energetic distribution of the exciton center-of-mass states:

1) The localization length $L_{\mathit{loc}}\sim {(|J_0|/\sigma )}^{2/3}$ at the band edge and as $L_{\mathit{loc}}\sim {(|J_0|/\sigma )}^{4/3}$ at the band center.

2) As a consequence of exchange narrowing [44, 45], the width of the density of states occupied by LEGSs scales as $\sigma /\sqrt{L_{\mathit{loc}}}\sim {\sigma }^{4/3}$. Similarly, the optical absorption is inhomogeneously narrowed with a line width ∼ σ^4/3.

3) The fraction of LEGSs scales as 1/L_loc ∼ σ^2/3.

These points are illustrated in Figure 3, which shows the Frenkel exciton density of states and optical absorption for a particular value of disorder. Although LEGSs are a small fraction of the total number of states, they dominate the optical absorption.

FIGURE 3

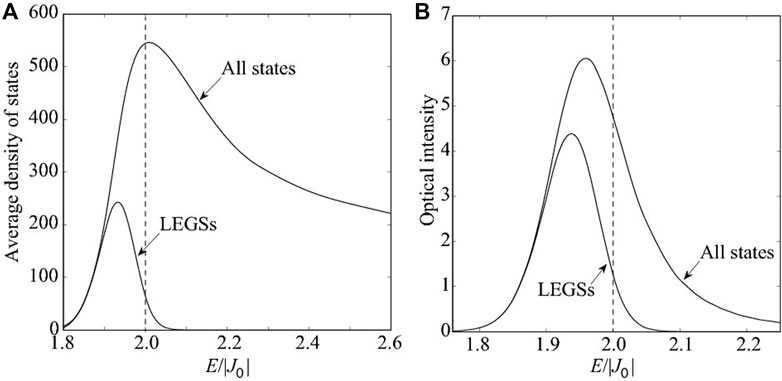
FIGURE 3. (A) The energy density of states and (B) the optical absorption (neglecting the vibronic progression) of the manifold of Frenkel excitons (where |σ_J/J₀| = 0.1). The width of the LEGSs density of states ∼|J₀‖σ_J/J₀|^4/3. Similarly, the width of the optical absorption from both the LEGSs and all states ∼|J₀‖σ_J/J₀|^4/3. The band edge for an ordered chain is at 2|J₀| (indicated by the dashed lines), so LEGSs generally lie in the Lifshitz (or Urbach) tail of the density of states, i.e., E < 2|J₀|.

This section has described LEGSs (or chromophores) as static objects defined by static disorder. However, as discussed in Section 5, dynamically torsional fluctuations also render the conformational disorder dynamic causing the LEGSs to evolve adiabatically. As a consequence, the chromophores “crawl” along the polymer chain.

3.3 Role of electron-nuclear coupling: Exciton-polarons

As well as disorder, another important process in determining exciton dynamics and spectroscopy is the coupling of an exciton to nuclear degrees of freedom; in a conjugated polymer these are fast C-C bond vibrations and slow monomer rotations. In this section we briefly review the origin of this coupling and then discuss exciton-polarons.

3.3.1 Origin of electron-nuclear coupling

When a nucleus moves, either by a linear displacement or by a rotation about a fixed point, there is a change in the electronic overlap between neighboring atomic orbitals. Assuming that neighboring p-orbitals lie in the same plane normal to the bond with a relative twist angle of θ, the resonance integral between a pair of orbitals separated by r is [46].

$\tilde{t}\left(r,\theta \right)=t\left(r\right)\cos \theta =\beta \exp \left(-\alpha r\right)\cos \theta ,(12)$

where t(r) = β exp (−αr) < 0. The kinetic energy contribution to the Hamiltonian is

${\widehat{H}}_{\text{ke}}=t\left(r\right)\cos \theta \times \widehat{T},(13)$

where the bond-order operator, $\widehat{T}$, is defined in Eq. 9. Treating r and θ as dynamical variables, suppose that the σ-electrons of a conjugated molecule and steric hinderances provide equilibrium values of r = r₀ and θ = θ₀, with corresponding elastic potentials of

$V_{\text{vib}}=\frac{1}{2}{K}_{\text{vib}}^{\sigma }{\left(r-r_0\right)}^2(14)$

and

$V_{\text{rot}}=\frac{1}{2}{K}_{\text{rot}}^{\sigma }{\left(\theta -{\theta }_0\right)}^2.(15)$

The coupling of the π-electrons to the nuclei changes these equilibrium values and the elastic constants.

To see this, we use the Hellmann-Feynman theorem to determine the force on the bond. The linear displacement force is

$\begin{array}{ll}\hfill f& =-\frac{\partial E}{\partial r}=-\langle \frac{\partial {\widehat{H}}_{\text{ke}}}{\partial r}\rangle \hfill \\ \hfill & =\alpha t\left(r\right)\cos \theta \langle \widehat{T}\rangle -K_{\text{vib}}^{\sigma }\left(r-r_0\right).\hfill \end{array}(16)$

Thus, to first order in the change of bond length, δr = (r − r₀), the equilibrium distortion is

$\delta r=\alpha t\left(r_0\right)\cos \theta ⟨\widehat{T}⟩/K_{\text{vib}}^{\sigma },(17)$

which is negative because it is favorable to shorten the bond to increase the electronic overlap.

Similarly, the torque around the bond is

$\begin{array}{ll}\hfill \mathrm{\Gamma }& =-\frac{\partial E}{\partial \theta }=-\langle \frac{\partial {\widehat{H}}_{ke}}{\partial \theta }\rangle \hfill \\ \hfill & =t\left(r\right)\sin \theta \langle \widehat{T}\rangle -K_{\text{rot}}^{\sigma }\left(\theta -{\theta }_0\right)\hfill \end{array}(18)$

and the equilibrium change of bond angle, δθ = (θ − θ₀), is

$\delta \theta =t\left(r\right)\sin {\theta }_0⟨\widehat{T}⟩/K_{\text{rot}}^{\sigma },(19)$

which is also negative, again because it is favorable to increase the electronic overlap. Thus, the π-electron couplings act to planarize the chain. The electron-nuclear coupling also changes the elastic constants. Assuming a harmonic potential, the new rotational spring constant is

$\begin{array}{ll}\hfill K_{\text{rot}}^{\pi }& =\frac{{\partial }^{2}E}{\partial {\theta }^2}\hfill \\ \hfill & =-t\left(r_0\right)\cos {\theta }_0⟨\widehat{T}⟩+K_{\text{rot}}^{\sigma }\hfill \end{array}(20)$

and thus $K_{\text{rot}}^{\pi }>K_{\text{rot}}^{\sigma }$ (because t (r₀) < 0).

Interestingly, as shown in Figure 4, because ${⟨\widehat{T}⟩}_{EX}>{⟨\widehat{T}⟩}_{GS}$ for the bridging bond in phenyl-based systems, the torsional angle is smaller and the potential is stiffer in the excited state (as a result of the benzenoid to quinoid distortion) [47].

FIGURE 4

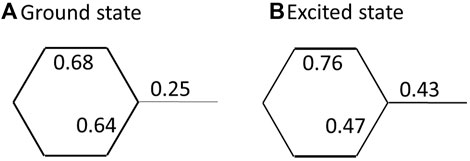
FIGURE 4. The π-bond order expectation values, $⟨\widehat{T}⟩$, for (A) the ground state and (B) the excited state, showing the benzenoid-quinoid transition. As Eq. 19 and Eq. 20 indicate, the larger bond order of the bridging bond in the excited state implies a smaller dihedral angle and a stiffer torsional potential than the ground state.

3.3.2 Exciton-polarons

An exciton that couples to a set of harmonic oscillators, e.g., bond vibrations or torsional oscillations, becomes “self-trapped”. Self-trapping means that the coupling between the exciton and oscillators causes a local displacement of the oscillator that is proportional to the local exciton density [48–51] (as illustrated in the next section). Alternatively, it is said that the exciton is dressed by a cloud of oscillators. Such a quasiparticle is named an exciton-polaron. As there is no barrier to self-trapping in one-dimensional systems [52], there is always an associated relaxation energy.

If the exciton and oscillators are all treated quantum mechanically, then in a translationally invariant system the exciton-polaron forms a Bloch state and is not localized. However, if the oscillators are treated classically, the non-linear feedback induced by the exciton-oscillator coupling self-localizes the exciton-polaron and “spontaneously” breaks the translational symmetry. This is a self-localized (or auto-localized) “Landau polaron” [53, 54]. Notice that self-trapping is a necessary but not sufficient condition for self-localization. Self-localization always occurs in the limit of vanishing oscillator frequency (i.e., the adiabatic or classical limit) and vanishing disorder [55].

Whether or not an exciton-polaron is self-localized in practice, however, depends on the strength of the disorder and the vibrational frequency of the oscillators. Qualitatively, an exciton coupling to fast oscillators (e.g., C-C bond vibrations) forms an exciton-polaron with an effective mass only slightly larger than a bare exciton [55]. For realistic values of disorder, such an exciton-polaron is not self-localized. This is illustrated in Figure 2A, which shows the three lowest solutions of the Frenkel-Holstein model (described in Section 4.1), known as vibrationally relaxed states (VRSs). As we see, the density of the VRSs mirrors that of the Anderson-localized LEGSs. Conversely, an exciton coupling to slow oscillators (e.g., bridging-bond rotations) forms an exciton-polaron with a large effective mass. Such an exction-polaron is self-localized (as described in Section 4.3. and shown in Figure 9).

4 Intrachain decoherence, relaxation and localization

Having qualitatively described the stationary states of excitons in conjugated polymers, we now turn to a discussion of exciton dynamics.

4.1 Role of fast C-C bond vibrations

After photoexcitation or charge combination after injection, the fastest process is the coupling of the exciton to C-C bond stretches. We now describe the resulting exciton-polaron formation and the loss of exciton-site coherence.

As we saw in Section 3.3, bond distortions couple to electrons. Using Eq. 13, it can be shown [22] that the coupling of local normal modes (e.g., vinyl-unit bond stretches or phenyl-ring symmetric breathing modes) to a Frenkel exciton is conveniently described by the Frenkel-Holstein model [22, 50],

${\widehat{H}}_{FH}={\widehat{H}}_F-A\hslash {\omega }_{\text{vib}}\sum _{n=1}^N{\tilde{Q}}_n{\widehat{N}}_n+\frac{\hslash {\omega }_{\text{vib}}}{2}\sum _{n=1}^N\left({\tilde{Q}}_n^2+{\tilde{P}}_n^2\right).(21)$

${\widehat{H}}_F$ is the Frenkel Hamiltonian, defined in Eq. 2, while $\tilde{Q}={(K_{\text{vib}}/\hslash {\omega }_{\text{vib}})}^{1/2}Q$ and $\tilde{P}={({\omega }_{\text{vib}}/\hslash K_{\text{vib}})}^{1/2}P$ are the dimensionless displacement and momentum of the normal mode. The second term on the right-hand-side of Eq. 21 indicates that the normal mode couples linearly to the local exciton density.² A is the dimensionless exciton-phonon coupling constant, which introduces the important polaronic parameter, namely the local Huang-Rhys factor

$S=\frac{A^2}{2}.(22)$

The final term is the sum of the elastic and kinetic energies of the harmonic oscillator, where ω_vib and K_vib are the angular frequency and force constant of the oscillator, respectively. The Frenkel-Holstein model is another example of a coarse-grained Hamiltonian which, in addition to coarse-graining the exciton motion, assumes that the atomistic motion of the carbon nuclei can be replaced by appropriate local normal modes.

Exciton-nuclear dynamics is often modeled via the Ehrenfest approximation, which treats the nuclear coordinates as classical variables moving in a mean field determined by the exciton. However, as described in Section 2, the Ehrenfest approximation fails to correctly describe ultra-fast dynamical processes. A correct description of the coupled exciton-nuclear dynamics therefore requires a full quantum mechanical treatment of the system. This is achieved by introducing the harmonic oscillator raising and lowering operators, ${\widehat{b}}_n^{†}$ and ${\widehat{b}}_n$, for the normal modes i.e., ${\tilde{Q}}_n\to {\widehat{\tilde{Q}}}_n=({\widehat{b}}_n^{†}+{\widehat{b}}_n)/\sqrt{2}$ and ${\tilde{P}}_n\to {\widehat{\tilde{P}}}_n=i({\widehat{b}}_n^{†}-{\widehat{b}}_n)\sqrt{2}$. The time evolution of the quantum system can then conveniently be simulated via the TEBD method, as briefly described in Section 2.

Since the photoexcited system has a different electronic bond order than the ground state, an instantaneous force is established on the nuclei. As described in Section 3.3, this force creates an exciton-polaron, whose spatial size is quantified by the exciton-phonon correlation function [57].

$C_n^{\text{ex}-\text{ph}}\left(t\right)\propto \sum _m⟨{\widehat{N}}_m{\widehat{\tilde{Q}}}_{m+n}⟩.(23)$

$C_n^{\text{ex}-\text{ph}}$ correlates the local phonon displacement, Q, with the instantaneous exciton density, N, n monomers away. $C_n^{\text{ex}-\text{ph}}(t)$, illustrated in Figure 5, shows that the exciton-polaron is established within 10 fs (i.e., within half the period of a C-C bond vibration) of photoexcitation. The temporal oscillations, determined by the C-C bond vibrations, are damped as energy is dissipated into the vibrational degrees of freedom, which acts as a heat bath for the exciton. The exciton-phonon spatial correlations decay exponentially, extending over ca. 10 monomers. This short range correlation occurs because the C-C bonds can respond relatively quickly to the exciton’s motion.³

FIGURE 5

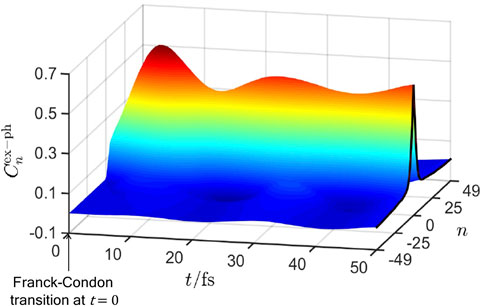
FIGURE 5. The time-dependence of the exciton-phonon correlation function, Eq. 23, after photoexcitation at time t = 0. It fits the form $C_n^{\text{ex}-\text{ph}}=C_0\exp (-n/\xi )$ as t → ∞, where ξ ∼ 10. n is a monomer index. The vibrational period is 20 fs.

The ultrafast establishment of quantum mechanically correlated exciton-phonon motion causes an ultrafast decay of off-diagonal-long-range-order (ODLRO) in the exciton site-basis density matrix. This is quantified via [58, 59].

$C_n^{\text{coh}}\left(t\right)=\sum _m\left|{\rho }_{m,m+n}\right|,(24)$

where ρ_m,m′ is the exciton reduced density matrix obtained by tracing over the vibrational degrees of freedom. $C_n^{\text{coh}}(t)$ is displayed in Figure 6 [60], showing that ODLRO is lost within 10 fs. The loss of ODLRO is further quantified by the coherence number, defined by

$N^{\text{coh}}=\sum _n{C}_n^{\text{coh}},(25)$

and shown in the inset of Figure 6. Again, N^coh decays to ca. 10 monomers in ca. 10 fs, reflecting the localization of exciton coherence resulting from the short range exciton-phonon correlations. As discussed later, the loss of ODLRO leads to ultrafast fluorescence depolarization [31].

FIGURE 6

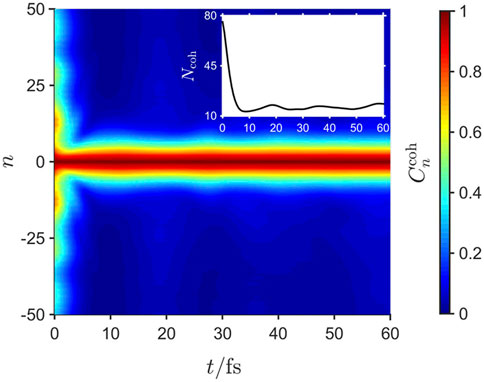
FIGURE 6. The time dependence of the exciton coherence correlation function, $C_n^{\text{coh}}$, Eq. 24. The time dependence of the associated coherence number, N^coh (Eq. 25), is shown in the inset. N^coh decays within 10 fs, i.e., within half a vibrational period. Reproduced from J. Chem. Phys. 148, 034901 (2018) with the permission of AIP publishing.

We emphasise that the prediction of an electron-polaron with short range correlations is a consequence of treating the phonons quantum mechanically, while the decay of exciton-site coherences is a consequence of the exciton and phonons being quantum mechanically entangled. Neither of these predictions are possible within the Ehrenfest approximation.

4.2 Role of system-environment interactions

For an exciton to dissipate energy it must first couple to fast internal degrees of freedom (as described in the last section) and then these degrees of freedom must couple to the environment to expell heat. For a low-energy exciton (i.e., a LEGS) this process will cause adiabatic relaxation on a single potential energy surface, forming a VRS [61–64]. As shown in Figure 3A, however, for a kinetically hot exciton (i.e., a QEES) this relaxation is through a dense manifold of states and is necessarily a nonadiabatic interconversion between different potential energy surfaces. As already stated in Section 2, the Ehrenfest approximation fails to correctly describe this process .⁴

Dissipation of energy from an open quantum system arising from system-environment coupling is commonly described by a Lindblad master equation [65],

$\frac{\partial \widehat{\rho }}{\partial t}=-\frac{i}{\hslash }\left[\widehat{H},\widehat{\rho }\right]-\frac{\gamma }{2}\sum _n\left({\widehat{L}}_n^{†}{\widehat{L}}_n\widehat{\rho }+\widehat{\rho }{\widehat{L}}_n^{†}{\widehat{L}}_n-2{\widehat{L}}_n\widehat{\rho }{\widehat{L}}_n^{†}\right),(26)$

where ${\widehat{L}}_n^{†}$ and ${\widehat{L}}_n$ are the Linblad operators, and $\widehat{\rho }$ is the system density operator. In practice, a direct solution of the Lindblad master equation is usually prohibitively expensive, as the size of Liouville space scales as the square of the size of the associated Hilbert space. Instead, Hilbert space scaling can be maintained by performing ensemble averages over quantum trajectories (evaluated via the TEBD method), where the action of the Linblad dissipator is modeled by quantum jumps [66].

In this section we assume that the C-C bond vibrations couple directly with the environment [31, 67], in which case the Linblad operators are the associated raising and lowering operators (i.e., ${\widehat{L}}_n\equiv {\widehat{b}}_n$, introduced in the last section). In addition,

$\widehat{H}={\widehat{H}}_{\text{FH}}+\frac{\gamma \hslash }{4}\sum _n\left({\widehat{\tilde{Q}}}_n{\widehat{\tilde{P}}}_n+{\widehat{\tilde{P}}}_n{\widehat{\tilde{Q}}}_n\right),(27)$

where the last term in Eq. 27 is added to ensure that the phonon oscillation satisfies [68] $\omega \to {({\omega }^2-{\gamma }^2/4)}^{1/2}$. (In Section 5 we discuss coupling of the torsional modes with the environment [69].)

The ultrafast localization of exciton ODLRO (or exciton-site decoherence) described in Section 4.1 occurs via the coupling of the exciton to internal degrees of freedom, namely the C-C bond vibrations. We showed in Section 3.3 (see Figure 2A) that this coupling does not cause exciton density localization. However, dissipation of energy to the environment causes an exciton in a QEES to relax onto a LEGS (i.e., onto a chromophore) and thus the exciton density becomes localized.

The spatial extent of the exciton density, averaged over an ensemble of quantum trajectories, is quantified by the correlation function [70], approximated by

$C_n^{\text{loc}}=\sum _m\left|\mathrm{\Psi }\left(m\right){\mathrm{\Psi }}^{\ast }\left(m+n\right)\right|.(28)$

Figure 7 shows the time dependence of $C_n^{\text{loc}}$ with an external dissipation time T = γ⁻¹ = 100 fs. The time scale for localization is seen from the time dependence of the exciton localization length [71],

$N_{\text{loc}}=\sum _n\left|n\right|C_n^{\text{loc}}/\sum _n{C}_n^{\text{loc}},(29)$

which corresponds to the average distance between monomers for which the exciton wavefunction overlap remains non-zero, and is given in the lower inset of Figure 7. Evidently, the coupling to the environment - and specifically, the damping rate - control the timescale for energy relaxation and exciton density localization onto chromophores. In contrast, the upper inset to Figure 7 shows an absence of localization without external dissipation, indicating that exciton density localization is an extrinsic process.

FIGURE 7

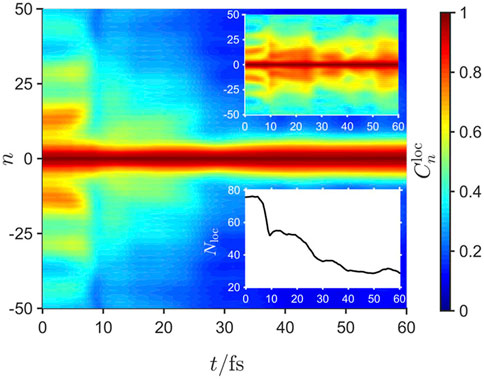
FIGURE 7. The time dependence of the exciton localization correlation function, $C_n^{\text{loc}}$ (Eq. 28), for an initial high-energy QEES. The main figure corresponds to the time evolution with the dissipation time T = γ⁻¹ = 100 fs. The time dependence of the exciton density localization number, N^loc (Eq. 29), is given in the lower inset. The upper inset corresponds to the time evolution without external dissipation showing that in this case exciton denisty localization does not occur. Reproduced from J. Chem. Phys. 148, 034901 (2018) with the permission of AIP publishing.

Figure 7 is obtained by averaging over an ensemble of trajectories. To understand the physical process of localization onto a chromophore, Figure 8 illustrates the exciton density of a single quantum trajectory for a photoexcited QEES (shown in Figure 2B). At a time ca. 20 fs a ‘quantum jump’ caused by the stochastic application of a Lindblad jump operator causes the exciton to localize onto the j = 2 LEGS, shown in Figure 2A, i.e., the high-energy extended state has randomly localized onto a chromophore because of a ‘measurement’ by the environment.

FIGURE 8

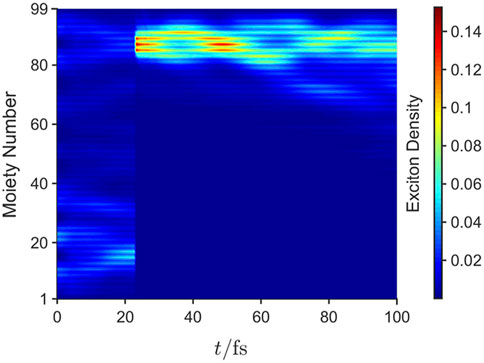
FIGURE 8. The time dependence of the exciton density for a single trajectory of the quantum jump trajectory method. The discontinuity in the density at ca. 20 fs is a ‘quantum jump’ caused by the stochastic application of a Lindblad jump operator. The dynamics were performed for an initial high energy QEES given in Figure 2B, showing localization onto the LEGSs (i.e., a chromophore) labeled j = 2 in Figure 2A. Reproduced from J. Chem. Phys. 148, 034901 (2018) with the permission of AIP publishing.

4.3 Role of slow bond rotations

By dissipating energy into the environment on sub-ps timescales, hot excitons relax into localized LEGSs, i.e., onto chromophores. The final intrachain relaxation and localization process now takes place, namely exciton-polaron formation via coupling to the torsional degrees of freedom. For this relaxation to occur bond rotations must be allowed, which means that this process is highly dependent on the precise chemical structure of the polymer and its environment.

Assuming that bond rotations are not sterically hindered, their coupling to the excitons is conveniently modeled (via Eq. 7 and 12 by supplementing the Frenkel-Holstein model (i.e., Eq. 21) by [73]

${\widehat{H}}_{\text{rot}}=-\sum _{n=1}^{N-1}B\left({\theta }_n^0\right)\times \left({\varphi }_{n+1}-{\varphi }_n\right){\widehat{T}}_{n,n+1}+\frac{1}{2}\sum _{n=1}^N\left(K_{\text{rot}}{\varphi }_n^2+L_n^2/I\right).(30)$

Here, ϕ is the angular displacement of a monomer from its groundstate equilibrium value and L is the associated angular momentum of a monomer around its bridging bonds.

The first term on the right-hand-side of Eq. 30 indicates that the change in the dihedral angle, Δθ_n = (ϕ_n+1 − ϕ_n), couples linearly to the bond-order operator, ${\widehat{T}}_{n,n+1}$, where

$B\left({\theta }_n^0\right)=J_{\mathit{SE}}\sin 2{\theta }_n^0(31)$

is the exciton-roton coupling constant and ${\theta }_n^0$ is the groundstate dihedral angle for the nth bridging bond. The final term is the sum of the elastic and kinetic energies of the harmonic oscillator.

The natural angular frequency of oscillation is ${\omega }_{\text{rot}}={(K_{\text{rot}}/I)}^{1/2}$, where K_rot is the elastic constant of the rotational oscillator and I is the moment of inertia, respectively. As discussed in Section 3.3, K_rot is larger for the bridging bond in the excited state than the groundstate, because of the increase in bond order. Also notice that both the moment of inertia (and thus ω_rot) of a rotating monomer and its viscous damping from a solvent are strongly dependent on the side groups attached to it. As discussed in the next section, this observation has important implications for whether the motion is under or over damped and on its characterstic timescales.

Unlike C-C bond vibrations, being over 10 times slower torsional oscillations can be treated classically [73]. Furthermore, since we are now concerned with adiabatic relaxation on a single potential energy surface, we may use the Ehrenfest approximation. Thus, using Eq. 30, the torque on each ring is

$\begin{array}{ll}\hfill {\mathrm{\Gamma }}_n& =-\frac{\partial ⟨{\widehat{H}}_{\mathit{rot}}⟩}{\partial {\varphi }_n}\hfill \\ \hfill & =-K_{\text{rot}}{\varphi }_n+{\lambda }_n\hfill \end{array}(32)$

where we define

${\lambda }_n=B\left({\theta }_{n-1}^0\right)\langle {\widehat{T}}_{n-1,n}\rangle -B\left({\theta }_n^0\right)\langle {\widehat{T}}_{n,n+1}\rangle .(33)$

Setting Γ_n = 0 gives the equilibrium angular displacements in the excited state as ${\varphi }_n^{\text{eq}}={\lambda }_n/K_{\text{rot}}$ ϕ_n is subject to the Ehrenfest equations of motion,

$I\frac{d{\varphi }_n}{dt}=L_n,(34)$

and

$\frac{d{L}_n}{dt}={\mathrm{\Gamma }}_n-\gamma L_n,(35)$

where the final term represents the damping of the rotational motion by the solvent.

4.3.1 A single torsional oscillator

Before considering a chain of torsional oscillators, it is instructive to review the dynamics of a single, damped oscillator subject to both restoring and displacement forces. The equation of motion for the angular displacement is

$\frac{d^2\varphi \left(t\right)}{d{t}^2}=-{\omega }_{\text{rot}}^2\left(\varphi \left(t\right)-{\varphi }_{\text{eq}}\right)-\gamma \frac{d\varphi \left(t\right)}{dt,}(36)$

where ϕ_eq = λ/K_rot is proportional to the displacement force.

In the underdamped regime [74], defined by γ < 2ω_rot,

$\varphi \left(t\right)={\varphi }_{\text{eq}}\left(1-\cos \left(\omega t\right)\exp \left(-\gamma t/2\right)\right),(37)$

where $\omega ={({\omega }_{\text{rot}}^2-{\gamma }^2/4)}^{1/2}$. In this regime, the torsional angle undergoes damped oscillations with a period T = 2π/ω and a decay time τ = 2/γ.

Conversely, in the overdamped regime [74], defined by γ > 2ω_rot,

$\varphi \left(t\right)={\varphi }_{\text{eq}}\left(1-\frac{1}{4\beta }\left({\gamma }_1\exp \left(-{\gamma }_{2}t/2\right)-{\gamma }_2\exp \left(-{\gamma }_{1}t/2\right)\right)\right),(38)$

where γ₁ = γ + 2β, γ₂ = γ − 2β and $\beta ={({\gamma }^2/4-{\omega }_{\text{rot}}^2)}^{1/2}$. Now, the torsional angle undergoes damped biexponential decay with the decay times τ₁ = 2/γ₁ and τ₂ = 2/γ₂. In the limit of strong damping, i.e., γ ≫ 2ω_rot, there is a fast relaxation time τ₁ = 1/γ = τ/2 and a slow relaxation time ${\tau }_2=\gamma /{\omega }_{\text{rot}}^2\gg \tau$. In this limit, as the slow relaxation dominates at long times, the torsional angle approaches equilibrium with an effective mono-exponential decay.

For a polymer without alkyl side groups, e.g., PPP and PPV, ω_rot ∼ γ ∼ 10¹³ s⁻¹ and are thus in the underdamped regime with sub-ps relaxation. However, polymers with side groups, e.g., P3HT, MEH-PPV and PFO, have a rotational frequency up to ten times smaller and a larger damping rate, and are thus in the overdamped regime [7].

4.3.2 A chain of torsional oscillators

An exciton delocalized along a polymer chain couples to multiple rotational oscillators resulting in collective oscillator dynamics. Eq. 31 and Eq. 33 indicate that torsional relaxation only occurs if the monomers are in a staggered arrangement in their groundstate, i.e., ${\theta }_n^0={(-1)}^n{\theta }^0$. In this case the torque acts to planarize the chain. Furthermore, since the torsional motion is slow, the self-trapped exciton-polaron thus formed is ‘heavy’ and in the under-damped regime becomes self-localized on a timescale of a single torsional period, i.e., 200–600 fs. In this limit the relaxed staggered bond angle displacement mirrors the exciton density. Thus, the exciton is localized precisely as for a ‘classical’ Landau polaron and is spread over $\sim 10$ monomers [73]. The time-evolution of the staggered angular displacement, ⟨ϕ_n⟩× (−1)ⁿ, is shown in Figure 9 illustrating that these displacements reach their equilibrated values after two torsional periods (i.e., t ≳ 400 fs). The inset also displays the time-evolution of the exciton density, ⟨N_n⟩, showing exciton density localization after a single torsional period ($\sim 200$ fs).

FIGURE 9

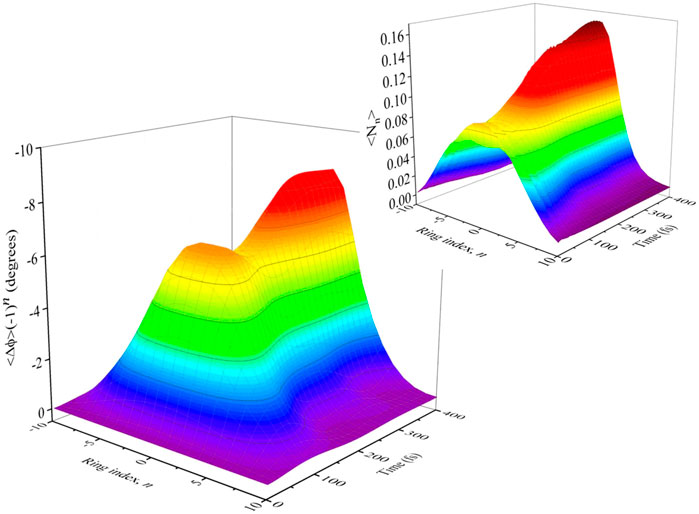
FIGURE 9. The time dependence of the staggered angular displacement, ⟨ϕ_n⟩× (−1)ⁿ. The change of dihedral angle is Δθ_n = (ϕ_n+1 − ϕ_n), showing local planarization for a PPP chain of 21 monomers. The inset shows the time dependence of the exciton density, ⟨N_n⟩, showing exciton density localization after a single torsional period ($\sim 200$ fs). In the long-time limit (i.e., t ≳ 400 fs) ⟨ϕ_n⟩∝⟨N_n⟩× (−1)ⁿ, illustrating classical (Landau) polaron formation. Reproduced from J. Chem. Phys. 149, 214107 (2018) with the permission of AIP publishing.

So far we have described how exciton coupling to torsional modes causes a spatially varying planarization of the monomers that acts as a one-dimensional potential which self-localizes the exciton. The exciton ‘digs a hole for itself’, forming an exciton-polaron [53]. Some researchers [11], however, argue that torsional relaxation causes an exciton to become more delocalized. A mechanism that can cause exciton delocalization occurs if the disorder-induced localization length is shorter than the intrinsic exciton-polaron size. Then, in this case for freely rotating monomers, the stiffer elastic potential in the excited state causes a decrease both in the variance of the dihedral angular distribution, ${\sigma }_{\theta }^2=k_{B}T/K_{\text{rot}}$, and the mean dihedral angle, θ₀. This, in turn, means that the exciton band width, |4J|, increases and the diagonal disorder [22], σ_J = J_SEσ_θ sin 2θ₀, decreases. Hence, the disorder-induced localization, $L_{\text{loc}}\sim {(|J|/{\sigma }_J)}^{2/3}$, increases (see Section 3.2).

4.4 Summary

The conclusions that we draw from Section 4 are that a band edge excitation (i.e., a LEGS, which is an exciton spanning a single chromophore) undergoes ultrafast exciton site decoherence via its coupling to fast C-C bond stretches. It subsequently couples to slow torsional modes causing planarization and exciton density localization on the chromophore. A hot exciton (i.e., a QEES) also undergoes ultrafast exciton site decoherence. However, exciton density localization within a chromophore only occurs after localization onto the chromophore via a stochastic interaction with the environment.

On conformationally disordered polymer, exciton site decoherence causes ultrafast fluorescence depolarization [31], as observed by Wells and Blank [3]. Subsequent exciton density localization causes additional fluorescence depolarization [2, 3, 75].

5 Intrachain exciton motion

The last section described the relaxation and localization of higher energy quasiextended excited states onto chromophores, and the subsequent torsional relaxation and localization on the chromophore into an exciton-polaron. We now consider the relaxation and dynamics of these relaxed excitons caused by dynamical disorder arising from the stochastic torsional fluctuations experienced by a polymer in a solvent.

Environmentally-induced intrachain exciton relaxation in poly(phenylene ethynylene) was modeled by Albu and Yaron [70] using the Frenkel exciton model supplemented by the torsional degrees of freedom, i.e., $\widehat{H}={\widehat{H}}_F+{\widehat{H}}_{\mathit{rot}}$ (given by Eq. 2 and 30, respectively). Fast vibrational modes were neglected because although they cause self-trapping, they do not cause self-localization, and these modes can be assumed to respond instantaneously to the torsional modes. The polymer-solvent interactions were modeled by the Langevin equation. For chains longer than the exciton localization length the excited-state relaxation showed biexponential behavior with a shorter relaxation time of a few ps and a longer relaxation time of tens of ps.

After photoexcitation of the n = 2 (charge-transfer) exciton in oligofluorenes, Clark et al. [76] reported torsional relaxation on sub-100 fs timescales. Since this timescale is faster than the natural rotational period of an undamped monomer, they ascribed it to the electronic energy being rapidly converted to kinetic energy via nonadiabatic transitions. They argue that this is analogous to inertial solvent reorganization.

Tozer and Barford [77] using the same model as Albu and Yaron to model intrachain exciton motion in PPP where the exciton dynamics were simulated on the assumption that at time t + δt the new exciton target state is the eigenstate of $\widehat{H}(t+\delta t)$ with the largest overlap with the previous target state at time t .⁵

A more sophisticated simulation of exciton motion in poly (p-phenylene vinylene) and oligothiophenes chains was performed by Burghardt and coworkers [21, 78–80] where high-frequency C-C bond stretches were also included, the solvent was modeled by a set of harmonic oscillators with an Ohmic spectral density, and the system was evolved via the multilayer-MCTDH method. Their results, however, are in quantitative agreement with those of Tozer and Barford in the “low-temperature” limit (discussed in Section 5.3), namely activationless, linearly temperature-dependent exciton diffusion with exciton diffusion coefficients larger, but close to experimental values.

The Brownian forces excerted by the solvent on the polymer monomers have two consequences. First, as already noted in Section 3.2, the instantaneous spatial dihedral angle fluctuations Anderson localize the Frenkel center-of-mass wavefunction. Second, the temporal dihedral angle fluctuations cause the exciton to migrate via two distinct transport processes.

At low temperatures there is small-displacement adiabatic motion of the exciton-polaron as a whole along the polymer chain, which we will characterize as a “crawling” motion. At higher temperatures the torsional modes fluctuate enough to cause the exciton to be thermally excited out of the self-localized polaron state into a more delocalized LEGS or quasi-band QEES. While in this more delocalized state, the exciton momentarily (transiently) exhibits quasi-band ballistic transport, before the wavefunction stochastically collapses into an exciton-polaron in a different region of the polymer chain (as already described in Section 4.2). We will characterize this large-scale displacement as a non-adiabatic “skipping” motion.

The thermally-activated, slow motion, large amplitude torsional fluctuations therefore play two competing roles. First, they localize the exciton (either by polaron formation or Anderson localization) and second they delocalize the exciton (either by crawling or skipping). This process of quantum transport in molecular systems in its various flavors is often referred to in the literature as environment-assisted quantum transport [81] or transient (de)localization [82], and it applies equally to excitons and charges [82–84].

The possible observation via two-dimensional coherence spectroscopy of torsionally-induced exciton dynamics has recently been discussed in Refs. [85, 86].

Before describing the details of these types of motion, we first describe a model of solvent dynamics and consider again exciton-polaron formation in a polymer subject to Brownian fluctuations.

5.1 Solvent dynamics

If the solvent molecules are subject to spatially and temporally uncorrelated Brownian fluctuations, then the monomer rotational dynamics are controlled by the Langevin equation

$\frac{d{L}_n\left(t\right)}{dt}={\mathrm{\Gamma }}_n\left(t\right)+R_n\left(t\right)-\gamma L_n\left(t\right),(39)$

where Γ_n(t) is the systematic torque given by Eq. 32.

R_n(t) is the stochastic torque on the monomer due to the random fluctuations in the solvent and γ is the friction coefficient for the specific solvent. From the fluctuation-dissipation theorem, the distribution of random torques is given by

$⟨R_m\left(t\right)R_n\left(0\right)⟩=2I\gamma k_{B}T{\delta }_{mn}\delta \left(t\right),(40)$

which are typically sampled from a Gaussian distribution with a standard deviation of ${\sigma }_R={(2I\gamma k_{B}T/\mathrm{\Delta }t)}^{\frac{1}{2}}$. As a consequence of these Brownian fluctuations the monomer rotations are characterized by the autocorrelation function [88],

$〈\delta \varphi \left(t\right)\delta \varphi \left(0\right)〉=〈{\delta \varphi }^2〉\left(\cos \left(\omega t\right)+\left(\frac{\gamma }{2\omega }\right)\sin \left(\omega t\right)\right)\exp \left(-\gamma t/2\right),(41)$

where $〈{\delta \varphi }^2〉=k_{B}T/K_{rot,}$ $K_{rot}$ is the stiffness, $\omega ={\left({\omega }_{rot}^2-{\gamma }^2/4\right)}^{1/2}$, and ${\omega }_{rot}={\left(K_{rot}/I\right)}^{1/2}$ is the angular frequency of the torsional mode.

The monomer rotations imply time-dependent dihedral angles, Δθ_n(t) = (ϕ_n+1(t) − ϕ_n(t)), which in turn - by virtue of Eq. 30 - causes time-dependent exciton transfer integrals. It is this time-dependence that drives the intrachain exciton dynamics.

5.2 Polaron formation

As we saw in Section 4.3, at zero temperature torsional modes couple to the exciton, forming an exciton-polaron. At finite temperatures, however, a combination of factors affect the localization of the exciton. First, the exciton will still attempt to form a polaron. However, the thermally induced fluctuations in the torsional angles will affect the size of this exciton-polaron, as there is a non-negligible probability that the exciton will be excited out of its polaron potential well into a more delocalized state at high enough temperatures. Second, the exciton states will be Anderson localized by the instantaneous torsional disorder.

Figure 10 shows how the average localization length varies with temperature both with and without coupling between the exciton and the torsional modes (i.e., “self-trapped” and “free” exciton, respectively). As described in Section 3.2, the localization length for the “free” exciton is determined by Anderson localization. For small angular displacements from equilibrium a Gaussian distribution of dihedral angles implies a Gaussian distribution of exciton transfer integrals. Then, as confirmed by the simulation results shown in Figure 10, from single-parameter scaling theory, $L_{\text{loc}}^{\text{free}}\propto {\sigma }_{\theta }^{-2/3}={⟨\delta {\theta }^2⟩}^{-1/3}\propto T^{-1/3}$.

FIGURE 10

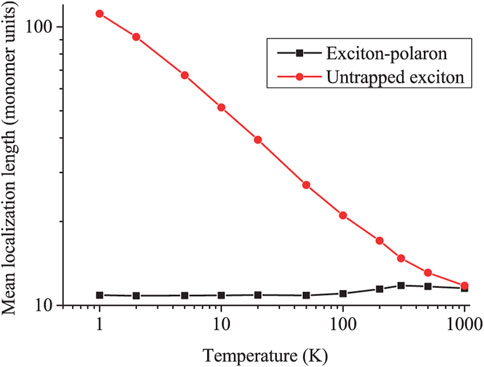
FIGURE 10. The exciton localization length as a function of temperature for the “free” (i.e., “untrapped”) exciton (red circles) and exciton-polaron (i.e., “self-trapped”) (black squares). Increasing the temperature causes a minor increase in the size of the exciton-polaron. This increase in size arises from the exciton escaping from the polaron potential well and being excited into a LEGS or QEES. The polaron binding energy is high enough for excitons in PPP that this is a rare occurrence even at high temperatures. The untrapped exciton localization length obeys $L_{\text{loc}}^{\text{free}}\propto T^{-1/3}$. The lengths coincide when k_BT ∼ the exciton-polaron binding energy. Reproduced from J. Chem. Phys. 143, 084102 (2015) with the permission of AIP publishing.

In contrast, the localization length of the “self-trapped” exciton slowly increases with temperature because of the thermal excitation of the exciton from the self-localized polaron to a more delocalized LEGS or QEES. The two values coincide when k_BT equals the exciton-polaron binding energy (i.e., T ∼ 1500 K in PPP).

5.3 Adiabatic “crawling” motion

At low temperatures (≲ 100 K) the exciton has only a small amount of thermal energy, and not enough to regularly break free from its polaronic torsional distortions. Thus, the exciton-polaron migrates quasi-adiabatically and diffusively as a single unit. This is a collective motion of the exciton and the torsional degrees of freedom, as the torsional planarization accompanies the exciton. Simulations confirm random walk motion [77], as the mean-square-distance traveled by the exciton-polaron is proportional to time, i.e., ⟨L²⟩ = 2D_A(T)t, where D_A is the diffusion coefficient. Since the migration of the exciton-polaron is an activationless process, at low temperatures it obeys the Einstein-Smoluchowski equation, D_A(T) = μk_BT, where μ is the mobility of the particle.

The time taken for an exciton to diffuse a distance L along the chain is determined by the equation for a one-dimensional random walk, i.e., τ_D = ⟨L²⟩/2D. As shown in Figure 10, the typical exciton-polaron localization length is $\sim 12$ monomers or $\sim 6$ nm in PPP. This characteristic length scale implies a characteristic timescale, namely the time taken for the exciton to diffuse along a chromophore length. As shown in Table 3, these timescales are typically 3–30 ps at room temperature depending on the solvent friction coefficient, being shorter at higher temperatures and smaller damping rates. As we show in Section 5, these timescales are an order of magnitude shorter than Förster transfer times in the condensed phase.

TABLE 3

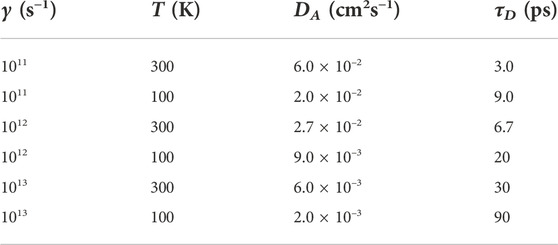
TABLE 3. Calculated intrachain adiabatic exciton diffusion coefficients, D_A, and times, τ_D, in PPP from Ref. [77]. τ_D is the time taken for an exciton to diffuse along a chromophore of linear size 6 nm in a solvent at temperature, T, with a damping rate γ. From simulations [77], τ_D ∼ γ^1/2/T. Hegger et al. [80] obtained D_A ∼ 10^–2 cm²s⁻¹ in oligothiophenes at 300 K and γ = 5 × 10¹² s⁻¹.

As the exciton-polaron migrates along the polymer chain it experiences a different potential energy landscape, so its energy will also fluctuate on a timescale ∼ τ_D. Interestingly, these timescales are consistent with the longer timescale found experimentally in biexponential fits of relaxation processes of polymers in solution (see Table 1) and correspond to the longer timescale simulated by Albu and Yaron [70] in longer polymers. As the inverse of these timescales is much smaller than the typical fluctuations in energy (given when ϕ⁰ = 0 by ${\sigma }_{ϵ}\sim J_{\mathrm{SE}}{\sigma }_{\varphi }^2\simeq 0.1$ eV), the associated emission spectra will exhibit inhomogeneous broadening.

5.4 Nonadiabatic “skipping” motion

At higher temperatures, adiabatic “crawling” migration of the exciton-polaron, as described above, still occurs. However, a second non-adiabatic mechanism for the dynamics plays an important role. This mechanism involves the exciton-polaron being excited to a high enough energy by the thermal fluctuations to be excited out of the polaron potential well, resulting in a breakdown of the polaron and the exciton to enter an untrapped local exciton ground state (LEGS), or a higher energy quasi-extended exciton state (QEES), as illustrated in Figure 2. Once in this more delocalized state the exciton has quasi-band characteristics and travels quasi-ballistically.

As described in Section 4.2, however, on a sub-ps timescale the hot, delocalized exciton will shed some of its excess kinetic energy and stochastically relax back into an exciton-polaron. As a result, the time-averaged exciton localization length calculations of Figure 10 show only a slight increase in localization length with increasing temperatures, as the majority of its lifetime is still spent in self-localized exciton-polarons.

The requirement that the exciton is excited out of the polaron potential well means that this process is activated. Thus, from a simple Fermi golden rule analysis it can be shown that [89].

$D_{NA}\left(T\right)\sim ⟨\delta {\theta }^2⟩\times {\ell }_{\mathit{QEES}}\times \exp \left(-\frac{\mathrm{\Delta }E}{k_{B}T}\right),(42)$

where ⟨δθ²⟩ is the variance of the dihedral angles, ℓ_QEES is the QEES localization length, and ΔE is the exciton-polaron binding energy. Since ⟨δθ²⟩∼ T and ℓ_QEES ∼ T^−1/3, this implies that

$D_{NA}\left(T\right)\sim T^{2/3}\exp \left(-\frac{\mathrm{\Delta }E}{k_{B}T}\right).(43)$

At 300 K D_NA is approximately twice as large as D_A and thus the overall diffusion coefficient is considerably enhanced by this skipping motion, which is schematically illustrated in Figure 11.

FIGURE 11

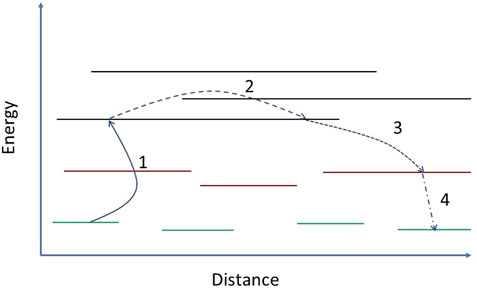
FIGURE 11. A schematic diagram representing intrachain transient exciton delocalization. The green, red and black horizontal lines represent the spatial extent of exciton-polarons, local exciton ground states (LEGSs) and quasiextended states (QEESs), respectively. (1) The exciton is thermally excited from its bound polaron state to a QEES. (2) Motion in the delocalized QEES is quasiballistic over long distances. (3) The exciton stochastically relaxes onto a LEGS (see Section 4.2). (4) Torsional relaxation causes an exciton-polaron (see Section 4.3).

The role of exciton transport in disordered one-dimensional systems via higher-energy quasi-band states has been discussed in Ref. [68], where in that work phonons in the condensed phase environment induced non-adiabatic transitions.

6 Interchain exciton motion

The stochastic, torsionally-induced intrachain exciton diffusion in polymers in solution described in the last section is not expected to be the primary cause of exciton diffusion in polymers in the condensed phase. Instead, owing to restricted monomer rotations and the proximity of neighboring chains, exciton transfer is determined by Coulomb-induced, Förster-like processes. Moreover, since dissipation rates are typically [63, 64] 10¹²–10¹³ s⁻¹, whereas exciton transfer rates are typically 10⁹–10¹¹ s⁻¹, except for timescales less than $\sim 1$ ps, exciton migration is an incoherent or diffusive process [90, 91].

We can derive the timescale after which incoherent processes dominate by considering a simple model of exciton transport in a cubic lattice, where each site represents a chromophore. Assuming an exciton transfer integral, J, between neighboring sites and an exciton dephasing rate, γ, Reineker [92] showed that the exciton mean-square displacement follows

$⟨r^2\left(t\right)⟩=3a^2\left(\frac{J^2}{{\hslash }^2\gamma }\right)\left(2t+\left[\exp \left(-2\gamma t\right)-1\right]\right),(44)$

where a is the lattice parameter. For short times, i.e., t ≪ γ⁻¹, the motion is ballistic:

$⟨r^2\left(t\right)⟩\to 6a^2{J}^2{t}^2,(45)$

whereas for long times, i.e., t ≫ γ⁻¹, the motion is diffusive:

$⟨r^2\left(t\right)⟩\to 6a^2\left(\frac{J^2}{{\hslash }^2\gamma }\right)t,(46)$

where J²/ℏ²γ is the ‘derived’ Förster transfer rate, k_F, and D = a²k_F is the diffusion coefficient. As shown in Ref. [90], for the short times t ≲ γ⁻¹ when coherent exciton transport is predicted, both exciton diffusion lengths and spectral diffusion are larger than for incoherent transport.

Early models of incoherent exciton transport assumed that the donors and acceptors are point-dipoles whose energy distribution is a Gaussian random variable [93–95]. An advantage of these models is that they allow for analytical analysis, for example predicting that the diffusion length increases with decreasing disorder and increasing temperature [96]. In particular, at high temperatures the pseudoequilibrium diffusion coefficient, D(T), satisfies [97].

$D\left(T\right)=D_0\exp \left[-{\left(T_0/T\right)}^2\right],(47)$

where T₀ is proportional to the width of the Gaussian disorder, while at low temperatures it is exponentially activated. The analytical results on model systems also reproduce some experimental features, such as the time-dependence of spectral diffusion. A disadvantage, however, is that there is no quantitative link between the model and actual polymer conformations and morphology.

More recent approaches have attempted to make the link between random polymer conformations and the energetic and spatial distributions of the donors and acceptors via the concept of extended chromophores [42, 98–100] and using transition densities to compute transfer integrals. However, the usual practice has been to arbitrarily define chromophores via a minimum threshold in the p-orbital overlaps, and then obtain a distribution of energies by assuming that the excitons delocalize freely on the chromophores thus defined.

As discussed in Section 3.2, an unambiguous link between polymer conformations and chromophores may be made by defining chromophores via the spatial extent of local exciton ground states (LEGSs). Using this insight, a more realistic first-principles model that accounts for polymer conformations can be developed [89, 101]. This is described in Section 6.1, while its predictions and comparisons to experimental observations are described in Section 6.2.

6.1 Modified Förster theory

The Förster resonance exciton transfer (FRET) rate from a donor (D) to an acceptor (A) has the general Golden rule form

$k_{DA}=\left(\frac{2\pi }{\hslash }\right){\left|J_{DA}\right|}^2\int D\left(E\right)A\left(E\right)dE,(48)$

where J_DA is the Coulomb-induced donor-acceptor transfer integral defined by Eq. 3. As we remarked in Section 3.1, the transition density vanishes for odd-parity singlet excitons; it also vanishes for all triplet excitons.

D(E) and A(E) are the donor and acceptor spectral functions, respectively, defined by

$D\left(E\right)=\sum _v{F}_{0v}^D\delta \left(E+E_{0v}^D\right)(49)$

and

$A\left(E\right)=\sum _v{F}_{0v}^A\delta \left(E-E_{0v}^A\right),(50)$

where F_0v is the effective Franck-Condon factor, defined in Eq. 52. $E_{0v}^A=(E_{00}^A+v\hslash {\omega }_{\mathit{vib}})$ is the excitation energy of the acceptor, while $E_{0v}^D=-(E_{00}^D-v\hslash {\omega }_{\mathit{vib}})$ is the de-excitation energy of the donor.

The link between actual polymer conformations and a realistic model of exciton diffusion is made by realising that the donors and acceptors for exciton transfer are LEGSs (i.e., chromophores). This assumption is based on the observation that exciton transfer occurs at a much slower rate than state interconversion, so the donors are LEGSs, while the spectral overlap between LEGSs and higher energy QEESs is small, so the acceptors are also LEGSs. Moreover, the energetic and spatial distribution of LEGSs is entirely determined by the conformational and site disorder, as described in Section 3.2. Finally, polaronic effects are incorporated by an effective Huang-Rhys factor for each chromophore and the Condon approximation may be assumed as C-C vibrational modes do not cause exciton self-localization.

Then, as proved rigorously in Ref. [89]:

1) J_DA is evaluated by invoking the Condon approximation and using the line-dipole approximation [15, 102].

$J_{DA}=\left(\frac{1}{4\pi {\epsilon }_r{\epsilon }_0}\right)\sum _{\begin{array}{c}n\in D\\ n^{\prime }\in A\end{array}}\frac{{\kappa }_{n{n}^{\prime }}}{R_{n{n}^{\prime }}^3}{\mu }_D{\mathrm{\Psi }}_D\left(n\right){\mu }_A{\mathrm{\Psi }}_A\left(n^{\prime }\right),(51)$

where Ψ(n) is the LEGS center-of-mass wavefunction on monomer n determined from the disordered Frenkel exciton model (Eq. 2). Since the spatial extent of Ψ(n) defines a chromophore, the sum over n and n′ is implicitly over monomers of a donor and acceptor chromophore, respectively. μ_X is the transition dipole moment of a single monomer of the donor (X = D) or acceptor (X = A) chromophores (so μ_XΨ_X(n) is the transition dipole moment of monomer n as part of the chromophore). κ_nn′ is the orientational factor, defined in Eq. 5, and R_nn’ is the separation of monomers on the donor and acceptor chromophores. The line-dipole approximation is valid when the monomer sizes are much smaller than their separation on the donor and acceptor chromophores; it reduces to the point-dipole approximation when the chromophore sizes are much smaller than their separation.

2) The spectral functions describe “polaronic” effects, by containing effective Franck-Condon factors which describe the chromophores coupling to effective modes with reduced Huang-Rhys parameters:

$F_{0v}=\frac{{\left(S_{\text{eff}}\right)}^v\exp \left(-S_{\text{eff}}\right)}{v!},(52)$

where S_eff = S/PN, S is the local Huang-Rhys parameter (defined by Eq. 22) and $\mathrm{P}\mathrm{N}={\left({\sum }_n|{\mathrm{\Psi }}_n{|}^4\right)}^{-1}$ is the participation number (or size) of the chromophore [20].

3) Similarly, the 0–0 transition energy is defined by E₀₀ = (E^vert − E^relax), where E^vert is determined from the Frenkel exciton model and E^relax = ℏωS_eff is the effective reorganisation energy for the effective mode.

6.2 Condensed-phase exciton diffusion via FRET

We might attempt to anticipate the results of the simulation of exciton diffusion from the properties of the exciton transfer rate, k_DA. When the chromophore size, L, is much smaller than the donor-acceptor separation, R, the point-dipole approximation is valid. In this limit k_DA ∼ L²/R⁶ and thus the hopping rate increases with increasing chromophore size, but is short range. Conversely, when the chromophore size is much larger than the donor-acceptor separation, the line-dipole approximation predicts that for straight, parallel or collinear chromophores [103–105] k_DA ∼ 1/(LR)² and thus the hopping rate decreases with increasing chromophore size, but is longer ranged.

In practice, Monte Carlo simulations assuming a statistical model of random polymer conformations find that the exciton hopping rate is essentially independent of disorder and hence of chromophore size. This is presumably because neither the assumption of straight, parallel chromophores nor point dipoles are generally valid. These simulations also show that the average time taken for the first exciton hop to occur after photoexcitation is $\sim 10$ ps, whereas the time intervals between hops just prior to radiative recombination is over 10 times longer, and indeed becoming so long that a radiative transition is competitive. This increase in hopping time intervals occurs because as an exciton diffuses through the polymer system it continuously looses energy. Thus, the energetic condition for exciton transfer to occur, namely E_A ≤ E_D, becomes harder to satisfy and in general the spectral overlap between the donor and acceptor decreases. As the excitons diffuse they eventually become trapped in ‘emissive’ chromophores, from which they radiate. As shown in Figure 12, these emissive chromophores occupy the low energy tail of the LEGSs density of states. Their quasi-Gaussian distribution explains spectral diffusion [95, 106]: a time-dependent change in the fluorescence energy, satisfying E ∝ − log  t.

FIGURE 12

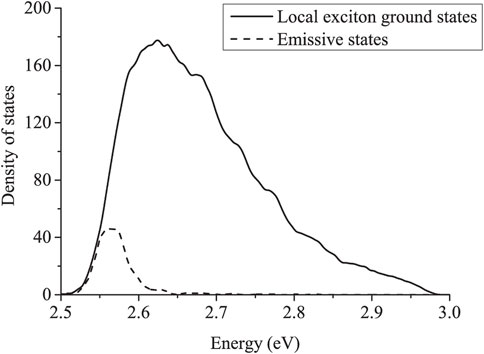
FIGURE 12. The density of states for absorbing LEGSs (solid line) and emitting trap states (dashed line) for an ensemble of PPV chains, with a Gaussian distribution of ϕ₀ and ϕ, as described in the main text. ⟨ϕ₀⟩ = 10°, ${\sigma }_{{\varphi }_0}=5^0$, and σ_ϕ = 5°. Reproduced from J. Chem. Phys. 141, 164103 (2014) with the permission of AIP publishing.

Typically, the average hop distance is between 4 nm (for strong disorder giving an average chromophore length of 8 nm) to 6 nm (for weak disorder giving an average chromophore length of 30 nm). On average, an exciton only makes four hops before radiating, and thus average diffusion lengths are between $\sim 8-12$ nm, being longer for more ordered systems. These theoretical predictions are consistent with experimental values obtained via various techniques [107–109] (see Köhler and Bässler [16] for further experimental references). The diffusion length is remarkably insensitive to disorder, and from simulation satisfies $L_D\sim L_{\text{loc}}^{1/4}\sim {\sigma }^{-1/6}$; a result that can be explained by the spatial distribution of chromophores in randomly coiled polymers [101].

An interesting prediction of Anderson localization is that for the same mean dihedral angle lower energy chromophores are shorter than higher energy chromophores. Now, as the intensity ratio of the vibronic peaks in the emission spectrum, I₀₀/I₀₁, is proportional to the chromophore size [20, 22, 110, 111], i.e.,

$\frac{I_{00}}{I_{01}}\propto \frac{1}{S_{\text{eff}}}=\frac{⟨\mathrm{P}\mathrm{N}⟩}{S},(53)$

spectral diffusion also implies that I₀₀/I₀₁ reduces in time, as a observed in time-resolved photoluminescence spectra in MEH-PPV (see Figure 3 of Ref. [106]). According to simulations [89], I₀₀/I₀₁ ∝ − log  t.

Some of the key features of exciton relaxation and dynamics described in this review are nicely encapsulated by Figure 13. This figure shows the simulated absorption to all absorbing states, the fluorescence via emission from all LEGSs (which occurs in the absence of exciton migration), and the time-integrated fluorescence following exciton migration and emission from ‘trap’ chromophores.

• The absorption spectrum and the emission spectrum assuming no exciton migration are broadly a mirror image. However, the absorption is broader and has a high energy tail as absorption occurs to both LEGSs and QEESs (as also shown in Figure 3B), whereas, from Kasha’s law, emission occurs only from LEGSs following interconversion from QEESs.

• The emission following exciton migration is red-shifted, because the emissive states are in the low-energy tail of the density of states (as shown in Figure 12).

• Since the disorder is static, the optical spectrum exhibits inhomogeneous broadening with a Gaussian distribution [112], narrowed because of exchange narrowing [44, 45].

• The inhomogeneous broadening of the post-migration emission is further narrowed, because the emissive states have a narrower density of states than LEGSs.

• Similarly the intensity ratio, I₀₀/I₀₁, decreases, because on average emissive chromophores have shorter conjugation lengths than LEGSs.

FIGURE 13

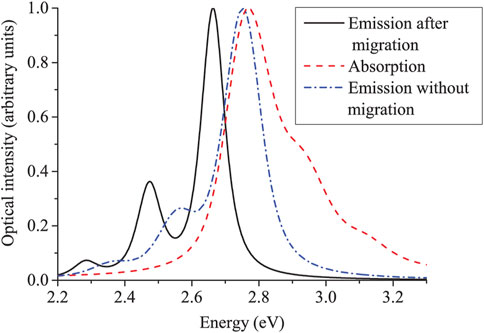
FIGURE 13. The calculated optical spectra of PPV assuming a statistical model of random polymer conformations. Exciton migration prior to emission causes a red-shift in energy, a narrowing of the inhomogeneous broadening, and a decrease in I₀₀/I₀₁. Reproduced from J. Chem. Phys. 141, 164103 (2014) with the permission of AIP publishing.

6.3 Transient exciton delocalization in the condensed phase

The previous section described exciton diffusion via FRET in typically conformationally disordered polymer systems. These systems have exciton diffusion lengths of ca. 10 nm. Recently, however, much longer diffusion lengths of ca. 300 nm have been reported in highly ordered poly (3-hexylthiophene) (P3HT) nanofiber films [113]. The mechanism proposed for this process by Beljonne et al. [114] is transient exciton delocalization (described in Section 5.4 for intrachain exciton diffusion), with the added ingredient of long-range exciton transfer integrals. Specifically, they propose that ordered P3HT chains form one-dimensional H-aggregate stacks. Then, low frequency, large amplitude interchain vibrational motion thermally induce transitions from low-energy localized exciton states to higher-energy delocalized states that span multiple P3HT chains along the stack. The transient occupation of these delocalized states followed by stochastic relaxation into localized states (as illustrated in Figure 11) facilitates long-range exciton hops. Crucially, this mechanism relies on the long-range (1/R) exciton transfer integrals, predicted when the chain size exceeds the interchain separations [102].

There can be little doubt, whatever the precise mechanism of exciton transfer (e.g., via FRET or vibrational motion), that highly ordered polymeric systems with bands of extended exciton states significantly facilitates exciton transport.

7 Summary and concluding remarks

We have reviewed the various exciton dynamical processes in conjugated polymer systems. In summary, they are:

• Following photoexcitation, the initial dynamical process in a conjugated polymer is the quantum correlation of the exciton with phonons associated with high-frequency C-C bond vibrations, thus creating an exciton-polaron. This quantum mechanical entanglement causes exciton-site decoherence, which is manifest as sub-10 fs fluorescence depolarization (see Section 4.1).

• Next, the energy that is transferred from the exciton to the nuclei is dissipated into the environment on a timescale determined by the strength of the system-bath interactions. For a hot, delocalized exciton (i.e., a QEES) the system-bath interactions cause the entangled exciton-nuclear wavefunction to stochastically ‘collapse’ into a particular localized exciton (i.e., a LEGS), causing the exciton density to be localized on a ‘chromophore’ (see Section 4.2).

• The fate of an exciton on a chromophore is now strongly dependent on the polymer chemical structure and the type of environment. For underdamped, freely rotating monomers, the coupling of the exciton to the low-frequency torsional modes creates a self-localized exciton-polaron, with associated planarization and exciton-density localization (see Section 4.3).

• For a polymer in solution, dynamical disorder, originating from stochastic, thermally-induced torsional fluctuations, causes two-types of motion. At lower temperature they cause the exciton-polaron to diffuse via a crawling motion along the polymer chain; a process known as environment-assisted quantum transport [81]. The diffusion coefficient is linearly proportional to temperature (see Section 5.3). At higher temperatures the larger torsional fluctuations cause the exciton to be thermally excited from the polaron, thereby momentarily (or transiently) occupying more delocalized states where the exciton skips (or surfs) quasi-ballistically. The exciton subsequently relaxes into a localized exciton-polaron by the process described in Section 4. This process is sometimes known as transient delocalization. In this regime the diffusion coefficient is exponentially activated (see Section 5.4).

• For a polymer in the condensed phase, the dominant post-ps process is Förster resonant energy transfer (FRET) and exciton diffusion. An exciton diffusing in the random energy landscape soon gets trapped in chromophores occupying the low-energy tail of the LEGSs density of states, exhibiting log  t spectral diffusion. An exciton typically diffuses $\sim 10$ nm before radiative decay, with the diffusion length weakly increasing with decreasing disorder (see Section 6.2).

• Finally, highly ordered polymer films, implying bands of thermally accessible quasiextended exciton states, facilitates exciton transport with diffusion lengths of $>100$ nm (see Section 6.3).

In this review we have argued that theoretical modeling of exciton dynamics over multiple time and length scales is only realistically possible by employing suitably parametrized coarse-grained exciton-phonon models. Moreover, to correctly account for the ultrafast processes of exciton-site decoherence and the relaxation of hot, delocalized excitons onto chromophores, the exciton and vibrational modes must be treated on the same quantum mechanical basis and importantly the Ehrenfest approximation must be abandoned. We have also repeatedly noted that spatial and temporal disorder play a key role in exciton spectroscopy and dynamics; and it is for this reason that exciton dynamics is conjugated polymers is essentially an incoherent process.

In a previous review [14] we explained how spectroscopic signatures are highly-dependent on polymer multiscale structures, and how—in principle—good theoretical modeling of excitons and spectroscopy can be used as a tool to predict these polymer structures. This review builds on that prospectus by describing how time-resolved spectroscopy can be understood via a theoretical description of exciton dynamics coupled to information on polymer multiscale structures. Again, the reverse proposition follows: time-resolved spectroscopy coupled to a theoretical description of exciton dynamics can be used to provide insights into polymer multiscale structures.

As stated in the Introduction, an understanding of the principles of exciton dynamics, relating this to multiscale polymer structures, and interpreting the associated spectroscopic signatures are all key ingredients to developing structure-function relationships and ultimately to developing rational design strategies for polymer electronic devices.

Author contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

Department of Chemistry, University of Oxford and Balliol College, University of Oxford.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹A related method is time-dependent density matrix renormalization group (TD-DMRG). This has been successfully applied to simulate singlet fission in carotenoids [36].

²There is also a weaker and less significant coupling of the normal mode to the exciton bond-order operator [22, 56].

³In contrast, in the classical limit (ω → 0) the nuclei respond infinitesimally slowly to the exciton, so that the correlation length and the exciton-polaron mass diverge causing exciton-polaron self-localization.

⁴In fact, the Ehrenfest approximation is the cause of the unphysical bifurcation of the exciton density onto separate chromophores found in Ehrenfest simulations of the relaxation dynamics of high energy photoexcited states [72].

⁵Although confirmed by solutions of the TDSE [77] this latter assumption was shown by Lee and Willard [87] to be potentially problematic for the nonadiabatic transport described in Section 5.4.

References

1. Grage MML, Zaushitsyn Y, Yartsev A, Chachisvilis M, Sundstrom V, Pullerits T. Ultrafast excitation transfer and trapping in a thin polymer film. Phys Rev B (2003) 67:205207. doi:10.1103/physrevb.67.205207

CrossRef Full Text | Google Scholar

2. Ruseckas A, Wood P, Samuel IDW, Webster GR, Mitchell WJ, Burn PL, et al. Ultrafast depolarization of the fluorescence in a conjugated polymer. Phys Rev B (2005) 72:115214. doi:10.1103/physrevb.72.115214

CrossRef Full Text | Google Scholar

3. Wells NP, Boudouris BW, Hillmyer MA, Blank DA. Intramolecular exciton relaxation and migration dynamics in poly(3-hexylthiophene). J Phys Chem C (2007) 111:15404–14. doi:10.1021/jp074657j

CrossRef Full Text | Google Scholar

4. Dykstra TE, Hennebicq E, Beljonne D, Gierschner J, Claudio G, Bittner ER, et al. Conformational disorder and ultrafast exciton relaxation in PPV-family conjugated polymers. J Phys Chem B (2009) 113:656–67. doi:10.1021/jp807249b

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Dykstra TE, Kovalevskij V, Yang XJ, Scholes GD. Excited state dynamics of a conformationally disordered conjugated polymer: A comparison of solutions and film. Chem Phys (2005) 318:21–32. doi:10.1016/j.chemphys.2005.04.001

CrossRef Full Text | Google Scholar

6. Yang XJ, Dykstra TE, Scholes GD. Photon-echo studies of collective absorption and dynamic localization of excitation in conjugated polymers and oligomers. Phys Rev B (2005) 71:045203. doi:10.1103/physrevb.71.045203

CrossRef Full Text | Google Scholar

7. Wells NP, Blank DA. Correlated exciton relaxation in poly(3-hexylthiophene). Phys Rev Lett (2008) 100:086403. doi:10.1103/physrevlett.100.086403

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Sperling J, Nemeth A, Baum P, Sanda F, Riedle E, Kauffmann HF, et al. Exciton dynamics in a disordered conjugated polymer: Three-pulse photon-echo and transient grating experiments. Chem Phys (2008) 349:244–9. doi:10.1016/j.chemphys.2008.02.046

CrossRef Full Text | Google Scholar

9. Consani C, Koch F, Panzer F, Unger T, Kohler A, Brixner T. Relaxation dynamics and exciton energy transfer in the low-temperature phase of MEH-PPV. J Chem Phys (2015) 142:212429. doi:10.1063/1.4918645

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Collini E, Scholes GD. Coherent intrachain energy migration in a conjugated polymer at room temperature. Science (2009) 323:369–73. doi:10.1126/science.1164016

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Westenhoff S, Beenken WJD, Friend RH, Greenham NC, Yartsev A, Sundstrom V. Anomalous energy transfer dynamics due to torsional relaxation in a conjugated polymer. Phys Rev Lett (2006) 97:166804. doi:10.1103/physrevlett.97.166804

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Banerji N, Cowan S, Vauthey E, Heeger AJ. Ultrafast relaxation of the poly(3-hexylthiophene) emission spectrum. J Phys Chem C (2011) 115:9726–39. doi:10.1021/jp1119348

CrossRef Full Text | Google Scholar

13. Busby E, Carroll EC, Chinn EM, Chang LL, Moule AJ, Larsen DS. Excited-state self-trapping and ground-state relaxation dynamics in poly(3-hexylthiophene) resolved with broadband pump-dump-probe spectroscopy. J Phys Chem Lett (2011) 2:2764–9. doi:10.1021/jz201168q

CrossRef Full Text | Google Scholar

14. Barford W, Marcus M. Perspective: Optical spectroscopy in π-conjugated polymers and how it can be used to determine multiscale polymer structures. J Chem Phys (2017) 146:130902. doi:10.1063/1.4979495

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Barford W. Electronic and optical properties of conjugated polymers. 2nd ed. Oxford: Oxford University Press (2013).

Google Scholar

16. Köhler A, Bässler H. Electronic processes in organic semiconductors: An introduction. 1st ed. Weinheim: Wiley VCH (2015).

Google Scholar

17. Barford W. Excitons in conjugated polymers: A tale of two particles. J Phys Chem A (2013) 117:2665–71. doi:10.1021/jp310110r

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Jang S. Dynamics of molecular excitons: Theories and applications. Elsevier (2020).

Google Scholar

19. Dimitriev OP. Dynamics of excitons in conjugated molecules and organic semiconductor systems. Chem Rev (2022) 122:8487–593. doi:10.1021/acs.chemrev.1c00648

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Barford W, Marcus M. Theory of optical transitions in conjugated polymers. I. Ideal systems. J Chem Phys (2014) 141:164101. doi:10.1063/1.4897984

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Binder R, Bonfanti M, Lauvergnat D, Burghardt I. First-principles description of intra-chain exciton migration in an oligo(para-phenylene vinylene) chain. 1. generalized Frenkel-Holstein Hamiltonian. J Chem Phys (2020). 152. 204119. doi:10.1063/5.0004510

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Marcus M, Tozer OR, Barford W. Theory of optical transitions in conjugated polymers. II. Real systems. J Chem Phys (2014) 141:164102. doi:10.1063/1.4897985

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Horsfield AP, Bowler DR, Ness H, Sanchez CG, Todorov TN, Fisher AJ. The transfer of energy between electrons and ions in solids. Rep Prog Phys (2006) 69:1195–234. doi:10.1088/0034-4885/69/4/r05

CrossRef Full Text | Google Scholar

24. Nelson TR, White AJ, Bjorgaard JA, Sifain AE, Zhang Y, Nebgen B, et al. Non-adiabatic excited-state molecular dynamics: Theory and applications for modeling photophysics in extended molecular materials. Chem Rev (2020) 120:2215–87. doi:10.1021/acs.chemrev.9b00447

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Tully JC. Molecular-dynamics with electronic-transitions. J Chem Phys (1990) 93:1061–71. doi:10.1063/1.459170

CrossRef Full Text | Google Scholar

26. Tully JC. Perspective: Nonadiabatic dynamics theory. J Chem Phys (2012) 137:22A301. doi:10.1063/1.4757762

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Beck MH, Jackle A, Worth GA, Meyer HD. The multiconfiguration time-dependent hartree (mctdh) method: A highly efficient algorithm for propagating wavepackets. Phys Rep (2000) 324:1–105. doi:10.1016/s0370-1573(99)00047-2

CrossRef Full Text | Google Scholar

28. Vidal G. Efficient classical simulation of slightly entangled quantum computations. Phys Rev Lett (2003) 91:147902. doi:10.1103/physrevlett.91.147902

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Vidal G. Efficient simulation of one-dimensional quantum many-body systems. Phys Rev Lett (2004) 93:040502. doi:10.1103/physrevlett.93.040502

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Schöllwock U. The density-matrix renormalization group in the age of matrix product states. Ann Phys (2011) 326:96–192. doi:10.1016/j.aop.2010.09.012

CrossRef Full Text | Google Scholar

31. Mannouch JR, Barford W, Al-Assam S. Ultra-fast relaxation, decoherence, and localization of photoexcited states in π-conjugated polymers. J Chem Phys (2018) 148:034901. doi:10.1063/1.5009393

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Kobayashi T. Relaxation in polymers. Singapore: World Scientific (1993).

Google Scholar

33. Loudon R. One-dimensional hydrogen atom. Proc R Soc A (2016) 472:20150534. doi:10.1098/rspa.2015.0534

CrossRef Full Text | Google Scholar

34. Barford W, Bursill RJ, Smith RW. Theoretical and computational studies of excitons in conjugated polymers. Phys Rev B (2002) 66:115205. doi:10.1103/physrevb.66.115205

CrossRef Full Text | Google Scholar

35. Barford W, Trembath D. Exciton localization in polymers with static disorder. Phys Rev B (2009) 80:165418. doi:10.1103/physrevb.80.165418

CrossRef Full Text | Google Scholar

36. Manawadu D, Valentine DJ, Marcus M, Barford W. Singlet triplet-pair production and possible singlet-fission in carotenoids. Journal of Physical Chemistry Letters (2022) 13:1344.

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Barford W, Lidzey DG, Makhov DV, Meijer AJH. Exciton localization in disordered poly(3-hexylthiophene). J Chem Phys (2010) 133:044504. doi:10.1063/1.3459099

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Anderson PW. Absence of diffusion in certain random lattices. Phys Rev (1958) 109:1492–505. doi:10.1103/physrev.109.1492

CrossRef Full Text | Google Scholar

39. Malyshev AV, Malyshev VA. Statistics of low energy levels of a one-dimensional weakly localized Frenkel exciton: A numerical study. Phys Rev B (2001) 63:195111. doi:10.1103/physrevb.63.195111

CrossRef Full Text | Google Scholar

40. Malyshev AV, Malyshev VA. Level and wave function statistics of a localized 1d frenkel exciton at the bottom of the band. J Lumin (2001) 94:369–72. doi:10.1016/s0022-2313(01)00303-9

CrossRef Full Text | Google Scholar

41. Makhov DV, Barford W. Local exciton ground states in disordered polymers. Phys Rev B (2010) 81:165201. doi:10.1103/physrevb.81.165201

CrossRef Full Text | Google Scholar

42. Athanasopoulos S, Hennebicq E, Beljonne D, Walker AB. Trap limited exciton transport in conjugated polymers. J Phys Chem C (2008) 112:11532–8. doi:10.1021/jp802704z

CrossRef Full Text | Google Scholar

43. Kramer B, Mackinnon A. Localization - theory and experiment. Rep Prog Phys (1993) 56:1469–564. doi:10.1088/0034-4885/56/12/001

CrossRef Full Text | Google Scholar

44. Knapp EW. Lineshapes of molecular aggregates - exchange narrowing and intersite correlation. Chem Phys (1984) 85:73–82. doi:10.1016/s0301-0104(84)85174-5

CrossRef Full Text | Google Scholar

45. Knapp EW. On the validity of the cumulant approximation for spectral-line profiles. Chem Phys Lett (1984) 108:342–6. doi:10.1016/0009-2614(84)85203-3

CrossRef Full Text | Google Scholar

46. Mulliken RS, Rieke CA, Orloff D, Orloff H. Formulas and numerical tables for overlap integrals. J Chem Phys (1949) 17:1248–67. doi:10.1063/1.1747150

CrossRef Full Text | Google Scholar

47. Beenken WJD, Lischka H. Spectral broadening and diffusion by torsional motion in biphenyl. J Chem Phys (2005) 123:144311. doi:10.1063/1.2049269

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Rashba EI. Theory of strong interactions of electron excitations with lattice vibrations in molecular crystals. 1. Optika I Spektroskopiya (1957) 2:75–87.

Google Scholar

49. Rashba EI. Theory of strong interactions of electron excitations with lattice vibrations in molecular crystals. 2. Optika I Spektroskopiya (1957) 2:88–98.

Google Scholar

50. Holstein T. Studies of polaron motion. Ann Phys (1959) 8:325–42. doi:10.1016/0003-4916(59)90002-8

CrossRef Full Text | Google Scholar

51. Holstein T. Studies of polaron motion. Ann Phys (1959) 8:343–89. doi:10.1016/0003-4916(59)90003-x

CrossRef Full Text | Google Scholar

52. Rashba EI, Sturge MD. Excitons. North-Holland Amsterdam (1982).

Google Scholar

53. Landau LD. The movement of electrons in the crystal lattice. Z Phys (1933) 3:664.

Google Scholar

54. Campbell DK, Bishop AR, Fesser K. Polarons in quasi-one-dimensional systems. Phys Rev B (1982) 26:6862–74. doi:10.1103/physrevb.26.6862

CrossRef Full Text | Google Scholar

55. Tozer OR, Barford W. Localization of large polarons in the disordered Holstein model. Phys Rev B (2014) 89:155434. doi:10.1103/physrevb.89.155434

CrossRef Full Text | Google Scholar

56. R. Binder, S. Romer, J. Wahl, and I. Burghardt, “An analytic mapping of oligomer potential energy surfaces to an effective Frenkel model,” Journal of Chemical Physics 141, 014101 (2014).

Google Scholar

57. Hoffmann M, Soos ZG. Optical absorption spectra of the Holstein molecular crystal for weak and intermediate electronic coupling. Phys Rev B (2002) 66:024305. doi:10.1103/physrevb.66.024305

CrossRef Full Text | Google Scholar

58. Kuhn O, Sundstrom V. Pump-probe spectroscopy of dissipative energy transfer dynamics in photosynthetic antenna complexes: A density matrix approach. J Chem Phys (1997) 107:4154–64. doi:10.1063/1.474803

CrossRef Full Text | Google Scholar

59. Smyth C, Fassioli F, Scholes GD. Measures and implications of electronic coherence in photosynthetic light-harvesting. Phil Trans R Soc A (2012) 370:3728–49. doi:10.1098/rsta.2011.0420

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Mannouch J. Exciton dynamics in π-conjugated polymer systems”, PhD thesis. Oxford: University of Oxford (2019).

Google Scholar

61. Tretiak S, Saxena A, Martin RL, Bishop AR. Conformational dynamics of photoexcited conjugated molecules. Phys Rev Lett (2002) 89:097402. doi:10.1103/physrevlett.89.097402

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Karabunarliev S, Bittner ER. Polaron-excitons and electron-vibrational band shapes in conjugated polymers. J Chem Phys (2003) 118:4291–6. doi:10.1063/1.1543938

CrossRef Full Text | Google Scholar

63. Sterpone F, Rossky PJ. Molecular modeling and simulation of conjugated polymer oligomers: Ground and excited state chain dynamics of ppv in the gas phase. J Phys Chem B (2008) 112:4983–93. doi:10.1021/jp711848q

PubMed Abstract | CrossRef Full Text | Google Scholar

64. De Leener C, Hennebicq E, Sancho-Garcia JC, Beljonne D. Modeling the dynamics of chromophores in conjugated polymers: The case of meh-ppv. J Phys Chem B (2009) 113:1311–22.

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Breuer H-P, Petruccione F. The theory of open quantum systems. Oxford: Oxford University Press (2002).

Google Scholar

66. Daley AJ. Quantum trajectories and open many-body quantum systems. Adv Phys (2014) 63:77–149. doi:10.1080/00018732.2014.933502

CrossRef Full Text | Google Scholar

67. Bednarz M, Malyshev VA, Knoester J. Intraband relaxation and temperature dependence of the fluorescence decay time of one-dimensional Frenkel excitons: The pauli master equation approach. J Chem Phys (2002) 117:6200–13. doi:10.1063/1.1499483

CrossRef Full Text | Google Scholar

68. Barchielli A, Vacchini B. Quantum Langevin equations for optomechanical systems. New J Phys (2015) 17:083004. doi:10.1088/1367-2630/17/8/083004

CrossRef Full Text | Google Scholar

69. Albu NM, Yaron DJ. Brownian dynamics model of excited-state relaxation in solutions of conjugated oligomers. J Phys Chem C (2013) 117:12299–306. doi:10.1021/jp400538g

CrossRef Full Text | Google Scholar

70. Spano FC, Meskers SCJ, Hennebicq E, Beljonne D. Using circularly polarized luminescence to probe exciton coherence in disordered helical aggregates. J Chem Phys (2008) 129:024704. doi:10.1063/1.2943647

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Tempelaar R, Spano FC, Knoester J, Jansen TLC. Mapping the evolution of spatial exciton coherence through time-resolved fluorescence. J Phys Chem Lett (2014) 5:1505–10. doi:10.1021/jz500488u

PubMed Abstract | CrossRef Full Text | Google Scholar

72. Tozer OR, Barford W. Exciton dynamics in disordered poly(p-phenylenevinylene). 1. ultrafast interconversion and dynamical localization. Journal of Physical Chemistry A (2012) 116:10310–18.

PubMed Abstract | CrossRef Full Text | Google Scholar

73. Barford W, Mannouch JR. Torsionally induced exciton localization and decoherence in π-conjugated polymers. J Chem Phys (2018) 149:214107. doi:10.1063/1.5054176

PubMed Abstract | CrossRef Full Text | Google Scholar

74. French AP. Vibrations and waves. London: Nelson (1971).

Google Scholar

75. Perez IG, Barford W. Ultrafast fluorescence depolarization in conjugated polymers. J Phys Chem Lett (2021) 12:5344–8. doi:10.1021/acs.jpclett.1c01354

PubMed Abstract | CrossRef Full Text | Google Scholar

76. Clark J, Nelson T, Tretiak S, Cirmi G, Lanzani G. Femtosecond torsional relaxation. Nat Phys (2012) 8:225–31. doi:10.1038/nphys2210

CrossRef Full Text | Google Scholar

77. Tozer OR, Barford W. Intrachain exciton dynamics in conjugated polymer chains in solution. J Chem Phys (2015) 143:084102. doi:10.1063/1.4929378

PubMed Abstract | CrossRef Full Text | Google Scholar

78. Binder R, Burghardt I. First-principles description of intra-chain exciton migration in an oligo(para-phenylene vinylene) chain. 2. ML-MCTDH simulations of exciton dynamics at a torsional defect. J Chem Phys (2020). 152. 1.

PubMed Abstract | CrossRef Full Text | Google Scholar

79. Binder R, Burghardt I. First-principles quantum simulations of exciton diffusion on a minimal oligothiophene chain at finite temperature. Faraday Discuss (2020) 221:406–27. doi:10.1039/c9fd00066f

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Hegger R, Binder R, Burghardt I. First-principles quantum and quantum-classical simulations of exciton diffusion in semiconducting polymer chains at finite temperature. J Chem Theor Comput (2020) 16:5441–55. doi:10.1021/acs.jctc.0c00351

CrossRef Full Text | Google Scholar

81. Rebentrost P, Mohseni M, Kassal I, Lloyd S, Aspuru-Guzik A. Environment-assisted quantum transport. New J Phys (2009) 11:033003. doi:10.1088/1367-2630/11/3/033003

CrossRef Full Text | Google Scholar

82. Fratini S, Mayou D, Ciuchi S. The transient localization scenario for charge transport in crystalline organic materials. Adv Funct Mater (2016) 26:2292–315. doi:10.1002/adfm.201502386

CrossRef Full Text | Google Scholar

83. Troisi A, Orlandi G. Charge-transport regime of crystalline organic semiconductors: Diffusion limited by thermal off-diagonal electronic disorder. Phys Rev Lett (2006) 96:086601. doi:10.1103/physrevlett.96.086601

PubMed Abstract | CrossRef Full Text | Google Scholar

84. Berencei L, Barford W, Clark SR. Thermally driven polaron transport in conjugated polymers. Phys Rev B (2022) 105:014303. doi:10.1103/physrevb.105.014303

CrossRef Full Text | Google Scholar

85. Barford W, Arber AN, McLennan F, Marcus M. Measuring time-dependent induced quantum coherences via two-dimensional coherence spectroscopy. Phys Rev A (2021) 104:063517. doi:10.1103/physreva.104.063517

CrossRef Full Text | Google Scholar

86. Brey D, Binder R, Martinazzo R, Burghardt I. Signatures of coherent vibronic exciton dynamics and conformational control in the two-dimensional electronic spectroscopy of conjugated polymers. Faraday Discuss (2022) 237:148–67. doi:10.1039/d2fd00014h

PubMed Abstract | CrossRef Full Text | Google Scholar

87. Lee EMY, Willard AP. Solving the trivial crossing problem while preserving the nodal symmetry of the wave function. Journal of Chemical Theory and Computation (2019) 15:4332–43.

PubMed Abstract | CrossRef Full Text | Google Scholar

88. Nitzan A. Chemical dynamics in condensed phases: Relaxation, transfer and reactions in condensed molecular systems. Oxford: Oxford University Press (2006).

Google Scholar

89. Barford W, Tozer OR. Theory of exciton transfer and diffusion in conjugated polymers. J Chem Phys (2014) 141:164103. doi:10.1063/1.4897986

PubMed Abstract | CrossRef Full Text | Google Scholar

90. Barford W, Duffy CDP. Role of quantum coherence and energetic disorder in exciton transport in polymer films. Phys Rev B (2006) 74:075207. doi:10.1103/physrevb.74.075207

CrossRef Full Text | Google Scholar

91. Hwang I, Scholes GD. Electronic energy transfer and quantum-coherence in π-conjugated polymers. Chem Mater (2011) 23:610–20. doi:10.1021/cm102360x

CrossRef Full Text | Google Scholar

92. Kenkre VM, Reineker P. Exciton dynamics in molecular crystals and aggregates. In: Springer tracts in modern physics. Berlin; New York: Springer-Verlag (1982).

CrossRef Full Text | Google Scholar

93. Movaghar B, Grunewald M, Ries B, Bässler H, Wurtz D. Diffusion and relaxation of energy in disordered organic and inorganic materials. Phys Rev B (1986) 33:5545–54. doi:10.1103/physrevb.33.5545

PubMed Abstract | CrossRef Full Text | Google Scholar

94. Movaghar B, Ries B, Grunewald M. Diffusion and relaxation of energy in disordered-systems - departure from mean-field theories. Phys Rev B (1986) 34:5574–82. doi:10.1103/physrevb.34.5574

PubMed Abstract | CrossRef Full Text | Google Scholar

95. Meskers SCJ, Hubner J, Oestreich M, Bassler H. Dispersive relaxation dynamics of photoexcitations in a polyfluorene film involving energy transfer: Experiment and Monte Carlo simulations. J Phys Chem B (2001) 105:9139–49. doi:10.1021/jp0113331

CrossRef Full Text | Google Scholar

96. Athanasopoulos S, Bässler H, Köhler A. Disorder vs delocalization: Which is more advantageous for high-efficiency organic solar cells? J Phys Chem Lett (2019) 10:7107–12. doi:10.1021/acs.jpclett.9b02866

PubMed Abstract | CrossRef Full Text | Google Scholar

97. Grunewald M, Pohlmann B, Movaghar B, Wurtz D. Theory of non-equilibrium diffusive transport in disordered materials. Philosophical Mag B (1984) 49:341–56. doi:10.1080/13642818408246522

CrossRef Full Text | Google Scholar

98. Beljonne D, Pourtois G, Silva C, Hennebicq E, Herz LM, Friend RH, et al. Interchain vs. intrachain energy transfer in acceptor-capped conjugated polymers. Proc Natl Acad Sci U S A (2002) 99:10982–7. doi:10.1073/pnas.172390999

PubMed Abstract | CrossRef Full Text | Google Scholar

99. Hennebicq E, Pourtois G, Scholes GD, Herz LM, Russell DM, Silva C, et al. Exciton migration in rigid-rod conjugated polymers: An improved forster model. J Am Chem Soc (2005) 127:4744–62. doi:10.1021/ja0488784

PubMed Abstract | CrossRef Full Text | Google Scholar

100. Singh J, Bittner ER, Beljonne D, Scholes GD. Fluorescence depolarization in poly[2-methoxy-5-((2-ethylhexyl)oxy)-1, 4-phenylenevinylene]: Sites versus eigenstates hopping. J Chem Phys (2009) 131:194905. doi:10.1063/1.3259549

PubMed Abstract | CrossRef Full Text | Google Scholar

101. Barford W, Bittner ER, Ward A. Exciton dynamics in disordered poly(p-phenylenevinylene). 2. exciton diffusion. J Phys Chem A (2012) 116:10319–27. doi:10.1021/jp307041n

PubMed Abstract | CrossRef Full Text | Google Scholar

102. Barford W. Exciton transfer integrals between polymer chains. J Chem Phys (2007) 126:134905. doi:10.1063/1.2714516

PubMed Abstract | CrossRef Full Text | Google Scholar

103. Wong KF, Bagchi B, Rossky PJ. Distance and orientation dependence of excitation transfer rates in conjugated systems: Beyond the Förster theory. J Phys Chem A (2004) 108:5752–63. doi:10.1021/jp037724s

CrossRef Full Text | Google Scholar

104. Das M, Ramasesha S. Fluorescent resonant excitation energy transfer in linear polyenes. J Chem Phys (2010) 132:124109. doi:10.1063/1.3367896

PubMed Abstract | CrossRef Full Text | Google Scholar

105. Barford W. Beyond Förster resonance energy transfer in linear nanoscale systems. J Phys Chem A (2010) 114:11842–3. doi:10.1021/jp107374r

PubMed Abstract | CrossRef Full Text | Google Scholar

106. Hayes GR, Samuel IDW, Phillips RT. Exciton dynamics in electroluminescent polymers studied by femtosecond time-resolved photoluminescence spectroscopy. Phys Rev B (1995) 52:11569–72. doi:10.1103/physrevb.52.r11569

PubMed Abstract | CrossRef Full Text | Google Scholar

107. Markov DE, Amsterdam E, Blom PWM, Sieval AB, Hummelen JC. Accurate measurement of the exciton diffusion length in a conjugated polymer using a heterostructure with a side-chain cross-linked fullerene layer. J Phys Chem A (2005) 109:5266–74. doi:10.1021/jp0509663

PubMed Abstract | CrossRef Full Text | Google Scholar

108. Lewis AJ, Ruseckas A, Gaudin OPM, Webster GR, Burn PL, Samuel IDW. Singlet exciton diffusion in MEH-PPV films studied by exciton-exciton annihilation. Org Electronics (2006) 7:452–6. doi:10.1016/j.orgel.2006.05.009

CrossRef Full Text | Google Scholar

109. Scully SR, McGehee MD. Effects of optical interference and energy transfer on exciton diffusion length measurements in organic semiconductors. J Appl Phys (2006) 100:034907. doi:10.1063/1.2226687

CrossRef Full Text | Google Scholar

110. Spano FC, Yamagata H. Vibronic coupling in J-aggregates and beyond: A direct means of determining the exciton coherence length from the photoluminescence spectrum. J Phys Chem B (2011) 115:5133–43. doi:10.1021/jp104752k

PubMed Abstract | CrossRef Full Text | Google Scholar

111. Yamagata H, Spano FC. Strong photophysical similarities between conjugated polymers and j-aggregates. J Phys Chem Lett (2014) 5:622–32. doi:10.1021/jz402450m

PubMed Abstract | CrossRef Full Text | Google Scholar

112. Mukamel S. Principles of nonlinear optical spectroscopy. New York ; Oxford: Oxford University Press (1995).

Google Scholar

113. Sneyd AJ, Fukui T, Palecek D, Prodhan S, Wagner I, Zhang YF, et al. Efficient energy transport in an organic semiconductor mediated by transient exciton delocalization. Sci Adv (2021) 7:eabh4232. ARTN eabh4232. doi:10.1126/sciadv.abh4232

PubMed Abstract | CrossRef Full Text | Google Scholar

114. Prodhan S, Giannini S, Wang LJ, Beljonne D. Long-range interactions boost singlet exciton diffusion in nanofibers of pi-extended polymer chains. J Phys Chem Lett (2021) 12:8188–93. doi:10.1021/acs.jpclett.1c02275

PubMed Abstract | CrossRef Full Text | Google Scholar