Superfluid density and two-component conductivity in hole-doped cuprates

While the pseudogap dominates the phase diagram of hole-doped cuprates, connecting the antiferromagnetic parent insulator at low doping to the strange metal at higher doping, its origin and relation to superconductivity remains unknown. In order to proceed, a complete understanding of how the single hole–initially localized in the Mott state–becomes mobile and ultimately evolves into a coherent quasiparticle at the end of the superconducting dome is required. In order to affect this development, we examine recent transport and spectroscopic studies of hole-doped cuprates across their phase diagram. In the process, we highlight a set of empirical correlations between the superfluid density and certain normal state properties of hole-doped cuprates that offer fresh insights into the emergence of metallicity within the CuO₂ plane and its influence on the robustness of the superconducting state. We conclude by arguing that the overall behavior is best understood in terms of two distinct current-carrying fluids, only one of which dominates the superconducting condensate and is gapped out below the pseudogap endpoint at a critical hole concentration p∗.

1 Introduction

At half-filling, the CuO₄ square-planar motif generic to all cuprates is insulating due to the strong on-site Coulomb repulsion that causes the single charge carrier within each unit cell to localize. Upon hole doping, the initial excess charge preferentially locates on the oxygen sites–giving rise to a charge-transfer insulator–which then couples antiferromagnetically with the localized charge on the copper site to create a band of Zhang-Rice singlets. With further doping, the charge-transfer gap collapses and long-range antiferromagnetic (AFM) order is destroyed, leading to a system of highly-frustrated short-range spin correlations and ultimately d-wave superconductivity. At the end of the superconducting (SC) dome, the charge initially localized in the Mott state becomes fully itinerant and a correlated Fermi liquid (FL) state with a large cylindrical Fermi surface containing the total carrier density emerges.

Despite a decades-long investigation, the above summary is almost the extent of our current understanding of the fate of the initially localized carrier as further holes are introduced into the CuO₂ plane. The starting point and endpoint are well established–it is the transition from localization to itinerancy as the number of doped holes (p) increases that is proving the biggest challenge. The fact that this transition incorporates the most enigmatic features of the cuprate problem; the normal state pseudogap, the strange metal and high temperature superconductivity itself makes steps to understand its evolution all the more pressing.

The aim of this Perspective is to highlight a number of intriguing correlations that shed new light, not only on the fate of the localized hole–as reflected in both single-particle probes like angle-resolved photoemission spectroscopy (ARPES) and scanning tunneling microscopy (STM) and collective responses like transport–but also on the impact of its enhanced mobility on the superconductivity and in particular, on the superfluid density. The totality of the transport behaviour across the cuprate phase diagram provides compelling evidence for the presence of two current-carrying fluids, one associated with coherent fermions, the other incoherent and possibly bosonic in nature. The relative occupation of these two entities and its evolution with doping suggests that the superfluid density is dominated by only one of these fluids. Finally, in order to motivate the development of a consistent theoretical description of this dichotomy, we highlight systems that exhibit such a two-fluid response before presenting results from a treatment of the Hubbard model on a 2 × 2 plaquette that captures a number of the essential elements seen in the cuprates. The overall picture that emerges is one that departs significantly from the standard BCS description.

2 Experimental survey

Despite the diverse and complex chemistry of the cuprates, the evolution of their physical (i.e., transport, thermodynamic and spectroscopic) properties across the phase diagram is found to be strikingly similar for all well-studied families. This remarkable uniformity suggests that Fermiology plays only a minor role in defining the overall behaviour, though certain unique aspects, such as the Lifshitz transition in La_2−xSr_xCuO₄ (LSCO) or the CuO chains in YBa₂Cu₃O_7−δ (Y123) or YBa₂Cu₄O₈ (Y124), need to be fully taken into account before a complete picture can emerge. In this experimental survey, we focus predominantly on the single-layered cuprates Tl₂Ba₂CuO_6+δ (Tl2201) and Bi_2+z−yPb_ySr_2−x−zLa_xCuO_6+δ (Bi2201) on which the bulk of our recent high-field transport studies have been performed, though for completeness, we also include complementary data obtained on LSCO, Y123, Y124 and single-layered HgBa₂CuO_6+δ (Hg1201). Moreover, in order to aid subsequent discussions, we redefine the phase diagram in Figure 1A in terms of the superfluid density n_s(0), rather than T_c. In this way, the SC dome can be divided simply into two regimes–pseudogapped (PG) and strange metal (SM)—rather than the usual three (underdoped, optimally doped and overdoped).

FIGURE 1

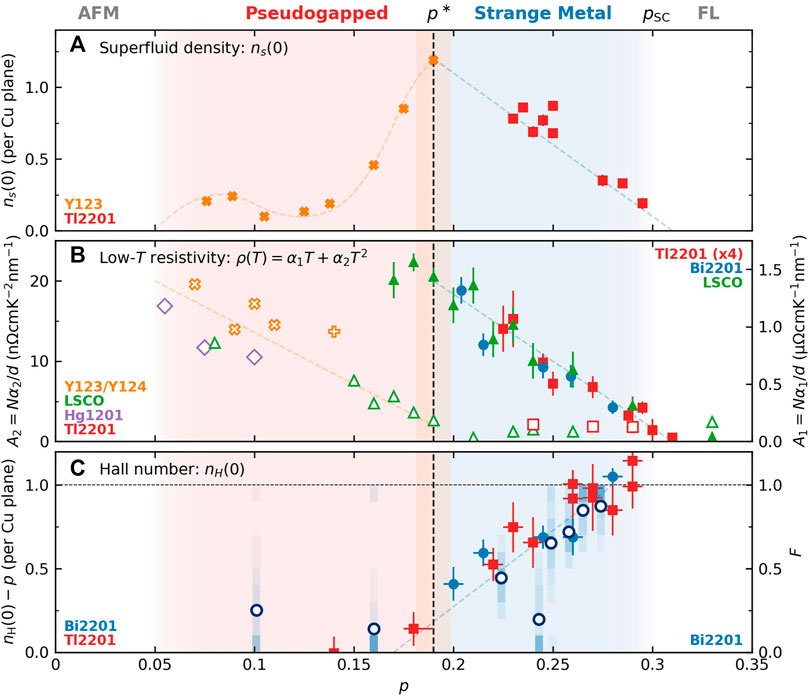
FIGURE 1. Correlations between superfluid density n_s(0) and various transport properties of hole-doped cuprates. (A) Evolution of n_s(0) (per Cu) with doping p in Y123 (orange crosses) and Tl2201 (red squares) obtained from measurements of the zero-temperature in-plane penetration depth λ_ab(0) (summarized in [33, 63]. In order to deduce n_s(0) in Y123, we used m* values obtained from high-field quantum oscillation studies over the doping range 0.10 $\le p\le$ 0.15 [64] and extrapolated to p* = 0.19 assuming that n_s(0) approaches 1 + p* there. For a description of how n_s(0) is obtained for Tl2201, please refer to Appendix A in [33]. All parameters used in these determinations are listed in the Supplementary Material. Note that the peak in n_s(0) at the pseudogap endpoint p* (vertical dashed line) delineates the pseudogapped (PG) regime, shaded in orange, from the strange metal (SM) regime, shaded in blue. (B) p-dependence of A₁ = Nα₁/d (right axis, solid points) and A₂ = Nα₂/d (left axis, open points), where d is the c-axis lattice constant, N is the number of CuO₂ planes per unit cell and α₁, α₂ are coefficients of the low-T zero-field resistivity ρ(T) = α₁T + α₂T². Open crosses (plusses) indicate data for Y123 (Y124), respectively. See Supplementary Material for the precise values and references related to these data points. (C) Comparison of n_H(0) − p, the p-dependence of the as-measured low-T Hall carrier number of Tl2201 and Bi2201 minus its corresponding p value (left axis, closed points [15]) and F, the fractional filling of the superconducting gap as measured recently by STM on Bi2201 (right axis, open points [36]). Shaded columns are histograms representing the local variations in the measured filling (as in [36]). In each panel, coloured dashed lines are guides to the eye.

The growth of n_s(0) with increasing p inside the PG regime–known as the Uemura relation–reflects the fact that the pseudogap itself is states-non-conserving, i.e. that states lost through the opening of the pseudogap (preferentially near the Brillouin zone edges) are not recovered below T_c [1]. The reduction in n_s(0) beyond p*, on the other hand, has commonly been attributed to pair breaking–the so-called dirty d-wave scenario–though recent studies on LSCO thin films have challenged this association [2, 3]. Robust correlations between n_s(0) and certain key transport coefficients–highlighted in Figure 1 and to be addressed in turn in the following sections–provide further clues as to the origin of this loss of condensate, with the nature of the carriers within the SM regime and proximity to the Mott state at half-filling playing pivotal roles.

2.1 Zero-field resistivity

In considering the in-plane resistivity ρ_ab(T), we find it more insightful to describe the doping evolution in reverse, i.e., with decreasing p, starting from the far overdoped side. Beyond the SC dome (p > p_SC where p_SC ∼ 0.30 is the doping at which superconductivity vanishes on the overdoped side), ρ_ab(T) displays a pure T² resistivity [4, 5] indicative of a correlated FL ground state. As p is reduced below p_SC, however, a finite T-linear term emerges with a coefficient A₁ that grows with decreasing p [6]. The striking correlation between A₁ and n_s(0) [7] within the SM regime–captured in panels A and B of Figure 1–is reminiscent of the correlation found in conventional BCS superconductors between T_c and λ_tr, the transport scattering rate linked to the electron-phonon coupling strength λ and the slope of the T-linear resistivity (at intermediate temperatures). The fact that a similar correlation exists in both hole- and electron-doped cuprates has motivated a prolonged and intense search for a corresponding λ in high-T_c cuprates. There is an important distinction to be made here, however. In cuprates, the T-linear resistivity extends down to anomalously low T (in marked contrast to expectations for a FL) and persists over a broad doping range (in marked contrast to expectations for a conventional quantum critical metal [8]). Moreover, the T-dependence of ρ_ab(T) in Bi2201 and LSCO was recently shown to be identical for samples with the same T_c (and therefore comparable p) values [9], despite the fact that the T- and p-dependencies of the spin and charge fluctuation spectra of both families are markedly different [10–13]. This simple result profoundly challenges claims that charge and/or spin fluctuations are responsible for the strange metallic behaviour seen in cuprates. Others have linked the ubiquitous nature of the low-T T-linear resistivity to the vague concept of Planckian dissipation [14] and a gradual loss of quasiparticle (QP) integrity across the SM regime [15], though how this QP integrity is lost remains an open question.

Plotting the temperature derivative dρ_ab/dT reveals that the evolution of ρ_ab(T) across the SM regime is best interpreted as the sum of two distinct (∼ T and T²) components [6, 9], rather than as a single component with an exponent intermediate between 1 and 2, as found, for example, in the heavy fermions. The T² component (A₂)—whose evolution across the SC dome is also captured in Figure 1B–is presumably a continuation of the QP-QP scattering term found beyond p_SC. Hence, a picture emerges in which the T² and T-linear components to ρ_ab(T) reflect, respectively, FL and non-FL contributions to the charge transport whose relative ratio evolves smoothly across the SM regime. Whether this duality reflects the presence of additive scattering rates, real-space differentiated segments or independent conducting channels, remains to be determined, though the former is difficult to reconcile with the evolution of the in-plane magnetoresistance (MR) and low-T Hall number as will be outlined in the following sections.

Acknowledging the over-simplicity of a pure two-fluid picture, one can nevertheless speculate as to which of these two fluids is the main contributor to the SC condensate. The growth in A₁ with decreasing p must reflect either enhanced scattering from the non-FL component (the corresponding λ) or an increased occupation of the non-QP sector. The striking correlation shown in Figure 1 between A₁ (a quantity determined both by scattering rate and carrier number) and n_s(0) (a carrier number) suggests strongly that it is the latter. Upon entering the PG regime, A₁ drops (almost precipitously) while A₂ increases sharply. This anti-correlation of the two coefficients implies that the states responsible for the SM component are the ones that are preferentially gapped out by the opening of the pseudogap (at the zone edges). The growth in A₂ then reflects the increasing dominance of the QP component to the total conductivity. The overall evolution of the two coefficients indicates that upon crossing p*, only part of the ‘strange’ sector is gapped out initially. Upon further reduction in p, the strange fluid shrinks further and faster than the reduction of the residual ‘normal’ fluid, leaving the latter once again as the dominant component (as it was for p ∼ p_SC). The corresponding reduction in n_s(0) with decreasing p across the PG regime appears then to tie the superfluid density to that component of the normal state exhibiting signatures of non-QP transport. In order to shed more light on the nature of this non-QP sector, we turn now to consider the evolution of the in-plane MR and Hall number across the phase diagram.

2.2 Magnetoresistance

The MR of most simple metals can be well described by conventional Boltzmann transport theory and follows Kohler scaling, whereby Δρ/ρ(0)—the fractional change of the resistivity in a magnetic field–is proportional to (H/ρ(0))² and where ρ(0) is the corresponding zero-field resistivity. Adherence to this scaling indicates that Δρ(H, T) and ρ(0, T) are governed by the same scattering rates. In cuprates, Kohler scaling is observed only beyond the SC dome [16]. Within the SM regime, however, the in-plane MR adopts an entirely different form of scaling–so-called quadrature or H/T scaling–that has also been observed in certain iron-based superconductors close to their respective quantum critical points [17, 18]. Specifically, the H² dependence at low fields transforms into an unsaturating H-linear dependence with a T-independent slope. At the same time, the coefficient (B) of the quadratic, low-field H² MR is found to exhibit a pure 1/T power-law dependence, in marked contrast to the 1/ρ(T) dependence one expects from Kohler scaling. Finally, in Tl2201 and Bi2201, the MR response is found to be independent of both field-orientation and impurity scattering [19]. While the H² to H-linear crossover can be reproduced within a modified Boltzmann treatment through the introduction of an impedance to cyclotron motion somewhere on the Fermi surface [20–23], all other aspects of the MR response represent a radical departure from the standard semi-classical picture.

The fact that the MR scales with 1/T (and not with 1/ρ(T) = 1/(ρ₀ + α₁T + α₂T²)) within the SM regime favours the two-fluid description introduced above. While ρ(T) is composed of two distinct T-dependent components, the MR response appears to be associated only with those carriers undergoing linear-in-T scattering or dissipation. The observed correlation [16] between α₁ and the magnitude of the H-linear MR further supports this singular association. The carriers responsible for the QP-like (ρ₀ + α₂T²) part of the zero-field resistivity, on the other hand, appear to play no role in the MR scaling. Of course, one cannot exclude a small orbital MR of the form predicted by Boltzmann transport in Bi2201 or Tl2201 [19], but this appears to be dwarfed completely by the quadrature component.

Across p*, the H-dependence of the MR remains qualitatively unchanged. The magnitude of the H-linear slope continues to increase with decreasing p, though now its continued rise appears to be tracking the loss of carriers inside the PG regime, as reflected in the growth of ρ₀ and, by correspondence, α₂ (Figure 1C). Single-power law scaling is still observed, albeit with an exponent that changes abruptly across p*—from H/T to H/T²—mirroring the crossover to a dominant quadratic T-dependence in ρ_ab(T) [24]. The sharpness of this crossover is reminiscent of the discontinuous collapse of the anti-nodal QP peak across p* seen by ARPES [25, 26]. It should be noted that although a return to quadratic resistivity suggests a recovery of conventional FL behaviour within the PG regime, the power-law scaling and in particular the absence of the residual resistivity component ρ₀ in the scaling of the MR is highly anomalous. It should also be stressed that such scaling is wholly incompatible with the notion of a single fluid with multiple scattering rates.

2.3 Hall number

The Hall number n_H, derived from measurements of the in-plane Hall coefficient R_H, serves as a convenient and informative quantifier of the mobile carrier density. For an isotropic, single-band metal R_H = V/n_He, where V is the unit cell volume and e the electronic charge. In lightly-doped LSCO (x < 0.08) [27], R_H is approximately T-independent below 300 K with a value set by n_H = p = x (see Figure 1B), indicating that initially, only the doped holes are mobile. In single particle probes, the opening of the pseudogap at p* is characterised by the formation of discontinuous Fermi arcs, preferentially located near the zone diagonals, whose arc-length also scales with p. Remarkably, the arcs themselves continue to host coherent quasiparticles, as evidenced by the observation of quantum oscillations [28]). At the other end of the SC dome, n_H(0) = 1 + p, where n_H(0) is the effective carrier number obtained from R_H in the high-field, low-T limit once superconductivity has been suppressed and any T-dependent in-plane anisotropy [29] washed out [15]. The value of n_H(0) in highly overdoped Tl2201 is consistent with quantum oscillations [30] and ARPES [31]. Thus, at this end of the SM regime, the hole that was originally localized in the Mott parent state becomes fully itinerant.

The crossover in n_H(0) from p to 1 + p was originally observed in Y123 and reported to be sharp and confined to a narrow doping region around p* [32]. In Bi2201 and Tl2201, however, this crossover was found to occur over a much broader doping range between p* and p_SC (see Figure 1B). While the role of the conducting CuO chains in modifying this crossover in Y123 remains to be clarified, the claim that the crossover in Tl2201 occurs beyond p* is strengthened by the observation that it coincides with a reduction in n_s(0) with increasing not decreasing p [33]. The fact that n_H(0) decreases upon lowering p before the PG itself opens suggests a profound disconnect between single-particle and particle-particle probes within the SM regime, possibly reflecting an increasing influence of current vertex corrections, though the coincidence of the reduction in n_H(0) and the growth in A₁ appears to support the aforementioned picture of a gradual and preemptive loss of QP integrity with underdoping.

The anti-correlation between n_H(0) and n_s(0) across the SM regime (panels A and C of Figure 1) is particularly striking and non-intuitive. In a clean BCS superconductor, all carriers are expected to participate in the SC condensate. As mentioned in the Introduction, the prevailing explanation for the reduction in n_s(0) is pair breaking induced by disorder coupled with a rapidly diminishing pairing amplitude Δ. This conventional viewpoint–based on the Landau BCS paradigm–fails to take into account, however, the highly anomalous nature of the normal state [7]. Moreover, the dirty d-wave scenario predicts a rapid reduction in T_c as the normal state scattering rate increases [34], in marked contrast with recent findings [35]. Last but not least, a similar correlation, shown here in Figure 1C for the first time, is also found between n_H(0) and F–the fraction of residual (zero-energy) states in the SC state deduced from STM [36]. The quantitative agreement between the two parameters in the same cuprate family (Bi2201) suggests that the states contributing to n_H(0) in the field-induced normal state do not form part of the SC condensate. Conversely, those states that emerge from the SC condensate upon application of a large magnetic field do not appear to exhibit an intrinsic Hall response of their own, due to them being localized [37], bosonic (particle-hole symmetric) or, if still fermionic, fundamentally incoherent.

3 Theoretical considerations

The picture emerging from this survey of recent high-field studies on hole-doped cuprates is of a transport current comprising two electron fluids–one coherent and FL-like (albeit correlated), the other non-FL-like and of unknown origin–whose relative ratio evolves smoothly across the phase diagram. Before discussing peculiarities in cuprates from a theoretical perspective, it is worthwhile to start with a general remark on the coexistence of two types of electronic liquids for interacting electrons in crystals. FL theory, together with its microscopic justification [38–40] has long been considered the ‘default’ many-body theory of conducting condensed matter. Recently, the concept of a ‘non-particle’ state was developed, mostly within the language of holographic duality [41, 42], which is argued to be a more appropriate framework to describe cuprates and other strange metals [7]. In both cases, the normal state of the system is described as a single liquid, either as a FL or a non-FL. It is not obvious therefore whether the hypothesis of a two-liquid state is consistent with general ideas of contemporary quantum many-body theory. Being very far from a complete theoretical description of the experimental situation, we are nevertheless able to give a positive answer to this question. To this aim, we will first make a general remark and then give two examples where the coexistence of two liquids in the same many-body system is reliably established.

We proceed by discussing the emerging physics in terms of the single-particle electron Green’s function [38–40]. To avoid possible misunderstanding, one should emphasise that this formalism contains full information on the many-particle system. In particular, it is sufficient to reproduce rigorously all equilibrium [43, 44] and non-equilibrium [45] properties of interacting fermionic systems. The simplest analysis can be done in terms of single-particle density matrix (let us stress again that, despite its ‘single-particle’ name, it characterizes the whole many-particle system). One can derive the following general expression [46] for the accelerating action of a constant uniform electric field E:

$\frac{d{j}_a}{dt}=e^2{E}_b\sum _{\mathbf{k},n}{m}_{ab}^{-1}\left(\mathbf{k},n\right){\rho }_n\left(\mathbf{k}\right),(1)$

where j is the electric current, t the time, e the electron charge and a, b are Cartesian indices,

$m_{ab}^{-1}\left(\mathbf{k},n\right)={\hslash }^{-2}\frac{{\partial }^2}{\partial k_a\partial k_b}⟨\mathbf{k}n\left|{\widehat{H}}_0\right|\mathbf{k}n⟩(2)$

plays the role of inverse effective mass tensor, $\left|\mathbf{k}n\right.⟩$ and ρ_n(k) are eigenfunctions and eigenvalues of the single-particle density matrix $\widehat{\rho }$ dependent on the wave vector k, n labels different eigenstates and plays the role of a ‘band index’ in the many-body description of crystalline solids [46], ${\widehat{H}}_0$ is the single-particle part of the Hamiltonian (we assume that the interaction Hamiltonian depends on coordinates only), and the k-summation in Eq. 1 is taken over the Brillouin zone. Equations 1 and 2 can be considered as a real-time equivalent of the optical f-sum rule frequently used to analyse strongly correlated systems [47].

The single-particle density matrix is nothing but the equal-time single-particle Green’s function $\widehat{G}$, and the latter, for energies close enough to the Fermi surface, can be decomposed into QP (that is, pole) and non-QP (incoherent) parts [38]. These two contributions to the density matrix corresponds to two contributions to Eq. 1. Rigorously speaking, the QP and non-QP parts of $\widehat{\rho }$ do not necessarily commute one with one another and thus do not share a common set of eigenfunctions, but at the level of the operator $\widehat{\rho }$, this decomposition is always possible and accurate.

Half-metallic ferromagnets [48] provide a neat example of a physical system in which two types of electron liquids coexist naturally and rigorously. Whereas for one spin projection, the electron subsystem is metallic and FL-like, for the other, non-QP states in the gap dominate close to the Fermi surface, their density of states being non-zero above the Fermi energy only for the minority-spin gap and below it for the majority-spin gap [48]. Importantly, their contribution to the occupation number ρ_n(k) is almost k-independent and thus these states are effectively currentless [46]. Nevertheless, they may contribute to photoemission and scanning probe spectra, tunneling, etc. [48], as confirmed experimentally [49, 50].

The case of half-metallic ferromagnets is useful as it provides us with a unique opportunity to prove the separation of electron liquids into QP and non-QP (or incoherent) components. Moreover, this separation is rigorous due to its connection to conserving quantities such as the total spin (we assume that spin-orbit effects are negligible). Unsurprisingly, the situation in cuprates is much more complicated however, and we need to find a closer analog, even if its consideration cannot be done with the same rigour. In this regard, the heavy fermion (or ‘Kondo lattice’) systems [51, 52] provide a useful bridge. In these systems, the 4f or 5f electrons are mostly atomic-like and form local magnetic moments but in some regime they become itinerant, contributing to the shape of the Fermi surface, charge transport etc. In some sense, these states can be considered as ‘Abrikosov pseudofermions’—usually a purely mathematical construction introduced as a way to represent local spin operators–that hybridize with the true conduction-band fermions and become real [53]. Therefore one needs to distinguish between large and small Fermi surface constructions with and without their contribution [52].

With this in mind, let us now return to the cuprate problem. The minimal model that is supposed to keep the essential elements of cuprate physics is the single-band t − t′ Hubbard model derived via mapping of density-functional computational results for various representatives of this family [54, 55]. The corresponding Hamiltonian has the form

$H=-\sum _{ij}{t}_{ij}{c}_{i\sigma }^{†}{c}_{j\sigma }+\sum _{i}U{n}_{i\uparrow }{n}_{i\downarrow }(3)$

where i, j are sites belonging to the simple square lattice, t_ij is an effective hopping that is supposed to be non-zero only for nearest- (t) and next-nearest-neighbours (t′) and U is the on-site Coulomb interaction parameter. Operators $c_{i\sigma }^{†}(c_{i\sigma })$ create (annihilate) fermions at site i with spin σ = ↑, ↓ and $n_{i\sigma }=c_{i\sigma }^{†}{c}_{i\sigma }$. The ratio t′/t is about 0.3 for most of the cuprates, with the exception of LSCO where it is closer to 0.15. Empirically, T_c grows with the value of t′/t [55]. The Hubbard parameter U is comparable with the bandwidth, so we deal with the most theoretically demanding case of intermediately strong correlations.

Arguably the simplest approach to correlated electrons is dynamical mean-field theory (DMFT) where the lattice problem is mapped onto a single-site effective impurity problem with self-consistent determined characteristics [56]. For cuprates, however, the minimal DMFT model should start with a 2 × 2 plaquette rather than a single site since the d-wave SC order parameter lives on bonds rather than on sites [57]. There have been an enormous number of cluster DMFT calculations, the corresponding references for which can be found in [58, 59]. Rather than discussing numbers, we focus here on an interesting observation [60]; that for the values of t′/t near 0.3 and a realistic value of U, the ground state of the minimal plaquette is degenerate, i.e. the ground states for two, three and four electrons on the plaquette coincide. As a result, the plaquette Green’s function has poles at energies close to zero which may be a physical realization of the soft hidden fermion mode suggested earlier phenomenologically [61]. This makes the system in some sense analogous to the Kondo lattice, and this degeneracy plays a role similar to spin degeneracy in the conventional Kondo problem. In particular, making the lattice from such resonant centers naturally explains the appearance of the pseudogap [58, 60].

In the context of the two-fluid concept discussed here, the most important theoretical observation was made in [59] at the numerically exact solution of the many-body problem for a larger, 4 × 4 size plaquette. It turns out that the binding energy of two holes per plaquette is very strongly dependent on the ratio t′/t and can reach values about 0.8t ≈ 0.3 eV which is more than an order of magnitude larger than T_c, as shown explicitly in Figure 2. This means that, at least, for some range of doping, holes build incoherent pairs already in the normal phase. Despite the holes being initially expected to form something similar to a charged Bose liquid, one can suppose that the interaction with the thermal bath makes this liquid rather more classical than of Bose-Einstein character [62].

FIGURE 2

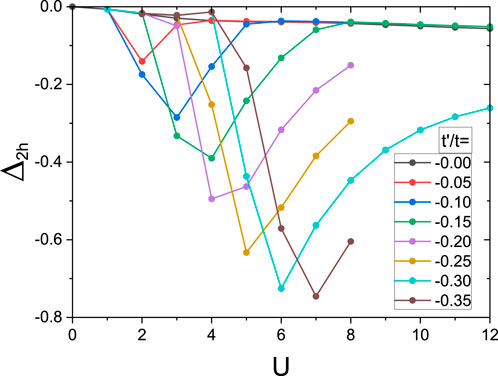
FIGURE 2. Pairing energy Δ_2h of two holes in a 4 × 4 cluster with periodic boundary condition as a function of U and t′. All energies are in units of t ≈ 0.35 eV. Reproduced with permission from [59].

Thus, in general one can propose the following phenomenological picture. The coherent or QP part of the fermionic spectrum is mostly responsible for electron transport in the normal state and completely responsible for its coherent manifestations such as quantum oscillations. The incoherent part, on the other hand, may be associated with the formation of two-hole bound states (one could call them bipolarons but we prefer to avoid any associations with phonons since they do not appear to be relevant in this simplified picture). At high enough temperatures, the Fermi liquid of coherent electron excitations acts as a dissipative environment for the ‘bipolarons’ preventing their Bose-Einstein condensation. The latter can nevertheless occur as the temperature decreases leading ultimately to superconductivity, while the coherent part remains largely untouched. While this picture provides a natural explanation for the presence of the two fluids, it remains to be explored how this incoherent part can play such a prominent role in the magnetic field response [19]. This will be the subject of future studies.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work was supported by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme, grant agreement nos 835279-CATCH-22 (N.E.H.) and 854843-FASTCORR (MK). NEH also acknowledges the support of EPSRC (grant ref. EP/V02986X/1). Finally, JA acknowledges the support of an EPSRC Doctoral Prize Fellowship (Ref. EP/T517872/1).

Acknowledgments

We thank Milan Allan and Alexander Lichtenstein for inspiring discussions.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.1021462/full#supplementary-material

References

1. Tallon JL, Loram JW. The doping dependence of T*: What is the real high-T_c phase diagram? Physica C: Superconductivity (2001) 349:53–68. doi:10.1016/S0921-4534(00)01524-0

CrossRef Full Text | Google Scholar

2. Božović I, He X, Wu J, Bollinger AT. Dependence of the critical temperature in overdoped copper oxides on superfluid density. Nature (2016) 510:309–11. doi:10.1038/nature19061

CrossRef Full Text | Google Scholar

3. Mahmood F, He X, Božović I, Armitage NP. Locating the missing superconducting electrons in the overdoped cuprates La_2−xSr_xCuO₄. Phys Rev Lett (2019) 122:027003. doi:10.1103/PhysRevLett.122.027003

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Manako T, Kubo Y, Shimakawa Y. Transport and structural study of Tl₂Ba₂CuO_6+δ single crystals prepared by the KCl flux method. Phys Rev B (1992) 46:11019–24. doi:10.1103/PhysRevB.46.11019

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Nakamae S, Behnia K, Mangkorntong N, Nohara M, Takagi H, Yates SJC, et al. Electronic ground state of heavily overdoped nonsuperconducting La_2−xSr_xCuO₄. Phys Rev B (2003) 68:100502. doi:10.1103/PhysRevB.68.100502

CrossRef Full Text | Google Scholar

6. Cooper RA, Wang Y, Vignolle B, Lipscombe OJ, Hayden SM, Tanabe Y, et al. Anomalous criticality in the electrical resistivity of La_2−xSr_xCuO₄. Science (2009) 323:603–7. doi:10.1126/science.1165015

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Phillips PW, Hussey NE, Abbamonte P. Stranger than metals. Science (2022) 377:eabh4273. doi:10.1126/science.abh4273

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Hussey NE, Licciardello S, Buhot J. A tale of two metals: Contrasting criticalities in the pnictides and hole-doped cuprates. Rep Prog Phys (2018) 81:052501. doi:10.1088/1361-6633/aaa97c

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Berben M, Smit S, Duffy C, Hsu YT, Bawden L, Heringa F, et al. Superconducting dome and pseudogap endpoint in Bi2201. Phys Rev Mater (2022) 6:044804. doi:10.1103/PhysRevMaterials.6.044804

CrossRef Full Text | Google Scholar

10. Wakimoto S, Yamada K, Tranquada JM, Frost CD, Birgeneau RJ, Zhang H. Disappearance of antiferromagnetic spin excitations in overdoped La_2−xSr_xCuO₄. Phys Rev Lett (2007) 98:247003. doi:10.1103/PhysRevLett.98.247003

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Minola M, Lu Y, Peng YY, Dellea G, Gretarsson H, Haverkort MW, et al. Crossover from collective to incoherent spin excitations in superconducting cuprates probed by detuned resonant inelastic x-ray scattering. Phys Rev Lett (2017) 119:097001. doi:10.1103/physrevlett.119.097001

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Peng YY, Fumagalli R, Ding Y, Minola M, Caprara S, Betto D, et al. Re-entrant charge order in overdoped (Bi, Pb)_2.12Sr_1.88CuO_6+δ outside the pseudogap regime. Nat Mater (2018) 17:697–702. doi:10.1038/s41563-018-0108-3

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Miao H, Fabbris G, Koch RJ, Mazzone DG, Nelson CS, Acevedo-Esteves R, et al. Charge density waves in cuprate superconductors beyond the critical doping. Npj Quan Mater (2021) 6:31. doi:10.1038/s41535-021-00327-4

CrossRef Full Text | Google Scholar

14. Legros A, Benhabib S, Tabis W, Laliberté F, Dion M, Lizaire M, et al. Universal T-linear resistivity and Planckian dissipation in overdoped cuprates. Nat Phys (2019) 15:142–7. doi:10.1038/s41567-018-0334-2

CrossRef Full Text | Google Scholar

15. Putzke C, Benhabib S, Tabis W, Ayres J, Wang Z, Malone L, et al. Reduced Hall carrier density in the overdoped strange metal regime of cuprate superconductors. Nat Phys (2021) 17:826–31. doi:10.1038/s41567-021-01197-0

CrossRef Full Text | Google Scholar

16. Berben M, Ayres J, Duffy C, Hinlopen RDH, Hsu YT, Leroux M, et al. (2022). Compartmentalizing the cuprate strange metal. arXiv:2203.04867 [cond-mat]. Available at: https://arxiv.org/pdf/2203.04867.pdf (Accessed March 10, 2022).

Google Scholar

17. Hayes IM, McDonald RD, Breznay NP, Helm T, Moll PJW, Wartenbe M, et al. Scaling between magnetic field and temperature in the high-temperature superconductor BaFe₂(As_1−xP_x)₂. Nat Phys (2016) 12:916–9. doi:10.1038/nphys3773

CrossRef Full Text | Google Scholar

18. Licciardello S, Maksimovic N, Ayres J, Buhot J, Čulo M, Bryant B, et al. Coexistence of orbital and quantum critical magnetoresistance in FeSe_1−xS_x. Phys Rev Res (2019) 1:023011. doi:10.1103/PhysRevResearch.1.023011

CrossRef Full Text | Google Scholar

19. Ayres J, Berben M, Čulo M, Hsu YT, van Heumen E, Huang Y, et al. Incoherent transport across the strange-metal regime of overdoped cuprates. Nature (2021) 595:661–6. doi:10.1038/s41586-021-03622-z

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Maksimovic N, Hayes IM, Nagarajan V, Analytis JG, Koshelev AE, Singleton J, et al. Magnetoresistance scaling and the origin of H-linear resistivity in BaFe₂(As_1−xP_x)₂. Phys Rev X (2020) 10:041062. doi:10.1103/PhysRevX.10.041062

CrossRef Full Text | Google Scholar

21. Grissonnanche G, Fang Y, Legros A, Verret S, Laliberté F, Collignon C, et al. Linear-in temperature resistivity from an isotropic planckian scattering rate. Nature (2021) 595:667–72. doi:10.1038/s41586-021-03697-8

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Hinlopen RDH, Ayres J, Hinlopen S, Hussey NE. B² to B-linear magnetoresistance due to impeded orbital motion. Phys Rev Res (2022) 4:033195. doi:10.1103/PhysRevResearch.4.033195

CrossRef Full Text | Google Scholar

23. Ataei A, Gourgout A, Grissonnanche G, Chen L, Baglo J, Boulanger ME, et al. (2022). Electrons with Planckian scattering obey standard orbital motion in a magnetic field. arXiv:2203.05035 [cond-mat]. Available at: https://arxiv.org/abs/2203.05035 (Accessed 9 Mar 2022).

CrossRef Full Text | Google Scholar

24. Proust C, Vignolle B, Levallois J, Adachi S, A NE. Fermi liquid behavior of the in-plane resistivity in the pseudogap state of YBa₂Cu₄O₈. Proc Natl Acad Sci U S A (2016) 113:13654–9. doi:10.1073/pnas.1602709113

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Tallon JL, Loram JW, Panagopoulos C. Pseudogap and quantum-transition phenomenology in HTS cuprates. J Low Temp Phys (2003) 131:387–94. doi:10.1023/a:1022970312795

CrossRef Full Text | Google Scholar

26. Chen SD, Hashimoto M, He Y, Song D, Xu KJ, He JF, et al. Incoherent strange metal sharply bounded by a critical doping in Bi2212. Science (2019) 366:1099–102. doi:10.1126/science.aaw8850

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Ando Y, Kurita Y, Komiya S, Segawa K. Evolution of the Hall coefficient and the peculiar electronic structure of the cuprate superconductors. Phys Rev Lett (2004) 92:197001. doi:10.1103/PhysRevLett.92.197001

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Sebastian SE, Proust C. Quantum oscillations in hole-doped cuprates. Annu Rev Condens Matter Phys (2015) 6:411–30. doi:10.1146/annurev-conmatphys-030212-184305

CrossRef Full Text | Google Scholar

29. Abdel-Jawad M, Kennett MP, Balicas L, Carrington A, Mackenzie AP, McKenzie RH, et al. Anisotropic scattering and anomalous normal-state transport in a high-temperature superconductor. Nat Phys (2006) 2:821–5. doi:10.1038/nphys449

CrossRef Full Text | Google Scholar

30. Vignolle B, Carrington A, Cooper RA, French MMJ, Mackenzie AP, Jaudet C, et al. Quantum oscillations in an overdoped high-T_c superconductor. Nature (2008) 455:952–5. doi:10.1038/nature07323

CrossRef Full Text | Google Scholar

31. Peets DC, Mottershead JDF, Wu B, Elfimov IS, Liang R, Hardy WN, et al. Tl₂Ba₂CuO_6+δ brings spectroscopic probes deep into the overdoped regime of the high-T_c cuprates. New J Phys (2007) 9:28. doi:10.1088/1367-2630/9/2/028

CrossRef Full Text | Google Scholar

32. Badoux S, Tabis W, Laliberté F, Grissonnanche G, Vignolle B, Vignolles D, et al. Change of carrier density at the pseudogap critical point of a cuprate superconductor. Nature (2016) 531:210–4. doi:10.1038/nature16983

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Čulo M, Duffy C, Ayres J, Berben M, Hsu YT, Hinlopen RDH, et al. Possible superconductivity from incoherent carriers in overdoped cuprates. Scipost Phys (2021) 11:012. doi:10.21468/SciPostPhys.11.1.012

CrossRef Full Text | Google Scholar

34. Lee-Hone NR, Özdemir HU, Mishra V, Broun DM, Hirschfeld PJ. Low energy phenomenology of the overdoped cuprates: Viability of the landau-bcs paradigm. Phys Rev Res (2020) 2:013228. doi:10.1103/physrevresearch.2.013228

CrossRef Full Text | Google Scholar

35. Mahmood F, Ingram D, He X, Clayhold JA, Božović I, Armitage NP. Effect of radiation-induced defects on the superfluid density and optical conductivity of overdoped La_2−xSr_xCuO₄. Phys Rev B (2022) 105:174501. doi:10.1103/PhysRevB.105.174501

CrossRef Full Text | Google Scholar

36. Tromp WO, Benschop T, Ge JF, Battisti I, Bastiaans KM, Chatzopoulos D, et al. (2022). Puddle formation, persistent gaps, and non-mean-field breakdown of superconductivity in overdoped (Pb,Bi)₂Sr₂CuO_6+δ. arXiv:2005.09470 [cond-mat]. Available at: https://arxiv.org/abs/2205.09740?context=cond-mat (Accessed 19 May 2022).

Google Scholar

37. Pelc D, Popčević P, Požeki M, Greven M, Barišić N. Unusual behavior of cuprates explained by heterogeneous charge localization. Sci Adv (2019) 5:eaau4538. doi:10.1126/sciadv.aau4538

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Abrikosov AA, Gorkov LP, Dzyaloshinski IE. Methods of quantum field theory in statistical physics. New York, NY: Dover (1975).

Google Scholar

39. Nozieres P. Theory of interacting Fermi systems. New York: W. A. Benjamin (1964).

Google Scholar

40. Migdal AB. Theory of finite Fermi systems and application to atomic nuclei. New York: John Wiley (1967).

Google Scholar

41. Zaanen J, Sun YW, Liu Y, Schalm K. Holographic duality in condensed matter physics. Cambridge U.K.: Cambridge University Press (2015).

Google Scholar

42. Hartnoll SA, Lucas A, Sachdev S. Holographic quantum matter. Cambridge MA: The MIT Press (2018).

Google Scholar

43. Luttinger JM, Ward JC. Ground-state energy of a many-fermion system. II. Phys Rev (1960) 118:1417–27. doi:10.1103/PhysRev.118.1417

CrossRef Full Text | Google Scholar

44. Carneiro GM, Pethick CJ. Specific heat of a normal Fermi liquid. II. Microscopic approach. Phys Rev B (1975) 11:1106–24. doi:10.1103/PhysRevB.11.1106

CrossRef Full Text | Google Scholar

45. Kadanoff LP, Baym G. Quantum statistical mechanics: Green’s function methods in equilibrium and nonequilibrium problems. New York: W. A. Benjamin (1962).

Google Scholar

46. Vonsovski SV, Katsnelson MI. Single-electron density matrix and the metal-insulator criterion for crystalline solids. Sov Phys Usp (1989) 32:720–2. doi:10.1070/PU1989v032n08ABEH002749

CrossRef Full Text | Google Scholar

47. Basov DN, Averitt RD, van der Marel D, Dressel M, Haule K. Electrodynamics of correlated electron materials. Rev Mod Phys (2011) 83:471–541. doi:10.1103/RevModPhys.83.471

CrossRef Full Text | Google Scholar

48. Katsnelson MI, Irkhin VY, Chioncel L, Lichtenstein AI, de Groot RA. Half-metallic ferromagnets: From band structure to many-body effects. Rev Mod Phys (2008) 80:315–78. doi:10.1103/RevModPhys.80.315

CrossRef Full Text | Google Scholar

49. Chioncel L, Sakuraba Y, Arrigoni E, Katsnelson MI, Oogane M, Ando Y, et al. Nonquasiparticle states in Co₂MnSi evidenced through magnetic tunnel junction spectroscopy measurements. Phys Rev Lett (2008) 100:086402. doi:10.1103/PhysRevLett.100.086402

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Fujiwara H, Terashima K, Sunagawa M, Yano Y, Nagayama T, Fukura T, et al. Origins of thermal spin depolarization in half-metallic ferromagnet CrO₂. Phys Rev Lett (2018) 121:257201. doi:10.1103/PhysRevLett.121.257201

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Stewart GR. Heavy fermion systems. Rev Mod Phys (1984) 56:755–87. doi:10.1103/RevModPhys.56.755

CrossRef Full Text | Google Scholar

52. Tsunetsugu H, Sigrist M, Ueda K. The ground-state phase diagram of the one-dimensional Kondo lattice model. Rev Mod Phys (1997) 69:809–64. doi:10.1103/RevModPhys.69.809

CrossRef Full Text | Google Scholar

53. Coleman P, Andrei N. Kondo-stabilised spin liquids and heavy fermion superconductivity. J Phys : Condens Matter (1989) 1:4057–80. doi:10.1088/0953-8984/1/26/003

CrossRef Full Text | Google Scholar

54. Andersen OK, Liechtenstein AI, Jepsen O, Paulsen F. LDA energy bands, low-energy Hamiltonians, t′, t′′, t_⊥(k), and J_⊥. J Phys Chem Sol (1995) 56:1573–91. doi:10.1016/0022-3697(95)00269-3

CrossRef Full Text | Google Scholar

55. Pavarini E, Dasgupta I, Saha-Dasgupta T, Jepsen O, Andersen OK. Band-Structure trend in hole-doped cuprates and correlation with $T_c^{\text{max}}$. Phys Rev Lett (2001) 87:047003. doi:10.1103/PhysRevLett.87.047003

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Georges A, Kotliar G, Krauth W, Rozenberg MJ. Dynamical mean-field theory of strongly correlated fermion systems and the limit of infinite dimensions. Rev Mod Phys (1996) 68:13–125. doi:10.1103/RevModPhys.68.13

CrossRef Full Text | Google Scholar

57. Lichtenstein AI, Katsnelson MI. Antiferromagnetism and d-wave superconductivity in cuprates: A cluster dynamical mean-field theory. Phys Rev B (2000) 62:R9283–6. doi:10.1103/PhysRevB.62.R9283

CrossRef Full Text | Google Scholar

58. Harland M, Brener S, Katsnelson MI, Lichtenstein AI. Exactly solvable model of strongly correlated d-wave superconductivity. Phys Rev B (2020) 101:045119. doi:10.1103/PhysRevB.101.045119

CrossRef Full Text | Google Scholar

59. Danilov M, van Loon EGCP, Brener S, Iskakov S, Katsnelson MI, Lichtenstein AI. Degenerate plaquette physics as key ingredient of high-temperature superconductivity in cuprates. Npj Quan Mater (2022) 7:50. doi:10.1038/s41535-022-00454-6

CrossRef Full Text | Google Scholar

60. Harland M, Katsnelson MI, Lichtenstein AI. Plaquette valence bond theory of high-temperature superconductivity. Phys Rev B (2016) 94:125133. doi:10.1103/PhysRevB.94.125133

CrossRef Full Text | Google Scholar

61. Sakai S, Civelli M, Imada M. Hidden Fermionic excitation boosting high-temperature superconductivity in cuprates. Phys Rev Lett (2016) 116:057003. doi:10.1103/PhysRevLett.116.057003

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Wheatley JM. Statistics in a dissipative medium. Phys Rev B (1990) 41:7301–3. doi:10.1103/PhysRevB.41.7301

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Bernhard C, Tallon JL, Blasius T, Golnik A, Niedermayer C. Anomalous peak in the superconducting condensate density of cuprate high-T_c superconductors at a unique doping state. Phys Rev Lett (2001) 86:1614–7. doi:10.1103/PhysRevLett.86.1614

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Ramshaw BJ, Sebastian SE, McDonald RD, Day J, Tan BS, Zhu Z, et al. Quasiparticle mass enhancement approaching optimal doping in a high-T_c superconductor. Science (2015) 348:317–20. doi:10.1126/science.aaa4990

PubMed Abstract | CrossRef Full Text | Google Scholar