Locally resonant metasurface for low-frequency transmissive underwater acoustic waves

Introduction: Acoustic metasurfaces for underwater wave manipulation have great potential use, but the strong solid-fluid interaction caused by impedance closeness between the structure and water brings design difficulty, especially in the low-frequency range.

Methods: Here a locally resonant metasurface for transmissive underwater acoustic waves is proposed using finite element method for which each metasurface unit consists of one channel and three subunits. Each subunit has one plate and two rubber spacers to form a resonator. By changing the height ratio of the plate over the subunit, arbitrary phase shifts within the full 2π coverage can be obtained at will with transmission ratio always higher than 60%.

Results: Three applications, including asymmetric transmission, self-bending, and source illusion, are chosen to validate the design methodology.

Discussion: Compared with previous transmissive type underwater metasurface, this design has the advantage of low frequency and simple fabrication. This work provides a novel paradigm of modulating waves for ocean exploration, underwater communication, and submarine stealth and antidetection.

1 Introduction

There are many achievements associated with using metamaterials and metasurfaces, particularly due to their extraordinary capabilities and subwavelength dimensions. Recently new discoveries in metasurfaces, including anisotropy, nonlocal effects, integer parity property, and exceptional points in a non-Hermitian system [1–6], have extended these capabilities by inducing high-efficiency manipulation [7–9], providing broadband operating ranges [10], and introducing asymmetric transmission [11, 12]. One interesting application is for acoustic metasurface. Most of the acoustic metasurfaces are designed to be used in air, where hard boundary assumptions are valid [13–15]. However, the impedance similarity between water and most solids invalidates such an assumption and makes more difficult underwater metasurface design. To conquer this diffficulty, Dong et al. [16] adopt bottom-up topology optimization method to conceive a broadband underwater pentamode shielding device. Several articles have focused on the manipulation of reflected underwater waves. Zhou et al. [17] investigate the nonlocal effect between the underwater metasurface units induced by the fluid-solid interaction and propose a nonlocal design based on diffraction theory to achieve large-angle anomalous reflection. The metasurface thickness is about 1/15 of the target wavelength. He et al. [18] present theoretical design, numerical simulation, and experimental demonstration of an underwater ultrasound cloaking carpet made of periodic grooves based on metagrating. The groove height is .248 times the wavelength. Dong et al. [19] use multiple elastic mode conversions to achieve reflective metasurfaces with broadband underwater sound absorption. Our team has also designed a resonator-based reflective metasurface for low-frequency underwater acoustic waves covering the full phase shift range [20]. The target frequency can be from 50 to 9000 Hz, which are achieved by changing the parameters of the design. We further improved this design by decreasing the thickness of the metasurface to only 1/61.7 of the target wavelength using rubber spacers [21]. Transmissive underwater metasurfaces have also attracted some interest. Fan and Mei [22] propose a metagrating and an inverse design method to obtain anomalous reflection and highly asymmetric transmission using diffraction theory. Compared to metasurfaces able to modulate phase shifts, the capability of such a metagrating is relatively limited and the metagrating layer is about half of the wavelength. Pentamode materials are another popular paradigm used in transmissive underwater manipulation. Tian et al. [23] employ pentamode materials and a gradient velocity to control refracted waves in a wide frequency range. The metasurface thickness is less than 1/10 of the target wavelength. Chen and Hu [24] design a similar metasuface with half-wavelength thickness and convert cylindrical waves to plane waves experimentally. However, such designs are usually complex to fabricate, and operate in a relatively high-frequency range, several or tens of kilo Hertz, which is inappropriate for long-distance signal communication.

We propose here for the first time a locally resonant metasurface for low-frequency transmissive underwater acoustic waves. The target frequency is as low as 300 Hz. Full phase shift can be covered by changing a single design parameter of one unit and the transmission ratio is always higher than 60%. Asymmetric transmission, self-bending, and source illusion are chosen as three applications to demonstrate the strong ability of the metasurface. This work offers a new means of designing underwater transmissive metasurface and contributes to underwater acoustic devices.

2 Design

One unit of the metasurface considered is illustrated in Figure 1A. It consists a fluid channel bounded of two steel columns, where one column is augmented by attaching three subunits as shown. Each subunit is a resonator made of a cavity capped by a steel plate connected to the supporting structure using two rubber fittings. When an acoustic wave enters the channel, it will induce vibration in the plates. Such vibrations result in a phase shift of the transmitted wave. Since the stiffness of the subunit plate affects the resonance, the ratio r of the plate height w to the subunit height a is chosen as the parameter to control the phase shift of the transmitted wave. The dimensions used here are a = .67 m and L = .4 m, which make the unit very compact compared with the target wavelength λ of 4.937 m. The detailed dimensions of one subunit is given in Supplementary Appendix SA.

FIGURE 1

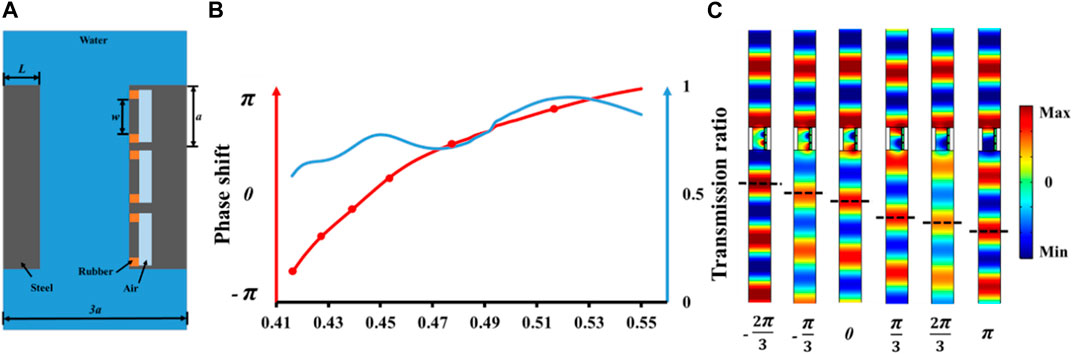
FIGURE 1. One metasurface unit: (A) the material and structure, (B) phase shift and amplitude transmission ratio as a function of ratio r for one unit, (C) normalized simulated pressure field of individual units with phase shift increase of π/3 for the r denoted by red points in (B).

The process of exposing the metasurface to waves is simulated using the commercial finite element software Comsol Multiphysics. Previous study has shown that underwater fluid-solid interaction can cause strong nonlocal influence between the metasurface units, leading to phenomena hard to predict analytically [17]. Periodic boundary conditions, which are widely used when simulating the response of airborne metasurface units, assume the nodes along the two boundaries share the same displacement. This is no longer always valid in underwater situations since the different neighboring unit has different influence [17]. For this reason, in our finite element model, periodic boundary conditions are imposed only on the two sides of the water area in Figure 1A, not on the steel part. The two columns are designed to be thick to minimize the nonlocal influence. The Acoustic-Solid Interaction module is used in Comsol and Perfect Matched Layers (PMLs) are put on the top and bottom of the water area (not shown). To make the model closer to reality, the loss effect induced by the rubber is also considered. The properties used for the steel and rubber are as follows. The associated Young’s moduli are 205 GPa and .05*(1 + .02i) GPa, the associate densities are 7,850 and 1,100 kg/m³, and the associated Poisson’s ratios are .28 and .4, respectively. Using the proposed finite element model, the phase shift and transmission ratio as functions of the ratio r are plotted in Figure 1B for the unit cell. The figure indicates that any arbitrary phase shift in the 2π range can be obtained by choosing a corresponding ratio r between .416 and .55. Also, the figure indicates that the amplitude transmission ratio is always above 60%, guaranteeing energy transmission efficiency. The normalized pressure profile of 6 units with equally distributed phase shift in the 2π range is displayed in Figure 1C, corresponding to the red dots in Figure 1B. Resonance mode shape around 300 Hz, displacement magnitude and energy flux at 300 Hz of the side with rubber and plate is displayed in Supplementary Appendix SB. We can see mainly the motion of the plate and the metasurface boundaries affect the wave transmission. The procedure to utilize the metasurface for a specific application can be generalized into three steps. First, based on the target application, the needed phase shift profile is calculated. Second, the profile is discretized and the corresponding parameter r for each segment is figured out using the interpolated function in Figure 1B. Finally, full-wave simulation of the proposed model is completed to make sure the application target is fulfilled with a tolerable error.

3 Applications

The first application considered for the proposed design is asymmetric transmission. When the unit width of the metasurface is far less than the target wavelength, the principle of a wave passing through the metasurface interface can be described by Generalized Snell’s Law

$\sin {\theta }_i=\sin {\theta }_t-G$

where ${\theta }_i$, ${\theta }_t$, and G are the incident angle, transmitted angle, and the reciprocal lattice vector, respectively. When the period length is comparable to the target wavelength with an incident angle larger than the critical angle, high order diffraction occurs and the Generalized Snell’s Law needs to be modified as

$\sin {\theta }_i=\sin {\theta }_t-nG$

where n is the diffraction order, an integer in the range ($-\infty ,1$]. The number of times the waves pass through the medium, L, can be calculated by

$L=m+n$

where m is the number of metasurface units in one supercell. This means whether the wave is transmitted or reflected is related to the integer parity of the number of units per period. Here we choose the incident angle to be $\pm$30° and m to be 3. The r values for the 3 units are .4143, .4385, and .4759 with an increment of phase shift to be 2π/3. When the incident angle is $-$30°, less than the critical angle, the wave can pass the metasurface directly with L = 1. When the incident angle is 30°, larger than the critical angle, high order diffraction happens and n = $-$1. In this case, L is equal to 2, meaning the wave passes the metasurface twice. No transmitted wave can be observed. The schematic diagram and full-wave simulations of asymmetric transmission are shown in Figure 2. It is worth mentioning that the loss in the rubber also helps the asymmetric transmission. One previous research has shown that asymmetric wave behavior can stem from loss-induced suppression of high-order diffraction in the airborne metasurface[11]. We also tried the full-wave simulation of the model with lossless rubber material (See Supplementary Appendix SC). Asymmetric transmission is still observed, but more waves can be transmitted after removing the loss effect. Therefore, if the asymmetric transmission is the target application of the metasurface, rubber with loss is a better choice than the lossless one.

FIGURE 2

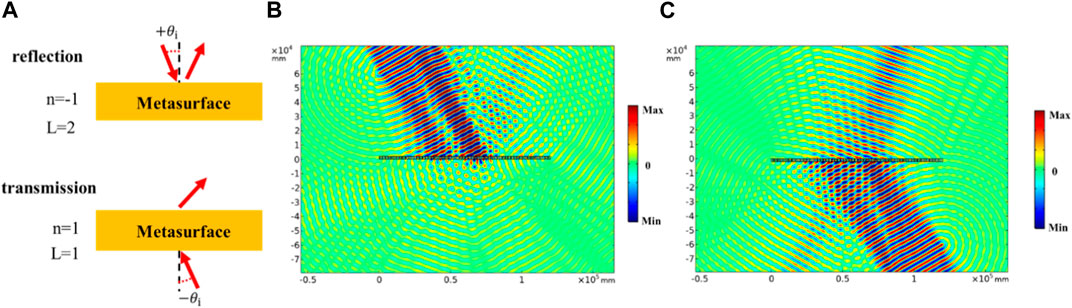
FIGURE 2. Asymmetric transmission: (A) schematic diagram, (B) normalized total acoustic pressure field under a wave with the incident angle equal to 30°, and (C) normalized total acoustic pressure field under a wave with the incident angle equal to $-$30°.

The second application is a self-bending beam, which is useful to bypass obstacles for underwater communication. By tracing individual caustic rays [25], the phase shift to form a circular bending beam can be calculated as

$\mathrm{\phi }\left(x\right)=-k\left(x-2Rk\sqrt{\frac{x}{R}}\right)(2)$

where k is the wave number, x describes the position of the metasurface unit and R is the radius of the objective circle. Here R is chosen to be 5λ and 50 metasurface units are adopted. The pressure distribution under a unit pressure vertical upward incident wave is displayed in Figure 3. The inset illustrates the parameter r values along the design. A bending beam is clearly observed. It deviates from the theoretical target line because 50 metasurface units are used instead of continuous phase shifts. This beam can easily travel around some obstacles without being reflected, validating this function for the designed metasurface.

FIGURE 3

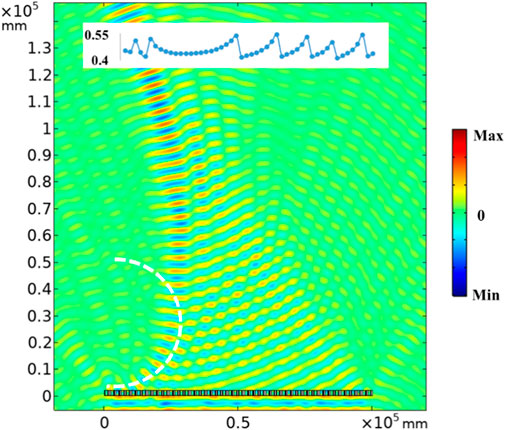
FIGURE 3. Normalized self-bending beam pressure distribution under an upward incident wave. The design target is the white half circle with a radius equal to 5λ. The inset shows the r values of the designed metasurface.

Another application of the metasurface is source illusion. For instance, a point source can be transformed to a prescribed wavefront. Here we surround the point source by the proposed metasurface in a circular pattern. To give an additional integer angular momentum to the point source, the phase shift introduced by the metasurface should be

$\mathrm{\phi }\left(x\right)=P\theta$

where P is the additional angular momentum and θ is the angular position with the point source at the origin. This means the wave experiences a phase shift of 2πP after traveling around one cycle in the azimuthal direction. The full-wave simulations of the acoustic field excited by a point source at the center are illustrated in Figure 4 with p = 6 or 4. Outside the metasurface circle, the cylindrical wave is reconstructed to a spiral wave with six or four branches, equal to the corresponding additional momentum L. The observer is unable to perceive the actual source type inside the metasurface circle, which verifies the function of the design.

FIGURE 4

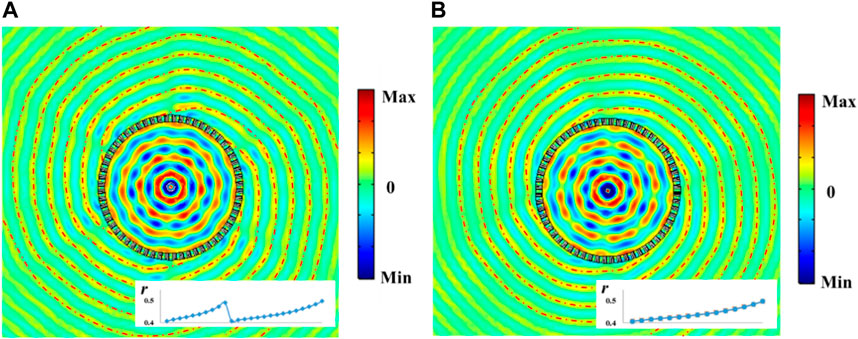
FIGURE 4. Source illusion: Normalized pressure field of a point source reconstructed to a spiral wave front with different angular momentums: (A) p = 6, (B) p = 4.

Although the metasurface is designed for 300 Hz, it can work in a relatively wide range. For instance, the self-bending beam function of the metasurface working under 260, 280, 320, and 350 Hz is shown in Figure 5. Obvious self-bending phenomena are observed in such frequency range. Another interesting observation is, the radius of the bending beam is related to the working frequency. The radius decreases as the frequency rises. This phenomenon is similar to the experimental results in [26], in which the focal length of the underwater metasurface also decreases as the frequency rises. This phenomenon endows such metasurfaces with one more degree of freedom, namely the frequency, to control the pressure field flexibly.

FIGURE 5

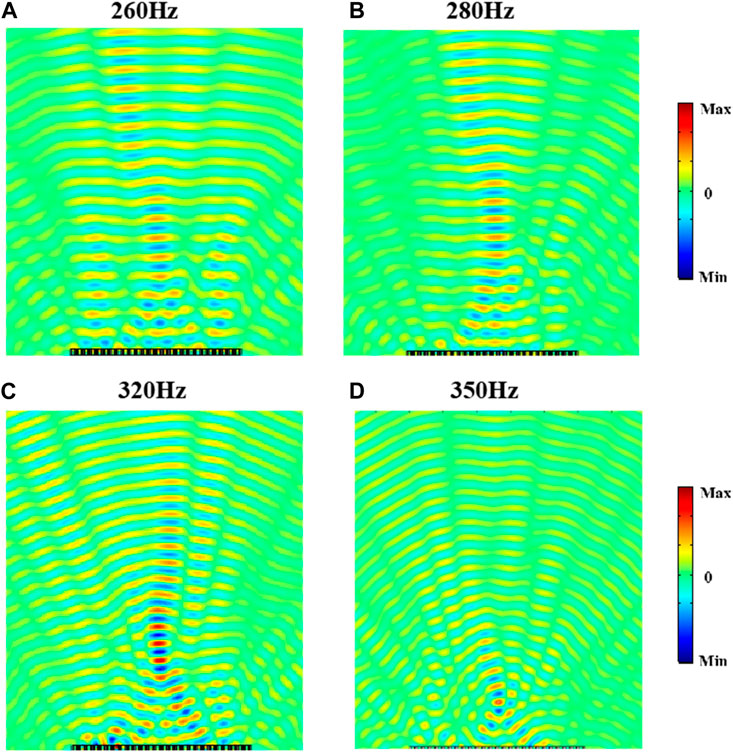
FIGURE 5. Normalized pressure field of the proposed self-bending beam metasurface structure working under different frequencies ((A–D) for 260 Hz, 280 Hz, 320 Hz and 350 Hz, respectively).

4 Conclusion

A locally resonant metasurface for manipulating low-frequency underwater waves is devised. In this design, the phase of the transmitted wave can be tailored by adjusting the height ratio of the steel resonating plate and the connecting rubber support in each metasurface unit. Asymmetric transmission, self-bending, and source illusion are chosen as demonstrations of applications of the design. Simulated results agree well with theoretical predictions. Three applications are demonstrated. Asymmetric transmission empowers an object to receive information from outside without sending out wave signals. Self-bending beams can help waves surpass obstacles to establish communication. The source illusion effect can be used for submarines to create misleading signals when there is a passive sonar being used to receive waves to detect them. Besides, here we design the dimensions of the metasurface unit by trial and error. Next, we plan to adopt optimization method by choosing efficiency as the objective function, design parameters as variables to find an optimal design. Similarly, we can adopt a multi-objective optimization method to further expand working bandwidth. The target wave pattern under different frequencies can be chosen as objective functions. This design has broad potential applications in areas of low-frequency underwater wave manipulation after further improvement.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author contributions

ZC and MN contributed to conception and design of the study. SG and ZG organized the database. QX performed the statistical analysis. ZC wrote the first draft of the manuscript. ZL provided funding. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work was supported by National Natural Science Foundation of China (Grant Nos 12172008 and 11991033).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.1098261/full#supplementary-material

References

1. Chen Z, Shao S, Negahban M, Li Z. Tunable metasurface for acoustic wave redirection, focusing and source illusion. J Phys D: Appl Phys (2019) 52(39):395503. doi:10.1088/1361-6463/ab2abd

CrossRef Full Text | Google Scholar

2. Liu Y, Liang Z, Zhu J, Xia L, Mondain-Monval O, Brunet T, et al. Willis metamaterial on a structured beam. Phys Rev X (2019) 9(1):011040. doi:10.1103/physrevx.9.011040

CrossRef Full Text | Google Scholar

3. Li B, Hu Y, Chen J, Su G, Liu Y, Zhao M, et al. Efficient asymmetric transmission of elastic waves in thin plates with lossless metasurfaces. Phys Rev Appl (2020) 14(5):054029. doi:10.1103/physrevapplied.14.054029

CrossRef Full Text | Google Scholar

4. Schwan L, Umnova O, Boutin C, Groby JP. Nonlocal boundary conditions for corrugated acoustic metasurface with strong near-field interactions. J Appl Phys (2018) 123(9):091712. doi:10.1063/1.5011385

CrossRef Full Text | Google Scholar

5. Lissek H, Rivet E, Laurence T, Fleury R. Toward wideband steerable acoustic metasurfaces with arrays of active electroacoustic resonators. J Appl Phys (2018) 123(9):091714. doi:10.1063/1.5011380

CrossRef Full Text | Google Scholar

6. Gerard NJRK, Li Y, Jing Y. Investigation of acoustic metasurfaces with constituent material properties considered. J Appl Phys (2018) 123(12):124905. doi:10.1063/1.5007863

CrossRef Full Text | Google Scholar

7. Li J, Diaz-Rubio A, Shen C, Jia Z, Tretyakov S, Cummer S. Highly efficient generation of angular momentum with cylindrical bianisotropic metasurfaces. Phys Rev Appl (2019) 11(2):024016. doi:10.1103/physrevapplied.11.024016

CrossRef Full Text | Google Scholar

8. Li J, Shen C, Diaz-Rubio A, Tretyakov SA, Cummer SA. Systematic design and experimental demonstration of bianisotropic metasurfaces for scattering-free manipulation of acoustic wavefronts. Nat Commun (2018) 9(1):1342. doi:10.1038/s41467-018-03778-9

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Quan L, Alù A. Passive acoustic metasurface with unitary reflection based on nonlocality. Phys Rev Appl (2019) 11(5):054077. doi:10.1103/physrevapplied.11.054077

CrossRef Full Text | Google Scholar

10. Zhu H, Patnaik S, Walsh TF, Jared BH, Semperlotti F. Nonlocal elastic metasurfaces: Enabling broadband wave control via intentional nonlocality. Proc Natl Acad Sci (2020) 117(42):26099–108. doi:10.1073/pnas.2004753117

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Li Y, Shen C, Xie Y, Li J, Wang W, Cummer SA, et al. Tunable asymmetric transmission via lossy acoustic metasurfaces. Phys Rev Lett (2017) 119(3):035501. doi:10.1103/PhysRevLett.119.035501

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Wang X, Fang X, Mao D, Jing Y, Li Y. Extremely asymmetrical acoustic metasurface mirror at the exceptional point. Phys Rev Lett (2019) 123(21):214302. doi:10.1103/physrevlett.123.214302

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Chen D-C, Zhu XF, Wei Q, Yao J, Wu DJ. Broadband tunable focusing lenses by acoustic coding metasurfaces. J Phys D: Appl Phys (2020) 53(25):255501. doi:10.1088/1361-6463/ab8247

CrossRef Full Text | Google Scholar

14. Liu P, Chen X, Xu W, Pei Y. Magnetically controlled multifunctional membrane acoustic metasurface. J Appl Phys (2020) 127(18):185104. doi:10.1063/1.5145289

CrossRef Full Text | Google Scholar

15. Han Y, Wang X, Xie G, Tang X, Chen T. Low-frequency sound-absorbing metasurface with a channel of nonuniform cross section. J Appl Phys (2020) 127(6):064902. doi:10.1063/1.5119408

CrossRef Full Text | Google Scholar

16. Dong H-W, Zhao SD, Miao XB, Shen C, Zhang X, Zhao Z, et al. Customized broadband pentamode metamaterials by topology optimization. J Mech Phys Sol (2021) 152:104407. doi:10.1016/j.jmps.2021.104407

CrossRef Full Text | Google Scholar

17. Zhou H-T, Fu WX, Wang YF, Wang YS. High-efficiency ultrathin nonlocal waterborne acoustic metasurface. Phys Rev Appl (2021) 15(4):044046. doi:10.1103/physrevapplied.15.044046

CrossRef Full Text | Google Scholar

18. He J, Jiang X, Ta D, Wang W. Experimental demonstration of underwater ultrasound cloaking based on metagrating. Appl Phys Lett (2020) 117(9):091901. doi:10.1063/5.0021002

CrossRef Full Text | Google Scholar

19. Dong H-W, Zhao SD, Oudich M, Shen C, Zhang C, Cheng L, et al. Reflective metasurfaces with multiple elastic mode conversions for broadband underwater sound absorption. Phys Rev Appl (2022) 17(4):044013. doi:10.1103/physrevapplied.17.044013

CrossRef Full Text | Google Scholar

20. Chen Z, Yan F, Negahban M, Li Z. Resonator-based reflective metasurface for low-frequency underwater acoustic waves. J Appl Phys (2020) 128(5):055305. doi:10.1063/5.0006523

CrossRef Full Text | Google Scholar

21. Chen Z, Yan F, Negahban M, Li Z. Extremely thin reflective metasurface for low-frequency underwater acoustic waves: Sharp focusing, self-bending, and carpet cloaking. J Appl Phys (2021) 130(12):125304. doi:10.1063/5.0041092

CrossRef Full Text | Google Scholar

22. Fan L, Mei J. Metagratings for waterborne sound: Various functionalities enabled by an efficient inverse-design approach. Phys Rev Appl (2020) 14(4):044003. doi:10.1103/physrevapplied.14.044003

CrossRef Full Text | Google Scholar

23. Tian Y, Wei Q, Cheng Y, Xu Z, Liu X. Broadband manipulation of acoustic wavefronts by pentamode metasurface. Appl Phys Lett (2015) 107(22):221906. doi:10.1063/1.4936762

CrossRef Full Text | Google Scholar

24. Chen Y, Hu G. Broadband and high-transmission metasurface for converting underwater cylindrical waves to plane waves. Phys Rev Appl (2019) 12(4):044046. doi:10.1103/physrevapplied.12.044046

CrossRef Full Text | Google Scholar

25. Li Y, Jiang X, Liang B, Cheng J, Zhang L. Metascreen-based acoustic passive phased array. Phys Rev Appl (2015) 4(2):024003. doi:10.1103/physrevapplied.4.024003

CrossRef Full Text | Google Scholar

26. Wu X, Xia X, Tian J, Liu Z, Wen W. Broadband reflective metasurface for focusing underwater ultrasonic waves with linearly tunable focal length. Appl Phys Lett (2016) 108(16):163502. doi:10.1063/1.4947437

CrossRef Full Text | Google Scholar