Measuring the Competitive Advantage of Countries Along the Belt and Road From the Perspective of Complex Social Networks

For the Belt and Road Initiative, “extensive consultation, joint contribution and shared benefits” is the basic principle, and the competitiveness heterogeneity is an important condition for cooperation. Based on the complex network theory, this paper constructs a complex network model of global value chain (GVC) division of labor system by using the Multi-Regional Input-output (MRIO) table, and reveals the variation trend of competitiveness of industrial sectors and economies on the GVC network by the National Competitive Advantage Index (NCAI). The results verify the effectiveness of BRI, and help countries along the B&R route to explore their comparative advantages and cooperation prospects with other countries. The research also provides a direction and reference for China to better implement the Initiative.

Introduction

Complex and profound changes are taking place in the world. The underlying impact of the international financial crisis keeps emerging; the world economy is recovering slowly, and global development is uneven; the international trade and investment landscape and rules for multilateral trade and investment are undergoing major adjustments; and countries still face big challenges to their development. The Belt and Road Initiative (BRI) refers to the Silk Road Economic Belt and 21st Century Maritime Silk Road proposed by Chinese President Xi Jinping in September and October 2013 respectively, aiming to share the development opportunities with countries along the route and achieve common prosperity [1].

The production systems of various countries and regions in the world have maintained relative independence for a long period of time. But with the continuous development of global economic integration, a global economic system has been established through the increasingly frequent trade exchanges among countries and regions. Also, the industrial value chains of different subsystems are interconnected, together forming the global value chain (GVC) network, an organic whole with specific functions. In recent years, the research on GVC network has been developing rapidly, and has been gradually extended from enterprise management level to industrial and national level. GVC network can not only reflect the topology of the global economic system, but also be highly applicable in theoretical framework and practical analysis. The promotion of the Multi-Regional Input-Output (MRIO) database has enabled the in-depth study on complex relationships among economies on the GVC network from the perspective of system science.

The measurement of GVC is a hot topic in the studies of complex relationships among economies in the GVC network. Most of the existing studies have used quantitative analysis methods in economics and statistics to conduct data studies from the macro level, and proposed a relatively systematic approach for GVC measurement [2–5]. From the perspective of system science, these methods are mainly based on reductionism—they measure the functions and positions of countries and sectors on the GVC through input-output analysis of established industrial and trade structures. However, they can hardly examine the structural relationships and operational mechanisms among industries within the GVC in a comprehensive and systematic way, or forecast the future trends of industrial transfer. Hence, except for the reductionist approach, systems theory shall be adopted to analyze socioeconomic issues, taking into account the complexity, structure, hierarchy and synergy within the global economic system.

This paper will therefore construct a Global Industrial Value Chain Network by using the complex network in the systems theory as the modeling framework and MRIO statistics as the database, and propose the National Competitive Advantage Index (NCAI) to reveal the competitive relationship, status and variation trend of industrial sectors and economies in the GVC, and identify the advantageous capacity. By analyzing the changes in NCAI of different countries before and after joining the Belt and Road Agreement, it provides a reference for countries to carry out cross-regional capacity cooperation, improve the quality and level of cooperation, and optimize economic structural adjustment.

Literature Review

Industrial Complementary Convergence and Integration

After the BRI was proposed, the comparative advantages and complementary relationship among industries in countries along the BRI have aroused the attention of many scholars. Kurihara and Fukushima found that industrial transfer can improve regional coordination, lift labor productivity in the places where industries are transferred, enhance diversification, and spur regional economic development [6]. By evaluating the effectiveness of infrastructure investment in Asian countries under the BRI at the global level, Yang et al. found that most of the countries or regions have embraced higher level of economic growth, welfare, export trade and trade conditions to different degrees, which has boosted China’s export trade and strengthened the trade interdependence among the countries along the BRI [7, 8]. Liu and Xin’s research have shown that the BRI will not only bring about changes in trade but also increase the total factor productivity of China’s provinces along the B&R route [9]. Taking the “Rong Ou” (Chengdu-Europe Fast Rail) strategy as an example, Deng et al. discusses how BRI can help capacity shift towards the inland provinces of China and promoted the rebound of trade with Europe [10]. Yao et al. analyzed the industrial convergence and synergistic development between China and countries along the B&R route by using social network analysis and MRIO tables. They found that not only the industrial integration between China and the BRI-related countries has been deepened and expanded, but also the economic circle brought by integration and interaction has been extended [11]. It can thus be concluded that BRI will bring about changes in the direction and scale of industrial transfer, especially for the less developed regions along the route. Every step forward under the BRI accelerates industrial restructuring and will affect whether the strategic goal of coordinated regional development can be achieved. However, few studies have touched upon the industrial competitive advantages and variation trends of countries or regions along the route, providing little guidance to countries or regions on industrial complementation and integration.

Application of Complex Networks in the Study of Industrial Relations

Complex network has been a trendy topic in fields such as statistical physics and social sciences. As the structural properties of real networks are understood better, various dynamical behaviors on networks, such as evolutionary game, disease propagation, synchronization, etc., have received wide attention. The study of complex net-work dynamics can provide insights into many phenomena in nature and human society [12, 13] such as the evolution and maintenance of cooperative behavior, traffic and communication congestion, and the spread of infectious diseases, and give feasible solutions.

In recent years, the study of economic systems using system theory has become a new trend. Many scholars have applied theoretical modeling, dynamics simulation and empirical research in studies based on the research paradigm of complex network theory from the perspectives of industrial development, industrial structure, industrial association, industrial organization, and industrial policy, which have greatly enriched the research content of industrial economics. All kinds of industrial complex network models have been constructed to describe the competitive [14–16] cooperative [17–20] and associative [21–25] relationships among industrial organizations, and a variety of network characteristic indicators and modelling algorithms used to explain specific economic phenomena. In terms of research scope, these studies are mainly limited to the industrial organization level. Most of the studies oversimplify the internal structure of industrial organizations by demonstrating them as un-weighted and undirected networks. The connected edges between nodes only reflect the topological structure and physical statistics features of the network system with a large number of nodes, yet rarely reveal the dynamics mechanisms of information, material and financial flows among economic entities in weighted, directed networks. The intricate techno-economic linkages between industries or enterprises are not reflected in a real sense, resulting in an inability to effectively explain the evolutionary laws of such networks.

Application of MRIO Data in the Study of Industrial Relations

At present, GVC network is witnessing growing trend of vertical division of labor and increasingly complex and close connection between industries, which makes it necessary to study the internal operation mechanism of regional economic system with the quantitative relationship of inputs and outputs between industries and even between countries. The matrix structure of IO data can be directly or slightly modified as the adjacency matrix of IO network model to describe in detail the flow and interaction of value added in all value chains in the economic system, which can then be used to analyze the industrial linkages at the meso level (national or regional IO tables) and macro level (global MRIO tables) of the industrial economy.

As MRIO database becomes widely applied, IO network is used to portraying the economic system not merely of a single country or region, but of inter-regional or even global economic system. For example, Ando measured the importance of industries under aggregate output shocks in the U.S. in the world input-output model [26]; Cerina et al. quantitatively analyzed the sub-network structure and dynamics characteristics of the global network based on community detection techniques, and then used the PageRank centrality algorithm and community core measurement algorithm to identify key industries and economies [27] Grazzini et al. defined the consumption impact index and GDP impact index and, on this basis, investigated the relationship between the robustness of the world input-output network and the relative amount of intermediate goods input [28] Amader and Cabral performed a network analysis on the value added from abroad in exported products and services at the country level and identified the special position of different countries on the GVC network through network structural measures [29] Araújo and Faustino quantitatively analyzed the closeness between industrial sectors through a bipartite graph and assessed the impact of the sovereign financial crisis on Portugal on this basis [30]; Xing et al. quantitatively analyzed the industrial influence of each economy on the GVC network in the MRIO network model with a biased random walk [31], conducted qualitative and quantitative analysis of various trade types and their proportions on the GVC network based on the concept of intermediates in social network analysis [32] and dug in the co-competitive relationships between industrial sectors implied in MRIO data based on citation net-work theory [33]; He et al. analyzed the consumption of resources and environment by industrial sectors in the Beijing-Tianjin-Hebei regional IO network [34]; Tsekeris used network measurement tools such as density, hierarchy, centrality and modularity to identify the main drivers of industrial structural change [35]; Soyyigit et al. introduced the HITS algorithm to the study of MRIO networks to determine the pivotal role of industrial sectors in global value chains and empirically analyzed the fossil fuel and olive oil markets [36, 37] In addition, some scholars have studied GVC networks based on MRIO data from the perspective of complex network theory, and there is a trend that many socioeconomic network research frameworks have emerged in the field of main-stream world economics. For example, Xiao introduces various network measurement tools to the GVC accounting system constructed by Koopman and Wang to analyze the sources of value added in total output from wider perspectives [38].

Network Analysis of GVC Through MRIO

The rise of GVC has naturally captured the attention of international trade economists who are eager to bridge the apparent gap between the new characteristics of the international organization of production and the standard methods used to collect, manipulate, and interpret international trade statistics. In particular, ingenious empirical methods have been proposed in a remarkable body of work to disentangle the value-added and intermediate inputs of international trade flows.

Among related studies, MRIO tables boast the feasibility in measuring both standard and vertical trades. With the availability and utilization of global MRIO database, especially MRIO tables, it is possible to construct quantitative indices to assess its impact on the GVC, because it better depicts the international source and use of intermediate goods than previous databases. As a result, distinctive approaches have been developed in a large number of researches to measure sectors’ function and status amid globalization. Important researches are as follows.

Hummels, et al., focusing on the use of imported inputs in producing export goods, proposed vertical specialization–the first empirical measure of participation in vertically specialized trade [2]. Antràs, et al. derived two distinct approaches to measure industrial upstreamness and proved their significant impacts on trade flows [39]. Fally made quantitative analyses on the average length of production chains, reflecting the number of stages required for production and the number of stages between production and final consumption [40]. Then, he and Hillberry extended the empirical research from across plants to across borders by employing the IDE-JETRO 4-dimensional IO tables [41]. Johnson and Noguera quantified cross-border production linkages with combined IO and bilateral trade data, and computed bilateral trades in value-added [42]. Koopman, et al. adjusted all previous measures of vertical specialization and value-added trade to analyze the back-and-forth trade of intermediates across multiple borders, and presented GVC position and participation indices to gauge the extent to which a national sector is involved in the global production chain. To empirically conduct gross export decomposition, they constructed a global ICIO mainly based on version 7 of the GTAP database [43]. Wang et al. decomposed total production activities with a new framework based on whether related value chains are for pure domestic demand, traditional international trade or simple and complex GVC activities and also introduced their unique but effective participation indices [44]. With the ICIO database updated, we can apply these research frameworks to generate a time series decomposition of gross trade flows into their value-added components.

Furthermore, in the latest research results, scholars analyzed GVC as a weighted network by using the MRIO database. Joao et al. represents GVC as weighted networks of foreign value added in exports and compute the bilateral foreign value added in exports (FV AiX) to quantify the interactions amongst countries in GVCs [45]. Angelidis et al. investigated competitive conditions in GVCs for a period of 15 years (2000–2014), focusing on sector structure, countries’ dominance and diversification. They examined the in- and out-weighted degree centrality and the in- and out-weight entropy in order to determine whether dominant countries are also diversified [46]. Against the backdrop of massive shock to GVC, Xing et al. introduce Weighted Betweenness Centrality of Edge based on Floyd-Warshall Algorithm (RFWA) to measure the Value-Added Pivotability of Input-Output Relations, which brings forth pivotability at domestic, international, and global levels [47].

In summation, the MRIO model reflects in detail the intricate production consumption relationships among industries in each economy in the form of a matrix balance sheet, which is conducive to modeling and analyzing GVC networks in conjunction with the complex network theory in system science, thus improving existing studies in terms of temporal continuity and spatial variability. It provides a powerful tool for research on vertical specialization, international trade and industrial structure optimization. This kind of cross-disciplinary research has already emerged in domestic and international academia.

Data and Modeling

MRIO Table

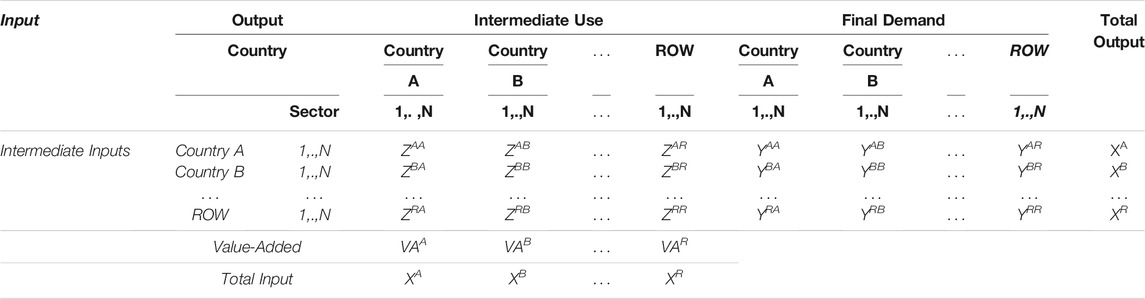
This paper utilizes MRIO data not only for its ability of reshowing flows of intermediate products, final goods, and services but also for possible comparison on the same basis, thanks to which the theoretical and empirical analyses on the GVC become possible. Let us consider a world economy with $m$ countries/regions $\left(u,v=\mathrm{1,2},\dots ,m\right)$, $n$ sectors within each country/region, and totally $N=m\times n$ sectors $\left(i,j=\mathrm{1,2},\dots ,N\right)$, as shown in Table 1.

TABLE 1

TABLE 1. The layout of MRIO table.

In the MRIO table, $Z^{uv}$ is a $n\times n$ matrix of intermediate inputs that are produced in country $u$ and used in country $v$, $Y^{uv}$ is a $n\times 1$ vector giving final products produced in country $u$ and consumed in country $v$, $X^u$ is also a $n\times 1$ vector giving gross outputs in country $u$, and $V{A}^u$ denotes a $n\times 1$ vector of direct value-added in country $u$ [5]. To depict the transmission of value stream on the GVC, we take the region of inter-country inter-^industry use and supply as the modeling data source, i.e., the $Z^{uv}$ matrix, in which row vectors record the allocation of outputs and column vectors the composition of demand.

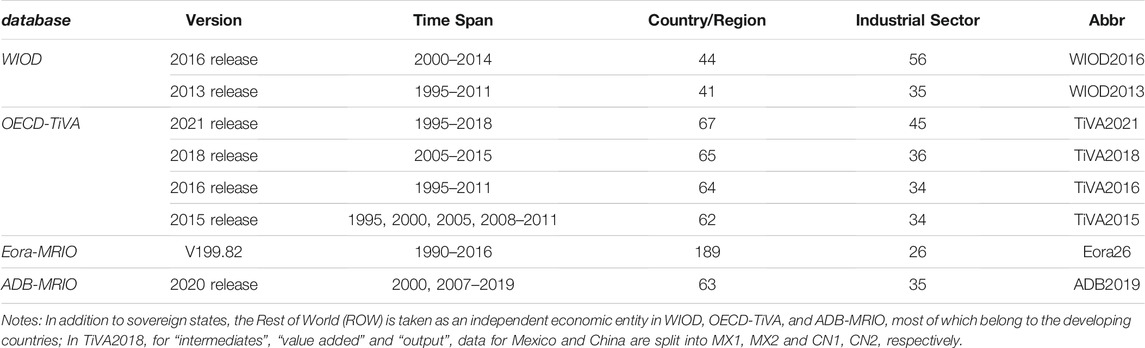
The existing MRIO databases include seven main categories, namely World Input-Output database (WIOD) [48], OECD-WTO database on Trade in Value-Added (TiVA), Eora Multi-Region Input-Output Table database (MRIOV199.82, and the simplified version with 26-sector harmonized classification is named Eora26) [49] Global Trade Analysis Program (GTAP), Asian International Input-Output Table (AIIOT), Asian Development Bank Multi-Regional Input-Output Tables (ADB-MRIO) and Externality Data and Input-Output Tools for Policy Analysis (EXIOPOL). However, only four of them cover both continuous period and wide range as shown in Table 2.

TABLE 2

TABLE 2. The basic information of each MRIO database.

As we all know, BRI is a hotly-debated topic in the field of the global economy, as well as GVC, which is a global development strategy proposed by Chinese government involving infrastructure construction and investments in 152 countries and international organizations in Asia, Europe, Africa, the Middle East, and the Americas. “Belt” refers to the overland routes for road and rail transportation, called “the Silk Road Economic Belt”; “Road” refers to the sea routes or the 21st Century Maritime Silk Road. From the Chinese government’s international viewpoints on politics and economy, BRI is supposed to the developing blueprint that meets the demands of relevant countries and delivers mutual benefits. However, some observers see it as a push for Chinese dominance in global affairs with a China-centered trading network, and even consider BRI as a potential threat to countries involved [50].

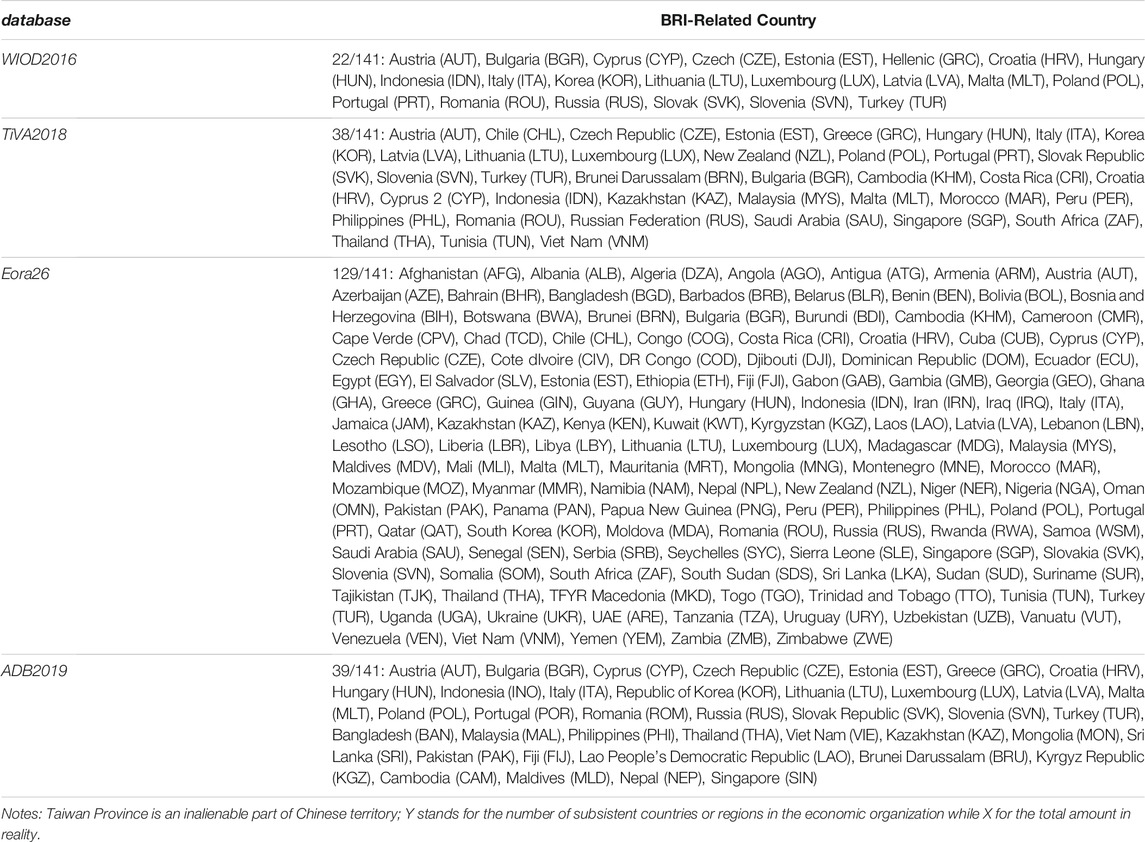
At the end of 2021, there are 141 countries that have signed cooperation agreements with China on Belt and Road Initiative—we call them BRI-related nations. Among MRIO databases (see Table 3), although Eora26 has the widest coverage of countries, including 129 BRI-related nations, its latest version ends with the year of 2016 and many countries didn’t join BRI at that time. We hence use ADB2019 to conduct an empirical analysis of industrial resource competition between them, because it contains the second largest number of countries and more years since 2013.

TABLE 3

TABLE 3. BRI-related country in MRIO database.

MRIO Network

MRIO data have proven itself to be a reliable source for analyzing economic globalization. Thanks to it, sectors all over the world can form a sophisticated GVC, bringing the advantages of simultaneous study on international and domestic economies in detail as a holistic network. To establish an industrial complex network, a sector within a region is considered as a node and the inter-industry IO relation as a tie, and its weight represents the sale and purchase relations between producers and consumers. Thus, a graph $G=(V,E,W)$ containing $n$ nodes is drawn to represent sectors within a nation or region and denote a node set $V$. Pairs of nodes are linked by ties to reflect their interdependencies, thereby forming an asymmetric edge set $E$. However, in valued graphs, a set $E$ can be replaced by weight set $W$, which can be extracted from the region of inter-country and inter-industry use and supply in MRIO table.

Note that, as shown in Figure 1A typical IO or MRIO table includes three different areas, namely value-added, intermediate use, and final demand. It is possible that the whole global economic system can be abstracted to a Multi-Layer Network as shown in Figure 1B, which includes three layers: the Value-Added Layer, the Intermediate Use Layer, and the Final Demand Layer. As shown in Figure 1C the intermediate use layer can be further treated as a puzzle that is made of many single-layer networks out of a multi-layer network, in which the nodes are the countries/regions, the layers are the industrial sectors, and links can be established from sellers to buyers within and across industrial sectors [51, 52]. It thus results in the graph G=(V, E, W), which contains N nodes, the set of nodes as V, the set of edges as E, and the set of weights as W. Because the set of weights W can be used to represent the set of edges E in a weighted network, this paper uses the N × N matrix which reflects the relationship between intermediate inputs and intermediate consumption among countries or regions in the ADB database as the weight set W. It can thus describe the sources of inputs and destinations of outputs in production activities of each industrial sector in the global economic system in a certain period (usually 1 year), and then reveal the interdependent and mutually constraining quantitative relationships among them. As shown in Figure 2, the German tertiary industry sector (manufacturing industry) has always had the largest betweenness centrality in the 12 years. Other larger nodes include the United States, Japan and China; the intermediary centrality of some countries has increased year by year, including Switzerland, Ireland, etc.; regarding the fourth industry sector (service industry), the intermediary centrality of the United States is far greater than that of other countries.

FIGURE 1

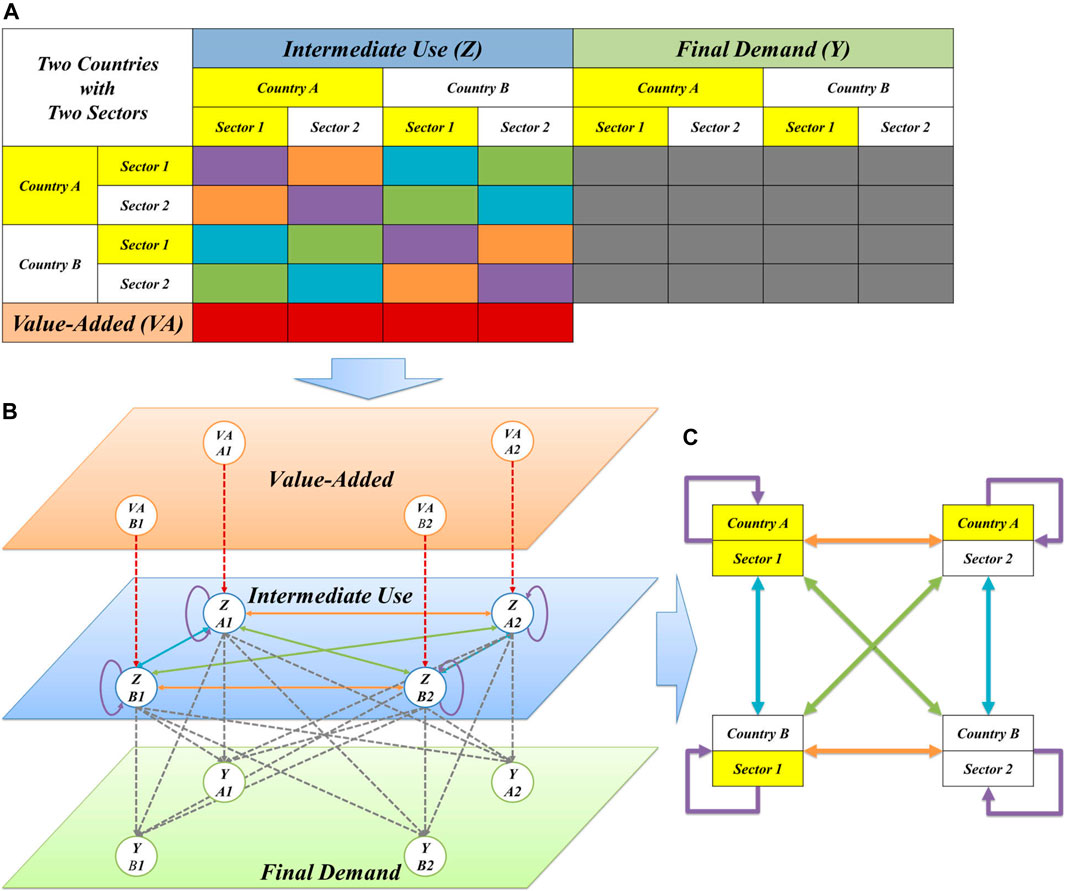
FIGURE 1. The relationship between MRIO Table and GVC network. (A) ICIO Table Including Two Countries with Two Sectors. (B) Tripartite Valued Graph Based on ICIO Table. (C) Graph Form of Intermediate Use Part.

FIGURE 2

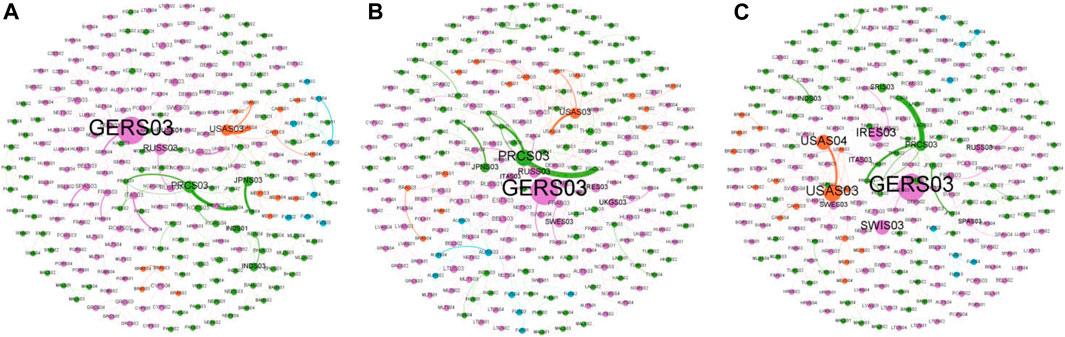
FIGURE 2. GIVCN-ADB2019 models. (A) Visualization of the global input-output model in 2007. (B) Visualization of the global input-output model in 2013. (C) Visualization of the global input-output model in 2019.

Notes: For the reason of visualization, we delete the weak industrial relevance based on the RFWA and combine industrial sectors into four-sector categories [53]^. The color of the node represents the different continents, the size of the node represents betweenness centrality, and the thickness of the edge represents the weight of the edge.

On this basis, this paper establishes the Global Industrial Value Chain Network (GIVCN model; labeled as GIVCN-ADB model because the ADB2019 database is used). The aim of this research is to portray how economies fight for the limited industrial resources, and GIVCN is hence needed to be transformed to embody the local competitive relations among industrial sectors. The GIVCN-ADB model includes 1,512 nodes, representing 35 industrial sectors in 62 countries/regions and RoW. Since the ADB2019 includes the world IO tables for 13 years from 2007 to 2019, 13 GIVCN-ADB models are constructed in this research accordingly.

Resource Allocation Process

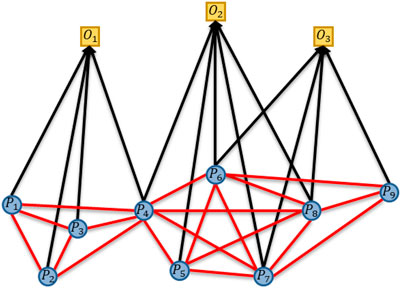
Bipartite Graph, or Bi-Graph, divides the node set of a simple graph $G$ as two nonempty sets $V_1$ and $V_2$ with no intersection in between. Let $V_1$ in $G=\left(V_1,V_2,E\right)$ as the node set of Participants, represented as $P$, and $V_2$ as that of the Objects, represented as $O$, then a bipartite graph $G=\left(P,O,E\right)$ is reached, in which, $E$ is the set of edges, $P=\left\{P_1,P_2,\cdots ,P_n\right\}$ $\left(i,j=\mathrm{1,2},\dots ,n\right)$ and $O=\left\{O_1,O_2,\cdots ,O_m\right\}$ $\left(h,k=\mathrm{1,2},\dots ,m\right)$ are the sets of two types of nodes, respectively. We take an example to describe its topological structure, where n = 9 and m = 3, as shown in Figure 3.

FIGURE 3

FIGURE 3. A two-mode network and its projection onto participants.

In Figure 3, the squares in the upper part are the objects (denoted by $O_1,O_2,\dots ,O_3$), while the circles below are the participants (denoted by $P_1,P_2,\dots ,P_9$), and the edges in black belong to the two-mode network. It is more than common to project a two-mode network onto one kind of nodes, and the resulting edges have been granted the property to reflect certain relationship. As we can see, the edges in red coming from the projection of two black edges constitute a one-mode network, namely Complete Object Subgraph. Sometimes, there should be weights on the edges, which are gained through the definition of co-occurrences and used to measure the potential relationship of two participants in the same object, or that of two objects in the same participant. For instance, it just likes the number of papers that two scientists (participants) wrote together, or the number of the same scientists that two papers (objects) have [54]. However, refined calculation on the weight of projected edge is very difficult, and we must use a specific method to solve a specific problem.

The bipartite graph has a wide application in complex network analysis, including cooperation and competition networks (mainly dealt with through affiliation networks), for either cooperation or competition is the common existence in social networks consisting of units of people. Padrón believed that this modeling process could bring distinctive simulation on the potential cooperation or competition relation [55]. In the field of GVC-related studies, scholars and politicians all want to figure out the inter-country and inter-industry competition and collaboration for the purposes of academic research and policy-making. If limited industrial resources lead to competition among downstream sectors, then limited market demand leads to cooperation among upstream sectors. Therefore, with the purpose of extracting the inter-industry collaborative relations, the Resource Allocation Process (RAP) is adopted in this paper as the algorithm of projection [56]. The following is the specific derivation process.

Firstly, we assume that the initial resource allocated to the $i$ -th participant is $f\left(P_i\right)\ge 0$, all the resources of $P$ flow in the direction of $O$, and the cumulative quota of the $k$ -th node in $O$ is:

$f\left(O_k\right)={\displaystyle \sum }_{i=1}^n\frac{a_{ik}f\left(P_i\right)}{K\left(P_i\right)}(1)$

where, $K\left(P_i\right)$ is the degree of $P_i$, $\left\{a_{ik}\right\}$ is a $n\times m$ matrix:

$a_{ik}=\{\begin{array}{cc}1& P_i{O}_k\in E\\ 0& otherwise\end{array}(2)$

The resources allocation process of $P\to O$ is shown in Figure 4.

FIGURE 4

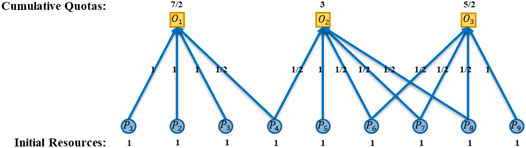
FIGURE 4. Primary Distribution: Initial Resources from Participants are Equally Distributed to Objects.

Notes: $O_1$ and relevant participants for an explanation are taken as example. For simplicity, we assume all participants here own an equal size of resources, i.e., $f\left(P_i\right)=1$. $P_1$ only connects to $O_1$, so $K\left(P_1\right)=1$, $a_{11}=1$, $a_{12}=0$, $a_{13}=0$. The same thing happens in $P_2$ and $P_3$. However, $P_4$ connects to both $O_1$ and $O_2$, so $K\left(P_4\right)=2$, $a_{41}=1$, $a_{42}=1$, $a_{43}=0$. Thus, $f\left(O_1\right)=1+1+1+\frac{1}{2}=\frac{7}{2}$. Similarly, $f\left(O_2\right)=3$ and $f\left(O_3\right)=\frac{5}{2}$.

With all the demand signals flowing back to set $P$, the consumed resource of $P_i$ is:

$f^{\text{'}}\left(P_i\right)={\displaystyle \sum }_{k=1}^m\frac{a_{ik}f\left(O_k\right)}{K\left(O_k\right)}={\displaystyle \sum }_{k=1}^m\frac{a_{ik}}{K\left(O_k\right)}{\displaystyle \sum }_{j=1}^n\frac{a_{jk}f\left(P_j\right)}{K\left(P_j\right)}(3)$

The RAP of $O\to P$ is shown in Figure 5.

FIGURE 5

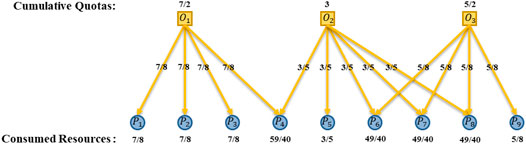
FIGURE 5. Secondary Distribution: Cumulative Quotas from Objects are Equally Satisfied by Participants.

Notes: When an object equally returns its cumulative quotas to relevant participants, the denominator is just the number of participants it owns. Thus, the consumed resource of participant is equal to the sum of quotas it gets from all objects, e.g., $f^{\text{'}}\left(P_1\right)=\frac{f\left(O_1\right)}{k\left(O_1\right)}=\frac{7}{8}$ and $f^{\text{'}}\left(P_4\right)=\frac{f\left(O_1\right)}{k\left(O_1\right)}+\frac{f\left(O_2\right)}{k\left(O_2\right)}=\frac{7}{8}+\frac{3}{5}=\frac{59}{40}$.

$f^{\text{'}}\left(P_i\right)\ne f\left(P_j\right)$ after implementing the RAP approach. This discrepancy stems from the nature of the resources themselves. That is, if objects could transfer resources without attenuation or loss, there will be no competition among relevant participants, e.g., papers and readers. But, if they could not, scarcity of resources will bring participants exclusive competition, e.g., banks and moneylenders. This kind of competitive relations among participants within Eq. 3 can be rewritten as:

$f^{\text{'}}\left(P_i\right)={\displaystyle \sum }_{j=1}^n{w}_{ij}^{P}f\left(P_j\right)(4)$

where, $w_{ij}^P$ is the relation strength produced in the two resource allocation processes between $P_i$ and $P_j$, and describes how the other participants’ occupation on resources affect $P_i$.

The $w_{ij}^P$ in Eq. 4 could be written as:

$w_{ij}^P=\frac{1}{K\left(P_j\right)}{\displaystyle \sum }_{k=1}^m\frac{a_{ik}{a}_{jk}}{K\left(O_k\right)}(5)$

Thus, the adjacency matrix $W^P={\left\{w_{ij}^P\right\}}_{n\times n}$ can be constructed for this complete object subgraph through RAP approach, as shown in Figure 6.

FIGURE 6

FIGURE 6. Competitive relations reflected by complete object subgraph. (A) Matrix-Form Linear Relation (B) the Topological Structure of Complete Object Subgraph. The values on the diagonal have no practical meaning for describing the inter-node competitive relations.

Notes: The values on the diagonal have no practical meaning for describing the inter-node competitive relations.

Further extension of RAP approaches can also be made to the condition of weighted edges in bipartite graphs, when resources are no longer distributed equally, with the weight representing the degree of membership of participant’s node to the object’s one. The formula is:

$w_{ij}^P=\frac{1}{S\left(P_j\right)}{\displaystyle \sum }_{k=1}^m\frac{w_{ik}{w}_{jk}}{S\left(O_k\right)}(6)$

where $S\left(P_j\right)$ is the weight of participant node $P_j$, $S\left(P_j\right)={\displaystyle \sum }_{k=1}^m{w}_{jk}$; $S\left(O_k\right)$ is the weight of object node $O_k$, $S\left(O_k\right)={\displaystyle \sum }_{i=1}^n{w}_{ik}$; $w_{ik}$ and $w_{jk}$ are the weights on edges connecting $P_i$ and $P_j$ with $O_k$, respectively.

In sum, the RAP approach reflects the scarcity of resources of network, and at the same time the limitation of resources taken by participant nodes from object nodes, enabling the complete object subgraph obtained through projection giving a clear indication on the competitive relations among participants.

GIRCN Model

IO table can well present the complicated interdependent relation among various industrial sectors from a global perspective, with a clear embodiment of the number of resources one sector may gain from its upstream sectors [57]. Studies on IO table mainly take advantage of its ability of depicting the topological structure of the economic system by measuring intermediate products as an indication of the inputs and outputs relation, so as to analyze the rules of value stream and industrial structural features. Bipartite graphs on the rows indicate the supply from upper to downstream industrial sectors and columns indicate on the demand from lower to upper ones. And it is obvious that the IO table is proficient in showing the cooperation or competition relation among different industrial sectors. However, there is no such relation among industrial sectors being reflected through direct structural measurement on the IO network, with adequate matrix transformations to be introduced for this goal.

If there exists more than one supplier or consumer for one single industrial sector, cooperation or competition will show up, for the scarcity of resources limits the flow of intermediate from upstream to downstream sectors. Traditional IO theory uses direct consumption coefficient and complete consumption coefficient to present this scarcity, with influence and reaction coefficients presenting the relations between one industrial sector and its environment. Yet it still bears the shortcoming that its focuses are restricted to the linear technical-economic relations among different industrial sectors and between the gross outputs and final usage, neglecting the scarcity of productive resources as constraints on cooperation and competition relations. This chapter contributes to set up modeling analysis with bipartite graph theory on the IO data, aiming at restoring the competition relation between downstream industrial sectors from the perspective of econophysics. The modeling framework is shown in Figure 7.

FIGURE 7

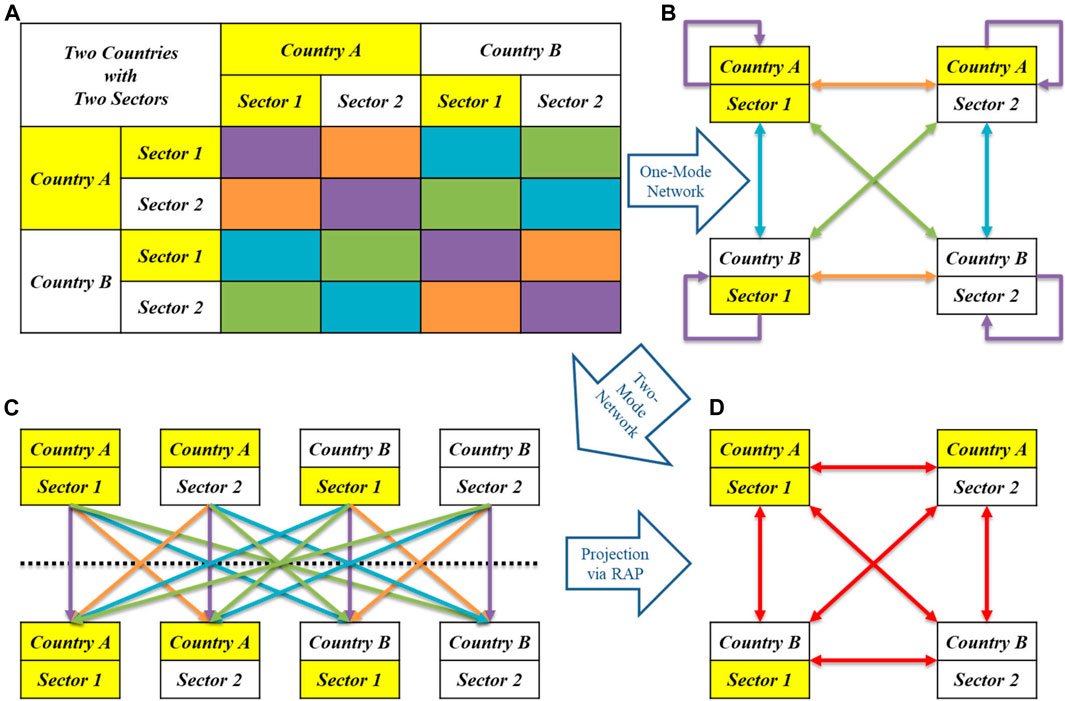
FIGURE 7. Modeling framework for reflecting inter-industry competitive relations in consideration of the scarcity of productive resources. (A) Inter-Country Input-Output Table (B) One-Mode Network Reflecting Economic Relations (C) Two-Mode Network Reflecting Economic Relations (D) One-Mode Network Reflecting Competitive Relations.

Notes: The flows in bipartite graphs direct from the participant nodes to the object nodes in common, but the IO/MRIO networks flow in the opposite direction from the upper stream sectors to the lower ones at the mercy of the transfer of the intermediate goods along the GVC, as shown in Figure 7C. Besides, we indicate different relations by colors, e.g., orange for domestic industrial IO trade, purple for domestic industrial self-consumption, green for international inter-industry trade, blue for international intra-industry trade and red for worldwide competition among industrial sectors.

Industrial sectors’ economic relations can be vividly depicted in the form of complex networks based on IO/MRIO data, as shown in Figures 7A,B. The sector’s self-consumption on its own intermediate outputs is usually indicated by self-loop. If we want to dig more information from IO/MRIO data, such as competitive status, it is necessary to reexamine IO/MRIO networks from another angle.

We need to change the one-mode network into a two-mode network, in order to separate the inner identity of each sector and prepare for the projection. In Figure 7C, the same sector distributes on the two sides of the dotted line, which means it belongs to both the upper stream and the lower stream. In other words, the upper stream sector in the IO/MRIO table could be referred to as the object nodes in the bipartite graph, while the lower one as the participant nodes. Now, self-loop becomes a common edge between the two identities of this sector.

Then, we adopt RAP mentioned above to extract competitive relations hidden in the IO/MRIO relations, as shown in Figure 7D. If any industrial sector enjoys with any other sector more than one upper stream industrial sector as production resources provider, there will be edges in the complete object subgraph depicting the competitive relations.

In the global economic system depicted by the GIVCN model, the downstream industrial sector consumes the limited output of the upstream industrial sector, making productive resources scarce. This scarcity is transmitted when several downstream industrial sectors simultaneously obtain productive resources from a common upstream industrial sector, leading to the competition between the downstream industrial sectors. This competitive relationship between industrial sectors implied in the GIVCN model can be represented by its complete project subgraph, mapped by the following equation:

$w_{ij}^P=\{\begin{array}{ccc}\frac{1}{{\overleftarrow{w}}_j}{\displaystyle \sum }_{k=1}^N\frac{w_{ki}{w}_{kj}}{{\overrightarrow{w}}_k}& ,& i\ne j\\ 0& ,& i=j\end{array}(7)$

where, $w_{ki}$ ($w_{kj}$) is the $k$ -th row and $i$ -th ($j$ -th) column element of the adjacency matrix of GIVCN model, representing the upstream sector $k$ and downstream sector $i$ ($j$) respectively; ${\overrightarrow{w}}_k$ is the gross outputs of upstream sector $k$, and it is numerically equal to the out-degree strength of node $k$ in GIVCN model, say ${\overrightarrow{w}}_k=S^{OUT}\left(k\right)={\displaystyle \sum }_{i=1}^N{w}_{ki}$; ${\overleftarrow{w}}_j$ is the gross inputs of downstream sector $j$, i.e., ${\overleftarrow{w}}_j=S^{IN}\left(j\right)={\displaystyle \sum }_{k=1}^N{w}_{kj}$; $w_{ij}^P$ is the competitive pressure of the sector $i$ against $j$; downstream sectors $i$ and $j$ are connected by an edge denoted by $e_{ij}^P$ in the complete object subgraph.

Until now, the edge set $E^P=\left\{e_{ij}^P\right\}$ and weight set $W^P=\left\{w_{ij}^P\right\}$ reflect all the competitive relations among sectors in the global economic system. We named the graph $G=\left(V,E^P,W^P\right)$ as the Global Industrial Resource Competition Network (GIRCN) hereafter, which is a sort of weighted and directed one-mode network without any self-loop of any node, as shown in Figure 8. The sectors with strong competitiveness in GIRCN are mainly manufacturing and service industries. Germany, Russia, the United Kingdom, and Switzerland have strong competitiveness in Europe; the main competitive countries in the Americas include the United States and Brazil; and Asia has strong competitiveness. Competitive advantages are the United States, Japan, South Korea, Thailand.

FIGURE 8

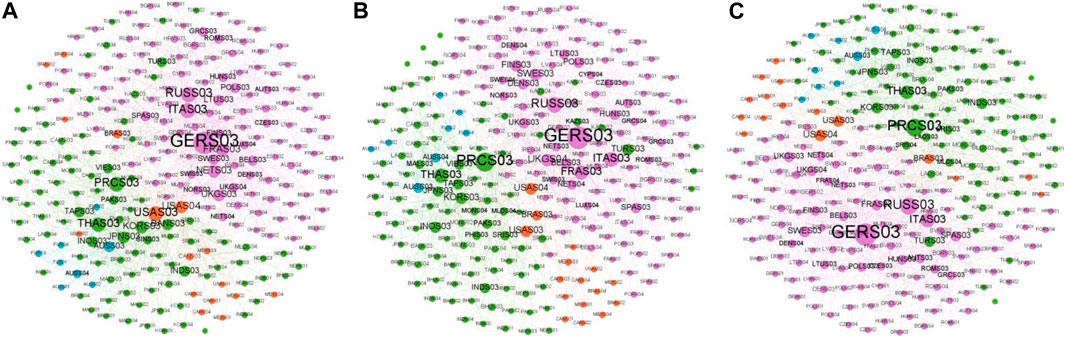
FIGURE 8. GIRCN-ADB2019 Models. (A) 2007 Global Industrial Resource Competition Network visualization. (B) 2013 Global Industrial Resource Competition Network visualization. (C) 2019 Global Industrial Resource Competition Network visualization.

Notes: For the reason of visualization, we delete the weak industrial relevance based on the RFWA and combine industrial sectors into four-sector categories. The color of the node represents the different continents, the size of the node represents out-degree, and the thickness of the edge represents the weight of the edge.

Measurement

According to our study on the application of the complex network theory [58], network-based algorithms and indices have great potential to enhance the understanding of the industrial sector’s position and function, given the network-form architecture of GVC. The inter-industry competitive status has been embodied in the GIRCN model, and out-strength and in-strength as simple yet important tools are hence introduced to quantify industrial sectors’ competitive strength and weakness on the GVC, based on which we further carry out econometric, static timing and simulation analyses.

CAI and NCAI

The weight set $W^P$ of GIRCN indicates the direct and indirect competitive relations among industrial sectors. It is noteworthy that this competitive relation is directed, which means $w_{ij}^P$ is the competitive strength of the industrial sector $i$ against $j$, while $w_{ji}^P$ is that of the opposite. Hence, it is defined in this section that the summation of the competitive advantages of an industrial sector to be its Competitive Advantage Index (CAI).

Judged from the perspective of complex networks, CAI is the out-strengths $S^{OUT}$ of nodes in the GIRCN model, to be calculated as follows:

$CAI\left(i\right)=S^{OUT}\left(i\right)={\displaystyle \sum }_{j=1}^N{w}_{ij}^P(8)$

Therefore, this paper proposes the National Competitive Advantage Index ($NCAI$) to measure the competitiveness of a country on GVC from the perspective of economic physics, whose formula is.

$NCAI\left(u\right)={\displaystyle \sum }_{i\in \tau \left(u\right)}CAI\left(i\right)(9)$

where $\tau \left(u\right)$ is a set of numbers standing for the row sequence number of a certain country/region in the adjacent matrix $Z^{uv}$. For instance, China is the 40th economy in EORA, so $\tau \left(8\right)=\left\{\mathrm{1015,1016},\cdots ,1040\right\}$ because each economy owns $n=26$ sectors. $NCAI\left(u\right)$ is used to measure the competitive advantage and weakness of country/region $u$.

Today, as the global economy integrates, the Comparative Advantage theory in classical economic theory can no longer adequately explain how the industrial sectors of an economy succeed or fail in the international environment. Scholars have gradually started to analyze the sources and formation of competitive advantages from the perspective of value chains [59]. This paper proposes the method to measure the competitive positions of industrial sectors on GVC, and reflects the intensity of two-way competition among downstream industrial sectors considering the scarce supply of intermediate goods in upstream industrial sectors, with the measurement of this competitive intensity being comparable.

Correlation Analysis

In this section, we will discuss the relationship between a country’s NCAI and its GDP, that is, how a network-based competitive advantage index affects a country’s macroeconomic performance. GDP data are converted into U.S. dollars at the exchange rate of the year and then calculated at comparable prices. In order to obtain a stationary series more easily, take the natural logarithm of the GDP of each country. In this paper, the distribution of NCAI and total GDP in 62 countries in the ADB database in 2007, 2013 and 2019 is linearly fitted, and the results show that the two are closely related, and the fitting indices R² are 0.58, 0.56 and 0.57, respectively. From the changing trend, the three sets of data have an obvious upward trend, that is, NCAI and GDP are positively correlated, which proves that the network indicators for measuring the country’s competitive advantage proposed in this article can reflect the country’s economic development level. In terms of the degree of fit, the R² values in 2007, 2013, and 2019 are very close, which proves the stability of the relationship between GDP and NCAI, and further proves that the NCAI proposed in this paper is robust as an indicator to measure global competitive advantage.

In the past 20 years, the World Economic Forum (WEF) has been evaluating the competitive advantages of countries. The “Global Competitiveness Index” was proposed by the WEF in 2005. It is a set of systems, policies and influencing factors that determine the productivity level of an economy. It uses 12 major competitiveness factors as measurement indicators. It comprehensively reflects the competitiveness of the world’s economies. The 12 key competitiveness factors are: legal and administrative structure, infrastructure, macroeconomic environment, health and basic education, higher education and training, commodity market efficiency, labor market efficiency, financial market development, technology readiness, market size, Business maturity and innovation. This article compares the GCI proposed by the World Economic Forum with the BRI-related country rankings from the NCAI, and the results are shown in Supplementary Material S1A. From the results, there are still differences in the rankings. Compared with the evaluation system proposed by WEF, the NCAI proposed in this paper focuses on analyzing the competitive advantages of countries/industries in the global production network. Therefore, NCAI can supplement the existing global competitiveness index system.

The evaluation indicators proposed in this article based on trade networks reflect the status of countries on the GVC. Global economic integration has greatly changed countries. China’s internal and external industrial institutions have changed the world economic structure. Therefore, a country’s competitive advantage in its international trade network will inevitably affect its level of economic development. All in all, the analysis framework of this article can reflect the internal mechanism of global economic development.

Results and Discussion

In recent years, with the deepening of economic globalization, the trend of regionalization of international trade has emerged. To a certain extent, regional economic cooperation can improve the risk resistance of member countries and alleviate the competitive pressure brought by global trade. The “Belt and Road” initiative provides a broad platform for Sino-foreign production capacity cooperation, which helps the positive promotion and development of global trade. This paper analyzes the NCAI trends of 40 countries that have signed the Belt and Road Agreement over the period 2007–2019. Using the R package Mfuzz V2.36.0, soft cluster analysis of noise resistance was carried out to further analyze the NCAI evolution mode and its mechanism.

The Mfuzz package was originally developed as a clustering method for processing gene expression or protein expression profile data, the core algorithm is based on Fuzzy C-Means Clustering (FCM) [60, 61]. In practical applications, other types of non-biological data can also be clustered and analyzed. This unsupervised cluster analysis can examine all variables simultaneously and identify international/regional regions among them with consistent NCAI change trends, helping us to more effectively tap into the complex trade information embedded in the sample data, which is important for the study of the dynamic evolution of global trade. The trends of NCAI changes over time in different countries are clustered into different modules (e.g., continuously rising, continuously falling, rising then falling and falling then rising, etc.), and finally six sets of clusters with different dynamics patterns are obtained, as shown in Figure 9. For the Belt and Road countries in each cluster, they have similar temporal expression characteristics, and the dynamics patterns differ significantly among the countries in different clusters.

FIGURE 9

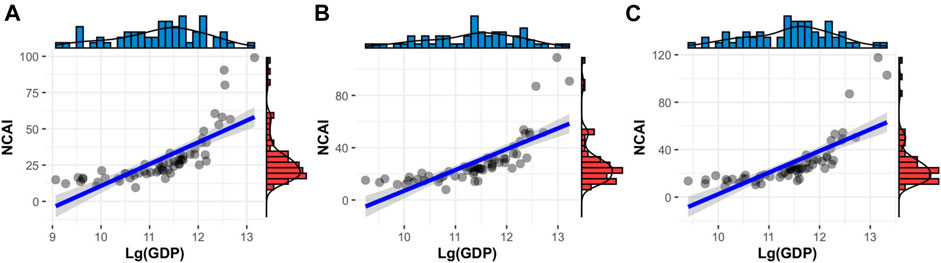
FIGURE 9. Correlation between NCAI and GDP. (A) Correlation between GDP and NCAI in 2007. (B) Correlation between GDP and NCAI in 2007. (C) Correlation between GDP and NCAI in 2007. The fitting indices R2 are 0.58, 0.56 and 0.57, respectively.

FIGURE 10

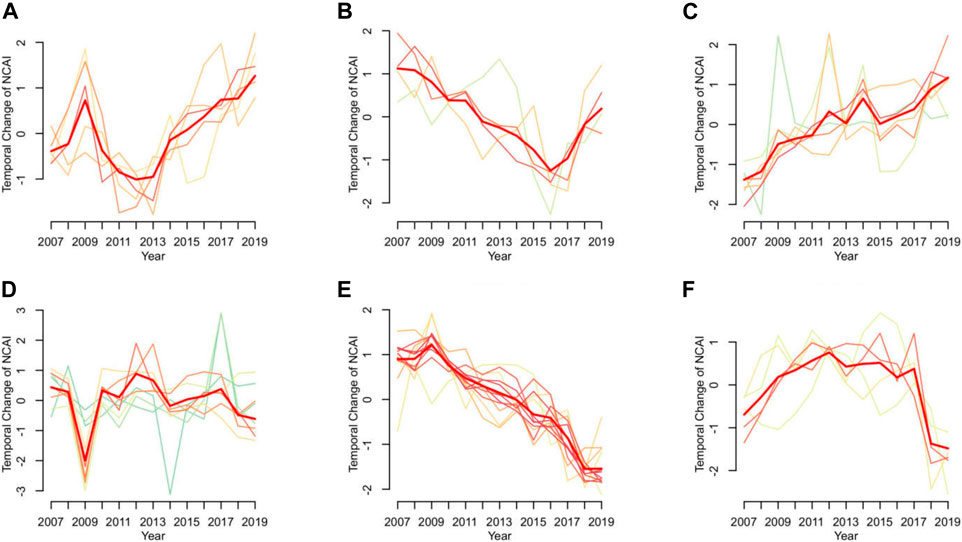
FIGURE 10. Six patterns of temporal change of NCAI. (A) Pattern I (B) Pattern II (C) Pattern III (D) Pattern IV (E) Pattern V (F) Pattern VI.

FIGURE 11

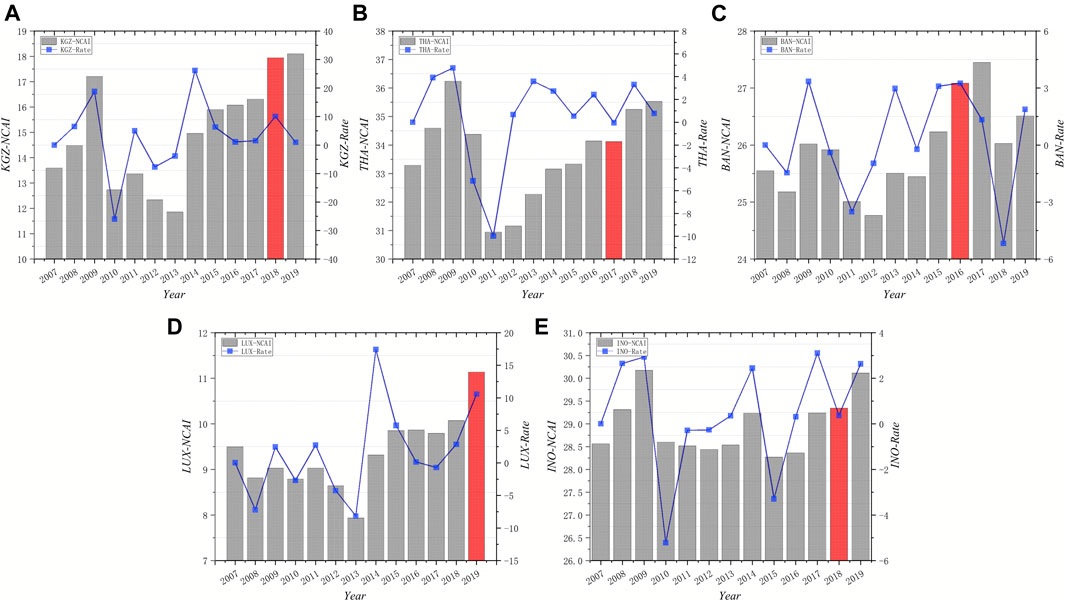
FIGURE 11. Pattern I of temporal change of NCAI. (A) Kazakhstan (B) Thailand (C) Bangladesh (D) Luxembourg (E) Indonesia.

FIGURE 12

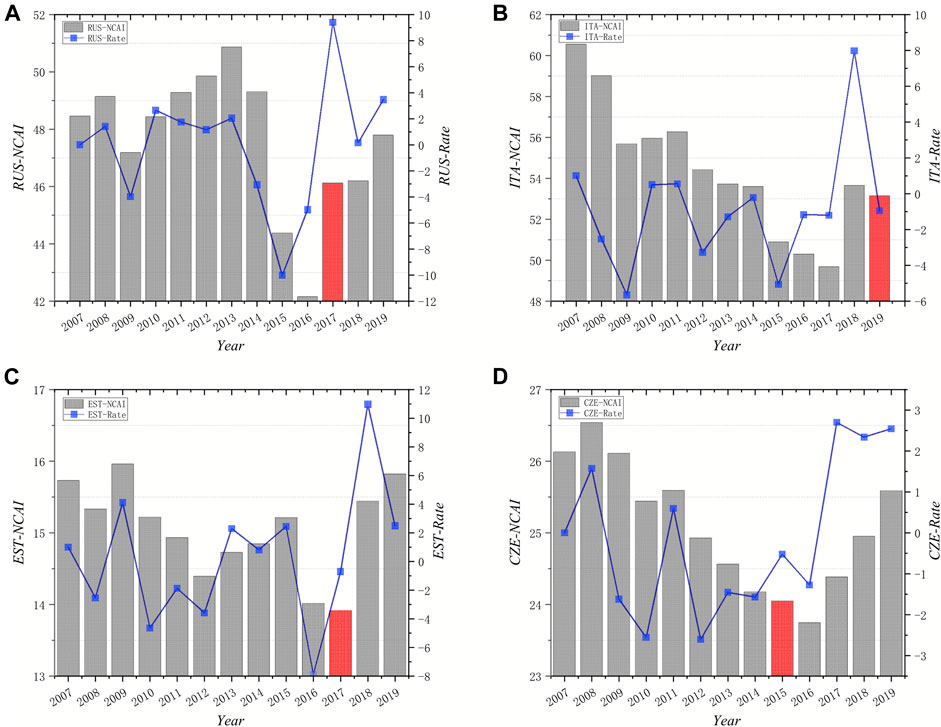
FIGURE 12. Pattern II of temporal change of NCAI. (A) Russia (B) Italy (C) Estonia (D) Czech Republic.

FIGURE 13

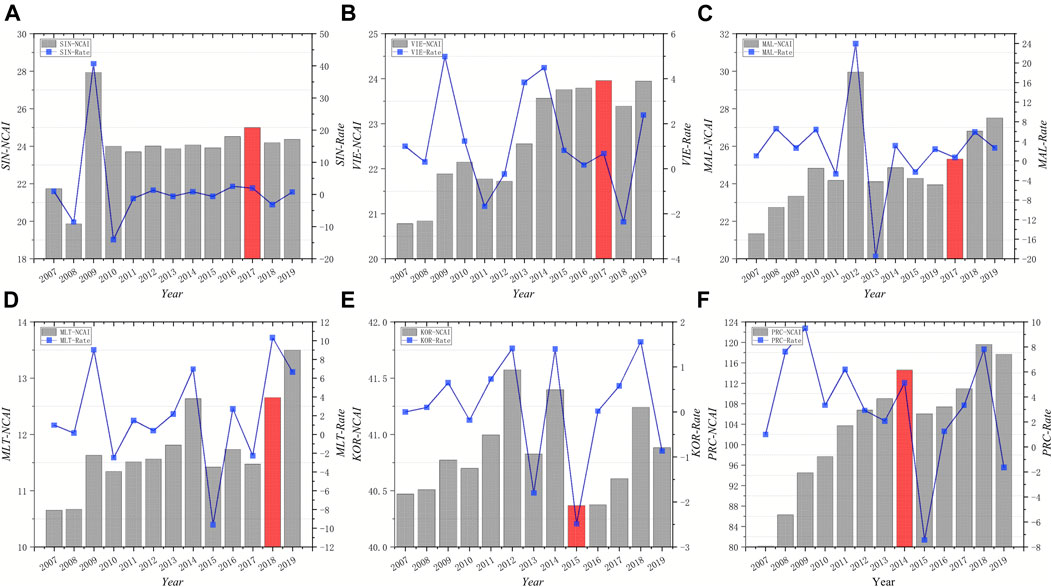
FIGURE 13. Pattern III of temporal change of NCAI. (A) Singapore (B) Viet Nam (C) Malaysia (D) Malta (E) Republic of Korea (F) China.

FIGURE 14

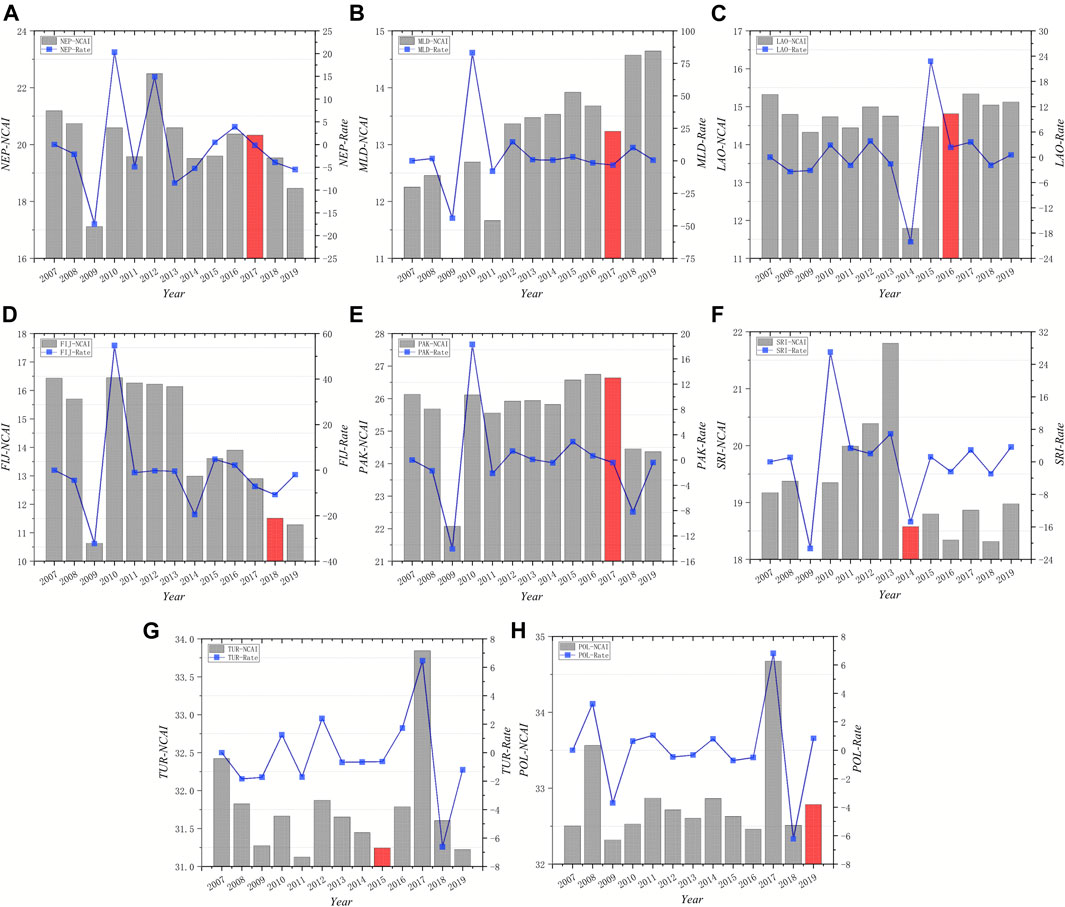
FIGURE 14. Pattern IV of temporal change of NCAI. (A) Nepal (B) Maldives (C) Lao (D) Fiji (E) Pakistan (F) Sri Lanka (G) Turkey (H) Poland.

FIGURE 15

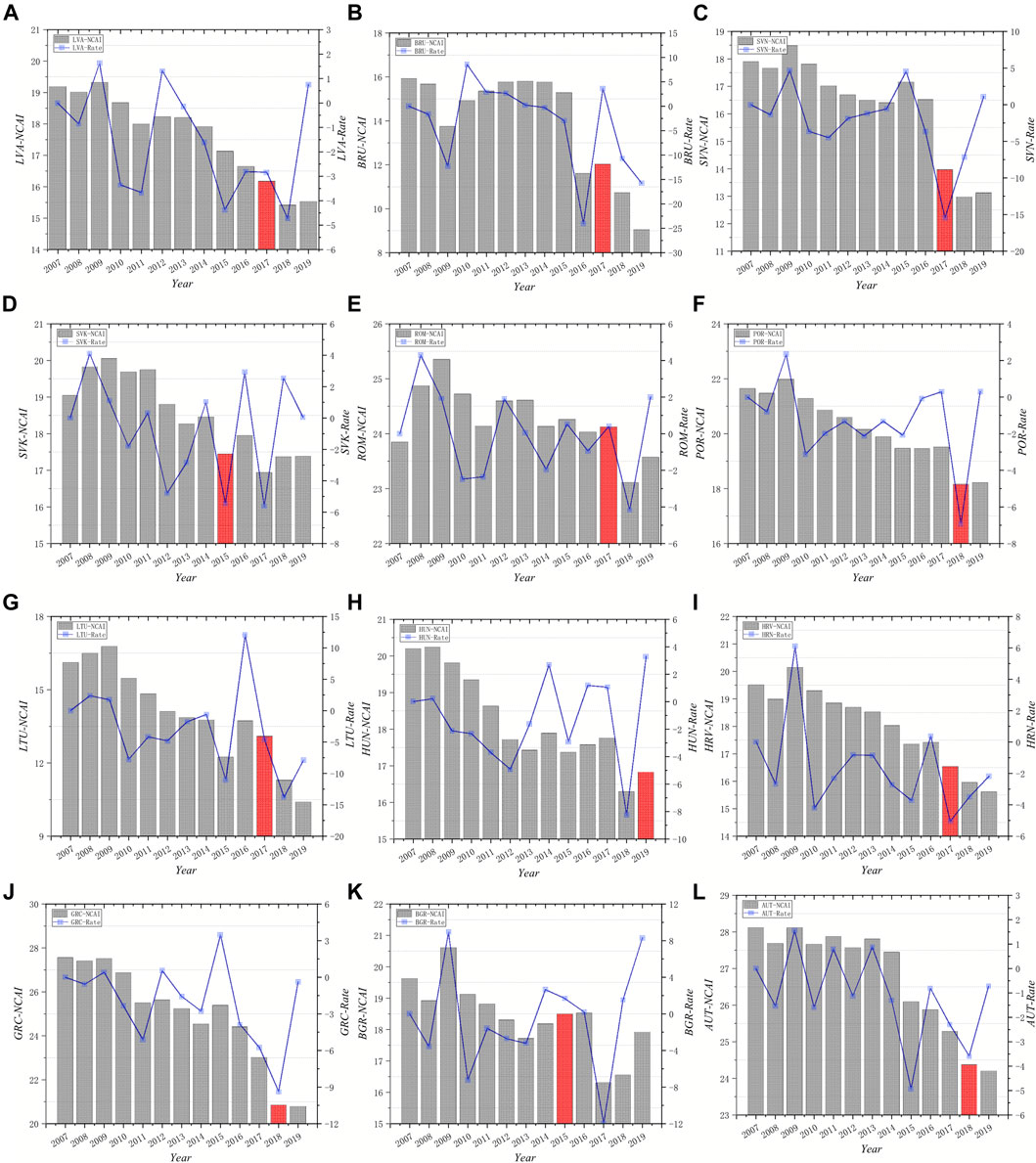
FIGURE 15. Pattern V of temporal change of NCAI. (A) Latvia (B) Brunei Darussalam (C) Slovenia (D) SlovakRepublic (E) Romania (F) Portugal (G) Lithuania (H) Hungary (I) Croatia (J) Greece (K) Bulgaria (L) Austria.

FIGURE 16

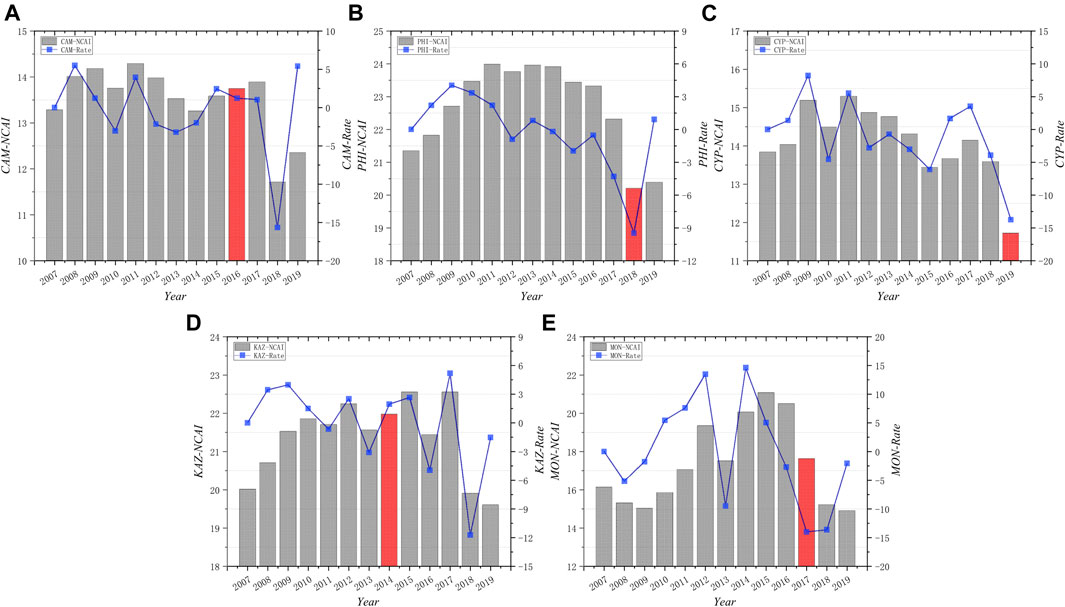
FIGURE 16. Pattern VI of temporal change of NCAI. (A) Cambodia (B) Philippines (C) Cyprus (D) Kazakhstan (E) Mongolia.

Pattern I includes Indonesia, Luxembourg, Bangladesh, Thailand, and Kyrgyz Republic. The NCAI of this group of countries rose to the highest point in the region in 2009, then began to decline and started to show an upward trend after falling to the lowest point in 2013. This group of economies performed better than other countries after the 2008 financial crisis, however, due to their backward and uneven development of industry and manufacturing, they are not competitive in the Belt and Road trade network. In the subsequent trade development gradually found export advantages, so the NCAI has a positive trend. In the subsequent trade development gradually found export advantages, so the NCAI has a positive trend. Indonesia, for example, has relatively stable export products with comparative advantages in terms of export scale such as coal and natural rubber, and the types of products in the international market are gradually diversified with the addition of man-made fibers and petroleum product residues, making the competitive advantage is enhanced.

Pattern II includes Czech Republic, Estonia, Italy, and Russia. The NCAI of this group of countries has been decreasing since 2007 until it started to increase during 2015–2017. This group of economies as a whole shows a decreasing and then increasing trend, with economic shocks from outside causing this change. Take Italy and Russia as examples. Italy, as the second manufacturing power in the EU after Germany and the second largest agricultural country after France, has a well-developed real economy. Hit by the global economic crisis and the European debt crisis, Italy’s GDP shrank by an average of 1.5 percentage points per year from 2008 to 2014. Since 2015, Italy’s economy has resumed growth, stimulated by the global economic rebound and relatively moderate fiscal policy and expansionary monetary policy. Russia has a strong competitive advantage with abundant natural resources and a strong industrial, scientific and technological base. However, Russia has also been affected by the world economic slowdown, falling oil prices and Western sanctions.

Pattern III includes China, Republic of Korea, Malta, Malaysia, Viet Nam, and Singapore. This group of countries has been showing an upward trend during the 12 years 2007–2019. China, Korea, and Singapore have an extremely important position in the global economic landscape as important countries and major economies in Asia. With a GDP of $91.064 billion in 2008 and $202.616 billion in 2016, Vietnam’s GDP growth rate remains strong on top of higher aggregates. This group of economies maintains strong competitiveness and growth momentum in global trade resulting in a steady rise in the country’s NCAI.

Pattern IV includes Poland, Turkey, Sri Lanka, Pakistan, Fiji, Lao, Maldives, Nepal. The growth rate of NCAI in this group of countries declined sharply in 2008–2009 and was in a fluctuating state afterwards. These countries were all affected by the subprime crisis in 2008, which hit their import and export trade. They are not highly competitive in the subsequent global trade. Take Laos and Nepal as examples. Among the Southeast Asian countries, Laos, a traditional agricultural country, is lagging behind in industry and later in services. It was not until 2010 when the national GDP growth rate started to pick up that the NCAI showed a slow upward trend. Nepal is a typical agricultural country, with a late start of industrial development, small scale, low mechanization level, reliance on imports for most industrial products, and little competitive advantage in trade.

Pattern V includes Austria, Bulgaria, Greece, Croatia, Hungary, Lithuania, Latvia, Portugal, Romania, Slovak Republic, Slovenia, Brunei Darussalam. The NCAI growth rate for this group of countries shows a fluctuating downward trend throughout. This group of economies is mostly EU countries. Europe’s productivity growth has been on a downward trend in recent decades, while the EU’s market share in the different production stages of the manufacturing value chain has declined, which has led to a gradual decline in competitive advantage in global trade.

Pattern VI includes Cyprus, Philippines, Kazakhstan, Mongolia, Cambodia. The growth rate of NCAI in this group of countries increased slowly until 2011 and started to decline after 2013. The external environment has a significant impact on the economic development of these countries, as they are mostly export-oriented economies with the export of commodities as their main pillar. However, after 2013, Kazakhstan’s oil sales declined due to increasing competition from Middle East oil producers and U.S. shale oil, so Kazakhstan’s GDP per capita declined or even declined, which greatly affected its competitive advantage.

Analysis on Pattern I

The competitiveness of countries under pattern I reached its first peak in 2009, the rate of change of NCAI then showed a mean-reversion mechanism, the absolute value of NCAI gradually climbed after it dropped to a minimum around 2013. In addition, the influence of each country has increased after joining BRI, such as Indonesia, Thailand, and Kazakhstan. These countries have a low level of economic development and industrial development and are downstream in the global production network, mainly exporting low value-added products, such as plastics, rubber, electromechanical products, oil, etc. After joining BRI, regional cooperation and trade have been developed, bringing improved infrastructure, industrial investment to the country. While consolidating its comparative advantages in multilateral trade, the technology creation effect brings advanced production technologies to each country. The added value of products has increased, the industrial structure has been optimized, and its competitiveness in the international trade network has been improved.

Analysis on Pattern II

Pattern II consists of developed countries with well-developed industrial systems and a high degree of foreign trade, making the country more exposed to the global economy. After joining BRI, NCAI shows a higher growth rate. Among them, the economic development of EU member states Czech, Estonia and Italy are highly dependent on exports, mainly exporting high value-added products such as machine-made products, all of which are closely traded with EU countries and account for more than 50% of total exports. However, affected by the subprime mortgage crisis and sovereign debt crisis, the EU economy has slowed down and faced a heavy crisis, which is manifested in the continuous decline of NCAI. After joining BRI, the scope and extent of trade tilted toward Asian countries, and the dependence on the European market decreased, and the rate of change of NCAI turned from negative to positive. Russia’s main trading partner country is China, with a low dependence on Europe. Unlike the other three countries, it maintained a higher competitive advantage until 2015, but falling oil prices, etc., also had a negative effect on its competitive advantage. After joining the BRI, the NCAI has improved significantly compared to 2016. It can be seen that the countries under Pattern II have the most significant impact on NCAI by joining BRI compared to other patterns, which helps to expand the market and improve competitiveness.

Analysis on Pattern III

The competitive advantage of each country in pattern III is on the rise, and all of them trade closely with the neighboring Asian countries. Compared with United States and other developed regions, they opened up to the outside world later. However, the economy was developed rapidly with the advantages of labor and resources in the early stage, mainly importing intermediate products and exporting final products. Less affected by the financial crisis in 2008, the growth rate of NCAI is higher in the observation period. After joining BRI, most countries also show positive rate of change. For example, since its reform and opening up, China has actively integrated into the global division of labor, participated in multilateral trade organizations, and has a huge domestic market potential, while focusing on the development of science and technology, which itself has a strong competitive advantage. It shows that NCAI is much higher than other countries. After establishing BRI, the competitive advantage declined in 2015, and then improved year by year, reaching a peak in 2018, and fell back slightly in 2019 due to the financial crisis. Vietnam has been reformed and opened up since 1986 and established a socialist market economy in 2001, focusing on the development of foreign trade. Malaysia introduces a new economic development plan every 5 years based on its development status. These economic policies of active participation in the global division of labor are manifested in the continuous rise of NCAI. After joining BRI, infrastructure such as transportation and communication has been improved, the environment of tourism and service industry, which are the main economic development, has been improving, and all NCAI has a high growth rate.

Analysis on Pattern IV

The NCAI of countries in pattern IV is generally low. Affected by the financial crisis in 2008, the rate of change was at a low value in 2009, and the overall fluctuation was high. These countries have a weak industrial base, lack of resources, and an imperfect industrial structure, with agriculture driving economic development in the early stage and the service sector taking the lead later. For example, Maldives relies on marine resources to develop tourism, Lao Laos has developed its service industry since the opening up of the country, and Sri Lanka’s service industry accounts for about 60% of GDP. BRI has transferred a large amount of steel production capacity to these countries for infrastructure construction, which has compensated for the shortage of domestic resources and improved its competitive advantage in the international arena. There are also some countries such as Pakistan. Not only do they face a severe international situation, but also domestic political turmoil and agriculture is affected by extreme weather, and the BRI has a limited impact on them. Overall, joining BRI has a limited effect on NCAI in this part of the world.

Analysis on Pattern V

The competitiveness of each country in pattern V fluctuates and decreases, after joining BRI, NCAI is still decreasing, but the rate of change has increased compared with the previous one, and the degree of decline of its competitive advantage has slowed down. Such as Latvia, Slovenia, Austria, Croatia, these countries are mostly EU countries with high economic level, developed industry, relatively well developed infrastructure, industrial structure, finance and tourism are their pillar industries, and the main trading partner countries are the neighboring European countries, which means that the economic development of the country is highly correlated with the development of the EU. The 2008 subprime mortgage crisis, economic development by the financial sector, followed by the sovereign debt crisis made the economy again hit, the potential bad debt crisis of banks in recent years has also affected the economic recovery of the EU, as shown by the continued reduction of the NCAI of each country. Because of its own well-developed industry and high degree of tourism development, joining the BRI has less effect on each EU country and has little impact on the change of NCAI. However, it also promotes trade with countries along the route, so the degree of decline in competitive advantage has slowed down and the rate of change has slightly increased.

Analysis on Pattern VI

Countries in Model VI have an imperfect industrial structure and rely mainly on a single industry for economic development. Most of them are export-oriented economies with high dependence on external markets. In terms of values, NCAI is low, most of the absolute values are below 20. For example, Kazakhstan is rich in resources, mainly oil, mining and coal, and is greatly affected by oil prices, in addition to the U.S. shale oil also poses a threat to its competitive advantage. Mongolia has a limited internal market, high external dependence, agriculture is the mainstay industry, and mainly exports livestock and textiles. Cambodia is mainly agricultural and relies mainly on foreign aid. Joining BRI can cope with the negative impact of the external crisis on economic development, but the industrial structure is too homogeneous to offset the impact on competitive advantage, and the role of BRI is relatively limited, as shown by the fluctuating changes in NCAI after joining BRI.

Conclusion

Empirical analysis has shown that China’s BRI has indeed brought dividends to some countries along the route on the GVC. In particular, some underdeveloped countries in Asia and Africa have problems such as lack of resources and imperfect industrial structure. Continuous cooperation with China in key areas has significantly improved their competitiveness. This further proves that BRI can provide good development opportunities for some countries along the route through complementing advantages, resource sharing, and capacity cooperation, and can help achieve common prosperity. Hence, BRI needs to be taken further, to share the dividends of China’s economic development with other countries along the route, and elevate the industrial competitiveness of countries along the route (especially less developed ones) on the GVC.

This empirical analysis not only helps outline the dynamic development process of each country’s industrial competitiveness on the GVC, but also can perform cluster analysis on the development trend of BRI-related countries to find different development trends. In this process, a detailed analysis of the internal and external conditions faced by the country has been carried out, and countries can formulate cooperation strategies with other countries or regions based on their own strengths and weaknesses. The premise of international cooperation is the complementarity and coupling of the two cooperating countries on the GVC, emphasizing the use of their respective advantages in technology, capital and resources to achieve mutual benefits and win-win situations.

Besides, this study also provides a reference for how China can better implement BRI. For example, in cooperation with some underdeveloped countries in Asia, most countries have rich oil and gas and mineral resources, but the industrial system is backward, the development technology is backward, and the development capacity is insufficient, China can cooperate with them in key areas such as oil and gas and mineral resources and meanwhile help them establish sound industrial, transportation and infrastructure systems. In cooperation with some EU countries, given the rapid development of the “Construction” sector, China can take advantage of the rapid development cycle of European infrastructure, and use its experiences in railroad industry to tap in the European rail transportation market. Meanwhile, China should also focus on the cooperation with European medium and high-end industries. In the cooperation with Africa, China should adhere to the humanitarian spirit, guide African industries to be more scientific and internationalized, and bring into play Africa’s comparative advantages on the GVC network.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding author.

Author Contributions

Conceptualization, YW and LX; methodology, WC; software, LX; validation, WC; formal analysis, YW; investigation, WC and CJ; writing—original draft preparation, YW and CJ; visualization, WC. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by National Natural Science Foundation of China (Grant No. 71971006, 71774008), Humanities and Social Science Foundation of Ministry of Education of the People’s Republic of China (Grant No. 19YJCGJW014).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.813005/full#supplementary-material

References

1.Office of the Leading Group for Promoting the Belt and Road Initiative. B & R Initiative-Belt and Road Portal. Available at: https://eng.yidaiyilu.gov.cn/ztindex.htm.

Google Scholar

2. Hummels D, Ishii J, Yi K-M. The Nature and Growth of Vertical Specialization in World Trade. J Int Econ (2001) 54:75–96. doi:10.1016/s0022-1996(00)00093-3

CrossRef Full Text | Google Scholar

3. Koopman R, Powers W, Wang Z, Wei SJ. Give Credit where Credit Is Due: Tracing Value Added in Global Production chains(No. W16426). Cambridge, MA: National Bureau of Economic Research (2010). doi:10.3386/w16426

CrossRef Full Text | Google Scholar

4. Wang Z, Wei SJ, Yu X, Zhu K. Measures of Participation in Global Value Chains and Global Business Cycles (No. W23222). Cambridge, MA: National Bureau of Economic Research (2017). doi:10.3386/w23222

CrossRef Full Text | Google Scholar

5. Wang Z, Wei SJ, Yu X, Zhu K. Characterizing Global Value Chains: Production Length and Upstreamness (No. W23261). Cambridge, MA: National Bureau of Economic Research (2017). doi:10.3386/w23261

CrossRef Full Text | Google Scholar

6. Kurihara Y, Fukushima A. Openness of the Economy, Diversification, Specialization, and Economic Growth. J Dev Stud (2016) 4:31–8. doi:10.15640/jeds.v4n1a3

CrossRef Full Text | Google Scholar

7. Yang G, Huang X, Huang J, Chen H. Assessment of the Effects of Infrastructure Investment under the belt and Road Initiative. China Econ Rev (2020) 60:101418. doi:10.1016/j.chieco.2020.101418

CrossRef Full Text | Google Scholar

8. Zou J, Liu C, Yin GQ, Tang Z. Spatial Patterns and Economic Effects of China’s Trade with Countries along the Belt and Road. Prog Phys Geogr (2015) 34:598–605. doi:10.11820/dlkxjz.2015.05.008

CrossRef Full Text | Google Scholar

9. Liu Z, Xin L. The Impact of the Belt and Road Construction on green Total Factor Productivity in China’s Key Provinces along the Route. Chin J. Popul. Resour. Environ. (2018) 28:87–97.

Google Scholar

10. Deng X. China’s Industrial Integration and Position along the Belt and Road, Industry Comparison, Regional Differences and Correlation Factors. J Southwest (2017) 38:121–5.

Google Scholar

11. Yao X, Pu Y, Wu G. China’s Level and Status of Industry Convergence in the Belt and Road Initiative, Industry Comparisons,Regional Gaps and Associated Factors. Res Transp Econ (2019) 9:172–86.

Google Scholar

12. Barabási AL, Albert R. Emergence of Scaling in Random Networks. Science (1999) 286:509–12. doi:10.1126/science.286.5439.509

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Albert R, Jeong H, Barabási A-L. Diameter of the World-wide Web. Nature (1999) 401:130–1. doi:10.1038/43601

CrossRef Full Text | Google Scholar

14. Lu D, Zhao W, Lu B, Zhang J. On the Structure and Characteristics of International Shipping Center Based on Complex Network Theory. Therm Sci Eng Prog (2012) 21:87–92. doi:10.1016/j.triboint.2011.11.010

CrossRef Full Text | Google Scholar

15. Wang J, Liao H. An Empirical Analysis of the Evaluation of Major Ports in the Coastal Urban Zone Based on AHP-RS. China Harb Eng (2012) 1:58–62. doi:10.3969/j.issn.1003-3688.2012.01.017

CrossRef Full Text | Google Scholar

16. Yang J. Competitive Relationships of Auto Industry and Rivalry Actions of Car Community Enterprises in China. Chin J. Catal. (2013) 10:49–55.

Google Scholar

17. Chmiel AM, Sienkiewicz J, Suchecki K, Hołyst JA. Networks of Companies and Branches in Poland. Physica A: Stat Mech its Appl (2007) 383:134–8. doi:10.1016/j.physa.2007.04.095

CrossRef Full Text | Google Scholar

18. Inoue H, Souma W, Tamada S. Analysis of Cooperative Research and Development Networks on Japanese Patents. J Informetrics (2010) 4:89–96. doi:10.1016/j.joi.2009.09.002

CrossRef Full Text | Google Scholar

19. Upper C. Simulation Methods to Assess the Danger of Contagion in Interbank Markets. J Financial Stab (2011) 7:111–25. doi:10.1016/j.jfs.2010.12.001

CrossRef Full Text | Google Scholar

20. Wang ZY, Li CF. Research on Stability of Eco-Industrial Symbiosis Network from a Perspective of Supernetwork. J Dalian Univ Technol (Social Sciences) (2013) 34:14–8.

Google Scholar

21. Acemoglu D, Ozdaglar A, Tahbaz-Salehi A. Cascades in Networks and Aggregate Volatility (No. W16516). Cambridge, MA: National Bureau of Economic Research (2010). doi:10.3386/w16516

CrossRef Full Text | Google Scholar

22. Burlon L. Ownership Networks and Aggregate Volatility. (Working Paper) No, 1004. Frankfurt am Main, Germany: Bank of Italy Temi di Discussione (2015). doi:10.2139/ssrn.2600875

CrossRef Full Text | Google Scholar

23. Mizuno T, Souma W, Watanabe T. Buyer-Supplier Networks and Aggregate Volatility. In: The Economics of Interfirm Networks. Tokyo: Springer (2015). doi:10.1007/978-4-431-55390-8_2

CrossRef Full Text | Google Scholar

24. Dhyne E, Rubínová S. The Supplier Network of Exporters: Connecting the Dots (No. 296). Brussels, Belgium: National Bank of Belgium Working Paper (2016).

Google Scholar

25. Fujii D Shock Propagations in Granular Networks. Los Angeles, CA: Elsevier (2016). USC-INET Research Paper No. 16-23. doi:10.2139/ssrn.2808094

CrossRef Full Text | Google Scholar

26. Ando S. Measuring US Sectoral Shocks in the World Input-Output Network. Econ Lett (2014) 125:204–7. doi:10.1016/j.econlet.2014.09.007

CrossRef Full Text | Google Scholar

27. Cerina F, Zhu Z, Chessa A, Riccaboni M. World Input-Output Network. PloS one (2015) 10:e0134025. doi:10.1371/journal.pone.0134025

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Grazzini J, Spelta A. An Empirical Analysis of the Global Input-Output Network and its Evolution (No. 31). Working Paper (2015).

Google Scholar

29. Amador J, Cabral S. Networks of Value-Added Trade. World Econ (2017) 40:1291–313. doi:10.1111/twec.12469

CrossRef Full Text | Google Scholar

30. Araújo T, Faustino R. The Topology of Inter-industry Relations from the Portuguese National Accounts. Physica A: Stat Mech its Appl (2017) 479:236–48. doi:10.1016/j.physa.2017.03.018

CrossRef Full Text | Google Scholar

31. Xing L, Dong X, Guan J. Global Industrial Impact Coefficient Based on Random Walk Process and Inter-country Input-Output Table. Physica A: Stat Mech its Appl (2017) 471:576–91. doi:10.1016/j.physa.2016.12.070

CrossRef Full Text | Google Scholar

32. Xing L, Xu X, Guan J, Dong X. Trade Brokerage Property of Industrial Sectors on the Global Value Chain. Mod Phys Lett B (2017) 31:1750212. doi:10.1142/s0217984917502128

CrossRef Full Text | Google Scholar

33. Xing L. Analysis of Inter-Country Input-Output Table Based on Citation Network: How to Measure the Competition and Collaboration between Industrial Sectors on the Global Value Chain. PloS one (2017) 12:e0184055. doi:10.1371/journal.pone.0184055

PubMed Abstract | CrossRef Full Text | Google Scholar

34. He X, Dong Y, Wu Y, Wei G, Xing L, Yan J. Structure Analysis and Core Community Detection of Embodied Resources Networks Among Regional Industries. Physica A: Stat Mech its Appl (2017) 479:137–50. doi:10.1016/j.physa.2017.02.068

CrossRef Full Text | Google Scholar

35. Tsekeris T. Global Value Chains: Building Blocks and Network Dynamics. Physica A: Stat Mech its Appl (2017) 488:187–204. doi:10.1016/j.physa.2017.06.019

CrossRef Full Text | Google Scholar

36. Soyyiğit S, Eren E. Complex Network Approach to International Trade of Fossil Fuel. Business Ind Eng (2016) 10:52–60. doi:10.5281/zenodo.1110862

CrossRef Full Text | Google Scholar

37. Soyyiğit S, Yavuzaslan K. Complex Network Analysis of International Olive Oil Market. Tur Agric Econ (2018) 24:117–29. doi:10.24181/tarekoder.453488

CrossRef Full Text | Google Scholar

38. Xiao H, Sun T, Meng B. Complex Network Analysis for Characterizing Global Value Chains in Equipment Manufacturing. PLOS ONE (2017) 12(1):e0169549. doi:10.1371/journal.pone.0169549

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Antràs P, Chor D, Fally T, Hillberry R. Measuring the Upstreamness of Production and Trade Flows. Am Econ Rev (2012) 102(3):412–6. doi:10.1257/aer.102.3.412

CrossRef Full Text | Google Scholar

40. Fally T. On the Fragmentation of Production in the US [R]. Boulder, CO: University of Colorado Working Paper (2011).

Google Scholar

41. Fally T, Hillberry R. Quantifying Upstreamness in East Asia: Insights from a Coasian Model of Production Staging [R]. Berkeley, CA: UC Berkeley ARE Working Paper (2013).

Google Scholar

42. Johnson RC, Noguera G. Accounting for Intermediates: Production Sharing and Trade in Value Added. J Int Econ (2012) 86(2):224–36. doi:10.1016/j.jinteco.2011.10.003

CrossRef Full Text | Google Scholar

43. Koopman R, Powers W, Wang Z, Wei S-J. Give Credit where Credit Is Due: Tracing Value Added in Global Production Chains. NBER Working Paper (2010). doi:10.3386/w16426

CrossRef Full Text | Google Scholar

44. Wang Z, Wei SJ, Yu X, Zhu K. Measures of Participation in Global Value Chains and Global Business Cycles [J]. NBER Working Pap (2017). doi:10.3386/w23222

CrossRef Full Text | Google Scholar

45. Amador J, Cabral S, Mastrandrea R, Ruzzenenti F. Who's Who in Global Value Chains? A Weighted Network Approach. Open Econ Rev (2018) 29(5):1039–59. doi:10.1007/s11079-018-9499-7

CrossRef Full Text | Google Scholar

46. Angelidis G, Ioannidis E, Makris G, Antoniou I, Varsakelis N. Competitive Conditions in Global Value Chain Networks: An Assessment Using Entropy and Network Analysis. Entropy (2020) 22(10):1068. doi:10.3390/e22101068

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Xing L, Han Y, Wang D. Measuring Economies' Pivotability on the Global Value Chain under the Perspective of Inter-country Input-Output Network. Mod Phys Lett B (2021) 35(17):2150289. doi:10.1142/s0217984921502894

CrossRef Full Text | Google Scholar

48. Timmer MP, Los B, Stehrer R, de Vries GJD. An Anatomy of the Global Trade Slowdown Based on the WIOD 2016 Release. GGDC research memorandum number 162. Groningen, Netherlands: University of Groningen (2016).

Google Scholar

49. Lenzen M, Moran D, Kanemoto K, Geschke A. Building Eora: A Global Multi-Region Input-Output Database at High Country and Sector Resolution. Econ Syst Res (2013) 25(1):20–49. doi:10.1080/09535314.2013.769938

CrossRef Full Text | Google Scholar

50. Chohan U. What Is One Belt One Road? A Surplus Recycling Mechanism Approach. Sydney, Australia: Social Science Electronic Publishing (2018). p. 205–19.

Google Scholar

51. Alves L A, Mangioni G, Rodrigues F, Panzarasa P, Moreno Y. Unfolding the Complexity of the Global Value Chain: Strength and Entropy in the Single-Layer, Multiplex, and Multi-Layer International Trade Networks. Entropy (2018) 20(12):909. doi:10.3390/e20120909

CrossRef Full Text | Google Scholar

52. Alves LGA, Cingolani I, Rodrigues FA, Panzarasa P, Moreno Y. The Nested Structural Organization of the Worldwide Trade Multi-Layer Network. Sci Rep (2019) 9(1):2866. doi:10.1038/s41598-019-39340-w

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Xing L, Han Y. Parameterless Pruning Algorithms for Similarity-Weight Network and its Application in Extracting the Backbone of Global Value Chain. J Data Inf Sci (2021) 7(1):1–19. doi:10.2478/jdis-2022-0002

CrossRef Full Text | Google Scholar

54. Newman MEJ. The Structure of Scientific Collaboration Networks. Proc Natl Acad Sci (2001) 98(2):404–9. doi:10.1073/pnas.98.2.404

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Padrón B, Nogales M, Traveset A. Alternative Approaches of Transforming Bimodal into Unimodal Mutualistic Networks. The Usefulness of Preserving Weighted Information. Basic Appl Ecol (2011) 12(8):713–21. doi:10.1016/j.baae.2011.09.004

CrossRef Full Text | Google Scholar

56. Zhou T, Ren J, Medo M, Zhang YC. Bipartite Network Projection and Personal Recommendation. Phys Rev E Stat Nonlin Soft Matter Phys (2007) 76:046115. doi:10.1103/PhysRevE.76.046115

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Leontif WW. Quantitative Input and Output Relations in the Economic Systems of the United States. Rev Econ Stat (1936) 18(3):105–25. doi:10.2307/1927837

CrossRef Full Text | Google Scholar

58. Xing L, Ye Q, Guan J. Spreading Effect in Industrial Complex Network Based on Revised Structural Holes Theory. Plos One (2016) 11(5):e0156270. doi:10.1371/journal.pone.0156270

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Porter M. Competitive Advantage of Nations. Comp Int Rev (1990) 1:14. doi:10.1002/cir.3880010112

CrossRef Full Text | Google Scholar

60. Futschik ME, Carlisle B. Noise-Robust Soft Clustering of Gene Expression Time-Course Data. J Bioinform Comput Biol (2005) 03:965–88. doi:10.1142/s0219720005001375

CrossRef Full Text | Google Scholar

61. Kumar L, Futschik ME. Mfuzz: A Software Package for Soft Clustering of Microarray Data. Bioinformation (2007) 2:5–7. doi:10.6026/97320630002005

PubMed Abstract | CrossRef Full Text | Google Scholar