- 1QPEC, The University of Tokyo, Tokyo, Japan
- 2RIKEN Center for Emergent Matter Sciences (CEMS), Saitama, Japan
- 3Department of Applied Physics, The University of Tokyo, Tokyo, Japan
We derive an effective three-orbital model for the infinite-layer nickelates based on the band structure obtained by the GW approximation (GWA), where we consider the Ni 3
Introduction
The discovery of nickel superconductors [1] has attracted renewed attention to superconductivity in strongly correlated electron systems [2–7]. So far, superconductivity has been found in film samples of doped infinite-layer nickelates RNiO2 (R = Nd, Pr, and La) [1, 8–16] and a quintuple-layer nickelate Nd6Ni5O12 [17]. Although the nature of the superconductivity is largely unknown, the pairing mechanism is likely to be unconventional: Theoretically, a phonon calculation for NdNiO2 has shown that the electron-phonon coupling is too weak to explain the superconductivity with a transition temperature on the order of 10 K [18]. Experimentally, both U- and V-shaped spectra have been observed using the scanning tunneling microscopy, depending on the location of the inhomogeneous surface of the doped NdNiO2 film [9]. Although the origin of the coexistence of the two different signals is controversial [19–23], the presence of the V-shape spectrum is consistent with an unconventional d-wave pairing. In fact, unconventional pairing mechanisms have been discussed since the early stages of the research [24–26].
In contrast with the conventional phonon-mediated superconductivity for which ab initio calculation based on density functional theory (DFT) plays a crucial role [27, 28], construction of low-energy models with few degrees of freedom is critically important for unconventional superconductivity since a detailed analysis of the correlation effects is mandatory. In the standard approach to derive a low-energy effective model from first principles, we first calculate the electronic structure with the local density approximation (LDA) or the generalized gradient approximation (GGA) in the framework of DFT. We then construct the maximally localized Wannier function (MLWF) [29, 30] for the low-energy states around the Fermi level and derive a tight-binding model. Next, we calculate the effective Coulomb interaction by the constrained random phase approximation (cRPA) [31, 32]. The matrix elements of the (partially) screened interaction are calculated for the Wannier basis, from which we estimate the Hubbard U and Hund coupling J in the multi-orbital Hubbard model [18, 24, 33, 34]. The cRPA is formulated in such a way that RPA calculation for the derived low-energy effective model reproduces a one-shot GW (G0W0) result [31, 32, 35].
To improve the accuracy of the parameters in the low-energy model, we can replace the Green’s function (G0) constructed from the DFT/LDA eigenenergies with the dressed Green’s function in the GW approximation (GWA).1 Such a derivation based on the GWA has been recently performed for the celebrated cuprate superconductors [37, 38]. While two types of orbitals, i.e., the Cu 3d and O 2p orbitals, form low-energy bands near the Fermi level, the GW self-energy correction increases the energy difference between the d and p orbitals and reduce the bandwidth of the d band. With these modifications, it has been shown with an extensive variational Monte Carlo (VMC) calculation that the experimental values of the Mott gap and magnetic moment of La2CuO4 are successfully reproduced [38, 39]. Given that the differences in the band structure between the DFT/LDA and that in the GWA are commonly seen in transition metal oxides where 3d and 2p orbitals with different correlation strengths coexist near the Fermi level, it would be of great interest to derive an effective low-energy model for infinite-layer nickelates based on the GWA.
In this study, we perform a first-principles derivation of the effective model for infinite-layer nickelates. In particular, we mainly focus on the dpp three-orbital models (single-orbital model is discussed in Appendix) because it is interesting to investigate how the GWA modifies the charge-transfer energy and correlation strength compared to the LDA-based downfolding.2 First, we calculate the band structure in the DFT/LDA and estimate the parameter of the effective model using the MLWF and cRPA technique. Next, we calculate the band structure in the GWA using the Green’s function of the LDA. We derive the effective model from the GW band structure and compare the results with those obtained from the LDA. We find that the GWA-based effective model is predicted to be more strongly-correlated with enhanced Mott-Hubbard type character. The model offers an interesting reference to be compared with that of the cuprates with the charge-transfer type character.
Methods
In this study, we calculate the parameter of the Hubbard Hamiltonian for the low-energy degree of freedom,
Here, the hopping term is represented by
where H is the Hamiltonian in the LDA or GWA and ϕℓR is the MLWF of the ℓth orbital localized at the unit cell R. The interaction term is given by
where WH is the effective interaction for the low-energy degree of freedom,
We calculate the effective interaction from the one-shot GWA band. In the one-shot GWA, we calculate the self-energy from the Green’s function G and the fully-screened interaction W,
where W is calculated from all the polarizations in the RPA P as follows,
The quasiparticle approximation of the Hamiltonian in the GWA is expressed as
where HLDA is the Hamiltonian in the LDA, Vxc is the exchange correlation potential in the LDA, and Z(ϵLDA) is the renormalization factor of Σ at the eigenenergy ϵLDA:
We calculate the electronic band structure of the YNiO2 using the experimental lattice parameters of LaNiO2, where
The cRPA and GW calculations use a mixed basis consisting of products of two atomic orbitals and interstitial plane waves [72]. In the cRPA and GW calculation, the 6 × 6 × 6 k-mesh is employed for YNiO2. we interpolate the mesh using the tetrahedron method to treat the screening effect accurately [73, 74]. We disentangle the target band from other bands when the target band crosses another band and construct orthogonalized two separated Hilbert spaces [75]. We include bands about from −25 to 120 eV for calculation of the screened interaction and the self-energy.
Result
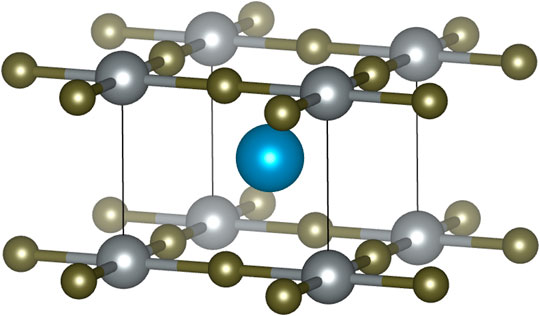
Figure 1 shows the crystal structure of the infinite-layer nickelates. The block layer is a single lanthanide cation and has large interstitial regions surrounded by cations. This is one of the reasons for the formation of electron pockets originating from the block layer, as described below.
Figure 2 shows the band structure of YNiO2 in the LDA. The band structure of YNiO2 is very similar to that of NdNiO2 if we eliminate the Nd 4f bands. The
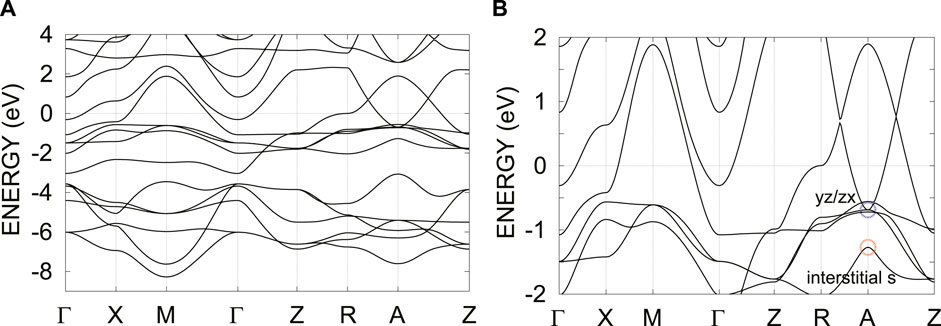
FIGURE 2. (A) DFT/LDA band structure for YNiO2 and (B) its magnified figure. The zero energy corresponds to the Fermi level.
The interstitial state is located at − 1.4 eV at the A point, and has a band inversion between yz/zx orbitals around the A point. Because of the inversion between bands with different numbers of degeneracies, the bands of the interstitial s and the yz/zx are continuously connected from the conduction band to the valence band. Since this band inversion is buried in the metallic band, it will be difficult to observe the surface state associated with the band inversion.
In this paper, we derive a three-orbital effective model consisting of the Ni
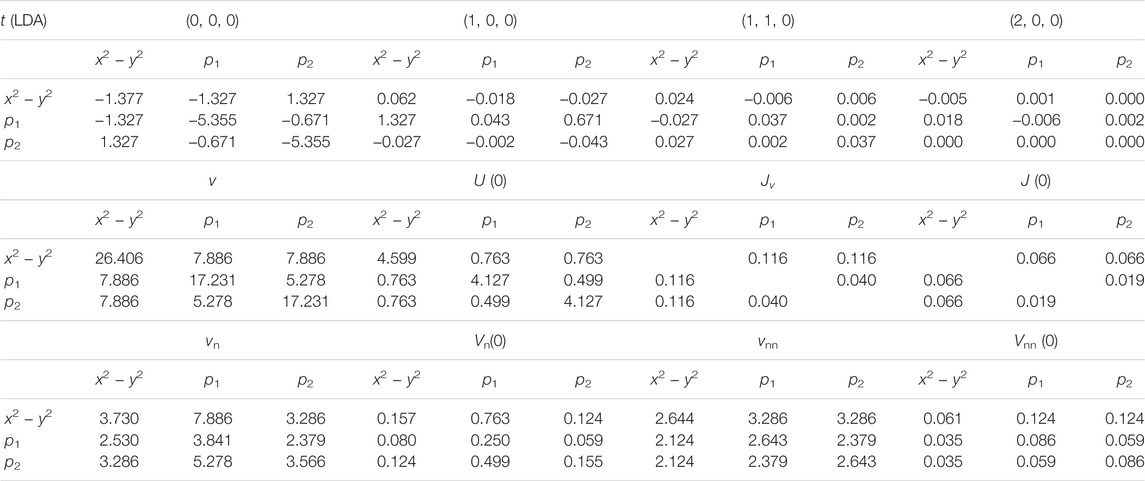
TABLE 1. Transfer integrals and effective interactions in the three-orbital Hamiltonian for YNiO2 (in eV). Both the one- and two-body part of the Hamiltonian are constructed based on the LDA band structure. v, U (0), Jv, and J (0) represent the bare Coulomb, the static values of the effective Coulomb, bare exchange interactions, and exchange interactions, respectively (at ω =0). The index “n” and “nn” represent the nearest unit cell (1,0,0) and the next-nearest unit cell (1,1,0), respectively.
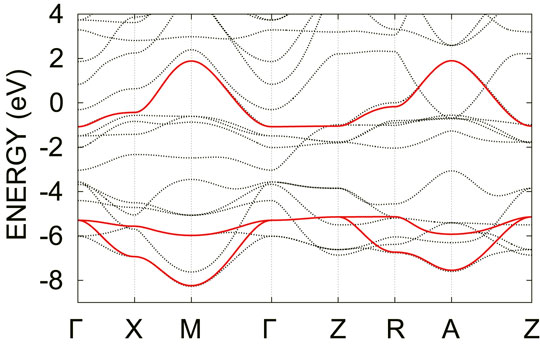
FIGURE 3. Electronic band structure of the three-orbital model in the LDA (solid lines). The zero energy corresponds to the Fermi level. For comparison, the band structures in the LDA is also given (dotted lines).
We then calculate the effective interaction for the three-orbital model by the cRPA method. The obtained effective interactions are summarized in Table 1. The bare Coulomb interaction v is slightly smaller than that of the copper oxides (Ni
We next show the band structure in the GWA in Figure 4. In the GWA, the energy difference between the strongly correlated Ni 3d orbitals and the weakly correlated O 2p orbitals is enhanced [33, 76]. Thereby, the energy gap between the d- and p-bands around −3 eV is increased. On the other hand, the bandwidth of the antibonding orbitals of the
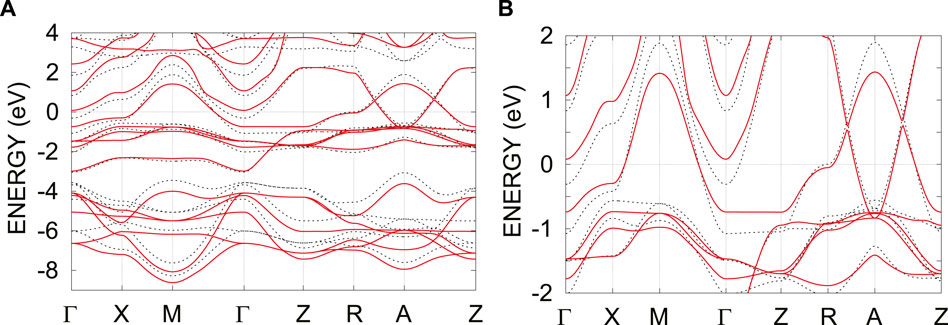
FIGURE 4. (A) GW band structure for YNiO2 and (B) its magnified figure (solid lines). For comparison, the band structures in the LDA is also given (dotted lines). The zero energy corresponds to the Fermi level.
In the GWA, the position of the valence band is lifted up from that in the LDA. In particular, the electron pocket originating from the d orbital in the block layer near the Γ point disappears. On the other hand, the bottom of the band originating from the interstitial state still creates the electron pocket around the A point even in the GWA.
We derive the three-orbital model (see Figure 5) and summarize the hopping parameters in Table 2. The difference in the on-site potential between the
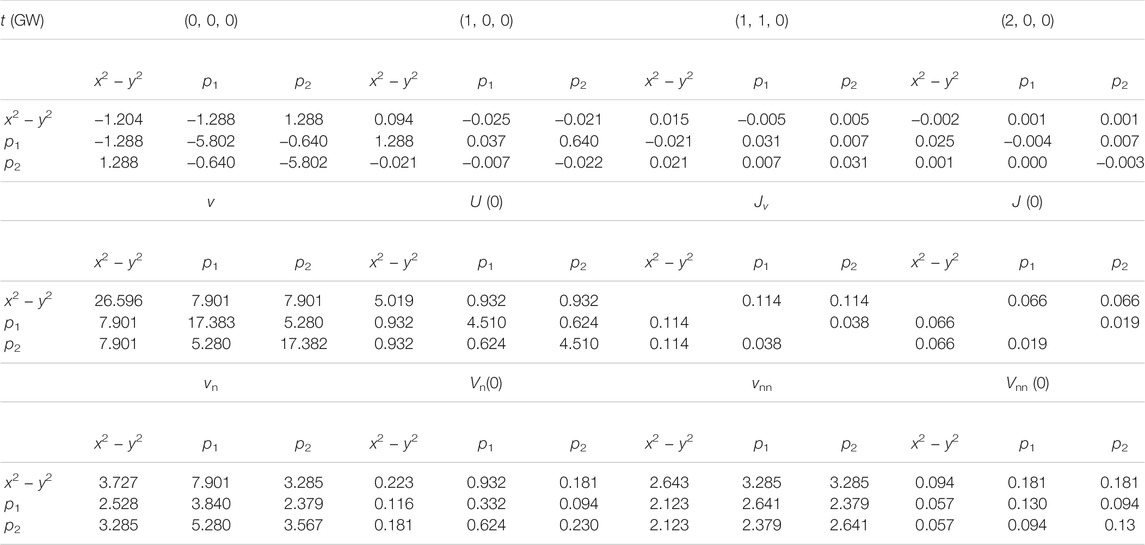
TABLE 2. Transfer integrals and effective interactions in the three-band Hamiltonian for YNiO2 (in eV). The one-body part is obtained from the GW band structure, and the effective interaction is the result of the cRPA calculation for the GW bands. v, U (0), Jv, and J (0) represent the bare Coulomb, the static values of the effective Coulomb, bare exchange interactions, and exchange interactions, respectively (at ω =0). The index “n” and “nn” represent the nearest unit cell [1,0,0] and the next-nearest unit cell [1,1,0] respectively.
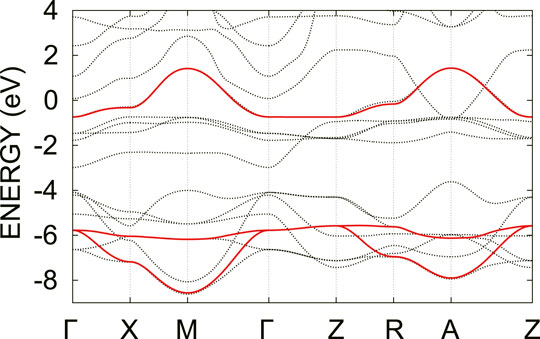
FIGURE 5. Electronic band structure of the three-orbital model in the GWA (solid lines). The zero energy corresponds to the Fermi level. For comparison, the band structures in the GWA is also given (dotted lines).
The screening effect of the system is reduced compared to that in the LDA mainly due to the increase of the charge-transfer energy, which increases the bare Coulomb interaction of the
Conclusion
We derived a three-orbital low-energy model for the infinite-layer nickelates based on the GWA. In the GWA, the O 2p bands locate deeper below the Fermi level, and the bandwidth of the Ni
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
MH conducted calculations. All authors contributed to writing the article.
Funding
We acknowledge funding through Grant-in-Aids for Scientific Research (JSPS KAKENHI) (Grant Nos 20K14423 (YN), 21H01041 (YN), and 19H05825 (RA)) and “Program for Promoting Researches on the Supercomputer Fugaku” (Basic Science for Emergence and Functionality in Quantum Matter —Innovative Strongly-Correlated Electron Science by Integration of “Fugaku” and Frontier Experiments) (Grant No. JPMXP1020200104) from MEXT.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The reviewer AF declared a shared affiliation, with no collaboration, with the authors, RA, MH, to the handling editor at time of review.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We thank Terumasa Tadano and Motoharu Kitatani for valuable discussions.
Footnotes
1It should be noted that although the cRPA method is free from the double counting problem for the interaction parameters, we have to apply the constrained GW (cGW) method to avoid the double counting in the self-energy [36].
2We note that there are several other effective models for infinite-layer nickelates that have been discussed, including a multi-band model that includes 3d orbitals other than the 3dx2−y2 orbital [40–52], a model that includes the contribution of rare-earth 4f electrons [53–56], and a model that includes the self-doping bands [57–59]. Here, we focus on the debate [40, 57, 60–67] on the classification of the Mott-Hubbard or charge-transfer regimes in Zaanen-Sawatzky-Allen phase diagram [68].
3We note that there is a proposal that the electron pocket at the A point can be eliminated by designing a different type of the block layer [33].
Appendix
For reference, we summarize the parameters in the single-orbital model in Tables A1 and A2. Special attention should be paid to the strength of the interaction in the GWA-based effective single-orbital model (see Ref. [38]). In the copper oxides, the correlation effect beyond the RPA between the d and p orbitals in the three-orbital model is not small. Therefore, in order to calculate the single-orbital model accurately, it is necessary to treat the screening effect originating from the bonding and nonbonding bands beyond the RPA. To do so, we need to solve the three-orbital model once with a low-energy solver such as the VMC and estimate the energy corrections between the d and p orbitals beyond the GWA. By combining such a correction with the GW self-energy correction, we can calculate the band structure beyond the GWA, and can estimate a single-orbital model with high accuracy (See Ref. [38] for details of the method). Because the nickelates have a qualitatively similar band structure to the cuprates, the reliability of the GWA-based single-orbital model for the nickelates also needs to be carefully examined: in particular, the correlation strength |U/t| might be overestimated.
References
1. Li D, Lee K, Wang BY, Osada M, Crossley S, Lee HR, et al. Superconductivity in an Infinite-Layer Nickelate. Nature (2019) 572:624–7. doi:10.1038/s41586-019-1496-5
2. Norman MR. Entering the Nickel Age of Superconductivity. Physics (2020) 13:85. doi:10.1103/physics.13.85
3. Pickett WE. The Dawn of the Nickel Age of Superconductivity. Nat Rev Phys (2021) 3:7–8. doi:10.1038/s42254-020-00257-3
4. Zhang J, Tao X. Review on quasi-2D Square Planar Nickelates. CrystEngComm (2021) 23:3249–64. doi:10.1039/d0ce01880e
5. Botana AS, Bernardini F, Cano A. Nickelate Superconductors: An Ongoing Dialog between Theory and Experiments. J Exp Theor Phys (2021) 132:618–27. doi:10.1134/s1063776121040026
8. Zeng S, Tang CS, Yin X, Li C, Li M, Huang Z, et al. Phase Diagram and Superconducting Dome of Infinite-Layer Nd1−xSrxNiO2 Thin Films. Phys Rev Lett (2020) 125:147003. doi:10.1103/PhysRevLett.125.147003
9. Gu Q, Li Y, Wan S, Li H, Guo W, Yang H, et al. Single Particle Tunneling Spectrum of Superconducting Nd1-xSrxNiO2 Thin Films. Nat Commun (2020) 11:6027. doi:10.1038/s41467-020-19908-1
10. Gao Q, Zhao Y, Zhou X-J, Zhu Z. Preparation of Superconducting Thin Films of Infinite-Layer Nickelate Nd0.8Sr0.2NiO2. Chin Phys. Lett. (2021) 38:077401. doi:10.1088/0256-307X/38/7/077401
11. Zhou XR, Feng ZX, Qin PX, Yan H, Wang XN, Nie P, et al. Negligible Oxygen Vacancies, Low Critical Current Density, Electric-Field Modulation, In-Plane Anisotropic and High-Field Transport of a Superconducting Nd0.8Sr0.2NiO2/SrTiO3 Heterostructure. Rare Metals (2021) 40:2847.
12. Li Y, Sun W, Yang J, Cai X, Guo W, Gu Z, et al. Impact of Cation Stoichiometry on the Crystalline Structure and Superconductivity in Nickelates. Front Phys (2021) 9:443. doi:10.3389/fphy.2021.719534
13. Osada M, Wang BY, Goodge BH, Lee K, Yoon H, Sakuma K, et al. A Superconducting Praseodymium Nickelate with Infinite Layer Structure. Nano Lett (2020) 20:5735–40. doi:10.1021/acs.nanolett.0c01392
14. Osada M, Wang BY, Lee K, Li D, Hwang HY. Phase Diagram of Infinite Layer Praseodymium Nickelate Pr1−xSrxNiO2 Thin Films. Phys Rev Mater (2020) 4:121801. doi:10.1103/PhysRevMaterials.4.121801
15. Osada M, Wang BY, Goodge BH, Harvey SP, Lee K, Li D, et al. Nickelate Superconductivity without Rare‐Earth Magnetism: (La,Sr)NiO 2. Adv Mater (2021) 33:2104083. doi:10.1002/adma.202104083
16. Zeng SW, Li CJ, Chow LE, Cao Y, Zhang ZT, Tang CS, et al. Superconductivity in Infinite-Layer Lanthanide Nickelates (2021). arXiv:2105.13492.
17. Pan GA, Ferenc Segedin D, LaBollita H, Song Q, Nica EM, Goodge BH, et al. Superconductivity in a Quintuple-Layer Square-Planar Nickelate. Nat Mater (2021). doi:10.1038/s41563-021-01142-9
18. Nomura Y, Hirayama M, Tadano T, Yoshimoto Y, Nakamura K, Arita R. Formation of a Two-Dimensional Single-Component Correlated Electron System and Band Engineering in the Nickelate Superconductor NdNiO2. Phys Rev B (2019) 100:205138. doi:10.1103/PhysRevB.100.205138
19. Adhikary P, Bandyopadhyay S, Das T, Dasgupta I, Saha-Dasgupta T. Orbital-selective Superconductivity in a Two-Band Model of Infinite-Layer Nickelates. Phys Rev B (2020) 102:100501. doi:10.1103/PhysRevB.102.100501
20. Wang Z, Zhang G-M, Yang Y-f., Zhang F-C. Distinct Pairing Symmetries of Superconductivity in Infinite-Layer Nickelates. Phys Rev B (2020) 102:220501. doi:10.1103/PhysRevB.102.220501
21. Kitamine N, Ochi M, Kuroki K. Designing Nickelate Superconductors with D8 Configuration Exploiting Mixed-Anion Strategy. Phys Rev Res (2020) 2:042032. doi:10.1103/PhysRevResearch.2.042032
22. Wu X, Jiang K, Sante DD, Hanke W, Schnyder AP, Hu J, et al. Surface S-Wave Superconductivity for Oxide-Terminated Infinite-Layer Nickelates (2020). arXiv:2008.06009.
23. Choubey P, Eremin IM. Electronic Theory for Scanning Tunneling Microscopy Spectra in Infinite-Layer Nickelate Superconductors. Phys Rev B (2021) 104:144504. doi:10.1103/PhysRevB.104.144504
24. Sakakibara H, Usui H, Suzuki K, Kotani T, Aoki H, Kuroki K. Model Construction and a Possibility of Cupratelike Pairing in a New D9 Nickelate Superconductor (Nd,Sr)NiO2. Phys Rev Lett (2020) 125:077003. doi:10.1103/PhysRevLett.125.077003
25. Hirsch JE, Marsiglio F. Hole Superconductivity in Infinite-Layer Nickelates. Physica C: Superconductivity its Appl (2019) 566:1353534. doi:10.1016/j.physc.2019.1353534
26. Wu X, Di Sante D, Schwemmer T, Hanke W, Hwang HY, Raghu S, et al. Robust Dx2−y2 -wave Superconductivity of Infinite-Layer Nickelates. Phys Rev B (2020) 101:060504. doi:10.1103/PhysRevB.101.060504
27. Giustino F. Electron-phonon Interactions from First Principles. Rev Mod Phys (2017) 89:015003. doi:10.1103/RevModPhys.89.015003
28. Flores-Livas JA, Boeri L, Sanna A, Profeta G, Arita R, Eremets M. A Perspective on Conventional High-Temperature Superconductors at High Pressure: Methods and Materials. Phys Rep (2020) 856:1–78. doi:10.1016/j.physrep.2020.02.003.A
29. Marzari N, Vanderbilt D. Maximally Localized Generalized Wannier Functions for Composite Energy Bands. Phys Rev B (1997) 56:12847–65. doi:10.1103/PhysRevB.56.12847
30. Souza I, Marzari N, Vanderbilt D. Maximally Localized Wannier Functions for Entangled Energy Bands. Phys Rev B (2001) 65:035109. doi:10.1103/PhysRevB.65.035109
31. Aryasetiawan F, Imada M, Georges A, Kotliar G, Biermann S, Lichtenstein AI. Frequency-dependent Local Interactions and Low-Energy Effective Models from Electronic Structure Calculations. Phys Rev B (2004) 70:195104. doi:10.1103/PhysRevB.70.195104
32. Imada M, Miyake T. Electronic Structure Calculation by First Principles for Strongly Correlated Electron Systems. J Phys Soc Jpn (2010) 79:2001. doi:10.1143/jpsj.79.112001
33. Hirayama M, Tadano T, Nomura Y, Arita R. Materials Design of Dynamically Stable D9 Layered Nickelates. Phys Rev B (2020) 101:075107. doi:10.1103/PhysRevB.101.075107
34. Nomura Y, Nomoto T, Hirayama M, Arita R. Magnetic Exchange Coupling in Cuprate-Analog D9 Nickelates. Phys Rev Res (2020) 2:043144. doi:10.1103/PhysRevResearch.2.043144
35. Hirayama M, Miyake T, Imada M, Biermann S. Low-energy Effective Hamiltonians for Correlated Electron Systems beyond Density Functional Theory. Phys Rev B (2017) 96:075102. doi:10.1103/physrevb.96.075102
36. Hirayama M, Miyake T, Imada M. Derivation of Static Low-Energy Effective Models by Anab Initiodownfolding Method without Double Counting of Coulomb Correlations: Application to SrVO3, FeSe, and FeTe. Phys Rev B (2013) 87:195144. doi:10.1103/PhysRevB.87.195144
37. Hirayama M, Yamaji Y, Misawa T, Imada M. Ab Initio effective Hamiltonians for Cuprate Superconductors. Phys Rev B (2018) 98:134501. doi:10.1103/PhysRevB.98.134501
38. Hirayama M, Misawa T, Ohgoe T, Yamaji Y, Imada M. Effective Hamiltonian for Cuprate Superconductors Derived from Multiscale Ab Initio Scheme with Level Renormalization. Phys Rev B (2019) 99:245155. doi:10.1103/PhysRevB.99.245155
39. Ohgoe T, Hirayama M, Misawa T, Ido K, Yamaji Y, Imada M. Ab Initio study of Superconductivity and Inhomogeneity in a Hg-Based Cuprate Superconductor. Phys Rev B (2020) 101:045124. doi:10.1103/PhysRevB.101.045124
40. Jiang M, Berciu M, Sawatzky GA. Critical Nature of the Ni Spin State in Doped NdNiO2. Phys Rev Lett (2020) 124:207004. doi:10.1103/PhysRevLett.124.207004
41. Zhang Y-H, Vishwanath A. Type-II t−J Model in Superconducting Nickelate Nd1−xSrxNiO2. Phys Rev Res (2020) 2:023112. doi:10.1103/PhysRevResearch.2.023112
42. Werner P, Hoshino S. Nickelate Superconductors: Multiorbital Nature and Spin Freezing. Phys Rev B (2020) 101:041104. doi:10.1103/PhysRevB.101.041104
43. Petocchi F, Christiansson V, Nilsson F, Aryasetiawan F, Werner P. Normal State of Nd1−xSrxNiO2 from Self-Consistent GW+EDMFT. Phys Rev X (2020) 10:041047. doi:10.1103/PhysRevX.10.041047
44. Hu L-H, Wu C. Two-band Model for Magnetism and Superconductivity in Nickelates. Phys Rev Res (2019) 1:032046. doi:10.1103/PhysRevResearch.1.032046
45. Lechermann F. Late Transition Metal Oxides with Infinite-Layer Structure: Nickelates versus Cuprates. Phys Rev B (2020) 101:081110. doi:10.1103/PhysRevB.101.081110
46. Lechermann F. Multiorbital Processes Rule the Nd1−xSrxNiO2 Normal State. Phys Rev X (2020) 10:041002. doi:10.1103/PhysRevX.10.041002
47. Lechermann F. Doping-dependent Character and Possible Magnetic Ordering of NdNiO2. Phys Rev Mater (2021) 5:044803. doi:10.1103/PhysRevMaterials.5.044803
48. Chang J, Zhao J, Ding Y. Hund-Heisenberg Model in Superconducting Infinite-Layer Nickelates. Eur Phys J B (2020) 93:220. doi:10.1140/epjb/e2020-10343-7
49. Wang Y, Kang C-J, Miao H, Kotliar G. Hund's Metal Physics: From SrNiO2 to LaNiO2. Phys Rev B (2020) 102:161118. doi:10.1103/PhysRevB.102.161118
50. Liu Z, Xu C, Cao C, Zhu W, Wang ZF, Yang J. Doping Dependence of Electronic Structure of Infinite-Layer NdNiO2. Phys Rev B (2021) 103:045103. doi:10.1103/PhysRevB.103.045103
51. Kang B, Melnick C, Semon P, Ryee S, Han MJ, Kotliar G, et al. Infinite-layer Nickelates as Ni-Eg Hund’s Metals (2021). arXiv:2007.14610.
52. Choi M-Y, Pickett WE, Lee K-W. Fluctuation-frustrated Flat Band Instabilities in NdNiO2. Phys Rev Res (2020) 2:033445. doi:10.1103/PhysRevResearch.2.033445
53. Jiang P, Si L, Liao Z, Zhong Z. Electronic Structure of Rare-Earth Infinite-Layer RNiO2(R=La,Nd). Phys Rev B (2019) 100:201106. doi:10.1103/PhysRevB.100.201106
54. Choi M-Y, Lee K-W, Pickett WE. Role of 4f States in Infinite-Layer NdNiO2. Phys Rev B (2020) 101:020503. doi:10.1103/PhysRevB.101.020503
55. Zhang R, Lane C, Singh B, Nokelainen J, Barbiellini B, Markiewicz RS, et al. Magnetic and F-Electron Effects in LaNiO2 and NdNiO2 Nickelates with Cuprate-like $$3{d}_{{x}^{2}-{y}^{2}}$$ Band. Commun Phys (2021) 4:118. doi:10.1038/s42005-021-00621-4
56. Bandyopadhyay S, Adhikary P, Das T, Dasgupta I, Saha-Dasgupta T. Superconductivity in Infinite-Layer Nickelates: Role of F Orbitals. Phys Rev B (2020) 102:220502. doi:10.1103/PhysRevB.102.220502
57. Hepting M, Li D, Jia CJ, Lu H, Paris E, Tseng Y, et al. Electronic Structure of the Parent Compound of Superconducting Infinite-Layer Nickelates. Nat Mater (2020) 19:381–5. doi:10.1038/s41563-019-0585-z
58. Zhang G-M, Yang Y-f., Zhang F-C. Self-doped Mott Insulator for Parent Compounds of Nickelate Superconductors. Phys Rev B (2020) 101:020501. doi:10.1103/PhysRevB.101.020501
59. Gu Y, Zhu S, Wang X, Hu J, Chen H. A Substantial Hybridization between Correlated Ni-D Orbital and Itinerant Electrons in Infinite-Layer Nickelates. Commun Phys (2020) 3:84. doi:10.1038/s42005-020-0347-x
60. Fu Y, Wang L, Cheng H, Pei S, Zhou X, Chen J, et al. Core-level X-ray Photoemission and Raman Spectroscopy Studies on Electronic Structures in Mott-Hubbard Type Nickelate Oxide NdNiO2 (2019). arXiv:1911.03177.
61. Goodge BH, Li D, Lee K, Osada M, Wang BY, Sawatzky GA, et al. Doping Evolution of the Mott–Hubbard Landscape in Infinite-Layer Nickelates. Proc Natl Acad Sci (2021) 118. doi:10.1073/pnas.2007683118
62. Kitatani M, Si L, Janson O, Arita R, Zhong Z, Held K. Nickelate Superconductors-A Renaissance of the One-Band Hubbard Model. Npj Quan Mater. (2020) 5:59. doi:10.1038/s41535-020-00260-y
63. Karp J, Hampel A, Zingl M, Botana AS, Park H, Norman MR, et al. Comparative many-body Study of Pr4Ni3O8 and NdNiO2. Phys Rev B (2020) 102:245130. doi:10.1103/PhysRevB.102.245130
64. Higashi K, Winder M, Kuneš J, Hariki A. Core-Level X-Ray Spectroscopy of Infinite-Layer Nickelate: LDA+DMFT Study. Phys Rev X (2021) 11:041009. doi:10.1103/PhysRevX.11.041009
65. Karp J, Botana AS, Norman MR, Park H, Zingl M, Millis A. Many-body Electronic Structure of NdNiO2 and CaCuO2. Phys Rev X (2020) 10:021061. doi:10.1103/PhysRevX.10.021061
66. Lang Z-J, Jiang R, Ku W. Strongly Correlated Doped Hole Carriers in the Superconducting Nickelates: Their Location, Local many-body State, and Low-Energy Effective Hamiltonian. Phys Rev B (2021) 103:L180502. doi:10.1103/PhysRevB.103.L180502
67. Worm P, Si L, Kitatani M, Arita R, Tomczak JM, Held K. Correlations Turn Electronic Structure of Finite-Layer Nickelates Upside Down (2021). arXiv:2111.12697.
68. Zaanen J, Sawatzky GA, Allen JW. Band Gaps and Electronic Structure of Transition-Metal Compounds. Phys Rev Lett (1985) 55:418–21. doi:10.1103/PhysRevLett.55.418
69. Crespin M, Isnard O, Dubois F, Choisnet J, Odier P. Lanio2: Synthesis and Structural Characterization. J Solid State Chem (2005) 178:1326–34. doi:10.1016/j.jssc.2005.01.023
70. Methfessel M, van Schilfgaarde M, Casali RA. Lecture Notes in Physics. editorH Dreysse 535. Berlin): Springer-Verlag (2000).
71. Ceperley DM, Alder BJ. Ground State of the Electron Gas by a Stochastic%20Method. Phys Rev Lett (1980) 45:566–9. doi:10.1103/PhysRevLett.45.566
72. van Schilfgaarde M, Kotani T, Faleev SV. Adequacy of Approximations inGWtheory. Phys Rev B (2006) 74:245125. doi:10.1103/physrevb.74.245125
73. Fujiwara T, Yamamoto S, Ishii Y. Generalization of the Iterative Perturbation Theory and Metal-Insulator Transition in Multi-Orbital Hubbard Bands. J Phys Soc Jpn (2003) 72:777–80. doi:10.1143/jpsj.72.777
74. Nohara Y, Yamamoto S, Fujiwara T. Electronic Structure of Perovskite-type Transition Metal oxidesLaMO3(M=Ti∼Cu)byU+GWapproximation. Phys Rev B (2009) 79:195110. doi:10.1103/physrevb.79.195110
75. Miyake T, Aryasetiawan F, Imada M. Ab Initioprocedure for Constructing Effective Models of Correlated Materials with Entangled Band Structure. Phys Rev B (2009) 80:155134. doi:10.1103/physrevb.80.155134
Keywords: nickelate superconductivity, density functional theory, GW approximation, ab initio downfolding, multi-orbital Hubbard model
Citation: Hirayama M, Nomura Y and Arita R (2022) Ab Initio Downfolding Based on the GW Approximation for Infinite-Layer Nickelates. Front. Phys. 10:824144. doi: 10.3389/fphy.2022.824144
Received: 29 November 2021; Accepted: 17 January 2022;
Published: 23 February 2022.
Edited by:
Junjie Zhang, Shandong University, ChinaReviewed by:
Atsushi Fujimori, Waseda University, JapanLiviu Chioncel, University of Augsburg, Germany
Copyright © 2022 Hirayama, Nomura and Arita. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Motoaki Hirayama, aGlyYXlhbWFAYXAudC51LXRva3lvLmFjLmpw
 Motoaki Hirayama1,2*
Motoaki Hirayama1,2* Yusuke Nomura
Yusuke Nomura Ryotaro Arita
Ryotaro Arita