Abstract
Emergency material allocation is an important issue in the urgent handling of public health emergencies. This article models the relief allocation and transportation route planning as an uncertain capacitated arc routing problem, which is a classic combinatorial optimization problem that considers stochastic factors such as uncertain demand and travel time in the service. The stochastic of demand leads to the route failure that the vehicle cannot serve the tasks successfully unexpected. Most existing research uses the independent recourse strategy. That is, each vehicle takes a back-and-forth trip separately when its remaining capacity cannot meet the actual demand of the task. This leads to a considerable recourse cost. However, a few studies have considered vehicular cooperation to deal with route failure, which is beneficial for pooling the capacity of multiple vehicles. In this paper, we propose a new recourse strategy called OneFAll that lets one vehicle take charge of all the failed tasks. In this case, other vehicles can finish the service once they are full. We develop the genetic programming hyper-heuristic with the OneFAll recourse strategy for solving the uncertain capacitated arc routing problem. The experimental studies show that our proposed method outperforms the existing genetic programming hyper-heuristic with the independent recourse strategy to the uncertain capacitated arc routing problem for the ugdb and uval benchmark instances. Moreover, our strategy outperforms the recourse strategy that failed tasks are returned to the unassigned task set for any vehicle to complete. This reflects that there exists resource waste if all vehicles are involved to repair the failed routes.
1 Introduction
In the urgent handling of public health emergencies, the medical resources, including protective equipments, disinfection materials, drugs, and medical supplies, are the material basis [1]. The allocation efficiency has a direct impact on the timely control and elimination of public health emergencies, and safeguarding the physical health and life security of the general public. However, if the allocation is not improper, the emergencies cannot be contained timely, which has a great effect on the recovery of social functions [2]. It is bound to cause enormous losses for our society.
From the perspective of management decision, emergency material allocation is a dynamic decision-making problem in the complex road networks that allocate relief materials from suppliers to disaster areas as soon as possible. The relief allocation and transportation route planning can be categorized under the domain of capacitated arc routing problem (CARP) [3], which is a classic optimization problem that has been thoroughly studied in the operations research and has a wide range of applications for many real-world situations [4, 5]. The pharmacies, quarantine offices, and community offices can be seen as demand points along the streets in the road network, which correspond to tasks in CARP. A fleet of equipped vehicles is appointed to meet the demands of these points, and both the vehicles that can be dispatched and their capacities are limited, which can be modeled as constraints in CARP. The goal is to design the most economical routes, which corresponds to optimizing the objective functions (e.g., minimizing costs) in CARP.
The emergency material allocation in the real world is much complex than the traditional CARP, which assumes that all the information in the environment such as the demands and traversal costs is static and can be exactly known in advance. However, this assumption does not always hold in the real world, especially in the environment of emergent disaster. In fact, the demands of tasks are uncertain, which are affected by many factors, such as the number of residents along the streets and the severity of the disaster. Hence, the exact value of demands cannot be exactly known beforehand. This may lead to that a vehicle reaches a task without enough capacity to meet the demand. Moreover, the roads may be interrupted or blocked, which leads to that the preplanned routes cannot be traversed. Hence, uncertain CARP (UCARP) has been a hot and active research topic in recent years [6]. Two of the above uncertainties are considered in UCARP, and they lead to two uncontrollable failures, i.e., the route failure and the edge failure, respectively.
For solving the UCARP, the existing approaches can be divided into three main categories [7, 8]: robust pro-active, completely reactive, and predictive–reactive. Among them, the completely reactive approaches aim to evolve policies, which can generate routes based on practical situations in real time. They have the advantages of flexibility and are very efficient in handling dynamic environments [9]. Among the completely reactive approaches, genetic programming (GP) has been proven to be an effective hyper-heuristic method (shorted as GPHH), which can automatically evolve routing policies for UCARP that are much better than the manually designed ones [10, 11]. For using GPHH to solve UCARP, an important issue is how to deal with failures, which could influence the efficiency of routing policies evolved by GPHH. For the edge failure, the most commonly used strategy is to find a detour to the destination. For the route failure, the situation is much more complex and has attracted more attention [12]. One of the naive recourse strategies to deal with route failure is that as soon as the capacity of the vehicle expires, the vehicle goes back to the depot to refill and then comes back to the interrupted place to continue the service [13]. This can be seen as an independent recourse strategy, and there is no collaboration between vehicles, which may lead to a considerable recourse cost. In recent years, collaborative transportation has been an emerging new mode, as it can bring together all the vehicles to improve the overall performance. Especially in the urgent disaster environment, the relief materials are very scarce and precious. There are not enough protective suits for workers or volunteers to participate in the rescue job. Hence, it is highly necessary to make full use of the cooperative abilities of vehicles in order to serve more tasks in a shorter time. That is to say, the independent recourse strategy is not suitable for urgent-disaster environments. We have to design more reasonable cooperative recourse strategies to deal with route failures, which have a great impact on the improvement of the whole efficiency.
Hence, we aim to propose a new recourse strategy for solving UCARP under the application of emergency material allocation in this paper. We develop a GPHH with the new recourse strategy to design routing policies for multi-vehicle UCARP. To be more specific, we have the following research objectives:
• To develop a new recourse strategy, named OneFAll, which considers cooperation between multiple vehicles.
• To develop a GPHH with the OneFAll recourse strategy to evolve routing policies for solving UCARP.
• To investigate the effectiveness of the OneFAll recourse strategy by comparing with existing state-of-the-art recourse strategies on benchmark UCARP datasets.
• To analyze the structure of the solutions obtained by different recourse strategies.
The rest of this paper is structured as follows. Section 2 presents the background including UCARP definition and related work. Section 3 describes the proposed OneFAll recourse strategy and the new GPHH algorithm for solving UCARP. Section 4 shows the experimental studies and analysis. Section 5 gives the conclusion and future work.
2 Background
2.1 Problem definition
A UCARP instance [
13,
14] can be represented by a connected graph
G= (
V,
E), where
Vis the set of vertices and
Eis the set of edges. Each edge
e∈
Eis associated with three features: a demand
d(
e)
0, a serving cost
sc(
e)
0, and a traversal cost (time to travel along the edge without serving it)
dc(
e)
0. Edges with positive demands are called
tasks. The set of all tasks is denoted as
T∈
E. A fleet of vehicles with a limited capacity
Qis located at a special vertex called depot
v0∈
Vat the beginning. In the real scenario, it is assumed that the number of vehicles is restricted. The goal of the problem is to find out a least-cost routing plan for the vehicles to serve all the tasks subject to the following constraints:
1. Each vehicle starts from the depot and comes back to the depot after serving all the tasks allocated to it. Vehicles can replenish its capacity each time when they pass by the depot.
2. Each task is served exactly once in either direction.
3. The total demand served by each vehicle in a single trip cannot exceed its capacity.
A
sampleof a UCARP instance is obtained by sampling a value for each random variable of the corresponding UCARP instance. For example, a sample
Iξof the UCARP instance
Iis obtained by sampling each random demand
dξ(
e) and each random traversal cost
dcξ(
e) under the environment (e.g., random seed)
ξ. For solving a UCARP instance sample, both the task demand and edge traversal cost are unknown until the task is served or the edge is traversed. These lead to two unavoidable failures:
• Edge failure: the edge ahead of the route is inaccessible.
• Route failure: the actual demand of the task to be served exceeds the remaining capacity of the vehicle.
In the case of edge failure, one can find a detour to the destination. If the edge is a task assigned to the vehicle, the vehicle will abandon this task and go to serve the next task according to the routing plan. The route failure is not such kind of easy to cope with. A typical recourse operator uses an independent recourse strategy [11, 13]. When a route failure occurs, the vehicle returns to the depot to refill its capacity and then comes back to finish the remaining service of the failed task. However, this may introduce a large amount of extra cost. We will give a detailed review about the current recourse strategies for route failure in Section 2.3. To summarize, avoiding a route failure is more challenging and has a greater impact on solution quality [12]. A good recourse strategy is expected to minimize the extra refill cost. Therefore, in this paper, we aim to propose an efficient recourse strategy to tackle the uncertain demands.
A solution to a UCARP instance sample can be represented as S = (X, Y). X = {X(1), X(2), …, X(m)} is a set of routes, where each route is a sequence of vertices starting and ending at the depot vertex (i.e., = = v0) and Lk is the number of vertices in the kth route. Y = {Y(1), Y(2), …, Y(m)} is a set of real-valued vectors indicating the fraction of service of each edge along the routes. Specifically, corresponds to X(k), where 0 1. means that the edge is a task and is fully served, and means that the edge is traveled through by the vehicle without being served. For other values of , it means that the edge is partially served at the current route.
The total cost of a solution (X, Y) is calculated as Eq. 1,where and stand for the and elements in the solution Sξ on the environment ξ.
Note that Sξ varies from one sample to another. For any sample ξ, a feasible solution Sξ can be generated by a pre-optimized (robust) solution or a routing policy that generates the solution in an online fashion. In this paper, we focus on the latter.
2.2 Approaches to uncertain CARP
Based on when the decisions are made, the approaches to solve uncertain routing problems are categorized into three categories [7, 8]: robust pro-active, completely reactive, and predictive–reactive.
The robust proactive typically can be divided into two stages. It first constructs predictive solutions to satisfy performance requirements based on the prediction of the environment. Then, the solutions are executed, and the recourse strategies are taken to deal with failures, as in two-stage stochastic programming with recourse. The optimization algorithms used in the first stage in existing studies are the branch-and-price algorithm [15], the memetic algorithm [16, 17] and the estimation of the distribution algorithm [18]. The recourse actions in the second stage are summarized in the following subsection.
The advantage of the proactive approaches is that they can provide a robust and predictable solution when applied to new environments. However, they are non-flexible and cannot cope with real-time adjustment.
The completely reactive approaches treat the problem as an online decision-making process and construct the final solution step by step using the decision-making rule (called routing policy in UCARP) [8]. Some common heuristics such as path scanning [19] can be seen as a completely reactive approach. The keys to the success of these approaches are to obtain a good decision-making policy and the decision-making process of the policy on instances (i.e., meta-algorithm). The two main approaches based on the completely reactive approach are the GP algorithm and the rollout algorithm.
GP [20] belongs to the evolutionary computation field, which aims to evolve computer programs. In GP, populations of computer programs are genetically bred using the Darwinian principle of survival of the fittest and using a genetic crossover operator appropriate for genetically mating computer programs [21]. As a hyper-heuristic method, GPHH has been applied to scheduling tasks. A GPHH program can be seen as a routing policy for routing problems [22], or a dispatching rule for job shop scheduling problems [23] for different decision environments. Weise et al. [22] first proposed to apply GPHH for the automated design of routing policy for solving static CARP and tested the performance of the evolved rules for dealing with random disappearance of tasks. Liu et al. [11] extended the GPHH for solving UCARP with a new meta-algorithm. Later on, many researchers have proposed the improved GPHH for solving UCARP from the aspect of developing more effective meta-algorithms [24, 25], evolving more interpretable routing policies [26, 27], and discovering the reusability of routing policies [28, 29].
The design of the rollout algorithm is motivated by the idea of policy iteration in dynamic programming. It is a decision-making process algorithm based on Monte Carlo simulation. Dror et al. [30] first modeled the vehicle routing problem with stochastic demands as a Markov decision process in theory, but they did not provide any computational results. Secomandi [31] first proposed the rollout algorithm to solve the vehicle routing problem defined in [30]. Later on, the rollout algorithm was improved by many researchers for solving uncertain vehicle routing problems [32–34].
The advantage of completely reactive approaches is that the solutions are generated online, so the solutions are flexible, which is especially effective in uncertain environments [35]. However, their disadvantage is that no baseline solution (i.e., a set of routes) is generated, which reduces the stability of routes and causes difficulty for planning and measuring in advance [7].
The predictive–reactive can be seen as a hybridization of the pro-active and the completely reactive. They include a baseline solution obtained by the pro-active part, and a reoptimization strategy in charge of real-time reaction. Liu et al. [14] designed the first predictive–reactive approach for solving UCARP. They proposed a new solution representation, which is composed of two components: a baseline task sequence and a recourse policy. Meanwhile, a cooperative coevolution framework is designed to optimize these two components simultaneously.
The advantage of predictive–reactive approaches is that they generally consider both the quality of the predictive baseline solution (efficiency) and the degree of change to be made on the baseline solution to adapt to the new environment (stability) [12, 14].
2.3 Recourse strategies for route failure
In [36], Gendreau et al. pointed out that the development of new recourse strategies is one of the most critical issues and challenges that need to be addressed to advance research in this area. By now, there are three main kinds of recourse strategies: the independent, the pairing, and the global.
In the independent recourse strategy, upon failure, the vehicle returns to the depot, replenishes its capacity, and resumes its planned route at the point of failure [11, 13]. While somewhat simplistic, this recourse strategy has some advantages. First, it yields relatively tractable models that enable the development of exact algorithms. Second, from the practical view, the independent recourse strategies warrant stable tactical routes, which are operationally desirable, as they require little deviations of drivers’ familiar driving environment and ensure that customers are consistently visited by the same drivers. Hence, it is the most widely used one for the routing problem with stochastic demands. However, the recourse actions are based on the realized demand of a route, independent of the demand realizations of the other routes. No cooperation between vehicles may cause a great degree of resource waste.
The pairing recourse strategy [37] considers a certain degree of collaboration between two vehicles. According to this strategy, the vehicles are paired to work, where one is identified as Type I and the other is Type II. When the Type I vehicle shows a failure, it returns to the depot. Moreover, the unserved tasks are appended to the end of the route of the Type II vehicle. The classical recourse policy is used to handle failure in the Type II route. Lei et al. [38] proposed another form of the paired strategy, where they allowed demands to be split between the paired routes while applying the classical recourse strategy upon failure. Erera et al. [39] proposed that customers were assigned to two planned routes, a primary and a backup. The recourse decisions allow reallocating customers to backup routes in the implementing of the planned routes. Their experiments verified that the paired recourse strategy can save the expected travel cost in a large degree.
The global recourse strategy aims to construct more collaborative forms of recourse involving multiple vehicles, which is likely to reduce the expected costs substantially. Unfortunately, only a few studies have considered the global recourse strategy to data. MacLachlan et al. [12] proposed that the failed tasks were returned back to the candidate task set. Any vehicle can potentially complete the remaining service at any time based on the routing policy. This can be seen as a kind of global recourse strategy. However, it may have the drawback that all vehicles could not cease their services until all the tasks are fulfilled. It may appear that many vehicles had to begin a second tour and only serve a few tasks (e.g., one or two), which may increase the total cost in a large degree. We compare our proposed strategy with this one in experiments and use a case study to show their differences.
Besides the above three categories, the preventive restocking strategy is also considered in many existing studies [40]. It assumes that whenever the residual capacity of a vehicle becomes low, the vehicle may execute a restocking trip to the depot actively. The preventive restocking can reduce the probability of route failures [36]. In our work, such strategy is used in the meta-algorithm to filter candidate tasks for the selection of vehicles [11]. Details are shown in Section 3.1.
As the information and communications technologies enable communications between vehicles [41], it is valuable to develop recourse strategies based on a high degree of vehicle collaboration. Moreover, taking the urgent disaster into consideration, the resources that can be used are limited and the basic requirement is to serve the area as larger as possible in the first time. Hence, we move a step forward to propose a new recourse strategy for route failure in the next section.
3 The proposed approach
First, the general framework of GPHH for evolving routing policies to solve UCARP is described in Figure 1.
FIGURE 1
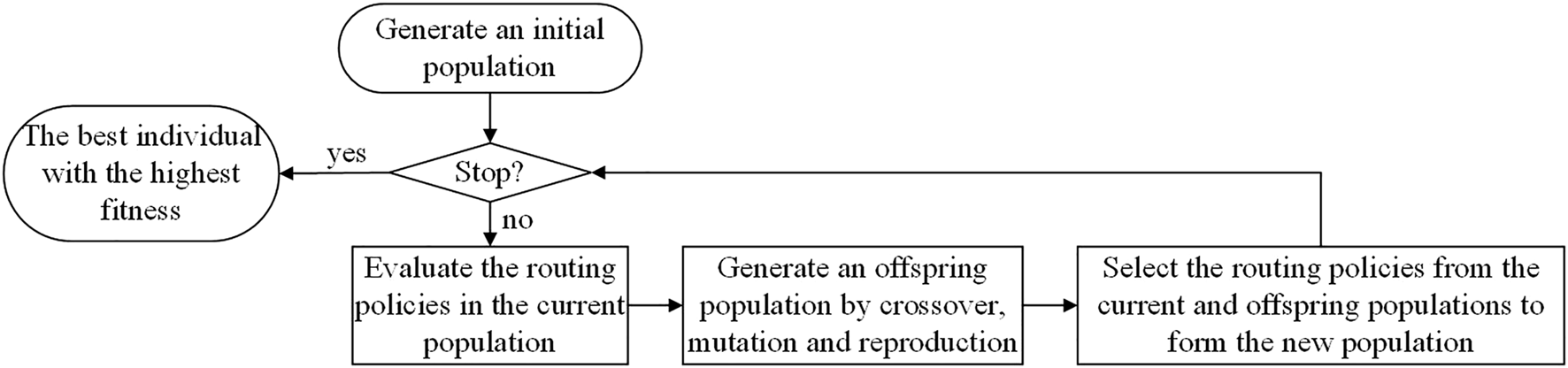
The flowchart of GPHH for UCARP.
In the GPHH, a routing policy is represented as a Lisp tree, which is used as a priority function to select the task from the candidate task sets for a vehicle to serve next. To evaluate the fitness of each routing policy, a meta-algorithm is designed to generate a feasible solution given a sampled UCARP instance Iξ and a routing policy h (⋅). At the beginning of the research, the meta-algorithm is designed as processes of building the routes one by one, which simulates a single-vehicle situation, where all the routes are executed by a single vehicle sequentially [11]. It cannot handle with the multi-vehicle UCARP, in which there are multiple vehicles on the road simultaneously. To fill this gap, Mei et al. [25] proposed the meta-algorithms that model a multi-vehicle decision-making process, where there can be any number of vehicles in service simultaneously. However, the strategies to deal with the route failure in multi-vehicle cases have been overlooked so far, which would influence the efficiency of the meta-algorithms. Considering the application of emergency material allocation, we proposed a new meta-algorithm with a new recourse strategy in the following.
3.1 The meta-algorithm with the new recourse strategy
For the emergency material allocation, a fleet of vehicles is appointed to allocate relief materials to communities distributed along streets in a certain area. These vehicles should complete the current tasks as soon as possible in order to traverse to the next area. Not all vehicles are needed to stay at the current area until all tasks are finished, as we want to help residents in wider areas. That is to say, when route failure occurs, only a few vehicles (e.g., one or two vehicles) need to stay at the current area to finish the remaining task; other vehicles can go to a new area straightforwardly.
Above all, an efficient cooperative recourse strategy in the emergency material allocation can be that vehicles are divided into two parts: flowing vehicles and stationary vehicles. Moreover, when route failure occurs, the failed tasks are returned back to the unassigned task set for any vehicles in the stationary category to potentially complete. For the vehicles in the flowing category, they just do one route, i.e., either when there is no candidate task for them to serve or when they encounter route failure, and they will finish the service. For the vehicles in the stationary category, they do not stop the service until all tasks are finished in the service. This proposal can also meet some other scenario in the real world. For example, some drivers want to do more job to earn more money.
Algorithm 1 describes the proposed meta-algorithm with the cooperative recourse strategy that executes a routing policy h (⋅) on a sampled UCARP instance Iξ to construct a feasible solution.
Algorithm 1
3.2 GPHH with the new meta-algorithm
The training process of GPHH with the new meta-algorithm is described in Algorithm 2. It follows the standard GP process. During fitness evaluation (line 9), given a training set {Iξ|ξ ∈ Ξtrain}, the fitness function of evaluating each routing policy h (⋅) is calculated as Eq. 2, i.e., the average total cost of the solutions obtained by applying this policy to the training samples.where C(Sξ, h (⋅)) is the total cost of the solution Sξ under the routing policy h (⋅).
Algorithm 2

4 Experimental study
In order to examine the effectiveness of the proposed recourse strategy, we compare with the basic GPHH with the independent recourse strategy (named GPHH) and GPHH with the reassigned strategy proposed in [12] (named GPHH-Re, which is described as a kind of global recourse strategy in Section 2.3).
4.1 Experiment settings
All the compared GPHH algorithms share the same parameter settings, as shown in Table 1. The terminal set is given in Table 2. The function set is {+, −, ×,/, max, min}. The function / is protected, which returns to 1 if divided by zero. The gdb and val datasets are two commonly used benchmark datasets in the area of UCARP. In the gdb dataset, the number of vertices varies from 7 to 27, and the number of the arcs varies from 11 to 55. The val dataset is much bigger than the gdb dataset, and its vertices and arcs numbers vary from 24 to 41, from 34 to 69, respectively. For the number of vehicles, we suppose that it equals to the total demands of all tasks dividing the capacity of the vehicle in each scenario in the experiments. Hence, combined with the proposed new recourse strategy in Section 3.1, we let one vehicle as the stationary and called the new algorithm as GPHH-OneFAll. The UCARP instance generator in [13] is used to generate the training and test instances based on the static gdb and val datasets. The stochastic traversal costs and demands follow the normal distribution , where μ is the deterministic value given in the static instance and λ is the uncertainty level. λ is set to 0.2 in our experiments. Especially, if the stochastic traversal cost dc(e) < 0, then it is set to ∞. That means that the arc becomes inaccessible. If the stochastic demand d(e) < 0, then it is set to 0. That means that the arc has no demand and is not a task in the current environment. In the experiments, each algorithm is trained on 5 randomly sampled instances in each generation, and the best routing policy h*(⋅) is tested on 500 unseen instances. The test performance of GPHH is defined as the average total cost over the 500 samples.
TABLE 1
| Parameter | Value |
|---|---|
| Population size | 1,024 |
| Generations | 51 |
| Tournament section size | 7 |
| Crossover rate | 0.8 |
| Mutation rate | 0.15 |
| Reproduction rate | 0.05 |
| Maximal tree depth | 8 |
The parameter settings.
TABLE 2
| Notation | Description |
|---|---|
| CFH | Cost From Here (the current node) to the head node of the candidate task |
| CR | Cost to Refill (from the current node to the depot) |
| CTD | Cost from the tail node of the candidate task To the Depot |
| CTT1 | Cost from the tail of the candidate task To its closest remaining unserved Task (the head) |
| DEM | DEMand of the candidate task |
| DEM1 | DEMand of the closet unserved task to the candidata task |
| FRT | Fraction of the Remaining (unserved) Tasks |
| FULL | FULLness of the vehicle (current load over capacity) |
| RQ | Remaining Capacity of the vehicle |
| SC | Serving Cost of the candidata task |
| ERC | a random constant number between 0 and 1 |
The terminal set.
4.2 Results
Table 3 and Table 4 show the test performances of the compared algorithms on the ugdb and uval UCARP instances, respectively. All the algorithms are run 20 times independently. The Wilcoxon rank-sum test with the significance level of 0.05 is conducted to compare GPHH-OneFAll with GPHH and GPHH-Re. The “(−)” means that the compared algorithms (i.e., GPHH or GPHH-Re) perform significantly worse than GPHH-OneFAll; otherwise, there is no significant difference between the two algorithms. The results with the minimum average are highlighted in bold.
TABLE 3
| Name | (|V|, |E|) | Vehicle no | GPHH | GPHH-Re | GPHH-OneFAll |
|---|---|---|---|---|---|
| ugdb1 | (12,22) | 5 | 351.34(7.03) (−) | 350.09 (5.55) (−) | 345.06 (6.21) |
| ugdb2 | (12,26) | 6 | 368.99 (4.46) (−) | 366.23 (5.50) (−) | 360.52 (3.53) |
| ugdb3 | (12,22) | 5 | 307.56(1.53) (−) | 305.39 (3.59) | 302.46 (7.60) |
| ugdb4 | (11,19) | 4 | 321.26 (1.98) (−) | 317.19 (1.67) | 317.50 (2.59) |
| ugdb5 | (13,26) | 6 | 423.67 (6.14) (−) | 422.05 (5.76) (−) | 418.09 (5.15) |
| ugdb6 | (12,22) | 5 | 347.50 (11.22) | 345.66 (8.58) | 345.83 (1.98) |
| ugdb7 | (12,22) | 5 | 351.41 (4.94) (−) | 347.22 (4.69) | 346.24 (4.26) |
| ugdb8 | (27,46) | 10 | 445.17 (8.04) (−) | 430.91 (7.90) (−) | 424.84 (6.04) |
| ugdb9 | (27,51) | 10 | 382.95 (8.83) (-) | 374.90 (8.63) | 369.73 (7.17) |
| ugdb10 | (12,25) | 4 | 296.47 (3.39) (-) | 291.97 (3.29) | 293.01 (2.58) |
| ugdb11 | (22,45) | 5 | 431.88 (5.93) (−) | 431.07 (5.27) (−) | 425.00 (5.85) |
| ugdb12 | (13,23) | 7 | 612.69 (14.59) (−) | 592.23 (7.96) | 595.61 (7.18) |
| ugdb13 | (10,28) | 6 | 576.08 (4.05) (−) | 572.21 (4.17) (−) | 568.04 (2.69) |
| ugdb14 | (7,21) | 5 | 107.77 (1.28) | 107.88 (1.37) | 107.34 (1.03) |
| ugdb15 | (7,21) | 4 | 58.10 (0.03) | 58.09 (0.03) | 58.08 (0.03) |
| ugdb16 | (8,28) | 5 | 136.23 (1.35) (−) | 136.05 (0.36) (−) | 133.17 (0.47) |
| ugdb17 | (8,28) | 5 | 91.07 (0.04) | 91.07 (0.03) | 91.06 (0.04) |
| ugdb18 | (9,36) | 5 | 167.86 (2.47) | 167.17 (1.61) | 166.50 (1.27) |
| ugdb19 | (8,11) | 3 | 61.58 (1.26) | 61.61 (1.37) | 61.69 (1.24) |
| ugdb20 | (11,22) | 4 | 127.31 (1.89) | 127.43 (1.17) | 127.24 (1.12) |
| ugdb21 | (11,33) | 6 | 164.15 (2.10) | 163.99 (2.21) | 164.10 (1.87) |
| ugdb22 | (11,44) | 8 | 209.60 (0.94) (−) | 208.52 (0.75) | 207.92 (0.78) |
| ugdb23 | (11,55) | 10 | 251.19 (1.86) (−) | 249.60 (1.47) (−) | 247.33 (1.32) |
| Mean | 286.60 | 283.41 | 281.58 |
Results on the ugdb dataset in terms of the average on the test set.
TABLE 4
| Name | (|V|, |E|) | Vehicle no. | GPHH | GPHH-Re | GPHH-OneFAll |
|---|---|---|---|---|---|
| uval1A | (24,39) | 2 | 176.68 (2.44) | 175.70 (2.18) | 175.76 (2.81) |
| uval1B | (24,39) | 3 | 184.88 (1.95) (−) | 184.54 (2.17) (−) | 182.87 (1.72) |
| uval1C | (24,39) | 8 | 314.63 (8.06) (−) | 303.24 (5.62) | 302.85 (6.68) |
| uval2A | (24,34) | 2 | 230.52 (3.47) | 232.40 (3.99) | 230.05 (3.39) |
| uval2B | (24,34) | 3 | 277.15 (3.72) | 276.54 (3.54) | 276.53 (3.19) |
| uval2C | (24,34) | 8 | 590.76 (15.67) (−) | 558.72 (17.22) | 558.70 (13.45) |
| uval3A | (24,35) | 2 | 81.75 (0.61) | 81.91 (0.78) | 81.86 (0.61) |
| uval3B | (24,35) | 3 | 97.51 (2.23) (−) | 95.92 (1.35) | 95.67 (1.58) |
| uval3C | (24,35) | 7 | 174.73 (5.04) (−) | 174.71 (7.24) (−) | 164.66 (7.61) |
| uval4A | (41,69) | 3 | 418.31 (5.79) | 422.05 (9.41) | 416.80 (5.70) |
| uval4B | (41,69) | 4 | 440.96 (4.41) | 439.39 (5.68) | 438.44 (3.10) |
| uval4C | (41,69) | 5 | 491.76 (9.16) (−) | 487.25 (5.85) (−) | 478.08 (5.87) |
| uval4D | (41,69) | 9 | 712.77 (10.05) (−) | 688.26 (23.45) (−) | 660.70 (19.11) |
| Mean | 322.49 | 316.97 | 312.54 |
Results on the uval dataset in terms of the average on the test set.
As shown in Table 3 and Table 4, it can be seen that the proposed GPHH-OneFAll outperformed GPHH on 22 out of the 36 instances and outperformed GPHH-Re on 12 out of the 36 instances. GPHH-OneFAll performed no worse than GPHH and GPHH-Re on any instances. Based on the results marked in bold, we can see that the GPHH algorithms with vehicle cooperations in recourse (i.e., GPHH-Re and GPHH-OneFAll) have better performance than the basic GPHH with the independent recourse strategy on almost all the instances. Only on two instances ugdb19 and uval3A whose vehicle number is small did the baseline GPHH obtain slightly better results. The experimental results show that the designed cooperative recourse strategy is useful for saving the total costs.
4.3 Further analysis
As we described in Section 2.3, GPHH-Re has the drawback that many vehicles may take a second small route to serve a few tasks because of the uncertainty. This usually increases the total cost. Furthermore, our proposed GPHH-OneFAll algorithm can overcome this drawback by appointing one vehicle to serve the remaining tasks if all other vehicles are full. To illustrate this idea more clearly, we randomly select a routing policy evolved by GPHH-Re and GPHH-OneFAll obtained from the ugdb13 instance, respectively. The two policies are applied on the same sampled scenario, whose detailed information (i.e., the tasks, the expected and the actual demands, the serving costs, and the actual traversal costs) is shown in Table 5.
TABLE 5
| Task | Demand | Actual | Serving cost | Actual traversal |
|---|---|---|---|---|
| (d) | demand (dξ) | sc | cost (dcξ) | |
| (v0, v4) | 12 | 11.93 | 7 | 4.82 |
| (v0, v5) | 2 | 1.41 | 18 | 15.76 |
| (v0, v6) | 13 | 11.76 | 4 | 5.13 |
| (v0, v7) | 12 | 14.57 | 24 | 20.25 |
| (v0, v8) | 16 | 11.75 | 11 | 8.18 |
| (v1, v0) | 13 | 15.24 | 15 | 15.38 |
| (v1, v2) | 11 | 10.26 | 5 | 5.7 |
| (v1, v4) | 7 | 9.24 | 12 | 9.61 |
| (v1, v7) | 13 | 15.57 | 13 | 21.62 |
| (v2, v0) | 16 | 18.38 | 8 | 8.2 |
| (v2, v5) | 7 | 7.21 | 1 | 0.92 |
| (v2, v6) | 5 | 4.84 | 10 | 9.18 |
| (v2, v7) | 3 | 3.17 | 24 | 24.67 |
| (v3, v0) | 13 | 17.45 | 6 | 5.66 |
| (v3, v1) | 4 | 4.55 | 3 | 2.91 |
| (v3, v2) | 7 | 8.87 | 28 | 34.13 |
| (v3, v4) | 15 | 16.46 | 2 | 1.45 |
| (v4, v5) | 9 | 9.65 | 20 | 23.01 |
| (v4, v6) | 5 | 6.37 | 42 | 39.36 |
| (v4, v8) | 5 | 5.38 | 12 | 10.5 |
| (v5, v6) | 8 | 9.19 | 9 | 8.64 |
| (v5, v8) | 3 | 2.1 | 13 | 15.23 |
| (v6, v7) | 9 | 8.61 | 16 | 10.67 |
| (v6, v8) | 3 | 3.23 | 60 | 55.69 |
| (v6, v9) | 14 | 10.73 | 5 | 5.68 |
| (v7, v8) | 7 | 6.95 | 22 | 18.51 |
| (v7, v9) | 8 | 5.61 | 99 | 152.56 |
| (v8, v9) | 5 | 5.52 | 20 | 20.38 |
The detailed information of one instance of ugdb13.
The routes generated by the two routing policies are shown in Figure 2. It can be seen that the total cost of the routes generated by GPHH-OneFAll (i.e., 568.67) is much shorter than that of GPHH-Re (i.e., 590.82). When looking into the details of the route, we discover that half of the vehicles (i.e., Vehicle 1, Vehicle 4, and Vehicle 6) in routes generated by GPHH-Re (Figure 2A) take second routes with serving only one or two tasks. However, in routes generated by GPHH-OneFAll, Vehicle2, Vehicle3, Vehicle4, and Vehicle6 directly return to the depot when their remaining capacities cannot meet the requirements of the unserved candidate tasks. Vehicle1 is appointed as the stationary vehicle, taking a second route to serve the remaining unserved tasks. The reason why Vehicle5 takes a second tour is that when serving the task (v6, v0), its capacity is refilled because v0 is the depot.
FIGURE 2
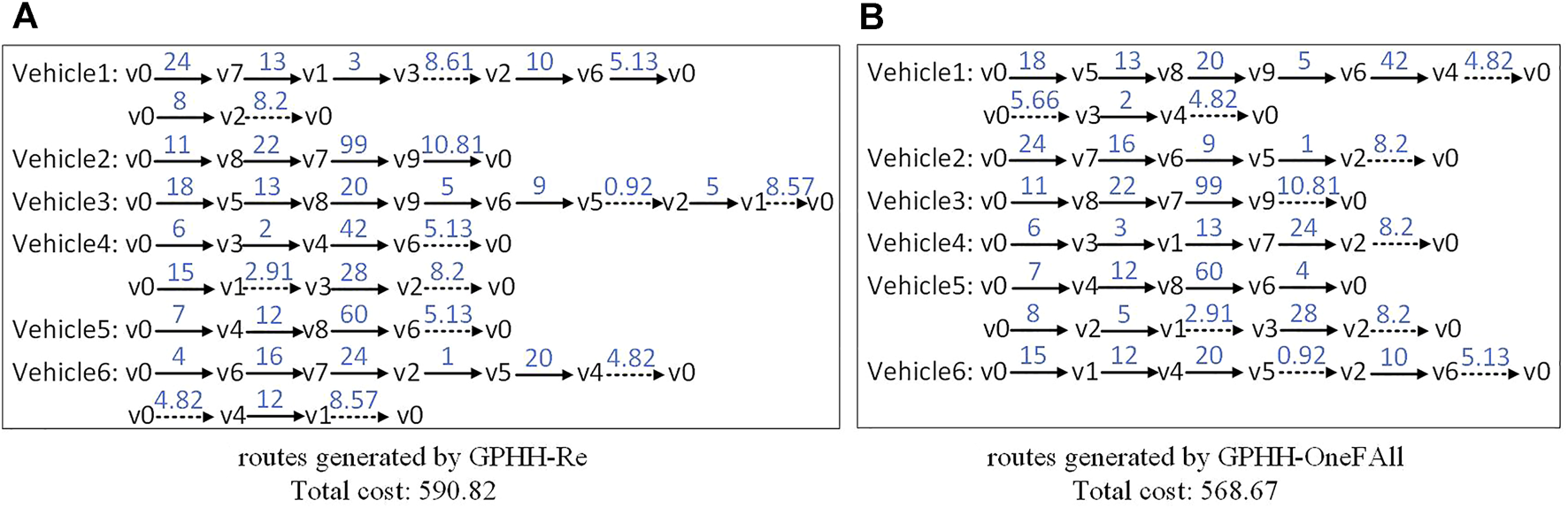
Examples of the routes generated by (A) GPHH-Re and (B) GPHH-OneFAll on the sampled ugdb13 instance in Table 5. The solid arrow connecting two vertices (vi, vj) means that (vi, vj) is a task and the vehicle travels from vi to vj to serve it, while the dotted arrow connecting two vertices (vi, vj) means that the vehicle travels from vi to vj following the shortest path between these two vertices without serving any tasks. The number above the solid arrow represents the serving cost, and the number above the dotted arrow represents the actual traversal cost of the shortest path.
5 Conclusion
In this paper, the emergency material allocation in the real world was formulated as UCARP, which was a classic combinatorial optimization problem under the uncertain environment. Addressing on the route failure caused by the uncertain demands of tasks, this paper proposed a new recourse strategy that divided the vehicles into two categories: flowing and stationary. The main idea of the new recourse strategy came from the real scenario that not all vehicles were needed to stay at the current area until all tasks were finished, as the goal was to help residents in wider areas. Moreover, it was easy to be applied to the real world. A GPHH algorithm based on the carefully designed meta-algorithm with the new recourse strategy for UCARP was proposed. In experiments, we let one vehicle to handle all the failed tasks or unserved tasks if other vehicles were full and called the new GPHH as GPHH-OneFAll. The experimental results showed that the proposed GPHH-OneFAll significantly outperformed the GPHH with existing recourse strategies.
For the future work, it is valuable to investigate the number of vehicles in each category, which may have a relationship with the total demands of tasks and the capacities of vehicles. As there is little knowledge on the manner of logistic companies that handle uncertain events, the recourse strategies remain mainly theoretical. Further work is to define more active recourse actions from the real data. Moreover, addressing on the global recourse strategies based on a high degree of vehicle coordination is also valuable to investigate.
Statements
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
YL and XL contributed to the conception and design of the study. SW organized the database and performed the statistical analysis. YL wrote the manuscript, and SW and XL contributed to the manuscript revision and read and approved the submitted version.
Funding
The work is sponsored by the National Natural Science Foundation of China (Nos. 61 976 181, 11 931 015) and the Shanghai Sailing Program (No. 21YF1416700).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1.
WangCDengYYuanZZhangCZhangFCaiQet alHow to Optimize the Supply and Allocation of Medical Emergency Resources during Public Health Emergencies. Front Phys (2020) 8:383. 10.3389/fphy.2020.00383
2.
CuiMHanDWangJ. An Efficient and Safe Road Condition Monitoring Authentication Scheme Based on Fog Computing. IEEE Internet Things J (2019) 6:9076–9084. 10.1109/JIOT.2019.2927497
3.
ZhangSZhangJZhaoJXinC. Robust Optimization of Municipal Solid Waste Collection and Transportation with Uncertain Waste Output: A Case Study. J Syst Sci Syst Eng (2021) 30:1–22. 10.1007/s11518-021-5510-8
4.
CorberánÁEgleseRHasleGPlanaISanchisJM. Arc Routing Problems: A Review of the Past, Present, and Future. Networks. (2021) 77:88–115. 10.1002/net.21965
5.
ThibbotuwawaABocewiczGNielsenPBanaszakZ. Unmanned Aerial Vehicle Routing Problems: A Literature Review. Appl Sci (2020) 10:4504. 10.3390/app10134504
6.
LiuJTangKYaoX. Robust Optimization in Uncertain Capacitated Arc Routing Problems: Progresses and Perspectives [Review Article]. IEEE Comput Intell Mag (2021) 16:63–82. 10.1109/mci.2020.3039069
7.
NguyenSMeiYMaHChenAZhangM. Evolutionary Scheduling and Combinatorial Optimisation: Applications, Challenges, and Future Directions. In: IEEE Congress on Evolutionary Computation; 2016 July 19–24. Vancouver, BC: IEEE (2016). p. 3053–60. 10.1109/cec.2016.7744175
8.
OuelhadjDPetrovicS. A Survey of Dynamic Scheduling in Manufacturing Systems. J Sched (2009) 12:417–31. 10.1007/s10951-008-0090-8
9.
WangSMeiYZhangMYaoX. Genetic Programming with Niching for Uncertain Capacitated Arc Routing Problem. IEEE Transactions on Evolutionary Computation (2022) 26 (1):73–87. 10.1109/TEVC.2021.3095261
10.
ArdehMAMeiYZhangM. Genetic Programming with Knowledge Transfer and Guided Search for Uncertain Capacitated Arc Routing Problem. IEEE Trans Evol Computat (2021). 10.1109/tevc.2021.3129278
11.
LiuYMeiYZhangMZhangZ. Automated Heuristic Design Using Genetic Programming Hyper-Heuristic for Uncertain Capacitated Arc Routing Problem. In: Proceedings of GECCO; 2017 July 15–19; Berlin, Germany. New York, NY: ACM (2017). p. 290–7. 10.1145/3071178.3071185
12.
MacLachlanJMeiYBrankeJZhangM. Genetic Programming Hyper-Heuristics with Vehicle Collaboration for Uncertain Capacitated Arc Routing Problems. Evol Comput (2020) 28:563–93. 10.1162/evco_a_00267
13.
MeiYTangKYaoX. Capacitated Arc Routing Problem in Uncertain Environments. In: IEEE Congress on Evolutionary Computation; 2010 July 18–23. Barcelona, Spain: IEEE (2010). p. 1–8. 10.1109/cec.2010.5586031
14.
LiuYMeiYZhangMZhangZ. A Predictive-Reactive Approach with Genetic Programming and Cooperative Coevolution for the Uncertain Capacitated Arc Routing Problem. Evol Comput (2020) 28:289–316. 10.1162/evco_a_00256
15.
ChristiansenCHLysgaardJWøhlkS. A branch-and-price Algorithm for the Capacitated Arc Routing Problem with Stochastic Demands. Operations Res Lett (2009) 37:392–8. 10.1016/j.orl.2009.05.008
16.
FleuryGLacommePPrinsC. Evolutionary Algorithms for Stochastic Arc Routing Problems. Berlin Heidelberg: Springer (2004). p. 501–12. 10.1007/978-3-540-24653-4_51
17.
WangJTangKYaoX. A Memetic Algorithm for Uncertain Capacitated Arc Routing Problems. In: 2013 IEEE Workshop on Memetic Computing; 2013 April 16–19; Singapore (2013). p. 72–9. 10.1109/mc.2013.6608210
18.
WangJTangKLozanoJAYaoX. Estimation of the Distribution Algorithm with a Stochastic Local Search for Uncertain Capacitated Arc Routing Problems. IEEE Trans Evol Computat (2016) 20:96–109. 10.1109/tevc.2015.2428616
19.
LacommePPrinsCRamdane-CherifW. Competitive Memetic Algorithms for Arc Routing Problems. Ann Operations Res (2004) 131:159–85. 10.1023/b:anor.0000039517.35989.6d
20.
KozaJR. Genetic Programming: On the Programming of Computers by Means of Natural Selection. Cambridge, MA, USA: MIT Press (1992).
21.
KozaJR. Genetic Programming as a Means of Programming Computers by Natural Selection. Stat Comput (1994) 4:87–112. 10.1007/bf00175355
22.
WeiseTDevertATangK. A Developmental Solution to (Dynamic) Capacitated Arc Routing Problems Using Genetic Programming. In: Proceedings of GECCO; 2012 July 7–11; Philadelphia, Pennsylvania. New York, NY: ACM (2012). p. 831–8. 10.1145/2330163.2330278
23.
XuBMeiYWangYJiZZhangM. Genetic Programming with Delayed Routing for Multiobjective Dynamic Flexible Job Shop Scheduling. Evolutionary Computation (2021) 29 (1):75–105. 10.1162/evco_a_00273
24.
MacLachlanJMeiYBrankeJZhangM. An Improved Genetic Programming Hyper-Heuristic for the Uncertain Capacitated Arc Routing Problem. In: Australasian Joint Conference on Artificial Intelligence; 2018 December 11–14; Wellington, New Zealand. Berlin, German: Springer (2018). p. 432–44. 10.1007/978-3-030-03991-2_40
25.
MeiYZhangM. Genetic Programming Hyper-Heuristics for Multi-Vehicle Uncertain Capacitated Arc Routing Problem. In: Proceedings of GECCO; 2018 July 15–19; Kyoto, Japan. New York, NY: ACM (2018). p. 141–2.
26.
WangSMeiYZhangM. Novel Ensemble Genetic Programming Hyper-Heuristics for Uncertain Capacitated Arc Routing Problem. In: Proceedings of GECCO; 2019 July 13–17; Prague, Czech Republic. New York, NY: ACM (2019). p. 1093–101. 10.1145/3321707.3321797
27.
WangSMeiYZhangM. A Multi-Objective Genetic Programming Hyper-Heuristic Approach to Uncertain Capacitated Arc Routing Problems. In: 2020 IEEE Congress on Evolutionary Computation (CEC); 2020 July 19–24; Glasgow, UK. Piscataway, NJ: IEEE (2020). p. 1–8. 10.1109/cec48606.2020.9185890
28.
ArdehMMeiYZhangM. Genetic Programming Hyper-Heuristic with Knowledge Transfer for Uncertain Capacitated Arc Routing Problem. In: Proceedings of GECCO; 2019 July 13–17; Prague, Czech Republic. New York, NY: ACM (2019). p. 334–5. 10.1145/3319619.3321988
29.
ArdehMAMeiYZhangM. A Parametric Framework for Genetic Programming with Transfer Learning for Uncertain Capacitated Arc Routing Problem. In: Australasian Joint Conference on Artificial Intelligence; 2020 November 29–30; Canberra, ACT, Australia. Berlin, German: Springer (2020). p. 150–62. 10.1007/978-3-030-64984-5_12
30.
DrorMLaporteGTrudeauP. Vehicle Routing with Stochastic Demands: Properties and Solution Frameworks. Transportation Sci (1989) 23:166–76. 10.1287/trsc.23.3.166
31.
SecomandiN. A Rollout Policy for the Vehicle Routing Problem with Stochastic Demands. Operations Res (2001) 49:796–802. 10.1287/opre.49.5.796.10608
32.
BertazziLSecomandiN. Faster Rollout Search for the Vehicle Routing Problem with Stochastic Demands and Restocking. Eur J Oper Res (2018) 270:487–97. 10.1016/j.ejor.2018.03.034
33.
GoodsonJCThomasBWOhlmannJW. Restocking-based Rollout Policies for the Vehicle Routing Problem with Stochastic Demand and Duration Limits. Transportation Sci (2016) 50:591–607. 10.1287/trsc.2015.0591
34.
NovoaCStorerR. An Approximate Dynamic Programming Approach for the Vehicle Routing Problem with Stochastic Demands. Eur J Oper Res (2009) 196:509–15. 10.1016/j.ejor.2008.03.023
35.
NguyenSZhangMJohnstonMTanKC. A Computational Study of Representations in Genetic Programming to Evolve Dispatching Rules for the Job Shop Scheduling Problem. IEEE Trans Evol Computat (2013) 17:621–39. 10.1109/TEVC.2012.2227326
36.
GendreauMJabaliOReiW. 50th Anniversary Invited Article-Future Research Directions in Stochastic Vehicle Routing. Transportation Sci (2016) 50:1163–73. 10.1287/trsc.2016.0709
37.
AkAEreraAL. A Paired-Vehicle Recourse Strategy for the Vehicle-Routing Problem with Stochastic Demands. Transportation Sci (2007) 41:222–37. 10.1287/trsc.1060.0180
38.
LeiHLaporteGGuoB. The Vehicle Routing Problem with Stochastic Demands and Split Deliveries. INFOR: Inf Syst Oper Res (2012) 50:59–71. 10.3138/infor.50.2.059
39.
EreraALSavelsberghMUyarE. Fixed Routes with Backup Vehicles for Stochastic Vehicle Routing Problems with Time Constraints. Networks (2009) 54:270–83. 10.1002/net.20338
40.
Salavati-KhoshghalbMGendreauMJabaliOReiW. A Rule-Based Recourse for the Vehicle Routing Problem with Stochastic Demands. Transportation Sci (2019) 53:1334–53. 10.1287/trsc.2018.0876
41.
HanDZhuYLiDLiangWSouriALiK-C. A Blockchain-Based Auditable Access Control System for Private Data in Service-Centric IoT Environment. IEEE Trans Industr Inform (2022) 18:3530–3540. 10.1109/TII.2021.3114621
Summary
Keywords
recourse strategy, uncertain capacitated arc routing problem, genetic programming hyper-heuristic, intelligent transportation, emergency material allocation
Citation
Liu Y, Wang S and Li X (2022) A New Cooperative Recourse Strategy for Emergency Material Allocation in Uncertain Environments. Front. Phys. 10:835412. doi: 10.3389/fphy.2022.835412
Received
14 December 2021
Accepted
10 January 2022
Published
22 February 2022
Volume
10 - 2022
Edited by
Zhanwei Du, University of Texas at Austin, United States
Reviewed by
Wenbin Pei, Victoria University of Wellington, New Zealand
Yu-Jie Xiong, Shanghai University of Engineering Sciences, China
Updates
Copyright
© 2022 Liu, Wang and Li.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xianghua Li, li_xianghua@nwpu.edu.cn
This article was submitted to Social Physics, a section of the journal Frontiers in Physics
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.