Investigating Effect of Coherent Emission Length on Pion Interferometry in High-Energy Collisions Using a Multiphase Transport Model

We study the two-pion Hanbury Brown–Twiss correlation functions for a partially coherent source constructed with the emission points and momenta of the identical pions generated by a multiphase transport model. A coherent emission length is introduced, the effects of which on the two-pion interferometry results in central Au-Au collisions at $\sqrt{s_{NN}}=200$ GeV, central Pb-Pb collisions at $\sqrt{s_{NN}}=2.76$ TeV, and p-p collisions at $\sqrt{s}=13$ TeV are investigated. It is found that the effect of coherent emission length reduces the two-pion correlation functions in the nucleus–nucleus collisions, leading to an average decrease of chaoticity parameter by approximately 15% in the high transverse momentum range. However, the influence of coherent emission length on the two-pion correlation functions in the p-p collisions is small, while the effect of coherent emission length on the chaoticity parameter is almost independent of the transverse momentum of pion pair in the p-p collisions.

1 Introduction

Pion Hanbury Brown–Twiss (HBT) interferometry has been widely used in high-energy collisions to detect the space-time structure of particle-emitting sources [1–6]. Since HBT correlation disappears for coherent emission of bosons, the intercept of the pion HBT correlation function near-zero relative momentum is sensitive to the coherence of the particle emission and can also be affected by many other factors [1–6]. Recent measurements of two-pion HBT correlations in p-p, p-Pb, and Pb-Pb collisions at the Large Hadron Collider (LHC) [7–11] and those of Au-Au and Cu-Cu collisions at the Relativistic Heavy Ion Collider (RHIC) [12–16] showed that the intercepts of the two-pion correlation functions near zero relative momentum are substantially less than 2. These observations and the suppression of the multi-pion correlation functions observed in the Pb-Pb collisions at the LHC [11, 17] indicate that the particle-emitting sources are perhaps partially coherent. However, there is no widely accepted explanation for these observations.

In Ref. 18, Bary and Zhang et al. analyzed the two- and multi-pion HBT correlations in a granular source with coherent pion emission droplets. They assumed that pions are emitted randomly from the evolving droplets in the granular source and that pion emissions from one droplet are coherent because of the closed emission points. They found that the intercepts of the pion HBT correlation functions at the relative momenta near zero have substantial decreases in the coherent granular source model. However, more detailed studies are needed to explain the experimental data. In this article, we study the two-pion HBT correlation functions for the partially coherent sources constructed with emission points and momenta of identical pions generated by a multiphase transport (AMPT) model [19, 20] for high-energy A-A and p-p collisions. Compared to a bulk evolution model, the AMPT as a cascade model can provide more detailed information about the particle production, interaction, and propagation in the source. It has been extensively employed in the simulation of high-energy p-p, p-A, and A-A collisions at the RHIC and LHC [19–32]. This study is our first step toward better understanding the relationship between HBT correlation and particle emission in the source.

The rest of this article is organized as follows. In Section 2, we present a brief introduction to the AMPT model and a description of the correlation function calculation for partially coherent sources. The HBT interferometry results for the sources in high-energy A-A and p-p collisions are presented in Section 3. Finally, a summary and discussion are provided in Section 4.

2 Model and Correlation Function Calculations

2.1 AMPT Model

The AMPT model has been extensively employed in the simulation of high-energy p-p, p-A, and A-A collisions at the RHIC and LHC [19–32]. The essential components of the AMPT model are initialization, parton transport, the hadronization mechanism, and hadron transport [20]. The initialization of the collisions is performed using the HIJING model [33]. Parton transport and hadron transport are described by the ZPC parton cascade model [34] and the ART model [35], respectively. In the string melting version of the AMPT model, which is used in this study, partons are hadronized by the quark coalescence mechanism [19, 20]. The model parameter μ of parton screening mass is taken to be 2.2814 fm⁻¹, and the strong coupling constant α_s is taken to be 0.47, corresponding to a parton-scattering cross section 6 mb [20]. The different values of the parton cross section were also used in analyzing the flow harmonics v_n (n = 2, 3) by comparing them with experimental data [19–24]. Because of partonic scattering, the v₂ results are great in the string melting AMPT model with a large parton scattering cross section [19, 20].

With the AMPT model, we can obtain the space-time emission points and momenta of identical pions and then calculate pion correlation functions. In Figure 1, we show the average spatial and temporal coordinates of the pion emissions versus pion transverse momentum in central Au-Au collisions at the RHIC energy $\sqrt{s_{NN}}=$200 GeV (Figures 1A,B), central Pb-Pb collisions at the LHC energy $\sqrt{s_{NN}}=$2.76 TeV (Figures 1C,D), and the p-p collisions at the LHC energy $\sqrt{s}=$13 TeV (Figures 1E,F). The solid and dashed lines are for the different values of the time limitation parameter t_L, which means that only the pions generated before t_L are sampled. The t_L values taken in our calculations are smaller than the cutoff time of 200 fm/c used in the model HBT analyses [20], so as to avoid the influence of long-lived resonance decay on the investigations.

FIGURE 1

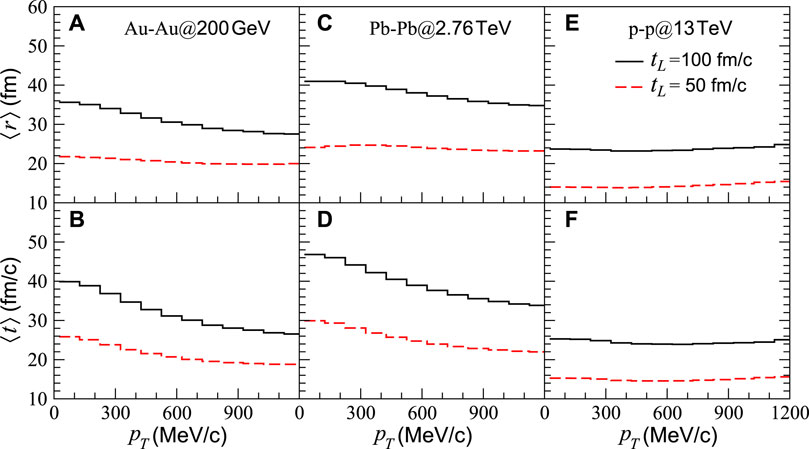
FIGURE 1. (A,B) Average spatial and temporal coordinates of pion emissions vs. pion transverse momentum in Au-Au collisions at $\sqrt{s_{NN}}=$200 GeV. (C,D) Average spatial and temporal coordinates of pion emissions vs. pion transverse momentum in Pb-Pb collisions at $\sqrt{s_{NN}}=$2.76 TeV. (E,F) Average spatial and temporal coordinates of pion emissions vs. pion transverse momentum in p-p collisions at $\sqrt{s}=$13 TeV. Solid and dashed lines denote the time limitation parameter t_L = 100 and 50 fm/c, respectively.

For the A-A collisions, both the average values of the spatial and temporal emission coordinates for t_L = 100 fm/c decrease with increasing transverse momentum, and the average of spatial coordinates for t_L = 50 fm/c is almost independent of transverse momentum. The average values of the spatial and temporal emission coordinates for t_L = 50 fm/c are smaller than those for t_L = 100 fm/c, and the average values of the spatial and temporal coordinates of the Pb-Pb collisions are larger than those of the Au-Au collisions. Compared to the average values in the A-A collisions, the results in the p-p collisions are smaller, and their variations with transverse momentum are flatter.

2.2 Calculation of Two-Pion Correlation Function

The two-pion HBT correlation function C(p₁, p₂) is defined as the ratio of the two-pion momentum distribution P(p₁, p₂) to the product of the single-pion momentum distribution P(p₁)P(p₂):

$C\left({\mathbf{p}}_1,{\mathbf{p}}_2\right)=\frac{P\left({\mathbf{p}}_1,{\mathbf{p}}_2\right)}{P\left({\mathbf{p}}_1\right)P\left({\mathbf{p}}_2\right)}.(1)$

For a chaotic pion-emitting source, P(p_i) (i = 1, 2) and P(p₁, p₂) can be expressed as [2]

$P\left({\mathbf{p}}_i\right)=\sum _{X_i}{A}^2\left({\mathbf{p}}_i,X_i\right),(2)$

$P\left({\mathbf{p}}_1,{\mathbf{p}}_2\right)=\sum _{X_1,X_2}{\left|\mathrm{\Phi }\left({\mathbf{p}}_1,{\mathbf{p}}_2;X_1,X_2\right)\right|}^2,(3)$

where A(p_i, X_i) is the magnitude of the amplitude for emitting a pion with momentum p_i at the four-coordinate X_i, and

$\begin{array}{ll}\hfill \mathrm{\Phi }\left({\mathbf{p}}_1,{\mathbf{p}}_2;X_1,X_2\right)& =\frac{1}{\sqrt{2}}\left[A\left({\mathbf{p}}_1,X_1\right)A\left({\mathbf{p}}_2,X_2\right)e^{i{p}_1\cdot X_1}{e}^{i{p}_2\cdot X_2}\right.\hfill \\ \hfill & \left.+A\left({\mathbf{p}}_1,X_2\right)A\left({\mathbf{p}}_2,X_1\right)e^{i{p}_1\cdot X_2}{e}^{i{p}_2\cdot X_1}\right],\hfill \end{array}(4)$

where p_i is the four-momentum.

For small relative momentum, q = p₁ − p₂, we can use A(K, X_i), instead of A(p_j, X_i) (i, j = 1, 2) [smoothed approximation, K = (p₁ + p₂)/2]. Then,

$\begin{array}{ccc}\hfill P\left({\mathbf{p}}_1,{\mathbf{p}}_2\right)& =\hfill & \sum _{X_1,X_2}{A}^2\left(\mathbf{K},X_1\right)A^2\left(\mathbf{K},X_2\right)\cos \left[\left(p_1-p_2\right)\cdot \left(X_1-X_2\right)\right]\hfill \\ \hfill & =\hfill & \sum _{X_1,X_2}{A}^2\left({\mathbf{p}}_1,X_1\right)A^2\left({\mathbf{p}}_2,X_2\right)\cos \left[\left(p_1-p_2\right)\cdot \left(X_1-X_2\right)\right].\hfill \end{array}(5)$

In high-energy nucleus–nucleus and proton–proton collisions at the RHIC and LHC, the systems are initially compressed in the beam direction (longitudinal or z direction) and then expanded longitudinally and transversely. Considering that the two pions emitted within a small longitudinal distance may be related, we assume that the pion emissions are coherent for the two pions with a relative longitudinal position $\mathrm{\Delta }z=\left|z_1-z_2\right|$ smaller than the length parameter L_C. Thus, for the partially coherent sources,

$P\left({\mathbf{p}}_1,{\mathbf{p}}_2\right)=\sum _{X_1,X_2}{A}^2\left({\mathbf{p}}_1,X_1\right)A^2\left({\mathbf{p}}_2,X_2\right)R\left({\mathbf{p}}_1,{\mathbf{p}}_2;X_1,X_2\right),(6)$

where

$R\left({\mathbf{p}}_1,{\mathbf{p}}_2;X_1,X_2\right)=\cos \left[\left(p_1-p_2\right)\cdot \left(X_1-X_2\right)\right],\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{\Delta }z>L_C,(7)$

and

$R\left({\mathbf{p}}_1,{\mathbf{p}}_2;X_1,X_2\right)=1,\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{\Delta }z<L_C.(8)$

We show in Figures 2A,B the two-pion correlation functions C(q) for the pion-emitting sources with the coherent emission length L_C = 0 (chaotic source), 1, and 2 fm in the Au-Au collisions at $\sqrt{s_{NN}}=$200 GeV in the transverse momentum ranges of K_T < 500 GeV/c and K_T > 500 GeV/c, respectively. Here, the temporal limitation parameter t_L is taken to be 100 fm/c. One can see that the effect of coherent emission length is greater in the higher momentum range than in the lower momentum range and decreases the correlation functions. The correlation functions in the higher transverse momentum range are wider than those in the lower transverse momentum range because the average source sizes at high transverse momenta are smaller than those at low transverse momenta. Figures 2C,D show the correlation functions for the sources with t_L = 50 fm/c. One can see that the correlation functions for t_L = 50 fm/c are wider than those for t_L = 100 fm/c because of the smaller source size for t_L = 50 fm/c. In Figure 2D, the correlation functions with nonzero L_C decrease slightly more than those in Figure 2B, relative to the correlation functions of the chaotic sources (L_C = 0 fm).

FIGURE 2

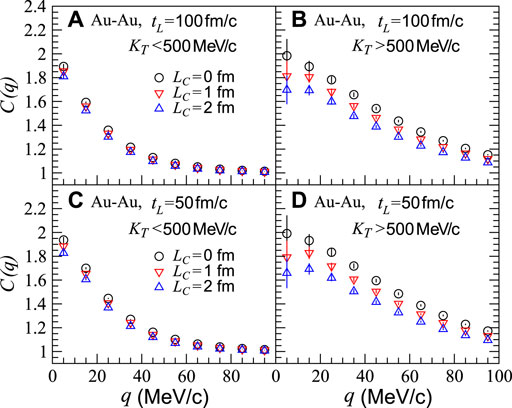
FIGURE 2. Two-pion correlation functions C(q) for pion-emitting sources with different coherent emission length values, L_C, in the transverse momentum ranges of K_T < 500 MeV/c and K_T > 500 MeV/c, respectively, in Au-Au collisions at $\sqrt{s_{NN}}=200$ GeV. Panels (A,B) apply to the temporal limitation parameter t_L = 100 fm/c, while panels (C,D) apply to t_L = 50 fm/c.

In high-energy p-p collisions, the statistics of the pions with high transverse momenta are smaller than those of the Au-Au collisions. In Figures 3A,B, we show the two-pion correlation functions in the p-p collisions at $\sqrt{s}=$13 TeV, for the pion-emitting sources with coherent emission lengths L_C = 0 (chaotic source), 0.5, and 1 fm in the transverse momentum ranges of K_T < 350 GeV/c and K_T > 0 GeV/c, respectively. Here, the temporal limitation parameter is taken to be t_L = 100 fm/c. The corresponding results for t_L = 50 fm/c are shown in Figures 3C,D. Compared to the correlation functions in the Au-Au collisions, the two-pion correlation functions in the p-p collisions are wider because the source sizes are smaller in p-p collisions. The effect of coherent emission length on the two-pion correlation functions in the p-p collisions is almost independent of the K_T range and the t_L parameter.

FIGURE 3

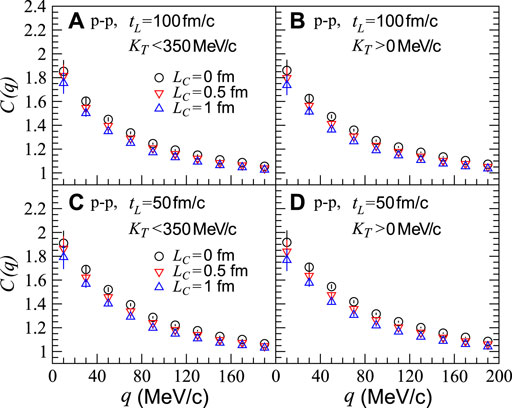
FIGURE 3. Two-pion correlation functions C(q) for pion-emitting sources with different coherent emission length values, L_C, in the transverse momentum ranges of K_T < 350 MeV/c and K_T > 0 MeV/c, respectively, in p-p collisions at $\sqrt{s}=13$ TeV. Panels (A,B) apply to the temporal limitation parameter t_L = 100 fm/c, while panels (C,D) apply to t_L = 50 fm/c.

3 Interferometry Results

In two-pion HBT analyses, the usual correlation function formula is

$C\left(q_{\text{out}},q_{\text{side}},q_{\text{long}}\right)=1+\lambda e^{-q_{\text{out}}^2{R}_{\text{out}}^2-q_{\text{side}}^2{R}_{\text{side}}^2-q_{\text{long}}^2{R}_{\text{long}}^2},(9)$

where R_out, R_side, and R_long are the Bertsch–Pratt variables [36, 37], which denote the components of the relative momentum q in the transverse “out” (parallel to the transverse momentum of the pion pair K_T), transverse “side” (in the transverse plane and perpendicular to K_T), and longitudinal (“long”) directions in the longitudinally comoving system (LCMS) frame [6], respectively. In Eq. 9, λ is the chaoticity parameter and R_out, R_side, and R_long are the HBT radii in the out, side, and long directions, respectively. By fitting the calculated three-dimensional correlation functions for the partially coherent sources with Eq. 9, one can obtain the values of the HBT radii and the chaoticity parameter.

3.1 Au-Au Collisions

In Table 1, we present the fitted results of the HBT radii (R_out, R_side, and R_long) and the chaoticity parameter λ in Eq. 9, for the sources with coherent emission lengths L_C = 0, 1, and 2 fm in central Au-Au collisions at $\sqrt{s_{NN}}=200$ GeV and in the transverse momentum ranges K_T < 500 MeV/c and K_T > 500 MeV/c. Here, the ratios of χ² to the number of bins fitted are also presented. The temporal limitation parameter t_L is taken to be 100 and 50 fm/c, and the event number is 10⁴.

TABLE 1

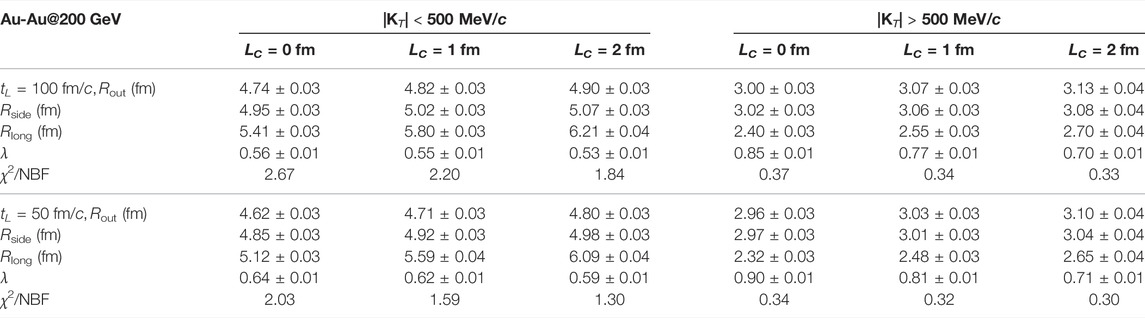
TABLE 1. Fitted results of HBT radii and λ parameter in Eq. 9 for sources with L_C = 0, 1, and 2 fm in central Au-Au collisions at $\sqrt{s_{NN}}=200$ GeV, in transverse momentum ranges K_T < 500 MeV/c and K_T > 500 MeV/c. t_L values are 100 and 50 fm/c, and ratios of χ² to the number of bins fitted are also presented.

One can see that the HBT radii increase slightly with increasing L_C, and the λ parameter decreases with increasing L_C. The HBT radii in the higher transverse momentum range are smaller than those in the lower transverse momentum range because the average source sizes are small at high transverse momenta (Figure 1A). In the lower transverse momentum range, the λ results are smaller than those in the higher transverse momentum range. The main reason is that the scattering interactions in the particle-emitting source reduce the intercepts of the correlation functions[20, 38], and this influence is weaker in the higher transverse momentum range where most pions are emitted early. The results of χ²/NBF indicate that the sources in the lower transverse momentum range are more different from a Gaussian source. For the sources with t_L = 50 fm/c, the HBT radii are slightly smaller than those of the sources with t_L = 100 fm/c. However, the λ results are slightly larger than those of the sources with t_L = 100 fm/c. It should be noted that the effect of coherent emission length on the chaoticity parameter λ becomes increasingly significant for sources with a smaller t_L value, which reduces the λ value by approximately 11% (for L_C = 1 fm) to 24% (for L_C = 2 fm) in the higher transverse momentum range.

We show in Figure 4 the projections of the two-pion correlation functions C(q_out, q_side, q_long) in the out, side, and long directions, for the sources in central Au-Au collisions at $\sqrt{s_{NN}}=200$ GeV and with t_L = 100 fm/c. The upper panels plot the transverse momentum range K_T < 500 MeV/c, and the bottom panels plot the transverse momentum range K_T > 500 MeV/c. The circle, up-triangle, and down-triangle symbols denote the coherent emission lengths L_C = 0, 1, and 2 fm, respectively. For each relative momentum direction, the projection of the correlation function is obtained from the three-dimensional correlation function by averaging the relative momenta in the other two directions over 0–20 MeV/c. The lines in the figure are the corresponding fitted curves of Eq. 9. The differences between the lines and corresponding symbols are due to the deviation from a Gaussian source distribution.

FIGURE 4

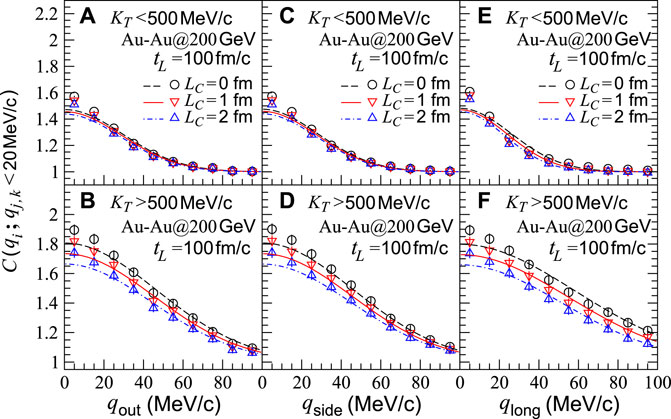
FIGURE 4. Two-pion correlation functions with respect to relative momenta q_i,j,k (i, j, and k = out, side, and long) for sources in central Au-Au collisions at $\sqrt{s_{NN}}=200$ GeV and with t_L = 100 fm/c. Upper panels plot transverse momentum range K_T < 500 MeV/c and bottom panels plot K_T > 500 MeV/c. Circle, up-triangle, and down-triangle symbols denote coherent emission lengths L_C = 0, 1, and 2 fm, respectively. Lines are fitted curves.

We show in Figure 5 the projections of the two-pion correlation functions C(q_out, q_side, q_long) in the out, side, and long directions, for the sources in central Au-Au collisions at $\sqrt{s_{NN}}=200$ GeV and with t_L = 50 fm/c. As in Figure 4, the projection in each direction is obtained from the three-dimensional correlation function by averaging the relative momenta in the other two directions over 0–20 MeV/c. The lines are the corresponding fitted curves of Eq. 9. Compared with the results in Figure 4, we find that the correlation functions in the K_T > 500 MeV/c range decrease slightly more with increasing L_C for the source with smaller t_L.

FIGURE 5

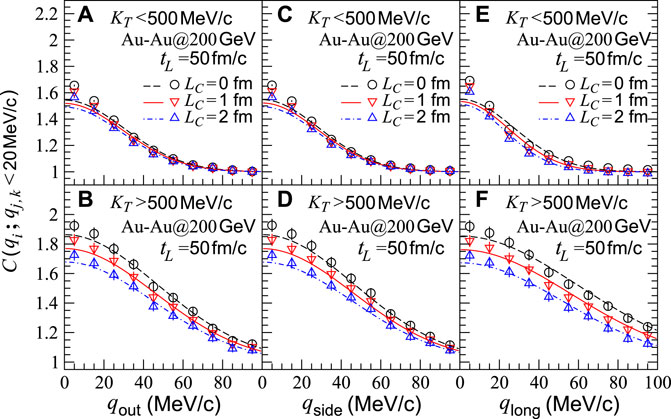
FIGURE 5. Two-pion correlation functions with respect to relative momenta q_i,j,k (i, j, and k = out, side, and long) for sources in central Au-Au collisions at $\sqrt{s_{NN}}=200$ GeV and with t_L = 50 fm/c. Upper panels plot transverse momentum range K_T < 500 MeV/c, and bottom panels plot K_T > 500 MeV/c. Circle, up-triangle, and down-triangle symbols denote coherent emission lengths L_C = 0, 1, and 2 fm, respectively. Lines are fitted curves.

3.2 Pb-Pb Collisions

In Table 2, we present the fitted results of the HBT radii (R_out, R_side, and R_long) and chaoticity parameter λ in Eq. 9 for the sources with the coherent emission lengths L_C = 0, 1, and 2 fm in central Pb-Pb collisions at $\sqrt{s_{NN}}=2.76$ TeV and in the transverse momentum ranges K_T < 500 MeV/c and K_T > 500 MeV/c. Here, the ratios of the χ² to the number of bins fitted are also presented. The parameter t_L is taken to be 50 fm/c, and the event number is 3 × 10³. Compared to the corresponding results for the Au-Au collisions, the HBT radii for the sources in the Pb-Pb collisions are larger, and the effect of coherent emission length on λ is slightly weaker. The two-pion correlation functions with respect to relative momenta q_out, q_side, and q_long are shown in Figure 6, for the sources in central Pb-Pb collisions at $\sqrt{s_{NN}}=2.76$ TeV and with t_L = 50 fm/c. Here, the lines are the fitted curves of Eq. 9.

TABLE 2

TABLE 2. Fitted results of HBT radii and λ parameter in Eq. 9 for sources with L_C = 0, 1, and 2 fm in central Pb-Pb collisions at $\sqrt{s_{NN}}=2.76$ TeV, in transverse momentum ranges K_T < 500 MeV/c and K_T > 500 MeV/c. The t_L value is 50 fm/c, and ratios of χ² to the number of bins fitted are also presented.

FIGURE 6

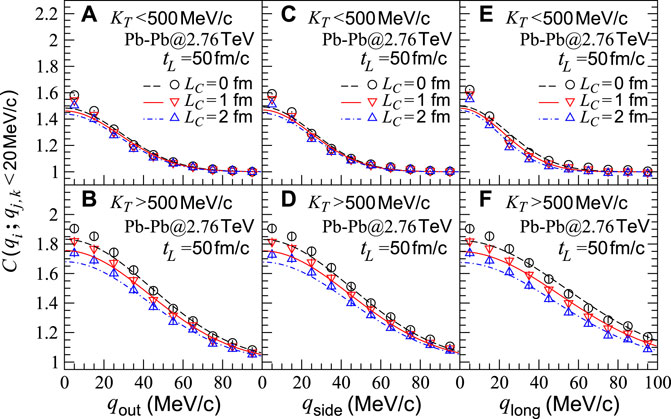
FIGURE 6. Two-pion correlation functions with respect to relative momenta q_i,j,k (i, j, and k = out, side, and long) for sources in central Pb-Pb collisions at $\sqrt{s_{NN}}=2.76$ TeV and with t_L = 50 fm/c. Upper panels plot the transverse momentum range K_T < 500 MeV/c, and bottom panels plot K_T > 500 MeV/c. Circle, up-triangle, and down-triangle symbols denote coherent emission lengths L_C = 0, 1, and 2 fm, respectively. Lines are fitted curves.

3.3 p-p Collisions

In Table 3, we present the fitted results of the HBT radii (R_out, R_side, and R_long) and the chaoticity parameter λ in Eq. 9, for the sources with the coherent emission lengths L_C = 0, 0.5, and 1 fm in p-p collisions at $\sqrt{s}=13$ TeV and in the transverse momentum ranges K_T < 350 MeV/c and K_T > 0 MeV/c. Here, the ratios of the χ² to the number of bins fitted are also presented. The temporal limitation parameter t_L is taken to be 50 fm/c. Because of the lesser pion multiplicity than that in the A-A collisions, the event number for the p-p collisions is taken to be 2 × 10⁵.

TABLE 3

TABLE 3. Fitted results of HBT radii and λ parameter in Eq. 9 for sources with L_C = 0, 0.5, and 1 fm in p-p collisions at $\sqrt{s}=13$ TeV, in transverse momentum ranges K_T < 350 MeV/c and K_T > 0 MeV/c. The t_L value is 50 fm/c, and ratios of χ² to the number of bins fitted are also presented.

One can see that the HBT radii for the sources in the p-p collisions are small. The radii increase slightly with increasing L_C, as is the sources in the nucleus–nucleus collisions. However, the effect of coherent emission length on λ parameter is small, and it reduces the λ value by approximately 8%. Because the average source size in the p-p collisions is almost independent of particle transverse momentum (Figure 1C), the effect of coherent emission length is almost the same in the two transverse momentum ranges. We show in Figure 7 the two-pion correlation functions with respect to relative momenta q_out, q_side, and q_long, for the sources in the p-p collisions and with t_L = 50 fm/c. The lines are the fitted curves of Eq. 9.

FIGURE 7

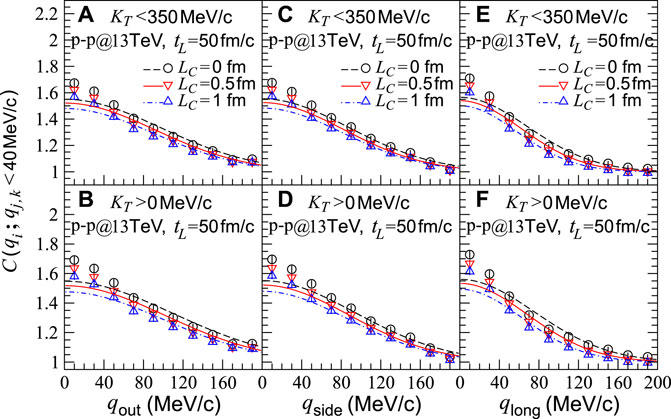
FIGURE 7. Two-pion correlation functions with respect to relative momenta q_i,j,k (i, j, and k = out, side, and long) for sources in p-p collisions at $\sqrt{s}=13$ TeV and with t_L = 50 fm/c. Upper panels plot for the transverse momentum range K_T < 350 MeV/c, and bottom panels plot K_T > 0 MeV/c. Circle, up-triangle, and down-triangle symbols denote coherent emission lengths L_C = 0, 0.5, and 1 fm, respectively. Lines are fitted curves.

4 Summary and Discussion

We construct a partially coherent source by introducing a coherent emission length for the identical pion emission points generated by the AMPT model. The effects of the coherent emission length on the two-pion interferometry results in central Au-Au collisions at $\sqrt{s_{NN}}=200$ GeV, central Pb-Pb collisions at $\sqrt{s_{NN}}=2.76$ TeV, and p-p collisions at $\sqrt{s}=13$ TeV are investigated. We find that the effect of coherent emission length reduces the two-pion correlation functions for the sources in the nucleus–nucleus collisions, leading to an average decrease of the chaoticity parameter λ by approximately 15% in the high transverse momentum range K_T > 500 GeV/c in the nucleus–nucleus collisions. However, the influence of coherent emission length on the two-pion correlation functions for the sources in the p-p collisions is small. The effect of coherent emission length on the λ parameter is almost independent of the transverse momentum of pion pair, K_T, in the p-p collisions.

As a microscopic transport model, the AMPT model can provide the emission coordinates and momenta of particles in the source and has been extensively used in high energy nucleus–nucleus, proton–proton, and proton–nucleus collisions to explain experimental observables. The method used in this study was able to construct the partially coherent sources and affect the analysis results of two-pion HBT interferometry, especially the λ parameter. However, it does not affect the explanations that the AMPT model provides for other observables. The particle-emitting sources produced in high-energy particle collisions may perhaps be partially coherent. The coherent fraction of the systems is related to the source size, temperature, particle multiplicity in the collision, and so on. This study is a first step toward understanding the influence of particle coherent emission on two-pion HBT correlations. More detailed studies on the two- and multiparticle (pions and kaons) HBT correlations in partially coherent sources and a better understanding of the coherent emission mechanism by comparing model and experimental HBT results will be of interest.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

W-NZ and S-YW contributed to conception and design of the study.

Funding

This research was supported by the National Natural Science Foundation of China (Grant No. 12175031).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank Zi-Wei Lin for useful discussions on the AMPT model.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.835592/full#supplementary-material

References

1. Gyulassy M, Kauffmann SK, Wilson LW. Pion Interferometry of Nuclear Collisions. I. Theory. Phys Rev C (1979) 20:2267–92. doi:10.1103/physrevc.20.2267

CrossRef Full Text | Google Scholar

2. Wong CY. Introduction to High-Energy Heavy-Ion Collisions. Singapore: World Scientific (1994). Chap. 17.

Google Scholar

3. Wienemann UA, Heinz U. Phys Rep (1999) 319:145.

4. Weiner R. Boson Interferometry in High-Energy Physics. Phys Rep (2000) 327:249–346. doi:10.1016/s0370-1573(99)00114-3

CrossRef Full Text | Google Scholar

5. Csörgő T. Heavy Ion Physics, 15 (2002). p. 1. arXiv:hep-ph/0001233.

Google Scholar

6. Lisa MA, Pratt S, Soltz R, Wiedemann U. Femtoscopy in Relativistic Heavy Ion Collisions: Two Decades of Progress. Annu Rev Nucl Part Sci (2005) 55:357–402. doi:10.1146/annurev.nucl.55.090704.151533

CrossRef Full Text | Google Scholar

7. Aamodt K. ALICE Collaboration). Phys Rev D (2010) 82:052001.

Google Scholar

8. Aamodt K. ALICE Collaboration). Phys Rev D (2011) 84:112004.

Google Scholar

9. Adam J. ALICE Collaboration). Phys Rev C (2015) 91:034906.

Google Scholar

10. Adam J. ALICE Collaboration). Phys Rev C (2015) 92:054908.

Google Scholar

11. Abelev B. ALICE Collaboration). Phys Rev C (2014) 89:024911.

Google Scholar

12. Adler C. STAR Collaboration). Phys Rev Lett (2001) 87:082301.

PubMed Abstract | Google Scholar

13. Adler SS. STAR Collaboration). Phys Rev Lett (2004) 93:152302.

PubMed Abstract | Google Scholar

14. Adams J. STAR Collaboration). Phys Rev C (2005) 71:044906.

Google Scholar

15. Abelev BI. STAR Collaboration). Phys Rev C (2009) 80:024905.

Google Scholar

16. Abelev BI. STAR Collaboration). Phys Rev C (2010) 81:024911.

Google Scholar

17. Adam J. (ALICE Collaboration). Phys Rev C (2016) 93:054908.

Google Scholar

18. Bary G, Zhang W-N, Ru P, Yang J. Analyses of Multi-Pion Bose-Einstein Correlations for Granular Sources with Coherent Pion-Emission Droplets *. Chin Phys. C (2021) 45:024106. doi:10.1088/1674-1137/abcd8d

CrossRef Full Text | Google Scholar

19. Lin ZW, Ko CM. Partonic Effects on the Elliptic Flow at Relativistic Heavy Ion Collisions. Phys Rev C (2002) 65:034904. doi:10.1103/physrevc.65.034904

CrossRef Full Text | Google Scholar

20. Lin ZW, Ko CM, Li BA, Zhang B, Pal S. Multiphase Transport Model for Relativistic Heavy Ion Collisions. Phys Rev C (2005) 72:064901. doi:10.1103/physrevc.72.064901

CrossRef Full Text | Google Scholar

21. Nasim M, Kumar L, Kumar P, Mohanty B. Energy Dependence of Elliptic Flow from Heavy-Ion Collision Models. Phys Rev C (2010) 82:054908. doi:10.1103/physrevc.82.054908

CrossRef Full Text | Google Scholar

22. Xu J, Ko CM. Effects of Triangular Flow on Di-hadron Azimuthal Correlations in Relativistic Heavy Ion Collisions. Phys Rev C (2011) 83:021903(R. doi:10.1103/physrevc.83.021903

CrossRef Full Text | Google Scholar

23. Bzdak A, Ma G-L. Elliptic and Triangular Flow Inp-Pb and Peripheral Pb-Pb Collisions from Parton Scatterings. Phys Rev Lett (2014) 113:252301. doi:10.1103/physrevlett.113.252301

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Ma GL, Lin ZW. Phys Rev C (2016) 93:054911. doi:10.1103/physrevd.93.083510

CrossRef Full Text

25. Li H, He L, Lin ZW, Molnar D, Wang F, Xie W. Origin of the Mass Splitting of Azimuthal Anisotropies in a Multiphase Transport Model. Phys Rev C (2017) 96:014901. doi:10.1103/physrevc.96.014901

CrossRef Full Text | Google Scholar

26. Nagle JL, Belmont R, Hill K, Koop JO, Perepelitsa DV, Yin P, et al. Minimal conditions for collectivity in e⁺e⁻ and p+p collisions. Phys Rev C (2018) 97:024909. doi:10.1103/physrevc.97.024909

CrossRef Full Text | Google Scholar

27. Nie MW, Huo P, Jia J, Ma GL. Multiparticle Azimuthal Cumulants in p+Pb Collisions from a Multiphase Transport Model. Phys Rev C (2018) 98:034903. doi:10.1103/physrevc.98.034903

CrossRef Full Text | Google Scholar

28. Haque MR, Nasim M, Mohanty B. Systematic Investigation of Azimuthal Anisotropy in Au+Au and U+U Collisions at $\sqrt{{s}_{{NN}}}=200\,\mathrm{GeV}$. J Phys G: Nucl Part Phys (2019) 46:085104. doi:10.1088/1361-6471/ab2ba4

CrossRef Full Text | Google Scholar

29. Shao T, Chen J, Ko CM, Lin ZW. Enhanced Production of Strange Baryons in High-Energy Nuclear Collisions from a Multiphase Transport Model. Phys Rev C (2020) 102:014906. doi:10.1103/physrevc.102.014906

CrossRef Full Text | Google Scholar

30. Magdy N, Lacey RA. Model Investigation of the Longitudinal Broadening of the Transverse Momentum Two-Particle Correlator. Phys Rev C (2021) 104:014907. doi:10.1103/physrevc.104.014907

CrossRef Full Text | Google Scholar

31. Magdy N, Evdokimov O, Lacey RA. A Method to Test the Coupling Strength of the Linear and Nonlinear Contributions to Higher-Order Flow Harmonics via Event Shape Engineering. J Phys G: Nucl Part Phys (2021) 48:025101. doi:10.1088/1361-6471/abcb59

CrossRef Full Text | Google Scholar

32. Zheng L, Zhang G-H, Liu Y-F, Lin Z-W, Shou Q-Y, Yin Z-B. Investigating High Energy Proton Proton Collisions with a Multi-phase Transport Model Approach Based on PYTHIA8 Initial Conditions. Eur Phys J C (2021) 81:755. doi:10.1140/epjc/s10052-021-09527-5

CrossRef Full Text | Google Scholar

33. Wang X-N, Gyulassy M. Hijing: A Monte Carlo Model for Multiple Jet Production inpp,pA, andAAcollisions. Phys Rev D (1991) 44:3501–16. doi:10.1103/physrevd.44.3501

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Zhang B. ZPC 1.0.1: a Parton cascade for Ultrarelativistic Heavy Ion Collisions. Comp Phys Commun (1998) 109:193–206. doi:10.1016/s0010-4655(98)00010-1

CrossRef Full Text | Google Scholar

35. Li B-A, Ko CM. Formation of Superdense Hadronic Matter in High Energy Heavy-Ion Collisions. Phys Rev C (1995) 52:2037–63. doi:10.1103/physrevc.52.2037

CrossRef Full Text | Google Scholar

36. Bertsch G, Gong M, Tohyama M, Bertsch GF. Pion interferometry as a probe of the plasma. Nuc Phys A (1989) 498:173c–179c. doi:10.1103/physrevc.37.1896

CrossRef Full Text | Google Scholar

37. Pratt S, Csörgő T, Zimányi J. Detailed Predictions for Two-Pion Correlations in Ultrarelativistic Heavy-Ion Collisions. Phys Rev C (1990) 42:2646–52. doi:10.1103/physrevc.42.2646

CrossRef Full Text | Google Scholar

38. Lin Z-w., Ko CM, Pal S. Partonic Effects on Pion Interferometry at the Relativistic Heavy-Ion Collider. Phys Rev Lett (2002) 89:152301. doi:10.1103/physrevlett.89.152301

PubMed Abstract | CrossRef Full Text | Google Scholar