Dependence Research on Multi-Layer Convolutions of Images

Convolutions are important structures in deep learning. However, theoretical analysis on the dependence among multi-layer convolutions cannot be found until now. In this paper, the image pixels before, in, and after multi-layer convolutions are of modified multifractional Gaussian noise (mmfGn). Thus, their Hurst parameters are calculated. Based on these, we applied mmfGn model to analyze the dependence of gray levels of multi-layer convolutions of the image pixels and demonstrate their short-range dependence (SRD) or long-range dependence (LRD), which can help researchers to design better network structures and image processing algorithm.

1 Introduction

Deep learning models are composed of multiple convolution layers to learn features of images [1, 2]. However, so far, the theoretical analysis on dependence among multi-layer convolutions have not been reported.

Fractional Brownian motion (fBm) is commonly used in modeling fractal time series. The fBm of the Weyl type is defined by [3–5]

$B_H\left(t\right)-B_H\left(0\right)=\frac{1}{\Gamma \left(H+0.5\right)}\left\{\underset{-\infty }{\overset{0}{{\displaystyle \int }}}\left[{\left(t-u\right)}^{H-0.5}-{\left(-u\right)}^{H-0.5}\right]dB\left(u\right)+\underset{0}{\overset{t}{{\displaystyle \int }}}{\left(t-u\right)}^{H-0.5}dB\left(u\right)\right\}(1)$

where 0 < H < 1 is the Hurst parameters.

Its auto-correlation function (ACF) of the Weyl type is

$C_{fBm}\left(\mathit{t},\mathit{s}\right)=\frac{V_H}{\left(H+0.5\right)\Gamma \left(H+0.5\right)}\left[|\mathit{t}{|}^{2H}+|\mathit{s}{|}^{2H}-|\mathit{t}-\mathit{s}{|}^{2H}\right](2)$

where

$V_H=\Gamma \left(1-2H\right)\frac{cos\pi H}{\pi H}(3)$

The fBm is nonstationary, but it has a stationary increment. The process fBm reduces to the standard Brownian motion when H = 0.5.

Based on the dependence theory, the main contributions of this paper are:

1) Discuss dependence of image multi-layer convolutions by assuming that gray levels of multi-layer convolutions of an image pixel are of modified multifractional Gaussian noise (mmfGn).

2) Calculate the time-varing Hurst parameters by point-by-point basis to discuss the dependence of different pixels.

The remainder of this paper is as follows: the second section introduces the preliminaries on fractional Gaussian noise (fGn) and mmfGn; the third section gives a case study. Finally, the conclusions and acknowledgments are given.

2 Preliminaries

2.1 Fractional Gaussian Noise

The fGn is the derivative of the fBm. Its ACF is:

$C_{fGn}\left(\mathit{\tau }\right)=\frac{V_H}{2}\left[{\left(\left|\mathit{\tau }\right|+1\right)}^{2H}+{\left(\left|\mathit{\tau }\right|-1\right)}^{2H}-2|\mathit{\tau }{|}^{2H}\right](4)$

where

$V_H=\Gamma (1-2H)\frac{cos\pi H}{\pi H}(5)$

fGn is of long-range dependence (LRD) for 0.5 < H < 1 and is of short-range dependence (SRD) for 0 < H < 0.5. If H = 0.5, fGn reduces to the white noise [5–7].

2.2 Modified Multifractional Gaussian Noise

Let G(t) be the mmfGn. The ACF of mmfGn is [6]

$C_{mmfGn}\left(\mathit{\tau }\right)=\frac{V_{H\left(t\right)}}{2}\left[{\left(\left|\mathit{\tau }\right|+1\right)}^{2H\left(t\right)}+\left|\right|\mathit{\tau }|-1{|}^{2H\left(t\right)}-2|\mathit{\tau }{|}^{2H\left(t\right)}\right](6)$

The condition of mmfGn to be of LRD is 0.5 < H(t) < 1, while to be of SRD is 0 < H(t) < 0.5.

Based on the local growth of the increment process, Peltier and Levy-Vehel gave H(t) estimator in Eqs 7 and 8 [8–11].

Let n be the number of data of a sample mmfGn and G(i) be the ith sample point. Let k (1 < k < n) be the length of the neighborhood used for estimating the functional parameter H(i). The H(i) will be estimated only for i = [k/2] + 1, [k/2] + 2, ..., n − 1 where [k/2] is the integral part of k/2. Let m = [n/k] be the integral part of n/k. Then the estimator of H(i) is [8]:

$\widehat{H}\left(i\right)=-\frac{log\left[\sqrt{\frac{\pi }{2}}{S}_k\left(i\right)\right]}{log\left(n-1\right)}(7)$

where

$S_k\left(i\right)=\frac{m}{n-1}{\displaystyle \sum }_{j=i-\left[k/2\right]}^{j=i+\left[k/2\right]}|G\left(j+1\right)-G\left(j\right)|(8)$

3 Case Study and Discussion

3.1 Data in Case Study

Tire.tif in matLab is chosen as test data. The image is convoluted 64 times by randomly generated 3 × 3 masks whose sum is equal to 1. Thus, the normalized gray levels in [0 1] of multi-layer convolutions on each pixel in the image will form a 64-dimensional column vector G = [G(1), G(2),..., G(63), G(64)]^T; see top image of Figure 1. We will discuss the dependence among the components of each 64-dimensional vector.

FIGURE 1

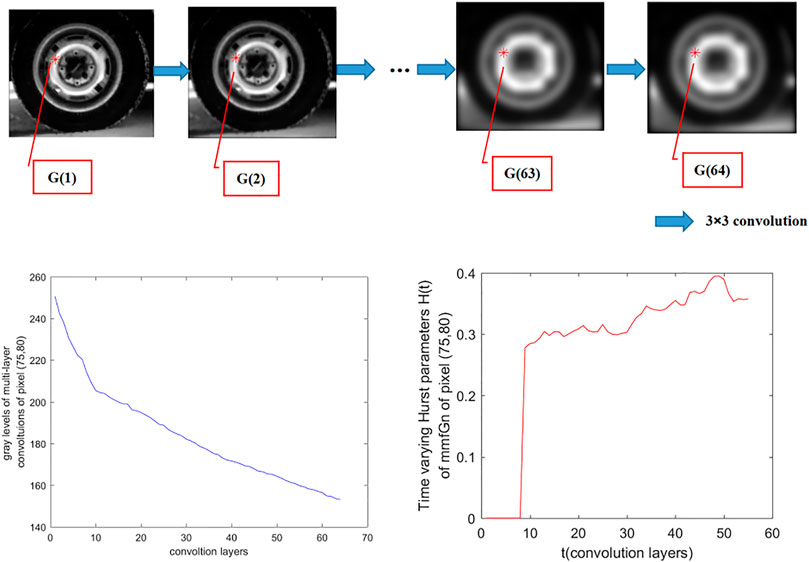
FIGURE 1. The 64-dimensional column vector G = [G(1), G(2),..., G(63), G(64)]^T whose components are the gray levels of multi-layer convolutions on pixel (75, 80). Top: the components of the 64-dimensional column vector on pixel (75, 80). Left bottom: the plot of the 64-dimensional vector whose x-axis represents the convolution layers and y-axis represents the gray levels of convolution layers on pixel (75, 80). Right bottom: time-varying Hurst parameters H(t) of mmfGn of the 64-dimensional column vector of pixel (75, 80) using Eqs 7 and 8 where n = 64, k = 16.

3.2 H(t) of mmfGn

We now study the dependence of samples among multi-layer convolution by computing H(t) of mmfGn for each 64-dimensional vector. That is, the 64-dimensional vector is of mmfGn; the time-varying Hurst parameter H(t) of samples should be calculated to feature the local similarity of the vectors.

The H(t) is calculated using Eqs 7 and 8: the sample number n = 64, and the length of the neighborhood k = 16. Thus, the Hurst parameter H(t) will be estimated only for t = 9, 10, ..., 55. H forms a 55-dimensional vector with 8 zeros on the 1st to 8th positions.

Tire.tif in MatLab is used to discuss the dependence of 64-dimensional vectors of a pixel. Since gray levels of multi-layer convolution of each of image pixel form a 64-dimensional vector whose time-varying Hurst parameter H(t) is a 55-dimensional vector, we can obtain a 3-dimensional matrix to record H(t) of image pixels with W × L × 55 where W is the width of the image and L is the length of the image.

The condition of mmfGn to be of LRD is 0.5 < H(t) < 1, while to be of SRD it is 0 < H(t) < 0.5.

Discussion

In order to discuss the dependence of different pixels of 64-dimensional vector G, two pixels are selected, and their time-varying Hurst parameter H(t) of mmfGn is shown in the bottom right of Figure 1 and the right of Figure 2. In Figure 1, the Hurst parameter H(t) of pixel (75, 80) is less than 0.5 for t = 1,...,55. Thus, G of pixel (75, 80) is of SRD. But the Hurst parameter H(t) of pixel (70, 171) is larger than 0.5 for t = 9,..., 55 in Figure 2. It is of LRD.

FIGURE 2

FIGURE 2. Left: the test image and the selected pixel (70, 171). Right: the time-varying Hurst parameters H(t) of pixel (70, 171).

From the above discussion, the dependence of 64-dimensional vectors of some pixel are of LRD, while for other pixels, they are of SRD.

We think the above dependence of image multi-layer convolution coincides with the nature of images and is a very promising character in designing a deep neural network. Maybe, we can design more powerful algorithms and networks with smaller computation cost.

Conclusion

The dependence of samples of multi-layer convolutions has been discussed. Based on the model of mmfGn, we found that each pixel with a 64-dimensional vector has the statistical dependence of either LRD or SRD on a pixel-by-pixel basis, relying on the value of H(t) of image pixels.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. LeCun Y, Bengio Y, Hinton G. Deep Learning. Nature (2015) 521:436–44. doi:10.1038/nature14539

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Rahman Minar M, Naher J. Recent Advances in Deep Learning: An Overview, CoRR, abs/1807.08169 (2018). Available from: http://arxiv.org/abs/1807.08169, 21 July 2018.

Google Scholar

3. Flandrin P. On the Spectrum of Fractional Brownian Motions. IEEE Trans Inform Theor (1989) 35(1):197–9. doi:10.1109/18.42195

CrossRef Full Text | Google Scholar

4. Li M. On the Long-Range Dependence of Fractional Brownian Motion. Math Probl Eng (2013) 2013, 5. doi:10.1155/2013/842197

CrossRef Full Text | Google Scholar

5. Li M. Fractal Time Series—A Tutorial Review. Math Probl Eng (2010) 2010, 26. doi:10.1155/2010/157264

CrossRef Full Text | Google Scholar

6. Li M. Modified Multifractional Gaussian Noise and its Application. Phys Scr (2021) 96(12):125002. Dec. 2021. doi:10.1088/1402-4896/ac1cf6

CrossRef Full Text | Google Scholar

7. Li M. Multi-fractional Generalized Cauchy Process and its Application to Teletraffic. Physica A: Stat Mech its Appl (2020) 550:123982. doi:10.1016/j.physa.2019.123982

CrossRef Full Text | Google Scholar

8. Peltier RF, Levy Vehel J. A New Method for Estimating the Parameter of Fractional Brownian Motion. RR-2396. Paris, France: INRIA (1994). (inria-00074279).

Google Scholar

9. Peltier RF. Levy-Vehel J. Multifractional Brownian Motion: Definition and Preliminaries Results. INRIA TR (1995) 2645, 43. https://hal.inria.fr/inria-00074045/document.

Google Scholar

10. He J, George C, Wu J, Li M, Leng J. Spatiotemporal BME Characterization and Mapping of Sea Surface Chlorophyll in Chesapeake Bay (USA) Using Auxiliary Sea Surface Temperature Data. Sci Total Environ (2021) 794(1 Nov):148670. doi:10.1016/j.scitotenv.2021.148670

PubMed Abstract | CrossRef Full Text | Google Scholar

11. He J. Application of Generalized Cauchy Process on Modeling the Long-Range Dependence and Self-Similarity of Sea Surface Chlorophyll Using 23 Years of Remote Sensing Data. Front Phys (2021) 9(28 September 2021):750347. doi:10.3389/fphy.2021.750347

CrossRef Full Text | Google Scholar