Abstract
Chiral quantum optics and Topological photonics are both emerging field of research, which have attracted great attention in recent years. Chiral quantum optics provides a new approach to achieve full quantum control of light-matter interaction in a novel manner, which has potential possibility for the implementation of complex quantum information networks. Meanwhile, topological photonics provides a novel route for designing and realizing optical device with unprecedented functionality, such as robust light propagation, the immunity to various structural imperfection, back-scattering suppression as well as unidirectional transmission. The application of topological photonics in chiral quantum optics will promote the whole performance of integrated quantum device with topological protection. In this review, we summarize the progress of chiral quantum optics and topological photonics firstly. Then, we mainly focus on the research of topological chiral edge states based on photonic quantum spin-Hall effect and photonic quantum valley-Hall effect. Furthermore, we introduce the recent work of chiral topological quantum interface formed by embedding quantum dot into the interface between two topologically distinct photonic crystal structures. At last, we give short outlook on the future development direction and prospect for application of topological chiral quantum interface.
Introduction
A single photon interacting with a single quantum emitter is the canonical setting of quantum optics, while the central goal of which is to develop techniques for complete control of light–matter interaction at single quanta level [1]. Chiral interfaces provide a new approach to quantum control of light–matter interaction. The coupling between light and emitter depends on the propagation direction of light and the polarization of the transition dipole moment of the emitter. Then the photon–emitter interaction becomes non-reciprocal, which means that forward- and backward-propagating photons interact differently with the emitter. The photon emission and absorption even becomes unidirectional in the most extreme case [1]. By suppressing the decoherence caused by the surrounding environment, it has potential possibility for the implementation of quantum many-body systems that promotes the speedy development of complex quantum information networks [2]. Many research groups have paid great attention to chiral quantum optics and started to explore intrinsic correlations relating to spin-momentum locking and unidirectional propagation [3–8]. Although numerous efforts have been made, several limitations still exist in this research area which seriously restrict the further development of on-chip integrated quantum networks and information processing. Quantum systems are more susceptible to changes of surrounding environment including external disturbance and internal structural imperfection, especially for more complex multi-body system. Fortunately, the advent of topological photonics provides new strategy for addressing the awkward problems and promoting the whole performance of integrated quantum device with topological protection.
Topological photonics has attracted extensive attention recently due to the unique optical behaviors, including robust light propagation, the immunity to various structural imperfection, back-scattering suppression as well as unidirectional transmission [9–16]. Most remarkably, chiral edge states with topological protection exist in the interface between two topologically distinct regions, allowing for the robust and directional propagation of light along the interface. Robust propagation of light in chiral edge states protected by topology is first demonstrated both theoretically and experimentally in Ref. [16] and then all kinds of intriguing physic phenomena based on photonic quantum Hall effect [18, 19], photonic quantum spin-Hall effect [20–23], and photonic quantum valley-Hall effect [24, 25] have been observed in different designed topological structures. Combining of chiral quantum optics with topological photonics to form chiral topological quantum interfaces promotes the further development of high-performance quantum integrated circuits and complex cascaded quantum systems [26, 27].
Herein, we review the recent progress in chiral topological quantum interface. Firstly, we provide a brief introduction of chiral quantum optics and topological photonics in Progress in Chiral Quantum Interface and Topological Photonics. Then we focus on chiral topological quantum interface combined with quantum emitters in Realization of Chiral Topological Quantum Interface. At last, we give a conclusion and a brief discussion for potential prospect in quantum integrated networks in Conclusion.
Progress in Chiral Quantum Interface and Topological Photonics
Chiral quantum optics as an emerging research field has attracted substantial attention. Some exotic physic phenomena in this field cannot be explained by conventional quantum optics. The advent of chiral quantum optics explains the intrinsic relationship between the unidirectional propagation of light and polarization of the emitter, which opens an intriguing research area and provides an in-depth understanding of light generation, propagation, and manipulation. If light with spin-momentum-locking can be coupled to the emitter with polarization-dependent dipole transition, the propagation direction of light will be determined even in some extreme case. Furthermore, propagation-direction-dependent emission, scattering, and absorption of photons from quantum emitters will be also obtained, which is a non-reciprocal process and a basic operation principle of chiral quantum optics [28, 29]. This chiral feature tends to appear in some specially designed nanostructures due to tightly transverse confinement of light, such as waveguides and nanobeams which will connect polarization property of the emitter and propagation direction of light due to spin-orbit coupling [30–32].
In recent years, chiral quantum optics has been investigated extensively and this spin-momentum-locked unidirectional propagation of light has been experimentally demonstrated in various dielectric [6, 8, 33–35] and plasmonic [36–39] photonic nanostructures. In these nanostructures, the strong transverse confinement of light, which is perpendicular to the propagation direction, naturally leads to a longitudinal component of the electric field. The transverse and longitudinal components of electric field produce π radian oscillations out of phase with each other, leading to an elliptically polarized electric field with spin angular momentum. The sign generated in this process determines the propagation direction of light which is forward or backward. Thus, the propagation direction of light reverses with the inversion of this sign. Considering the interaction between spin-momentum-locked light and quantum emitter, only when the polarization of transition dipole moment of the emitter is matched with local polarization of propagation direction of light, can the directional emission be appearing at this point. Some exactly engineered photonic crystal waveguides and nanocavities have been demonstrated as a promising platform to tailor interaction between light and matter due to their ability to lock polarization of photons to their propagation direction and realize unidirectional transmission of emitted photons [40–43]. For example, a broken-symmetry glide-plane waveguide can provide circularly polarized field mode at the maximum of field intensity, which cannot be observed in other conventional waveguides [44]. A number of associated experiments have been implemented. Besides, this chiral light-matter interaction between photonic nanostructure and quantum emitter has also been realized in other structures, such as nanobeam waveguides [34, 45], optical resonators [46, 47], and metamaterials [48]. Here, more details about systematic theoretical research and applications for chiral quantum interface in conventional nanostructures have been reviewed in Ref. [49].
A well-defined chiral quantum interface can not only enhance chiral light-matter interaction but also suppress massive transport loss. But disappointingly, the back-scattering loss and imperfect directionality caused by inherent fabrication impurities and disorders have negative influences on operation efficiency and information fidelity of quantum photonic circuits, which become extremely worse for long transmission length. Fortunately, topological photonic structures have great ability to solve these problems owing to their immunity to structural imperfections and robust propagation of light.
In 2005, Haldane and Raghu introduced the concept of topology to the realm of photonics [50, 51]. Then a new class of research perspective named topological photonics is opened up, which enables the massive potential possibility for realizing various functional integrated photonic devices and on-chip integrated photonic circuits with built-in protection. Topological photonics has attracted widespread interest once proposed as it provides a new paradigm in the further development of various robust photonic devices for integrated quantum photonic circuits and quantum computing [9–13]. The robust edge states protected by band topology enable the highly potential possibility for chiral light-matter interaction [52–55], which have been observed in various photonic systems, including 1D photonic structures based on SSH model and AAH model [56, 57], 2D topological photonic structures based on metamaterials, synthetic gauge field and ring resonator arrays [58–61] as well as complicated higher dimensional photonic structures [62]. Nevertheless, some limitations existing in these topological structures impose serious restrictions on the further development of topological photonic devices and cannot satisfy on-chip integration requirements. Firstly, some structures made of gyromagnetic or bianisotropic materials in photonic quantum Hall systems with time-reversal broken can only exhibit unidirectional edge states under a strong magnetic field and cannot be applied in the optical range due to weak magnetic response [17–19, 59, 63, 64]. Besides, some special designs such as synthetic gauge field and ring resonator arrays are so complicated with huge difficulty in nanofabrication and on-chip integration, which is not similarly compatible with other photonic devices [60, 61, 65–70].
Two-dimensional semiconductor photonic crystal structures are promising candidates to solve these problems, as they are easier to achieve robust topological edge states with unidirectional transmission and anti-back-scattering and are less stringent about current nanofabrication techniques. Moreover, multiple defects and disorders can be introduced by deforming the shape and size of individual cells to investigate and verify some robust characteristics [71, 72]. Additionally, various operating wavelengths like telecommunication wavelength or even optical regime and different band structures can be simply realized by engineering structural parameters like lattice constant, air hole’s radius, and dielectric cylinders [73–79]. Therefore, these 2D photonic crystal structures are known as extremely infusive platform to achieve various integrated photonic devices for on-chip integrated photonic circuits, like topological circulators [80], on-chip channel filters [71], and slow-light waveguides [81].
Here we just give a brief introduction to topological photonics. Next, we mainly focus on the progress of chiral topological quantum interface based on photonic quantum spin-Hall effect and photonic quantum valley-Hall effect. More details about the recent progress and applications of topological photonics have been reviewed in Refs. [11, 16, 82].
Realization of Chiral Topological Quantum Interface
An interface formed by connecting two topologically distinct photonic structures supports chiral edge state with directional propagation and immunity to back-scattering, which is easy to constitute chiral topological quantum interface when combined with quantum emitters like quantum dots (QDs). The prerequisite for implementing this chiral quantum interface in topological photonic is the appearance of chiral topological edge states with spin-momentum locking and directional transmission. The topological semiconductor photonic crystal structures have successfully aroused immense attention due to their compatibility with nano-manufacturing technology and ease of implementation for on-chip integrated photonic device [20]. Moreover, these structures can be directly integrated with quantum emitters such as quantum dots (QDs) to constitute chiral topological quantum interface with robustness to some structural imperfection, which enables to immensely improve the whole performance of integrated photonic devices and quantum networks [73, 83]. In this section, we will review the two-dimensional semiconductor photonic crystal structures and the polarization properties of chiral edge states in the photonic quantum spin-Hall systems and photonic quantum valley-Hall systems, respectively. Furthermore, we will introduce the recent work of chiral topological quantum interfaces formed by embedding quantum dots into the interface between two topologically distinct photonic crystal structures.
Chiral Topological Quantum Interface Based on Photonic Quantum Spin-Hall Effect
Chiral edge states can be realized in two-dimensional photonic crystal structures based on photonic quantum spin-Hall effect. These edge states protected by band topology can propagate in opposite directions at the interface between two kinds of topological distinct photonic crystals. In 2015, Wu et al. provided the theoretical basis of chiral topological edge states in a photonic quantum spin-Hall system and proposed the concept of pseudo time-reversal symmetry for the first time [84]. The considered honeycomb lattice with rotational symmetry composed of six-sites unit cells can fold two Dirac cones at K and K’ points into doubly degenerate Dirac cones at Г point in the first Brillouin zone. A topological nontrivial bandgap with nonzero topology invariant can be opened by simply deforming the honeycomb while maintaining the hexagonal clusters and C6 rotational symmetry unchanged, as shown in Figures 1A,B. Simultaneously, the photonic band dispersion experience an opened state, a closed state, and a reopened state when generally changing lattice constant from larger to smaller, which directly results in a topological phase transition and a band inversion identified as p± and d± states. When an interface consisting of two regions with different band topology is considered, two cross-bands connecting the upper and bottom bulk band lead to two pseudo spin states with opposite group velocities appearing within the bandgap as shown in Figure 1C. These in-gap edge states can be well located at the interface and exponentially decay into the bulk. Moreover, it is explicitly concluded from energy flow represented by Poynting vector shown in Figure 1D that these two pseudo spin-up and spin-down states respectively correspond to the left-hand and right-hand circular polarizations of in-plane magnetic fields for TM mode and also have a one-to-one correspondence with the propagation direction of electromagnetic energy, which is the fundamental of photonic quantum spin-Hall effect [85, 86].
FIGURE 1
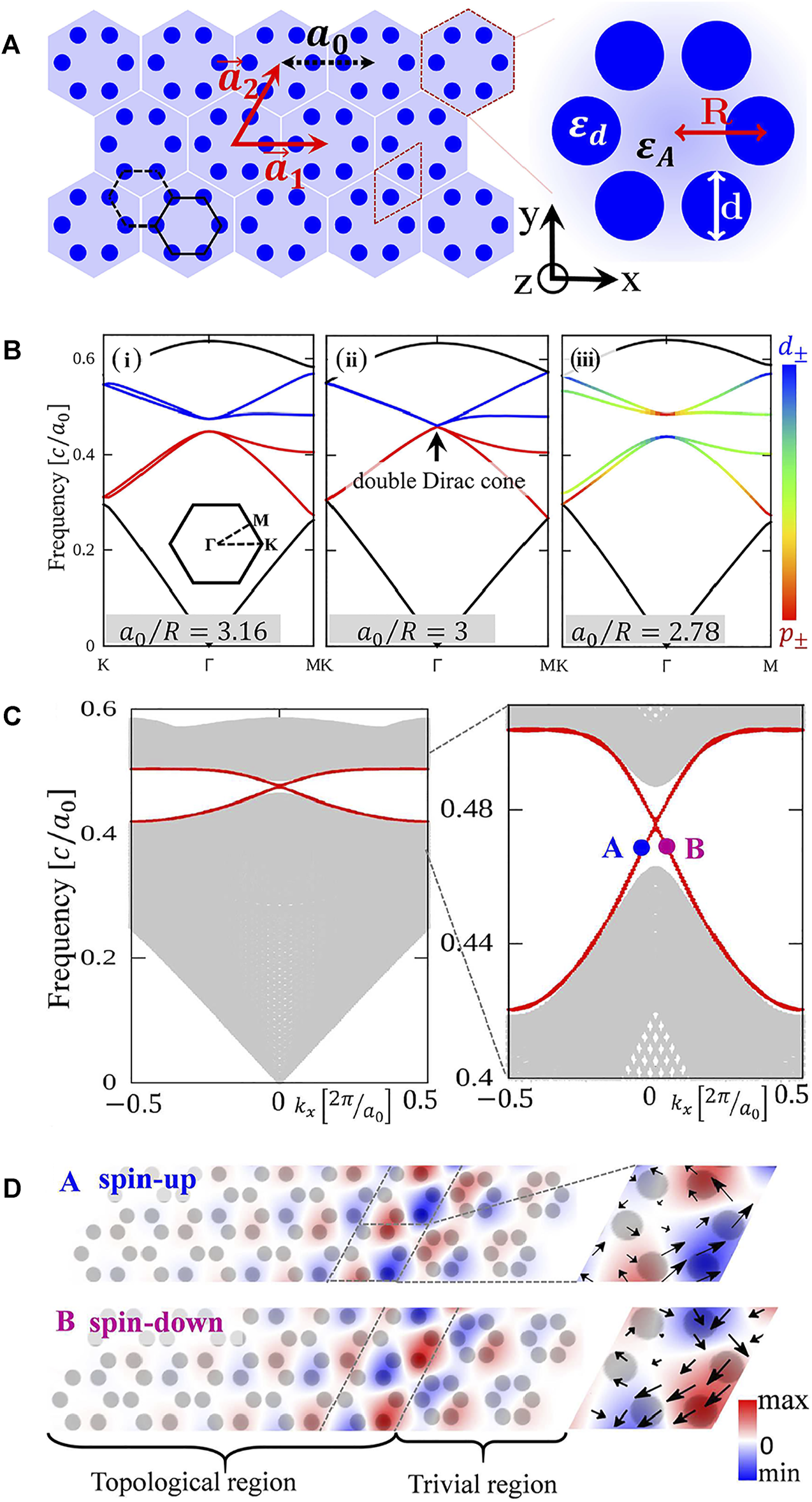
(A) Topological photonic crystal structure with honeycomb lattice composed of six cylindrical pillars in each unit cell [84]. (B) Band structure in the first Brillouin zone for transverse electromagnetic mode with expanding or shrinking the honeycomb lattice. (C) Dispersion relation in the topological interface. The gray regions indicate bulk modes and the red curves indicate topological edge states within the bandgap. (D) Distribution of electric field intensity Ez at A and B points marked in (C).
After that, various semiconductor photonic crystal structures with C6 rotation symmetry and pseudo time-reversal symmetry that support chiral edge states at the interface have been intensively investigated both theoretically and experimentally [87–89]. Nanostructures based on cylindrical pillars made of Si or Al2O3 materials in the air have been demonstrated experimentally to realize two opposite pseudo spin edge states and unidirectional propagation of edge states [21, 90]. Although their operating wavelength can be extended to near-infrared or even visible range, several limitations still exist just as the cylinder structures are difficult to achieve in-plane transverse confinement of light. The above problems can be solved well by adding metallic plates. However, the enormous metal loss seriously deteriorates the performance of the photonic devices [84]. Moreover, nano-manufacturing technology and integration with other topological devices are challenging. Another simpler design approach has also been proposed to constitute all-dielectric topological photonic crystal structures with honeycomb lattice via etching air hole array on a dielectric slab, which is highly desirable for chip-scale integration devices [20, 91, 92].
With deformed honeycomb lattices topological photonic crystal structures, Barik et al. experimentally explored the chiral topological quantum interface for the first time in photonic quantum spin-Hall system, as shown in Figure 2A [83]. Emitted polarization-dependent photons from quantum dots coupled to two opposite pseudo spin edge states, exhibiting directional propagation and robust characteristic even in the presence of a 60° sharp bend. Chiral emission is achieved as shown in Figure 2B. Moreover, the single-photon behaviors at such topological interface have been experimentally demonstrated. Subsequently, Jalali et al. proposed theoretically and investigated experimentally GaAs topological ring resonator combined with InGaAs quantum dots, in which topological nontrivial photonic structure of hexagonal array with expanded lattice is surrounded by topological trivial photonic structure with shrunk lattice as in Figure 2C [72]. As shown in Figure 2D, the chiral emission is clearly observed via the electric field intensity distribution and the propagation direction of edge modes is closely associated with the polarization property of dipole sources. Moreover, the mode structures of the optical ring resonator remain unchanged when the location of the excitation point is changed in the vicinity of the interface. Therefore, this kind of topological ring resonator embedded with quantum dots can be effectively coupled with a bus waveguide to form some novel photonic device like add-drop filter, which represents an important building block for integrated quantum photonics.
FIGURE 2
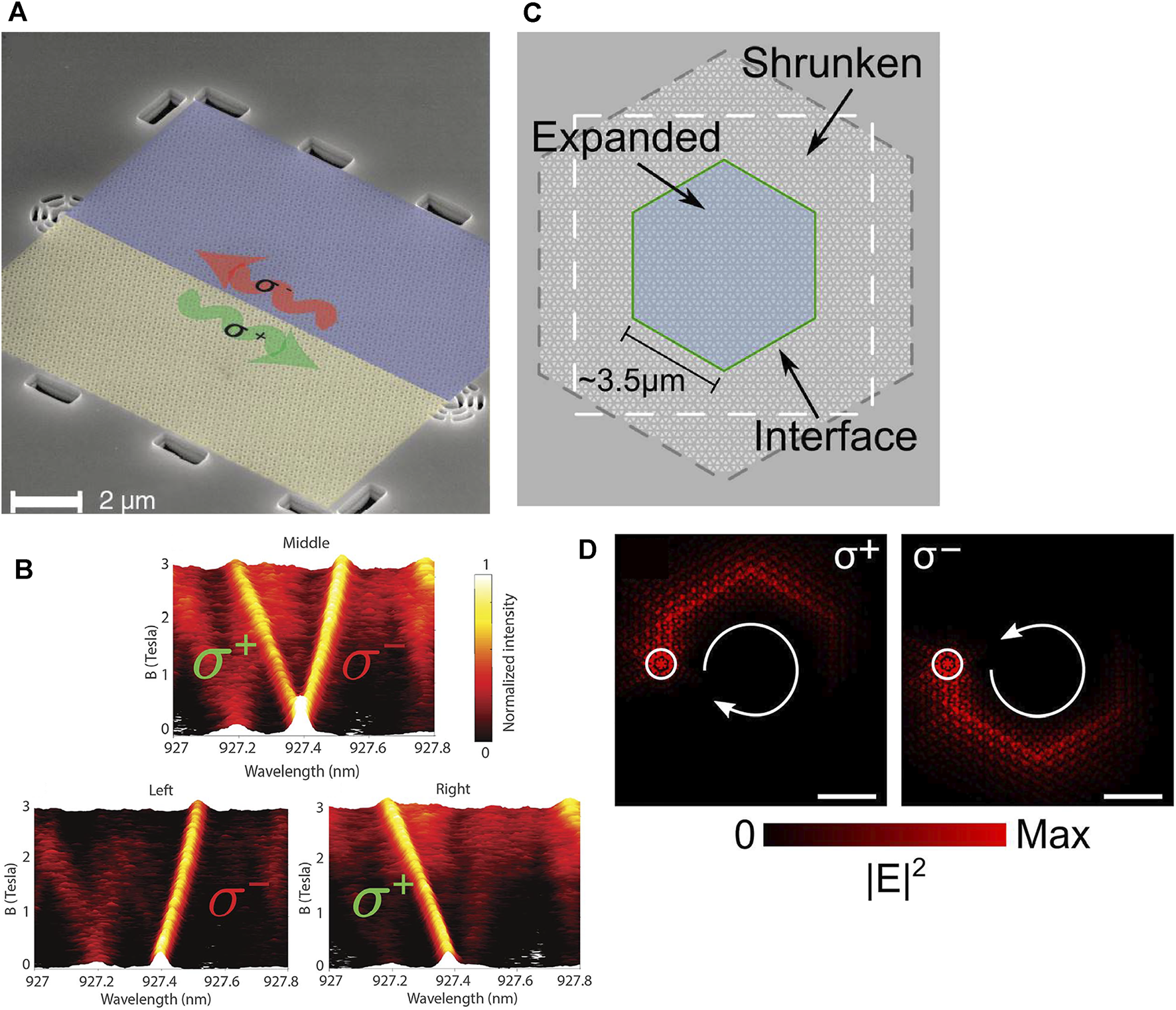
(A) Schematic of the chiral quantum interface formed by connecting two photonic crystal structures with different band topologies indicated by blue and yellow [83]. (B) Emission and transmission spectrum collected from the position of a quantum dot, left and right grating output couplers as a function of the magnetic field, respectively. (C) Schematic of the ring resonator constituted by embedding a topological nontrivial region of hexagonal shape with expanded honeycomb lattice (blue area) in the center of the topological trivial region with shrunk honeycomb lattice (grey area). The green solid line indicates the interface between two topologically distinct photonic crystal regions [72]. (D) The electric field intensity distribution of two pseudo spin edge modes with opposite polarization excited by inversely polarized dipole sources represented by the white open circle.
Additionally, a new class of topologically engineered photonic crystal waveguides have been proposed and demonstrated recently, the guided modes of which have been identified as both chiral [6, 11] and resistant to back-scattering in 60-degree bends [71, 81, 93–95]. Quantum chiral-light matter interface has been demonstrated based on the quantum spin-Hall effect [96].
Chiral Topological Quantum Interface Based on Photonic Quantum Valley-Hall Effect
Another promising platform for realizing chiral quantum interface in topological photonics is valley photonic crystal (VPhC) based on the photonic analogous of quantum valley-Hall effect. This kind of valley photonic crystal is originally proposed in an all-Si photonic crystal platform with triangular lattices made of Si rods [97]. An interface or an edge constituted by two perturbed structures with a triangular Si rod in the hexagonal unit cell supports highly confined robust edge wave with immunity to back-scattering, which has the ability for realizing photonic topological insulator (PTI) and has immense potential for developing robust optical delay line with arbitrary-shape cavity. Subsequently, Chen et al. discussed the unidirectional excitation of valley bulk state with intrinsic chirality and topological phase transition in a valley photonic crystal platform with honeycomb lattice of circular Si rods [75]. In addition, other types of valley photonic crystals have been proposed with some special structural designs, such as staggered bianisotropic response with different bianisotropic coefficients but identical rod radii [98], valley surface-wave photonic crystals on a single metal surface made of metallic rods with different height [76], topological edge states along the armchair and zigzag domain walls composed of topologically distinct honeycomb lattices [79].
In the photonic valley-Hall system, the topological invariant used to characterize band topology of differently perturbed lattices is referred to the valley Chern number with the definition of , which is the integration of Berry curvature over half of the first Brillouin zone at K or K’ points and is quantified as ±1/2. The difference between the valley Chern numbers determines the number of edge state at each valley. According to the bulk-edge correspondence and the difference of valley Chern numbers, only one helical edge state crosses the whole bandgap region between the first and second bulk band at the single valley, shown in Figures 3A,B. Another edge state with opposite group velocity and opposite helicity exists at the other valley due to time-reversal symmetry and the symmetry of band structure with respect to wave vector (kx) in the momentum space. It is different from that of photonic quantum spin-Hall system in that photonic bands of these edge states are both below the light line, which directly ensures highly efficient in-plane confinement of light and reflection-free propagation.
FIGURE 3
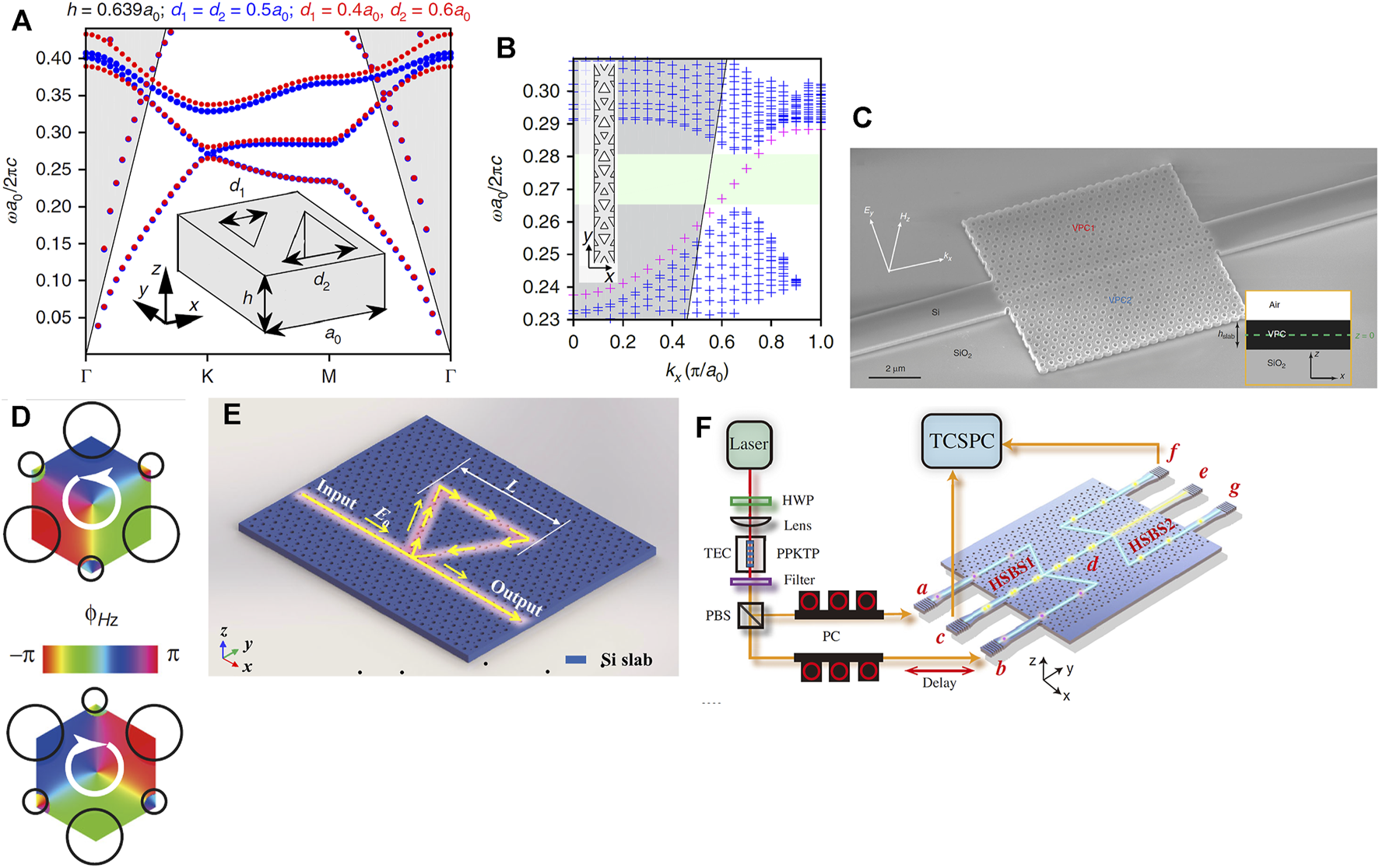
(A) Band structures of the valley photonic crystal slab with triangular air holes. The inset represents the unit cell structure composed of two unequal triangular air holes [95]. (B) Band diagram of edge states in the interface between two distinct valley photonic crystals. The magenta curve indicates the edge state. The green and blue regions indicate the bandgap and bulk bands, respectively. (C) Schematic of the topological chiral interface by connecting two topologically distinct valley photonic crystal regions marked by “VPC1” and “VPC2” [99]. (D) Calculated phase distribution of Hz field for differently perturbed honeycomb lattice. (E) Schematic of the topological notch filter containing a triangular-loop ring resonator, in which only one edge state propagates forward and then directionally coupled to the ring resonator mode due to valley-polarization locking [71]. (F) Experimental setup and structural image of a complex topological structure with two harpoon-shaped beam splitters [100].
Shalaev et al. experimentally demonstrated planar silicon photonic crystal structure with topological protection in telecommunication wavelength [95]. The honeycomb lattice with rhombic unit cell of two equilateral triangular air holes is considered in this work. When the sides of two triangular holes are equal and have C6 symmetry, a Dirac zone for TE mode appears at K and K’ points in the momentum space, which is protected by time- and spatial-reversal symmetry. When perturbing the unit cell by changing the side length of these two triangular air holes to break the spatial inversion symmetry, the degeneracy around the Dirac points is lifted and a controllable photonic bandgap is opened resulting in the presence of a topological valley phase. Besides, this type of photonic crystal structure possesses a nonzero Berry curvature with opposite signs at K and K’ points. When the size of two triangular holes in the same unit cell is exchanged, the sign of Berry curvature is simultaneously flipped. A similar work that validates robust propagation of light is also implemented by constructing three various topological interfaces with flat-, Z-, and Ω-shape [99]. The experimental and simulation results illustrate that the high transmission spectra within the bandgap region are maintained flat-top, which means that broadband robust transportation can be achieved due to the suppression of inter-valley scattering [99]. More importantly, the selective excitation of valley-chirality-locked edge states existing an interface between two topologically distinct valley photonic crystals is demonstrated experimentally in this work, as shown in Figure 3C. The unit cell of these two different structures, consisting of two nonequivalent circular air holes, directly breaks the inversion symmetry and opens a photonic bandgap for TE-like polarization. It is shown from simulated Hz phase distribution in Figure 3D that the vortex phase increases clockwise or anticlockwise by 2π around the center of the unit cell for different photonic crystal structures, which directly corresponds to right- or left-handedness circular polarization and simultaneously has a straightforward relationship with valley pseudo spin, that is, valley degree of freedom (DOF). Thus, the valley-polarization-dependent edge state is selectively excited by controlling the chirality of light and highly efficient unidirectional coupling is expected to be achieved via vortex fields of chiral edge states.
Apart from the topological waveguide with straight interface or several sharp bends, other complicated topological photonic devices including circulators are also investigated. Gu et al. both theoretically and experimentally proposed a ring resonator with topological protection, which is constituted by a closed triangular-shape topological edge formed by two topologically distinct photonic crystal structures [71]. Due to valley-polarization locking, only one edge mode propagates forward along the straight interface and propagates clockwise along the ring resonator, as shown in Figure 3E. Besides, Chen et al. experimentally demonstrated a topological harpoon-shaped beam splitters (HSBS) with 50/50 splitting ratio in valley photonic crystal fabricated on SOI wafer [100]. Two-photon quantum interference based on Hong-Ou-Mandel is realized with a high visibility of 0.956. This kind of device is also verified to possess outstanding scalability and feasibility because it can combine two or even more above harpoon-shaped beam splitters to constitute more complex quantum networks as shown in Figure 3F. Moreover, topological slow-light waveguides made of Si valley photonic crystals are theoretically and experimentally demonstrated [101, 102]. The light propagation with topological protection and back-scattering-free in the slow light regime possesses widespread application prospects ranging from enhancing optical gain to nonlinearity for realizing active topological photonic devices and photonic integrated circuits [103, 104].
Although considerable efforts in Si-based valley photonic crystal slabs have been achieved both theoretically and experimentally with a wide range of application prospects in integrated Si photonics, it is challenging for chiral topological quantum interfaces combined with quantum emitters such as quantum dots. The III-V compound semiconductor materials provide incomparable superiority because they are convenient to directly integrate with various quantum emitters and enable the implementation of chiral emission and transmission of photons from quantum emitters. In 2019, Yamaguchi et al. experimentally realized a valley photonic crystal waveguide on a GaAs slab with embedded InAs quantum dot, as shown in Figure 4A. The embedded InAs quantum dot acts as an internal light source used not only for characterizing guiding mode of edge state at the topological interface between two topologically distinct regions with different modulated honeycomb lattices, but also for emitting single photons to realize directional emission and coupling with edge mode [105]. A bright radiation spot appearing at output port of the non-trivial interface is observed in Figure 4B by the micro-photoluminescence measurements, which indicates that light emitted from quantum dots can propagate along the topological interface. And the high transmittance from output port also suggests the robust propagation of light within the bandgap. The high confinement of light at the interface is also verified by changing excitation positions relative to the center of the interface. Even in the presence of sharp bends, the light only from the emission of quantum dot can propagate along the Z-shaped interface without any back-scattering. These crucial results lay the foundation for realizing chiral emission and directional coupling between edge mode and quantum emitter as well as for exploring the chiral quantum ring resonator with topological protection.
FIGURE 4
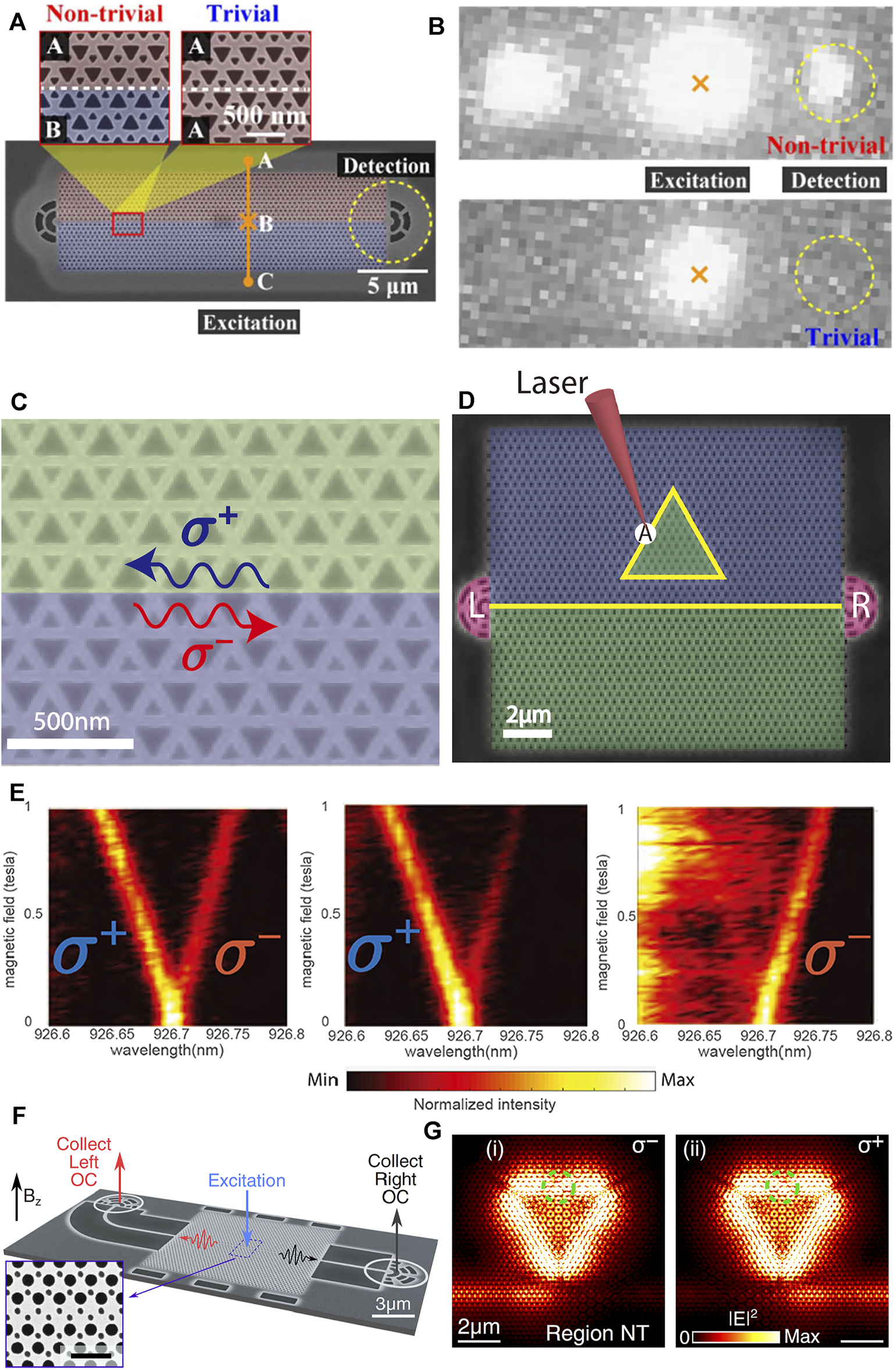
(A) Schematic of a Z-shaped valley photonic crystal waveguide with two grating output couplers at the two ends [105]. (B) Measured photoluminescence images of non-trivial and trivial interfaces. (C) Schematic of the topological interface formed by two valley photonic crystals with the same bulk band but different topology properties, supporting two various edge states with opposite chirality [106]. (D) Structural image of the topological ring resonator composed of a triangular loop and a straight waveguide terminated by two grating output couplers marked by “L” and “R”. The mark of “A” indicates the position of excitation. (E) Measured photoluminescence spectra from A position, left grating, and right grating, respectively. (F) Schematic of the topological ring resonator (RR) with triangular shape coupled to a straight waveguide (WG), terminated by two nanobeam waveguides and two grating output couplers [94]. (G) Calculated electric field profile of the topological ring resonator when excited by a dipole source with opposite circular polarization of σ- and σ+.
Recently, Barik et al. experimentally constituted a topological ring resonator composed of chiral interface between two differently perturbed valley photonic crystal regions on a GaAs slab with embedded InAs quantum dots, as shown in Figure 4C [106]. The unidirectional coupling between quantum emitter and the resonator modes is observed in the simulation and experimental results. It is displayed in Figure 4D that the formed topological interface support two counter-propagating edge modes with opposite helicity, which leads to the emergence of resonator modes with opposite circular polarization. The light within the photonic bandgap can be highly confined at the boundary. And there is not any back-scattering at the three sharp corners owing to topological protection. It is observed from the calculated Poynting vector that when the ring resonator is excited by the dipole with right circular polarization (σ-), the electric field propagates clockwise along the triangular loop and then couples to the right part of the straight waveguide while the ring resonator is excited by the dipole with left circular polarization (σ+), the electric field propagates counterclockwise around the triangular loop and then couples to the left part of the straight waveguide. The reason is that the same band topology of the region below the straight waveguide and inside the triangular loop results in the same chirality at the interface. When applying a magnetic field on quantum dot, the two spectrally resolved branches with different transition dipole moments are formed due to Zeeman splitting, which corresponds to the opposite circular polarization, as displayed in Figure 4E. Moreover, when the emission lines of the quantum dot are resonant with resonator modes, the Purcell enhancement factor of 3.4 is obtained and thus the emission from thequantum dot is significantly enhanced. This work opens a new paradigm to engineer the chiral light-matter interaction in valley photonic crystal platforms. Various intriguing phenomena containing the generation of entangled spin states, photonic clusters states, and superradiant are supposed to be achieved in a new manner [107–109].
After that, Mehrabad et al. also experimentally demonstrated a chiral ring resonator in valley photonic crystal of honeycomb lattice on GaAs slab with an embedded layer of InGaAs quantum dots [94]. The topological structure with a bearded-shaped interface is displayed in Figure 4F. The light with σ- state couples to the left part of the topological waveguide and the light with σ+ state couples to the other part, which indicates that the propagation direction of light at the bearded-shape interface is determined by the chirality of the circular polarization of photons from quantum dot. Chiral emission and unidirectional coupling with topologically nontrivial guiding modes are simultaneously achieved. Based on robust propagation of light around sharp bends, a triangular-loop ring resonator with a straight topological waveguide below is constituted, the high Q factors of which can reach 12,500 and 4,000 in simulation and experimental results, respectively. It is shown as the simulation results in Figure 4G that a dipole with opposite circular polarization placed at the highly chiral point on the ring resonator interface excites different polarized resonator modes and the generated light field couples evanescently to the bus topological waveguide, in which the propagation of light is dependent on the chirality of the dipole polarization. These works have demonstrated the feasibility of chiral coupling for topological ring resonators and facilitated the further development of chiral light-matter interaction for various spinful photonic devices.
Besides the chiral ring resonators with topological protection combined with quantum emitters being essential components for integrated quantum networks, other topological integrated devices such as filters with quantum characteristics are also in urgent need of exploration. Mehrabad et al. proposed a topological add-drop filter composed of a rhombus-shaped ring resonator and a pair of access waveguides named as “through” and “drop” waveguides, as shown in Figure 5A [80]. When the quantum dot at the interface is excited, the photons with various transition dipole momentum are coupled to different output ports under a nonzero magnetic field, which demonstrates chiral behavior and directional coupling between the ring resonator and quantum dot. Simulated results in Figure 5B demonstrate the chiral behavior again, enabling the realization of a bidirectional chiral router. Additionally, the second-order correlation function of g(2)(0) = 0.14 indicates that the single-photon property of the single quantum dot emission can be well preserved during the whole propagating and coupling process of photons. Consequently, these kinds of valley photonic crystal structures combined with quantum emitters reveal the inherent mechanism of chiral control of light-matter interaction at the single-photon level and possess a widespread application for high-performance on-chip topological filters and circulators with in-built protection against structural imperfections and arbitrary-shape bending, which promote the future development of chiral integrated quantum photonic circuits [110].
FIGURE 5
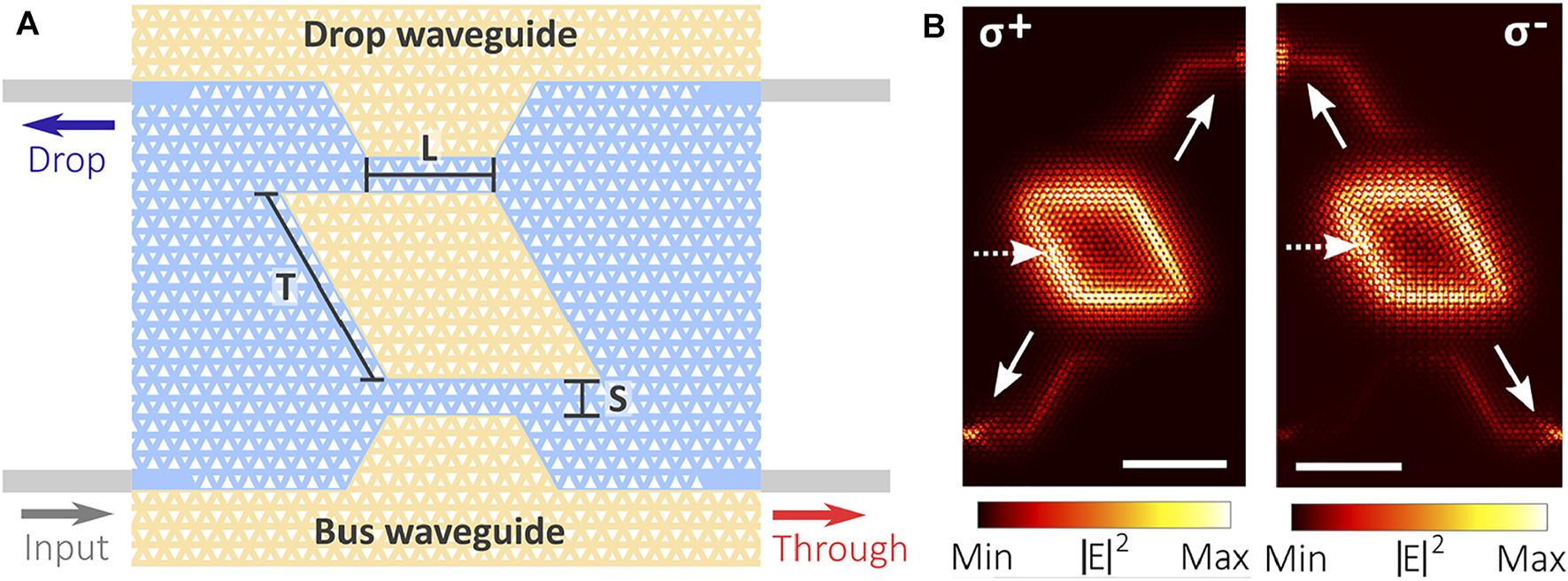
(A) Schematic of a topological add-drop filter containing a rhombus-shaped ring resonator and a pair of access waveguides with the output ports marked by “Through” and “Drop” [80]. (B) Calculated electric field intensity distribution when the device is excited by a dipole source with σ+ and σ- polarization.
Conclusion
On-chip chiral quantum light-matter interface provides a promising platform for efficient spin-photon coupling, non-reciprocal photonic elements, and quantum logic architectures. In this review, we mainly focus on the topological chiral quantum interfaces based on photonic quantum spin-Hall effect and photonic quantum valley-Hall effect. Various integrated devices including topological quantum ring resonators and filters are discussed concretely.
At present, the quantum chiral edge state has been realized both numerically and experimentally. But the experimental work on the topological quantum chiral interface with quantum emitter is still deficient. Therefore, relevant experimental research will be the focus in the near future. Besides, the combined quantum emitters are not solely limited to quantum dots, which can be extended to other types of quantum emitters such as defects in two-dimensional materials and color defects in diamonds. Furthermore, the application prospects based on topological quantum chiral interfaces will be the important development directions. Various ring resonators based on the topologically protected interface are formed with arbitrary shapes owing to robustness against various sharp bends, which can leave more space for high-density integrated quantum networks. Considering the spin-orbit interaction and more complex information-carrying capacity, the light beams with multiple degrees of freedom are in urgent need of development for the future implementation of high-speed and more secure multi-dimensional information communications and quantum teleportation systems.
At last, we would like to give a short discuss on the applications prospect of topological chiral interface. The platform of topologically robust and chiral interface between a photonic resonator and a quantum emitter could provide a robust and scalable pathway to engineer chiral light-matter interaction between multiple emitters coupled to a single resonator, without fine tuning of system parameters. The combination of quantum emitters and chiral topological interfaces can not only constitute various functional photonic devices, but also facilitate the development of effective single photon sources. The preeminent characteristics of these topological edge states especially topological ring resonators improve the light-emitting properties of quantum emitters themselves and the single photon behaviors can be well preserved during the whole robust propagation of light, leading to the effective and efficient coupling to other quantum devices. This undoubtedly increases the possibility of the on-chip quantum circuit implementation. Furthermore, various nanophotonic devices containing ultracompact filters and circulators with excellent performance based on topological quantum chiral interfaces will experience rapid development in the future, which are basic elements for achieving compact quantum integrated circuits. Although the photonic devices consisting of a single ring resonator have been intensely investigated, more complex photonic devices with diverse functionality based on multiple ring resonators possess enormous application prospects for complicated and changeable quantum computing and quantum information processing. In a chiral waveguide, photon-matter interactions between emitters are location-independent [110], which could promote the coupling of multiple solid-state emitters via photons while overcoming scalability issues associated with random emitter position, enabling large-scale super-radiant states and spin-squeezing. Finally, a versatile platform to explore many-body quantum physics at a topological edge, create chiral spin networks, and realize fractional quantum Hall states of light can be developed [111], which provide a new approach to study QED in a new regime.
Statements
Author contributions
PJ conceived the idea. PJ, NM, XQ, and HZ prepared the draft. All authors contributed to the discussion and revision of the manuscript.
Funding
This work was funded by the Central University Basic Research Fund (19CX02056A).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1.
LodahlPMahmoodianSStobbeSRauschenbeutelASchneeweissPVolzJet alChiral Quantum Optics. Nature (2017) 541:473–80. 10.1038/nature21037
2.
EisertJFriesdorfMGogolinC. Quantum many-body Systems Out of Equilibrium. Nat Phys (2015) 11:124–30. 10.1038/nphys3215
3.
ShomroniIRosenblumSLovskyYBechlerOGuendelmanGDayanB. All-optical Routing of Single Photons by a One-Atom Switch Controlled by a Single Photon. Science (2014) 345:903–6. 10.1126/science.1254699
4.
SayrinCJungeCMitschRAlbrechtBO’SheaDSchneeweissPet alNanophotonic Optical Isolator Controlled by the Internal State of Cold Atoms. Phys Rev X (2015) 5:041036. 10.1103/PhysRevX.5.041036
5.
RosenblumSBechlerOShomroniILovskyYGuendelmanGDayanB. Extraction of a Single Photon from an Optical Pulse. Nat Photon (2016) 10:19–22. 10.1038/nphoton.2015.227
6.
MitschRSayrinCAlbrechtBSchneeweissPRauschenbeutelA. Quantum State-Controlled Directional Spontaneous Emission of Photons into a Nanophotonic Waveguide. Nat Commun (2014) 5:1–5. 10.1038/ncomms6713
7.
JungeCO’SheaDVolzJRauschenbeutelA. Strong Coupling between Single Atoms and Nontransversal Photons. Phys Rev Lett (2013) 110:213604. 10.1103/PhysRevLett.110.213604
8.
LuxmooreIJWasleyNARamsayAJThijssenACTOultonRHuguesMet alInterfacing Spins in an InGaAs Quantum Dot to a Semiconductor Waveguide Circuit Using Emitted Photons. Phys Rev Lett (2013) 110:037402. 10.1103/PhysRevLett.110.037402
9.
LuLJoannopoulosJDSoljačićM. Topological Photonics. Nat Photon (2014) 8:821–9. 10.1038/nphoton.2014.248
10.
KhanikaevABShvetsG. Two-dimensional Topological Photonics. Nat Photon (2017) 11:763–73. 10.1038/s41566-017-0048-5
11.
WuYLiCHuXAoYZhaoYGongQ. Applications of Topological Photonics in Integrated Photonic Devices. Adv Opt Mater (2017) 5:1700357. 10.1002/adom.201700357
12.
XieB-YWangH-FZhuX-YLuM-HWangZDChenY-F. Photonics Meets Topology. Opt Express (2018) 26:24531–50. 10.1364/OE.26.024531
13.
OzawaTPriceHMAmoAGoldmanNHafeziMLuLet alTopological Photonics. Rev Mod Phys (2019) 91:015006. 10.1103/RevModPhys.91.015006
14.
RiderMSPalmerSJPocockSRXiaoXArroyo HuidobroPGianniniV. A Perspective on Topological Nanophotonics: Current Status and Future Challenges. J Appl Phys (2019) 125:120901. 10.1063/1.5086433
15.
KimMJacobZRhoJ. Recent Advances in 2D, 3D and Higher-Order Topological Photonics. Light Sci Appl (2020) 9:1–30. 10.1038/s41377-020-0331-y
16.
IwamotoSOtaYArakawaY. Recent Progress in Topological Waveguides and Nanocavities in a Semiconductor Photonic crystal Platform [Invited]. Opt Mater Express (2021) 11:319–37. 10.1364/OME.415128
17.
WangZChongYJoannopoulosJDSoljačićM. Observation of Unidirectional Backscattering-Immune Topological Electromagnetic States. Nature (2009) 461:772–5. 10.1038/nature08293
18.
MaTKhanikaevABMousaviSHShvetsG. Guiding Electromagnetic Waves Around Sharp Corners: Topologically Protected Photonic Transport in Metawaveguides. Phys Rev Lett (2015) 114:127401. 10.1103/PhysRevLett.114.127401
19.
BahariBNdaoAValliniFEl AmiliAFainmanYKantéB. Nonreciprocal Lasing in Topological Cavities of Arbitrary Geometries. Science (2017) 358:636–40. 10.1126/science.aao4551
20.
ParappurathNAlpeggianiFKuipersLVerhagenE. Direct Observation of Topological Edge States in Silicon Photonic Crystals: Spin, Dispersion, and Chiral Routing. Sci Adv (2020) 6:eaaw4137. 10.1126/sciadv.aaw4137
21.
XieBSuGWangH-FLiuFHuLYuS-Yet alHigher-order Quantum Spin Hall Effect in a Photonic crystal. Nat Commun (2020) 11:1–8. 10.1038/s41467-020-17593-8
22.
BliokhKYSmirnovaDNoriF. Quantum Spin Hall Effect of Light. Science (2015) 348(6242):1448–51. 10.1126/science.aaa9519
23.
GuoKWuJChenFZhouKLiuSGuoZ. Second Harmonic Generation Enhancement and Directional Emission from Topological Corner State Based on the Quantum Spin Hall Effect. Opt Express (2021) 29:26841–50. 10.1364/OE.432660
24.
BleuOSolnyshkovDDMalpuechG. Quantum valley Hall Effect and Perfect valley Filter Based on Photonic Analogs of Transitional Metal Dichalcogenides. Phys Rev B (2017) 95:235431. 10.1103/PhysRevB.95.235431
25.
YangYYamagamiYYuXPitchappaPWebberJZhangBet alTerahertz Topological Photonics for On-Chip Communication. Nat Photon (2020) 14:446–51. 10.1038/s41566-020-0618-9
26.
CarmichaelHJ. Quantum Trajectory Theory for Cascaded Open Systems. Phys Rev Lett (1993) 70:2273–6. 10.1103/PhysRevLett.70.2273
27.
GardinerCW. Driving a Quantum System with the Output Field from Another Driven Quantum System. Phys Rev Lett (1993) 70:2269–72. 10.1103/PhysRevLett.70.2269
28.
MitschRSayrinCAlbrechtBSchneeweissPRauschenbeutelA. Directional Nanophotonic Atom-Wwaveguide Interface Based on Spin-Oorbit Interaction of Light (2014). arXivAvailable at: https://arxiv.org/abs/1406.0896 (Accessed December 13, 2021).
29.
ColesRJPriceDMDixonJERoyallBClarkeEKokPet alChirality of Nanophotonic Waveguide with Embedded Quantum Emitter for Unidirectional Spin Transfer. Nat Commun (2016) 7:1–7. 10.1038/ncomms11183
30.
BliokhKYNoriF. Transverse and Longitudinal Angular Momenta of Light. Phys Rep (2015) 592:1–38. 10.1016/j.physrep.2015.06.003
31.
BliokhKYRodríguez-FortuñoFJNoriFZayatsAV. Spin-orbit Interactions of Light. Nat Photon (2015) 9:796–808. 10.1038/nphoton.2015.201
32.
AielloABanzerPNeugebauerMLeuchsG. From Transverse Angular Momentum to Photonic Wheels. Nat Photon (2015) 9:789–95. 10.1038/nphoton.2015.203
33.
LuxmooreIJWasleyNARamsayAJThijssenACTOultonRHuguesMet alOptical Control of the Emission Direction of a Quantum Dot. Appl Phys Lett (2013) 103:241102. 10.1063/1.4845975
34.
PetersenJVolzJRauschenbeutelA. Chiral Nanophotonic Waveguide Interface Based on Spin-Orbit Interaction of Light. Science (2014) 346:67–71. 10.1126/science.1257671
35.
Rodríguez-FortuñoFJBarber-SanzIPuertoDGriolAMartínezA. Resolving Light Handedness with an On-Chip Silicon Microdisk. ACS Photon (2014) 1:762–7. 10.1021/ph500084b
36.
LeeS-YLeeI-MParkJOhSLeeWKimK-Yet alRole of Magnetic Induction Currents in Nanoslit Excitation of Surface Plasmon Polaritons. Phys Rev Lett (2012) 108:213907. 10.1103/PhysRevLett.108.213907
37.
LinJMuellerJPBWangQYuanGAntoniouNYuanX-Cet alPolarization-controlled Tunable Directional Coupling of Surface Plasmon Polaritons. Science (2013) 340:331–4. 10.1126/science.1233746
38.
Rodríguez-FortuñoFJMarinoGGinzburgPO’ConnorDMartínezAWurtzGAet alNear-field Interference for the Unidirectional Excitation of Electromagnetic Guided Modes. Science (2013) 340:328–30. 10.1126/science.1233739
39.
O’ConnorDGinzburgPRodríguez-FortuñoFJWurtzGAZayatsAV. Spin-orbit Coupling in Surface Plasmon Scattering by Nanostructures. Nat Commun (2014) 5:1–7. 10.1038/ncomms6327
40.
ColesRJPrtljagaNRoyallBLuxmooreIJFoxAMSkolnickMS. Waveguide-coupled Photonic crystal Cavity for Quantum Dot Spin Readout. Opt Express (2014) 22:2376–85. 10.1364/OE.22.002376
41.
ArcariMSöllnerIJavadiALindskov HansenSMahmoodianSLiuJet alNear-unity Coupling Efficiency of a Quantum Emitter to a Photonic crystal Waveguide. Phys Rev Lett (2014) 113:093603. 10.1103/PhysRevLett.113.093603
42.
FongCFOtaYArakawaYIwamotoSKatoYK. Chiral Modes Near Exceptional Points in Symmetry Broken H1 Photonic crystal Cavities. Phys Rev Res (2021) 3:043096. 10.1103/PhysRevResearch.3.043096
43.
MahmoodianSPrindal-NielsenKSöllnerIStobbeSLodahlP. Engineering Chiral Light-Matter Interaction in Photonic crystal Waveguides with Slow Light. Opt Mater Express (2017) 7:43–51. 10.1364/OME.7.000043
44.
SöllnerIMahmoodianSHansenSLMidoloLJavadiAKiršanskėGet alDeterministic Photon-Emitter Coupling in Chiral Photonic Circuits. Nat Nanotech (2015) 10:775–8. 10.1038/nnano.2015.159
45.
XiaoSWuSXieXYangJWeiWShiSet alPosition-dependent Chiral Coupling between Single Quantum Dots and Cross Waveguides. Appl Phys Lett (2021) 118:091106. 10.1063/5.0042480
46.
Martin-CanoDHaakhHRRotenbergN. Chiral Emission into Nanophotonic Resonators. Acs Photon (2019) 6:961–6. 10.1021/acsphotonics.8b01555
47.
TangLTangJZhangWLuGZhangHZhangYet alOn-chip Chiral Single-Photon Interface: Isolation and Unidirectional Emission. Phys Rev A (2019) 99:043833. 10.1103/PhysRevA.99.043833
48.
YadavRKLiuWIndukuriSRKCVasistaABKumarGVPAgarwalGSet alObservation of Photonic Spin-Momentum Locking Due to Coupling of Achiral Metamaterials and Quantum Dots. J Phys Condens Matter (2020) 33:015701. 10.1088/1361-648X/abb650
49.
LodahlPMahmoodianSStobbeSRauschenbeutelASchneeweissPVolzJet alChiral Quantum Optics. Nature (2017) 541:473–80. 10.1038/nature21037
50.
HaldaneFDMRaghuS. Possible Realization of Directional Optical Waveguides in Photonic Crystals with Broken Time-Reversal Symmetry. Phys Rev Lett (2008) 100:013904. 10.1103/PhysRevLett.100.013904
51.
RaghuSHaldaneFDM. Analogs of Quantum-Hall-Effect Edge States in Photonic Crystals. Phys Rev A (2008) 78:033834. 10.1103/PhysRevA.78.033834
52.
YanBXieJLiuEPengYGeRLiuJet alTopological Edge State in the Two-Dimensional Stampfli-triangle Photonic Crystals. Phys Rev Appl (2019) 12:044004. 10.1103/PhysRevApplied.12.044004
53.
CaoTFangLCaoYLiNFanZTaoZ. Dynamically Reconfigurable Topological Edge State in Phase Change Photonic Crystals. Sci Bull (2019) 64:814–22. 10.1016/j.scib.2019.02.017
54.
El-GanainyRLevyM. Optical Isolation in Topological-Edge-State Photonic Arrays. Opt Lett (2015) 40:5275–8. 10.1364/OL.40.005275
55.
JiC-YLiuG-BZhangYZouBYaoY. Transport Tuning of Photonic Topological Edge States by Optical Cavities. Phys Rev A (2019) 99:043801. 10.1103/PhysRevA.99.043801
56.
GongYGuoLWongSBennettAJOhSS. Tailoring Topological Edge States with Photonic crystal Nanobeam Cavities. Sci Rep (2021) 11:1–9. 10.1038/s41598-020-79915-6
57.
KeYQinXMeiFZhongHKivsharYSLeeC. Topological Phase Transitions and Thouless Pumping of Light in Photonic Waveguide Arrays. Laser Photon Rev (2016) 10:995–1001. 10.1002/lpor.201600119
58.
ChenW-JJiangS-JChenX-DZhuBZhouLDongJ-Wet alExperimental Realization of Photonic Topological Insulator in a Uniaxial Metacrystal Waveguide. Nat Commun (2014) 5:1–7. 10.1038/ncomms6782
59.
ChengXJouvaudCNiXMousaviSHGenackAZKhanikaevAB. Robust Reconfigurable Electromagnetic Pathways within a Photonic Topological Insulator. Nat Mater (2016) 15:542–8. 10.1038/nmat4573
60.
BandresMAWittekSHarariGPartoMRenJSegevMet alTopological Insulator Laser: Experiments. Science (2018) 359:359. 10.1126/science.aar4005
61.
FangKYuZFanS. Realizing Effective Magnetic Field for Photons by Controlling the Phase of Dynamic Modulation. Nat Photon (2012) 6:782–7. 10.1038/nphoton.2012.236
62.
LuLJoannopoulosJDSoljačićM. Topological States in Photonic Systems. Nat Phys (2016) 12:626–9. 10.1038/nphys3796
63.
WangZChongYDJoannopoulosJDSoljačićM. Reflection-free One-Way Edge Modes in a Gyromagnetic Photonic crystal. Phys Rev Lett (2008) 100:013905. 10.1103/PhysRevLett.100.013905
64.
KhanikaevABHossein MousaviSTseW-KKargarianMMacDonaldAHShvetsG. Photonic Topological Insulators. Nat Mater (2013) 12:233–9. 10.1038/nmat3520
65.
RechtsmanMCZeunerJMTünnermannANolteSSegevMSzameitA. Strain-induced Pseudomagnetic Field and Photonic Landau Levels in Dielectric Structures. Nat Photon (2013) 7:153–8. 10.1038/nphoton.2012.302
66.
TzuangLDFangKNussenzveigPFanSLipsonM. Non-reciprocal Phase Shift Induced by an Effective Magnetic Flux for Light. Nat Photon (2014) 8:701–5. 10.1038/nphoton.2014.177
67.
HafeziMMittalSFanJMigdallATaylorJM. Imaging Topological Edge States in Silicon Photonics. Nat Photon (2013) 7:1001–5. 10.1038/nphoton.2013.274
68.
MittalSFanJFaezSMigdallATaylorJMHafeziM. Topologically Robust Transport of Photons in a Synthetic Gauge Field. Phys Rev Lett (2014) 113:087403. 10.1103/PhysRevLett.113.087403
69.
MittalSGoldschmidtEAHafeziM. A Topological Source of Quantum Light. Nature (2018) 561:502–6. 10.1038/s41586-018-0478-3
70.
HafeziMDemlerEALukinMDTaylorJM. Robust Optical Delay Lines with Topological protection. Nat Phys (2011) 7:907–12. 10.1038/nphys2063
71.
GuLYuanQZhaoQJiYLiuZFangLet alA Topological Photonic Ring-Resonator for On-Chip Channel Filters. J Lightwave Technol (2021) 39:5069–73. 10.1109/JLT.2021.3082558
72.
Jalali MehrabadMFosterAPDostRClarkeEPatilPKFarrerIet alA Semiconductor Topological Photonic Ring Resonator. Appl Phys Lett (2020) 116:061102. 10.1063/1.5131846
73.
SlobozhanyukAPKhanikaevABFilonovDSSmirnovaDAMiroshnichenkoAEKivsharYS. Experimental Demonstration of Topological Effects in Bianisotropic Metamaterials. Sci Rep (2016) 6:1–7. 10.1038/srep22270
74.
WuXMengYTianJHuangYXiangHHanDet alDirect Observation of valley-polarized Topological Edge States in Designer Surface Plasmon Crystals. Nat Commun (2017) 8:1–9. 10.1038/s41467-017-01515-2
75.
ChenX-DZhaoF-LChenMDongJ-W. Valley-contrasting Physics in All-Dielectric Photonic Crystals: Orbital Angular Momentum and Topological Propagation. Phys Rev B (2017) 96:020202. 10.1103/PhysRevB.96.020202
76.
GaoZYangZGaoFXueHYangYDongJet alValley Surface-Wave Photonic crystal and its Bulk/edge Transport. Phys Rev B (2017) 96:201402. 10.1103/PhysRevB.96.201402
77.
GaoFXueHYangZLaiKYuYLinXet alTopologically Protected Refraction of Robust Kink States in valley Photonic Crystals. Nat Phys (2018) 14:140–4. 10.1038/nphys4304
78.
RechtsmanMCZeunerJMPlotnikYLumerYPodolskyDDreisowFet alPhotonic Floquet Topological Insulators. Nature (2013) 496:196–200. 10.1038/nature12066
79.
NohJHuangSChenKPRechtsmanMC. Observation of Photonic Topological valley Hall Edge States. Phys Rev Lett (2018) 120:063902. 10.1103/PhysRevLett.120.063902
80.
MehrabadMJFosterAMartinNDostRClarkeEPatilPet alA Chiral Topological Add-Drop Filter for Integrated Quantum Photonic Circuits (2021). arXivAvailable at: https://ui.adsabs.harvard.edu/abs/2021arXiv211007277J (Accessed December 16, 2021).
81.
XieXYanSDangJYangJXiaoSWangYet alTopological Cavity Based on Slow-Light Topological Edge Mode for Broadband Purcell Enhancement. Phys Rev Appl (2021) 16:014036. 10.1103/PhysRevApplied.16.014036
82.
YanQHuXFuYLuCFanCLiuQet alQuantum Topological Photonics. Adv Opt Mater. (2021) 9:2001739. 10.1002/adom.202001739
83.
BarikSKarasahinAFlowerCCaiTMiyakeHDeGottardiWet alA Topological Quantum Optics Interface. Science (2018) 359:666–8. 10.1126/science.aaq0327
84.
WuL-HHuX. Scheme for Achieving a Topological Photonic crystal by Using Dielectric Material. Phys Rev Lett (2015) 114:223901. 10.1103/PhysRevLett.114.223901
85.
HasanMZKaneCL. Colloquium: Topological Insulators. Rev Mod Phys (2010) 82:3045–67. 10.1103/RevModPhys.82.3045
86.
QiX-LZhangS-C. Topological Insulators and Superconductors. Rev Mod Phys (2011) 83:1057–110. 10.1103/RevModPhys.83.1057
87.
YangYHangZH. Topological Whispering Gallery Modes in Two-Dimensional Photonic crystal Cavities. Opt Express (2018) 26:21235–41. 10.1364/OE.26.021235
88.
SauerEVascoJPHughesS. Theory of Intrinsic Propagation Losses in Topological Edge States of Planar Photonic Crystals. Phys Rev Res (2020) 2:043109. 10.1103/PhysRevResearch.2.043109
89.
GorlachMANiXSmirnovaDAKorobkinDZhirihinDSlobozhanyukAPet alFar-field Probing of Leaky Topological States in All-Dielectric Metasurfaces. Nat Commun (2018) 9(1):1–8. 10.1038/s41467-018-03330-9
90.
YangYXuYFXuTWangH-XJiangJ-HHuXet alVisualization of a Unidirectional Electromagnetic Waveguide Using Topological Photonic Crystals Made of Dielectric Materials. Phys Rev Lett (2018) 120:217401. 10.1103/PhysRevLett.120.217401
91.
AndersonPDSubramaniaG. Unidirectional Edge States in Topological Honeycomb-Lattice Membrane Photonic Crystals. Opt Express (2017) 25:23293–301. 10.1364/OE.25.023293
92.
BarikSMiyakeHDeGottardiWWaksEHafeziM. Two-dimensionally Confined Topological Edge States in Photonic Crystals. New J Phys (2016) 18:113013. 10.1088/1367-2630/18/11/113013
93.
ArreguiGGomis-BrescoJSotomayor-TorresCMGarciaPD. Quantifying the Robustness of Topological Slow Light. Phys Rev Lett (2021) 126:027403. 10.1103/PhysRevLett.126.027403
94.
Jalali MehrabadMFosterAPDostRClarkeEPatilPKFoxAMet alChiral Topological Photonics with an Embedded Quantum Emitter. Optica (2020) 7:1690–6. 10.1364/OPTICA.393035
95.
ShalaevMIWalasikWTsukernikAXuYLitchinitserNM. Robust Topologically Protected Transport in Photonic Crystals at Telecommunication Wavelengths. Nat Nanotech (2019) 14:31–4. 10.1038/s41565-018-0297-6
96.
HauffNHughesSJeannicHLLodahlPRotenbergN. Chiral Quantum Optics in Broken-Symmetry and Topological Photonic crystal Waveguides (2021). arXivAvailable at: https://arxiv.org/abs/2111.02828 (Accessed December 8, 2021).
97.
MaTShvetsG. All-Si valley-Hall Photonic Topological Insulator. New J Phys (2016) 18:025012. 10.1088/1367-2630/18/2/025012
98.
DongJ-WChenX-DZhuHWangYZhangX. Valley Photonic Crystals for Control of Spin and Topology. Nat Mater (2017) 16:298–302. 10.1038/nmat4807
99.
HeX-TLiangE-TYuanJ-JQiuH-YChenX-DZhaoF-Let alA Silicon-On-Insulator Slab for Topological valley Transport. Nat Commun (2019) 10:1–9. 10.1038/s41467-019-08881-z
100.
ChenYHeX-TChengY-JQiuH-YFengL-TZhangMet alTopologically Protected valley-dependent Quantum Photonic Circuits. Phys Rev Lett (2021) 126:230503. 10.1103/PhysRevLett.126.230503
101.
YoshimiHYamaguchiTKatsumiROtaYArakawaYIwamotoS. Experimental Demonstration of Topological Slow Light Waveguides in valley Photonic Crystals. Opt Express (2021) 29:13441–50. 10.1364/OE.422962
102.
YoshimiHYamaguchiTOtaYArakawaYIwamotoS. Slow Light Waveguides in Topological valley Photonic Crystals. Opt Lett (2020) 45:2648–51. 10.1364/OL.391764
103.
EkSLunnemannPChenYSemenovaEYvindKMorkJ. Slow-light-enhanced Gain in Active Photonic crystal Waveguides. Nat Commun (2014) 5:1–8. 10.1038/ncomms6039
104.
CorcoranBMonatCGrilletCMossDJEggletonBJWhiteTPet alGreen Light Emission in Silicon through Slow-Light Enhanced Third-Harmonic Generation in Photonic-crystal Waveguides. Nat Photon (2009) 3:206–10. 10.1038/nphoton.2009.28
105.
YamaguchiTOtaYKatsumiRWatanabeKIshidaSOsadaAet alGaAs valley Photonic crystal Waveguide with Light-Emitting InAs Quantum Dots. Appl Phys Express (2019) 12:062005. 10.7567/1882-0786/ab1cc5
106.
BarikSKarasahinAMittalSWaksEHafeziM. Chiral Quantum Optics Using a Topological Resonator. Phys Rev B (2020) 101:205303. 10.1103/PhysRevB.101.205303
107.
SipahigilAEvansRESukachevDDBurekMJBorregaardJBhaskarMKet alAn Integrated diamond Nanophotonics Platform for Quantum-Optical Networks. Science (2016) 354:847–50. 10.1126/science.aah6875
108.
BhattiDSchneiderROppelSvon ZanthierJ. Directional Dicke Subradiance with Nonclassical and Classical Light Sources. Phys Rev Lett (2018) 120:113603. 10.1103/PhysRevLett.120.113603
109.
PichlerHChoiSZollerPLukinMD. Universal Photonic Quantum Computation via Time-Delayed Feedback. Proc Natl Acad Sci USA (2017) 114:11362–7. 10.1073/pnas.1711003114
110.
PichlerHRamosTDaleyAJZollerP. Quantum Optics of Chiral Spin Networks. Phys Rev A (2015) 91:042116. 10.1103/PhysRevA.91.042116
111.
BarikS. Chiral Quantum Optics Using Topological Photonics. [PhD’s thesis]. Maryland: University of Maryland (2020).
Summary
Keywords
chiral quantum optics, topological photonics, chiral topological quantum interfaces, integrated quantum devices, quantum dot
Citation
Jiang P, Ma N, Qiao X and Zhang H (2022) Recent Progress in Chiral Topological Quantum Interface. Front. Phys. 10:845579. doi: 10.3389/fphy.2022.845579
Received
30 December 2021
Accepted
10 January 2022
Published
25 January 2022
Volume
10 - 2022
Edited by
Cuicui Lu, Beijing Institute of Technology, China
Reviewed by
Hongu Zhang, Beijing Institute of Technology, China
Sayed Elshahat, Beijing Institute of Technology, China
Updates
Copyright
© 2022 Jiang, Ma, Qiao and Zhang.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ping Jiang, pjiang@upc.edu.cn
This article was submitted to Optics and Photonics, a section of the journal Frontiers in Physics
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.