- School for Theoretical Physics, School of Physics and Electronics, Hunan University, Changsha, China
Critical exponent γ ⪰ 1.1 characterizes the behavior of the mechanical compressibility of a real fluid when the temperature approaches the critical one. It results in zero Gaussian curvature of the local shape of the critical point on the thermodynamic equation of state surface, which imposes a new constraint upon the construction of the potential equation of state of the real fluid from the empirical data. All known empirical equations of the state suffer from a weakness that the Gaussian curvature of the critical point is negative definite instead of zero.
It is believed that God created the universe according to a geometric plan, and geometry is everywhere. Physics is the most fundamental scientific discipline with its main goal to understand the universe, and geometry is deeply rooted in every branch of physics. The present work concentrates on the relationship between thermodynamics and geometry. The modern version of thermodynamics can be reformulated in terms of contact geometry [1], and the so-called geometry of thermodynamics has been put forward, which describes the space of thermodynamic parameters by the Riemannian metric [2–4]. The influence of the curved space on the critical behavior of the two-dimensional Ising model is identified [5], and geometric critical exponents are definable in classical and quantum phase transitions [6]. Latest advances include the geometrical methods employed in the analysis of quantum phase transitions and non-equilibrium dissipative phase transitions [7], the new formalism of thermodynamic geometry employed in investigating phase transition points, and the critical behavior of a Gauss–Bonnet-AdS black hole in four-dimensional spacetime [8]. Thus, the new relationship between thermodynamics and geometry is always interesting, and we report a new requirement on the construction of the empirical equation of state (EoS) based on the differential geometry of the surfaces.
The elaboration of a form of the empirical EoS best fitting the experimental data and also meeting the theoretical requirements has been an important issue for more than one century [9–15]. For a real fluid, an open theoretical problem is, in the close neighborhood of the critical point, what is the better form of the EoS? For instance, it is well-known that both the van der Waals EoS and the general theory of the Landau theory of phase transitions predict the compressibility critical exponent γ = γ′ to be 1, and all known empirical EoS fail to exactly reproduce the experimental values γ = 1.2 ∼ 1.3 ≳ γ′ = 1.1 ∼ 1.2 [16, 17]. Recently, we have conjectured that the Gaussian curvature of the local shape of the vapor-liquid critical point is zero [18]. In the present study, we first prove that the conjecture is true and secondly report the construction of a fluid EoS, which has γ = γ′ = 3, which is quantitatively different from the experimental values but leads to the zero Gaussian curvature of the vapor-liquid critical point.
The fluid of a pure substance belongs to the so-called pVT system, which means that the EoS usually takes following simplest form:
where p, V, T denote the pressure, volume, and temperature, respectively. In general, at the critical point
In other words, the values
In geometry, the EoS (1) can be viewed as a two-dimensional surface in the flat pVT space, and its shape can be completely characterized by the mean and the Gaussian curvature [19]. It is then interesting to explore the local shape of the vapor-liquid critical point via these two curvatures. In calculation, the dimensionless EoS surface Equation 1 must be used, in which all quantities
At the critical point, conditions (2) apply, and we have the mean curvature HC and the Gaussian curvature KC, respectively:
The compressibility or a mechanical response function,
leads to
Near the critical point, the experiments suggest, with γ ≈ γ′ ∼ 1.2 [16, 17],
In consequence, we have
which can be rewritten into the following, in terms of the Gaussian curvature from (5):
Thus, for real fluids, the Gaussian curvature of the local shape of the critical point of the EoS surface is zero.
In contrast, all known empirical EoS at the critical point give the negative values of the Gaussian curvature KC ≺ 0, whose typical results are listed in Table 1, from which we see that none of them can reproduce KC = 0. In the last line of Table 1, the Shamsundar–Lienhard EoS [14] is special, because it is a principle (“The shape of the (experimental data) figure tells us that a cubic-like equation must be of the form” [14]) rather than an explicit form of an EoS. Though these empirical EoS in Table 1 do not exhaust all possibilities, we are safe to say that KC = 0 is beyond the current form of the Landau theory of phase transitions because it generally predicts γ = γ′ = 1, thus KC ≺ 0 for

TABLE 1. Mean and Gaussian curvature of the critical points for empirical or semi-empirical EoS. Symbol v denotes the molar volume, a and b are repulsive and attractive parameters, respectively, y = b/4v, and a(T) depends on temperature and other substance parameters [9, 15]. Only one typical value of the substance parameter in a(T) is used in the calculations.
Now, we present an EoS with KC = 0. Our constructed EoS takes following form:
where
It is quantitatively different from the compressibility critical exponent for the real fluid. The origin of the difference may lie in that we use the continuous form of the EoS rather than the discontinous ones, which shall be explored in the future.
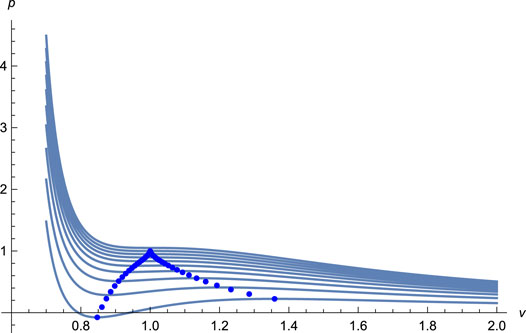
FIGURE 1. The isotherms (solid lines) with T = 0.60, 0.65, 0.70, …, 1.05 from undermost to upmost, and the spinodal curve (solid dots) for EoS (11). The EoS captures the essential feature of the vapor-liquid phase transition for the existence of the van der Waals loops, clearly indicating a first-order phase transition in the liquid system.
So far, there are at least three requirements in the form of EoS for the real fluid: 1) in large volume limit, the EoS reproduces the ideal gas law [14]; 2) at both ends of a vapor-liquid coexistence line, there are onset and outset value for volume for gas and liquid state and a coexisting pressure [14]; and 3) the Gaussian curvature of the critical point is zero. All these constraints directly come from experiments. There may be other constraints on the form of the EoS, which may arise from the theoretical requirements, such as Maxwell area construction for the van der Waals loop [14], which must nevertheless be used case by case.
In summary, geometry not only offers a better understanding and deeper insight into the mathematical structure of thermodynamics but also presents an accurate and convenient means to characterize various properties of thermodynamic states. We report that the local shape of the vapor-liquid critical point on the thermodynamic surface has zero Gaussian curvature, which has long been hidden in the compressibility critical exponent γ ≻ 1. It can be used to distinguish different empirical models and impose this requirement on the construction of the new EoS. A new form of the EoS capturing the essential feature of the vapor-liquid phase transition with γ ≻ 1 is successfully elaborated. Without explicitly carrying it out, we are confident that the theoretical value γ = γ′ = 3 for the compressibility critical exponent can be explained within the higher order of the Landau theory of phase transitions.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.
Author Contributions
JY and QL contributed to the conception and design of the study. WD organized the database. QL wrote the first draft of the manuscript. All authors contributed to manuscript revision and read and approved the submitted version.
Funding
This work was financially supported by the National Natural Science Foundation of China under Grant no. 11675051.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
3. Gilmore R. Length and Curvature in the Geometry of Thermodynamics. Phys Rev A (1984) 30:1994–7. doi:10.1103/physreva.30.1994
4. Ruppeiner G. Riemannian Geometry in Thermodynamic Fluctuation Theory. Rev Mod Phys (1995) 67:605–59. doi:10.1103/revmodphys.67.605
5. Shima H, Sakaniwa Y. Geometric Effects on Critical Behaviours of the Ising Model. J Phys A: Math Gen (2006) 39:4921–33. doi:10.1088/0305-4470/39/18/010
6. Kumar P, Sarkar T. Geometric Critical Exponents in Classical and Quantum Phase Transitions. Phys Rev E Stat Nonlin Soft Matter Phys (2014) 90:042145. doi:10.1103/PhysRevE.90.042145
7. Carollo A, Valenti D, Spagnolo B. Geometry of Quantum Phase Transitions. Phys Rep (2020) 838:1–72. doi:10.1016/j.physrep.2019.11.002
8. Hosseini Mansoori SA. Thermodynamic Geometry of the Novel 4-D Gauss-Bonnet AdS Black Hole. Phys Dark Universe (2021) 31:100776. doi:10.1016/j.dark.2021.100776
9. Wei YS, Sadus RJ. Equations of State for the Calculation of Fluid-phase Equilibria. Aiche J (2000) 46:169–96. doi:10.1002/aic.690460119
10. Kontogeorgis GM, Privat R, Jaubert JN. Taking Another Look at the van der Waals Equation of State-Almost 150 Years Later. J Chem Eng Data (2019) 64:4619–37. doi:10.1021/acs.jced.9b00264
11. Lebowitz JL, Waisman EM. Statistical Mechanics of Simple Fluids: Beyond Van Der Waals. Phys Today (1980) 33:24–30. doi:10.1063/1.2913994
12. Reid RC, Prausnitz JM, Poling BE. The Properties of Gases and Liquids. New York: McGraw-Hill (1987).
13. Lienhard JH, Shamsundar N, Biney PO. Spinodal Lines and Equations of State: A Review. Nucl Eng Des (1986) 95:297–314. doi:10.1016/0029-5493(86)90056-7
14. Shamsundar N, Lienhard JH. Equations of State and Spinodal Lines - a Review. Nucl Eng Des (1993) 141:269–87. doi:10.1016/0029-5493(93)90106-j
15. Anderko A. 4 Cubic and generalized van der waals equations. Exp Thermodynamics (2000) 5:75–126. doi:10.1016/s1874-5644(00)80015-6
16. Toda M, Kubo R, Saito N. Statistical Physics I: Equilibrium Statistical Mechanics. 2nd ed. Berlin: Sringer-Verlag (2012).
18. Yu JS, Zhou X, Chen JF, Du WK, Wang X, Liu QH. Local Shape of the Vapor-Liquid Critical Point on the Thermodynamic Surface and the van der Waals Equation of State. Front Phys (2021) 9:679083. doi:10.3389/fphy.2021.679083
Keywords: critical point, critical exponent, fluid system, Gaussian curvature, equation of state
Citation: Yu JS, Du WK and Liu QH (2022) Geometrical Aspect of Compressibility Critical Exponent. Front. Phys. 10:850296. doi: 10.3389/fphy.2022.850296
Received: 07 January 2022; Accepted: 11 March 2022;
Published: 19 April 2022.
Edited by:
Fernando A. Oliveira, University of Brasilia, BrazilReviewed by:
Gennady Chitov, Université de Sherbrooke, CanadaDmitrii Tayurskii, Kazan Federal University, Russia
Copyright © 2022 Yu, Du and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Q. H. Liu, cXVhbmh1aWxpdUBnbWFpbC5jb20=
 J. S. Yu
J. S. Yu W. K. Du
W. K. Du Q. H. Liu
Q. H. Liu