- School of Physical Science and Technology, Ningbo University, Ningbo, China
The theoretical framework for the uncertainty relation of Hermitian operators is perfect and has been applied in many fields. At the same time, non-Hermitian operators are also widely used in some other fields. However, the uncertainty relation of non-Hermitian operators remains to be explored. K.W. Bong and his co-workers proposed the theory of unitary uncertainty relation and verified it in the experiment [Phys. Rev. Lett. 120, 230402 (2018)]. In this work, we generalized this unitary uncertainty relation theory and proposed uncertainty relations of non-Hermitian operators. Due to the difficulties in the direct measurement of non-Hermitian operators in the uncertainty relations, we simplified the uncertainty relation of two non-Hermitian operators with pure states and proposed a realizable experimental measurement scheme by using the Mach–Zehnder interferometer. When the two non-Hermitian operators are unitary, our result can reduce to Bong et al.’s result. Furthermore, for two non-Hermitian operators but not unitary, we obtained a generalized and analogous result of theirs.
1 Introduction
Uncertainty relations are the basis of quantum theory. It was first proposed by Heisenberg [1] and was rewritten by Kennard [2] and Weyl [3] as the uncertainty relation between position and momentum. Robertson generalized this to any two observables [4]. Schrödinger strengthened the inequality and put forward the Schrödinger uncertainty relation [5] as
where ⟨(ΔO)2⟩ stands for the variance of observable O, {A, B} represents the anticommutator of observables A and B, and [A, B] is their commutator. Uncertainty relations have been used in many quantum information tasks, including quantum key distribution [6, 7], deeply quantum systems [8–10], quantum random number generation [11, 12], entanglement witness [13], Einstein–Podolsky–Rosen (EPR) steering [14, 15], quantum metrology [16], and so on.
In quantum theory, we know that those observable measurements of physics are represented by Hermitian operators and can be faithfully represented on measuring instruments. In fact, there are non-Hermitian operators that are not Hermitian conjugated, and these non-Hermitian operators can be observed by weak measurements [17]. Certainly, the measurement of non-Hermitian operators is not limited to this; weak values of non-Hermitian operators can also be derived from bound state scattering [18]. The problem of eigenvalues of non-Hermitian operators can also be solved by introducing generalized ladder operators [19]. In reality, non-Hermitian operators can be used in many ways such as quantum open systems [20], quantum optics [21], quantum cosmology [22], and many other fields. Furthermore, pseudo-Hermitian operators belong to non-Hermitian operators, which have many applications [23, 24].
The uncertainty relation of unitary operators can reflect the basic characteristics of the quantum world to some extent. In Ref. [25], the authors proposed the uncertainty relation of the unitary operator, satisfying the certain commutative condition in finite dimensions. However, it is not applicable in high dimensions, so Bagchi and Pati put forward the uncertainty relation of general unitary operators, which can be applied to high dimensions [26]. In order to get a more general case, the uncertainty relation of general unitary operators has been experimentally tested [27]. Furthermore, Bong and his co-workers put forward an uncertainty relation: strong unitary and overlap relation, and demonstrated their theory in the experiment [28]. The subtlety of this theory lies in that it greatly simplifies the measurement of the experiment and provides a very valuable experimental idea for reference. In addition, the theory of the strong unitary uncertainty relation has also been discussed in Ref. [29] and has been experimentally realized in Ref. [30].
Unitary operators are a kind of non-Hermitian operators, and the theory about the uncertainty relation of unitary operators has been relatively mature. But what about the uncertainty relations of more general non-Hermitian operators? For non-Hermitian operators, their eigenvalues are complex and cannot be directly observed in experiments. Therefore, we made corresponding changes to the measurement method of non-Hermitian operators. The general derivation of the uncertainty relation of general non-Hermitian operators is given in Ref. [17], but this form lacks experimental protocols to measure this uncertainty relation.
In this study, we proposed uncertainty relations of non-Hermitian operators and designed an experimental scheme to facilitate measurement for two non-Hermitian operators with pure states. The article is organized as follows: First, we briefly proved the uncertainty relation of non-Hermitian operators. Second, we provided an example of the uncertainty relation of two non-Hermitian operators in a pure state, explained how to measure the uncertainty relation of two non-Hermitian operators in an experiment, and proposed a measurement scheme by using the Mach–Zehnder interferometer. Finally, we discussed and summarized the content of the article.
2 Uncertainty Relations for Non-Hermitian Operators
To propose the uncertainty relation for non-Hermitian operators, we first need to define the variance of a non-Hermitian operator. In Refs. [17, 31], the variance of a non-Hermitian operator O under a state ρ is defined as ⟨(ΔO)2⟩≔⟨(O† − ⟨O†⟩) (O− ⟨O⟩)⟩ = ⟨O†O⟩ − ⟨O†⟩⟨O⟩, where ⟨O⟩ = Tr (ρO). Based on this definition, we can prove the following uncertainty relation for non-Hermitian operators:
Proposition 1. Two non-Hermitian operators A and B are considered in a d-dimensional Hilbert space; the uncertainty relations for two non-Hermitian operators are
where ⟨(ΔA)2⟩≔⟨A†A⟩ − ⟨A†⟩⟨A⟩ and ⟨(ΔB)2⟩≔⟨B†B⟩ − ⟨B†⟩⟨B⟩.
Proof. Let us define a 2 × 2 matrix M as
Now, let us prove that M is a semi-definite positive matrix. An arbitrary vector (a,b)T is considered, where a and b are two arbitrary complex numbers; of both numbers, one has
where the operator C is defined as
Since for an arbitrary vector (a,b)T, the result ⟨C†C⟩ is always non-negative, and M is semi-definite positive.If a matrix is semi-definite positive, then its determinant is non-negative. Thus, we have
with
Therefore, the uncertainty relations for two non-Hermitian operators (2) have been proved. □
Remark. The uncertainty relation (2) has also been proved in Ref. [17]. When A and B are Hermitian operators, the uncertainty relation (2) reduces to the Schrödinger uncertainty relation (1) since
holds. Moreover, we generalized proposition 1 to the case of n non-Hermitian operators.
Proposition 2. Consider n non-Hermitian operators
where the matrix M is defined as
Proof. The proof is similar to proposition 1. Let us prove that M is a semi-definite positive matrix. An arbitrary vector
where the operator C is defined as
3 Uncertainty Relations for Two Non-Hermitian Operators in Pure States
Now, we focused on the uncertainty relations for two non-Hermitian operators (2) in pure states. Two non-Hermitian operators A and B are considered in a d-dimensional Hilbert space; if the state is a pure state |ϕ⟩, then
where P is a project operator defined as
and
Therefore, the uncertainty relations for two non-Hermitian operators (2) with a pure state |ϕ⟩ become
Moreover, if the dimension of the Hilbert space d = 2 (a single qubit system), the rank of P is 1. Thus, P can be rewritten as P = |ϕ⊥⟩⟨ϕ⊥|, where |ϕ⊥⟩ is the orthogonal state of |ϕ⟩ in the single qubit system. Thus, the uncertainty relation (14) becomes
It is obvious that the “ = ” always holds in (15).
Based on the aforementioned proof, one can conclude that we can always obtain equality in (2) when we only consider pure states in a one-qubit system.
4 Test Uncertainty Relation for Two Non-Hermitian Operators
The uncertainty relation for two non-Hermitian operators in a one-qubit system is discussed, and the uncertainty relation is experimentally tested via weak measurements. Since the variance of a non-Hermitian operator in a state is a concave function of the state, we focused on the uncertainty relation in pure states.
4.1 Theory
Two non-Hermitian operators A and B are considered in a single-qubit system. Suppose the polar decompositions of the non-Hermitian operators A and B are
where SA and SB are two positive semi-definite operators and UA and UB are unitary operators. Thus, the variances of A and B in a pure state |ϕ⟩ are
where |ψ⟩≔UA|ϕ⟩ and |χ⟩≔UB|ϕ⟩. Moreover, the right hand side of (2) becomes
In the following, for the simplicity of experiments, we chose the non-Hermitian operators A and B as
Thus,
Now the left hand side of the uncertainty relation (2) becomes
Meanwhile, the right hand side of the uncertainty relation (2) becomes
Therefore, the uncertainty relation (2) reduces to
Let us define |φ1⟩≔|ϕ⟩, |φ2⟩≔A|ϕ⟩ = σz|ψ⟩, |φ3⟩≔B|ϕ⟩ = σx|χ⟩, and Tjk = ⟨φj|φk⟩; the uncertainty relation (2) becomes
Since
where Φ is the phase of T23T12T31, and Re (T23T12T31) is the real part of T23T12T31. Thus, Eq. 29 is equivalent to
From cos Φ ≤ 1, one has a weaker uncertainty relation of (32),
Remark. If A = UA and B = UB, then the uncertainty relations (32) and (33) reduce to the case of unitary operators discussed in Ref. [28]. This theory has a much broader scope and can deal with a wide variety of situations.
4.2 Scheme
Now we discussed how to test the uncertainty relation (32) and its weaker form (33) by using the Mach–Zehnder interferometer. According to the theory and measurement ideas proposed by Bong [28] and Nirala [32], the uncertainty relation of non-Hermitian operators can also be expressed by calculating the interference visibility.
In principle, we can test the uncertainty relation of non-Hermitian operators for any n. Here, we chose a special case of n = 2, which requires preparation of a strictly pure state |ψ⟩ and tomographic reconstruction of |ψ⟩, A|ψ⟩, and B|ψ⟩.
Non-Hermitian operators A and B are considered for example. As shown in Figure 1, the main component of our setup is the Mach–Zehnder interferometer. For the single-photon source, we have a choice to use a continuous-wave diode laser to pump an optically nonlinear beta barium borate (BBO) crystal. Then, photon pairs are generated by noncollinear type-I spontaneous parametric down-conversion (SPDC). The idler photon (Trigger) heralds the presence of a signal photon. The A and B operators can be implemented by using combinations of optical components in the laboratory such as half-wave plates (HWPs) and quarter-wave plates (QWPs). We used phase shifters on two branches to adjust the optical path difference with a certain angle θ.
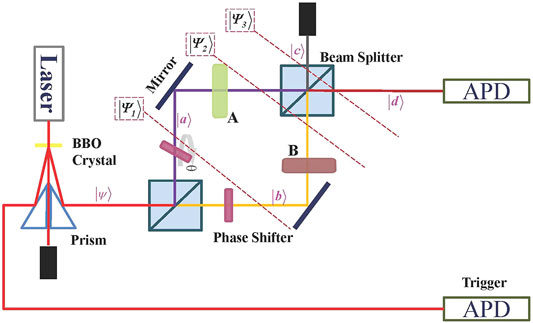
FIGURE 1. This scheme can test the uncertainty relation for two non-Hermitian operators (A and B) by using the Mach–Zehnder interferometer. Pairs of single photons are generated using a BBO crystal. The signal single-photon state is prepared in |ψ⟩. After entering a displaced Mach–Zehnder interferometer at a 5050 beam splitter, the photon traverses the interferometer. B in the transmitted arm is represented in (yellow), and A in the reflected arm is represented in (purple).
It is considered that |ψ⟩ is the input state of the first beam splitter, which is further changed as
where |a⟩ and |b⟩ are path states corresponding to reflection and transmission, respectively. We placed the optical elements of the operators A and B on the corresponding arms. Before passing through the second beam splitter, the state changes into
After passing through the second beam splitter, the ports are denoted by |c⟩ and |d⟩. Here, when the two beams finally meet at the beam splitter, there is a phase difference ϵ between the two arms due to propagation. The formation of ϵ is independent of A and B operations.
The detection device is at port |d⟩, which means that what we detected is the component of the total state. This can be carried out by applying the projector Πd = |d⟩⟨d| to the entire state, so the component of the detection arm state is
Finally, the strength of the detector port is determined by
where we suppose that
Hence, we can obtain the interference visibility γ. Based on Eq. 38, the maximal and minimal values of Nd can be obtained by varying θ,
The interference visibility γ is defined as
Since A†A and B†B are Hermitian operators, these two Hermitian operators can be directly measured by von Neumann measurements. The values of ⟨A†⟩ and ⟨B⟩ are similarly determined from the corresponding interference visibilities γ(A, I), γ(I, B), where I denotes the identity operator. Moreover, when A = σzUA, B = σxUB, the interference visibility is given by γ(A, B) = |⟨A†B⟩|. Generally speaking, the expected value that we need to measure is a complex number, it is necessary to measure its real part and imaginary part separately, but it is not usually possible to measure both of them simultaneously. However, our method is to directly measure the modulus of a complex number, and the uncertainty relations (29) and (33) are required to measure the modulus.
5 Discussion and Conclusion
As shown in Figure 1, we tested the uncertainty relation of non-Hermitian operators very conveniently. However, this is only a theoretical diagram of the experimental design. If the experimental design scheme is to be applied in real experiments, the Mach–Zehnder interferometer can be displaced by a Sagnac interferometer, which can reduce the influence of the external environment on the experiment.
In conclusion, the uncertainty relation of non-Hermitian operators in any quantum state can be measured. This broadens the practical scope of uncertainty relations, and non-Hermitian operators also have experimentally observable uncertainty relations. The theory would be less restrictive and could be applied to other open systems. In addition, it can be used to solve scattering problems and entanglement problems.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author Contributions
XZ and CZ contributed to the conception and design of the study. XZ wrote the first draft of the manuscript. CZ wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.
Funding
This work is supported by the National Natural Science Foundation of China (Grant No. 11734015) and the K. C. Wong Magna Fund in Ningbo University.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Heisenberg W. Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Z Physik (1927) 43:172–98. doi:10.1007/bf01397280
2. Kennard EH. Zur Quantenmechanik Einfacher Bewegungstypen. Z Physik (1927) 44:326–52. doi:10.1007/bf01391200
6. Koashi M. Simple Security Proof of Quantum Key Distribution Based on Complementarity. New J Phys (2009) 11:045018. doi:10.1088/1367-2630/11/4/045018
7. Berta M, Christandl M, Colbeck R, Renes JM, Renner R. The Uncertainty Principle in the Presence of Quantum Memory. Nat Phys (2010) 6:659–62. doi:10.1038/nphys1734
8. Tomamichel M, Renner R. Uncertainty Relation for Smooth Entropies. Phys Rev Lett (2011) 106:110506. doi:10.1103/physrevlett.106.110506
9. Wollman EE, Lei CU, Weinstein AJ, Suh J, Kronwald A, Marquardt F, et al. Quantum Squeezing of Motion in a Mechanical Resonator. Science (2015) 349:952–5. doi:10.1126/science.aac5138
10. Ding ZY, Huan Y, Dong W, Hao Y, Jie Y, Liu Y. Experimental Investigation of Entropic Uncertainty Relations and Coherence Uncertainty Relations. Phys Rev A (2020) 101:032101. doi:10.1103/physreva.101.032101
11. Vallone G, Marangon DG, Tomasin M, Villoresi P. Quantum Randomness Certified by the Uncertainty Principle. Phys Rev A (2014) 90:052327. doi:10.1103/physreva.90.052327
12. Zhu C, Hongyi Z, Xiao Y, Xiongfeng M. Source-Independent Quantum Random Number Generation. Phys Rev X (2016) 6:011020.
13. Mario B, Patrick JC, Stephanie W. Entanglement-assisted Guessing of Complementary Measurement Outcomes. Phys Rev A (2014) 90:062127.
14. Walborn SP, Salles A, Gomes RM, Toscano F, Souto Ribeiro PH. Revealing Hidden Einstein-Podolsky-Rosen Nonlocality. Phys Rev Lett (2011) 106:130402. doi:10.1103/physrevlett.106.130402
15. James S, Curtis JB, Stephen PW, Eric GC, John CH. Einstein-Podolsky-Rosen Steering Inequalities from Entropic Uncertainty Relations. Phys Rev A (2013) 87:062103.
16. Giovannetti V, Lloyd S, Maccone L. Advances in Quantum Metrology. Nat Photon (2011) 5:222–9. doi:10.1038/nphoton.2011.35
17. Pati AK, Singh U, Sinha U. Measuring Non-hermitian Operators via Weak Values. Phys Rev A (2015) 92:052120. doi:10.1103/physreva.92.052120
18. Matzkin A. Weak Measurements in Non-hermitian Systems. J Phys A: Math Theor (2012) 45:444023. doi:10.1088/1751-8113/45/44/444023
19. l’Yi WS. Non-Hermitian Quantum Canonical Variables and the Generalized Ladder Operators. Phys Rev A (1996) 53:1251–6. doi:10.1103/physreva.53.1251
20. Feshbach H. Unified Theory of Nuclear Reactions. Ann Phys (1958) 5:357–90. doi:10.1016/0003-4916(58)90007-1
21. Aharonov Y, Massar S, Popescu S, Tollaksen J, Vaidman L. Adiabatic Measurements on Metastable Systems. Phys Rev Lett (1996) 77:983–7. doi:10.1103/physrevlett.77.983
22. Rostami T, Jalalzadeh S, Moniz PV. Quantum Cosmological Intertwining: Factor Ordering and Boundary Conditions from Hidden Symmetries. Phys Rev D (2015) 92:023526. doi:10.1103/physrevd.92.023526
23. Zhan X, Wang K, Xiao L, Bian Z, Zhang Y, Sanders BC, et al. Experimental Quantum Cloning in a Pseudo-unitary System. Phys Rev A (2020) 101:010302. doi:10.1103/physreva.101.010302
24. Chen YC, Gong M, Xue P, Yuan HD, Zhang CJ. Quantum Deleting and Cloning in a Pseudo-unitary System. Front Phys (2021) 16:53601. doi:10.1007/s11467-021-1063-z
25. Massar S, Spindel P. Uncertainty Relation for the Discrete Fourier Transform. Phys Rev Lett (2008) 100:190401. doi:10.1103/physrevlett.100.190401
26. Bagchi S, Pati AK. Uncertainty Relations for General Unitary Operators. Phys Rev A (2016) 94:042104. doi:10.1103/physreva.94.042104
27. Xiao L, Wang K, Zhan X, Bian Z, Li J, Zhang Y, et al. Experimental Test of Uncertainty Relations for General Unitary Operators. Opt Express (2017) 25:17904. doi:10.1364/oe.25.017904
28. Bong K-W, Tischler N, Patel RB, Wollmann S, Pryde GJ, Hall MJW. Strong Unitary and Overlap Uncertainty Relations: Theory and Experiment. Phys Rev Lett (2018) 120:230402. doi:10.1103/physrevlett.120.230402
29. Bing Y, Naihuan J, Xianqing LJ. Strong Unitary Uncertainty Relations. Phys Rev A (2019) 100:022116.
30. Qu D, Wang K, Xiao L, Zhan X, Xue P. Experimental Demonstration of strong Unitary Uncertainty Relations. Opt Express (2021) 29:29567. doi:10.1364/oe.438774
31. Anandan J. Geometric Phase for Cyclic Motions and the Quantum State Space Metric. Phys Lett A (1990) 147:3–8. doi:10.1016/0375-9601(90)90003-7
Keywords: uncertainty relations, non-Hermitian operators, Mach–Zehnder interferometer, Robertson–Schrödinger uncertainty relations, Heisenberg uncertainty relations
Citation: Zhao X and Zhang C (2022) Uncertainty Relations of Non-Hermitian Operators: Theory and Experimental Scheme. Front. Phys. 10:862868. doi: 10.3389/fphy.2022.862868
Received: 26 January 2022; Accepted: 16 March 2022;
Published: 19 April 2022.
Edited by:
Ming-Liang Hu, Xi’an University of Posts and Telecommunications, ChinaReviewed by:
Ming Li, China University of Petroleum, ChinaJuan He, Fuyang Normal University, China
Jin-Ming Liu, East China Normal University, China
Ali Asadian, Institute for Advanced Studies in Basic Sciences (IASBS), Iran
Copyright © 2022 Zhao and Zhang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Chengjie Zhang, Y2hlbmdqaWUuemhhbmdAZ21haWwuY29t
 Xinzhi Zhao
Xinzhi Zhao Chengjie Zhang
Chengjie Zhang