Porous Media Microstructure Determines the Diffusion of Active Matter: Experiments and Simulations

Introduction

The transport of living, colloidal-sized species through crowded environments plays a crucial function in many natural and synthetic processes. For example, the transport of bacteria through soil plays a beneficial role in bioremediation [1, 2], and novel drug delivery mechanisms seek to utilize the proliferation of S. typhimurium to access tumor tissues that have been conventionally out of reach [3, 4]. In contrast, the transport of pathogens into wounds sites and mucosa can lead to life-threatening infections without proper treatment [5–7]. The effective transport properties of bacteria in crowded environments depend on the interplay between the swimmer motility and the boundaries that make up the porous material [8]. Many forms of microscopic life enhance their transport via directed self-propulsion, including E. coli bacteria, spermatozoa cells, and C. reinhardtii algae [9–11]. Recent advancements in micro/nanoscale synthesis have also led to the creation of artificial swimmers that are excellent tools in the study of autonomous self-propulsion [12–19]. Understanding the motion of these living and synthetic “active matter” constituents embedded within heterogeneous materials is a challenging problem because of the complex interactions between the swimmer and the material boundaries. For porous materials composed of polymer networks, particle transport may be affected by steric hindrance, nonspecific interactions (hydrophobicity, electrostatics), and specific interactions (ligand-receptor binding) [20, 21]. This behavior is not unique to polymer networks; introducing even a dilute concentration of immobile obstacles with purely excluded-volume interactions provides a substantial slowdown to diffusive flux [22–24].

In addition to the interactions experienced by non-motile Brownian particles, active particles accumulate at physical boundaries due to their persistent self-motion, characterized by a boundary layer near the surface. This accumulation occurs even in the absence of attractive interactions; the active particles propel freely until hitting a surface and continue to propel themselves toward the surface until they reorient and escape into the bulk fluid. This behavior has been observed experimentally and in simulations of rods and spheres, both with and without hydrodynamic interactions [25–40]. A mechanistic understanding of how the local accumulation near physical boundaries affects the macroscopic mobility of active matter through heterogeneous and tortuous materials is lacking. In this work, we study the impact of boundary accumulation on the effective diffusivity of active matter by analyzing the motion of active Brownian particles (ABPs) in a system of rigid 2D obstacles. The presence of boundaries in active systems reduces the effective long-time self diffusivity by an amount that depends on the average swimming speed (U₀) and the average reorientation time (τ_R). This is in sharp contrast to passive Brownian particles, which do not accumulate along boundaries, and whose effective diffusivity depends primarily on the packing fraction of the obstacles [23, 41].

Many studies on active matter transport focus on the effect of alignment along surfaces due to steric or hydrodynamic torques aligning the swimmer parallel or perpendicular to boundaries [27, 36, 38, 40, 42–46]. However, a connection between transport and surface accumulation of active matter [28, 32–34, 37, 47, 48] without any imposed torques has not been fully explored. For active systems, the precise shape and curvature of the boundary can have a strong effect on motility induced accumulation [33, 34, 49]. This increased accumulation corresponds to more time spent “trapped” in the boundary layer, which inhibits the transport of active matter in tight pores. Therefore, we hypothesize that active swimmers experience a strong reduction in the relative diffusivity in porous media due to the synergistic effects of active boundary accumulation and boundary shape.

While many existing theories predict the diffusive transport of passive Brownian particles through porous media [20, 22, 50–54], the unique accumulation of active matter along boundaries—especially at regions of large curvature—leads to unexpected diffusive slowdowns that are not captured in traditional theories. In this work, we combine Janus particle experiments, Brownian dynamics simulations, and theory to demonstrate that the transport of active matter in heterogeneous materials is a strong function of the obstacle shape, curvature, and microstructure. Experimentally, we rely upon optical tracking of active particle trajectories, which has been a powerful tool to study both living and artificial swimmers in porous environments [49, 55–62], and allows for direct comparisons to particle based simulations [63–71]. In addition to advancing our basic understanding of active matter transport, our work provides a mechanism to control the transport of active matter in heterogeneous materials.

Results

To obtain a mechanistic understanding of boundary layer accumulation and slowdown of active matter in heterogeneous materials, we combined Janus particle experiments, Brownian dynamics (BD) simulations, and analytical theory. In our experiments, we immobilized 6.5 μm lipid bilayer-coated silica particles in a random distribution at the bottom of an imaging chamber at ϕ ≈ 12% area fraction. We added a dilute concentration of 4 μm silica Janus particles, coated on one side with a thin layer of platinum and the other side with a lipid bilayer containing fluorescently-labeled lipids (see Materials and Methods). The silica beads sedimented to the bottom of the imaging chamber, so our experiments are conducted in 2D. The lipid bilayers on the obstacles and Janus half-coating contain different fluorescent dyes, which enabled us to track both types of particles simultaneously in different fluorescence channels. Upon adding 2% hydrogen peroxide in Milli-Q water, the Janus particles self-propelled [72–74] with speed U₀ = 0.84 ± 0.01 μm/s and reorientation time τ_R = 14 ± 2 s. The self-propulsive speed and the reorientation time were determined via the mean instantaneous velocity and a fit to the known mean squared displacement (see in Materials and Methods). We conducted time lapse imaging and tracked the positions of the obstacles and the Janus particles using a tracking algorithm [75]. In Figure 1, we show the motion of a single Janus particle moving through a random array of obstacles, punctuated by an obstructed motion of over 1 min in a local grouping of obstacles creating a concave boundary. Eventually, the Janus particle reoriented, propelled away from the concave boundary, and resumed an active random walk (Figure 1H).

FIGURE 1

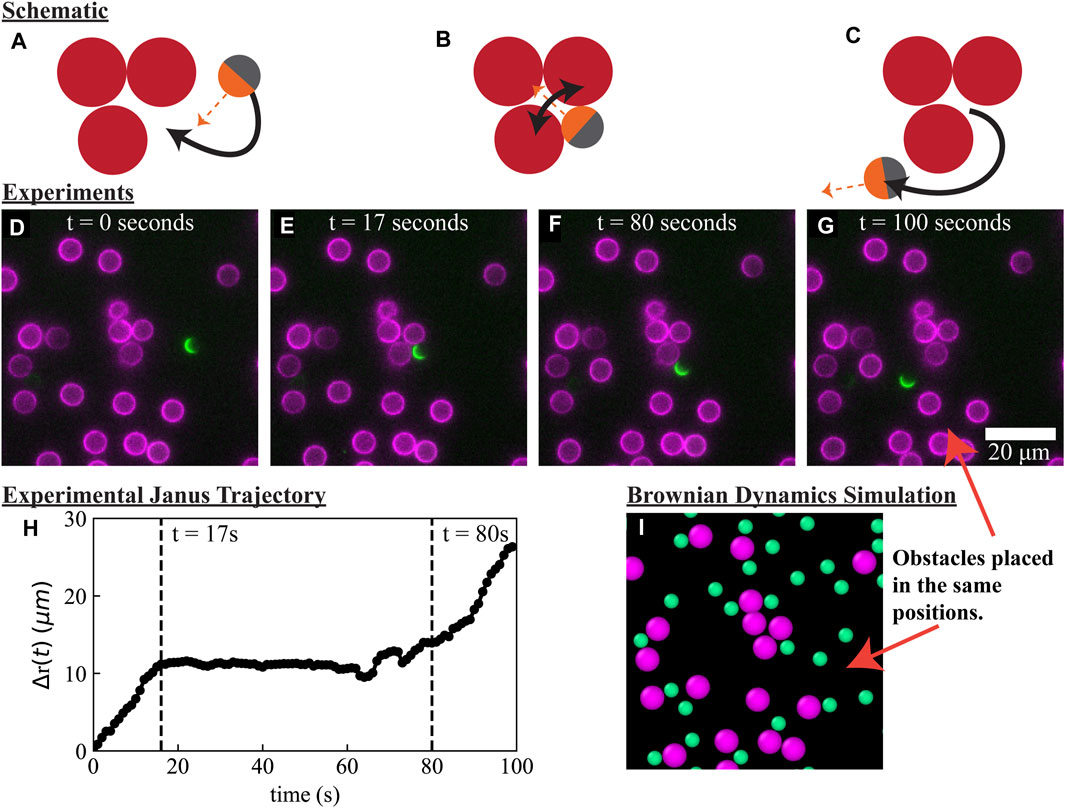
FIGURE 1. Active particles experience a significant slowdown near obstacle boundaries and a reduction in effective diffusivity in a random array of fixed obstacles. (A–C): Schematic demonstrating the obstructed motion of an active particle near a grouping of three obstacles. (D–G): Experimental images of a 4 μm Janus particle (green semicircle) moving through 6.5 μm obstacle particles (magenta). (H) Displacement of the active Janus particle (green semicircle) tracked for 100 s. (I) Brownian Dynamics (BD) simulation snapshot of active Brownian particles moving through a recreated copy of the same porous media as in the experiments. More individual particle trajectories are available in the Supplementary Information (Supplementary Figure S1).

To corroborate our experiments, we developed BD simulations in which the motion of ABPs are evolved following the overdamped Langevin equation (see Materials and Methods). We compare the experimental mean squared displacement (MSD) with simulated active Brownian particle MSD to determine if this simple model quantitatively captures the transport behavior observed in the Janus particle experiments in Figure 2. Comparing the two MSDs also allowed us to determine that the entropic effect of immobile obstacles was the cause of the diffusivity reduction, and not some unaccounted for mechanism (e.g. hydrodynamic forces or interparticle attractions). To simulate a dilute system, the active Brownian particles interact with obstacle particles via a purely repulsive potential, but do not interact with each other (“ideal gas” particles). We chose the active particle swimming speed and reorientation time to match our Janus particles, and we placed obstacles of the same size in the same positions as the experiments. By using the experimental obstacle particle positions as inputs into our simulations, we recapitulated our precise experimental system in the simulations (Figure 1I). Consistent with our experimental observations, we also observed a similar accumulation of particles in local groupings of obstacles that form a concave boundary.

FIGURE 2

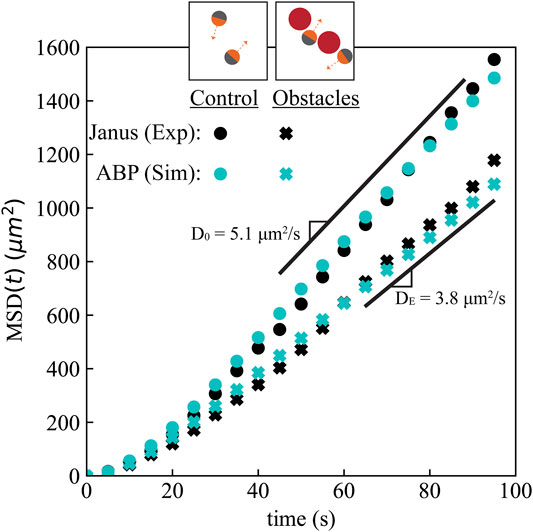
FIGURE 2. The effective diffusivity of active particles decreased by 25% in a random array of fixed obstacles at ϕ ≈12% area fraction. The mean squared displacement (MSD) of 4 μm active Janus colloids in experiments (black symbols) agrees with that in our BD simulation of the equivalent system using the active Brownian particle (ABP) model (cyan symbols), for both the control case without obstacles (circles) and with a random distribution of 6.5 μm obstacles (cross marks). Labelled diffusivities correspond to the fit to the slope at times past 50 s in the experiments. Standard error of the mean for the MSDs is available in the Supplementary Figure S2. Additional MSD simulation data for different ABP activities is available in Supplementary Figure S3.

To quantify the effect of active particle accumulation and slowdown near boundaries, we computed the mean squared displacement (MSD) of the active particles in our experiments and BD simulations, MSD(t) = ⟨|r(t) − r (0)|²⟩, where r(t) is the position of the active particle at time t. We obtained the slope of the MSD at large times to find the long-time self diffusivity of the active particles in the experiments and simulations, $D={\lim }_{t\to \infty }(1/4)\left(\mathrm{d}\mathrm{M}\mathrm{S}\mathrm{D}/\mathrm{d}t\right)$. As shown in Figure 2, we found that the effective diffusivity of active Janus particles decreases by 25% in the presence of fixed obstacles, from D₀ = 5.1 ± 0.2 μm²/s (without obstacles) to D_E = 3.8 ± 0.2 μm²/s (with obstacles). An ABP in a dilute suspension in two dimensions has a self diffusivity of $D_0=D_T+U_0^2{\tau }_R/2$ without any obstacles present, where D_T is the thermal Brownian diffusivity of an isolated particle. Our BD simulations agreed quantitatively with the experimental values when we used identical activity parameters with obstacles placed in the same positions, confirming that our active Brownian particle simulations are a proficient model of the experiments. For passive Brownian particles in a dilute packing of rigid obstacles, the effective diffusivity reduces to D_T (1 − ϕ) [22]. Therefore, our 25% reduction in the effective diffusivity for active particles is about twice as large as the relative reduction experienced by passive Brownian particles at the same obstacle packing fraction, ϕ ≈ 12%.

In our experiments, we noticed that several 6.5 μm obstacle particles formed local groupings with narrow constrictions (Figure 3A), even at semi-dilute packing fractions (ϕ ≈ 12%). Indeed, we quantified the crowding by finding the number of other obstacle neighbors located within a surface-to-surface distance of 4 μm (Figure 3B). We observed that the Janus particles spent significantly more time in the concave region of these emergent shapes as opposed to the convex side (Figure 3C). We therefore hypothesized that the presence of these structures with curved geometries plays an important role in reducing the effective transport properties of active particles beyond the 1 − ϕ correction observed in passive particles. Furthermore, we anticipated that the role of obstacle geometry on the effective diffusivity is much larger for active particles undergoing persistent self-propulsion compared to passive particles translating due to thermal Brownian motion.

FIGURE 3

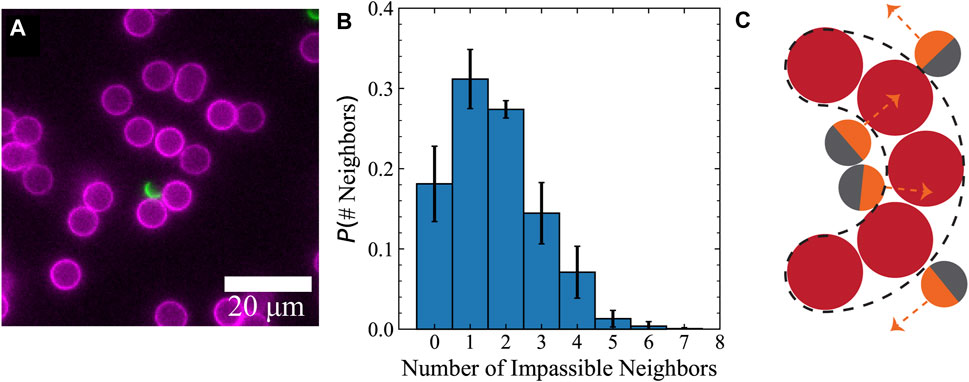
FIGURE 3. Active Janus particles spent a significant amount of time near obstacle clusters that formed curved boundaries with narrow constriction sites. (A) Image of an active Janus particle interacting with a grouping of obstacles that forms a curved boundary with concavity. (B) Histogram quantifying obstacle particle grouping. Number of impassible neighbors is found by counting all the obstacle neighbors within distance 4 μm from a reference obstacle’s surface. Groups of obstacles within this distance are impassible by a Janus swimmer with diameter 4 μm. Error bars are the standard deviation from six independent experiments. (C) Schematic demonstrating the concave shape formed by the packing of obstacles.

To test our hypothesis and to develop a micromechanical understanding of the role of obstacle geometry on active particle diffusion, we analyzed the distribution of active particles near obstacle boundaries, P (x, y, θ, t), which satisfies the Smoluchowski equation

$\frac{\partial P}{\partial t}+\nabla \cdot \left(U_0\mathbf{q}P-D_T\nabla P\right)-D_R\frac{{\partial }^{2}P}{\partial {\theta }^2}=0,(1)$

where U₀ is the self-propulsive speed of the active particles, q = [ cos(θ), sin(θ)] is the unit orientation vector indicating the direction of self-propulsion, and D_T and D_R = 1/τ_R are the translational and rotational diffusivity, respectively. Eq. 1 is subject to the no-flux boundary condition along the obstacle surface, $\widehat{\mathbf{n}}\cdot [U_0\mathbf{q}P-D_T\nabla P]=0$, and periodic boundary conditions across the unit cell. The probability distribution is normalized, ∭P dxdydθ = 1. We computed the density and polar order fields of active particles at steady state (∂P/∂t = 0) by solving Eq. 1 using the finite element method via the software Freefem++ [76].

We obtained steady-state density and polarization fields by taking orientational integrals over the full probability distribution,

$n\left(x,y\right)={\int }_0^{2\pi }P\left(x,y,\theta \right)\mathrm{d}\theta ,(\mathrm{2a})$

$\mathbf{m}\left(x,y\right)={\int }_0^{2\pi }P\left(x,y,\theta \right)\mathbf{q}\left(\theta \right)\mathrm{d}\theta ,(\mathrm{2b})$

We numerically solved the full Smoluchowski equation for a point-sized active particle around fixed obstacles with different shapes. For a circular obstacle, we observed a small accumulation of active particles near the surface, as shown in Figure 4A. In contrast, for a curved obstacle, we observed a significant increase in the number density n (x, y) and polar order vector m (x, y) near the obstacle surface, especially at regions of large concavity (Figures 4D–F). Our results in Figure 4 are presented for a mild activity of U₀τ_R/δ = 1, where $\delta =\sqrt{D_T{\tau }_R}$ is the microscopic length describing how far the active particle thermally diffuses before it reorients. Even for mild activity, we observed a 40% increase in density accumulation along the inner surface compared to only 12% near the circular obstacle. The active Janus particles in our experiments have an activity of U₀τ_R/δ = 100, which would cause an even larger increase in the density and polar order enhancement at concave boundaries. Our Smoluchowski analysis suggests that the obstacle arrangement and shape play a critical role in governing local trapping of active particles in porous media.

FIGURE 4

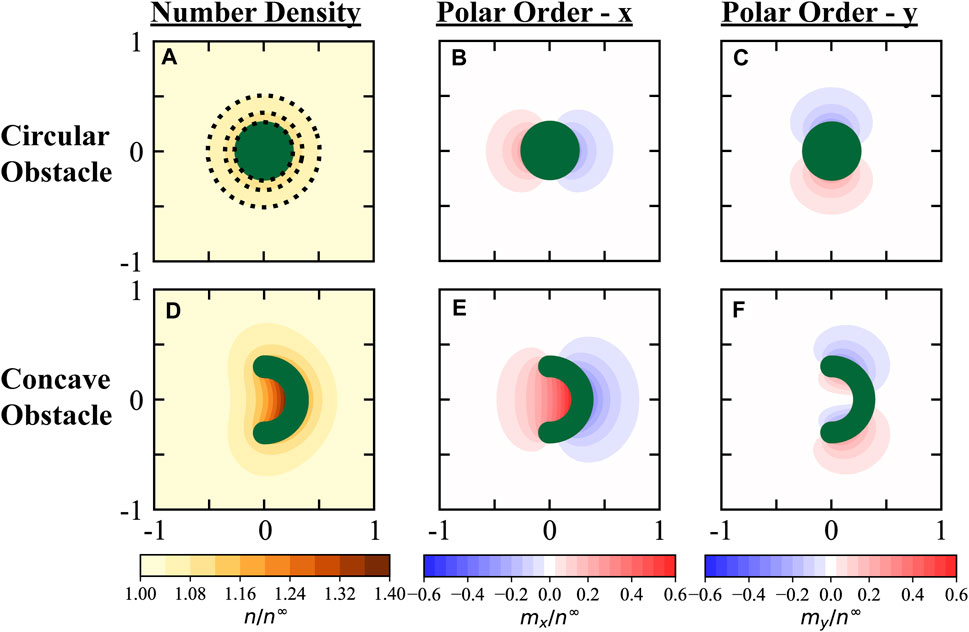
FIGURE 4. Active constituents accumulate along boundaries due to their persistent self-motion, with a significant increase in density and polar order along curved boundaries with large concavity. (A–C): Density and polarization fields around a circular obstacle (radius over run length $R/(U_0{\tau }_R)=\sqrt{7}/4$) with dashed lines to guide the eye around the faint increase in contours. The fields are normalized by n^∞, the bulk concentration of active particles far away from the boundary. (D–F): the concentration and polarization fields around a curved obstacle with large concavity (R_inner/(U₀τ_R)=1/2, R_outer/(U₀τ_R)=1). A convex, circular obstacle experiences a 12% increase in active particle accumulation, while a concave shape in the same active bath experiences a 40% increase in active particle accumulation at the inner side, indicating that the specific arrangement and shape of obstacles play a key role in the effective diffusivity of active particles. We used the same obstacle area fraction of σ $\approx 5.5\%$ and activity U₀τ_R/δ =1 in both cases, where $\delta =\sqrt{D_T{\tau }_R}$ is the microscopic length.

Motivated by our micromechanical understanding of active particles near curved obstacles (Figure 4), we hypothesized that the effective diffusivity of active particles in an array of obstacles should depend on the specific shape of the obstacles. To these ends, we conducted BD simulations of active Brownian particles moving through a square lattice of obstacles, carefully varying the curvature while preserving the packing fraction to keep the excluded volume constant within a unit cell. As a model obstacle shape with smoothly-varying curvature, we utilized the “Cassini Oval” (Figures 5B–D), which is described by the equation

$\left[{\left(x+a\right)}^2+y^2\right]\left[{\left(x-a\right)}^2+y^2\right]=b^4,(\mathrm{3a})$

$A=2b^{2}E\left(\frac{a^4}{b^4}\right),(\mathrm{3b})$

${\kappa }^{*}=\frac{1}{b}\left(\frac{2a^2/b^2-1}{\sqrt{1-a^2/b^2}}\right)(\mathrm{3c})$

where a and b are two shape parameters (a < b), κ* is the maximum curvature in the shape, A is the shape area, and E(x) is the complete elliptic integral of the second kind. The Cassini Oval is a modification of the traditional ellipse with the product of the distance to two foci (located at x = ±a) kept constant at b². The shape extends laterally and shrinks vertically as it is deformed at constant area, which would generate anisotropies and slowdowns in the effective diffusivity for even passive Brownian particles. Since we wish to isolate the effects of curvature, and not the artifacts from lateral elongation of the shape, we performed BD simulations on both passive and active Brownian particles to quantify the effects of curvature and shape elongation. Passive Brownian particles with purely excluded-volume interactions do not accumulate along boundaries, so any change in their diffusivity is due to shape elongation within the unit cell. We have conducted BD simulations at different activities and obstacle packing fractions, and found that the effective diffusivity is well-approximated by the expression D₀ (1 − ϕ) for dilute packing fractions, where D₀ is the bulk diffusivity in 2D in the absence of any obstacles. This is a proficient analytical expression for all activities at dilute obstacle densities (See Supplementary Figures S4, S5). However, at larger packing fractions of obstacles greater than ϕ ≈ 5%, we observe deviations in this expression as a function of varying activity parameters. For example, as (U₀τ_R)κ* > 1, the scaled diffusivity decreases compared to the passive case, due to the reduced swim diffusivity in the boundary layer.

FIGURE 5

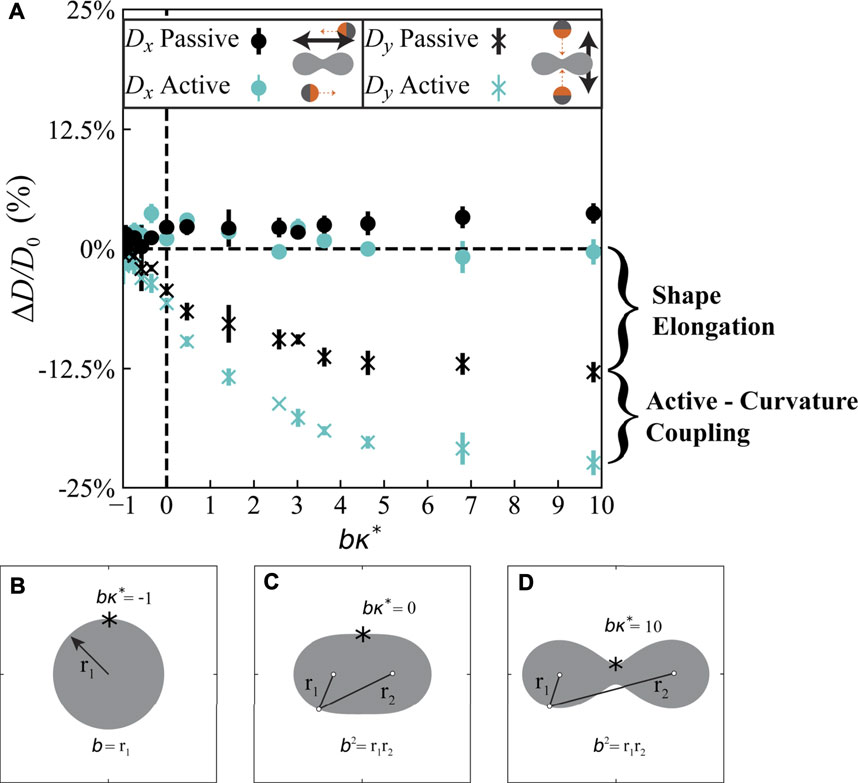
FIGURE 5. Curved obstacles with a large concavity generate a significant slowdown in diffusive transport of active particles compared to purely convex shapes at the same packing fraction. (A) Scaled diffusivity deviation as a function of shape concavity for the Cassini Oval shape described by Eq. 3, where bκ* is the non-dimensional curvature at the top of the inclusion. The diffusivity along the direction facing the concavity, D_y, decreases by 24% for the active particles for highly concave obstacles compared to 12.5% for the passive Brownian particles, indicating that the coupling between the active force and curvature plays a key role. Total packing fraction is fixed at ϕ ≈5.5%, and error bars are the standard deviation of three independent trials. (B–D): Schematics of area preserving Cassini Ovals for three different parameter sets. The two foci are separated a distance of 2a. Beyond a critical distance, $a=b/\sqrt{2}$, the shape becomes concave.

To isolate the diffusivity reduction due to obstacle shape, we computed a scaled diffusivity deviation given by

$\frac{\mathrm{\Delta }D}{D_0}=\frac{D_E-\tilde{D}}{D_0},(4)$

where D_E is the effective diffusivity measured from the MSD, $D_0=D_T+U_0^2{\tau }_R/2$ is the diffusivity without any obstacles, and $\tilde{D}=D_0(1-\varphi )$ is a first correction to the diffusion constant due to excluded volume effects of circles in a square lattice [22]. In Figure 5, we show our BD simulation results for an obstacle packing of ϕ = 5.5%. Using active particles of diameter σ, we set the activity as U₀τ_R/σ = 100, $\delta /\sigma =5\sqrt{2}$, and the shape area as A/σ² = 400π. As the concave curvature of the obstacle increased, we found a large reduction in the effective diffusivity along the direction facing the concavity (D_y) whereas the diffusivity along the other direction (D_x) remained approximately constant. As the local curvature of the shape increased, the conserved area moves off to the sides, slightly thinning its vertical projection and expanding its horizontal projection. The effect of obstacle shape elongation on the effective diffusivity is measured by the deviation in the passive case (black circles and crosses in Figure 5A). In the active case, there is an additional contribution that we designate as the active-curvature coupling.

As shown in our data for D_y in Figure 5A, the active-curvature coupling contribution to the effective diffusivity is equally as large as the diffusivity reduction due to obstacle shape elongation. Due to their persistent self-propulsion, the active particles experience a large accumulation of density and polar order fields near boundaries with large concavity, consistent with our Smoluchowski analysis in Figure 4. The magnitude of this boundary layer accumulation is a strong function of curvature and activity, and we have observed that the effect becomes more important at high activity and semi-dilute obstacle packing (see Supplementary Figures S4, S5). Our results validate our hypothesis that the shape and curvature of the obstacles play a critical role in governing the effective mobility of active particles in porous materials. The physical mechanism behind this phenomenon is that active matter accumulates along boundaries, especially along curved and concave surfaces, where active particles are trapped. Therefore, the specific shape and arrangement of obstacles within a porous material modulate the effective diffusivity of the active particles in a manner that is more significant compared to passive Brownian particles.

Discussion

In this work, we discovered that the obstacle packing fraction alone is insufficient to provide an accurate prediction of effective active particle diffusivity. The specific shape and distribution of physical obstacles plays a critical role in determining active transport. The microscopic details of the external boundary strongly influences the macroscopic observables like the long-time self diffusivity. Both in our experiments and simulations, a random packing of obstacles led to concave structures with narrow constriction sites that gave rise to a significant accumulation of active particles. We showed that the local slowdown of active particles within the boundary layers has a direct effect on their overall mobility across the porous material. We focused on obstacle curvature and microstructure as metrics for predicting the effective diffusivity, which is complementary to other porosity metrics, like chord-length distributions [77] or tortuosity measurements [52].

Our scientific basis for focusing on the obstacle shape and curvature was inspired by the strong connection between active matter accumulation and its force generation along boundaries [32, 74, 78, 79]. For example, Burkholder and Brady derived a macrotransport based model to connect fluctuations in surface accumulation and the enhancement in diffusivity of passive spherical tracers [80]. Furthermore, the surface accumulation is highly dependent on surface curvature [28, 31, 33, 34]; the accumulation on certain parts of an asymmetric shape can lead to a pressure imbalance and net translation of anisotropic colloidal tracers [11, 81]. These studies showed that active matter can impart forces on its environment; however, in our work, we focused on how the micromechanical details of the environment, like curved boundaries, can alter the dynamical properties of the active particles. We validated that a strong coupling between surface curvature and active matter accumulation decreases the diffusivity of active particles by a much larger relative degree than the slowdown expected for equivalent passive Brownian particles.

The surface accumulation of active particles around a single obstacle with small curvature ((U₀τ_R), δ ≪ 1/κ) is shown by Yan and Brady [33]:

$\frac{n_{\text{surf}}}{n^{\infty }}=1+\frac{{\ell }^2}{2{\delta }^2}+\kappa {\ell }^2{\lambda }^{\prime }+\mathcal{O}{\left(\kappa {\ell }^2{\lambda }^{\prime }\right)}^2,(5)$

where n^∞ is the bulk concentration of active particles, κ is the curvature in units of inverse obstacle length, ℓ = U₀τ_R is the run length, and ${\lambda }^{\prime }=\sqrt{\left(1+\frac{1}{2}\right.{(\ell /\delta )}^2}/\delta$ is the inverse screening length of the boundary layer. As the curvature goes from κ = 0 (e.g. a flat wall) to a convex curvature κ < 0 (e.g. the outside of a circle), the surface accumulation decreases proportionally. However, if regions of the shape have a concave curvature κ > 1 (e.g. the inside of a circle), the accumulation increases. To first order in curvature, the accumulation described in Eq. 5 predicts no net force on an asymmetric surface [33], and higher order curvature expansions are needed to get a nonzero force. The need for large curvatures is consistent with our simulations (Figure 5), where we found that the active-curvature coupling effect on the diffusivity is small until the nondimensional curvature is large, κℓ ≫ 1, (see Supplementary Figure S4). For our most curved obstacle in Figure 5D, our analysis from Eq. 5 leads us to define our grouping of κℓ²λ′ ≈ 7 × 10³. The effect of active-curvature coupling is expected to increase dramatically in dense, tortuous media, leading to the mechanism of hopping and trapping transport. Other mechanisms of motility, such as the run-reverse mechanism seen in bacteria and archaea [82, 83], can enable swimmers to avoid the slowdown resulting from boundary accumulation and enhance transport between highly curved pores [64].

We focused on the effects of immobile obstacles with purely excluded volume interactions. However, soft porous materials present a rich opportunity for future study. Boundary fluctuations of soft surfaces are important for particle transport in mucus, hydrogels, and other polymeric networks [20, 84, 85]. Active particles have been shown to induce large deformations on soft membranes [86, 87], changing the curvature and transport drastically. Hydrogel networks and sediments in 3D provide an additional degree of freedom for a swimmer to avoid obstacles. In 2D, close packing of disks precludes transport; however, a close packing of spheres in 3D allows for bicontinous percolation, resulting in a reduced but nonzero diffusivity.

Our work opens up opportunities for future experimental work to control active matter diffusion via the design of obstacle shape and arrangement. Convex, nonspherical inclusions can be used to control transport and create anisotropic spreading of bacteria along a predefined axis. Novel sorting mechanisms have already been developed using asymmetric blockers [37], and the method could be extended to sort mixtures of swimmers with different types of motility [88]. Precise consideration of the activity-curvature coupling on transport serves as a promising route to increase the efficacy of these sorting methods, and may lead to more accurate predictions of bacterial transport coefficients.

Materials and Methods

Experiment Preparation

Lipid-coated silica beads were created by coating silica micro-beads with a supported lipid bilayer (SLB). Small unilamellar vesicles (SUVs) were prepared by rehydrating a lipid sheet composed of a mixture of phospholipids with pure deionized water to a concentration of 0.2 mg/ml. For the Janus particles, we used 1,2-dioleoyl-sn-glycero-3-phos-phocholine (DOPC) with 5% of 1,2-dioleoyl-sn-glycero-3-phospho-l-serine (DOPS) and 0.3% of Atto 488-1,2-dioleoyl-sn-glycero-3-phosphoethanolamine (DOPE-Atto 488) fluorescent dye. For the obstacle particles, we used DOPC with 5% of 1,2-dioleoyl-3-trimethylammonium-propane (DOTAP) and 0.3% of Atto 647-DOPE (DOPE-Atto 647). After rehydrating the lipids for 30 min, the solution was vigorously vortexed, sonicated at low-power (20% power) using a tip sonicator (Branson SFX250 Sonifier). The resulting SUV solution was buffered with a MOPS buffer (50 mM MOPS, 100 mM sodium chloride, pH 7.5). DOPC (catalog number: 850375), DOPS (catalog number: 840035), and DOTAP (catalog number: 890890) were purchased from Avanti polar lipids. DOPE-Atto 488 and DOPE-Atto 647 were purchased from ATTO-TEC GmbH. Silica microspheres (4.0μm; catalog code: SS05002 and 6.5μm; catalog code: SS06N) were purchased from Bangs Laboratories.

Silica microspheres with diameters 4 and 6.5 μm were cleaned using a 3:2 mixture of sulfuric acid:hydrogen peroxide (Piranha) for 30 min in a bath sonicator, and were spun down at 1000g and washed 3 times before being resuspended in pure water. We fabricated Janus particles from the cleaned 4 μm particles by depositing a monolayer on a glass slide, and coating half of the particle surface with a 2 nm-thick layer of chromium and 8 nm-thick layer of platinum using an E-beam evaporator at a deposition rate of 0.1 $\mathring{A}/s$. To form SLBs on the Janus particles and the beads, 50 μL of SUV solution was mixed gently with 10 μL of clean bead suspension. The bead/SUV mixture was incubated for 15 min at room temperature while allowing the beads to sediment to the bottom of the tube. Beads were washed 5 times with pure deionized water by gently adding/removing the liquid without resuspending the beads into solution. We verified the fluidity of the SLB by imaging beads on a glass coverslip at high laser intensity, where the diffusion of labeled lipids was visible after photo-bleaching a small region.

For the 4 μm Janus particles, the SLBs coated only half of the particle surface exposed to clean silica. The side with the platinum did not get coated with an SLB. When these SLB half-coated Janus particles were deposited in a 2% solution of hydrogen peroxide, the particles self-propelled pointing away from their platinum half-coating via self-diffusiophoresis. Since silica is more dense than water, the Janus particles moved in 2D along the bottom of the imaging chamber. Within the time frame of our experimental measurements, we did not observe any significant degradation of the SLB from hydrogen peroxide.

For the 6.5 μm obstacle particles, we obtained a uniform SLB across the entire surface of the silica bead. We added a positively-charged DOTAP lipid to the SLB to facilitate a strong electrostatic attraction between the obstacle particles and the borosilicate coverslip substrate. We found that most obstacle particles remained fixed along the bottom substrate with no observable Brownian motion. We did not observe any adhesion or fusion of the SLBs between the obstacles and the Janus particles.

The SLB-coated obstacle particles were added into the imaging chamber at a desired density, followed by the SLB half-coated Janus particles. We added 2% hydrogen peroxide into the chamber and conducted time lapse imaging. All imaging was carried out on an inverted Nikon Ti2-Eclipse microscope (Nikon Instruments) using an oil-immersion objective (Apo ×60, numerical aperture (NA) 1.4, oil). Lumencor SpectraX Multi-Line LED Light Source was used for excitation (Lumencor, Inc.). Fluorescent light was spectrally filtered with emission filters (515/30 and 680/42, Semrock, IDEX Health and Science) and imaged on a Photometrics Prime 95 CMOS Camera (Teledyne Photometrics). Experimental results presented in this work are an average over six independent replicates of systems with obstacles and three independent replicates of systems without obstacles as a control.

Particle Tracking in Experiments

To determine the effect of the porous media on transport, we measured the Janus particle trajectories with and without the presence of the fixed obstacles. We used a modified MATLAB script based on IDL code by Crocker and Grier [75] to track the individual Janus particles by identifying each particle center and tracking its trajectory over time using an image stack with one frame taken every second. We removed any macroscopic drifts by enforcing that the mean displacement over all particles was zero at any time. We filtered out any Janus particles that were immobile due to defects of the particle (defined as moving less than 30 μm over 100 s or if it moved in only one direction via macroscopic drifts). In all experimental results, we tracked the particles for times t > 7τ_R. We obtained the Janus particle mean swim speed, U₀, and reorientation time, τ_R, using the control experiments in the absence of obstacles. We obtained the mean swim speed by averaging all tracked particles’ velocity over time,

$U_0=⟨\frac{\mathrm{\Delta }r}{\mathrm{\Delta }t}⟩.(6)$

The mean swim speed was determined to be U₀ = 0.84 ± 0.01 μm/s with the reported error as the standard error of the mean. We obtained the reorientation time by measuring the bulk diffusivity for the control experiment in the absence of obstacles,

$D_0=D_T+\frac{U_0^2{\tau }_R}{2},(7)$

where D_T ≈ 0.1 μm²/s is the thermal Brownian diffusivity for 4 μm diameter spheres using the Stokes-Einstein-Sutherland relation [89–91]. We note that the thermal Brownian diffusivity is negligible compared to the self-propulsive component. Using the experimental measurement of the bulk diffusivity, D₀ = 5.1 μm²/s, we obtained the reorientation time and standard deviation τ_R = 14 ± 2 s using Eq. 7. As a separate measurement, we computed τ_R using the Janus particle orientation autocorrelation in 2D,

$⟨\mathbf{q}\left(t\right)\cdot \mathbf{q}\left(0\right)⟩=e^{-t/{\tau }_R}.(8)$

We obtained the Janus particle orientations directly from particle tracking, and we obtained a reorientation time τ_R ≈ 10 s using Eq. 8. This measurement is similar to the value we obtained using Eq. 7, especially considering the difficulty in finding the orientation using the velocity vector. We concluded that the particles are behaving as active Brownian particles in 2D. In principle, the Janus particles are located along a 2D plane but can reorient in 3D. However, the platinum coating makes the catalytic half-surface more heavy and causes the Janus particles to tilt downwards, making the particle move effectively in 2D. We note that the direction of self-propulsion points away from the platinum half-surface, so the configuration of the platinum half-surface pointing vertically down appears to be an unstable state.

Brownian Dynamics Simulations

The parameters (U₀, τ_R) obtained from the control experiment are then used as inputs into our Brownian dynamics simulations in Figure 2. In Figure 5, the parameters were chosen as described in the caption. We implemented our simulations using HOOMD-blue, a molecular dynamics (MD) simulation package in Python [92]. We focused on the dilute limit of a single active Brownian particle (ABP) in 2D interacting with fixed hard-sphere obstacles. Hydrodynamic interactions are ignored in these simulations. The ABP model describes a swimmer with constant propulsion force but white noise torques [11, 93–96]. Hard-sphere like interactions between the obstacles and the ABPs were implemented using the Weeks-Chandler-Andersen (WCA) [97] potential (Eq. 10). For the nonspherical Cassini Oval, the structure was formed using overlapping rigid surface particles offset so that the surfaces of the particles formed the boundaries of the Cassini Oval.

The ABPs were initialized and integrated according to the overdamped Langevin equations of motion:

$\frac{d{\mathbf{x}}_i}{dt}=\sqrt{2D_T}{\mathit{\eta }}_i\left(t\right)+\frac{{\mathbf{F}}_{wca}\left(x_i,x_j\right)}{\zeta }+U_0\mathbf{q}(\mathrm{9a})$

$\frac{d{\theta }_i}{dt}=\sqrt{2D_R}{\xi }_i\left(t\right)(\mathrm{9b})$

where F_wca is the force on the particle from all potentials and constraints, ζ is the drag coefficient, q = [ cos θ, sin θ] is the unit vector describing particle orientation in 2D, D_R = 1/τ_R is the rotational diffusion coefficient, and (η_i, ξ_i) are random variables obeying the zero mean and variance consistent with the fluctuation-dissipation theorem. We used a timestep of Δt = 0.001 s, and set the thermal diffusivity to match our experiments at D_T = 0.1 μm²/s. The drag coefficient and the energy scale of the potential were chosen such that force induced velocity at contact is $\frac{24\epsilon }{\zeta {\sigma }_{avg}}=0.6\mu m/s$, which is similar in magnitude as the self-propelled velocity U₀. The WCA force is given by

${\mathbf{F}}_{wca}=-\nabla V_{wca}(\mathrm{10a})$

$V_{wca}\left(r_{ij}\right)=4\epsilon \left[{\left(\frac{\sigma }{r_{ij}}\right)}^{12}-{\left(\frac{\sigma }{r_{ij}}\right)}^6\right]+\epsilon ,r\le 2^{1/6}\sigma .(\mathrm{10b})$

The particle diameters σ_ABP and σ_obs were preset to 4 and 6.5 μm for Figure 2, and for Figure 5 they were chosen to be small compared to the radius of the disk shown in Figure 5B, σ/R = 1/20. We used periodic boundary conditions to simulate a continuous domain. Simulations are visualized using OVITO [98].

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

KM and ST conceived of the study; KM and ST designed research; KM performed finite element calculations; KM and YX performed simulations and analyzed data; ST performed experiments; ST supervised the study; and KM, YX, and ST wrote the paper.

Funding

This material is based upon work supported by the Air Force Office of Scientific Research under award number FA9550-21-1-0287. KM is supported by the National Science Foundation Graduate Research Fellowship under Grant No. 1650114. Use was made of computational facilities purchased with funds from the National Science Foundation (OAC-1925717) and administered by the Center for Scientific Computing (CSC). The CSC is supported by the California NanoSystems Institute and the Materials Research Science and Engineering Center (MRSEC; NSF DMR 1720256) at UC Santa Barbara.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to thank Parth Shah for help in Janus particle synthesis, Dr. Joseph Barakat for a careful reading of this manuscript, and Prof. Ahmad K. Omar for enlightening conversations and insights that helped to conceive of this project.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.869175/full#supplementary-material

References

1. Gannon JT, Mingelgrin U, Alexander M, Wagenet RJ. Bacterial Transport through Homogeneous Soil. Soil Biol Biochem (1991) 23:1155–60. doi:10.1016/0038-0717(91)90028-I

CrossRef Full Text | Google Scholar

2. Adadevoh JST, Triolo S, Ramsburg CA, Ford RM. Chemotaxis Increases the Residence Time of Bacteria in Granular Media Containing Distributed Contaminant Sources. Environ Sci Technol (2016) 50:181–7. doi:10.1021/acs.est.5b03956

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Toley BJ, Forbes NS. Motility Is Critical for Effective Distribution and Accumulation of Bacteria in Tumor Tissue. Integr Biol (2012) 4:165–76. doi:10.1039/c2ib00091a

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Kasinskas RW, Forbes NS. Salmonella typhimurium Specifically Chemotax and Proliferate in Heterogeneous Tumor Tissue In Vitro. Biotechnol Bioeng (2006) 94:710–21. doi:10.1002/bit.20883

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Ribet D, Cossart P. How Bacterial Pathogens Colonize Their Hosts and Invade Deeper Tissues. Microbes Infect (2015) 17:173–83. doi:10.1016/j.micinf.2015.01.004

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Gu SX, Lentz SR. Fibrin Films: Overlooked Hemostatic Barriers against Microbial Infiltration. J Clin Invest (2018) 128:3243–5. doi:10.1172/JCI121858

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Kao CY, Lin WH, Tseng CC, Wu AB, Wang MC, Wu JJ. The Complex Interplay Among Bacterial Motility and Virulence Factors in Different Escherichia coli Infections. Eur J Clin Microbiol Infect Dis (2014) 33:2157–62. doi:10.1007/s10096-014-2171-2

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Martínez-Calvo A, Trenado-Yuste C, Datta SS. Active Transport in Complex Environments (Preprint). arXiv:2108.07011v2 (2021).

Google Scholar

9. Chaban B, Hughes HV, Beeby M. The Flagellum in Bacterial Pathogens: For Motility and a Whole Lot More. Semin Cel Developmental BiologyBiomineralisation Motorisation Pathog (2015) 46:91–103. doi:10.1016/j.semcdb.2015.10.032

CrossRef Full Text | Google Scholar

10. Woolley D. Motility of Spermatozoa at Surfaces. Reproduction (2003) 126:259–70. doi:10.1530/rep.0.1260259

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Bechinger C, Di Leonardo R, Löwen H, Reichhardt C, Volpe G, Volpe G. Active Particles in Complex and Crowded Environments. Rev Mod Phys (2016) 88:045006. doi:10.1103/RevModPhys.88.045006

CrossRef Full Text | Google Scholar

12. Golestanian R, Liverpool TB, Ajdari A. Propulsion of a Molecular Machine by Asymmetric Distribution of Reaction Products. Phys Rev Lett (2005) 94:220801. doi:10.1103/PhysRevLett.94.220801

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Howse JR, Jones RAL, Ryan AJ, Gough T, Vafabakhsh R, Golestanian R. Self-Motile Colloidal Particles: From Directed Propulsion to Random Walk. Phys Rev Lett (2007) 99:048102. doi:10.1103/PhysRevLett.99.048102

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Sanchez S, Ananth AN, Fomin VM, Viehrig M, Schmidt OG. Superfast Motion of Catalytic Microjet Engines at Physiological Temperature. J Am Chem Soc (2011) 133:14860–3. doi:10.1021/ja205012j

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Soto R, Golestanian R. Self-Assembly of Catalytically Active Colloidal Molecules: Tailoring Activity through Surface Chemistry. Phys Rev Lett (2014) 112:068301. doi:10.1103/PhysRevLett.112.068301

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Ma X, Jannasch A, Albrecht U-R, Hahn K, Miguel-López A, Schäffer E, et al. Enzyme-Powered Hollow Mesoporous Janus Nanomotors. Nano Lett (2015) 15:7043–50. doi:10.1021/acs.nanolett.5b03100

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Ma X, Hahn K, Sanchez S. Catalytic Mesoporous Janus Nanomotors for Active Cargo Delivery. J Am Chem Soc (2015) 137:4976–9. doi:10.1021/jacs.5b02700

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Dreyfus R, Baudry J, Roper ML, Fermigier M, Stone HA, Bibette J. Microscopic Artificial Swimmers. Nature (2005) 437:862–5. doi:10.1038/nature04090

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Bricard A, Caussin JB, Das D, Savoie C, Chikkadi V, Shitara K, et al. Emergent Vortices in Populations of Colloidal Rollers. Nat Commun (2015) 6:7470. doi:10.1038/ncomms8470

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Cai LH, Panyukov S, Rubinstein M. Hopping Diffusion of Nanoparticles in Polymer Matrices. Macromolecules (2015) 48:847–62. doi:10.1021/ma501608x

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Witten J, Ribbeck K. The Particle in the Spider’s Web: Transport through Biological Hydrogels. Nanoscale (2017) 9:8080–95. doi:10.1039/C6NR09736G

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Mangeat M, Guérin T, Dean DS. Effective Diffusivity of Brownian Particles in a Two Dimensional Square Lattice of Hard Disks. J Chem Phys (2020) 152:234109. doi:10.1063/5.0009095

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Saxton M. Anomalous Diffusion Due to Obstacles: a Monte Carlo Study. Biophysical J (1994) 66:394–401. doi:10.1016/S0006-3495(94)80789-1

CrossRef Full Text | Google Scholar

24. Alonso-Matilla R, Chakrabarti B, Saintillan D. Transport and Dispersion of Active Particles in Periodic Porous media. Phys Rev Fluids (2019) 4:043101. doi:10.1103/PhysRevFluids.4.043101

CrossRef Full Text | Google Scholar

25. Volpe G, Gigan S, Volpe G. Simulation of the Active Brownian Motion of a Microswimmer. Am J Phys (2014) 82:659–64. doi:10.1119/1.4870398

CrossRef Full Text | Google Scholar

26. Wysocki A, Elgeti J, Gompper G. Giant Adsorption of Microswimmers: Duality of Shape Asymmetry and wall Curvature. Phys Rev E (2015) 91:050302. doi:10.1103/PhysRevE.91.050302

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Elgeti J, Gompper G. Self-propelled Rods Near Surfaces. EPL (Europhysics Letters) (2009) 85:38002. doi:10.1209/0295-5075/85/38002

CrossRef Full Text | Google Scholar

28. Elgeti J, Gompper G. Wall Accumulation of Self-Propelled Spheres. EPL (Europhysics Letters) (2013) 101:48003. doi:10.1209/0295-5075/101/48003

CrossRef Full Text | Google Scholar

29. Elgeti J, Winkler RG, Gompper G. Physics of Microswimmers—Single Particle Motion and Collective Behavior: a Review. Rep Prog Phys (2015) 78:056601. doi:10.1088/0034-4885/78/5/056601

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Wensink HH, Löwen H. Aggregation of Self-Propelled Colloidal Rods Near Confining walls. Phys Rev E (2008) 78:031409. doi:10.1103/PhysRevE.78.031409

CrossRef Full Text | Google Scholar

31. Wang M. Effect of Boundaries on Noninteracting Weakly Active Particles in Different Geometries. Phys Rev E (2021) 103:042609. doi:10.1103/PhysRevE.103.042609

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Yan W, Brady JF. The Force on a Boundary in Active Matter. J Fluid Mech (2015) 785:R1. doi:10.1017/jfm.2015.621

CrossRef Full Text | Google Scholar

33. Yan W, Brady JF. The Curved Kinetic Boundary Layer of Active Matter. Soft Matter (2018) 14:279–90. doi:10.1039/c7sm01643c

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Smallenburg F, Löwen H. Swim Pressure on walls with Curves and Corners. Phys Rev E (2015) 92:032304. doi:10.1103/PhysRevE.92.032304

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Takatori SC, Yan W, Brady JF. Swim Pressure: Stress Generation in Active Matter. Phys Rev Lett (2014) 113:028103. doi:10.1103/PhysRevLett.113.028103

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Berke AP, Turner L, Berg HC, Lauga E. Hydrodynamic Attraction of Swimming Microorganisms by Surfaces. Phys Rev Lett (2008) 101:038102. doi:10.1103/PhysRevLett.101.038102

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Martinez R, Alarcon F, Aragones JL, Valeriani C. Trapping Flocking Particles with Asymmetric Obstacles. Soft Matter (2020) 16:4739–45. doi:10.1039/C9SM02427A

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Giacché D, Ishikawa T, Yamaguchi T. Hydrodynamic Entrapment of Bacteria Swimming Near a Solid Surface. Phys Rev E (2010) 82:056309. doi:10.1103/PhysRevE.82.056309

CrossRef Full Text | Google Scholar

39. Galajda P, Keymer J, Chaikin P, Austin R. A Wall of Funnels Concentrates Swimming Bacteria. J Bacteriol (2007) 189:8704–7. doi:10.1128/JB.01033-07

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Molaei M, Barry M, Stocker R, Sheng J. Failed Escape: Solid Surfaces Prevent Tumbling of escherichia Coli. Phys Rev Lett (2014) 113:068103. doi:10.1103/PhysRevLett.113.068103

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Kalnin J, Kotomin E, Maier J. Calculations of the Effective Diffusion Coefficient for Inhomogeneous media. J Phys Chem Sol (2002) 63:449–56. doi:10.1016/S0022-3697(01)00159-7

CrossRef Full Text | Google Scholar

42. Li G, Tang JX. Accumulation of Microswimmers Near a Surface Mediated by Collision and Rotational Brownian Motion. Phys Rev Lett (2009) 103:078101. doi:10.1103/PhysRevLett.103.078101

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Sipos O, Nagy K, Di Leonardo R, Galajda P. Hydrodynamic Trapping of Swimming Bacteria by Convex walls. Phys Rev Lett (2015) 114:258104. doi:10.1103/PhysRevLett.114.258104

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Das S, Garg A, Campbell AI, Howse J, Sen A, Velegol D, et al. Boundaries Can Steer Active Janus Spheres. Nat Commun (2015) 6:8999. doi:10.1038/ncomms9999

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Takagi D, Palacci J, Braunschweig AB, Shelley MJ, Zhang J. Hydrodynamic Capture of Microswimmers into Sphere-Bound Orbits. Soft Matter (2014) 10:1784–9. doi:10.1039/C3SM52815D

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Morin A, Lopes Cardozo D, Chikkadi V, Bartolo D. Diffusion, Subdiffusion, and Localization of Active Colloids in Random post Lattices. Phys Rev E (2017) 96:042611. doi:10.1103/PhysRevE.96.042611

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Das S, Gompper G, Winkler RG. Confined Active Brownian Particles: Theoretical Description of Propulsion-Induced Accumulation. New J Phys (2018) 20:015001. doi:10.1088/1367-2630/aa9d4b

CrossRef Full Text | Google Scholar

48. Kjeldbjerg CM, Brady JF. Theory for the Casimir Effect and the Partitioning of Active Matter. Soft Matter (2021) 17:523–30. doi:10.1039/D0SM01797C

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Volpe G, Buttinoni I, Vogt D, Kümmerer HJ, Bechinger C. Microswimmers in Patterned Environments. Soft Matter (2011) 7:8810–5. doi:10.1039/C1SM05960B

CrossRef Full Text | Google Scholar

50. Reguera D, Rubí JM. Kinetic Equations for Diffusion in the Presence of Entropic Barriers. Phys Rev E (2001) 64:061106. doi:10.1103/PhysRevE.64.061106

CrossRef Full Text | Google Scholar

51. Brenner H, Edwards DA. Macrotransport Processes. Elsevier (1993). doi:10.1016/C2009-0-25915-0

CrossRef Full Text | Google Scholar

52. Shen L, Chen Z. Critical Review of the Impact of Tortuosity on Diffusion. Chem Eng Sci (2007) 62:3748–55. doi:10.1016/j.ces.2007.03.041

CrossRef Full Text | Google Scholar

53. Burada PS, Hänggi P, Marchesoni F, Schmid G, Talkner P. Diffusion in Confined Geometries. ChemPhysChem (2009) 10:45–54. doi:10.1002/cphc.200800526

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Ning L, Liu P, Ye F, Yang M, Chen K. Diffusion of Colloidal Particles in Model Porous media. Phys Rev E (2021) 103:022608. doi:10.1103/PhysRevE.103.022608

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Perez LJ, Bhattacharjee T, Datta SS, Parashar R, Sund NL. Impact of Confined Geometries on Hopping and Trapping of Motile Bacteria in Porous media. Phys Rev E (2021) 103:012611. doi:10.1103/PhysRevE.103.012611

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Bhattacharjee T, Datta SS. Bacterial Hopping and Trapping in Porous media. Nat Commun (2019) 10:2075. doi:10.1038/s41467-019-10115-1

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Figueroa-Morales N, Dominguez-Rubio L, Ott TL, Aranson IS. Mechanical Shear Controls Bacterial Penetration in Mucus. Scientific Rep (2019) 9:9713. doi:10.1038/s41598-019-46085-z

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Truong VK, Mainwaring DE, Murugaraj P, Nguyen DHK, Ivanova EP. Impact of Confining 3-D Polymer Networks on Dynamics of Bacterial Ingress and Self-Organisation. J Mater Chem B (2015) 3:8704–10. doi:10.1039/c5tb01880c

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Bansil R, Celli JP, Hardcastle JM, Turner BS. The Influence of Mucus Microstructure and Rheology in Helicobacter pylori Infection. Front Immunol (2013) 4. doi:10.3389/fimmu.2013.00310

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Wu H, Greydanus B, Schwartz DK. Mechanisms of Transport Enhancement for Self-Propelled Nanoswimmers in a Porous Matrix. Proc Natl Acad Sci (2021) 118. doi:10.1073/pnas.2101807118

CrossRef Full Text | Google Scholar

61. Licata NA, Mohari B, Fuqua C, Setayeshgar S. Diffusion of Bacterial Cells in Porous Media. Biophysical J (2016) 110:247–57. doi:10.1016/j.bpj.2015.09.035

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Brun-Cosme-Bruny M, Bertin E, Coasne B, Peyla P, Rafaï S. Effective Diffusivity of Microswimmers in a Crowded Environment. J Chem Phys (2019) 150:104901. doi:10.1063/1.5081507

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Sandoval M, Dagdug L. Effective Diffusion of Confined Active Brownian Swimmers. Phys Rev E - Stat Nonlinear, Soft Matter Phys (2014) 90:062711. doi:10.1103/PhysRevE.90.062711

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Kurzthaler C, Mandal S, Bhattacharjee T, Löwen H, Datta SS, Stone HA. A Geometric Criterion for the Optimal Spreading of Active Polymers in Porous media. Nat Commun (2021) 12:7088. doi:10.1038/s41467-021-26942-0

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Chepizhko O, Peruani F. Diffusion, Subdiffusion, and Trapping of Active Particles in Heterogeneous Media. Phys Rev Lett (2013) 111:160604. doi:10.1103/PhysRevLett.111.160604

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Reichhardt C, Olson Reichhardt CJ. Active Matter Transport and Jamming on Disordered Landscapes. Phys Rev E (2014) 90:012701. doi:10.1103/PhysRevE.90.012701

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Reichhardt CJO, Reichhardt C. Avalanche Dynamics for Active Matter in Heterogeneous media. New J Phys (2018) 20:025002. doi:10.1088/1367-2630/aaa392

CrossRef Full Text | Google Scholar

68. Jakuszeit T, Croze OA, Bell S. Diffusion of Active Particles in a Complex Environment: Role of Surface Scattering. Phys Rev E (2019) 99:012610. doi:10.1103/PhysRevE.99.012610

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Chamolly A, Ishikawa T, Lauga E. Active Particles in Periodic Lattices. New J Phys (2017) 19:115001. doi:10.1088/1367-2630/aa8d5e

CrossRef Full Text | Google Scholar

70. Volpe G, Volpe G. The Topography of the Environment Alters the Optimal Search Strategy for Active Particles. Proc Natl Acad Sci (2017) 114:11350–5. doi:10.1073/pnas.1711371114

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Yuan C, Chen A, Zhang B, Zhao N. Activity–crowding Coupling Effect on the Diffusion Dynamics of a Self-Propelled Particle in Polymer Solutions. Phys Chem Chem Phys (2019) 21:24112–25. doi:10.1039/C9CP04498A

PubMed Abstract | CrossRef Full Text | Google Scholar

72. Paxton WF, Kistler KC, Olmeda CC, Sen A, St Angelo SK, Cao Y, et al. Catalytic Nanomotors: Autonomous Movement of Striped Nanorods. J Am Chem Soc (2004) 126:13424–31. doi:10.1021/ja047697z

PubMed Abstract | CrossRef Full Text | Google Scholar

73. Howse JR, Jones RAL, Ryan AJ, Gough T, Vafabakhsh R, Golestanian R. Self-motile Colloidal Particles: From Directed Propulsion to Random Walk. Phys Rev Lett (2007) 99:048102. doi:10.1103/PhysRevLett.99.048102

PubMed Abstract | CrossRef Full Text | Google Scholar

74. Takatori SC, De Dier R, Vermant J, Brady JF. Acoustic Trapping of Active Matter. Nat Commun (2016) 7:1–7. doi:10.1038/ncomms10694

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Crocker JC, Grier DG. Methods of Digital Video Microscopy for Colloidal Studies. J Colloid Interf Sci (1996) 179:298–310. doi:10.1006/jcis.1996.0217

CrossRef Full Text | Google Scholar

76. Hecht F. New Development in Freefem++. J Numer Mathematics (2012) 20. doi:10.1515/jnum-2012-0013

CrossRef Full Text | Google Scholar

77. Torquato S, Lu B. Chord-length Distribution Function for Two-phase Random media. Phys Rev E (1993) 47:2950–3. doi:10.1103/PhysRevE.47.2950

PubMed Abstract | CrossRef Full Text | Google Scholar

78. Takatori SC, Brady JF. Swim Stress, Motion, and Deformation of Active Matter: Effect of an External Field. Soft Matter (2014) 10:9433–45. doi:10.1039/C4SM01409J

PubMed Abstract | CrossRef Full Text | Google Scholar

79. Omar AK, Wang ZG, Brady JF. Microscopic Origins of the Swim Pressure and the Anomalous Surface Tension of Active Matter. Phys Rev E (2020) 101:012604. doi:10.1103/PhysRevE.101.012604

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Burkholder EW, Brady JF. Tracer Diffusion in Active Suspensions. Phys Rev E (2017) 95:052605. doi:10.1103/PhysRevE.95.052605

PubMed Abstract | CrossRef Full Text | Google Scholar

81. Kaiser A, Peshkov A, Sokolov A, ten Hagen B, Löwen H, Aranson IS. Transport Powered by Bacterial Turbulence. Phys Rev Lett (2014) 112:158101. doi:10.1103/PhysRevLett.112.158101

PubMed Abstract | CrossRef Full Text | Google Scholar

82. Son K, Guasto JS, Stocker R. Bacteria Can Exploit a Flagellar Buckling Instability to Change Direction. Nat Phys (2013) 9:494–8. doi:10.1038/nphys2676

CrossRef Full Text | Google Scholar

83. Thornton KL, Butler JK, Davis SJ, Baxter BK, Wilson LG. Haloarchaea Swim Slowly for Optimal Chemotactic Efficiency in Low Nutrient Environments. Nat Commun (2020) 11:4453. doi:10.1038/s41467-020-18253-7

PubMed Abstract | CrossRef Full Text | Google Scholar

84. Bodrenko IV, Salis S, Acosta-Gutierrez S, Ceccarelli M. Diffusion of Large Particles through Small Pores: From Entropic to Enthalpic Transport. J Chem Phys (2019) 150:211102. doi:10.1063/1.5098868

PubMed Abstract | CrossRef Full Text | Google Scholar

85. Ledesma-Aguilar R, Yeomans JM. Enhanced Motility of a Microswimmer in Rigid and Elastic Confinement. Phys Rev Lett (2013) 111:138101. doi:10.1103/PhysRevLett.111.138101

PubMed Abstract | CrossRef Full Text | Google Scholar

86. Takatori SC, Sahu A. Active Contact Forces Drive Nonequilibrium Fluctuations in Membrane Vesicles. Phys Rev Lett (2020) 124:158102. doi:10.1103/PhysRevLett.124.158102

PubMed Abstract | CrossRef Full Text | Google Scholar

87. Vutukuri HR, Hoore M, Abaurrea-Velasco C, van Buren L, Dutto A, Auth T, et al. Active Particles Induce Large Shape Deformations in Giant Lipid Vesicles. Nature (2020) 586:52–6. doi:10.1038/s41586-020-2730-x

PubMed Abstract | CrossRef Full Text | Google Scholar

88. Khatami M, Wolff K, Pohl O, Ejtehadi MR, Stark H. Active Brownian Particles and Run-And-Tumble Particles Separate inside a Maze. Scientific Rep (2016) 6:37670. doi:10.1038/srep37670

PubMed Abstract | CrossRef Full Text | Google Scholar

89. Sutherland W. Lxxv. A Dynamical Theory of Diffusion for Non-electrolytes and the Molecular Mass of Albumin. Lond Edinb Dublin Philosophical Mag J Sci (1905) 9:781–5. doi:10.1080/14786440509463331

CrossRef Full Text | Google Scholar

90. von Smoluchowski M. Zur kinetischen theorie der brownschen molekularbewegung und der suspensionen. Annalen der Physik (1906) 326:756–80. doi:10.1002/andp.19063261405

CrossRef Full Text | Google Scholar

91. Einstein A. Eine neue bestimmung der moleküldimensionen. Annalen der Physik (1906) 324:289–306. doi:10.1002/andp.19063240204

CrossRef Full Text | Google Scholar

92. Anderson JA, Glaser J, Glotzer SC. HOOMD-Blue: A Python Package for High-Performance Molecular Dynamics and Hard Particle Monte Carlo Simulations. Comput Mater Sci (2020) 173:109363. doi:10.1016/j.commatsci.2019.109363

CrossRef Full Text | Google Scholar

93. Takatori SC, Brady JF. Forces, Stresses and the (Thermo?) Dynamics of Active Matter. Curr Opin Colloid Interf Sci (2016) 21:24–33. doi:10.1016/j.cocis.2015.12.003

CrossRef Full Text | Google Scholar

94. Shaebani MR, Wysocki A, Winkler RG, Gompper G, Rieger H. Computational Models for Active Matter. Nat Rev Phys (2020) 2:181–99. doi:10.1038/s42254-020-0152-1

CrossRef Full Text | Google Scholar

95. Marchetti MC, Joanny JF, Ramaswamy S, Liverpool TB, Prost J, Rao M, et al. Hydrodynamics of Soft Active Matter. Rev Mod Phys (2013) 85:1143–89. doi:10.1103/RevModPhys.85.1143

CrossRef Full Text | Google Scholar

96. Solon AP, Cates ME, Tailleur J. Active Brownian Particles and Run-And-Tumble Particles: A Comparative Study. Eur Phys J Spec Top (2015) 224:1231–62. doi:10.1140/epjst/e2015-02457-0

CrossRef Full Text | Google Scholar

97. Weeks JD, Chandler D, Andersen HC. Role of Repulsive Forces in Determining the Equilibrium Structure of Simple Liquids. J Chem Phys (1971) 54:5237–47. doi:10.1063/1.1674820

CrossRef Full Text | Google Scholar

98. Stukowski A. Visualization and Analysis of Atomistic Simulation Data with OVITO–The Open Visualization Tool. Model Simulation Mater Sci Eng (2009) 18:015012. doi:10.1088/0965-0393/18/1/015012

CrossRef Full Text | Google Scholar