- 1 Department of Bioengineering, University of California, Merced, Merced, CA, United States
- 2 Department of Mechanical Engineering, University of California, Merced, Merced, CA, United States
Semi-flexible filaments interacting with molecular motors and immersed in rheologically complex and viscoelastic media constitute a common motif in biology. Synthetic mimics of filament-motor systems also feature active or field-activated filaments. A feature common to these active assemblies is the spontaneous emergence of stable oscillations as a collective dynamic response. In nature, the frequency of these emergent oscillations is seen to depend strongly on the viscoelastic characteristics of the ambient medium. Motivated by these observations, we study the instabilities and dynamics of a minimal filament-motor system immersed in model viscoelastic fluids. Using a combination of linear stability analysis and full non-linear numerical solutions, we identify steady states, test the linear stability of these states, derive analytical stability boundaries, and investigate emergent oscillatory solutions. We show that the interplay between motor activity, filament and motor elasticity, and fluid viscoelasticity allows for stable oscillations or limit cycles to bifurcate from steady states. When the ambient fluid is Newtonian, frequencies are controlled by motor kinetics at low viscosities, but decay monotonically with viscosity at high viscosities. In viscoelastic fluids that have the same viscosity as the Newtonian fluid, but additionally allow for elastic energy storage, emergent limit cycles are associated with higher frequencies. The increase in frequency depends on the competition between fluid relaxation time-scales and time-scales associated with motor binding and unbinding. Our results suggest that both the stability and oscillatory properties of active systems may be controlled by tailoring the rheological properties and relaxation times of ambient fluidic environments.
1 Introduction
Biology is replete with examples of rigid and semi-flexible filaments, that singly or as aggregate bundles, interact with molecular motors in intracellular or extracellular settings. For instance, actin-myosin systems are crucial for cell function, development and growth [1–5] and in the transport of DNA [2]. Structured filament-motor systems comprised of microtubules and axonemal dynein motor arrays drive sperm locomotion [6–8] and algal motility [9]. These also constitute crucial components of healthy respiratory and reproductive tracts [10–15]. In the synthetic realm, motor assays and reconstituted biofilament networks frequently feature molecular motors translating, deforming and bending filaments [16–18].
A striking and well-studied feature of these filament-motor systems is the emergence of stable oscillations under favorable conditions. Examples include oscillatory instabilities in muscles and sarcomeres [19–21] and in microtubule assays involving NCD motors [22, 23], the periodic undulations of eukaryotic cilia [7, 8], and spontaneous oscillations during asymmetric cell division that involve microtubules interacting with cortical force generators [24–26]. These temporally varying patterns may follow complicated periodic functions, and are furthermore very tunable. Often, the onset of these oscillations may be controlled by quenching the system by depleting the molecular motors (the active agents driving these oscillations) of their energy source (ATP or Ca2+). All these systems are open systems with continuous energy input, and highly non-linear. In all, these observations suggest that the onset of these oscillations may be interpreted as instabilities to a base state triggered by system changes.
Biological filaments and motors usually inhabit fluidic or gel-like media with non-Newtonian properties and viscoelastic properties. Such complex fluid environments can directly impact these active systems by exerting time-dependent stresses. For instance, a filament moving in a Newtonian fluid feels viscous drag stresses exerted by the ambient medium. A filament moving in viscoelastic environments will be subject to more complicated time dependent forces that include dissipative (viscous) and non-dissipative (elastic) components. Recent work on cilia in the green alga Chlamydomonas reinhardtii that enables whole-cell locomotion suggests a strong influence of the viscosity and complex rheology of the ambient fluidic medium [9, 27]. Sketched in Figure 1A is a schematic summarizing experiments from [9] that depicts the variation in ciliary beat frequency of an algal cell in Newtonian (red) and polymeric (blue) fluids. Frequencies are seen to be significantly higher in the viscoelastic polymeric fluid compared to a Newtonian fluid with the same viscosity. Similarly strong effects of viscoelasticity on ciliary beat frequency are seen in the human mucociliary tract. In diseased states or when there is ciliary dysfunction—as seen for instance in cystic fibrosis (CF), primary ciliary dyskinesia (PCD) or chronic obstructive pulmonary disease (COPD)—the mucus layer submerges cilia in an extremely viscoelastic environment that impacts their beating [10, 12–14].
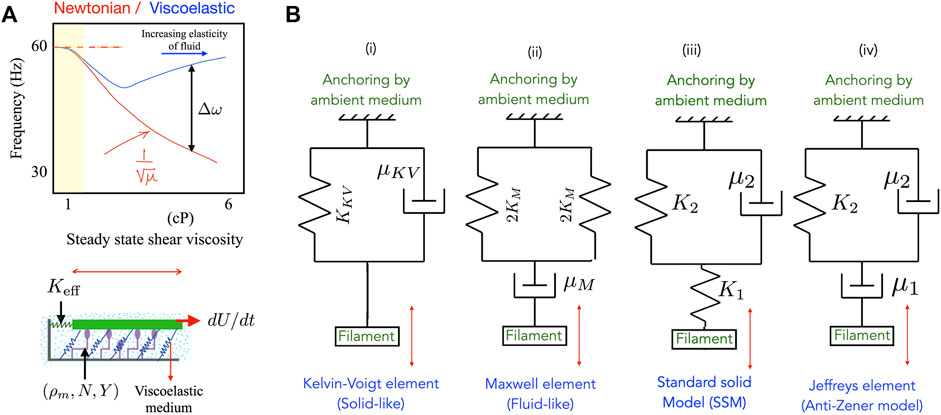
FIGURE 1. (A) (Top) A schematic summarizing experimental observations of ciliary frequencies on bi-ciliated alga Chlamydomonas reinhardtii moving in model viscoelastic fluids [9] made by adding polymer to a Newtonian solvent. The observed ciliary beat frequency in polymeric fluids is much higher than in Newtonian fluids with the same viscosity. (Bottom) Schematic of the animated motor-filament segment that forms the basis of the minimal motor-filament system. Active motors (purple) may be in one of two states–attached to the segment (in green) or detached. Passive cross-linkers are shown in blue and are treated as linearly elastic springs. The resistance to motion of the test segment exerted by its neighbors are combined into an effective elastic resistance (spring constant K eff). The ambient medium in which the assembly is embedded is viscoelastic. In the minimal model this medium may be treated as a Maxwell medium or as a Kelvin-Voigt medium. (B) Representations of the viscoelastic ambient media considered in this article—here the spring stiffness K (if present) for each material is related to the elastic modulus of the material comprising the medium. (i) A Kelvin-Voigt material, (ii) a Maxwell fluid, and (iii) a generalized standard solid element. The anti-Zener Jeffrey element in (iv) results in a more complicated relationship involving second derivatives of the strain rather than first derivatives as in (i)-(iii).
Thus the effect of the rheology of the ambient fluid needs to be understood in order to predict the dynamical response in these biological filament-motor systems. There is however a significant gap in our understanding of these aspects since it is experimentally difficult to independently vary fluid viscosity and elasticity. Abstracting the ingredients crucial to the examples of actively driven motor-filament systems allows us to identify three main ingredients that may control system-level mesoscale and macroscale dynamics–1) passive elasticity, from intrinsic filament-motor elasticity, 2) rheological properties of the embedding medium, and 3) associated motor mechanochemistry and kinetics. Here, we will combine these elements to build a simple phenomenological model for a filament-motor aggregate interacting with model fluidic media. To enable analytical progress, we assume the ambient fluid to correspond to one of three canonical types–a Newtonian fluid, a Kelvin-Voigt gels or a Maxwell medium. Using our minimal model we investigate the onset, stability and control of oscillations and address associated questions: 1) how do variations in the fluid induced mechanical stresses affect the manner in which the internal biomechanical state of the molecular motors in the aggregate is modulated, 2) how do these modulations impact the onset of oscillations, and when may they stabilize an otherwise unstable system, and 3) how does fluid rheology affect the frequency of emergent oscillations and their amplitude? Biological filament-motor systems are of course much more complex than the minimal model analyzed here. Nonetheless, minimal models offer an essential tool for understanding basic biophysical mechanisms. In this sense, the simple minimal model analyzed here using model fluids represents an important step towards more complete computational models.
2 Minimal Model
Our model system is shown in Figure 1A (bottom pane). We model the filament bundle—referred to henceforth as (composite) filament—as a rigid sheet that is at a certain fixed height from an underlying flat substrate. In the reduced setting analyzed here, the sheet has length ℓ A , thickness b A ≪ ℓ A and lateral extent w A satisfying ℓ A ≫ w A ≫ b A . The view shown in the figure is from the side, the axial dimension is the length and the lateral dimension into the paper (corresponding to the lateral extent, b) is treated as a neutral direction. The area of the segment that faces the underlying substrate is ℓ A w A . Biofilaments and aggregates may have slender cylindrical geometries; the area ℓ A w A is thus to be interpreted as the projected area of the aggregate that faces the substrate.
The filament is held a fixed distance away from an underlying flat substrate by passive, permanently attached linear springs (blue springs) with areal density ρ p, stiffness K p, and equilibrium length ℓ p. These passive springs resist shearing deformations and lateral translation of the filament. Additionally, the filament also interacts with a collection of model molecular motor proteins that are shown in purple in the figure. These motors are grafted to the lower plate with an areal density ρ m. We treat these molecular motors as active linear elastic springs with spring constant k m and equilibrium rest length ℓ m. The tail of each motor is permanently attached to the substrate and thus we do not allow for diffusion of the motors. Motor heads meanwhile can periodically adhere to the filament and when attached generate forces displacing the filament laterally. We choose the inter-motor spacing to be small enough, and densities high enough that a continuum description of filament-motor interactions suffices. Finally, for ease of analysis without loss of generality, we set ℓ m = ℓ p = 0.
To aid in the analysis, we model motor-filament interactions using two-state cross-bridge models [8, 19, 21]. Each motor is either attached state or detached. Detached motors can attach to the filament in a forward-leaning position with specified attachment probabilities. They then quickly undergo a conformational change, which makes them strained. As the filament moves, so does the motor and this results in the extension of the motor and thus extension of the internal spring (with spring constant k m ). Attached motors can detach any time, and the statistics of this process is embodied via microscopic strain dependent detachment probabilities. The transitions between attached and detached states – the kinetics of the mechanochemical cycle – are thus determined by motor kinetics, and specifically the attachment and detachment probabilities (rates). Detailed microscale equations modeling the mechanochemistry and motor-filament interactions in systems such as these have been derived and used by others and by us (c.f [19, 28] and references therein). Briefly summarized, motor kinetics may be described by a set of population balances relating the attached and the detached probability densities to the attachment and detachment fluxes via microscopic transition rates. For simplicity we neglect motor diffusion, and consider the noiseless mean-field limit, where the number of motors (and the density) is large (high) enough that fluctuations in the time average of the density of attached motors are small compared to the mean value. When the distribution in extension of attached motors is sharply peaked about the typical (average) length, transients to this distribution occur over times very small compared to the averaged macroscopic time scale. The extension of attached motors is then peaked about the mean value with small deviations from the mean. We assume that detached motors relax to a delta function with the change occurring instantaneously. Coarse-graining the microscale dynamical equations provides a mean-field continuum description for the (mean) attached motor fraction, and the mean attached motor extension.
3 Governing Equations for the Minimal Model
Following the physical picture described in §2, we next derive equations governing the dynamics for our minimal system - an elastically constrained filament-motor assembly embedded in a viscoelastic fluid. To enable analytical progress, we assume that the rheology of the embedding fluidic medium behaves in one of three ways: as 1) a Newtonian fluid, as 2) a Kelvin-Voigt material, or as a 3) Maxwell medium. Based on these, filament-motor and filament-medium interactions may be modeled analytically.
Consider again the schematic in Figure 1A. As mentioned earlier, the (composite) filament interacts with motors via a projected area ℓ A w A where w A is the width in the neutral direction. To model the effect of external elastic constraints on the filament, we choose to anchor the filament to a boundary with a linear elastic anchoring spring with stiffness K eff and rest length L o . We ignore edge effects and choose a reference frame with origin at the left attachment point where the spring is anchored. Due to the action of the motors, the rigid filament moves horizontally; with its motion resisted by the anchoring spring and the passive substrate attached springs. Filament motion is also resisted by fluid drag forces arising from the ambient viscoelastic medium. As a result of these restoring forces, when forced by attached molecular motors, the equilibrium stable state of the filament can either be one of rest or a time dependent state.
We define the displacement of material points on the plate relative to the rest state (where no motors are attached to the filament and the spring is not strained) by U∗ = L − L
o
; the speed of the plate is
The active force
Here the mean attachment rate
Given N and Y ∗, the effective active force per motor in Eq. 1 is given by
We next model the fluid interaction term,
1. Newtonian fluid: In the simplest case where the medium is a Newtonian fluid, the fluid drag per unit length acting on the plate depends just on the local shear rate at the plate surface. Since our intention is to capture qualitative aspects we proceed with scaling laws. Let us assume that the shear rate induced in the fluid at the filament surface is uniform along the filament and the velocity field penetrates to a distance ℓ N so that an aerage measure of the local strain rate is (1/ℓ N )dU ∗/dt ∗. An approximate equation for the drag force is then
with μ N being the Newtonian viscosity. The reduction is consistent with an effective drag coefficient approximation used for motion of bodies at low Reynolds number (with drag force proportional to the instantaneous speed). Note that the segment length ℓ A , segment width w A and length ℓ N are all assumed to be constants. This is a major simplification since this penetration depth can be time dependent.
2. Kelvin-Voigt fluid: When the embedding medium is a networked gel-like medium with both elastic and viscous features, the drag forces depend both on plate velocities as well as displacements. One may consider these displacement contributions to arise as a result of restoring forces as the plate moves relative to a fixed meshed elastic network. We choose a Kelvin-Voigt like model with a single retardation time scale and equilibrium mesh size ℓ KV represented by
relating the strain to the stress. Evaluating this at the surface of the plate and assuming no slip, we obtain (measuring strain in mesh lengths, and assuming a continuum formulation holds)
3. MaxwelL gel: For a viscoelastic Maxwell-like with a single relaxation time scale and a mesh length ℓ M, we have the relationship
or
Evaluating this at the surface of the plate and assuming no slip, we obtain (again measuring strain in units of mesh length and assuming a continuum formulation holds so that
Equations 1,5,6,7 assume that the ambient medium is always quasi-statically coupled to motion of the upper plate. A similar analysis may be done for the Zener standard solid model of the type illustrated in Figures 1B–iv, but we do not pursue this in the current work.
We emphasize that Equations 5–7 ignore transient stress fields induced as the viscous/viscoelastic boundary layer forms near the moving filament and associated time-dependent features. A more accurate description would necessitate solving the full Navier-Stokes equation with the appropriate constitutive equation relating the stress in the fluid to the strain and strain rate and is beyond the aim of this paper.
To obtain scaled equations that allow the identification of important non-dimensional parameters, we scale time with
with dimensionless parameter β quantifying motor density while dimensionless parameters
In this article we will consider not consider models resulting in a second derivative of U. The linear stability analysis can however be extended to the Jeffrey element, albeit with slightly more involved algebra.

TABLE 2. Dimensionless parameters quantifying the ambient medium stress on moving filament. Here, ℓ
A
and w
A
are the length and width of the filament aggregate interacting with motors and allow one to go from the stress to a force description. Displacements are scaled with
Following previous work, we model motor kinetics as responding to the deformation experienced by attached motors [1, 2, 19]. Attached motors behaving as slip bonds with a strain dependent detachment probability. This functionality is encoded in the detachment rate
In Equation 11, the dimensionless parameter
In our model, bending is ignored and the filament composite/aggregate is considered rigid and inextensible. While our model is not directly applicable to ciliary oscillations, using some numerical estimates relevant to filaments and motors in cilia provides understanding of the magnitudes of the parameters in the model. Our model also may allow us to interpret how oscillations may arise within and along an initially straight passive cilium. Localized elastically weak regions may result in cilia fragments driven by dynein arrays moving against their neighbors. In this scenario, we estimate k
m
∼ 10−3 N/m, the effective linear density ρ
m
w
A
∼ O (108) m−1, w
A
∼ 40−60 nm, k
N ∼ 16–100 pN μm−1 and w
A
ρ
N ∼ 105–107 m−1 [1, 29]. The value of K
eff depends on the material. Microtubules are relatively stiff with large persistent lengths and the Young’s modulus E ∼ 1.2 GPa providing the stiffness per length K
eff ∼ Gw
A
. For microtubules driven by dynein, previous studies report a persistence length
4 Results and Discussion
4.1 Dynamics of the Unconstrained System
Before analyzing the dynamics of the constrained filament-motor system, we briefly address the dynamics of an unconstrained system. Accordingly, we set ρ p = 0, K eff = 0 and study the dynamics of the animated filaments on a rigid surface on which motors are grafted, as in motility assays. Short fragments in these assays are typically rigid enough that they move without bending. Long fragments on the other hand are susceptible to buckling instabilities as previous studied experimentally and analytically [18, 31–36] in these and similar systems involving driven active filaments.
Here, we invert the problem and study the dynamics of the motor variables (Y, N) as functions of the speed Z = dU/dT. In other words, we restrict ourselves to time scales where the dynamics of the motor kinetics is slaved to the speed of the filament. The speed Z may be envisioned as an independently controlled variable; we then enquire how steady values of N and Y depend on Z and if these solutions are linearly stable. Eq. 10 is irrelevant in this limit, and Equations 8, 9 become.
When Z = 0, Equations 13, 14 admit steady state solutions (N s , Y s ) given by
For each value of Z ≠ 0, other steady solutions different from Eq. 15 exist. To study both the steady solutions and their stability, we use an in-house numerical continuation implemented in Matlab
@
. Treating Z as the free variable, we plot steady solutions to Equations 13, 14 and investigate the stability of the solutions for various values of Ψ and
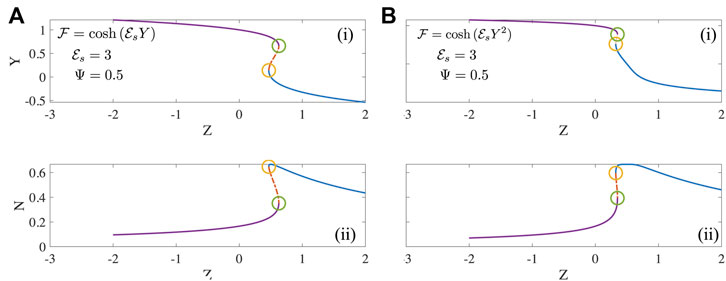
FIGURE 2. The mean motor extension Y and fraction of motors that are attached N as a function of Z steady solutions to Eqs 13, 14 for two forms of the detachment function (A)
Numerical investigation reveals that the existence and extent of the unstable region depends on the form of the detachment curve. When the detachment function is constant or a decreasing function of extension Y, no unstable regions exist. In these cases, typically each value of Z is associated with a unique value of N and Y. However when the detachment function is an increasing function of Y, some parts of the steady state solutions becomes unstable as seen in Figure 2. This is manifest clearly in bistability, evident for instance in the curves of N vs. Z with three possible values of Z (two stable, one unstable) corresponding to a single value of Z. A value of N = 0.4 in Figure 2A-(ii) and 2(b)-(ii) for instance is unstable and is susceptible to disturbances that can push the state to either the upper branch or the lower branch each with the same value of Z. The origin of this instability is the emergence of effective negative spring constants due to motor activity; such features have been studied previously [19].
4.2 Analytical Results: Oscillatory Instabilities and Emergent Frequencies
The question that arises naturally next is how K eff > 0 impacts this response. To answer this question, we turn next to the stationary base state of the full Equations 8–11 and the linear stability of the base state given by Eq. 12. We find that the base state exhibits linear instability for certain regions in parameter space. We derive analytical expressions for the locus of these critical points—the neutral stability curves. Classical linear stability analysis shows at these critical points, stable oscillatory solutions emerge via the Hopf-Andronov-Poincare bifurcation [37]. Limit cycles emanate at these points with fixed frequencies and small amplitude. We calculate the frequencies of these emergent solutions analytically and investigate their dependence on dimensionless parameters defined earlier. Predictions of our linear stability analysis are confirmed by full non-linear solutions of the equations.
To identify the stability of the stationary (base) state (Eq. 12), we analyze how small imposed perturbations to this state evolve in time. We introduce a small (amplitude) parameter ϵ ≪ 1 and write
Substituting (Eq. 16) in Eqs 8-11, expanding all terms, and retaining only terms that are O(ϵ), we get the three coupled linear ODE’s:
Substituting next
in Eqs 17-19, we obtain coupled algebraic equations for
where
The growth rates σ of Eq. 21 depend crucially on the signs of b and c. We note that a and d are always positive. Since coefficients a − d are real, Equation 21 has—from the fundamental theorem of algebra—three roots. One of these is purely real and the other two may be complex conjugate. Since we set
Restricting ourselves to the subspace of solutions that comprise 1 real root and a complex conjugate pair, we write (σ 1), σ 2 = σ + iω and σ 3 = σ − iω. When the base state is stable we have σ 1 < 0 and σ < 0. We seek incipient oscillatory instabilities such that emergent solutions may be stable and oscillating. At the onset of instability—that is on the neutral stability curve—this implies the condition σ = 0. The imaginary part ω may then be identified as the frequency of the emergent solutions.
4.2.1 Results From Stability Analysis
1. No drag from medium: Consider the simplest degenerate case where the medium does not exert any forces on the motor-filament system. In this case, we have
For constant Ψ and
2. Newtonian fluid: For the simplest drag-producing medium - a Newtonian fluid - we have
with first two left hand side terms being resisting (passive) forces and the third term the driving (active) force; the right hand is zero here due to the absence of inertia as explained earlier.The frequency of the bifurcating limit cycles at onset is given by
Combining (Eqs 23) and (24) yields
and so,
while
Thus for very high viscosity μ
N, the frequency scales as
From the analytical expression for the neutral stability curve, we deduce that for oscillatory instabilities to exist we require that
3. Kelvin-Voigt medium: Here, the drag force depends on the displacement and the rate of displacement. Thus we have
For fixed motor parameters and fixed value of
where we have defined the shift in frequency relative to a purely Newtonian fluid, Δω KV ≡ (ω KV − ω N ). We can also derive the expression for the neutral stability curve
4. MaxwelL medium: For the Maxwell medium, the displacement rate is linearly coupled to the drag force and the rate of change of the drag force. We have for this case,
From an estimation of constants a − d, we rule out the possibility of a fold-Hopf bifurcation, that is a fold bifurcation coincident with the Andronov-Hopf-Poincare bifurcation. However we can still satisfy conditions for the existence of an oscillatory instability. Further analysis (see Supplementary Appendix A) indicates a mathematical possibility for non-oscillatory instability for very high values of
We therefore look for a subset of critical points for which exactly 1 real negative root (σ 1) and a complex conjugate pair (±iω) with zero real part (σ = 0) exists for the cubic. The neutral stability curve is defined by the locus of points that simultaneously satisfy ad − bc = 0. The frequency at onset is given by
Since
Before concluding this section, we address the biophysical origin of the oscillations. The simplest scenarios—the case of no fluid, and that of a Newtonian fluid—provide hints as to the destabilizing mechanism. Linearizing (Eqs 8)–(11) about the base state (Eq. 12) provides (in frequency space) a relationship between the displacement U and an effective compliance that includes contributions from the active motor-based interactions with the filament as well as the fluid response. When there is no drag/resistive force at all from the medium, we find that the instability arises when the active compliance has a negative effective elastic coefficient i. e, active motor induced elasticity overcomes the passive elastic resistances. This provides a mechanism by which system-level oscillations are initiated. Meanwhile the dissipative components of the system—i. e, viscous effects–limit the amplitude of the oscillations. Thus stable limit cycles can emerge. Interestingly no fluid or external medium is needed to initiate and sustain oscillations in this model system.
We have three independent parameters here that determine if oscillations exists–β, Ψ and
4.3 Comparison to Non-linear Solutions
4.3.1 Amplitudes and Frequencies of Limit Cycles Vary Away From Critical Point
The linear stability analyses in Section 4.1, Section 4.2 provide information on the stability boundaries for the stationary steady state (Eq. 12) and also on the emergent frequencies of the bifurcating limit cycles at critical points on these boundaries, the neutral stability curves. The frequency when parameters correspond to positions in phase space far away from the neutral stability curves will of course differ from the values at criticality. When all parameters are kept fixed, and just one parameter–say for example, β varies, the amplitude of the limit cycles is expected to scale
Our analysis also suggests that smooth modulation of the frequencies may be implemented once past the critical point but linear stability alone is insufficient to validate this. Furthermore the linear stability analysis does not show how the amplitude of the oscillations changes with parameters. The amplitude is dominated by non-linear terms. Thus to understand how non-linearity affects frequencies and amplitudes far from critical points, we solved Equations 8–11 numerically using Matlab
@
. Equations 8–11 constitute a stiff set of equations especially in the limit of small
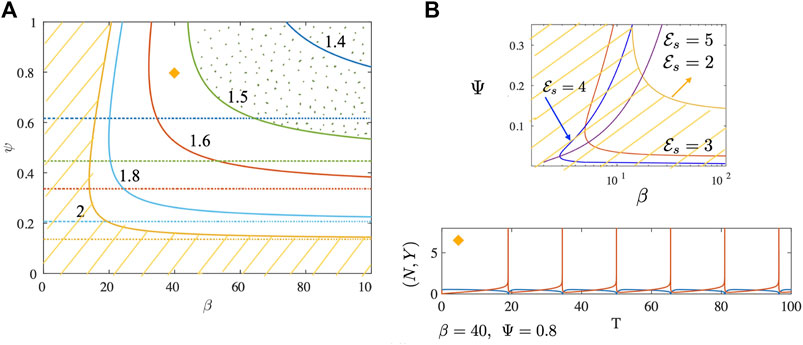
FIGURE 3. (A) Neutral stability curves separating linearly stable from unstable regions are shown for the no drag case. Plotted as solid curves are results for different values of
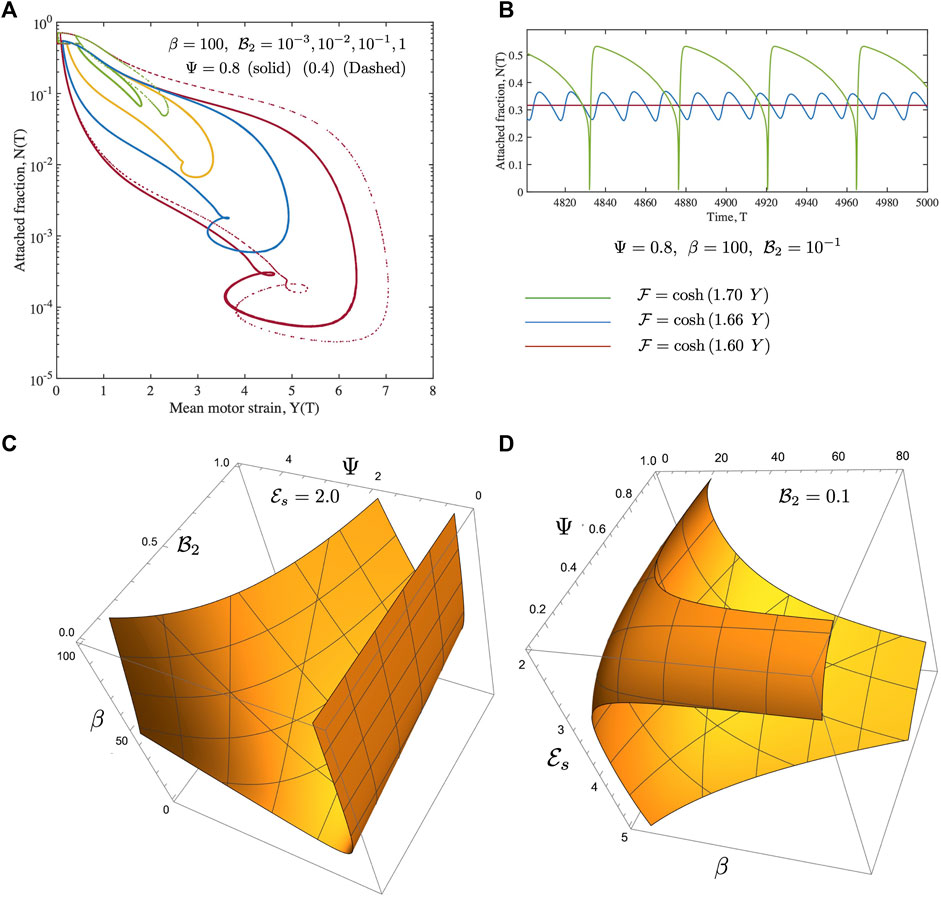
FIGURE 4. (A) Phase-plots over complete cycles obtained from fully non-linear solutions for the Newtonian case are shown. The detachment function is cosh (2Y) and the motor activity parameter (density) β =100. We note that as
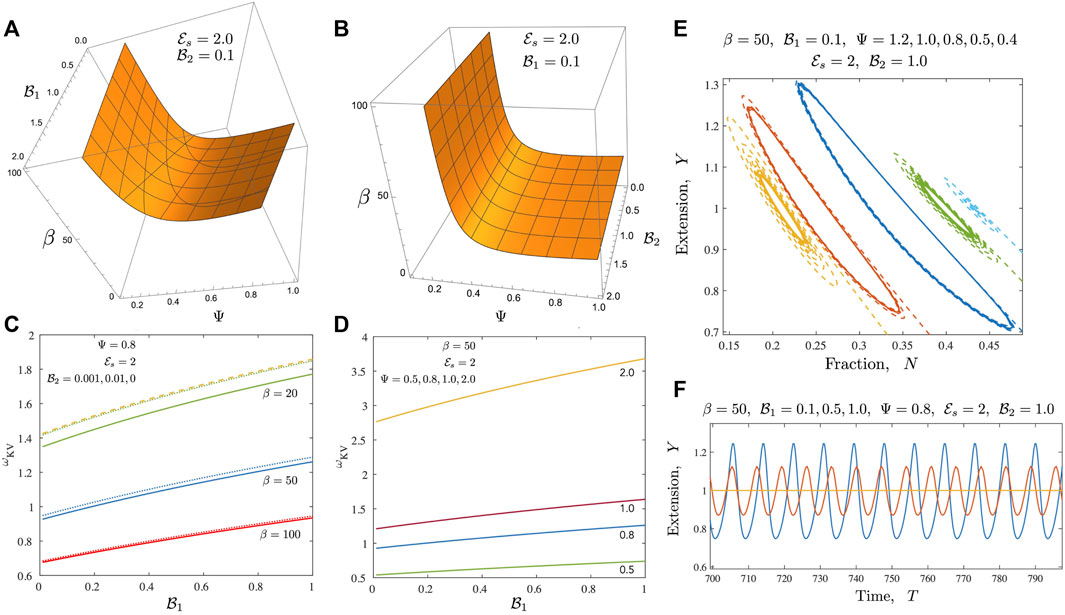
FIGURE 5. Results for the case of a Kelvin-Voigt medium (A,B) Neutral stability curves from the linear stability analysis shown here for the Newtonian case when
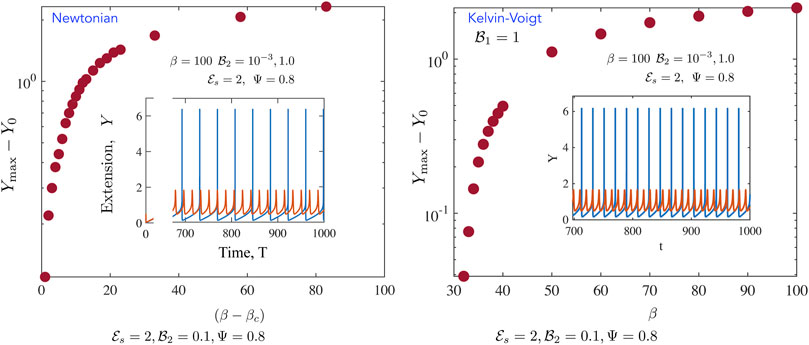
FIGURE 6. Representative metrics for the fully non-linear periodic solutions for the (left) Newtonian, and (right) Kelvin-Voigt cases (Newtonian, left) We calculate the maximum value of Y
max over a cycle and plot Y
max −1 as a function of β − β
c
where the critical value of beta for these parameters
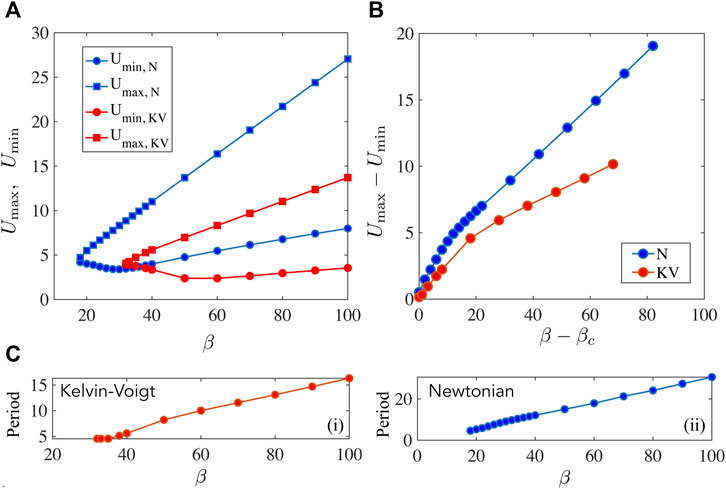
FIGURE 7. Non-linear solutions for Newtonian and Kelvin-Voigt media compared with the focus on the filament displacements U and period of oscillations. (A) Here we plot U
max and U
min, the maximum and minimum values attached by U(t) over a cycle when the oscillations have stabilized, as a function of β. Parameters are
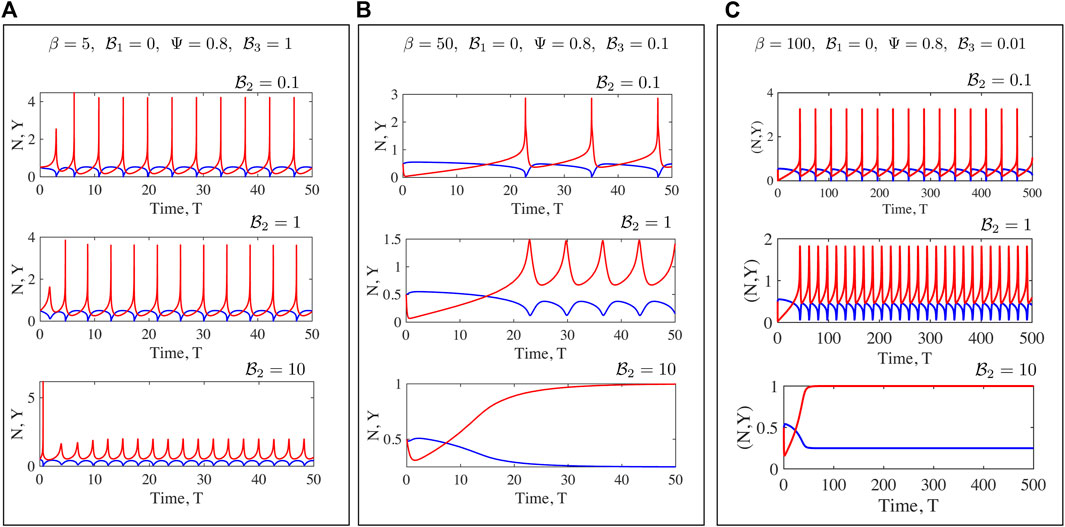
FIGURE 8. Fully non-linear solutions for the Maxwell medium. Here to focus on the rheological parameters
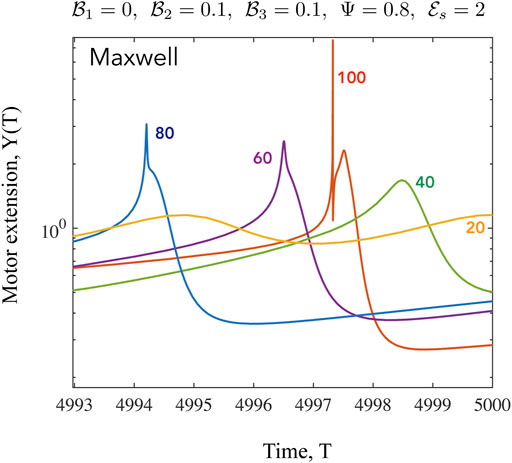
FIGURE 9. Time series of the mean motor extension Y for the Maxwell case shown for β =20,40,60,80,100. Here we focus on the shape of the function close to the point where Y = Y max. When β to close to its critical value, the oscillations are harmonic as seen from the form of Y(T) for β =20. As the value of β increases, the periodic profiles becomes highly asymmetric and also develop double maxima and double minima, especially evident for β =100. The high values of Y are associated with very low values of N when very few motors are attached, with these motors extended significantly.
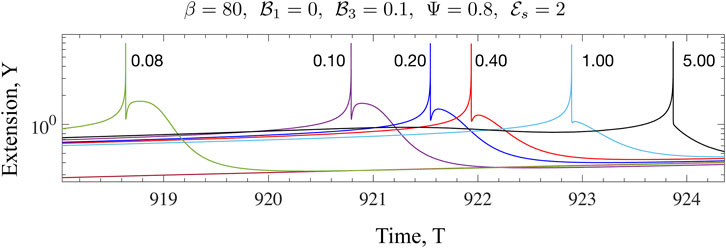
FIGURE 10. The effect of increased dissipation (viscosity) on the form of Y(T) for the Maxwell model is illustrated here. The value of β is much larger than the critical value for the onset of oscillations. Fixing
4.3.2 Supercritical Hopf Bifurcations and Fluid Limited Oscillation Amplitudes
Let us start with the two reference cases first. For the case of no fluid drag, the active energy input into the system by continuous motor activity is eventually dissipated away by internal motor friction with the anchoring spring as well as the passive links serving as intermediate storage agents. The motor activity derived internal friction is associated with the energy loss when motors detach and eventually go back to their rest length. We note that oscillations can feature very sharp gradients in Y. Over a cycle, the attached motor fraction N can become very small reaching relative values of O (10−4) as seen in Figure 4A (albeit for non-zero
Introducing viscoelastic effects changes the dynamics in a variety of ways. When the ambient medium follows Kelvin-Voigt like response (a reasonable simple approximation to a gel), the ability to store energy increases for
We further probe the variation in amplitudes away from the critical point and present results in Figures 6, 7. Figure 6 focusses on the motor variables (or the motor state) for both the Newtonian model and the Kelvin Voigt model. In both cases, we confirm that limit cycles emerge via supercritical bifurcations [37]. Figure 6A illustrates this feature; plotted here is the quantity |Y max(T) − Y 0| and we find that this tends to 0 as β → β c . Emergent oscillations also onset, as required for this class of bifurcations, with fixed non-zero frequency. When β ≫ β c , the amplitude saturates. This saturation is likely due to a combination of two features. First, even though the number of active motors increases with increasing β, attached motors generate passive resistance when pulled backwards and limit the amplitude of the oscillations. Secondly, increased amplitudes result in a zipper effect—almost all motors rapidly disengage and detach together. Figure 6B illustrates that the emergent oscillations when the ambient medium is a Kelvin-Voigt medium also arise from supercritical bifurcations. We note increased frequencies as well as slightly larger amplitudes. Figures 6A,B suggest that in the absence of any energy constraints (an open system where energy limitations are not present), limit cycles can in viscoelastic media can exhibit larger amplitudes and higher frequencies than in the Newtonian case.
Until now we have focussed on how the motor variables Y and N are impacted by the fluid rheology dependent parameters. In experimental realizations of the filament motor system, one typically finds it easier to track filament related positions. For instance we may envision marking one end of the filament via florescent markers and tracking the position as a function of time. In Figure 7, we therefore illustrate how the filament displacement U varies over a period of a stable oscillation. For simplicity we treat all variables except β as constants and plot U
max ≡max [U(T)], U
min ≡min [U(T)], the characteristic amplitude |U
max − U
min| and the period T
p
defined implicitly via U (T + T
p
) = U(T) for stable oscillations. For the Newtonian case, we fix
4.3.3 Differences Between the Maxwell and Kelvin-Voigt Models
Numerical solutions for oscillations in a Maxwell fluid indicate that the onset of oscillations and frequencies may be more readily tuned than for the Kelvin-Voigt case. Oscillations are enabled at even O (1) values of β provided
We have discussed the frequencies as well as the amplitudes (measured via suitable norms) of emergent oscillations until now. We conclude this section by focussing on the shape of the limit cycle and the asymmetries that may manifest. A motivation for looking at this in closer detail comes from the possibility of using synthetic versions of motor-filament systems as switching or triggering devices. One may imagine connecting this active viscoelastic unit in series to a dynamical system that uses the input dU/dT and/or U to provide downstream responses/signals. In Figures 9, 10 we examine the variation in the shape of the limit cycles for the specific case of the ambient fluid being a Maxwell fluid. In Figure 9 close to onset, the variations in Y(T) are smooth, and in fact almost sinusoidal as one moves towards the critical point. Increasing β makes the profile asymmetric; the mean motor extension attains large extensions (Y > 1) and compressions but the profile develops three extrema with two maxima and 1 minimum as seen by comparing the curves for β = 80 and β = 20. Figure 10 illustrates how the asymmetric double peaked shaped may be smoothened by increased viscosity (here by increasing the value of
5 Summary and Conclusion
Here, we studied a minimal system comprised of an active bio-filament segment working against an elastic spring and immersed in model complex materials. A mean-field macroscale continuum description of filament-motor interactions was employed based on a cross-bridge model—however, other models can be readily used instead (see [28] for a general model that allows motors to undergo initial conformations as well as move relative to the filament). We used a combination of analytical and numerical methods to extract the conditions under which rheology of the fluid may be exploited to both shift the onset of instabilities, and modulate ensuing frequencies and amplitudes. We found that steady base states yield to stable oscillatory states or limit cycles. These solutions arise via supercritical Hopf-Andronov-Poincare’ bifurcations with exponentially damped oscillation change to small limit cycle oscillation about the steady state. Linear stability results were validated and complemented with full time-dependent solutions that provide an indication of the manner in which the amplitude of these oscillations changes.
A shortcoming in our theoretical approach is that in the process of formulating analytically tractable equations, complex biochemical and biomechanical aspects are highly simplified. We have not considered noise and stochastic aspects of the problem that may be important for small to moderate values of β and/or low attachment rates [28]. While our model does not include motor driven filament bending which dominates in oscillatory dynamics of biological and synthetically devised ciliary structures, reduced dimensional and spatially dependent versions have been used to investigate oscillations of cilia in Newtonian fluids [8, 9, 29, 31, 36]. However, ciliary or flagellar motion in viscoelastic fluids remains an open challenge. Elastic and viscous responses of for a viscoelastic fluid made by adding polymers to a Newtonian solvent fluid may depend on concentration differently. Thus in a polymeric fluid the ratio
The governing equations we utilized employed simplifications that allow for analytical and independent exploration of fluid viscoelastic properties (both its effective viscosity and elasticity, measured appropriately and encapsulated in parameters
Our results are also relevant to understanding the rheology and dynamical response of biological and synthetic muscles, and in devising actuators for soft-robots [38–41]. In general, active responses to imposed external stimuli or perturbations are analyzed using an effective frequency-dependent dynamic moduli in these systems. The minimal approach we have used here–modeling the ambient fluid in terms of minimal models with spring-like and dashpot-like elements—provide a clear means to evaluate these dynamic response functions (or transfer functions).
While direct comparison to ciliary experiments requires a spatially varying version of our model, there are experimental setups that can be used to check the theoretical predictions we have made. Motility assays offer an easy way to study the spatial dynamics of gliding microtubules or actin filaments. These filaments are animated by molecular motors that are grafted on the substrate and periodically attach to the filaments propelling them via tangential forces. Oscillations have been observed in filaments that are temporarily pinned in these systems with frequencies comparable to the values calculated in this paper for Newtonian fluids. In [18] we interpreted and analyzed bending oscillations for long filaments in Newtonian settings via a combination of linear stability analysis and non-linear computations. By using 1) very short rigid (non-bendable) filaments, 2) model viscoelastic fluids as the nutrient media in which the gliding takes place, and 2) additional polymeric binders that can attach to the filament and play the role of passive adhesive springs [42, 43], one can adapt current protocols and establish a setup that mimics closely the model analyzed in this paper. A natural next step would be the test of the model predictions from in these adapted gliding motility assays.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
The project was conceived by AG. Theoretical calculations were done by AM and AG. Numerical analysis was conducted by AM and JT. All authors contributed to the final form of the manuscript.
Funding
AG acknowledges funding from the National Science Foundation via awards NSF-CBET-2047210 and NSF-MCB-2026782. JT was supported by funding from NSF-MCB-2026782.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.895536/full#supplementary-material
References
1. Howard J. Mechanics of Motor Proteins and the Cytoskeleton. Sunderland: Sinauer Associates (2001).
2. Grill SW, Kruse K, Jülicher F. Theory of Mitotic Spindle Oscillations. Phys Rev Lett (2005) 94(10):108104. doi:10.1103/physrevlett.94.108104
3. Bizzi E, Chapple W, Hogan N. Mechanical Properties of Muscles: Implications for Motor Control. Trends Neurosciences (1982) 5:395–8. doi:10.1016/0166-2236(82)90221-1
4. Hogan N. Adaptive Control of Mechanical Impedance by Coactivation of Antagonist Muscles. IEEE Trans Automat Contr (1984) 29:681–90. doi:10.1109/TAC.1984.1103644
5. Walcott S. Muscle Activation Described with a Differential Equation Model for Large Ensembles of Locally Coupled Molecular Motors. Phys Rev E (2014) 90:042717. doi:10.1103/PhysRevE.90.042717
6. Witman GB. Introduction to Cilia and Flagella. In: RA Bloodgood, editor. Ciliary and Flagellar Membranes. New York: Plenum (1990). p. 1–30. doi:10.1007/978-1-4613-0515-6_1
7. Machin KE. The Control and Synchronization of Flagellar Movement. Proc Roy Soc B (1963) 158(970):88–104.
8. Brokaw CJ. Molecular Mechanism for Oscillation in Flagella and Muscle. Proc Natl Acad Sci U.S.A (1975) 72(8):3102–6. doi:10.1073/pnas.72.8.3102
9. Qin B, Gopinath A, Yang J, Gollub JP, Arratia PE. Flagellar Kinematics and Swimming of Algal Cells in Viscoelastic Fluids. Sci Rep (2015) 5:9190. doi:10.1038/srep09190
10. Sears PR, Thompson K, Knowles MR, Davis CW. Human Airway Ciliary Dynamics. Am J Physiology-Lung Cell Mol Physiol (2013) 304:L170–L183. doi:10.1152/ajplung.00105.2012
11. Kempeneers C, Seaton C, Chilvers MA. Variation of Ciliary Beat Pattern in Three Different Beating Planes in Healthy Subjects. Chest (2017) 151:993–1001. doi:10.1016/j.chest.2016.09.015
12. Knowles MR, Leigh MW, Carson JL, Davis SD, Dell SD, Ferkol TW, et al. Mutations ofDNAH11in Patients with Primary Ciliary Dyskinesia with normal Ciliary Ultrastructure. Thorax (2012) 67:433–41. doi:10.1136/thoraxjnl-2011-200301
13. Papon J-F, Bassinet L, Cariou-Patron G, Zerah-Lancner F, Vojtek A-M, Blanchon S, et al. Quantitative Analysis of Ciliary Beating in Primary Ciliary Dyskinesia: a Pilot Study. Orphanet J Rare Dis (2012) 7:78. doi:10.1186/1750-1172-7-78
14. Thomas B, Rutman A, O'Callaghan C. Disrupted Ciliated Epithelium Shows Slower Ciliary Beat Frequency and Increased Dyskinesia. Eur Respir J (2009) 34:401–4. doi:10.1183/09031936.00153308
15. Ringers C, Olstad EW, Jurisch-Yaksi N. The Role of Motile Cilia in the Development and Physiology of the Nervous System. Phil Trans R Soc B (2019) 375:20190156. doi:10.1098/rstb.2019.0156
16. Sanchez T, Welch D, Nicastro D, Dogic Z. Cilia-like Beating of Active Microtubule Bundles. Science (2001) 333(6041):456–9. doi:10.1126/science.1203963
17. Sanchez T, Chen DTN, DeCamp SJ, Heymann M, Dogic Z. Spontaneous Motion in Hierarchically Assembled Active Matter. Nature (2012) 491(7424):431–4. doi:10.1038/nature11591
18. Fily Y, Subramanian P, Schneider TM, Chelakkot R, Gopinath A. Buckling Instabilities and Spatio-Temporal Dynamics of Active Elastic Filaments. J R Soc Interf (2020) 17(165):20190794. doi:10.1098/rsif.2019.0794
19. Vilfan A, Frey E. Oscillations in Molecular Motor Assemblies. J Phys Condens Matter (2005) 17(47):S3901–S3911. doi:10.1088/0953-8984/17/47/018
20. Nguyen KD, Sharma N, Venkadesan M. Active Viscoelasticity of Sarcomeres. Front Robot AI (2018) 5:69. doi:10.3389/frobt.2018.00069
21. Vilfan A, Duke T. Synchronization of Active Mechanical Oscillators by an Inertial Load. Phys Rev Lett (2003) 91:114101. doi:10.1103/physrevlett.91.114101
22. Endow SA, Higuchi H. A Mutant of the Motor Protein Kinesin that Moves in Both Directions on Microtubules. Nature (2000) 406:913–6. doi:10.1038/35022617
23. Badoual M, Jülicher F, Prost J. Bidirectional Cooperative Motion of Molecular Motors. Proc Natl Acad Sci U.S.A (2002) 99:6696–701. doi:10.1073/pnas.102692399
24. Grill SW, Gönczy P, Stelzer EHK, Hyman AA. Polarity Controls Forces Governing Asymmetric Spindle Positioning in the Caenorhabditis elegans Embryo. Nature (2001) 409:630–3. doi:10.1038/35054572
25. Colombo K, Grill SW, Kimple RJ, Willard FS, Siderovski DP, Gönczy P. Translation of Polarity Cues into Asymmetric Spindle Positioning in Caenorhabditis elegans Embryos. Science (2003) 300:1957–61. doi:10.1126/science.1084146
26. Grill SW, Howard J, Schäffer E, Stelzer EHK, Hyman AA. The Distribution of Active Force Generators Controls Mitotic Spindle Position. Science (2003) 301:518–21. doi:10.1126/science.1086560
27. Li C, Qin B, Gopinath A, Arratia PE, Thomases B, Guy RD. Flagellar Swimming in Viscoelastic Fluids: Role of Fluid Elastic Stress Revealed by Simulations Based on Experimental Data. J R Soc Interf (2017) 14(135):20170289. doi:10.1098/rsif.2017.0289
28. Gopinath A, Chelakkot R, Mahadevan L. Filament Extensibility and Shear Stiffening Control Persistence of Strain and Loss of Coherence in Cross-Linked Motor-Filament Assemblies. bioRxiv (2020). doi:10.1101/423582
29. Camalet S, Jülicher F. Generic Aspects of Axonemal Beating. New J Phys (2000) 2:24.1–24.23. doi:10.1088/1367-2630/2/1/324
30. Patteson AE, Gopinath A, Goulian M, Arratia PE. Running and Tumbling with E. coli in Polymeric Solutions. Sci Rep (2015) 5(1):15761–11. doi:10.1038/srep15761
31. Hamilton E, Pellicciotta N, Feriani L, Cicuta P. Motile Cilia Hydrodynamics: Entrainment versus Synchronization when Coupling through Flow. Phil Trans R Soc B (2019) 375:20190152. doi:10.1098/rstb.2019.0152
32. Sangani A, Gopinath A. Elastohydrodynamical Instabilities of Active Filaments, Arrays and Carpets Analyzed Using Slender Body Theory. Phys. Rev. Fluids (2020). 5(8):083101.
33. Fatehiboroujeni S, Gopinath A, Goyal S. Nonlinear Oscillations Induced by Follower Forces in Prestressed Clamped Rods Subjected to Drag. J Comp Non Dyn (2018) 13(12):121005. doi:10.1115/1.4041681
34. Fatehiboroujeni S, Gopinath A, Goyal S. Follower Forces in Pre-stressed Fixed-Fixed Rods to Mimic Oscillatory Beating of Active Filaments. In: Proceedings of the ASME 2018 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Volume 6: 14th International Conference on Multibody Systems, Nonlinear Dynamics, and Control; August 26–29, 2018; Quebec City, Quebec, Canada (2018). ASME DETC2018-85449, V006T09A033. doi:10.1115/detc2018-85449
35. Chelakkot R, Gopinath A, Mahadevan L, Hagan MF. Flagellar Dynamics of a Connected Chain of Active, Polar, Brownian Particles. J R Soc Interf (2014) 11(92):20130884. doi:10.1098/rsif.2013.0884
36. Chakrabarti B, Saintillan D. Spontaneous Oscillations, Beating Patterns, and Hydrodynamics of Active Microfilaments. Phys Rev Fluids (2019) 4:043102. doi:10.1103/physrevfluids.4.043102
37. Strogatz SH. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering. Reading, Mass: Addison-Wesley (1994).
38. Anderson IA, Gisby TA, McKay TG, O’Brien BM, Calius EP. Multi-functional Dielectric Elastomer Artificial Muscles for Soft and Smart Machines. J Appl Phys (2012) 112:041101. doi:10.1063/1.4740023
39. Buerger SP, Hogan N. Complementary Stability and Loop Shaping for Improved Human-Robot Interaction. IEEE Trans Robot (2007) 23:232–44. doi:10.1109/TRO.2007.892229
40. George NT, Irving TC, Williams CD, Daniel TL. The Cross-Bridge Spring: Can Cool Muscles Store Elastic Energy? Science (2013) 340:1217–20. doi:10.1126/science.1229573
41. Hines L, Petersen K, Lum GZ, Sitti M. Soft Actuators for Small-Scale Robotics. Adv Mater (2017) 29:1603483–43. doi:10.1002/adma.201603483
42. Sharma P, Ghosh S, Bhattacharya S. Microrheology of a Sticking Transition. Nat Phys (2008) 4:960–6. doi:10.1038/nphys1105
Keywords: spontaneous oscillations, active instabilities, rheology, motor assemblies, complex matter
Citation: Tamayo J, Mishra A and Gopinath A (2022) Ambient Fluid Rheology Modulates Oscillatory Instabilities in Filament-Motor Systems. Front. Phys. 10:895536. doi: 10.3389/fphy.2022.895536
Received: 14 March 2022; Accepted: 06 May 2022;
Published: 21 June 2022.
Edited by:
Liheng Cai, University of Virginia, United StatesReviewed by:
Xingbo Yang, Harvard University, United StatesPoornachandra Sekhar Burada, Indian Institute of Technology Kharagpur, India
Copyright © 2022 Tamayo, Mishra and Gopinath. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Arvind Gopinath, YWdvcGluYXRoQHVjbWVyY2VkLmVkdQ==
† These authors have contributed equally to this work
 Joshua Tamayo
Joshua Tamayo Anupam Mishra
Anupam Mishra Arvind Gopinath
Arvind Gopinath