Continuous and Discrete Deformation Modes of Mechanical Metamaterials With Ring-Like Unit Cells

Structures with multiple deformation paths provide a promising platform for robotics and reprogrammable mechanical and thermal deformation materials. Reconfigurations with a multi-path can fulfill many tasks (e.g., walking and grasping) and possess multiple properties (e.g., targeted Poisson’s ratio and thermal expansion coefficient). Here, we proposed a new ring-like kirigami structure and theoretically and experimentally found that for a basic unit, there are four discrete deformation patterns and a continuous shearing deformation pattern; thus, there are a large number of discrete deformation patterns for a multi-unit combination with geometrical compatibility coupled with a shearing deformation mode. Moreover, targeted Poisson’s ratios (either + or -) in the x- and y-directions can be realized by inversely designing the geometrical parameters for a certain deformation path. Additionally, we showed the capability of constructing 2D and 3D cellular structures in various patterns with the proposed ring-like units. The multiple deformation modes demonstrated here open up avenues to design new reprogrammable materials and robots across various scales.

Introduction

Material deformation can provide motion, function, and power for diverse applications. For robotics, the deformation of a material enables the realization of gripping motions, walking motions, sensing capabilities, and muscle-like actuating forces [1–3]. Material deformation also provides a platform to realize a negative Poisson’s ratio [4], negative thermal expansion [5], negative compressibility [6], and negative stiffness [7–9]. The design of multiple deformation modes provides a flexible way to create mechanical metamaterial switching between soft and stiff states [10], the mechanical properties of which depend more on their own architectures but less on molecular or chemical compositions [11]. These metamaterials have been studied for their potential applications in vibration isolation [12–15], biomedical devices [16], protective systems [17], energy absorption [18, 19], and wave attenuation [20]. Recently, origami has been used to create deployable mechanical metamaterials with unusual “negative” properties coded in the inherent architecture [21–30]. For example, negative Poisson’s ratio and negative stiffness are easily realized in a reentrant origami-based structure [31] compared to traditional design methods.

Generally, materials with a positive Poisson’s ratio undergo a transverse contraction when stretched, while materials with a negative Poisson’s ratio experience a transverse expansion when stretched [32]. Although the deformation mechanism of mechanical metamaterials with either positive and negative Poisson’s ratios has been investigated in previous studies [7, 10, 17, 20, 22, 31–33], critical aspects have been overlooked: 1) whether any combinations of Poisson’s ratio can be realized in different directions, 2) how the targeted Poisson’s ratios are structurally realized, and 3) how the number of deformation patterns of a cellular structure increases with the configurations of unit cells in different deformation paths. This mechanism may result in more applications. For example, in a recent study, we found that there is a relation between Poisson’s ratio and the thermal expansion coefficient in kirigami-based materials [34]; thus if any combinations of Poisson’s ratio can be realized, then that of the thermal expansion coefficient can be realized in a designed material. Also, this auxetic design has some merit for the biomedical application. When the structure is used as implant in the intervertebral disc, the uniaxial compression would not cause a cross-section expansion, and thus, it would not squeeze the surrounding tissues and can avoid aching.

Here, our proposed ring-like kirigami structure can be easily transformed into a concave shape in one direction for a negative Poisson’s ratio and a convex shape in another direction for a positive Poisson’s ratio. Compared to the origami-based designs [35, 36], our kirigami-based design enables us to straightforwardly generate a convex and concave pattern for the same structural unit. In this way, we can obtain any combinations of Poisson’s ratios along two orthometric directions in the 2D Poisson’s ratio space due to the different planar design angles and deformation modes in the two directions. In this sense, the Poisson’s ratios can be independently tuned and inversely designed [37]. Additionally, in theory and experiment, we find that a basic ring-like unit has four discrete deformation patterns and a continuous shearing deformation pattern, and a structure with four basic units has 16 discrete deformation patterns. Furthermore, additional potential deformation patterns can be realized by plenty of multi-unit combinations (with 8, 16, or 32 … basic units). Finally, we showed that a 3D cellular structure with multiple deformation modes can be built by stacking 2D cellular structures layer by layer.

Materials and Methods

Unit Design

Here, we designed a ring-like unit cell with multiple deformation modes. In Figure 1A, the ring-like unit cell comprises four “z”-shaped structures (also in the gray frame in Figure 1C), which are folded with mountain (solid line) and valley (dashed line) creases and formed into 3D configurations from the 2D patterns by taping the edges (see purple edges in Figure 1A and see also Supplementary Figure S1), where the opposite “z”-shaped structures are centrosymmetric. ${\gamma }_1$ and ${\gamma }_2$ are important planar design angles on the facets of the opposite “z”-shaped structures, as shown in Figure 1A. For a regular unit, the “z”-shaped structure with ${\gamma }_1$ is perpendicular to that with ${\gamma }_2$, that is, $\beta =90°$. The length parameters $m$, $n$, and $q$ are identical for the four “z”-shaped structures (in this study, $m=n=2q$), and only the angle parameters ${\gamma }_1$ and ${\gamma }_2$ are different. Deformation angles ${\theta }_1$ and ${\theta }_2$ are defined as the dihedral angles between two facets, corresponding to the “z”-shaped structures with ${\gamma }_1$ and ${\gamma }_2$, respectively (Figure 1B top, pink, and blue dihedrals). Based on the requirement of geometrical compatibility (the same height in z-direction), there is a relation between ${\theta }_1$ and ${\theta }_2$ (Figure 1B bottom; see Eq. 11). The panels of the kirigami structure are assumed to be rigid. The Miura origami is a specific case of our kirigami design, which is shown in Section 8 of SI.

FIGURE 1

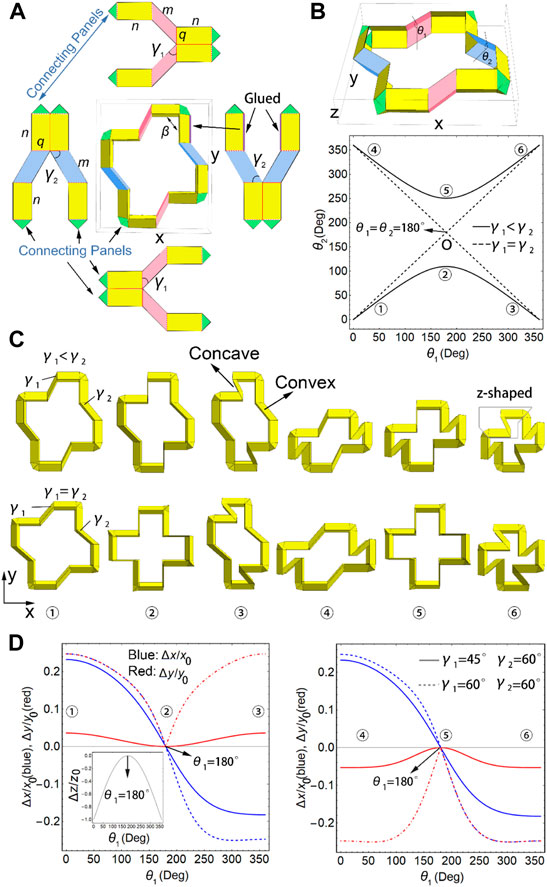
FIGURE 1. Ring-like unit design. (A) Ring-like unit comprising four “z”-shaped structures with their 2D folding patterns and lengths ($m$, $n$, and $q$) and their angle parameters (${\gamma }_1$ and ${\gamma }_2)$. (B) Definition of the deformation angles ${\theta }_1$ and ${\theta }_2$ and their relations (in deformation paths, $\mathrm{①}\to \mathrm{②}\to \mathrm{③}$ and $\mathrm{④}\to \mathrm{⑤}\to \mathrm{⑥}$) for ${\gamma }_1<{\gamma }_2$ and ${\gamma }_1={\gamma }_2$. (C) Structural configurations $\mathrm{①}\sim \mathrm{⑥}$. (D) Nominal strains $\frac{\Delta x}{x_0}$ (blue lines) and $\frac{\Delta y}{y_0}$ (red lines) as functions of the deformation angle ${\theta }_1$ with ${\gamma }_1={\gamma }_2=60°$ (nonsolid lines, including blue dashed and red dot–dashed lines) and ${\gamma }_1=45°$ and ${\gamma }_2=60°$ (solid lines). Inset, nominal strains $\frac{\Delta z}{z_0}$ as a function of ${\theta }_1$. For all units here, $\beta =90°$.

Sample Fabrication

The ring-like unit samples were fabricated using the Strathmore 500 Series 3-ply Bristol card stock that was laser cut based on a design pattern generated using Mathematica 11.2. The edges of the given panels were glued to be connected (Figure 1A) to build 3D units for flexible foldability. See SI Section 6 for details.

Calculation Methods

The calculation methods for the sizes of a ring-like unit and four-unit combination comprising four ring-like units and the design method for targeted Poisson’s ratios are given in SI Sections 1–4.

Sample Size Measurement

The top box, camera, and bottom box were connected and moved together with the test head under the control of a universal testing machine. The sample was put on a motionless substrate. When the bottom box touched the sample, it was deformed and captured using a camera. Then, the binary images of the sample at different times were obtained, and the sample in each image was enclosed within a minimum enclosed rectangle, and then, the x- and y-sizes were obtained. Finally, the real size of the sample was obtained by using a conversion factor of 0.4167 mm/pixel. The experimental setup is shown in Figure 3F.

Results and Discussion

Here, we used Mathematica 11.2 software to simulate the deformation using geometrical relation equations (see SI) to obtain the vertex coordinates and then the facets of the structures at different deformation angles.

Unit Cell Deformation

Once ${\theta }_1$ is fixed, the height in the z-direction of the whole ring-like structure is determined, and then, ${\theta }_2$ is determined. With different initial settings of ${\theta }_1={\theta }_2=0$ and ${\theta }_1=360°-{\theta }_2=0$, there are two deformation paths, that is, $\mathrm{①}\to \mathrm{②}\to \mathrm{③}$ and $\mathrm{④}\to \mathrm{⑤}\to \mathrm{⑥}$, in the ${\theta }_1- {\theta }_2$ space (see Figure 1B for the plot and Figure 1C for the configurations of $\mathrm{①}\sim \mathrm{⑥}$). For ${\gamma }_1<{\gamma }_2$, the two paths are disconnected. However, for ${\gamma }_1={\gamma }_2$, the two paths are connected at point O, and points $\mathrm{②}$ and $\mathrm{⑤}$ overlap, resulting in the connected “X”-shaped paths (Figure 1B plot). Figure 1C shows the discrete configuration examples $\mathrm{①}\sim \mathrm{⑥}$ of a unit with ${\gamma }_1<{\gamma }_2$ and ${\gamma }_1={\gamma }_2$ and the convex (${\theta }_2<180°$) and concave (${\theta }_1>180°$) parts in a unit cell. Figures 1B,C show that these discrete configurations are realized by continuously changing ${\theta }_1$. In fact, for ${\gamma }_1<{\gamma }_2$, configuration $\mathrm{②}$ can be switched to $\mathrm{⑤}$ with panel bending, and vice versa. Here, we study only the case of ${\gamma }_1\le {\gamma }_2$, as the case of ${\gamma }_1\ge {\gamma }_2$ can be known by swapping the current ${\gamma }_1$ and ${\gamma }_2$, which means that the unit is rotated by $90°$. See SI Sections 1 and 2 for the detailed geometric model.

Here, the ring-like units possess various deformation behaviors in the x- and y-directions. Figure 1D shows the isotropic deformations for ${\gamma }_1={\gamma }_2=60°$ along paths $\mathrm{①}\to \mathrm{②}$ and $\mathrm{⑤}\to \mathrm{⑥}$, where the nominal x- and y-strains are equal ($\frac{\Delta x}{x_0}=\frac{\Delta y}{y_0}$, see the overlapped blue and red nonsolid lines, where the nonsolid lines are pertaining to ${\gamma }_1={\gamma }_2=60°$, and the solid lines are pertaining to ${\gamma }_1=45°$ and ${\gamma }_2=60°$), and the anisotropic deformations ($\frac{\Delta x}{x_0}\ne \frac{\Delta y}{y_0}$) for ${\gamma }_1={\gamma }_2=60°$ along paths $\mathrm{②}\to \mathrm{③}$ and $\mathrm{④}\to \mathrm{⑤}$ and for ${\gamma }_1=45°$ and ${\gamma }_2=60°$ along all paths. The nominal z-strain is always symmetrical about ${\theta }_1=180°$ (see Figure 1D inset). Here, the nominal strain is defined as $\frac{\Delta s}{s_0}=\frac{s}{s_0}-1$, where $s=x,y,z$ denotes the dimension and $s_0=s{|}_{{\theta }_1=180°}$ denotes the initial dimension. Figure 1D implies that we may obtain arbitrary combinations of different Poisson’s ratios along the x- and y-directions. The relations between the nominal z-strain and the nominal x- and y-strains are shown in Supplementary Figure S3, which is a variant of Figure 1D.

There are two degrees of freedom (DOFs) of the ring-like unit, that is, ${\theta }_1$ and $\beta$. To explain the two DOFs, Figures 2a and c show that the ring-like unit can be skewed by $\beta \ne 90°$ with fixed ${\theta }_1$ compared to that with $\beta =90°$ (Figure 2B), with the opposite “z”-shaped structures remain parallel. We defined the dimensions of the units by aligning the AB side in the y-direction, as shown in Figure 2A, and found that with the continuous change of $\beta$, the ring-like unit shows a continuous shearing deformation mode. The size changes in the x- and y-directions under different values of $\beta$ are shown in Figures 2E, F, respectively. This shows that ${\theta }_1$ controls the opening and closing mode of the structure, while $\beta$ controls the shearing mode.

FIGURE 2

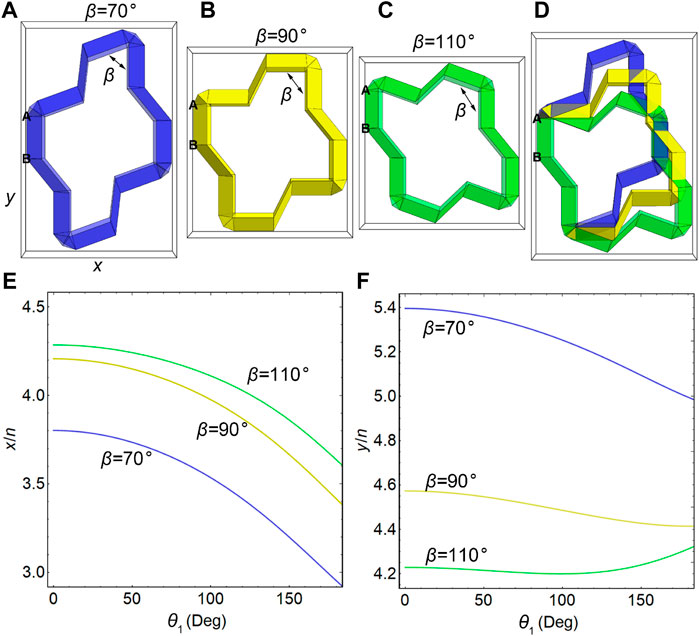
FIGURE 2. Shearing deformation modes of the ring-like unit. Configurations of the ring-like unit with (A) $\beta =70°$, (B) $90°$, and (C) $110°$. (D) Overlapped configurations of (A–C). The dimensionless size, (E) $x/n$ and (F) $y/n$, as functions of the deformation angle ${\theta }_1$ with (A) $\beta =70°$, (B) $90°$, and (C) $110°$. Here, ${\gamma }_1=45°$ and${\gamma }_2=60°.$

To demonstrate the analytical geometrical model with experimental data, we compressed a paper-made ring-like unit (Figure 3) in the z-direction using a universal testing machine. Here, the unit with ${\gamma }_1=45°$ and ${\gamma }_2=60°$ is programmed into four discrete patterns ($\mathrm{①}$, $\mathrm{③}$, $\mathrm{④}$, and$\mathrm{⑥}$ corresponding to Figure 1C; the sample cannot stay at ${\theta }_1=180°$, i.e., transitional patterns $\mathrm{②}$ and $\mathrm{⑤}$) and compressed in the z-direction. From the top, a camera is used to obtain a video of the unit deformation process to calculate the x- and y-dimensions (see Figure 3F for the experimental setup and Supplementary Videos S1–4). The measured x- and y-dimensions are shown in Figures 3A–D and compared to the analytical curves. When the unit is shrunk in a given direction under compression, the scraping and friction between the unit and substrate become apparent; thus, the measured dimensions oscillate around the analytical values (see Figures 3B–D). Figure 3E is used to show the sample layout direction compared with the model. The results of the model and experiment agree with each other well. The experimental setup is shown in Figure 3F.

FIGURE 3

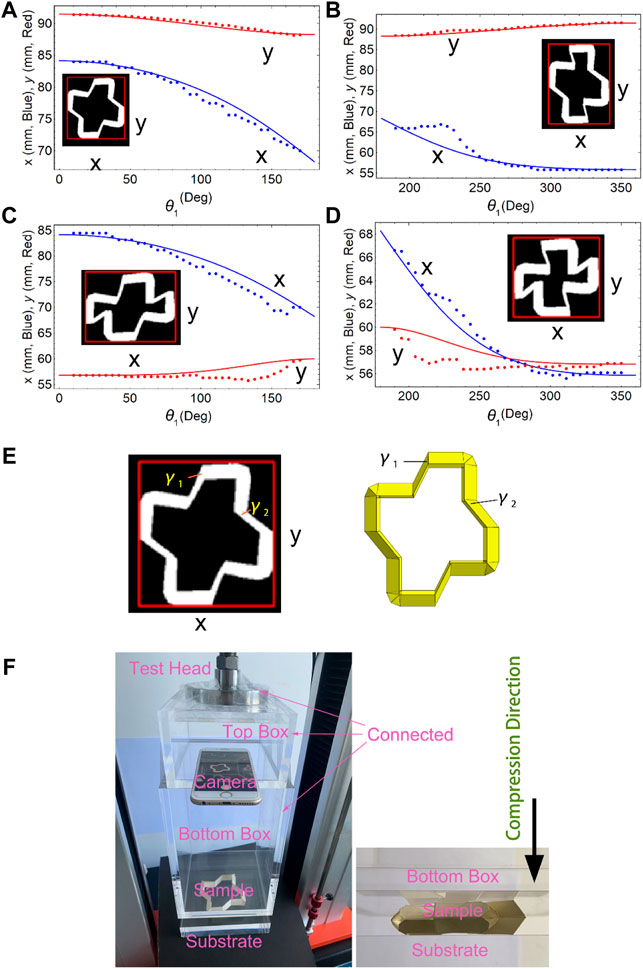
FIGURE 3. Experimental verification. Dimensions of a unit with ${\gamma }_1=45°$, ${\gamma }_2=60°$, and $\beta =90°$ under compression in the z-direction for four patterns: (A) $\mathrm{①}$, (B) $\mathrm{③}$, (C) $\mathrm{④}$, and (D) $\mathrm{⑥}$ (curves, analytical model; points, measured data). (E) ${\gamma }_1$ and ${\gamma }_2$ in the binary image and structural model. (F) Experimental setup.

Inverse Design for the Desired Poisson’s Ratio

After validating the analytical model, we focused on the inverse design of a unit with $\beta =90°$ for targeted Poisson’s ratios as the x- and y-dimensions can be clearly defined with $\beta =90°$ (see Figure 2B). Poisson’s ratios in the x- and y-directions under compression in the z-direction are calculated by ${\nu }_{zx}=-\frac{dx/x}{dz/z}$ and ${\nu }_{zy}=-\frac{dy/y}{dz/z}$ [31] based on the definition in Figure 1B. Even with ${\gamma }_1={\gamma }_2$, the ring-like unit shows various Poisson’s ratios in different paths. In Figure 4A, with ${\gamma }_1={\gamma }_2=60°$ for deformation path $\mathrm{①}\to \mathrm{②}$, we have ${\nu }_{zx}>0$ and ${\nu }_{zy}>0$; for $\mathrm{②}\to \mathrm{③}$, ${\nu }_{zx}<0$ and ${\nu }_{zy}>0$; for $\mathrm{④}\to \mathrm{⑤}$, ${\nu }_{zx}>0$ and ${\nu }_{zy}<0$; and for $\mathrm{⑤}\to \mathrm{⑥}$, ${\nu }_{zx}<0$ and ${\nu }_{zy}<0$. Therefore, we can expect more various Poisson’s ratios of a unit cell with ${\gamma }_1\ne {\gamma }_2$. Taking ${\gamma }_2=60°$ as example, we plotted Poisson’s ratio curves (${\nu }_{zx}-{\nu }_{zy}$ relations) with ${\gamma }_1=60°$, $59°$, and $55°$ for paths $\mathrm{①}\to \mathrm{②}$, $\mathrm{②}\to \mathrm{③}$, $\mathrm{④}\to \mathrm{⑤}$, and $\mathrm{⑤}\to \mathrm{⑥}$ as shown in Figure 4B. If we plot the ${\nu }_{zx}-{\nu }_{zy}$ curves within ${\gamma }_1\le {\gamma }_2=60°$, the curves would fill the regions A (pink), B (blue), C (yellow), and D (green), which are the half of ${\nu }_{zx}-{\nu }_{zy}$ space (i.e., regions A, B, C, and D and regions A′, B′, C′, and D′ are symmetric about ${\nu }_{zx}={\nu }_{zy}$, see Figure 4B). Also, this does not limit to ${\gamma }_2=60°$, which implies that the curves would fill the other half of ${\nu }_{zx}-{\nu }_{zy}$ space (i.e., regions A’+B’+C’+D′) by swapping the x-size and y-size (or swapping ${\gamma }_1$ and ${\gamma }_2$), which means that a unit cell is rotated by $90°$. For example, if the design parameters ${\gamma }_1=\tau$ and ${\gamma }_2=\omega$ obtain the point $({\nu }_{zx},{\nu }_{zy})=({\nu }_{\tau },{\nu }_{\omega })$ in the Poisson’s ratio space, then the point $({\nu }_{zx},{\nu }_{zy})=({\nu }_{\omega },{\nu }_{\tau })$ can be obtained by ${\gamma }_1=\omega$ and ${\gamma }_2=\tau$.

FIGURE 4

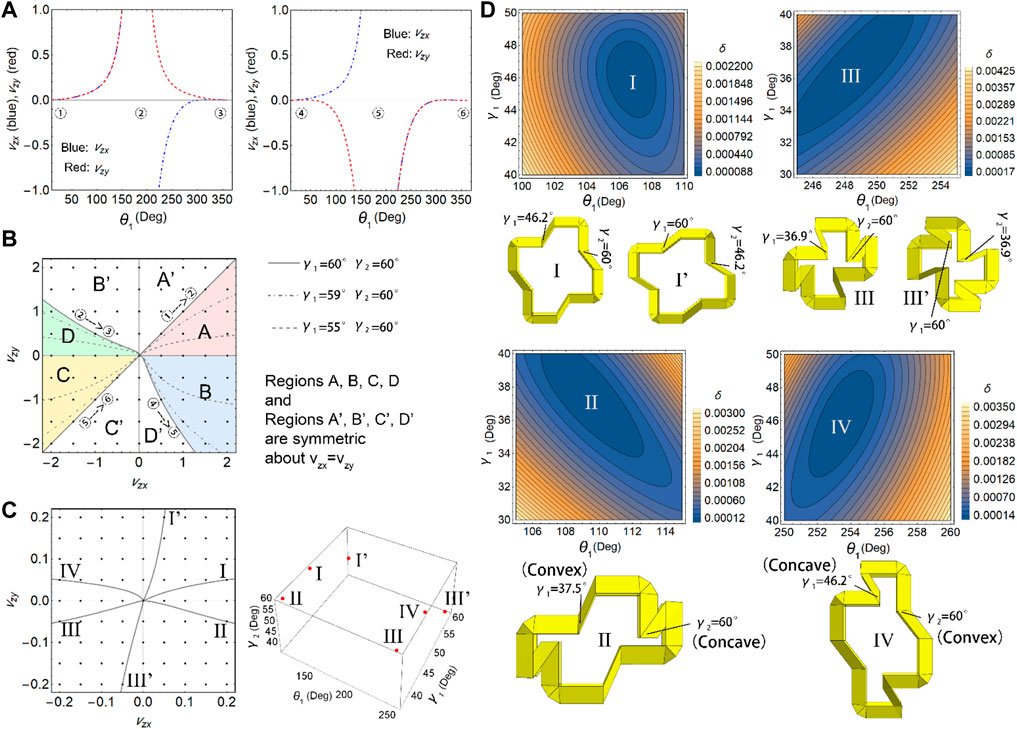
FIGURE 4. Optimal design for the targeted Poisson’s ratios in the x- and y-directions. (A) Poisson’s ratios along different deformation paths with ${\gamma }_1={\gamma }_2=60°$. (B) With ${\gamma }_1<{\gamma }_2=60°$, the region in the 2D Poisson’s ratio space where the curve $({\nu }_{zx},{\nu }_{zy}$) can reach are plotted. Pink region, deformation from $\mathrm{①}\to \mathrm{②}$; green region, $\mathrm{②}\to \mathrm{③}$; blue region, $\mathrm{④}\to \mathrm{⑤}$; and yellow region, $\mathrm{⑤}\to \mathrm{⑥}$. (C) Optimal design for selected Poisson’s ratios $({\nu }_x,{\nu }_y)=(0.2, 0.05)$, $(0.05, 0.2)$, $(0.2, -0.05)$, $(-0.2, -0.05)$, $(-0.05, -0.2)$, and $(-0.2, 0.05)$ at points I, I′, II, III, III′, and IV in the Poisson’s ratio space, respectively, and the corresponding optimal parameters (red points) in the design space. (D) Searching for the optimal parameters in the design space with ${\gamma }_2=60°$. Top: contour plots of $\delta$; bottom, configurations. For I, ${\theta }_1=106.8°$, ${\theta }_2=84°$, ${\gamma }_1=46.2°$, and ${\gamma }_2=60°$. For I′, ${\theta }_2=106.8°$, ${\theta }_1=84°$, ${\gamma }_2=46.2°$, and ${\gamma }_1=60°$. For II, ${\theta }_1=109.3°$, ${\theta }_2=290.0°$, ${\gamma }_1=37.5°$, and ${\gamma }_2=60°$. For III, ${\theta }_1=248.8°$, ${\theta }_2=290.2°$, ${\gamma }_1=36.9°$, and ${\gamma }_2=60°$. For III′, ${\theta }_2=248.8°$, ${\theta }_1=290.2°$, ${\gamma }_2=36.9°$, and ${\gamma }_1=60°$. For IV, ${\theta }_1=253.6°$, ${\theta }_2=83.7°$, ${\gamma }_1=46.2°$, and ${\gamma }_2=60°$.

The optimization of the structures for given Poisson’s ratios in the x- and y-directions can be achieved by minimizing the error, $\delta ={({\nu }_{zx}-{\nu }_x)}^2+{({\nu }_{zy}-{\nu }_y)}^2$, subjected to $0<{\theta }_1$, ${\theta }_2<360°$, and $0<{\gamma }_1\le {\gamma }_2<90°$ (see SI for details), where $({\nu }_x,{\nu }_y)$ are the targeted Poisson’s ratios. To test this method, we chose six points, I, I′, II, III, III′, and IV, in the Poisson’s ratio space to represent the six targeted pairs of Poisson’s ratios, as shown in Figure 4C, where points I, II, III, and IV are four vertices of a rectangle, and I′ and III′ are the symmetrical points of I and III about ${\nu }_{zx}={\nu }_{zy}$. As a result, we obtained${\theta }_1=106.8°$, ${\theta }_2=84°$, ${\gamma }_1=46.2°$, and ${\gamma }_2=60°$ for point I with $({\nu }_x,{\nu }_y)=(0.2, 0.05)$. At point I′ with $({\nu }_x,{\nu }_y)=(0.05, 0.2)$, we have the structure with ${\theta }_2=106.8°$, ${\theta }_1=84°$, ${\gamma }_2=46.2°$, and ${\gamma }_1=60°$, which is shown as the structure I′ in Figure 4D. Other optimal design results for points II, III, III′, and IV are also shown in Figures 4C,D (with the resulting parameters listed in the caption of Figure 4), where Figure 4C shows the ${\nu }_{zx}-{\nu }_{zy}$ curves passing through the six targeted points (left) and the corresponding parameters in the 3D design space $({\theta }_1,{\gamma }_1,{\gamma }_2)$ (right), and Figure 4D presents the contour plots and minima of $\delta$ and the corresponding structural configurations. Taking configurations II and IV as examples, the convex and concave parts result in positive and negative Poisson’s ratios, respectively, but the specific values are determined by the design angles ${\gamma }_1$ and ${\gamma }_2$. This optimization method provides an effective tool to design a ring-like unit with targeted Poisson’s ratios, and the minimum value of $\delta$ can be less than ${10}^{-12}$ for each case.

Multiple Deformation Patterns of 2D Cellular Structures

After understanding the deformation mechanism of one ring-like unit, here we focus on that with multiple units. Four identical ring-like units can be combined to form a four-unit combination, which can be periodically replicated to construct a 2D cellular structure, as shown in Figure 5A (in the gray shade, the four-unit combination is displayed with a yellow–pink–yellow–pink pattern because the diagonal ring-like units are with the same configuration). Although the four ring-like units are identically designed with ${\gamma }_1=45°$, ${\gamma }_2=60°$, and $\beta =90°$, four deformation patterns of each ring-like unit (see Figure 1C, $\mathrm{①}$, $\mathrm{③}$, $\mathrm{④}$, and $\mathrm{⑥}$) make $4\times 4=16$ discrete patterns for the four-unit combination. Figure 5B introduces one pattern of four-unit combinations in detail, and the other 15 patterns are shown in Figure 5C. Figure 5B shows the relation between the dimensionless sizes $x_c/n$ and $y_c/n$ (where $x_c$ and $y_c$ are defined as the sizes of the four-unit combination in the x- and y-directions, see also Supplementary Figure S2 and Eq. (14)). The four-unit combination is with two ring-like units in pattern $\mathrm{①}$ (yellow) and the other two in pattern $\mathrm{③}$ (pink) (see Figure 5B). Here, the four ring-like units have the same value of ${\theta }_1$ within $0\le {\theta }_1\le 180°$ to maintain the same height in the z-direction, which is necessary given the geometrical compatibility requirements for building 3D cellular structures. In the plot of Figure 5B, there is a sharp corner in the $x_c/n-y_c/n$ curve since, before the corner (stage 1), the yellow unit dominates the $x_c$ value, and then, the pink unit dominates the $x_c$ value (stage 2). Similar sharp corners, as well as smooth $x_c/n-y_c/n$ curves, can be found in the other 15 patterns in Figure 5C. In fact, the 16 patterns can be divided into four groups based on the pattern of the diagonal ring-like units in yellow (groups #1, #2, #3, and #4 in Figure 5C, where the symbol “#a, b” means No. b in group #a), and within each group, the pattern of the yellow unit remains unchanged. Some size ranges related to the x- and y-dimensions of the four-unit combination are identical. For example, in group #2, the first two plots and last two plots individually have the same $x_c$ range, while the first and fourth plots and the second and third plots individually have the same $y_c$ range. This implies that different four-unit combinations may be again connected through the side with identical sizes to create a new unit (comprising 4n (n = 2, 3, 4, … ) basic ring-like units), then the number of deformation patterns of the resulting structure is greatly increased. This operation can be recursively implemented within a group (see the combination of #3.1 and #3.4 in Figure 5D) or across groups (see the combination of #3.1 and #2.1 in Figure 5D).

FIGURE 5

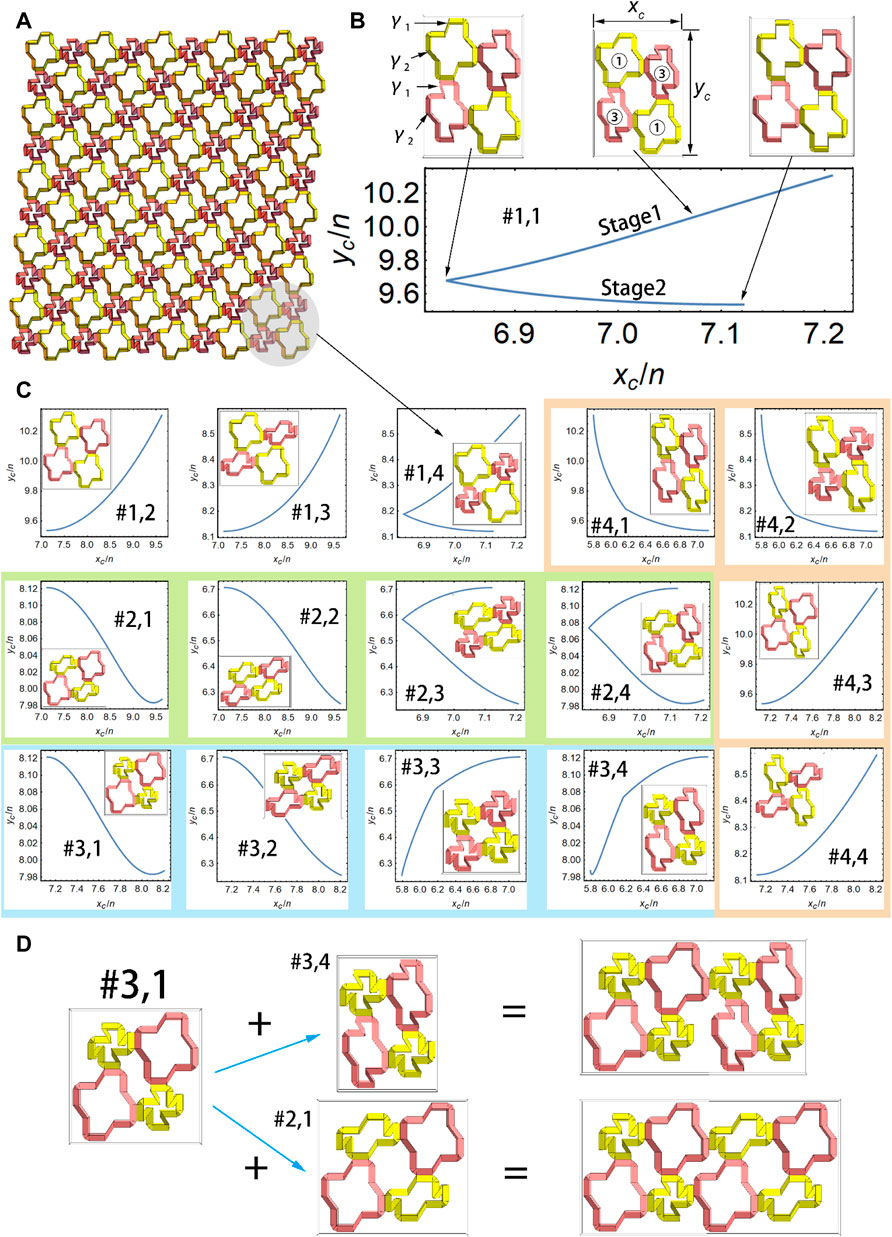
FIGURE 5. Multiple deformation patterns of 2D cellular structures. (A) 2D cellular structures comprising $5\times 5$ four-unit combinations. (B) One deformation pattern of a four-unit combination comprising four ring-like units. (C) Other 15 deformation patterns of the four-unit combination. Each deformation pattern is represented by a $x_c/n-y_c/n$ curve. For all units, the value of ${\theta }_1$ is the same, and $0\le {\theta }_1\le 180°$. The 16 patterns can be divided into four groups, shown against white (group #1), green (group #2), blue (group #3), and orange (group #4) backgrounds. (D) Combination within a group: #3.1 and #3.4; combination across groups: #3.1 and #2.1.

The shearing deformation of the 2D cellular structures with $\beta \ne 90°$ compared to the non-shearing case with $\beta =90°$ is shown in Figure 6. Three representatives of the 16 discrete patterns are chosen, as shown in Figures 6A–C, and the top edges of the upper-left-most yellow structures are aligned with the y-direction (Figure 6A). This is to show a rotation-like effect of the 2D cellular structures with shearing deformations, although the directions of key sides are fixed. This figure shows the potential ability to control mechanical waves in the shearing directions (see the possible shearing forces in Figure 6B), which is beyond the topic of this work but will be an interesting further work. The structures in Figure 6 (column 1–3) are shown on the x–y plane, and they can be stacked in the z-direction layer by layer to build 3D cellular structures (see Figure 6, column 4).

FIGURE 6

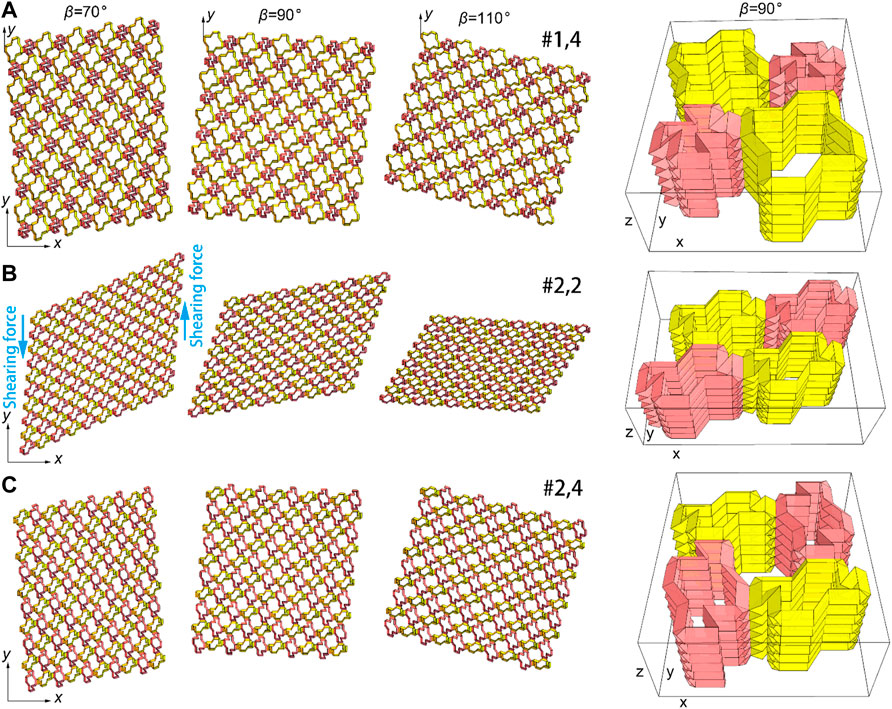
FIGURE 6. Shearing deformation modes of the 2D cellular structure. Three of the 16 discrete patterns in Figure 5C, (A) #1.4 (B) #2.2 (C) #2.4; column 1–3, 2D cellular structures with $\beta =70°,90°,\text{ and }110°$; column 4, 3D cellular structures with $\beta =90°$.

Another Method for Building 2D and 3D Cellular Structures

Finally, we explore another design of cellular structures consisting of multiple ring-like units with $\beta =90°$ (see Figure 7). Different from the manner in Figure 6, the 2D cellular structure is constructed by symmetrically connecting the ring-like units with the same pattern in the x- and y-direction, and the 3D cellular structure is also built by stacking 2D structures. Similar to the units discussed earlier, both the 2D and 3D structures are flat-foldable. By taking advantage of our analysis of a unit cell, we can design new 2D and 3D cellular structures exhibiting anisotropic and isotropic deformation in the x–y plane under uniaxial compression/tension in the z-direction. Similar to a ring-like unit with ${\gamma }_1=45°$ and ${\gamma }_2=60°$ (Figure 1D, solid lines), a 3D cellular structure comprising the same units shows two anisotropic deformation behaviors: for $\mathrm{②}\to \mathrm{①}$, we have ${\nu }_{zx}>0$ and ${\nu }_{zy}>0$ but ${\nu }_{zx}\ne {\nu }_{zy}$; and for $\mathrm{②}\to \mathrm{③}$, ${\nu }_{zx}<0$ and ${\nu }_{zy}>0$ (Figure 7A); likewise, the 3D cellular structure shows two other anisotropic deformation behaviors: for $\mathrm{⑤}\to \mathrm{④}$, ${\nu }_{zx}>0$, and ${\nu }_{zy}<0$; and for $\mathrm{⑤}\to \mathrm{⑥}$, ${\nu }_{zx}<0$ and ${\nu }_{zy}<0$ but ${\nu }_{zx}\ne {\nu }_{zy}$ (Figure 7B). Although ${\nu }_{zx}$ and ${\nu }_{zy}$ have the same sign, their values are different because of ${\gamma }_1\ne {\gamma }_2$ (see also a ring-like unit in Figure 1D with ${\gamma }_1=45°$ and ${\gamma }_2=60°$, solid lines). Moreover, isotropic behaviors can be realized with the same value of ${\gamma }_1$ and ${\gamma }_2$. Figure 7C shows two isotropic deformation behaviors with ${\gamma }_1={\gamma }_2=60°$: for $\mathrm{②}\to \mathrm{①}$, ${\nu }_{zx}>0$ and ${\nu }_{zy}>0$; for $\mathrm{②}\to \mathrm{⑥}$, ${\nu }_{zx}<0$, and ${\nu }_{zy}<0$ (see also a ring-like unit in paths $\mathrm{②}\to \mathrm{①}$ and $\mathrm{⑤}\to \mathrm{⑥}$ in Figure 1D with ${\gamma }_1={\gamma }_2=60°$, nonsolid lines, notice that configurations $\mathrm{②}$ and $\mathrm{⑤}$ are identical, as shown in Figures 1B,C). These cellular structures also have only one DOF with $\beta =90°$ (folding and unfolding by manipulating one parameter, i.e., the deformation angle ${\theta }_1$; see Figure 1B), which can be easily controlled as an origami robot. Using this construction method, we can realize the deformation behavior of a 3D cellular structure only based on that of a single unit.

FIGURE 7

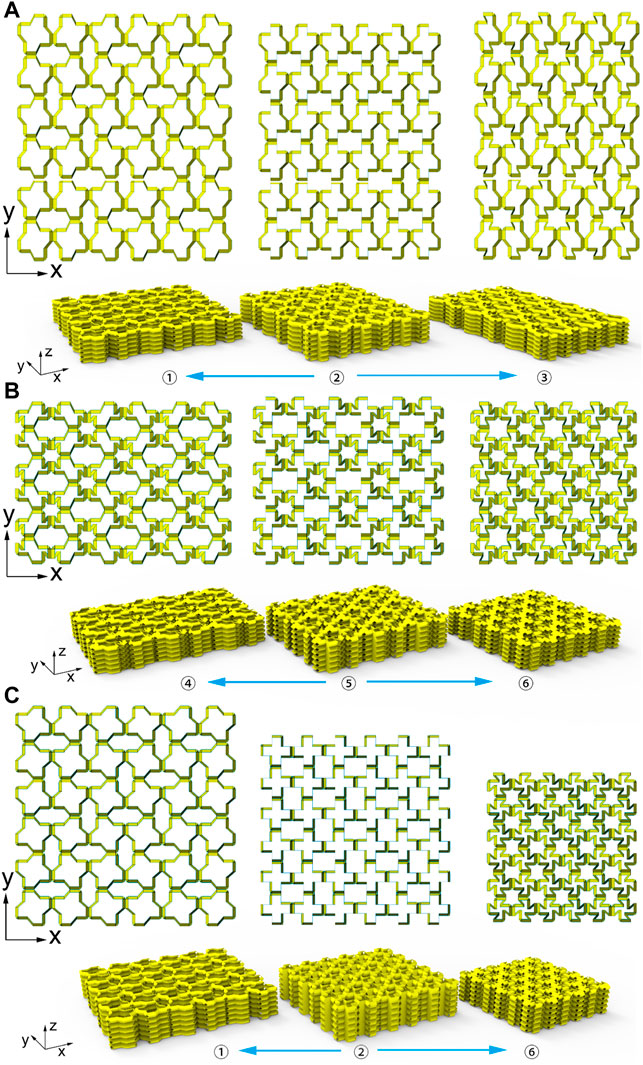
FIGURE 7. Three patterns of 3D cellular structures. (A) Deformation paths $\mathrm{②}\to \mathrm{① and ②}\to \mathrm{③}$ with ${\gamma }_1=45°$ and ${\gamma }_2=60°$. (B) Deformation paths $\mathrm{⑤}\to \mathrm{④ and ⑤}\to \mathrm{⑥}$ with ${\gamma }_1=45°$ and ${\gamma }_2=60°$. (C) Deformation paths $\mathrm{②}\to \mathrm{① and ②}\to \mathrm{⑥}$ with ${\gamma }_1={\gamma }_2=60°$. Anisotropic pattern: (A) and (B); isotropic pattern: (C). Top: 2D metamaterials with $6\times 6$ units. Bottom: 3D metamaterials with $6\times 6\times 6$ units.

The cellular structures in Figure 7 with 6 × 6 × 6 units look like 2.5D because for each unit, the height is less than the length or the width. But in essence, the structures are 3D since the layers can be continuously stacked along the z-direction, such as with 6 × 6 × 12 units. Here, we used 6 × 6 × 6 units for clear visualization.

Conclusion

We have investigated the unique kinematics of kirigami-based 3D metamaterials with ring-like units. We foundd that the various combinations of Poisson’s ratios (values and signs) can be obtained with different combinations of the design angles ${\gamma }_1$ and ${\gamma }_2$ and targeted Poisson’s ratios can be realized by choosing the proper deformation paths. Additionally, we numerically and experimentally verified the analytical geometrical model of the ring-like unit cell. Interestingly, we showed multiple continuous and discrete deformation patterns for a ring-like unit and a multi-unit combination. These 2D and 3D cellular structures, offering multiple deformation patterns, show great potential for various engineering applications, from robotics, and impact absorbers to biomedical implants.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author Contributions

NY designed and performed the research; JZ and SW processed the data; NY and YY analyzed the data and wrote the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (11872046), the Scientific Research Funding of Shantou University (NTF19012), the 2020 LKSF Cross-Disciplinary Research Projects (2020LKSFG01D), the Natural Science Foundation of Guangdong, China (2021A1515010318, 2022A1515011024, and 2018A030307030), the Key Project of Guangdong Provincial Department of Education (2021ZDZX2007), and the Science and Technology Project of Guangdong, China (180917114960497).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.909536/full#supplementary-material

References

1. Lee K, Wang Y, Zheng C. Twister Hand: Underactuated Robotic Gripper Inspired by Origami Twisted tower. IEEE Trans Robot (2020) 36:488–500. doi:10.1109/tro.2019.2956870

CrossRef Full Text | Google Scholar

2. Hu W, Lum GZ, Mastrangeli M, Sitti M. Small-scale Soft-Bodied Robot with Multimodal Locomotion. Nature (2018) 554:81–5. doi:10.1038/nature25443

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Kanik M, Orguc S, Varnavides G, Kim J, Benavides T, Gonzalez D, et al. Strain-programmable Fiber-Based Artificial Muscle. Science (2019) 365:145–50. doi:10.1126/science.aaw2502

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Wu W, Hu W, Qian G, Liao H, Xu X, Berto F. Mechanical Design and Multifunctional Applications of Chiral Mechanical Metamaterials: a Review. Mater Des (2019) 180:107–950. doi:10.1016/j.matdes.2019.107950

CrossRef Full Text | Google Scholar

5. Boatti E, Vasios N, Bertoldi K. Origami Metamaterials for Tunable thermal Expansion. Adv Mater (2017) 29:1700360. doi:10.1002/adma.201700360

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Mirzaali MJ, Pahlavani H, Zadpoor AA. Auxeticity and Stiffness of Random Networks: Lessons for the Rational Design of 3D Printed Mechanical Metamaterials. Appl Phys Lett (2019) 115:021901. doi:10.1063/1.5096590

CrossRef Full Text | Google Scholar

7. Dudek KK, Gatt R, Dudek MR, Grima JN. Negative and Positive Stiffness in Auxetic Magneto-Mechanical Metamaterials. Proc R Soc A (2018) 474:20180003. doi:10.1098/rspa.2018.0003

CrossRef Full Text | Google Scholar

8. Yang H, Ma L. Multi-stable Mechanical Metamaterials with Shape-Reconfiguration and Zero Poisson's Ratio. Mater Des (2018) 152:181–90. doi:10.1016/j.matdes.2018.04.064

CrossRef Full Text | Google Scholar

9. Tan X, Wang B, Zhu S, Chen S, Yao K, Xu P, et al. Novel Multidirectional Negative Stiffness Mechanical Metamaterials. Smart Mater Struct (2019) 29:015037. doi:10.1088/1361-665x/ab47d9

CrossRef Full Text | Google Scholar

10. Yang N, Chen C-W, Yang J, Silverberg JL. Emergent Reconfigurable Mechanical Metamaterial Tessellations with an Exponentially Large Number of Discrete Configurations. Mater Des (2020) 196:109143. doi:10.1016/j.matdes.2020.109143

CrossRef Full Text | Google Scholar

11. Dudek KK, Gatt R, Grima JN. 3D Composite Metamaterial with Magnetic Inclusions Exhibiting Negative Stiffness and Auxetic Behaviour. Mater Des (2020) 187:108403. doi:10.1016/j.matdes.2019.108403

CrossRef Full Text | Google Scholar

12. Sui N, Yan X, Huang TH, Xu J, Yuan FG, Jing Y. A Lightweight yet Sound-Proof Honeycomb Acoustic Metamaterial. Appl Phys Lett (2015) 106:171–905. doi:10.1063/1.4919235

CrossRef Full Text | Google Scholar

13. Lee C-M, Goverdovskiy VN. A Multi-Stage High-Speed railroad Vibration Isolation System with "negative" Stiffness. J Sound Vibration (2012) 331:914–21. doi:10.1016/j.jsv.2011.09.014

CrossRef Full Text | Google Scholar

14. Le TD, Ahn KK. Experimental Investigation of a Vibration Isolation System Using Negative Stiffness Structure. Int J Mech Sci (2013) 70:99–112. doi:10.1016/j.ijmecsci.2013.02.009

CrossRef Full Text | Google Scholar

15. Nagarajaiah S, Pasala DTR, Reinhorn A, Constantinou M, Sirilis AA, Taylor D. Adaptive Negative Stiffness: a New Structural Modification Approach for Seismic protection. Amr (2013) 639-640:54–66. doi:10.4028/www.scientific.net/amr.639-640.54

CrossRef Full Text | Google Scholar

16. Kuribayashi K, Tsuchiya K, You Z, Tomus D, Umemoto M, Ito T, et al. Self-deployable Origami Stent Grafts as a Biomedical Application of Ni-Rich TiNi Shape Memory alloy Foil. Mater Sci Eng A (2006) 419:131–7. doi:10.1016/j.msea.2005.12.016

CrossRef Full Text | Google Scholar

17. Imbalzano G, Linforth S, Ngo TD, Lee PVS, Tran P. Blast Resistance of Auxetic and Honeycomb sandwich Panels: Comparisons and Parametric Designs. Compos Structures (2018) 183:242–61. doi:10.1016/j.compstruct.2017.03.018

CrossRef Full Text | Google Scholar

18. Dudek KK, Wolak W, Gatt R, Grima JN. Impact Resistance of Composite Magnetic Metamaterials. Sci Rep (2019) 9:3963. doi:10.1038/s41598-019-40610-w

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Zhang L, Feih S, Daynes S, Chang S, Wang MY, Wei J, et al. Energy Absorption Characteristics of Metallic Triply Periodic Minimal Surface Sheet Structures under Compressive Loading. Additive Manufacturing (2018) 23:505–15. doi:10.1016/j.addma.2018.08.007

CrossRef Full Text | Google Scholar

20. Scarpa F, Yates JR, Ciffo LG, Patsias S. Dynamic Crushing of Auxetic Open-Cell Polyurethane Foam. Proc Inst Mech Eng C: J Mech Eng Sci (2002) 216:1153–6. doi:10.1243/095440602321029382

CrossRef Full Text | Google Scholar

21. Li M, Shen L, Jing L, Xu S, Zheng B, Lin X, et al. Origami Metawall: Mechanically Controlled Absorption and Deflection of Lightflection of Light. Adv Sci (2019) 6:1901434. doi:10.1002/advs.201901434

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Wang H, Zhao D, Jin Y, Wang M, Mukhopadhyay T, You Z. Modulation of Multi-Directional Auxeticity in Hybrid Origami Metamaterials. Appl Mater Today (2020) 20:100715. doi:10.1016/j.apmt.2020.100715

CrossRef Full Text | Google Scholar

23. Reis PM, Jaeger HM, Van Hecke M. Designer Matter: A Perspective. Extreme Mech Lett (2015) 5:25–9. doi:10.1016/j.eml.2015.09.004

CrossRef Full Text | Google Scholar

24. Fang H, Wang KW, Li S. Asymmetric Energy Barrier and Mechanical Diode Effect from Folding Multi-Stable Stacked-Origami. Extreme Mech Lett (2017) 17:7–15. doi:10.1016/j.eml.2017.09.008

CrossRef Full Text | Google Scholar

25. He YL, Zhang PW, You Z, Li ZQ, Wang ZH, Shu XF. Programming Mechanical Metamaterials Using Origami Tessellations. Composites Sci Tech (2020) 189:108015. doi:10.1016/j.compscitech.2020.108015

CrossRef Full Text | Google Scholar

26. Zhai Z, Wang Y, Jiang H. Origami-inspired, On-Demand Deployable and Collapsible Mechanical Metamaterials with Tunable Stiffness. Proc Natl Acad Sci U.S.A (2018) 115:2032–7. doi:10.1073/pnas.1720171115

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Liu B, Silverberg JL, Evans AA, Santangelo CD, Lang RJ, Hull TC, et al. Topological Kinematics of Origami Metamaterials. Nat Phys (2018) 14:811–5. doi:10.1038/s41567-018-0150-8

CrossRef Full Text | Google Scholar

28. Zhang J, Karagiozova D, You Z, Chen Y, Lu G. Quasi-static Large Deformation Compressive Behaviour of Origami-Based Metamaterials. Int J Mech Sci (2019) 153-154:194–207. doi:10.1016/j.ijmecsci.2019.01.044

CrossRef Full Text | Google Scholar

29. Brunck V, Lechenault F, Reid A, Adda-Bedia M. Elastic Theory of Origami-Based Metamaterials. Phys Rev E (2016) 93:033005. doi:10.1103/PhysRevE.93.033005

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Yang N, Silverberg JL. Decoupling Local Mechanics from Large-Scale Structure in Modular Metamaterials. Proc Natl Acad Sci U.S.A (2017) 114:3590–5. doi:10.1073/pnas.1620714114

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Yasuda H, Yang J. Reentrant Origami-Based Metamaterials with Negative Poisson's Ratio and Bistability. Phys Rev Lett (2015) 114:185502. doi:10.1103/physrevlett.114.185502

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Ruzzene M, Scarpa F, Soranna F. Wave Beaming Effects in Two-Dimensional Cellular Structures. Smart Mater Struct (2003) 12:363–72. doi:10.1088/0964-1726/12/3/307

CrossRef Full Text | Google Scholar

33. Qin G, Qin Z. Negative Poisson's Ratio in Two-Dimensional Honeycomb Structures. Npj Comput Mater (2020) 6:51. doi:10.1038/s41524-020-0313-x

CrossRef Full Text | Google Scholar

34. Yang N, Zhang M, Zhu R. 3D Kirigami Metamaterials with Coded thermal Expansion Properties. Extreme Mech Lett (2020) 40:100912. doi:10.1016/j.eml.2020.100912

CrossRef Full Text | Google Scholar

35. Wang H, Zhao D, Jin Y, Wang M, Mukhopadhyay T, You Z. Modulation of Multi-Directional Auxeticity in Hybrid Origami Metamaterials. Appl Mater Today (2020) 20:100715. doi:10.1016/j.apmt.2020.100715

CrossRef Full Text | Google Scholar

36. Pratapa PP, Liu K, Paulino GH. Geometric Mechanics of Origami Patterns Exhibiting Poisson's Ratio Switch by Breaking Mountain and valley Assignment. Phys Rev Lett (2019) 122:155501. doi:10.1103/physrevlett.122.155501

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Xue R, Li R, Du Z, Zhang W, Zhu Y, Sun Z, et al. Kirigami Pattern Design of Mechanically Driven Formation of Complex 3D Structures through Topology Optimization. Extreme Mech Lett (2017) 15:139–44. doi:10.1016/j.eml.2017.03.004

CrossRef Full Text | Google Scholar