Propagation and Focusing Properties of Vortex Beams Based on Light Ray Tracing

1 Introduction

Vortex beams, with a spiral phase term of exp(ilφ) (where l is the topological charge) [1, 2], can carry an optical orbital angular momentum (OAM) of lℏ per photon, in addition to the intrinsic spin angular momentum. Vortex beams have excited a surge of academic interest because they bring a new degree of freedom for photons with unbounded quantum states, and great success has been achieved in the creation and manipulation of optical OAM. In optical tweezers, vortex beams can trap microparticles and make them move orbitally, and this intrinsic OAM takes the form of a tangential component to the beam’s linear momentum density that can be transferred to illuminated objects [3–6]. In optical communications, OAM can be used as a new freedom degree of modulation/multiplexing to further increase the transmission capacity and density [7, 8]. In addition, vortex beams have been used to fabricate chiral structures in metals and spiral patterns in anisotropic polarization-dependent azobenzene polymers or 3D chiral microstructures in isotropic polymers [9–11]. In recent years, advanced control over OAM modes by changing the sign and value of the topological charge as the beam propagates has been explored, and these degrees of flexibility in beam manipulation are generic and can be utilized in many applications [12, 13].

The most common vortex beams are Laguerre–Gaussian beams or Bessel–Gaussian beams, which are eigensolutions of Helmholtz equations and have strict analytical forms, and their propagation and evolution behaviors in free space can be predicted precisely [14–16]. However, for specific vortex beams, such as the vortex beam with top-hat form intensity [16], a new kind of power-exponent-phase vortex beam [17], abruptly autofocusing vortex beams [18, 19], and even the beams with azimuthally nonuniform OAM [20, 21], although their propagating and focusing behavior can be derived by numerical methods, the exact analytical solution of the beam propagation is still not available, which makes the research on beam propagation characteristics encounter some difficulties. The ray-tracing method based on geometric optics, in which the intensity of light is treated as bundles of light rays traced during scattering, absorption, and multiple reflections, is a convenient and intuitive tool in optical research.

In this study, we studied and derived analytically the relation between the propagation distance and radius (and rotation angle) of vortex beams with top-hat form intensity in the propagating (or focusing) process, and the results can help us understand intuitively the propagation behaviors and focusing characteristics for this specific vortex beam based on ray tracing in the geometrical optics. The proposed method can accurately reproduce the complete dynamic characteristics of the propagation and focusing process of the vortex beam, and the method is also suitable for studying other specific vortex beams.

2 Vortex Beam Propagation Through the Homogeneous Medium Based on Light Ray Tracing

In geometrical optics, the straight propagation of light leads to two basic concepts: light ray and wavefront. As is known, the light ray is always perpendicular to the wavefront and travels in a straight line in the homogeneous and isotropic medium for the plane waves. However, the wavefront of a vortex beam is a helical surface, and it can be written as follows:

$kz-l\phi =C,(1)$

where C is a constant, k = 2πn/λ (λ is the wavelength of the vortex beam, and n is the refractive index of the medium), z is the propagation distance, and φ is the azimuth coordinate in the transverse plane. Because the light ray travels in straight lines in a homogeneous medium and perpendicular to the wavefront (as shown in Figure 1), the normal direction AP of a helical surface at a certain point A(x₀, y₀, 0) can be written as follows:

$\frac{x_z-x_0}{F_x\left(x_0,y_0,0\right)}=\frac{y_z-y_0}{F_y\left(x_0,y_0,0\right)}=\frac{z}{F_z\left(x_0,y_0,0\right)},(2)$

where F(x, y, z) = kz − lφ − C, F_x = ∂F/∂x, F_y = ∂F/∂y, and F_z = ∂F/∂z, then F_x, F_y, and F_z can be represented as follows:

$\begin{array}{cc}\hfill F_x\left(x_0,y_0,0\right)& =l{y}_0/r_0^2,\hfill \\ \hfill F_y\left(x_0,y_0,0\right)& =-l{x}_0/r_0^2,\hfill \\ \hfill F_z\left(x_0,y_0,0\right)& =k,\hfill \end{array}(3)$

where $r_0=\sqrt{x_0^2+y_0^2}$, which is the initial radius of the light ray at the z = 0 plane. According to Eqs 2, 3, the coordinate of point P for the light ray AP can be written as follows:

$\begin{array}{cc}\hfill x_z& =l{y}_{0}z/\left(k{r}_0^2\right)+x_0,\hfill \\ \hfill y_z& =-l{x}_{0}z/\left(k{r}_0^2\right)+y_0.\hfill \end{array}(4)$

FIGURE 1

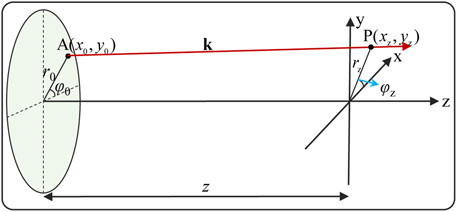
FIGURE 1. Schematic diagram of a light ray’s propagation for a vortex beam in the homogeneous medium.

According to Eq. 4, the propagation properties of the light ray in space for the vortex beam can be derived. Figure 2A reflects the evolution of the light ray in a three-dimensional (3D) view for a vortex beam with l = 10 and r₀ = 1 mm. We can see that the direction of each light ray is different, and the unit vector direction of the light ray AP in the cylindrical coordinate system can be represented as follows:

${\mathbf{e}}_{\text{AP}}=\frac{l}{\sqrt{l^2+k^2{r}_0^2}}\frac{lz}{\sqrt{l^2{z}^2+k^2{r}_0^4}}{\mathbf{e}}_r-\frac{l}{\sqrt{l^2+k^2{r}_0^2}}\frac{k{r}_0^2}{\sqrt{l^2{z}^2+k^2{r}_0^4}}{\mathbf{e}}_{\phi }+\frac{k{r}_0}{\sqrt{l^2+k^2{r}_0^2}}{\mathbf{e}}_z.(5)$

According to Eq. 5, it can be seen that the radial component of the unit vector increases when r₀ decreases, but the longitudinal component is just the opposite. Because of the radial component, the rays at the center of the vortex beam diverge with the increase in the propagation distance during the propagation process, resulting in the zero intensity at the center of vortex beams. According to Eq. 4, the distance r_z between the point P and the origin of the xyz coordinate system (see Figure 1) can be written as follows:

$r_z=\sqrt{l^2{z}^2/\left(k^2{r}_0^2\right)+r_0^2},(6)$

where z is the propagation distance of the vortex beam as the light ray travels to the point P. Figure 2B shows the relationship between r_z with the topological charge l (or z) with the given value of z (or l). On the left of Figure 2B (or the right of Figure 2B), it can be seen that the increase rate of r_z with the propagation distance z (or topological charge l) increases when r₀ decreases for the given l (or z). As a result, a dark spot in the center of the vortex beam appears as it propagates.

FIGURE 2

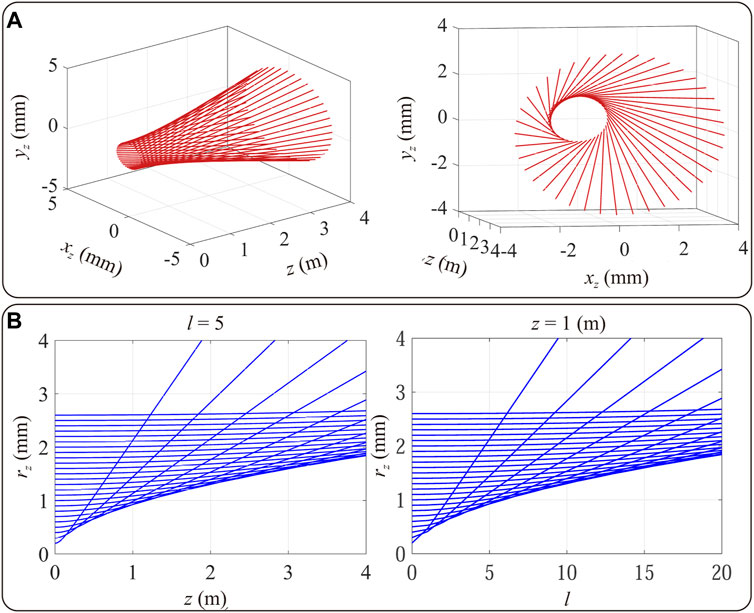
FIGURE 2. Simulated propagation properties of light rays in free space for a vortex beam based on the ray-tracing method.(A) Distributions of light rays in three-dimensional space for different views. (B) Relationship between the parameter r_z and the propagation distance z in the case of l = 5 (left), and the relationship between the parameter r_z and the topological number l in the case of z = 1 m (right).

In order to verify the correctness of our theoretical analysis and derivation, we have carried out the corresponding experiments, as shown in Figure 3A. In our experiment, a linearly polarized flat-top light beam (532 nm) is incident on the spatial light modulator (SLM), on which a forked holographic grating is loaded (where z = 0 m), and the +1 and −1 diffraction orders carry a spiral phase with the opposite topological charges. We then selected one of the diffraction orders and observed the intensity change during the propagation process with the help of a CCD. For easy comparison, we just generated different ring beams instead of whole beams (as shown in Figures 3B1–B5), which is realized by defining a ring-shape transmission function and inside which the forked holographic grating is loaded. As the rings have different radii, which are 0.86, 1.29, 1.72, 2.15, and 2.58 mm, respectively, the selected diffraction order also have different radius but with the same width 0.43 mm). Figures 3B6–B10 show the corresponding far-field intensity pattern at z = 1 m. We can see that the smaller the radius of the ring in the initial position (z = 0) is, the larger the radius of the vortex beam (main ring with the highest intensity) at a given propagation distance (z = 1 m) becomes, which are well in accord with the theoretical conclusions.

FIGURE 3

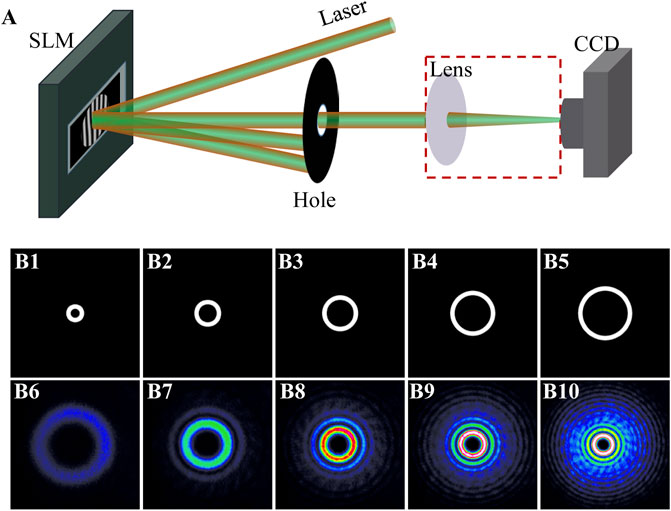
FIGURE 3. Experimental setup and results for propagation and evolution of a vortex beam. (A) Schematic representation of the experimental setup. (B1–B5) Transmission rings with different outer radii of 0.86, 1.29, 1.72, 2.15, and 2.58 mm in the case of the same ring width of 0.43 mm, respectively. (B6–B10) Corresponding measured intensity distribution in the case of l = 5 and the propagation distance z = 1 m, respectively. All images have the same dimension of 6.2 mm × 6.2 mm.

According to Eq. 6, we can get an inequation as follows:

$r_z=\sqrt{l^2{z}^2/\left(k^2{r}_0^2\right)+r_0^2}\ge \sqrt{2lz/k}=r_{\text{min}},(7)$

where r_min is the radius of the dark spot of the vortex beam. According to Eq. 7, r_min is proportional to the root of z and l, which are shown by the blue solid line in Figures 4A1, B1, respectively. To prove the relationship between r_min and l, we measured the value of r_min with different topological charges l, which is from 0 to 20 in the experiment, and the results are marked by the red “+” in Figure 4A1 and the measured intensity distributions for vortex beam with l=1,4,8 are shown in Figures 4A2–A4. We also measured the experimental results of r_min at different propagation distances (z), as shown by the red “+” in Figure 4B1. And Figures 4B2–B4 are the measured intensity for l=5 at propagating distance z are 0.5,1.5 and 2.5 m. According to Figure 4, we can find that the experimental value of r_min is slightly smaller than the theoretical one, and the reason is that we do not consider the diffraction of vortex beams. However, the variation trend of r_min with z or l in the experiment agrees with the theoretical results.

FIGURE 4

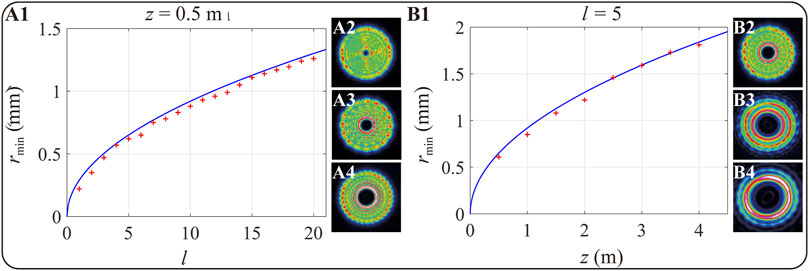
FIGURE 4. Evolutionary process of the minimum radius of the dark ring of a vortex beam variation with l and z in the experiment. The relationship between r_min and (A1) the topological number l and (B1) the propagation distance z. The blue solid line is the simulation result, and the “+” marks are the experimental results. The measured intensity distributions for the vortex beam (A2–A4) at the propagation distance z = 0.5 m with the topological number l are 1, 4, and 8, and (B2–B4) the topological number l = 5 and the propagation distance z are 0.5, 1.5 and 2.5 m, respectively. All images have the same dimension of 6.2 mm × 6.2 mm.

According to Eq. 4 and Figure 1, the rotation angle Δφ_z of point P with respect to point A along the z axis can be written as follows:

$\begin{array}{cc}\hfill \mathrm{\Delta }{\phi }_z& ={\phi }_z-{\phi }_0={\tan }^{-1}\frac{y_z/x_z-y_0/x_0}{1+y_z{y}_0/\left(x_z{x}_0\right)}\hfill \\ \hfill & =-{\tan }^{-1}\frac{lz}{k{r}_0^2}.\hfill \end{array}(8)$

According to Eq. 8, the absolute value of Δφ_z increases as the topological charge l increases, but it decreases as the initial radius r₀ increases. Point P rotates clockwise (or anticlockwise) with respect to the initial point A if l is positive (or negative), and Δφ_z is equal to 90⁰ as z = +∞. The theoretical predictions and experimental confirmations are shown in Figure 5. In Figure 5A, we have shown the theoretical predictions of the rotation angles for vortex beams with different topological charges (l = −20, −10, 0, 10, and 20, respectively) at different propagation distances (z = 0.5 and 1 m, respectively) with r₀ = 1.5 mm. Figures 5B1–B6 illustrates the corresponding experimental measured results of a₁-a₆ in Figure 5A by the truncated semicircular vortex beam. It is clear that the theoretical and the experimental results have some differences; however, the variation tendency is the same. For a specific radial position r₀ (white dotted circle in Figure 5B), the rotation angle of a semicircular beam located at the propagation distance z = 1 m is larger than that at z = 0.5 m in the case of the same topological number l, and the semicircular beam rotates clockwise (anticlockwise) in the case of l > 0 (l < 0), as shown in Figures 5B1–B6. To compare Figure 5B1, B2, we can see the rotation angle is larger if the topological charge is larger with the same propagation distance z = 1 m. In summary, we observed that the experimental results in Figure 5 are in accordance with the theoretical results in Eq. 8.

FIGURE 5

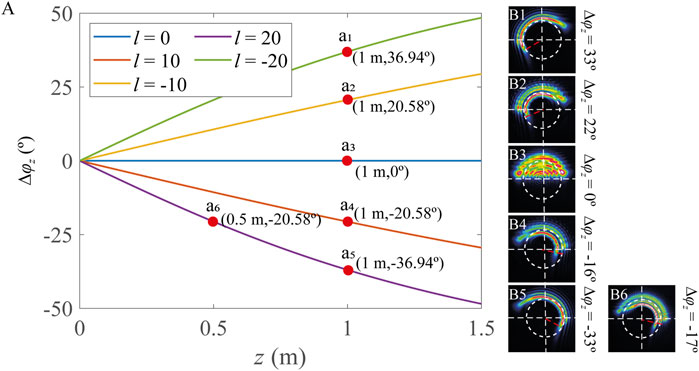
FIGURE 5. Rotation angle predicted by theoretical derivations and the corresponding experimental results for vortex beams with different topological charges. (A) Rotation angle for vortex beams with different topological charges (l equal to 0, 10, −10, 20, and −20) at the propagation distance. (B1–B6) Corresponding measured intensity distributions and the rotation angles of (a1-a6) for truncated vortex beams. All images have the same dimension of 6.2 mm × 6.2 mm.

3 Focusing Properties of Vortex Beams Based on Light Ray Tracing

As is well known, the focusing properties of vortex beams can be calculated by diffraction integration. However, it is more intuitive to understand the focusing behavior of the vortex beam based on the ray-tracing method. As shown in Figure 6, we suppose that a light ray of the vortex beam propagates from the initial point A(x₀, y₀, 0) located in the plane of z = 0 to point P(x′, y′, z₀) located in the plane of z = z₀; then, it is deflected by the focusing lens located at z = z₀. The direction of light ray AP is the same as that of the wave-vector k, which can be written as follows:

$\mathbf{k}=k_x{\mathbf{e}}_x+k_y{\mathbf{e}}_y+k_z{\mathbf{e}}_z,(9)$

where

$\begin{array}{cc}\hfill k_x& =k\left(x^{\prime }-x_0\right)/\sqrt{{\left(x^{\prime }-x_0\right)}^2+{\left(y^{\prime }-y_0\right)}^2+z_0^2},\hfill \\ \hfill k_y& =k\left(y^{\prime }-y_0\right)/\sqrt{{\left(x^{\prime }-x_0\right)}^2+{\left(y^{\prime }-y_0\right)}^2+z_0^2},\hfill \\ \hfill k_z& =k{z}_0/\sqrt{{\left(x^{\prime }-x_0\right)}^2+{\left(y^{\prime }-y_0\right)}^2+z_0^2}.\hfill \end{array}(10)$

In a cylindrical coordinate system, which has three unit vectors, i.e., e_r, e_φ, and e_z, the coordinate of point P can be written as (r′, φ′, z₀). The transformation relationship between e_r, e_φ and e_x, e_y in the cartesian coordinate system can be written as follows:

$\begin{array}{c}\hfill {\mathbf{e}}_x=\cos {\phi }^{\prime }{\mathbf{e}}_r-\sin {\phi }^{\prime }{\mathbf{e}}_{\phi },\\ \hfill {\mathbf{e}}_y=\sin {\phi }^{\prime }{\mathbf{e}}_r+\cos {\phi }^{\prime }{\mathbf{e}}_{\phi }.\end{array}(11)$

When substituting Eq. 11 into Eq. 9, k can be written as follows:

$\mathbf{k}=\left(k_x\cos {\phi }^{\prime }+k_y\sin {\phi }^{\prime }\right){\mathbf{e}}_r+\left(-k_x\sin {\phi }^{\prime }+k_y\cos {\phi }^{\prime }\right){\mathbf{e}}_{\phi }+k_z{\mathbf{e}}_z.(12)$

By replacing x_z, y_z, and z with x′, y′ , and z₀ in Eq. 4, we can get the following:

$\begin{array}{cc}\hfill x^{\prime }& =l{y}_0{z}_0/\left(k{r}_0^2\right)+x_0,\hfill \\ \hfill y^{\prime }& =-l{x}_0{z}_0/\left(k{r}_0^2\right)+y_0.\hfill \end{array}(13)$

When substituting Eq. 13 into Eq. 10, we can get the following:

$\begin{array}{cc}\hfill k_x& =kl{y}_0/\left(r_0\sqrt{l^2+r_0^2{k}^2}\right),\hfill \\ \hfill k_y& =-kl{x}_0/\left(r_0\sqrt{l^2+r_0^2{k}^2}\right),\hfill \\ \hfill k_z& =k^2{r}_0/\sqrt{l^2+r_0^2{k}^2}.\hfill \end{array}(14)$

According to Eq. 13, we can obtain

$\begin{array}{cc}\hfill \cos {\phi }^{\prime }& =x^{\prime }/\sqrt{{\left(x^{\prime }\right)}^2+{\left(y^{\prime }\right)}^2}=\left(l{y}_0{z}_0/r_0+x_{0}k{r}_0\right)/\sqrt{l^2{z}_0^2+k^2{r}_0^4},\hfill \\ \hfill \sin {\phi }^{\prime }& =y^{\prime }/\sqrt{{\left(x^{\prime }\right)}^2+{\left(y^{\prime }\right)}^2}=\left(-l{x}_0{z}_0/r_0+y_{0}k{r}_0\right)/\sqrt{l^2{z}_0^2+k^2{r}_0^4}.\hfill \end{array}(15)$

By further substituting Eqs 14, 15 into Eq. 12, we can obtain the following:

$\mathbf{k}=\frac{k}{\sqrt{l^2+r_0^2{k}^2}}\left(\frac{l^2{z}_0}{\sqrt{l^2{z}_0^2+k^2{r}_0^4}}{\mathbf{e}}_r-\frac{kl{r}_0^2}{\sqrt{l^2{z}_0^2+k^2{r}_0^4}}{\mathbf{e}}_{\phi }+k{r}_0{\mathbf{e}}_z\right).(16)$

As the light ray is deflected by the lens, its direction is then changed from k/k to k′/k, and e_r and e_z are deflected by an angle of θ, with respect to the optical axis of the lens (which is coincided with the axis of the vortex beam). As a result, e_r and e_z were as follows: ${\mathbf{e}}_r^{\prime }$ and ${\mathbf{e}}_z^{\prime }$, respectively; then, k′ can be written as follows:

${\mathbf{k}}^{\prime }=\frac{k}{\sqrt{l^2+r_0^2{k}^2}}\left(\frac{l^2{z}_0}{\sqrt{l^2{z}_0^2+k^2{r}_0^4}}{\mathbf{e}}_r^{\prime }-\frac{kl{r}_0^2}{\sqrt{l^2{z}_0^2+k^2{r}_0^4}}{\mathbf{e}}_{\phi }^{\prime }+k{r}_0{\mathbf{e}}_z^{\prime }\right).(17)$

The light ray after deflection propagates to point B, and point B in the light ray PB is the nearest point to the z axis or the optical axis. The projection of the line segment PB at ${\mathbf{e}}_z^{\prime }$ is the line segment PO, which is the focal length f of the focusing lens. According to Eq. 17, the projection of the line segment PB in the direction of ${\mathbf{e}}_r^{\prime }$ and ${\mathbf{e}}_{\phi }^{\prime }$ can be written as follows:

$\begin{array}{cc}\hfill s_r^{\prime }& =f{l}^2{z}_0/\left(k{r}_0\sqrt{l^2{z}_0^2+k^2{r}_0^4}\right),\hfill \\ \hfill s_{\phi }^{\prime }& =-fkl{r}_0^2/\left(k{r}_0\sqrt{l^2{z}_0^2+k^2{r}_0^4}\right).\hfill \end{array}(18)$

FIGURE 6

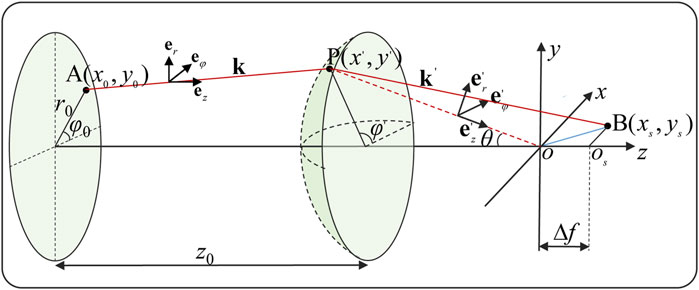
FIGURE 6. Focusing sketch diagram of a light ray for a vortex beam. The light ray propagates from the initial point A to point P and is then deflected by lens and arrives at point B.

For the cylindrical system, the unit vector in the direction of the straight line OB can be represented as follows:

${\mathbf{e}}_{\text{OB}}=\left(s_r^{\prime }{\mathbf{e}}_r^{\prime }+s_{\phi }^{\prime }{\mathbf{e}}_{\phi }^{\prime }\right)/s_{\text{OB}},(19)$

where s_OB is the length of the line segment OB and $s_{\text{OB}}=\sqrt{{(s_r^{\prime })}^2+{(s_{\phi }^{\prime })}^2}$. By substituting ${\mathbf{e}}_r^{\prime }=\cos \theta {\mathbf{e}}_r+\sin \theta {\mathbf{e}}_z$ into Eq. 19, we can get the following equation:

${\mathbf{e}}_{\text{OB}}=\left(s_r^{\prime }\cos \theta {\mathbf{e}}_r+s_r^{\prime }\sin \theta {\mathbf{e}}_z+s_{\phi }^{\prime }{\mathbf{e}}_{\phi }\right)/s_{\text{OB}}.(20)$

According to Eq. 11, Eq. 20 can be rewritten as follows:

${\mathbf{e}}_{\text{OB}}/s_{\text{OB}}=\left(s_r^{\prime }\cos \theta \cos {\phi }^{\prime }-s_{\phi }^{\prime }\sin {\phi }^{\prime }\right){\mathbf{e}}_x+\left(s_r^{\prime }\cos \theta \sin {\phi }^{\prime }+s_{\phi }^{\prime }\cos {\phi }^{\prime }\right){\mathbf{e}}_y+s_r^{\prime }\sin \theta {\mathbf{e}}_z.(21)$

According to Eq. 21, the coordinates of point B in the Cartesian coordinate system (with the origin O and the coordinate axes x, y, and z) can be written as follows:

$\begin{array}{cc}\hfill x_s& =s_r^{\prime }\cos \theta \cos {\phi }^{\prime }-s_{\phi }^{\prime }\sin {\phi }^{\prime },\hfill \\ \hfill y_s& =s_r^{\prime }\cos \theta \sin {\phi }^{\prime }+s_{\phi }^{\prime }\cos {\phi }^{\prime }.\hfill \end{array}(22)$

Based on Eq. 15 and Eq. 18, Eq. 22 can be written as follows:

$\begin{array}{cc}\hfill x_s& =\frac{f{l}^2{z}_0\cos \theta \left(l{y}_0{z}_0/r_0+x_{0}k{r}_0\right)}{k{r}_0\left(l^2{z}_0^2+k^2{r}_0^4\right)}+\frac{fl{r}_0\left(-l{x}_0{z}_0/r_0+y_{0}k{r}_0\right)}{l^2{z}_0^2+k^2{r}_0^4},\hfill \\ \hfill y_s& =\frac{f{l}^2{z}_0\cos \theta \left(-l{x}_0{z}_0/r_0+y_{0}k{r}_0\right)}{k{r}_0\left(l^2{z}_0^2+k^2{r}_0^4\right)}-\frac{fl{r}_0\left(l{y}_0{z}_0/r_0+x_{0}k{r}_0\right)}{l^2{z}_0^2+k^2{r}_0^4}.\hfill \end{array}(23)$

According to Eq. 23, the distance between point B and point O_s can be obtained as follows:

$r_s=\sqrt{{\left(x_s\right)}^2+{\left(y_s\right)}^2}=\frac{|l|}{k\sin \theta }\sqrt{\frac{l^2{z}_0^2{\cos }^2\theta }{k^2{r}_0^4}+1}=\frac{|l|f}{k\sqrt{{\left(l{z}_0/k{r}_0\right)}^2+r_0^2}}\sqrt{\frac{l^2{z}_0^2}{k^2{r}_0^4}\left(1-\frac{{\left(l{z}_0/k{r}_0\right)}^2+r_0^2}{f^2}\right)+1},(24)$

where sin θ = r′/f, and r′ = $\sqrt{{(x^{\prime })}^2+{(y^{\prime })}^2}$ is the pupil radius of the focusing lens. According to Eq. 24, r_s decreases with the increase in r₀, which means that the maximum radius r₀ of the vortex beam in the plane z = 0 corresponds to the minimun ring radius r_s of the focal spot. The intensity near the center of the focal spot is zero, and the shape of focal spot is similar to a donut.

According to Eq. 24, we can see that the radius r_s of the dark spot in the focal plane is proportional to the topological charge l and the focal length f of the focusing lens but inversely proportional to the spot radius of the incident vortex beam.

In the experiment shown in Figure 3, we set the distance (z₀) between the lens and SLM to be 0.5 m, the maximum spot radius (r₀) of the vortex beam in the plane of SLM is 2.6 mm, and the focal length of the lens is equal to 400 mm. Based on Eq. 24 and the aforementioned parameters, we derived the relationship between the radius of the dark focal spot and the topological charge l, as shown by the blue line of Figure 7A. Then, we measured the variation of the radius of the dark spot with the topological charge l, which changes from 2 to 20, and the results are marked by the red “+” in Figure 7A, and Figures 7B–D are the intensity distributions in the focal field for vortex beams with l=4,8,12. It can be seen that the experimental results are slightly smaller than the simulation results, which is because we do not take the diffraction into account; however, the experimental and simulation results have the same tendency.

FIGURE 7

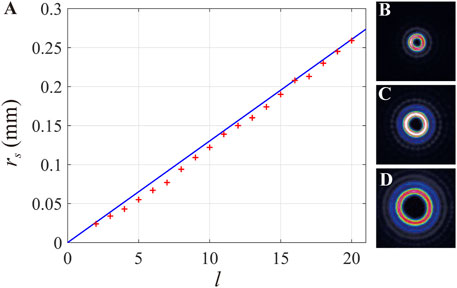
FIGURE 7. Relationship between the radius r_s of the dark spot in the focal field and the topological charge of l. (A) Blue solid line is the simulation result, and the red “+” marks are the experimental results. (B–D) are, respectively, the intensity distributions in the focal field for vortex beams with the topological number l to be 4, 8, and 12. (B–D) have the same dimensions of 1 mm × 1 mm.

From Eq. 21, we can see that the position of the minimum focal spot for a vortex beam is not located in the focal plane of the focusing lens as z₀ ≠ 0 but in the plane with a distance of Δf away from the focal plane. According to Eq. 21, we can get the expression of Δf as follows:

$\mathrm{\Delta }f=s_r^{\prime }\sin \theta =l^2{z}_0/\left(k^2{r}_0^2\right).(25)$

According to Eq. 25, Δf is proportional to the square of l and z₀ but inversely proportional to the square of the initial radius r₀ of the light ray. If z₀ = 0, then Δf = 0, which means that the position of the minimum spot does not shift.

According to Eq. 23, when a vortex beam propagates from the initial plane at z = 0 to the plane which is away from the focal plane with a distance of Δf, we can get the rotation angle Δφ_s of a certain point in the spot as follows:

$\mathrm{\Delta }{\phi }_s=-\pi +\left({\phi }_s-{\phi }_0\right)=-\pi +{\tan }^{-1}\left[\frac{\tan {\phi }_s-\tan {\phi }_0}{1+\tan {\phi }_s\tan {\phi }_0}\right],(26)$

where tan φ_s = y_s/x_s. Based on Eq. 23, we can get the following:

$\mathrm{\Delta }{\phi }_s=\pi +{\tan }^{-1}\left[\frac{l{z}_0\cos \theta +k^2{r}_0^4/\left(l{z}_0\right)}{k{r}_0^2\left(2-\cos \theta \right)}\right].(27)$

According to Eq. 27, we can see that the rotation angle Δφ_s is equal to − π/2 (or π/2) for a negative (or positive) l. This result can be used to intuitively explain the results in [8].

For the given parameters z₀ = 0.5 m, f = 400 mm, and r₀ = 2.6 mm, we can calculate the value of Δφ_s, according to Eq. 27. The calculation result shows that the focal spot rotates clockwise about 93.6° (or 97.1°) with respect to the direction at the initial plane in the case of l = 10 (or l = 20), while for the negative l (e.g., l = −10 or l = −20), the rotation angle is opposite. To verify the theory analysis, we carried out the corresponding experiments. In the experiment, we just generated truncated half or quarter part of a vortex beam and then measured its intensity distribution in the focal plane; the results are shown in Figure 8. It is clear that for the negative or positive l, the rotation of the focal spot is slightly larger than 90°, and the direction is opposite. Meanwhile, the clockwise rotation angle $(\sim 95°)$ of the focal spot in the case of l = 20 is greater than that $(\sim 92°)$ in the case of l = 10. The experimental and theoretical results agree with each other very well, and it proves that the ray-tracing method is effective in predicting the evolution behavior of structured beams during the focusing process.

FIGURE 8

FIGURE 8. Experimentally observed focusing property of vortex beams. (A1) and (B1) are the sketch diagrams of a half and a quarter circular pupil at z = 0 planes, respectively. (A2–A5) are the intensity distributions in the focal field for vortex beams with a half circular pupil in the case of the topological charge l to be −10, 10, −20, and 20, respectively, and (B2–B5) are the corresponding measured intensity distributions for the vortex beam with a quarter circular pupil. (A) and (B) have the same dimensions of 1 mm × 1 mm.

4 Conclusion

In conclusion, we derived analytically the propagation and focusing of vortex beams with top-hat intensity in the homogeneous medium by use of the light ray-tracing method, based on which some propagation behaviors and focusing characteristics of vortex beams can be understood intuitively. For example, the central dark spot of the vortex beam increases with the propagation distance and the topological number, and the relationship between the radius of the dark spot, the topological number, and the propagation distance can be derived. The experiment proves that vortex beams can rotate as it travels in the homogeneous medium, and the rotation angle is related to the propagation distance and the topological number. We can intuitively understand that the vortex beam can be focusing into a donut shape at the focal plane, and we can get the relationship between the radius of the dark spot at the center of the donut shape and the focal length of the lens, the topological charge, and the size of the incident vortex beam. In addition, the proposed method can be also applied to other specific vortex beams, and the results are helpful to understand the propagation and evolution of specific vortex beams.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.

Author Contributions

M-QC and C-HT proposed the idea. M-QC completed the theory and experiment. QW organized the database. C-HT and Y-NL gave some suggestions in numerical simulations and experiments. M-QC, QW, and C-HT wrote the manuscript. All authors contributed to the final manuscript revision.

Funding

This work was supported by the National Key R&D Program of China (2017YFA0303800 and 2017YFA0303700) and the National Natural Science Foundation of China (12074196, 11774183, and 11904152).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Allen L, Beijersbergen MW, Spreeuw RJC, Woerdman JP. Orbital Angular Momentum of Light and the Transformation of Laguerre-Gaussian Laser Modes. Phys Rev A (1992) 45:8185–9. doi:10.1103/PhysRevA.45.8185

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Yao AM, Padgett MJ. Orbital Angular Momentum: Origins, Behavior and Applications. Adv Opt Photon (2011) 3:161–204. doi:10.1364/AOP.3.000161

CrossRef Full Text | Google Scholar

3. Gieseler J, Gomez-Solano JR, Magazzù A, Pérez Castillo I, Pérez García L, Gironella-Torrent M, et al. Optical Tweezers - From Calibration to Applications: A Tutorial. Adv Opt Photon (2021) 13:74–241. doi:10.1364/AOP.394888

CrossRef Full Text | Google Scholar

4. Grier DG. A Revolution in Optical Manipulation. Nature (2003) 424:810–6. doi:10.1038/nature01935

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Dholakia K, Čižmár T. Shaping the Future of Manipulation. Nat Photon (2011) 5:335–42. doi:10.1038/nphoton.2011.80

CrossRef Full Text | Google Scholar

6. Padgett M, Bowman R. Tweezers with a Twist. Nat Photon (2011) 5:343–8. doi:10.1038/NPHOTON.2011.81

CrossRef Full Text | Google Scholar

7. Fu S, Zhai Y, Zhou H, Zhang J, Wang T, Liu X, et al. Experimental Demonstration of Free-Space Multi-State Orbital Angular Momentum Shift Keying. Opt Express (2019) 27:33111–9. doi:10.1364/OE.27.033111

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Wang J, Yang J-Y, Fazal IM, Ahmed N, Yan Y, Huang H, et al. Terabit Free-Space Data Transmission Employing Orbital Angular Momentum Multiplexing. Nat Photon (2012) 6:488–96. doi:10.1038/NPHOTON.2012.138

CrossRef Full Text | Google Scholar

9. Ambrosio A, Marrucci L, Borbone F, Roviello A, Maddalena P. Light-Induced Spiral Mass Transport in Azo-Polymer Films under Vortex-Beam Illumination. Nat Commun (2012) 3:1–9. doi:10.1038/ncomms1996

CrossRef Full Text | Google Scholar

10. Toyoda K, Miyamoto K, Aoki N, Morita R, Omatsu T. Using Optical Vortex to Control the Chirality of Twisted Metal Nanostructures. Nano Lett (2012) 12:3645–9. doi:10.1021/nl301347j

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Ni J, Wang C, Zhang C, Hu Y, Yang L, Lao Z, et al. Three-Dimensional Chiral Microstructures Fabricated by Structured Optical Vortices in Isotropic Material. Light Sci Appl (2017) 6:e17011. doi:10.1038/lsa.2017.11

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Dorrah AH, Rosales-Guzmán C, Forbes A, Mojahedi M. Evolution of Orbital Angular Momentum in Three-Dimensional Structured Light. Phys Rev A (2018) 98:043846. doi:10.1103/PhysRevA.98.043846

CrossRef Full Text | Google Scholar

13. Dorrah AH, Zamboni-Rached M, Mojahedi M. Controlling the Topological Charge of Twisted Light Beams with Propagation. Phys Rev A (2016) 93:063864. doi:10.1103/PhysRevA.93.063864

CrossRef Full Text | Google Scholar

14. Schechner YY, Piestun R, Shamir J. Wave Propagation with Rotating Intensity Distributions. Phys Rev E (1996) 54:R50–R53. doi:10.1103/PhysRevE.54.R50

CrossRef Full Text | Google Scholar

15. Srinivas P, Perumangatt C, Lal N, Singh RP, Srinivasan B. Investigation of Propagation Dynamics of Truncated Vector Vortex Beams. Opt Lett (2018) 43:2579–82. doi:10.1364/OL.43.002579

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Wang X-L, Lou K, Chen J, Gu B, Li Y, Wang H-T. Unveiling Locally Linearly Polarized Vector Fields with Broken Axial Symmetry. Phys Rev A (2011) 83:063813. doi:10.1103/PhysRevA.83.063813

CrossRef Full Text | Google Scholar

17. Shen D, Wang K, Zhao D. Generation and Propagation of a New Kind of Power-Exponent-Phase Vortex Beam. Opt Express (2019) 27:24642–53. doi:10.1364/OE.27.024642

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Yan X, Guo L, Cheng M, Li J. Controlling Abruptly Autofocusing Vortex Beams to Mitigate Crosstalk and Vortex Splitting in Free-Space Optical Communication. Opt Express (2018) 26:12605–19. doi:10.1364/OE.26.012605

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Davis JA, Cottrell DM, Sand D. Abruptly Autofocusing Vortex Beams. Opt Express (2012) 20:13302–10. doi:10.1364/oe.20.013302

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Li X, Ma H, Yin C, Tang J, Li H, Tang M, et al. Controllable Mode Transformation in Perfect Optical Vortices. Opt Express (2018) 26:651–62. doi:10.1364/OE.26.000651

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Zhang H, Li X, Ma H, Tang M, Li H, Tang J, et al. Grafted Optical Vortex with Controllable Orbital Angular Momentum Distribution. Opt Express (2019) 27:22930–8. doi:10.1364/OE.27.022930

PubMed Abstract | CrossRef Full Text | Google Scholar