- Department of Chemical Engineering, University of New Hampshire, Durham, NH, United States
We report coarse-grained Langevin dynamics simulations of homogeneous mixtures of lobed colloidal particles with opposite charges. We show that dumbbell, trigonal planar, tetrahedral, square planar, trigonal bipyramidal, and octahedral shaped particles form distinct self-assemblies including chains, sheets, crystalline, and spherical structures. The dumbbell and square planar particles predominantly form chains and sheets while other particles form network-like self-assembled morphologies. At higher temperatures and lower charges, non-planar particles form three-dimensional aggregates. We further report on packing arrangements of particles which lead to differences in porosities within self-assembled morphologies. Our results show that the trigonal planar particles form larger porous structures. The self-assembled structures that we report are potentially useful in designing porous biomaterials for biomedical applications.
Introduction
Self-assembly is an approach where the components of a system spontaneously assemble without the application of external forces [1, 2]. The self-assembled structure gains its stability from the interactions among its constituents. Colloidal particles are one such class of materials which have been widely studied for their tendency to form larger clusters with distinct morphologies [3–5]. The interactions of significance in these assemblies include van der Waals interactions (vdW) [6], electrostatic interactions [7], steric effects [8], and solvation forces [9, 10]. Colloidal systems have served as models in understanding fundamental and applied problems including phase behavior [11], glass transition [12, 13], crystal nucleation [14, 15], and biomedical applications [16–18].
Self-assemblies of patchy colloidal particles are known for their distinct shapes and novel applications [19–22]. The placement of patches on colloidal particles leads to selective and tunable interactions that allow control over the morphologies of the structures formed via self-assembly [23, 24]. These patches can take the form of lobes that protrude from the surface of colloidal particles. As a result, the lobes can dictate the phase behavior and porosity of a given self-assembled structure due to their size, number, location, and inter-particle interactions, in addition to environmental conditions [25]. Our previous simulation studies have shown that the incorporation of lobes in colloidal particles results in the formation of structures with enhanced porosity due to an increase in the excluded volume created by the non-spherical shapes of particles [18, 25–29].
Interest in the synthesis and self-assembly of colloidal particles with lobes has been increasing in recent years [30–40]. A pioneering study by Wang et al. [31] reported the synthesis of colloidal particles with lobes in positions that mimic hybridized atomic orbitals, which provide three-dimensional bonding symmetries resulting in novel self-assembled structures. Liu and colleagues [32] have synthesized dumbbell-shaped particles and observed that when the particle lobes are DNA-coated, these particles self-assemble to form Kagome lattices, brick-wall-like lattices, or a co-existence of these two arrangements, based on the temperature of the system. Wolters et al. [39] synthesized two-lobed particles with a “Mickey Mouse” shape and reported that these particles self-assemble to form tube-like structures.
Simulations have also been conducted for studying the assemblies of tri-block patchy colloidal particles of tetrahedral and octahedral shapes which result in the formation of colloidal crystals of body centered cubic and cubic diamonds [41]. Simulations of dumbbell-shaped particles show the formation of micelles, vesicles or bilayers with a change in size ratio, separation between two dumbbell spheres and volume fraction [42]. Further, using experimental and computational approaches, dumbbell-shaped particles were shown to stabilize microspheres against aggregation [43]. Simulations of spherical patchy particles have highlighted the dependence of the interaction strength, patch coverage, and density as the key factors in forming two-dimensional self-assemblies [29, 44]. However, lobed patchy particles and their mixtures have been underexplored for the creation of porous colloidal self-assemblies.
We have previously reported simulation studies on the self-assembly of lobed colloidal particles [18, 25–28]. We considered different particle types, as in the current work (dumbbell, trigonal planar, square planar, tetrahedral, trigonal bipyramidal, and octahedral), and investigated their morphologies and porosities where the lobes of these particles are either neutral, charged, or functionalized. Many of these particle types have been successfully designed using experimental approaches, thereby highlighting the feasibility of creating larger lobes instead of patches [31, 34, 45–47]. However, in one of our previous studies in which the lobed particles with charges were studied [27], the positive and the negative charges are placed on different lobes of the same particle to have a net charge of zero on the particle, but experimentally designing lobed particles where different lobes on the same particle can be functionalized differently is significantly challenging. In contrast, it is conceivable that all lobes on a given particle can be functionalized uniformly to have complementary interactions between a pair of distinctly-functionalized particles.
In this work, we introduce a new design of lobed colloidal particles with uniformly-charged lobes where we assign either an overall positive or an overall negative charge to all lobes of a given type of particle (Figures 1A-F) to mimic complementary interactions between the lobes. For observing self-assembly due to complementary interactions, we studied 1:1 mixtures of the same type of particles where half of the particles in the mixture have positively-charged lobes and the other half have negatively-charged lobes, thus studying an overall electrically neutral system. Along with investigating the role of the particle design, charges, and temperature on the phase behavior and porosity, we also focus on packing modes of particles which lead to differences in porosities of the self-assembled structures.
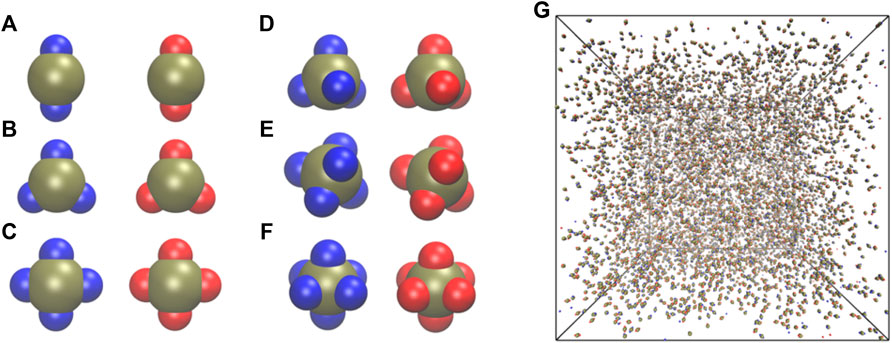
FIGURE 1. Snapshots of particle geometries studied in this work: (A) Dumbbell
Models and Methods
Model
We conducted Langevin molecular dynamics simulations to study the self-assembly behavior of six different types of lobed particles with oppositely-charged lobes. These particles with distinct shapes include dumbbell
Non-Bonded Interactions
The self-assembly of charged colloidal particles is mediated by non-bonded short-range interactions short-range interactions as well as long-range electrostatic interactions [48]. The model used in our simulations accounts for both types of interactions. The seed-seed (S-S), lobe-lobe (L-L), and seed-lobe (S-L) non-bonded interactions are modeled by using the shifted Lennard-Jones (SLJ) potential (Eq. 1). The SLJ potential was chosen to model the non-bonded interactions because the diameters of the colloidal particles of interest are in the μm range. Therefore, the interactions are computed between the surfaces of the particles rather than between the centers of the particles [49].
In this equation, ϵij denotes the depth of the potential well for a pair of particles i and j, and σ denotes the distance of the closest approach. The equation is used to model the pairwise interaction potentials when rij < rcut + δ. Here, rcut signifies a cut-off distance and δ = (σi + σj)/2–1, where σi and σj are the particle diameters. When rij ≥ (rcut + δ), non-bonded interactions are neglected, i.e., USLJ (rij) = 0. The depth of the pair-potential well for interactions between the positive and negative lobes is fixed as three in reduced units, while it was kept as one for all other pairs, similar to our previous work on particles with charges on the lobes [27]. The short-ranged repulsions are treated by setting the cut-off distance (rcut) as
where, qi and qj are the charges on a pair of particles i and j, respectively, ϵ0 is the permittivity of the free space, and ϵr the relative permittivity. For electrostatic screening, ϵr represents the dielectric permitivity of bulk water at ambient conditions (equal to 80).
Simulation Details
We conducted coarse-grained Langevin dynamics simulations for all systems using the HOOMD-Blue software [55]. We computed the electrostatic interactions by using the particle-particle-particle-mesh (PPPM) method [54, 56]. Each system is composed of 8,000 particles of the same type (4,000 each with positively-charged and negatively-charged lobes, respectively) and the length of the simulation domain is 160σL along each direction in all simulations. Overall, we simulated six distinct systems, each at four distinct temperatures and three distinct charge values. Specifically, we performed simulations of all six types of particles at four different temperature conditions (kBT = 0.1, 0.4, 0.7, and 1.0, in reduced units) with three different magnitudes for the charges on the lobes (±2, ±4, and ±6 in reduced units). We note that kBT = 1.0 corresponds to T = 298 K [22]. Therefore, kBT = 0.1, 0.4, and 0.7 correspond to 29.8, 119.2, and 208.6 K, respectively.
We generated initial conditions for different systems by simulating each system for 10,000 steps at kBT = 3.0, a sufficiently higher temperature to prevent any self-assembly at all conditions and to randomize the initial configurations (Figure 1G). In all simulations, we used an integration time-step of 0.005 and a simulation length of 5 × 107 steps. We confirmed the stability of a given self-assembled structure by analyzing the convergence of the potential energy per particle and the total number of clusters (Supplementary Figure S1) as a function of the number of time-steps. The self-assembled clusters are formed by those particles whose centers of masses are within 3.25σL from each other. The cluster calculation was carried out using the freud software [57].
Pore Diameter and Interplanar Angle Measurements
We analyzed two types of pores in our self-assembled morphologies, the interstitial (Figure 2A) and the intra-network pores (Figure 2B). The interstitial pores arise in the system due to the formation of large three-dimensional self-assembled morphologies. The available spaces within these aggregates correspond to interstitial pores. The interstitial pore size is calculated by carving out a cube from a three-dimensional aggregate and the pores within the cube (zoomed view in Figure 2A) are characterized as representative of the self-assembled morphology. The intra-network pores exist due to the formation of interconnected structures (chains, sheets and random aggregates) within the simulation domain. We consider the entire simulation domain for capturing the sizes of intra-network pores formed from different types of particles. We used the Zeo++ software [58–60] to compute the pore size diameter by measuring the diameter of the largest free sphere (DLFS) which can freely diffuse through a self-assembled porous structure. For this, we considered a probe radius equivalent to
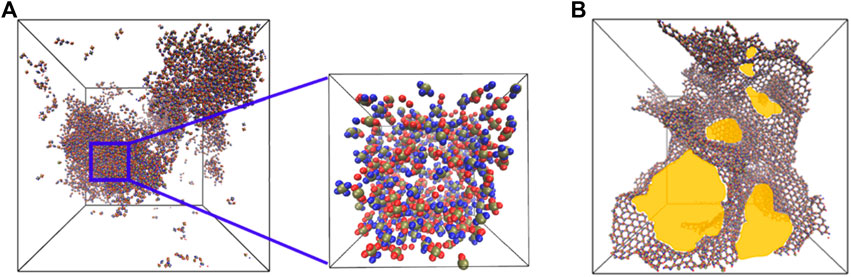
FIGURE 2. (A) A snapshot highlighting the interstitial pores formed in three-dimensional aggregates. The zoomed-view shows a cube carved out of larger aggregates and used in the calculation of the sizes of interstitial pores. (B) A snapshot highlighting the intra-network pores (yellow) observed in self-assembled structures.
To characterize the packing arrangements among particles in self-assembled morphologies, we also computed the distributions of the interplanar angles between the planes formed by S–L+–L− and L+–L−–S groups of particles, where L+ and L− denote the positively-charged and negatively-charged lobes, respectively, and S signifies the central seed particle on which the lobes are placed. The interplanar angle values span the range between -180° and +180° which correspond to the interior/exterior angles between the two planes.
Results and Discussion
We studied self-assembly for six different types of lobed particles which differ in their number of lobes (Figure 1) as well as their positions and charges. We systematically studied the effect of temperature (kBT = 0.1, 0.4, 0.7, and 1.0) and charges (2, 4, or 6 units) on the lobes with a focus on homogeneous mixtures of particles where half of the particles have positively-charged lobes and the remaining half have negatively-charged lobes. The time-evolution of the potential energy per particle and the total number of clusters in each system for a given condition of q and kBT are shown in Supplementary Figure S1. Similar convergence trends were observed for all systems. However, we note that patchy interactions may lead to the formation of kinetically trapped structures [61–63], especially at lower temperatures. Therefore, alternate methodologies [64, 65] could be explored in future studies to further probe such structures.
Self-Assembled Morphologies
We analyzed the final configurations obtained at the end of the simulations for each system according to their morphologies. In Figure 3, we summarize the phase behavior of different morphologies formed by these mixtures under all temperature and charge conditions.
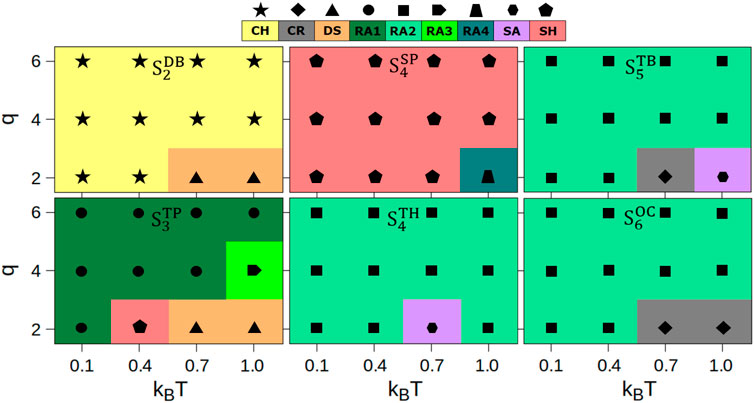
FIGURE 3. Phase behavior in homogeneous mixtures of charged lobed particles at all charge (q) and temperature (kBT) conditions. Each type of morphology is color coded: chains (CH), crystalline self-assemblies (CR), random aggregates (RA1, RA2, RA3, RA4), sheets (SH), and spherical aggregates (SR). The conditions at which self-assembly is not observed are labeled as DS, the dissociated state.
These data reveal the formation of various types of network-like particle assemblies including chains (CH), different types of random aggregates (RA1, RA2, RA3, RA4), and two-dimensional sheets (SH), or three-dimensional clusters including crystalline (CR) and spherical aggregates (SA). The random aggregates termed RA1 and RA3 are formed by the planar particles
The relative occurrence of distinct phases in simulations of charged particles without mixing, as reported in our previous work [27], and homogeneous mixtures of charged particles from this work is shown in Supplementary Figure S2 (magenta bars, previous work; green bars, this work). The fractional occurrence (expressed as a percentage) is computed by comparing the formation of a specific phase with respect to the total number of phases formed in simulations. The homogeneous mixtures reported in this work have higher occurrences of some (CH, CR, RA1, RA2, and RA3) morphologies, and comparable occurrences of other (SA and SH) morphologies. The RA4 morphology is only observed in homogeneous mixtures albeit at a significantly lower fraction compared to other morphologies.
Structural Motifs in Self-Assembled Morphologies
For dumbbell-shaped particles with two lobes
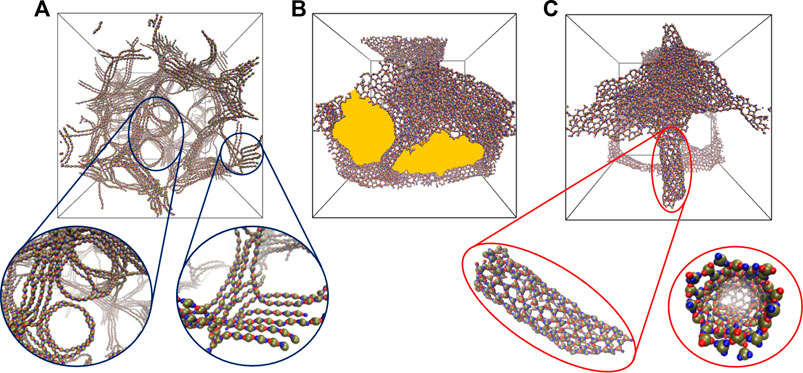
FIGURE 4. Snapshots highlighting self-assembled networks formed by the particles with two
As the number of lobes increases, as in the case of
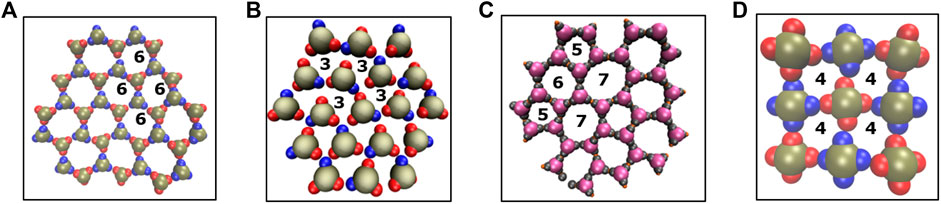
FIGURE 5. A comparison of structural motifs in sheet-like morphologies reported in this study and our previous work [18, 27]. (A–C) Ring-like arrangements of particles with three lobes are shown: six membered rings (panel A, current work), three membered rings (panel B, previous work [27]), and five or seven membered rings (panel C, previous work [18]). (D) Four membered rings formed by the square planar
In Supplementary Figure S5, we show the systematic evolution of morphologies formed by the
Further, the particles with four lobes either have a square-planar
In contrast, the
Similar network-like morphologies originating from the RA2-type configurations are found in the assemblies of lobed particles with 5 or 6 lobes (
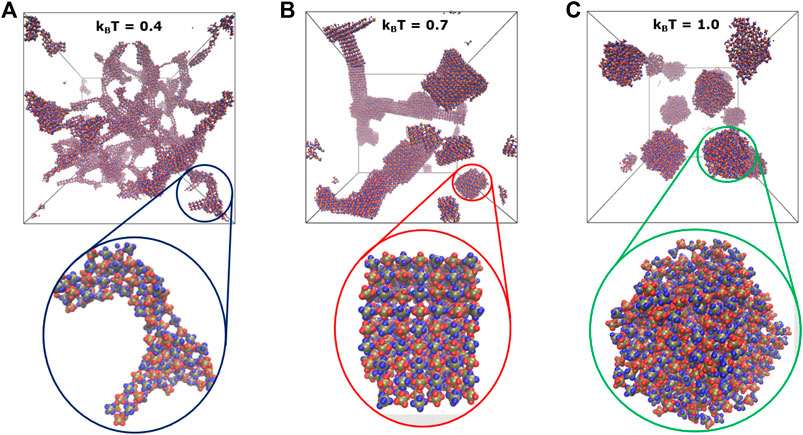
FIGURE 6. Shown are the snapshots highlighting temperature-dependent shape transitions in self-assemblies formed by the
Interstitial and Intra-Network Pore Sizes
To probe the porosity of a given self-assembled structure, we computed the pore sizes (measured using the diameter of the largest free sphere DLFS as a metric) for all assemblies at all conditions of charges and temperatures (Supplementary Figure S7). This analysis considered all particle shapes and the conditions responsible for the formation of pores of various diameters. The smaller pores originate from the interstitial space between particles in three-dimensional aggregates, while the larger pores originate from the intra-network void space in a given network-like morphology. Among all charge (q) and temperature values, the pore-sizes with larger diameters are observed for q = 4, kBT = 0.7 and 1.0.
In Figure 7, we show the trends in pore sizes (DLFS) for both interstitial and intra-network pores for self-assemblies formed by particles with three or more lobes (
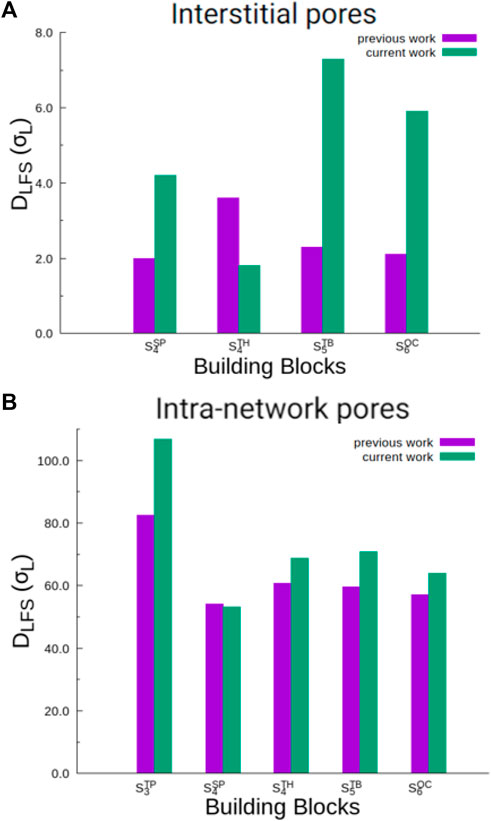
FIGURE 7. A comparison of interstitial pore diameters [panel (A)] and intra-network pore diameters [panel (B)], computed based on data from this study and our previous work on charged lobed particles [27]. Data are shown for only those particle types which form interstitial or intra-network pores in both studies. In Supplementary Figure S7, we also present pore diameters for self-assemblies of all particle types at all conditions from this study.
On comparing intra-network pores (Figure 7B), we find that the network-like self-assemblies formed by particle mixtures studied in our current work have larger pores in most cases except for the
Particle Packing Modes: Interplanar Angles
To further probe the correlation between the porosity and the packing arrangements of particles within self-assemblies, we computed the distributions of the inter-planar angles between the planes S−L+−L− and L+−L−−S that are formed by the seed (S) and positively-charged as well as negatively-charged lobes (L+/L−) (Figure 8). The inter-planar angle distributions for the
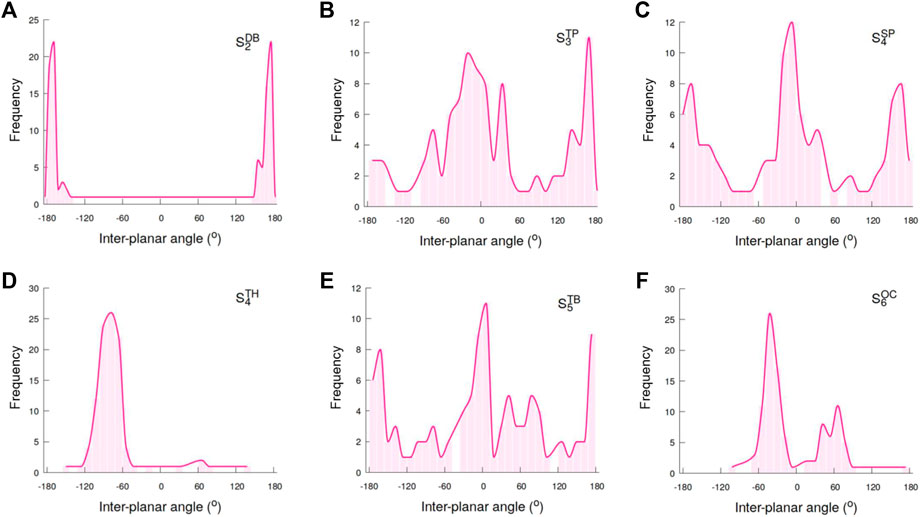
FIGURE 8. Shown are the distributions of the inter-planar angles in self-assemblies formed by (A) dumbbell, (B) trigonal planar (C) square planar, (D) tetrahedral, (E) trigonal bipyramidal, and (F) octahedral shaped particles.
The angle distributions for the
The trigonal bipyramidal particles with five lobes
Conclusion
We studied self-assembly in homogeneous mixtures of particles with oppositely-charged lobes and probed their pore forming tendencies. In these mixtures, each particle has all the lobes either positively-charged or negatively-charged to resemble functionalized lobed particles with complementary interactions that are potentially experimentally realizable in comparison to the particles where the lobes on the same particle have different charges [27]. We observed the formation of morphologies with interstitial as well as intra-network pores, where the pores in the latter morphologies are an order of magnitude larger than in the former morphologies. Among all the particles studied, the
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
HV: conceptualization, supervision, funding acquisition, and draft editing. AS and BR: modeling, simulation, analysis, and draft preparation. All authors contributed to the article and approved the submitted version.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We acknowledge the National Science Foundation (NSF) EPSCoR award (OIA-1757371; HV) for financial support as well as for providing the hetereogenous CPU/GPU supercomputing facility at the University of New Hampshire (UNH).
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.936385/full#supplementary-material
References
1. Whitesides GM, Grzybowski B. Self-assembly at All Scales. Science (2002) 295:2418–21. doi:10.1126/science.1070821
2. Sacanna S, Pine DJ, Yi G-R. Engineering Shape: the Novel Geometries of Colloidal Self-Assembly. Soft Matter (2013) 9:8096–106. doi:10.1039/c3sm50500f
3. Matijevic E. Monodispersed Metal (Hydrous) Oxides - a Fascinating Field of Colloid Science. Acc Chem Res (1981) 14:22–9. doi:10.1021/ar00061a004
4. Matijevic E. Preparation and Properties of Uniform Size Colloids. Chem Mater (1993) 5:412–26. doi:10.1021/cm00028a004
5. Matijevic E. Uniform Inorganic Colloid Dispersions. Achievements and Challenges. Langmuir (1994) 10:8–16. doi:10.1021/la00013a003
6. Vold MJ. The effect of adsorption on the van der waals interaction of spherical colloidal particles. J Colloid Sci (1961) 16:1–12. doi:10.1016/0095-8522(61)90057-5
7. Moncho-Jordá A, Martínez-López F, González AE, Hidalgo-Álvarez R. Role of Long-Range Repulsive Interactions in Two-Dimensional Colloidal Aggregation: Experiments and Simulations. Langmuir (2002) 18:9183–91. doi:10.1021/la0258805
8. Min Y, Akbulut M, Kristiansen K, Golan Y, Israelachvili J. The Role of Interparticle and External Forces in Nanoparticle Assembly. Nat Mater (2008) 7:527–38. doi:10.1038/nmat2206
9. Lotito V, Zambelli T. Approaches to Self-Assembly of Colloidal Monolayers: A Guide for Nanotechnologists. Adv Colloid Interf Sci (2017) 246:217–74. doi:10.1016/j.cis.2017.04.003
10. van Dommelen R, Fanzio P, Sasso L. Surface Self-Assembly of Colloidal Crystals for Micro- and Nano-Patterning. Adv Colloid Interf Sci (2018) 251:97–114. doi:10.1016/j.cis.2017.10.007
11. Lu PJ, Weitz DA. Colloidal Particles: Crystals, Glasses, and Gels. Annu Rev Condens Matter Phys (2013) 4:217–33. doi:10.1146/annurev-conmatphys-030212-184213
12. Pham KN, Puertas AM, Bergenholtz J, Egelhaaf SU, Moussaïd A, Pusey PN, et al. Multiple Glassy States in a Simple Model System. Science (2002) 296:104–6. doi:10.1126/science.1068238
13. Weeks ER, Crocker JC, Levitt AC, Schofield A, Weitz DA. Three-dimensional Direct Imaging of Structural Relaxation Near the Colloidal Glass Transition. Science (2000) 287:627–31. doi:10.1126/science.287.5453.627
14. Schall P, Cohen I, Weitz DA, Spaepen F. Visualization of Dislocation Dynamics in Colloidal Crystals. Science (2004) 305:1944–8. doi:10.1126/science.1102186
15. Schall P, Cohen I, Weitz DA, Spaepen F. Visualizing Dislocation Nucleation by Indenting Colloidal Crystals. Nature (2006) 440:319–23. doi:10.1038/nature04557
16. Ghosh Chaudhuri R, Paria S. Core/shell Nanoparticles: Classes, Properties, Synthesis Mechanisms, Characterization, and Applications. Chem Rev (2012) 112:2373–433. doi:10.1021/cr100449n
17. Gao L, Gan H, Meng Z, Gu R, Wu Z, Zhang L, et al. Effects of Genipin Cross-Linking of Chitosan Hydrogels on Cellular Adhesion and Viability. Colloids Surf B: Biointerfaces (2014) 117:398–405. doi:10.1016/j.colsurfb.2014.03.002
18. Gorai B, Rocha BC, Vashisth H. Design of Functionalized Lobed Particles for Porous Self-Assemblies. JOM (2021) 73:2413–22. doi:10.1007/s11837-021-04715-w
19. Ravaine S, Duguet E. Synthesis and Assembly of Patchy Particles: Recent Progress and Future Prospects. Curr Opin Colloid Interf Sci (2017) 30:45–53. doi:10.1016/j.cocis.2017.05.002
20. Pawar AB, Kretzschmar I. Fabrication, Assembly, and Application of Patchy Particles. Macromol Rapid Commun (2010) 31:150–68. doi:10.1002/marc.200900614
21. Bharti B, Rutkowski D, Han K, Kumar AU, Hall CK, Velev OD. Capillary Bridging as a Tool for Assembling Discrete Clusters of Patchy Particles. J Am Chem Soc (2016) 138:14948–53. doi:10.1021/jacs.6b08017
22. Long AW, Ferguson AL. Nonlinear Machine Learning of Patchy Colloid Self-Assembly Pathways and Mechanisms. J Phys Chem B (2014) 118:4228–44. doi:10.1021/jp500350b
23. Zhang Z, Glotzer SC. Self-assembly of Patchy Particles. Nano Lett (2004) 4:1407–13. doi:10.1021/nl0493500
24. Kraft DJ, Groenewold J, Kegel WK. Colloidal Molecules with Well-Controlled Bond Angles. Soft Matter (2009) 5:3823. doi:10.1039/b910593j
25. Paul S, Vashisth H. Self-assembly Behavior of Experimentally Realizable Lobed Patchy Particles. Soft Matter (2020) 16:8101–7. doi:10.1039/d0sm00954g
26. Paul S, Vashisth H. Self-assembly of Lobed Particles into Amorphous and Crystalline Porous Structures. Soft Matter (2020) 16:1142–7. doi:10.1039/c9sm01878f
27. Rocha BC, Paul S, Vashisth H. Enhanced Porosity in Self-Assembled Morphologies Mediated by Charged Lobes on Patchy Particles. J Phys Chem B (2021) 125:3208–15. doi:10.1021/acs.jpcb.0c11096
28. Paul S, Vashisth H. Self-assembly of Porous Structures from a Binary Mixture of Lobed Patchy Particles. Front Phys (2021) 9:767623. doi:10.3389/fphy.2021.767623
29. Mathews K RA, Mani E. Stabilizing Ordered Structures with Single Patch Inverse Patchy Colloids in Two Dimensions. J Phys Condens Matter (2021) 33:195101. doi:10.1088/1361-648x/abf0c0
30. Blenner D, Stubbs J, Sundberg D. Multi-lobed Composite Polymer Nanoparticles Prepared by Conventional Emulsion Polymerization. Polymer (2017) 114:54–63. doi:10.1016/j.polymer.2017.02.080
31. Wang Y, Wang Y, Breed DR, Manoharan VN, Feng L, Hollingsworth AD, et al. Colloids with Valence and Specific Directional Bonding. Nature (2012) 491:51–5. doi:10.1038/nature11564
32. Liu M, Zheng X, Grebe V, He M, Pine DJ, Weck M. Two‐Dimensional (2D) or Quasi‐2D Superstructures from DNA‐Coated Colloidal Particles. Angew Chem Int Ed (2021) 60:5744–8. doi:10.1002/anie.202014045
33. van Ravensteijn BGP, Kegel WK. Tuning Particle Geometry of Chemically Anisotropic Dumbbell-Shaped Colloids. J Colloid Interf Sci (2017) 490:462–77. doi:10.1016/j.jcis.2016.11.045
34. Meester V, Verweij RW, van der Wel C, Kraft DJ. Colloidal Recycling: Reconfiguration of Random Aggregates into Patchy Particles. ACS Nano (2016) 10:4322–9. doi:10.1021/acsnano.5b07901
35. Sacanna S, Pine DJ. Shape-anisotropic Colloids: Building Blocks for Complex Assemblies. Curr Opin Colloid Interf Sci (2011) 16:96–105. doi:10.1016/j.cocis.2011.01.003
36. Liu M, Dong F, Jackson NS, Ward MD, Weck M. Customized Chiral Colloids. J Am Chem Soc (2020) 142:16528–32. doi:10.1021/jacs.0c07315
37. Liu M, Zheng X, Grebe V, Pine DJ, Weck M. Tunable Assembly of Hybrid Colloids Induced by Regioselective Depletion. Nat Mater (2020) 19:1354–61. doi:10.1038/s41563-020-0744-2
38. Zheng X, Wang Y, Wang Y, Pine DJ, Weck M. Thermal Regulation of Colloidal Materials Architecture through Orthogonal Functionalizable Patchy Particles. Chem Mater (2016) 28:3984–9. doi:10.1021/acs.chemmater.6b01313
39. Wolters JR, Avvisati G, Hagemans F, Vissers T, Kraft DJ, Dijkstra M, et al. Self-assembly of "Mickey Mouse" Shaped Colloids into Tube-like Structures: Experiments and Simulations. Soft Matter (2015) 11:1067–77. doi:10.1039/c4sm02375g
40. Kraft DJ, Vlug WS, van Kats CM, van Blaaderen A, Imhof A, Kegel WK. Self-assembly of Colloids with Liquid Protrusions. J Am Chem Soc (2008) 131:1182–6. doi:10.1021/ja8079803
41. Morphew D, Shaw J, Avins C, Chakrabarti D. Programming Hierarchical Self-Assembly of Patchy Particles into Colloidal Crystals via Colloidal Molecules. ACS Nano (2018) 12:2355–64. doi:10.1021/acsnano.7b07633
42. Avvisati G, Vissers T, Dijkstra M. Self-assembly of Patchy Colloidal Dumbbells. J Chem Phys (2015) 142:084905. doi:10.1063/1.4913369
43. Wolters JR, Verweij JE, Avvisati G, Dijkstra M, Kegel WK. Depletion-induced Encapsulation by Dumbbell-Shaped Patchy Colloids Stabilize Microspheres against Aggregation. Langmuir (2017) 33:3270–80. doi:10.1021/acs.langmuir.7b00014
44. Sato M. Effect of the Interaction Length on Clusters Formed by Spherical One-Patch Particles on Flat Planes. Langmuir (2021) 37:4213–21. doi:10.1021/acs.langmuir.1c00102
45. Sacanna S, Korpics M, Rodriguez K, Colón-Meléndez L, Kim SH, Pine DJ, et al. Shaping Colloids for Self-Assembly. Nat Commun (2013) 4:1688. doi:10.1038/ncomms2694
46. Gong Z, Hueckel T, Yi G-R, Sacanna S. Patchy Particles Made by Colloidal Fusion. Nature (2017) 550:234–8. doi:10.1038/nature23901
47. Lin Y-C, Tripathi AK, Tsavalas JG. Tunable Multilobe Particle Geometry by Annealing-Assisted Emulsion Polymerization. ACS Appl Polym Mater (2022) 4:313–26. doi:10.1021/acsapm.1c01312
48. Glotzer SC, Solomon MJ, Kotov NA. Self-assembly: From Nanoscale to Microscale Colloids. Aiche J (2004) 50:2978–85. doi:10.1002/aic.10413
49. Marson RL, Phillips CL, Anderson JA, Glotzer SC. Phase Behavior and Complex crystal Structures of Self-Assembled Tethered Nanoparticle Telechelics. Nano Lett (2014) 14:2071–8. doi:10.1021/nl500236b
50. Santos PHS, Campanella OH, Carignano MA. Brownian Dynamics Study of Gel-Forming Colloidal Particles. J Phys Chem B (2010) 114:13052–8. doi:10.1021/jp105711y
51. Santos PHS, Campanella OH, Carignano MA. Effective Attractive Range and Viscoelasticity of Colloidal Gels. Soft Matter (2013) 9:709–14. doi:10.1039/c2sm26585k
52. Chremos A, Jeong C, Douglas JF. Influence of Polymer Architectures on Diffusion in Unentangled Polymer Melts. Soft Matter (2017) 13:5778–84. doi:10.1039/c7sm01018d
53. Liu T, VanSaders B, Keating JT, Glotzer SC, Solomon MJ. Effect of Particles of Irregular Size on the Microstructure and Structural Color of Self-Assembled Colloidal Crystals. Langmuir (2021) 37:13300–8. doi:10.1021/acs.langmuir.1c01898
54. LeBard DN, Levine BG, Mertmann P, Barr SA, Jusufi A, Sanders S, et al. Self-assembly of Coarse-Grained Ionic Surfactants Accelerated by Graphics Processing Units. Soft Matter (2012) 8:2385–97. doi:10.1039/c1sm06787g
55. Anderson JA, Glaser J, Glotzer SC. Hoomd-blue: A python Package for High-Performance Molecular Dynamics and Hard Particle Monte Carlo Simulations. Comput Mater Sci (2020) 173:109363. doi:10.1016/j.commatsci.2019.109363
56. Hockney RW, Goel SP, Eastwood JW. Quiet High-Resolution Computer Models of a Plasma. J Comput Phys (1974) 14:148–58. doi:10.1016/0021-9991(74)90010-2
57. Ramasubramani V, Dice BD, Harper ES, Spellings MP, Anderson JA, Glotzer SC. Freud: A Software Suite for High Throughput Analysis of Particle Simulation Data. Comp Phys Commun (2020) 254:107275. doi:10.1016/j.cpc.2020.107275
58. Willems TF, Rycroft CH, Kazi M, Meza JC, Haranczyk M. Algorithms and Tools for High-Throughput Geometry-Based Analysis of Crystalline Porous Materials. Microporous Mesoporous Mater (2012) 149:134–41. doi:10.1016/j.micromeso.2011.08.020
59. Pinheiro M, Martin RL, Rycroft CH, Jones A, Iglesia E, Haranczyk M. Characterization and Comparison of Pore Landscapes in Crystalline Porous Materials. J Mol Graphics Model (2013) 44:208–19. doi:10.1016/j.jmgm.2013.05.007
60. Pinheiro M, Martin RL, Rycroft CH, Haranczyk M. High Accuracy Geometric Analysis of Crystalline Porous Materials. CrystEngComm (2013) 15:7531–8. doi:10.1039/c3ce41057a
61. Zhang J, Luijten E, Granick S. Toward Design Rules of Directional Janus Colloidal Assembly. Annu Rev Phys Chem (2015) 66:581–600. doi:10.1146/annurev-physchem-040214-121241
62. Dias CS, Braga C, Araújo NAM, Telo da Gama MM. Relaxation Dynamics of Functionalized Colloids on Attractive Substrates. Soft Matter (2016) 12:1550–7. doi:10.1039/c5sm02754c
63. Hagan MF, Elrad OM, Jack RL. Mechanisms of Kinetic Trapping in Self-Assembly and Phase Transformation. J Chem Phys (2011) 135:104115. doi:10.1063/1.3635775
64. Nykypanchuk D, Maye MM, van der Lelie D, Gang O. DNA-Guided Crystallization of Colloidal Nanoparticles. Nature (2008) 451:549–52. doi:10.1038/nature06560
65. Paquet E, Viktor HL. Molecular Dynamics, Monte Carlo Simulations, and Langevin Dynamics: A Computational Review. Biomed Res Int (2015) 2015:1–18. doi:10.1155/2015/183918
Keywords: self-assembly, charged lobed particles, particle mixtures, porous structures, long range interactions
Citation: Srivastava A, Rocha BC and Vashisth H (2022) Self-Assembly in Mixtures of Charged Lobed Particles. Front. Phys. 10:936385. doi: 10.3389/fphy.2022.936385
Received: 05 May 2022; Accepted: 17 June 2022;
Published: 19 July 2022.
Edited by:
Rodrigo Sánchez, Metropolitan Autonomous University, MexicoReviewed by:
Nuno A. M. Araújo, University of Lisbon, PortugalPrateek Kumar Jha, Indian Institute of Technology Roorkee, India
Copyright © 2022 Srivastava, Rocha and Vashisth. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Harish Vashisth, aGFyaXNoLnZhc2hpc3RoQHVuaC5lZHU=
†These authors have contributed equally to this work
 Arpita Srivastava†
Arpita Srivastava† Brunno C. Rocha
Brunno C. Rocha Harish Vashisth
Harish Vashisth