Odd viscosity in chiral passive suspensions

1 Introduction

Chiral active fluids are typical nonequilibrium systems consisting of self-spinning constituents [1–3]. In recent years, they have attracted increasing attention because of intriguing dynamics and collective behaviors such as turbulence [4], phase separation [5–7], surface wave [2, 8], and unidirectional edge current [9–13]. One essential property to explain such behaviors is the so-called Hall or odd viscosity, which stems from the inherent breaking of parity and time-reversal symmetries and does not produce any entropy or heat as dissipative viscosity [14, 15]. Prior work on the odd viscosity ranges from phenomenological to topological and rheological scopes. In most of such work, the self-spinning constituents are sufficiently small, so that the chiral active fluids are treated as continuum phases. Then their behaviors can be described by hydrodynamic equations with an additional assumed odd term, where the odd viscosity physically characterizes the orthogonal stress response of the system to the imposed flow (i.e., eigendirections of the rate of deformation tensor) [16–22].

In the field of rheology, the first normal stress difference, as one of viscometric functions, has been widely studied [23–25]. It also describes the orthogonal stress response to the imposed flow, but is commonly discussed for conventional complex fluids such as viscoelastic fluids and dense suspensions. We have clarified the relation between the odd viscosity and the first normal stress difference in the recent work [7]. In general, the latter can be decomposed into even and odd components. The even one results from the microstructures constructed by interacting fluid constituents, whereas the odd one is equivalent to the odd viscosity, which is nonzero when the parity and time-reversal symmetries of the system break. Our work reported that both of such even and odd components were nonzero for chiral active suspensions, indicating the mixed feature of conventional complex fluids and chiral viscous fluids [7]. Nevertheless, the understanding of rheology of chiral active suspensions is still lacking. Another open question is whether a suspension needs to be active (i.e., with self-spinning or externally-driven constituents) or not to have non-zero odd viscosity.

In this paper, we examine the odd viscosity in passive suspensions composed of chirally-shaped particles with finite size, by carrying out computational simulations in both simple shear and planar extensional flows [26]. The particles are modeled by ratchets with unidirectional (clockwise or anticlockwise) teeth and supposed to undergo asymmetric contact interactions. This means the contact can be either frictional or frictionless depending on the teeth and sliding directions of the particles. In Section 2, we detail the main simulation methods, including the modeling of particle dynamics and background flows, simulation parameters and conditions, and rheological characterization. Section 3 presents the simulation results in terms of average contact number of the particles, reorientation angles, and even and odd components of essential rheological coefficients.

2 Simulation method

2.1 Particle dynamics

For N spherical particles that are suspended in liquid solvent, they experience forces and torques due to Stokes drag (F_S and T_S), hydrodynamic inter-particle interactions (F_H and T_H), and frictional contact (F_C and T_C). When the flow time scale is shorter than the Brownian time scale, we can neglect both inertia and thermal fluctuations. Such a regime is also accessible in experiments [27–29]. As a result, the force and torque balances on particle i (= 1, …, N) are given by

${\mathit{F}}_{\text{S},i}+{\mathit{F}}_{\text{H},i}+\sum _{j\ne i}{\mathit{F}}_{\text{C},ij}=\mathrm{0},(1)$

${\mathit{T}}_{\text{S},i}+{\mathit{T}}_{\text{H},i}+\sum _{j\ne i}{\mathit{T}}_{\text{C},ij}=\mathrm{0}.(2)$

Here, the Stokes force and torque are given by

${\mathit{F}}_{\text{S},i}=-6\pi {\eta }_{0}a\left({\mathit{U}}_i-{\mathit{U}}^{\infty }\left({\mathit{x}}_i\right)\right),(3)$

${\mathit{T}}_{\text{S},i}=-8\pi {\eta }_0{a}^3\left({\mathbf{\Omega }}_i-{\mathbf{\Omega }}^{\infty }\left({\mathit{x}}_i\right)\right),(4)$

where η₀ represents the solvent viscosity, a the particle radius, U_i and Ω_i the velocity and angular velocity of particle i, respectively, and U^∞(x_i) and Ω^∞(x_i) the velocity and angular velocity of the background fluid at particle position x_i, respectively. For the inter-particle hydrodynamic interactions, we assume that they only arise from lubrication effects. This is justified for dense suspensions subjected to contact forces, where the far-field or many-body hydrodynamic interactions play minor roles. The 6N lubrication force and torque vectors (F_H ≡{F_H,1, …, F_H,N} and T_H ≡{T_H,1, …, T_H,N}) are coupled with the 6N particle velocity and angular velocity vectors (U ≡{U₁, …, U_N} and Ω ≡{Ω₁, …, Ω_N}) in the form of

$\left(\begin{array}{c}\hfill {\mathit{F}}_{\text{H}}\hfill \\ \hfill {\mathit{T}}_{\text{H}}\hfill \end{array}\right)=-{\mathsf{R}}_{\text{L}}\cdot \left(\begin{array}{c}\hfill \mathit{U}-{\mathit{U}}^{\infty }\left(\mathit{x}\right)\hfill \\ \hfill \mathbf{\Omega }-{\mathbf{\Omega }}^{\infty }\left(\mathit{x}\right)\hfill \end{array}\right)+{\mathsf{R}}_{\text{L}}^{\prime }:{\mathsf{E}}^{\infty },(5)$

where ${\mathsf{R}}_{\text{L}}$ and ${\mathsf{R}}_{\text{L}}^{\prime }$ are the configuration-dependent resistance matrices for the hydrodynamic lubrication, and ${\mathsf{E}}^{\infty }$ denotes the rate-of-strain tensor [30]. In the current work, the resistance matrices are simply described by the leading terms of the pairwise short-range lubrication interaction [31].

For two particles in contact, their interaction is described by a simple spring-and-dashpot model [32, 33], where the normal and tangential components of the contact force are given by

${\mathit{F}}_{\text{C},ij}^{\left(\mathrm{n}\right)}=k_{\text{n}}{h}_{ij}{\mathit{n}}_{ij}+{\gamma }_{\text{n}}{\mathit{U}}_{ij}^{\left(\mathrm{n}\right)},(6)$

${\mathit{F}}_{\text{C},ij}^{\left(\mathrm{t}\right)}=k_{\text{t}}{\mathit{\xi }}_{ij}.(7)$

Here, k_n and k_t are the normal and tangential spring constants, respectively, h_ij and n_ij represent the surface separation and center-to-center unit vector between the particles, respectively, γ_n is the damping constant, ${\mathit{U}}_{ij}^{(\mathrm{n})}\equiv {\mathit{n}}_{ij}{\mathit{n}}_{ij}\cdot \left({\mathit{U}}_j-{\mathit{U}}_i\right)$ is the relative normal velocity, and ξ_ij denotes the tangential stretch vector. The contact forces fulfill Coulomb’s friction law $|{\mathit{F}}_{\text{C},ij}^{(\mathrm{t})}|\le \mu |{\mathit{F}}_{\text{C},ij}^{(\mathrm{n})}|$ with the static friction coefficient μ. In addition, we note that ξ_ij = 0 in the absence of contact (h_ij > 0). After the particles contact at time t₀ (h_ij ≤ 0), the tangential stretch vector evolves as ${\mathit{\xi }}_{ij}(t)={\int }_{t_0}^t{\mathit{U}}_{ij}^{(\mathrm{t})}dt$, with the relative tangential velocity defined by ${\mathit{U}}_{ij}^{(\mathrm{t})}\equiv (\mathsf{I}-{\mathit{n}}_{ij}{\mathit{n}}_{ij})\cdot [{\mathit{U}}_j-{\mathit{U}}_i-(a{\mathbf{\Omega }}_i+a{\mathbf{\Omega }}_j)\times {\mathit{n}}_{ij}]$. Here $\mathit{I}$ is the identity tensor. Then the tangential contact torque in Eq. 2 is obtained by

${\mathit{T}}_{\text{C},ij}=a{\mathit{n}}_{ij}\times {\mathit{F}}_{\text{C},ij}^{\left(\mathrm{t}\right)}.(8)$

2.2 Simulation parameters and conditions

Our work takes into account four different types of particles, i.e., ratchet-like particles with clockwise teeth (ratchet I), ratchet-like particles with anticlockwise teeth (ratchet II), smooth particles, and gear-like rough particles (see Figure 1A). In computational modeling, all of these particles are spheres without any physical teeth or bumps. They differ from each other only in terms of different mathematical models for the inter-particle contact. For example, we assume the smooth particles are frictionless, i.e., μ = 0, and their contact interactions are only along the normal direction. In contrast, the gear-like particles are infinitely-frictional, i.e., μ = ∞, and their contact sliding is constrained. For ratchet-like particles, imaginary and chiral-directional ratchet teeth are endowed. Namely, the contact is infinitely-frictional when a ratchet slides in the same direction with its tooth at the contact point, and is frictionless otherwise.

FIGURE 1

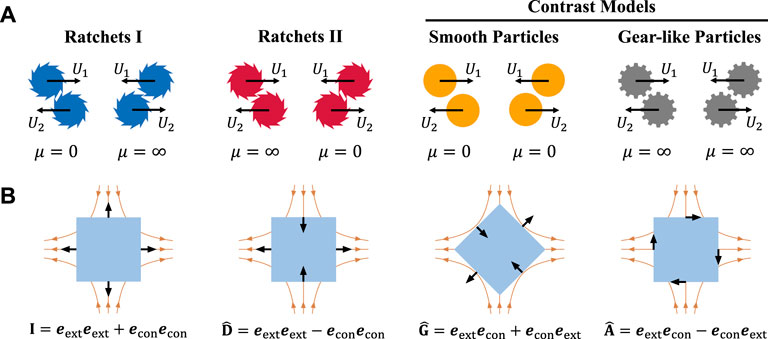
FIGURE 1. (A) Schematic of four particle models: ratchets I (with clockwise teeth), ratchets II (with anticlockwise teeth), smooth particles, and gear-like particles. When two ratchets tangentially contact and their teeth at the contact point are anti-parallel and parallel to their relative velocity, we assume the contacts are frictionless (μ = 0) and infinitely-frictional (μ = ∞), respectively. The smooth and gear-like particles (for contrast only) experience zero and infinite friction, respectively. (B) Schematic of stress components and corresponding basis tensors. The black arrows indicate the stress directions, whereas the orange lines and arrows represent the embedded extensional flow including the contraction (vertical) and extension (horizontal) axes.

Suspensions of the particles of the same type are exposed to simple shear and planar extensional flows, which are constructed with the Lees–Edwards [34] and Kraynik–Reinelt periodic boundary conditions [26, 35], respectively. The velocity field of the simple shear flow can be expressed as ${\mathit{U}}^{\infty }(\mathit{x})={\mathbf{\Omega }}^{\infty }\times \mathit{x}+{\mathsf{E}}^{\infty }\cdot \mathit{x}$. When the shear rate $\dot{\gamma }$ is constant, we have the nonzero elements $U_x^{\infty }=\dot{\gamma }y$, ${\mathrm{\Omega }}_z^{\infty }=-\dot{\gamma }/2$, and $E_{xy}^{\infty }=E_{yx}^{\infty }=\dot{\gamma }/2$. For the planar extensional flow, on the other hand, the velocity field is given by ${\mathit{U}}^{\infty }(\mathit{x})={\mathsf{E}}^{\infty }\cdot \mathit{x}$ and a constant extensional rate $\dot{\epsilon }$ leads to the nonzero elements $U_x^{\infty }=\dot{\epsilon }y$, $U_y^{\infty }=-\dot{\epsilon }x$, and $E_{xy}^{\infty }=-E_{yx}^{\infty }=\dot{\epsilon }$.

Simulations are carried out for N = 3000 bidisperse particles (with radii a and 1.4a and with equal areal fractions) that are constrained in a monolayer (x-y plane). The constants $\dot{\gamma }$ and $\dot{\epsilon }$ are taken to be positive. We set k_n and k_t (only for the cases of μ = ∞) to sufficiently large values that keep both the maximum overlap and tangential displacement smaller than 5% of the particle radius. The particle areal fraction varies in the range of 0.3 ≤ ϕ ≤ 0.75. For each set of simulation conditions and parameters, five parallel runs are performed starting from different random initial configurations.

2.3 Rheological characterization

The stress tensor of passive suspension can be obtained as

$\mathit{\sigma }=2{\eta }_0{\mathsf{E}}^{\infty }-\frac{1}{V}\sum _{i>j}{\mathit{r}}_{ij}\left({\mathit{F}}_{\text{H},ij}+{\mathit{F}}_{\text{C},ij}\right),(9)$

where V and r_ij represent the total volume of the suspension and center-to-center vector between particles i and j, respectively. According to the theoretical framework discussed in reference [36], the stress tensor in two-dimensional systems can be decomposed in terms of basis tensors as

$\mathit{\sigma }=-p\mathsf{I}+\dot{s}\left(\eta \widehat{\mathsf{D}}+\lambda \widehat{\mathsf{G}}+\zeta \widehat{\mathsf{A}}\right),(10)$

where p represents the pressure (including the isotropic stress due to contact forces), η the suspension viscosity, $\dot{s}$ ($=\dot{\gamma }$ or $2\dot{\epsilon }$) the flow rate, and λ and ζ the non-dissipative response function and rotational viscosity, respectively. The basis tensors are defined as $\widehat{\mathsf{D}}\equiv {\mathit{e}}_{\text{ext}}{\mathit{e}}_{\text{ext}}-{\mathit{e}}_{\text{con}}{\mathit{e}}_{\text{con}}$, $\widehat{\mathsf{G}}\equiv {\mathit{e}}_{\text{ext}}{\mathit{e}}_{\text{con}}+{\mathit{e}}_{\text{con}}{\mathit{e}}_{\text{ext}}$, and $\widehat{\mathsf{A}}\equiv {\mathit{e}}_{\text{ext}}{\mathit{e}}_{\text{con}}-{\mathit{e}}_{\text{con}}{\mathit{e}}_{\text{ext}}$, where e_ext and e_con are the unit vectors for the extension and contraction axes of the imposed flow. We note that the basis tensors are orthogonal to each other and their corresponding stress components are shown in Figure 1B. Besides, for suspensions without self-spinning elements, as in the current work, the term with ζ can be dropped.

Then the rotation of principal axes of σ in the flow plane with respect to those of $\widehat{\mathsf{D}}$ is quantified by the reorientation angle

$\theta \equiv \arctan \left[\lambda /\left(\eta +\sqrt{{\eta }^2+{\lambda }^2}\right)\right],(11)$

which is proportional to the ratio λ/η, or equivalently, N₁/σ_xy [36]. Here the first normal stress difference, N₁ ≡ σ_xx − σ_yy, is one typical signature indicating the presence of elasticity in complex fluids [25, 37]. It can alternatively be characterized through the first normal stress coefficient Ψ₁ defined by

${\mathrm{\Psi }}_1\equiv \frac{N_1}{|\dot{\gamma }|}=\frac{\dot{\gamma }}{|\dot{\gamma }|}\lambda .(12)$

However, when planar extensional flows are imposed, λ does not depend on the sign of $\dot{\epsilon }$ and the characterization in terms of Ψ₁ is unnecessary. Therefore, we only study the non-dissipative response function λ for the planar extensional flows. In order to further analyze the effect of shape chirality on any quantity Λ of interest, we decompose it into the even and odd components in terms of the flow rate as

${\Lambda }_{\text{even}}\equiv \frac{1}{2}\left[\Lambda \left(\dot{s}\right)+\Lambda \left(-\dot{s}\right)\right],(13)$

${\Lambda }_{\text{odd}}\equiv \frac{1}{2}\left[\Lambda \left(\dot{s}\right)-\Lambda \left(-\dot{s}\right)\right].(14)$

When Λ = Ψ₁/2, the odd component Λ_odd corresponds to the odd viscosity [7].

3 Results

Both simple shear and planar extensional flows can give rise to particle contacts along the contraction axis. Especially for dense suspensions, emergent particle microstructures and complex force chains (or networks) are determinant on the macroscopic rheological properties [38, 39]. Here, we first focus on the simulations where simple shear flows are applied and then step to the case of planar extensional flow. For each flow type, the rheological property is studied in terms of particle microstructure, (shear or extensional) viscosity, and non-dissipative response function.

Figure 2A presents the dependence of average contact number Z on the particle areal fraction ϕ, for the case where a simple shear flow is imposed. For low areal fractions (ϕ ≤ 0.5), we see that Z < 1 and the curves of ratchets I and II are in accordance with the curves of smooth and gear-like particles, respectively. This observation is expected because the same contact modes are assigned to the ratchets I and smooth particles, and to the ratchets II and gear-like particles (refer to the left column of each particle type in Figure 1A). Besides, the condition of simple shear flow and low areal fraction causes most of the particles to get into contact with only one neighbor. However, the average contact number becomes Z > 1 when ϕ increases. The curves of ratchets I and II then gradually coincide and eventually stay in the middle of the curves of the frictionless and gear-like particles.

FIGURE 2

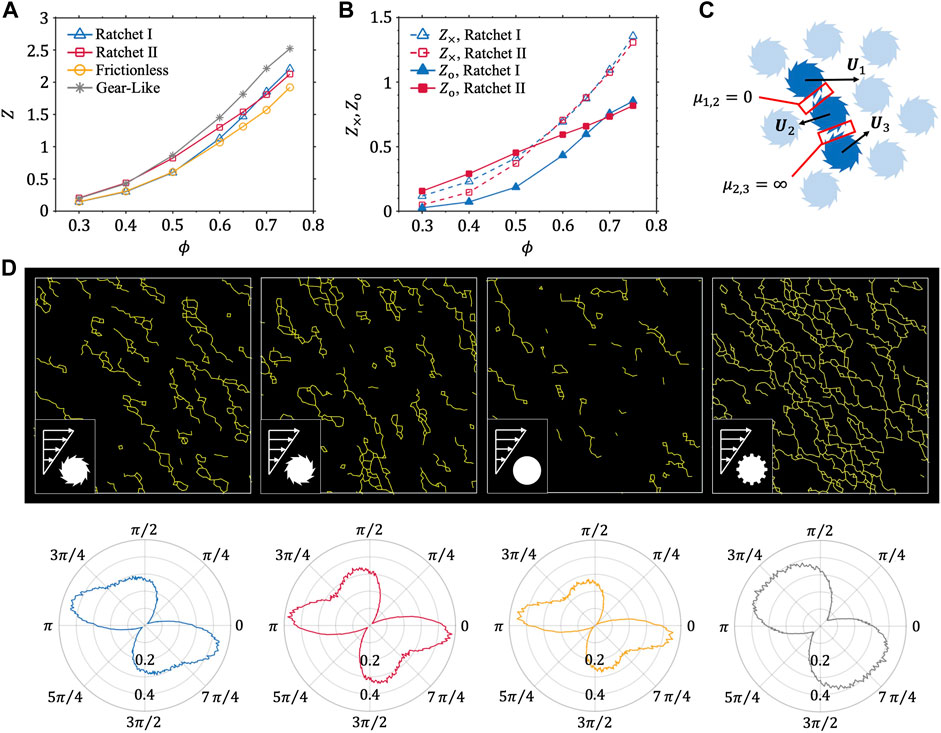
FIGURE 2. (A) Average contact number Z as a function of particle areal fraction ϕ for various particle models. (B) Average number of frictionless (Z_×) and infinitely-frictional (Z_o) contacts as a function of particle areal fraction ϕ for ratchets I and II. In (A) and (B), error bars are not shown because they are smaller than the symbols. (C) Schematic of contact interaction between ratchets in the dense limit, where frictionless and infinitely-frictional contacts emerge simultaneously. Here U₁, U₂, and U₃ denote the velocities of three contacted particles, whereas μ_1,2 and μ_2,3 represent the static friction coefficients for particles 1 and 2 and for particles 2 and 3, respectively. (D) Representative snapshots of force chain distribution (top) and corresponding polar plot of the angular contact distribution (bottom) in simple shear flows, for particle areal fraction ϕ = 0.65 and various particle models. Inserts denote the particle type and the velocity gradient of the simple shear flow. The radial axis of the polar plots represents the distribution probability P(θ).

In order to explain such a phenomenon, we separately plot the average numbers of frictionless (Z_×) and infinitely-frictional (Z_o) contacts for different ratchet systems. As shown in Figure 2B, both Z_× and Z_o increase with ϕ, but the former becomes preponderant at large values of ϕ. Particularly, unlike ratchets I for which the frictionless contacts are dominant throughout the areal fractions studied, ratchets II experience a switch of the main contact type. For large ϕ values, both Z_× and Z_o are independent of the particle chirality. This result not only explains the convergence of the curves of ratchets I and II (in Figure 2A), but also reveals that frictionless and infinitely-frictional contacts coexist within dense ratchet suspensions.

Figure 2C illustrates the representative contact scheme for dense ratchet suspensions, where U₁, U₂, and U₃ denote the velocities of three ratchet particles in contact. Because of the particle chirality and irregular local motions, ratchets 1 and 2 undergo the frictionless contact (μ_1,2 = 0), whereas ratchets 2 and 3 experience the infinitely-frictional contact (μ_2,3 = ∞). From the representative snapshots of contact network shown in Figure 2D (top row), one can observe that the ratchet suspensions of ϕ = 0.65 include profound multi-particle contacts. Furthermore, we estimate the angular distributions of the inter-particle contacts, as exhibited at the bottom row of Figure 2D. The radial axis is the distribution probability given by

$P\left(\theta \right)\equiv N_{\text{c}}\left(\theta \right)/\left(N\mathrm{\Delta }\theta \right),(15)$

where N_c(θ) represents the contact number at angle θ and Δθ denotes the angle interval. The result shows that the principal contact orientation of the gear-like particles is roughly along the contraction axis (θ = 3π/4 and 7π/4). But those for the other three particle types skew towards the anticlockwise direction.

Next we characterize the relative shear viscosity for different suspensions in the simple shear flow. Because of the close relation between the contact network and viscosity [26], the curves in Figure 3A show the similar shapes with those presented in Figure 2A. In details, the relative shear viscosities of ratchets I and II gradually coincide when ϕ increases and finally take the values between those of the smooth and gear-like particles. Compared with the other three types of particles, the gear-like particles show a dramatic increase of the shear viscosity at ϕ = 0.75. This is explained by the proximity to the frictional jamming point [40], which depends on the particle type as well as the value of the static friction coefficient [33].

FIGURE 3

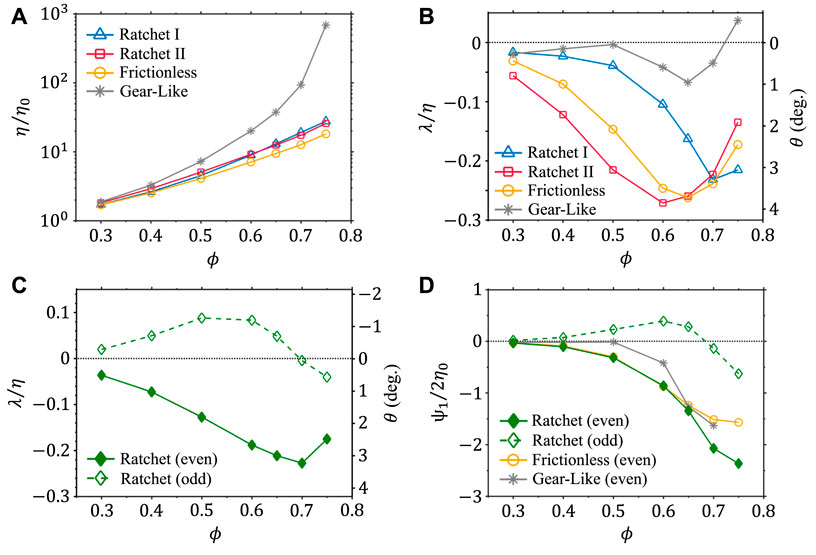
FIGURE 3. (A) Relative shear viscosity η/η₀ and (B) ratio of non-dissipation response function to shear viscosity λ/η and corresponding reorientation angle θ as a function of particle areal fraction ϕ for various particle models. (C) Even and odd components of the ratio λ/η as a function of ϕ for ratchet particles. (D) Scaled first normal stress coefficient as a function of ϕ for various particle models. In the figures, error bars are not shown because they are smaller than the symbols.

Figure 3B shows the ratio of non-dissipative response function to shear viscosity λ/η, or equivalently, N₁/σ_xy, and the corresponding reorientation angle θ as a function of ϕ for various particle suspensions. The curves of the frictionless and infinitely-frictional particles are in accord with the prior results [37, 41]. Additionally, the θ values at ϕ = 0.65 coincide with the result of the angular contact distributions (see the bottom row of Figure 2D), which demonstrates the close relation between the particle contacts (or microstructures) and responsive stress of the suspension. However, the curves of ratchets I and II are distinct, suggesting the dependence of the reorientation angle on the particle chirality. We employ Eqs. 13, 14 to decompose λ/η into even and odd components for the ratchet particles. As seen in Figure 3C, the even component takes negative values and its dependence on the areal fraction is typical of λ/η for achiral particle suspensions [42]. In contrast, the finite odd component shows a completely different behavior, with positive values for ϕ ≤ 0.65 and negative values for ϕ ≥ 0.7. The vanishing odd component is near ϕ = 0.7, where the even component experiences the minimum point. We emphasize that except for ϕ = 0.7, the odd component is non-negligible as compared with the even component.

In Figure 3D, we also calculate the even and odd components of the scaled first normal stress coefficient Ψ₁/(2η₀). One can see that the ratchet particles have the similar even components with the frictionless particles for ϕ ≤ 0.6, but smaller even components for ϕ ≥ 0.65. The odd component for the ratchet particles shows the similar behavior with the odd component of λ/η shown in Figure 3C. Such results demonstrate that the features of conventional complex fluids and chiral viscous fluids coexist in the passive ratchet suspensions.

In the following, we study the suspension rheology in the planar extensional flows. The average contact numbers Z for different suspensions are shown in Figure 4A. We observe that throughout the areal fraction studied, the Z values for ratchets I and II are similar and intermediate as compared with those for the frictionless and gear-like particles. Such a phenomenon, not seen for the simple shear flows, is because the planar extensional flows are symmetric with respect to the contraction and extension axes. Therefore, for both ratchets I or II, half of the particles undergo the frictionless contact and the other half experience the infinitely-frictional contact. This explains the phenomena shown in Figure 4B, where extensional viscosities for the ratchets I and II show the similar behaviors and the intermediate values with respect to those for the frictionless and gear-like particles.

FIGURE 4

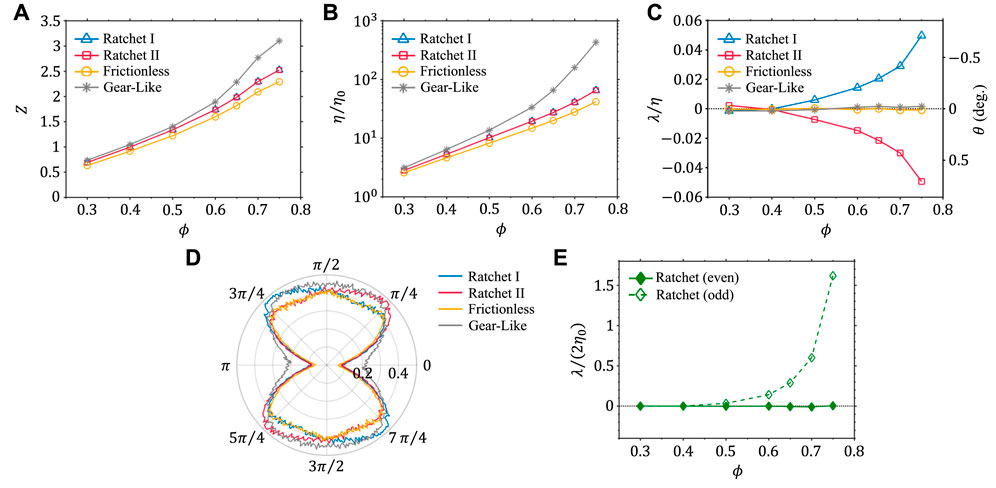
FIGURE 4. (A) Average contact number Z, (B) relative extensional viscosity η/η₀, and (C) ratio of non-dissipation response function to extensional viscosity λ/η and corresponding reorientation angle θ as a function of particle areal fraction ϕ for various types of particles in imposed planar extensional flows. (D) Polar plot of the angular contact distribution for various types of particles in imposed planar extensional flows. The radial axis represents the distribution probability P(θ). (E) Even and odd components of scaled non-dissipation response function λ/(2η₀) as a function of ϕ for ratchet particles. In the figures, error bars are not shown because they are smaller than the symbols.

Since the first normal stress difference N₁ and coefficient Ψ₁ are introduced for simple shear flows, we cannot use them for planar extensional flows. Instead, we directly investigate the dependence of the ratio λ/η and the corresponding reorientation angle on the particle areal fraction ϕ. In Figure 4C, we see that the reorientation angles for the frictionless and gear-like particles are almost zero. Nevertheless, the reorientation angles of ratchets I and II increase and decrease for large $\varphi$, respectively. This is because the shape chirality of the ratchet particle breaks the time-reversal symmetry in the planar extensional flow, resulting in the asymmetric contact network (or particle microstructures) around the contraction and extension axes (see Figure 4D). Moreover, by taking the decomposition of the scaled non-dissipative response function λ/(2η₀) for the ratchet particles, we observe the vanishing even component but prominent odd component that increases with ϕ (see Figure 4E). Such a result demonstrates that the reorientation angle in the planar extensional flows is purely due to the existence of the odd viscosity.

4 Discussions and conclusion

Although the nonzero odd viscosity is obtained for chiral passive suspensions, we underline that its dependence on the particle areal fraction ϕ varies for different flow types. As exhibited in the result section, the simple shear and planar extensional flows give rise to the non-monotonic changes and monotonic increase of the odd viscosity with ϕ, respectively. This difference is due to the flow-induced microstructures, which affect the non-dissipative response function λ and then make the odd viscosity flow-type-dependent. Besides, we demonstrate that the odd viscosity can also be characterized when the fluid constituents are not externally rotated (by active torques or imposed flows). Applying planar extensional flows is suggested to be a straightforward examination of the odd viscosity of a fluid.

In order to give a universal framework for the relevant rheological characterizations, we schematically present in Figure 5 the responsive stress and the corresponding reorientation angle for four different fluid systems. Since the reorientation angle does not rely on the rotational stress response, our framework only considers the symmetric part of the stress sym σ. Meanwhile, both the cases of simple shear and planar extensional flows are taken into account.

FIGURE 5

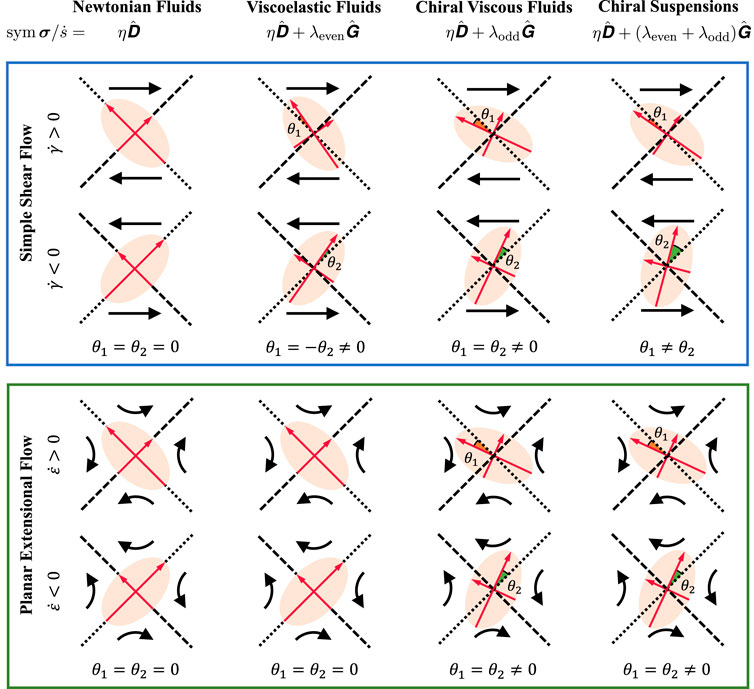
FIGURE 5. Schematics of response stress of different fluids in simple shear and planar extensional flows. The red arrows represent the principal axes of the response stress in the flow plane, whereas the black arrows denote the direction of imposed strain. The symbols λ_even and λ_odd denote the even and odd components of non-dissipative response function λ. The subscripts 1 and 2 indicate the reorientation angles for the positive and negative shear or extensional rate, respectively.

As seen in the first column, stable Newtonian fluids have a uniform distribution of constituents and thus constant viscosity. The principal axes of sym σ should align exactly with those of $\widehat{\mathsf{D}}$. However, for sheared conventional complex fluids (including viscoelastic fluids and dense suspensions), the emergence of internal constituent microstructures leads the principal axes of sym σ to differ from those of $\widehat{\mathsf{D}}$. Then one will obtain a nonzero response function λ_even (i.e., the even component of the first normal stress coefficient) and the corresponding reorientation angles satisfying θ₁ = −θ₂ ≠ 0. We note that such behaviors are not typical for planar extensional flows, because both of the flow field and resultant microstructures are symmetric with respect to the contraction and extension axes. For chiral viscous fluids, the principal axes of the responsive stress rotate for both simple shear and planar extensional flows. However, the origin is purely due to the intrinsic chirality, leading to the loss of parity and time-reversal symmetries of the fluid. As a result, the direction of the reorientation angle is independent of the shear or extensional rates, i.e., θ₁ = θ₂ ≠ 0. The response function is the odd component of the first normal stress coefficient λ_odd or the odd viscosity. Finally, in chiral suspensions (either active or passive), both microstructures and chirality contribute to the tilted principal axes of the responsive stress from those of $\widehat{\mathsf{D}}$. Thus, the response function is the first normal stress coefficient (i.e., λ_even + λ_odd) for the simple shear flows, and is λ_odd for the planar extensional flows.

In conclusion, by carrying out computational simulations, we have studies the rheology of passive chiral suspensions in simple shear and planar extensional flows. The results of the shear and extensional viscosities show the intermediate values between those for the smooth and gear-like particles. The dependence of the shear viscosity on the particle chirality is significant at low particle areal fractions but negligible for high areal fractions. Importantly, the chiral passive suspensions show nonzero even and odd components of the non-dissipative response function, suggesting the mixed feature of conventional complex fluids and chiral viscous fluids. Such even and odd components have comparable contributions to the reorientation angle of the system stress. We hope our work will extend the field of rheology and progress the understanding of chiral fluids.

Data availability statement

The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.

Author contributions

ZZ, MY, SK, and RS contributed to design the project and wrote the manuscript. ZZ performed the numerical simulations and data analysis.

Funding

The work was supported by the startup fund of Wenzhou Institute, University of Chinese Academy of Sciences (No. WIUCASQD2020002 and No. WIUCASQD2021041), National Nature Science Foundation of China (No. 1217042129 and No. 12174390), and the Research Fund for International Scientists, National Nature Science Foundation of China (No. 12150610463).

Acknowledgments

ZZ acknowledges the Postdoctor Association of WIUCAS for helpful discussions. The authors also acknowledge Giulio Giusteri for valuable suggestions.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Tsai JC, Ye F, Rodriguez J, Gollub JP, Lubensky T. A chiral granular gas. Phys Rev Lett (2005) 94:214301. doi:10.1103/physrevlett.94.214301

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Soni V, Bililign ES, Magkiriadou S, Sacanna S, Bartolo D, Shelley MJ, et al. The odd free surface flows of a colloidal chiral fluid. Nat Phys (2019) 15:1188–94. doi:10.1038/s41567-019-0603-8

CrossRef Full Text | Google Scholar

3. Scholz C, Engel M, Pöschel T. Rotating robots move collectively and self-organize. Nat Commun (2018) 9:931–8. doi:10.1038/s41467-018-03154-7

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Reeves CJ, Aranson IS, Vlahovska PM. Emergence of lanes and turbulent-like motion in active spinner fluid. Commun Phys (2021) 4:92–9. doi:10.1038/s42005-021-00596-2

CrossRef Full Text | Google Scholar

5. Shen Z, Lintuvuori JS. Hydrodynamic clustering and emergent phase separation of spherical spinners. Phys Rev Res (2020) 2:013358. doi:10.1103/physrevresearch.2.013358

CrossRef Full Text | Google Scholar

6. Massana-Cid H, Levis D, Hernández RJH, Pagonabarraga I, Tierno P. Arrested phase separation in chiral fluids of colloidal spinners. Phys Rev Res (2021) 3:L042021. doi:10.1103/physrevresearch.3.l042021

CrossRef Full Text | Google Scholar

7. Zhao Z, Wang B, Komura S, Yang M, Ye F, Seto R. Emergent stripes of active rotors in shear flows. Phys Rev Res (2021) 3:043229. doi:10.1103/physrevresearch.3.043229

CrossRef Full Text | Google Scholar

8. Abanov A, Can T, Ganeshan S. Odd surface waves in two-dimensional incompressible fluids. Scipost Phys (2018) 5:010. doi:10.21468/scipostphys.5.1.010

CrossRef Full Text | Google Scholar

9. van Zuiden BC, Paulose J, Irvine WT, Bartolo D, Vitelli V. Spatiotemporal order and emergent edge currents in active spinner materials. Proc Natl Acad Sci U S A (2016) 113:12919–24. doi:10.1073/pnas.1609572113

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Souslov A, Dasbiswas K, Fruchart M, Vaikuntanathan S, Vitelli V. Topological waves in fluids with odd viscosity. Phys Rev Lett (2019) 122:128001. doi:10.1103/physrevlett.122.128001

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Yang X, Ren C, Cheng K, Zhang H. Robust boundary flow in chiral active fluid. Phys Rev E (2020) 101:022603. doi:10.1103/physreve.101.022603

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Liu P, Zhu H, Zeng Y, Du G, Ning L, Wang D, et al. Oscillating collective motion of active rotors in confinement. Proc Natl Acad Sci U S A (2020) 117:11901–7. doi:10.1073/pnas.1922633117

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Yang Q, Zhu H, Liu P, Liu R, Shi Q, Chen K, et al. Topologically protected transport of cargo in a chiral active fluid aided by odd-viscosity-enhanced depletion interactions. Phys Rev Lett (2021) 126:198001. doi:10.1103/physrevlett.126.198001

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Avron J. Odd viscosity. J Stat Phys (1998) 92:543–57. doi:10.1023/a:1023084404080

CrossRef Full Text | Google Scholar

15. Banerjee D, Souslov A, Abanov AG, Vitelli V. Odd viscosity in chiral active fluids. Nat Commun (2017) 8:1573–12. doi:10.1038/s41467-017-01378-7

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Ganeshan S, Abanov AG. Odd viscosity in two-dimensional incompressible fluids. Phys Rev Fluids (2017) 2:094101. doi:10.1103/physrevfluids.2.094101

CrossRef Full Text | Google Scholar

17. Liao Z, Han M, Fruchart M, Vitelli V, Vaikuntanathan S. A mechanism for anomalous transport in chiral active liquids. J Chem Phys (2019) 151:194108. doi:10.1063/1.5126962

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Hargus C, Klymko K, Epstein JM, Mandadapu KK. Time reversal symmetry breaking and odd viscosity in active fluids: Green–kubo and nemd results. J Chem Phys (2020) 152:201102. doi:10.1063/5.0006441

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Epstein JM, Mandadapu KK. Time-reversal symmetry breaking in two-dimensional nonequilibrium viscous fluids. Phys Rev E (2020) 101:052614. doi:10.1103/physreve.101.052614

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Han M, Fruchart M, Scheibner C, Vaikuntanathan S, de Pablo JJ, Vitelli V. Fluctuating hydrodynamics of chiral active fluids. Nat Phys (2021) 17:1260–9. doi:10.1038/s41567-021-01360-7

CrossRef Full Text | Google Scholar

21. Hosaka Y, Komura S, Andelman D. Nonreciprocal response of a two-dimensional fluid with odd viscosity. Phys Rev E (2021) 103:042610. doi:10.1103/physreve.103.042610

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Hosaka Y, Komura S, Andelman D. Hydrodynamic lift of a two-dimensional liquid domain with odd viscosity. Phys Rev E (2021) 104:064613. doi:10.1103/physreve.104.064613

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Coleman BD, Markovitz H, Noll W. Viscometric flows of non-Newtonian fluids: Theory and experiment, vol. 5. Cambridge: Cambridge Univ Press (1966).

Google Scholar

24. Bird RB, Armstrong RC, Hassager O. Dynamics of polymeric liquids. Vol. 1: Fluid mechanics. New York, NY: John Wiley & Sons (1987).

Google Scholar

25. Dbouk T, Lobry L, Lemaire E. Normal stresses in concentrated non-brownian suspensions. J Fluid Mech (2013) 715:239–72. doi:10.1017/jfm.2012.516

CrossRef Full Text | Google Scholar

26. Seto R, Giusteri GG, Martiniello A. Microstructure and thickening of dense suspensions under extensional and shear flows. J Fluid Mech (2017) 825:R3. doi:10.1017/jfm.2017.469

CrossRef Full Text | Google Scholar

27. Zarraga IE, Hill DA, Leighton DT. The characterization of the total stress of concentrated suspensions of noncolloidal spheres in Newtonian fluids. J Rheology (2000) 44:185–220. doi:10.1122/1.551083

CrossRef Full Text | Google Scholar

28. Stickel JJ, Powell RL. Fluid mechanics and rheology of dense suspensions. Annu Rev Fluid Mech (2005) 37:129–49. doi:10.1146/annurev.fluid.36.050802.122132

CrossRef Full Text | Google Scholar

29. Boyer F, Guazzelli É, Pouliquen O. Unifying suspension and granular rheology. Phys Rev Lett (2011) 107:188301. doi:10.1103/physrevlett.107.188301

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Brady JF, Bossis G. Stokesian dynamics. Annu Rev Fluid Mech (1988) 20:111–57. doi:10.1146/annurev.fl.20.010188.000551

CrossRef Full Text | Google Scholar

31. Ball R, Melrose JR. A simulation technique for many spheres in quasi-static motion under frame-invariant pair drag and brownian forces. Physica A: Stat Mech its Appl (1997) 247:444–72. doi:10.1016/s0378-4371(97)00412-3

CrossRef Full Text | Google Scholar

32. Luding S. Cohesive, frictional powders: Contact models for tension. Granul Matter (2008) 10:235–46. doi:10.1007/s10035-008-0099-x

CrossRef Full Text | Google Scholar

33. Mari R, Seto R, Morris JF, Denn MM. Shear thickening, frictionless and frictional rheologies in non-brownian suspensions. J Rheol (N Y N Y) (2014) 58:1693–724. doi:10.1122/1.4890747

CrossRef Full Text | Google Scholar

34. Lees AW, Edwards SF. The computer study of transport processes under extreme conditions. J Phys C: Solid State Phys (1972) 5:1921–8. doi:10.1088/0022-3719/5/15/006

CrossRef Full Text | Google Scholar

35. Kraynik A, Reinelt D. Extensional motions of spatially periodic lattices. Int J Multiphase Flow (1992) 18:1045–59. doi:10.1016/0301-9322(92)90074-q

CrossRef Full Text | Google Scholar

36. Giusteri GG, Seto R. A theoretical framework for steady-state rheometry in generic flow conditions. J Rheol (N Y N Y) (2018) 62:713–23. doi:10.1122/1.4986840

CrossRef Full Text | Google Scholar

37. Seto R, Giusteri GG. Normal stress differences in dense suspensions. J Fluid Mech (2018) 857:200–15. doi:10.1017/jfm.2018.743

CrossRef Full Text | Google Scholar

38. Larson RG. The structure and rheology of complex fluids, vol. 150. New York: Oxford University Press (1999).

Google Scholar

39. Seto R, Mari R, Morris JF, Denn MM. Discontinuous shear thickening of frictional hard-sphere suspensions. Phys Rev Lett (2013) 111:218301. doi:10.1103/physrevlett.111.218301

PubMed Abstract | CrossRef Full Text | Google Scholar

40. O’Hern CS, Silbert LE, Liu AJ, Nagel SR. Jamming at zero temperature and zero applied stress: The epitome of disorder. Phys Rev E (2003) 68:011306. doi:10.1103/physreve.68.011306

CrossRef Full Text | Google Scholar

41. Royer JR, Blair DL, Hudson SD. Rheological signature of frictional interactions in shear thickening suspensions. Phys Rev Lett (2016) 116:188301. doi:10.1103/physrevlett.116.188301

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Cwalina CD, Wagner NJ. Material properties of the shear-thickened state in concentrated near hard-sphere colloidal dispersions. J Rheol (N Y N Y) (2014) 58:949–67. doi:10.1122/1.4876935

CrossRef Full Text | Google Scholar