Enhancing the teleportation of quantum Fisher information under correlated amplitude damping decoherence

1 Introduction

Quantum teleportation is an important branch in the field of quantum communication. Its original idea was first proposed by Bennett et al. in 1993 [1]. Since then, the research and application of quantum teleportation have attracted great attention and great progress has also been made in experiments [2–7]. Recently, the teleportation of quantum Fisher information (QFI) was widely investigated [8]. QFI plays a central role in quantum estimation theory where the main task is to estimate the value of an unknown parameter. According to the quantum Cramer-Rao theorem [9], the precision of parameter estimation is inversely proportional to the square root of QFI. This means that the larger the QFI is, the higher the precision of parameter estimation would be. In the past 2 decades, rapid developments in the field of quantum metrology also deepen the understanding of QFI [10, 11]. Moreover, as a specific measure of the information content of quantum states, QFI also has a wide range of applications in other quantum information processes, including but not limited to entanglement detection [12, 13], quantum thermodynamics [14], quantum teleportation [15] and quantum machine learning [16].

However, in the process of quantum teleportation, quantum system will inevitably interact with the surrounding environment. This interaction will lead to the loss of coherence and the decay of entanglement, which results in the distortion of teleportation [17–20]. The same is true for the teleportation of QFI [8, 21–24]. In Ref. [21], the author has studied the teleportation of QFI in consideration of vacuum fluctuation. The influence of thermal noise caused by the Unruh effect on the teleportation of QFI has been discussed in Ref. [22]. Guo et al. have investigated the teleportation of QFI under the Davies-type Markov environment [23]. In Refs. [8, 25], the amplitude damping decoherence has been studied and the schemes to improve the teleportation of QFI have been proposed. However, much of the research up to now are based on the assumption that the noisy channel used for teleportation is memoryless and the two consecutive use of the channel are independent.

In practice, an actual physical system is more or less correlated in continuous uses, especially when the transmission rate is high [26–30]. Interestingly, although the qubits in the CAD noise suffer from decoherence, the correlated effects are beneficial to suppress the decay of coherence [31–34]. Many studies have focused on the influence of correlated noise in quantum information processing, and put forward many schemes to suppress the CAD decoherence. Xiao et al. have investigated the protection of entanglement from CAD by WM [31]. Huang and Zhang demonstrate the protection of measurement-induced nonlocality and local quantum uncertainty from CAD by WM and post-measurement reversal [32]. Enhancing entanglement of assistance using WM and quantum measurement reversal (QMR) under CAD noise has been studied in Ref. [33]. In addition, the teleportation under CAD noise has been investigated and one scheme to suppress decoherence using WM has been proposed [34].

Here, we consider the teleportation of QFI using Werner state as quantum channels under the CAD decoherence. Our study differs from Refs. [22–24], in which the performance of the QFI under the uncorrelated decoherence is discussed. The focus of our paper is to examine how correlated effects affect the teleportation of QFI. According to our results, we find that the correlated effects are beneficial to the teleportation of QFI in the CAD decoherence. Our study also differs from Refs. [31–34], in which the combination of WM and QMR is presented to improve the teleportation. In this paper, two schemes based on WM and EAM are proposed to make further efforts on enhancing the QFI. In particular, a comprehensive comparison indicates that the EAM strategy outperforms the WM strategy on the teleportation of QFI. We also discuss how correlated effects affect the teleportation of QFI in WM and EAM schemes.

This paper is organized as follows: In Section 2, the teleportation of QFI under CAD decoherence is investigated. In Section 3, the scheme for enhancing the teleportation of QFI by WM and QMR is proposed. In Section 4, based on EAM and QMR, we present another scheme to enhance the teleportation of QFI. And the comparison of the two schemes is presented in Section 5. Finally, a summary is given in Section 6.

2 Teleportation of QFI under CAD noise

The teleportation of QFI under CAD noise is investigated in this section. Alice wants to send the QFI of parameter ϕ encoded in an unknown quantum state to Bob, which is

$|{\mathrm{\Psi }}_{in}\rangle =\cos \frac{\theta }{2}|0\rangle +\sin \frac{\theta }{2}{e}^{i\varphi }|1\rangle .(1)$

where θ is the polarization parameter and ϕ is the phase parameter. To realize the teleportation of QFI, an initially entangled state must be established between Alice and Bob. Here, the shared entangled state is a degraded Bell state, i.e., Werner state, which plays an important role in entanglement purification [17] and delocalized state [35].

$\rho =\mu |{\mathrm{\Psi }}^{+}\rangle \langle {\mathrm{\Psi }}^{+}|+\frac{1-\mu }{4}{\mathrm{I}}_4.(2)$

where $\mu \in \left[\mathrm{0,1}\right]$, $|{\mathrm{\Psi }}^{+}\rangle =\frac{1}{\sqrt{2}}(|00\rangle +|11\rangle )$ and I₄ is a 4 × 4 identity matrix. Assume that this entangled state is prepared by a third-party Charlie. When Charlie distributes the entangled particles to Alice and Bob, they first pass through a common channel with AD noise in successive, and then pass through a noise-free private channel respectively. Note that for the uncorrelated AD noise, its action over one channel use is irrelevant to all other uses. The total evolution map can be expressed as a tensor product of the individual evolution: ${\epsilon }_N={\epsilon }_1^{\otimes N}$. However, the correlated effects should be considered when the common channel is used continuously. The tensorial decomposition is not applicable, i.e., ${\epsilon }_N\ne {\epsilon }_1^{\otimes N}$. Therefore, in the process of establishing entangled channel, the Werner state is influenced by CAD noise. It can be expressed as [36].

${\epsilon }_{\mathrm{C}\mathrm{A}\mathrm{D}}\left(\rho \right)=\left(1-\eta \right)\sum _{i,j=0}^1{E}_{ij}\rho E_{ij}^{†}+\eta \sum _{k=0}^1{A}_k\rho A_k^{†},(3)$

where η is the correlated parameter and $\eta \in \left[\mathrm{0,1}\right]$. Obviously, we can get the uncorrelated AD noise by setting η = 0 and the fully correlated amplitude damping (FCAD) noise by setting η = 1. AD noise is a widely discussed model in various real-world physical evolutions that describes the ubiquitous energy dissipation process between quantum systems and environment [37]. It is represented by Kraus operators

$E_0=\left(\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \sqrt{1-\gamma }\hfill \end{array}\right),E_1=\left(\begin{array}{cc}\hfill 0\hfill & \hfill \sqrt{\gamma }\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right),(4)$

where γ is the decoherence strength of the AD noise and $\gamma \in \left[\mathrm{0,1}\right]$. The Kraus operators of the correlated part are obtained by solving the correlated Lindblad equation [38]

$A_0=\left(\begin{array}{cccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \sqrt{1-\gamma }\hfill \end{array}\right),A_1=\left(\begin{array}{cccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \sqrt{\gamma }\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right).(5)$

We note that the Kraus operator A₀ cannot be expressed as a tensor product of two 2 × 2 matrices. In fact, it depicts the typical “spooky” action of the public channel: |00⟩, |01⟩ and |10⟩ will go through the channel undisturbed, while |11⟩ suffers the amplitude damping decoherence.

Substituting Eqs 2, 4, 5 into Eq. 3, we can obtain

$\begin{array}{cc}\hfill & {\epsilon }_{\mathrm{C}\mathrm{A}\mathrm{D}}\left(\rho \right)=\left(\begin{array}{cccc}\hfill {\epsilon }_{11}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\epsilon }_{14}\hfill \\ \hfill 0\hfill & \hfill {\epsilon }_{22}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\epsilon }_{33}\hfill & \hfill 0\hfill \\ \hfill {\epsilon }_{41}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\epsilon }_{44}\hfill \end{array}\right),\hfill \end{array}(6)$

where ${\epsilon }_{11}=\frac{\bar{\eta }(1+\mu )(1+{\gamma }^2)+2\gamma \bar{\eta }\bar{\mu }+\eta (1+\mu )(1+\gamma )}{4}$, ${\epsilon }_{22}={\epsilon }_{33}=\frac{\bar{\eta }\bar{\mu }\bar{\gamma }+(1+\mu )\gamma \bar{\gamma }\bar{\eta }+\eta \bar{\mu }}{4}$, ${\epsilon }_{44}=\frac{\bar{\gamma }(1+\mu )(\bar{\eta }\bar{\gamma }+\eta )}{4}$, ${\epsilon }_{14}={\epsilon }_{41}^{\ast }=\frac{\mu (\bar{\eta }\bar{\gamma }+\eta \sqrt{\bar{\gamma }})}{2}$.

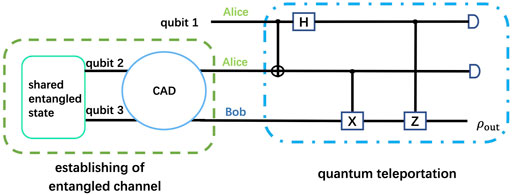
Then, through the quantum teleportation protocol shown in Figure 1, the state received by Bob is

$\begin{array}{cc}\hfill & {\rho }_{\text{out}}=\left(\begin{array}{cc}\hfill {\cos }^2\frac{\theta }{2}\left({\epsilon }_{11}+{\epsilon }_{44}\right)+{\sin }^2\frac{\theta }{2}\left({\epsilon }_{22}+{\epsilon }_{33}\right)\hfill & \hfill \cos \frac{\theta }{2}\sin \frac{\theta }{2}{e}^{-i\varphi }\left({\epsilon }_{14}+{\epsilon }_{41}\right)\hfill \\ \hfill \cos \frac{\theta }{2}\sin \frac{\theta }{2}{e}^{i\varphi }\left({\epsilon }_{14}+{\epsilon }_{41}\right)\hfill & \hfill {\cos }^2\frac{\theta }{2}\left({\epsilon }_{22}+{\epsilon }_{33}\right)+{\sin }^2\frac{\theta }{2}\left({\epsilon }_{11}+{\epsilon }_{44}\right)\hfill \end{array}\right),\hfill \end{array}(7)$

On the other hand, Zhong et al. [39] presented a simple and explicit description of QFI for the single-qubit state

$\begin{array}{cc}\hfill & F_{\varphi }=\left\{\begin{array}{cc}\hfill {\left|{\partial }_{\varphi }\vec{r}\right|}^2+\frac{{\left(\vec{r}\cdot {\partial }_{\varphi }\vec{r}\right)}^2}{1-|\vec{r}{|}^2},\hfill & \text{\hspace{0.17em}if\hspace{0.17em}}|\vec{r}|<1,\hfill \\ \hfill {\left|{\partial }_{\varphi }\vec{r}\right|}^2,\hfill & \text{\hspace{0.17em}if\hspace{0.17em}}|\vec{r}|=1,\hfill \end{array}\right.\hfill \end{array}(8)$

where $\vec{r}={\left(r_x,r_y,r_z\right)}^T$ is the real Bloch vector of the single-qubit state $\rho =\frac{1}{2}(1+\vec{r}\cdot \widehat{\sigma })$ with $\widehat{\sigma }=\left({\widehat{\sigma }}_x,{\widehat{\sigma }}_y,{\widehat{\sigma }}_z\right)$ denoting the Pauli matrices. The Bloch vector of state shown in Eq. 7 is

$r_x=2{\epsilon }_{14}\sin \theta \cos \varphi ,(9)$

$r_y=2{\epsilon }_{14}\sin \theta \sin \varphi ,(10)$

$r_z=\cos \theta \left({\epsilon }_{11}+{\epsilon }_{44}-{\epsilon }_{22}-{\epsilon }_{33}\right).(11)$

Then, we can obtain the teleported QFI under the CAD decoherence

$\begin{array}{c}\hfill F_{\mathrm{C}\mathrm{A}\mathrm{D}}={\mu }^2{\left(\bar{\eta }\bar{\gamma }+\eta \sqrt{\bar{\gamma }}\right)}^2{\sin }^2\theta .\end{array}(12)$

FIGURE 1

FIGURE 1. (color online) The circuit of quantum teleportation under CAD noise.

In Figure 2A, we have plotted the teleported QFI as a function of μ and γ for η = 0.8. It is straightforward to note that F_CAD rapidly decreases with the increase of decoherence strength γ. That is to say, the decoherence seriously reduces the transmission of QFI. On the other hand, in order to figure out the effect of correlated parameter, Figure 2B is plotted to shown F_CAD as a function of η and γ for μ = 0.8. It is found that F_CAD decays more slowly as η increases. This result means that the correlated effects enable to enhance the teleported QFI which is subject to CAD noise.

FIGURE 2

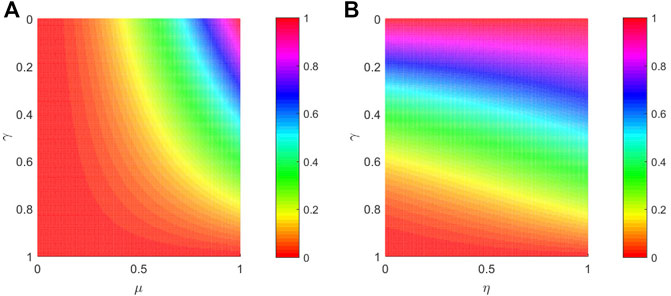
FIGURE 2. (color online) (A) Teleported QFI F_CAD as a function of γ and μ with η = 0.8. (B) Teleported QFI F_CAD as a function of γ and η with μ = 0.8. The polarization parameter θ is $\frac{\pi }{2}$.

3 WM scheme

In above, the influence of CAD decoherence on the teleportation of QFI has been examined. We find that even though the correlated effect could enhance the teleported QFI, the unfavorable effects of CAD decoherence still remain. In this section, we introduce the techniques of WM and QMR to reduce the adverse effects of CAD noise. WM is associated with positive-operator valued measure (POVM) [40, 41]. The most notable virtue of WM is that it is not fully destructive, implying that the quantum state can be recovered. Then, QMR operation is designed to recover the initial state. The specific process is as follows: before Charlie sends the entangled qubits to Alice and Bob, two WMs are performed on the qubits, respectively. After qubits two and three arrive at Alice and Bob through the CAD channel, the QMRs are carried out on these two qubits by Alice and Bob. The processes can be expressed as the following map

$\begin{array}{c}\hfill {\rho }_{\mathrm{W}\mathrm{M}}={\mathrm{M}}_{\mathrm{Q}\mathrm{M}\mathrm{R}}\left[{\epsilon }_{\mathrm{C}\mathrm{A}\mathrm{D}}\left({\mathrm{M}}_{\mathrm{W}\mathrm{M}}\rho {\mathrm{M}}_{\mathrm{W}\mathrm{M}}^{†}\right)\right]{\mathrm{M}}_{\mathrm{Q}\mathrm{M}\mathrm{R}}^{†},\end{array}(13)$

where

$\begin{array}{cc}\hfill & {\mathrm{M}}_{\mathrm{W}\mathrm{M}}=\left(\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \sqrt{\bar{p}}\hfill \end{array}\right)\otimes \left(\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \sqrt{\bar{p}}\hfill \end{array}\right),\hfill \end{array}(14)$

$\begin{array}{cc}\hfill & {\mathrm{M}}_{\mathrm{Q}\mathrm{M}\mathrm{R}}=\left(\begin{array}{cc}\hfill \sqrt{\bar{q}}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right)\otimes \left(\begin{array}{cc}\hfill \sqrt{\bar{q}}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right),\hfill \end{array}(15)$

where p and q are the strength of WM and QMR, respectively. $p,q\in \left[\mathrm{0,1}\right]$. Here, we define $\bar{\mathrm{O}}=1-\mathrm{O}$ for arbitrary parameter O. Finally, Alice and Bob share the state

$\begin{array}{cc}\hfill & {\rho }_{\mathrm{W}\mathrm{M}}=\left(\begin{array}{cccc}\hfill {\epsilon }_{11}^{\prime }\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\epsilon }_{14}^{\prime }\hfill \\ \hfill 0\hfill & \hfill {\epsilon }_{22}^{\prime }\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\epsilon }_{33}^{\prime }\hfill & \hfill 0\hfill \\ \hfill {\epsilon }_{41}^{\prime }\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\epsilon }_{44}^{\prime }\hfill \end{array}\right),\hfill \end{array}(16)$

where ${\epsilon }_{11}^{\prime }=\frac{U{\bar{q}}^2}{U{\bar{q}}^2+2V\bar{q}+W}$, ${\epsilon }_{22}^{\prime }={\epsilon }_{33}^{\prime }=\frac{V\bar{q}}{U{\bar{q}}^2+2V\bar{q}+W}$, ${\epsilon }_{44}^{\prime }=\frac{W}{U{\bar{q}}^2+2V\bar{q}+W}$, ${\epsilon }_{14}^{\prime }={{\epsilon }_{41}^{\prime }}^{\ast }=\frac{2X\bar{q}}{U{\bar{q}}^2+2V\bar{q}+W}$, and $U=\bar{\eta }(1+\mu )(1+{\gamma }^2{\bar{p}}^2)+2\gamma \bar{\eta }\bar{\mu }\bar{p}+\eta (1+\mu )(1+\gamma {\bar{p}}^2)$, $V=\bar{\mu }\bar{\eta }\bar{\gamma }\bar{p}+(1+\mu )\bar{\eta }\gamma \bar{\gamma }{\bar{p}}^2+\bar{\mu }\eta \bar{p}$, $W=\bar{\gamma }{\bar{p}}^2(1+\mu )(\eta +\bar{\eta }\bar{\gamma })$, $X=\mu \bar{\eta }\bar{\gamma }\bar{p}+\mu \eta \bar{p}\sqrt{\bar{\gamma }}$.

Following the quantum teleportation protocol shown in Figure 1, we can get the state received by Bob

$\begin{array}{cc}\hfill & {\rho }_{\text{out}}^{\prime }=\left(\begin{array}{cc}\hfill {\cos }^2\frac{\theta }{2}\left({\epsilon }_{11}^{\prime }+{\epsilon }_{44}^{\prime }\right)+{\sin }^2\frac{\theta }{2}\left({\epsilon }_{22}^{\prime }+{\epsilon }_{33}^{\prime }\right)\hfill & \hfill \cos \frac{\theta }{2}\sin \frac{\theta }{2}{e}^{-i\varphi }\left({\epsilon }_{14}^{\prime }+{\epsilon }_{41}^{\prime }\right)\hfill \\ \hfill \cos \frac{\theta }{2}\sin \frac{\theta }{2}{e}^{i\varphi }\left({\epsilon }_{14}^{\prime }+{\epsilon }_{41}^{\prime }\right)\hfill & \hfill {\cos }^2\frac{\theta }{2}\left({\epsilon }_{22}^{\prime }+{\epsilon }_{33}^{\prime }\right)+{\sin }^2\frac{\theta }{2}\left({\epsilon }_{11}^{\prime }+{\epsilon }_{44}^{\prime }\right)\hfill \end{array}\right).\hfill \end{array}(17)$

Similarly, one can obtain the Bloch vector of Eq. 17 and calculate the teleported QFI by Eq. 8

$\begin{array}{c}\hfill F_{\mathrm{W}\mathrm{M}}=\frac{16X^2{\bar{q}}^2}{{\left(U{\bar{q}}^2+2V\bar{q}+W\right)}^2}{\sin }^2\theta .\end{array}(18)$

To transfer the most amount of QFI from Alice to Bob, we should select a proper strength of QMR. The optimal QMR strength q can be obtained by solving the equation ∂F_WM/∂q = 0 under the condition that ∂²F_WM/(∂q)² < 0. The result turns out to be

$\begin{array}{c}\hfill q_{\mathrm{W}\mathrm{M}}^{\text{opt}}=1-\sqrt{\frac{W}{U}},\end{array}(19)$

and the corresponding QFI is

$\begin{array}{c}\hfill F_{\mathrm{W}\mathrm{M}}^{\text{opt}}=\frac{4X^2}{{\left(V+\sqrt{WU}\right)}^2}{\sin }^2\theta .\end{array}(20)$

Figure 3 shows the result of QFI as a function of decoherence strength γ under CAD noise with the assistance of WM and QMR. It is noted that the teleported QFI rapidly decreases to 0 without the operations of WM and QMR (i.e., p = 0 and q = 0). When the operation of QMR is performed (i.e., p = 0), the teleported QFI can be enhanced. Remarkably, it can be further improved with the combination of WM and QMR (i.e., p = 0.5 and p = 0.9 and $q=q_{\mathrm{W}\mathrm{M}}^{\text{opt}}$). Particularly, we find the larger the measurement strength of WM is, the better the improvement of the teleported QFI would be. A more clearer description of the role of p is shown in Figure 4A, where the curve of $F_{\mathrm{W}\mathrm{M}}^{\text{opt}}$ is shown as a function of p and μ with the correlated parameter η = 0.8 and the decoherence strength γ = 0.6. It can be seen that the teleported QFI can be monotonically increased with the increase of p for the Werner state.

FIGURE 3

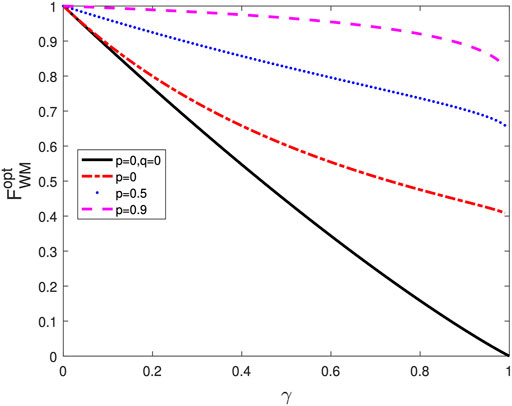
FIGURE 3. (color online) Teleported QFI $F_{\mathrm{W}\mathrm{M}}^{\text{opt}}$ as a function of γ for different p with μ = 1 and η = 0.8. When p = 0, p = 0.5 and p = 0.9, the corresponding strength of QMR is $q=q_{\text{WM}}^{\text{opt}}$. The polarization parameter θ is π/2.

FIGURE 4

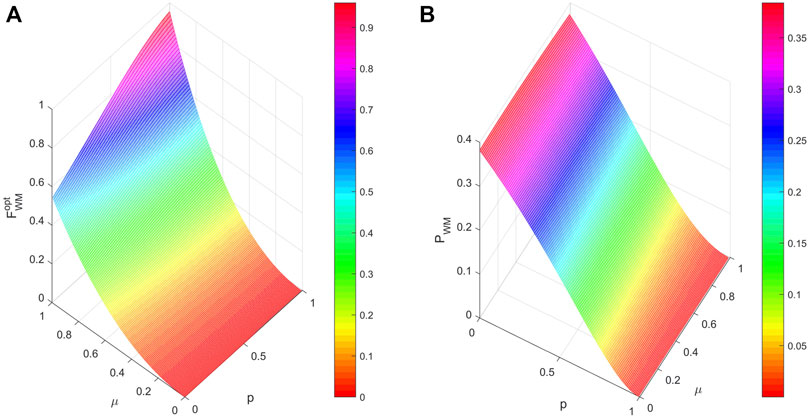
FIGURE 4. (color online) (A) The teleported QFI $F_{\mathrm{W}\mathrm{M}}^{\text{opt}}$ and (B) The success probability P_WM as a function of p and μ. The other parameters γ = 0.6, η = 0.8 and θ = π/2.

Since both WM and QMR operations are non-unital, thus the price of enhancement of the teleported QFI is based on the probability of the scheme. The success probability of this scheme can be obtained as

$\begin{array}{c}\hfill P_{\mathrm{W}\mathrm{M}}=\frac{2W+2V\sqrt{\frac{W}{U}}}{\left(1+\mu \right)\left(1+{\bar{p}}^2\right)+2\bar{\mu }\bar{p}}.\end{array}(21)$

Figure 4B shows the behavior of success probability P_WM as a function of p and μ with γ = 0.6 and η = 0.8. Obviously, P_WM decreases with the increase strength of WM. That is to say, the great improvement of teleported QFI is achieved at the cost of low success probability.

The curious question that comes up is: Are the correlated effects still contributing for the teleportation of QFI in the WM scheme? In order to clarify this question, we plot $F_{\mathrm{W}\mathrm{M}}^{\text{opt}}$ and P_WM as function of η for various values of p in Figures 5A,B, respectively. A careful observation shows that the effect of the correlation on the teleportation of QFI becomes more subtle. It is different from the result in Figure 2B, in which the correlated effects always enhance the teleported QFI without WM and QMR. If the strength of WM is not very strong, correlated effects significantly enhance the teleported QFI. However, $F_{\mathrm{W}\mathrm{M}}^{\text{opt}}$ does not increase monotonically as η increases when p → 1 (red solid line), as shown in Figure 5A. This indicates that the combined WM and QMR cannot completely retrieve the initial QFI for the CAD noise (0 < η < 1) even in the limit case p → 1. This result will exceed one’s expectation since the combined WM and QMR has been widely used to battle against decoherence and restore the initial quantum resources, such as entanglement, quantum discord as well as QFI in Refs. [31, 41, 42]. We argue that the perfect recovery just occurs in the uncorrelated AD and FCAD cases, but not works in the partially CAD case.

FIGURE 5

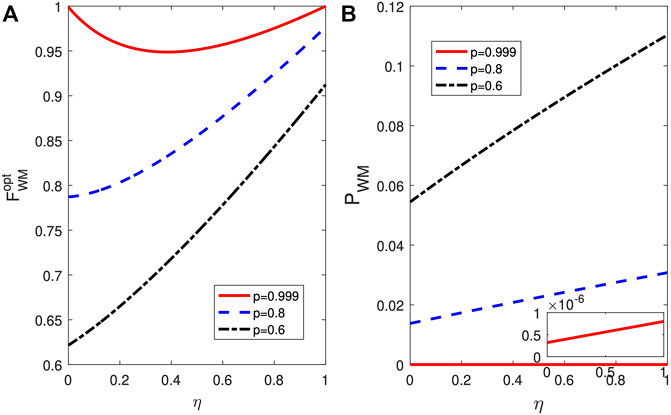
FIGURE 5. (color online) (A) The teleported QFI $F_{\mathrm{W}\mathrm{M}}^{\text{opt}}$ and (B) The success probability P_WM as a function of η. The other parameters γ = 0.6, μ = 1 and θ = π/2.

The underlying mechanism can be understood as follows. From Eqs 3–5, it is found that only one decoherence process |11⟩ → (| 10⟩, |01⟩) → |00⟩ is involved for uncorrelated AD noise (η = 0), while another decoherence process |11⟩ → |00⟩ is involved for FCAD noise (η = 1). Considering |00⟩ is immune to AD, FCAD and CAD decoherence, the pre-posed WM operation is devised to decrease the weights of states |11⟩, |10⟩ and |01⟩, which equivalently increases the weight of lazy state |00⟩. It was because of such a weight interchange that the state after WM consequentially becomes insensitive to the decoherence. In order to restore the initial information, the post-posed QMR is performed to re-balance the severely deviated weights between |11⟩, |10⟩, |01⟩ and |00⟩. Choosing the proper strength of QMR, the initial information can be totally recovered for AD and FCAD noise by WM and QMR. However, for CAD noise, the two decoherence processes mentioned above are involved simultaneously that cannot be distinguished by QMR. Therefore, the initial information cannot be completely recovered. In this context, the correlated effects are not always helpful to the WM enhanced teleportation of QFI. Fortunately, the magnitude of success probability is proportional to the correlated factor η since it is not related to the distinction of the two decoherence processes.

4 EAM scheme

In this section, we explore another strategy for enhancing the teleported QFI by EAM and QMR. In this scheme, the EAM operation is performed on the environment [43, 44]. The procedure is as follows: a detector is added to monitor the exciton changes of the environment when the entangled qubits pass through the CAD noise. We discard the result of clicks (including both one and two clicks) while keep the result corresponding to the no click. The quantum state corresponding to no click is picked out by EAM. To restore the initial QFI, the operations of QMRs shown in Eq. 15 are performed on the qubits 2 and 3, respectively. The final state shared by Alice and Bob yields to

$\begin{array}{cc}\hfill & {\rho }_{\mathrm{E}\mathrm{A}\mathrm{M}}=\left(\begin{array}{cccc}\hfill {\epsilon }_{11}\prime \prime \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\epsilon }_{14}\prime \prime \hfill \\ \hfill 0\hfill & \hfill {\epsilon }_{22}\prime \prime \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\epsilon }_{33}\prime \prime \hfill & \hfill 0\hfill \\ \hfill {\epsilon }_{41}\prime \prime \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\epsilon }_{44}\prime \prime \hfill \end{array}\right),\hfill \end{array}(22)$

where ${\epsilon }_{11}\prime \prime =\frac{U^{\prime }{\bar{q}}^2}{U^{\prime }{\bar{q}}^2+2V^{\prime }\bar{q}+W^{\prime }}$, ${\epsilon }_{22}\prime \prime ={\epsilon }_{33}\prime \prime =\frac{V^{\prime }\bar{q}}{U^{\prime }{\bar{q}}^2+2V^{\prime }\bar{q}+W^{\prime }}$, ${\epsilon }_{44}\prime \prime =\frac{W^{\prime }}{U^{\prime }{\bar{q}}^2+2V^{\prime }\bar{q}+W^{\prime }}$, ${\epsilon }_{14}\prime \prime ={{\epsilon }_{41}\prime \prime }^{\ast }=\frac{2X^{\prime }\bar{q}}{U^{\prime }{\bar{q}}^2+2V^{\prime }\bar{q}+W^{\prime }}$, and $U^{\prime }=\bar{\eta }(1+\mu )(4-\gamma -\mu \gamma )+\eta (1+\mu )(4-4\gamma +{\gamma }^2+\mu {\gamma }^2)$, $V^{\prime }=\bar{\eta }\bar{\gamma }\bar{\mu }(4-\gamma -\mu \gamma )+\eta \bar{\mu }(4-4\gamma +{\gamma }^2+\mu {\gamma }^2)$, $W^{\prime }=\bar{\eta }{\bar{\gamma }}^2(1+\mu )(4-\gamma -\mu \gamma )+\eta \bar{\gamma }(1+\mu )(4-4\gamma +{\gamma }^2+\mu {\gamma }^2)$, $X^{\prime }=\bar{\eta }\bar{\gamma }\mu (4-\gamma -\mu \gamma )+\eta \mu \sqrt{\bar{\gamma }}(4-4\gamma +{\gamma }^2+\mu {\gamma }^2)$.

Then, following the quantum teleportation protocol shown in Figure 1, the state received by Bob is

$\begin{array}{cc}\hfill & {\rho }_{\text{out}}^{″}=\left(\begin{array}{cc}\hfill {\cos }^2\frac{\theta }{2}\left({\epsilon }_{11}\prime \prime +{\epsilon }_{44}\prime \prime \right)+{\sin }^2\frac{\theta }{2}\left({\epsilon }_{22}\prime \prime +{\epsilon }_{33}\prime \prime \right)\hfill & \hfill \cos \frac{\theta }{2}\sin \frac{\theta }{2}{e}^{-i\varphi }\left({\epsilon }_{14}\prime \prime +{\epsilon }_{41}\prime \prime \right)\hfill \\ \hfill \cos \frac{\theta }{2}\sin \frac{\theta }{2}{e}^{i\varphi }\left({\epsilon }_{14}\prime \prime +{\epsilon }_{41}\prime \prime \right)\hfill & \hfill {\cos }^2\frac{\theta }{2}\left({\epsilon }_{22}\prime \prime +{\epsilon }_{33}\prime \prime \right)+{\sin }^2\frac{\theta }{2}\left({\epsilon }_{11}\prime \prime +{\epsilon }_{44}\prime \prime \right)\hfill \end{array}\right).\hfill \end{array}(23)$

Similarly, the QFI of the teleported state could be obtained

$\begin{array}{c}\hfill F_{\mathrm{E}\mathrm{A}\mathrm{M}}=\frac{16{X^{\prime }}^2{\bar{q}}^2}{{\left(U^{\prime }{\bar{q}}^2+2V^{\prime }\bar{q}+W^{\prime }\right)}^2}{\sin }^2\theta ,\end{array}(24)$

The optimal strength of QMR can be obtained by solving the equation ∂F_EAM/∂q = 0 under the condition that ∂²F_EAM/(∂q)² < 0. The result turns out to be

$\begin{array}{c}\hfill q_{\mathrm{E}\mathrm{A}\mathrm{M}}^{\text{opt}}=1-\sqrt{\frac{W^{\prime }}{U^{\prime }}},\end{array}(25)$

and the corresponding QFI is

$\begin{array}{c}\hfill F_{\mathrm{E}\mathrm{A}\mathrm{M}}^{\text{opt}}=\frac{4{X^{\prime }}^2}{{\left(V^{\prime }+\sqrt{W^{\prime }{U}^{\prime }}\right)}^2}{\sin }^2\theta .\end{array}(26)$

Figure 6 shows the result of the teleported QFI as a function of γ under CAD noise with the assistance of EAM and QMR for μ = 1. It is noted that the teleported QFI is improved only the EAM is performed (i.e., q = 0). However, such a improvement disappears when γ → 1. Utilizing the combination of EAM and QMR $(q=q_{\mathrm{E}\mathrm{A}\mathrm{M}}^{\text{opt}})$, we can further enhance the teleported QFI regardless of the value of γ. From Eq. 26, it is found that $F_{\mathrm{E}\mathrm{A}\mathrm{M}}^{\text{opt}}$ is related to the correlated parameter η.

FIGURE 6

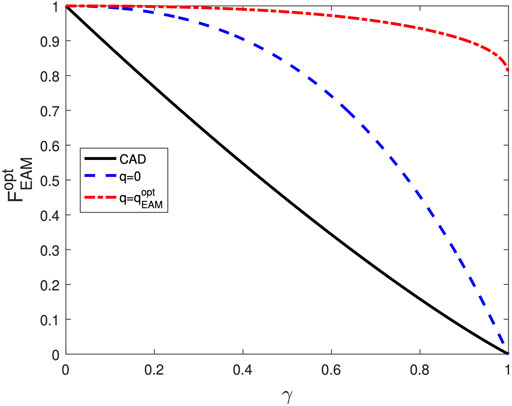
FIGURE 6. (color online) The teleported QFI $F_{\mathrm{E}\mathrm{A}\mathrm{M}}^{\text{opt}}$ as a function of γ with μ = 1 and η = 0.8. The optimal QMR strength $q_{\mathrm{E}\mathrm{A}\mathrm{M}}^{\text{opt}}=1-\sqrt{\frac{W^{\prime }}{U^{\prime }}}$. The polarization parameter θ is π/2.

In order to more clearly describe the role of the correlated factor, Figure 7A is plotted to show $F_{\mathrm{E}\mathrm{A}\mathrm{M}}^{\text{opt}}$ as a function of μ and η. Similar to Figure 5A, the teleported QFI $F_{\mathrm{E}\mathrm{A}\mathrm{M}}^{\text{opt}}$ reaches its maximal value (i.e., the initial value of QFI μ² sin²θ) in the uncorrelated AD and FCAD cases. While in the partially correlated regions (i.e., 0 < η < 1), the combination of EAM and QMR cannot restore the total QFI. The underlying reason can be attributed to the fact that QMR cannot distinguish the two decoherence processes mentioned above. Considering that the EAM and QMR are also probabilistic operations, the success probability is

$\begin{array}{c}\hfill P_{\mathrm{E}\mathrm{A}\mathrm{M}}=\frac{2W^{\prime }+2V^{\prime }\sqrt{\frac{W^{\prime }}{U^{\prime }}}}{\left(4-4\gamma +{\gamma }^2+\mu {\gamma }^2\right)\left(4-\gamma -\mu \gamma \right)}.\end{array}(27)$

FIGURE 7

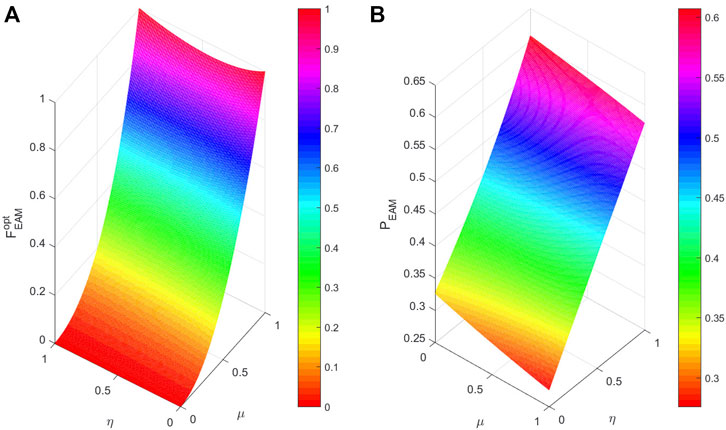
FIGURE 7. (color online) (A) Teleported $F_{\mathrm{E}\mathrm{A}\mathrm{M}}^{\text{opt}}$ as a function of μ and η. (B) The success probability P_EAM as a function of μ and η. The QMR strength $q_{\mathrm{E}\mathrm{A}\mathrm{M}}^{\text{opt}}=1-\sqrt{\frac{W^{\prime }}{U^{\prime }}}$. The polarization parameter θ is π/2.

Figure 7B reveals that there has been a marked increase in the success probability with increasing η.

5 Comparison between the WM scheme and the EAM scheme

So far, we have found that both WM and EAM schemes can significantly enhance the teleportation of QFI under CAD noise in a probabilistic way. Particularly, in these two schemes, the improvement of QFI is based on the sacrifice of success probability. A detailed comparison seems necessary to show which one is better. To quantitatively determine the superiority of probabilistic schemes, a quantity of average improvement of QFI that balances the enhanced QFI and success probability is introduced.

$\begin{array}{c}\hfill F_{\mathrm{i}\mathrm{m}\mathrm{p}}^{\mathrm{a}\mathrm{v}}=F_{\mathrm{E}\mathrm{A}\mathrm{M}}^{\mathrm{o}\mathrm{p}\mathrm{t}}\times P_{\mathrm{E}\mathrm{A}\mathrm{M}}-F_{\mathrm{W}\mathrm{M}}^{\mathrm{o}\mathrm{p}\mathrm{t}}\times P_{\mathrm{W}\mathrm{M}},\end{array}(28)$

where the subscript “imp” denotes the EAM scheme’s improvement over the WM scheme.

In Figure 8A, We have plotted $F_{\mathrm{i}\mathrm{m}\mathrm{p}}^{\mathrm{a}\mathrm{v}}$ as a function of p and γ with η = 0.8 and μ = 1. Remarkably, it is intriguing to notice that $F_{\mathrm{i}\mathrm{m}\mathrm{p}}^{\mathrm{a}\mathrm{v}}$ is always positive. As we discussed in Section 3, the larger strength of WM corresponds to the larger QFI, but with a smaller success probability. Figure 8A tells us that the EAM scheme performs better than the WM scheme on the average improvement of QFI regardless of the strength of WM. We conjecture that WM which is performed before CAD noise only collects the information from system, whereas EAM can gather the information from both system and environment since it is acted after CAD noise. Therefore, EAM scheme is superior to WM scheme. It also should be noted that $F_{\mathrm{i}\mathrm{m}\mathrm{p}}^{\mathrm{a}\mathrm{v}}$ monotonically increases with the increase of η for a given γ, as shown in Figure 8B. This means that although the correlated effects may not be able to enhance the teleported QFI and success probability at the same time in both WM and EAM schemes, the average improvement in EAM scheme is more pronounced.

FIGURE 8

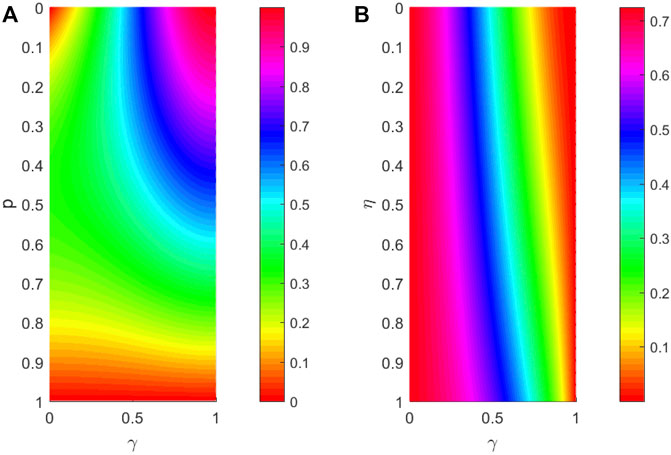
FIGURE 8. (color online) (A)$F_{\mathrm{i}\mathrm{m}\mathrm{p}}^{\mathrm{a}\mathrm{v}}$ as a function of γ and p with μ = 1 and η = 0.8. (B)$F_{\mathrm{i}\mathrm{m}\mathrm{p}}^{\mathrm{a}\mathrm{v}}$ as a function of γ and η with μ = 1 and p = 0.8. The polarization parameter θ is π/2.

6 Conclusion

In summary, we have investigated the teleportation of QFI using Werner state as the quantum channel under the CAD decoherence. It is found that the correlated effects is helpful to increase the teleported QFI in CAD noise. Furthermore, we have proposed two schemes for improving the teleportation of QFI. The first scheme is based on the combination of WM and QMR. The second scheme is based on the aid of EAM and QMR. The teleported QFI can be improved significantly by taking advantage of these two schemes. Remarkably, the correlated effects can increase the success probability of these two schemes. A detailed comparison leads us to the conclusion that the EAM scheme beats the WM scheme in terms of enhancing the teleported QFI under CAD decoherence. Our work would be helpful for understanding the CAD decoherence in other quantum information processing tasks.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

Y-LL and YL conceived the paper’s physical model and idea, and Y-LL and LY carried out the calculation and numerical analysis. Y-LL and Y-BZ supervised the work. All authors contributed to the interpretation of the work and the preparation of the manuscript.

Funding

This work is supported by the Funds of Jiangxi Provincial Natural Science Foundation under Grant No. 20212ACB211004, the National Natural Science Foundation of China under Grant No. 61765007, and the Program of Qingjiang Excellent Young Talents of Jiangxi University of Science and Technology.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Bennett CH, Brassard G, Crpeau C, Jozsa R, Peres A, Wootters WK, et al. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys Rev Lett (1993) 70:1895–9. doi:10.1103/PhysRevLett.70.1895

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Gottesman D, Chuang IL. Demonstrating the viability of universal quantum computation using teleportation and single-qubit operations. Nature (1999) 402:390–3. doi:10.1038/46503

CrossRef Full Text | Google Scholar

3. Bouwmeester D, Pan JW, Mattle K, Eibl M, Weinfurter H, Zeilinger A, et al. Experimental quantum teleportation. Nature (1997) 390:575–9. doi:10.1038/37539

CrossRef Full Text | Google Scholar

4. Braunstein SL, Kimble HJ. Teleportation of continuous quantum variables. Phys Rev Lett (1998) 80:869–72. doi:10.1103/PhysRevLett.80.869

CrossRef Full Text | Google Scholar

5. Ursin R, Jennewein T, Aspelmeyer M, Kaltenbaek R, Lindenthal M, Walther P, et al. Quantum teleportation across the danube. Nature (2004) 430:849. doi:10.1038/430849a

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Jin XM, Ren JG, Yang B, Yi ZH, Zhou F, Xu XF, et al. Experimental free-space quantum teleportation. Nat Photon (2010) 4:376–81. doi:10.1038/nphoton.2010.87

CrossRef Full Text | Google Scholar

7. Pirandola S, Eisert J, Weedbrook C, Furusawa A, Braunstein SL. Advances in quantum teleportation. Nat Photon (2015) 9:641–52. doi:10.1038/nphoton.2015.154

CrossRef Full Text | Google Scholar

8. Xiao X, Yao Y, Zhong WJ, Li YL, Xie YM. Enhancing teleportation of quantum Fisher information by partial measurements. Phys Rev A (2016) 93:012307. doi:10.1103/PhysRevA.93.012307

CrossRef Full Text | Google Scholar

9. Braunstein SL, Caves CM. Statistical distance and the geometry of quantum states. Phys Rev Lett (1994) 72:3439–43. doi:10.1103/PhysRevLett.72.3439

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Giovannetti V, Lloyd S, Maccone L. Advances in quantum metrology. Nat Photon (2011) 5:222–9. doi:10.1038/nphoton.2011.35

CrossRef Full Text | Google Scholar

11. Meyer JJ. Fisher information in noisy intermediate-scale quantum applications. Quantum (2021) 5:539. doi:10.22331/q-2021-09-09-539

CrossRef Full Text | Google Scholar

12. Li N, Luo SL. Entanglement detection via quantum Fisher information. Phys Rev A (2013) 88:014301. doi:10.1103/PhysRevA.88.014301

CrossRef Full Text | Google Scholar

13. Akbari-Kourbolagh Y, Azhdargalam M. Entanglement criterion for multipartite systems based on quantum Fisher information. Phys Rev A (2019) 99:012304. doi:10.1103/PhysRevA.99.012304

CrossRef Full Text | Google Scholar

14. Shitara T, Ueda M. Determining the continuous family of quantum Fisher information from linear-response theory. Phys Rev A (2016) 94:062316. doi:10.1103/PhysRevA.94.062316

CrossRef Full Text | Google Scholar

15. El Anouz K, El Allati A, El Baz M. Teleporting quantum Fisher information for even and odd coherent states. J Opt Soc Am B (2020) 37:38. doi:10.1364/JOSAB.37.000038

CrossRef Full Text | Google Scholar

16. Haug T, Bharti K, Kim MS. Capacity and quantum geometry of parametrized quantum circuits. PRX Quan (2021) 2:040309. doi:10.1103/PRXQuantum.2.040309

CrossRef Full Text | Google Scholar

17. Bennett CH, Brassard G, Popescu S, Schumacher B, Smolin JA, Wootters WK, et al. Purification of noisy entanglement and faithful teleportation via noisy channels. Phys Rev Lett (1996) 76:722–5. doi:10.1103/PhysRevLett.76.722

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Oh S, Lee S, Lee HW. Fidelity of quantum teleportation through noisy channels. Phys Rev A (2002) 66:022316. doi:10.1103/PhysRevA.66.022316

CrossRef Full Text | Google Scholar

19. Laura TK, Christian TS, Miguel AL. Noisy quantum teleportation: An experimental study on the influence of local environments. Phys Rev A (2014) 90:042332. doi:10.1103/PhysRevA.90.042332

CrossRef Full Text | Google Scholar

20. Alejandro F. High-dimensional quantum teleportation under noisy environments. Phys Rev A (2019) 100:062311. doi:10.1103/PhysRevA.100.062311

CrossRef Full Text | Google Scholar

21. Jin Y. The effects of vacuum fluctuations on teleportation of quantum Fisher information. Sci Rep (2017) 7:40193. doi:10.1038/srep40193

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Jafarzadeh M, Rangani JH, Amniat-Talab M. Teleportation of quantum resources and quantum Fisher information under Unruh effect. Quan Inf Process (2018) 17:165. doi:10.1007/s11128-018-1922-x

CrossRef Full Text | Google Scholar

23. Guo YN, Peng HP, Yang C, Xie Q, Zeng K. Davies theory for teleportation of quantum Fisher information under decoherence. Laser Phys Lett (2019) 16:125202. doi:10.1088/1612-202X/ab5529

CrossRef Full Text | Google Scholar

24. Guo YN, Zeng K, Chen PX. Teleportation of quantum Fisher information under decoherence channels with memory. Laser Phys Lett (2019) 16:095203. doi:10.1088/1612-202X/ab2f33

CrossRef Full Text | Google Scholar

25. Li YL, Sun FX, Yang J, Xiao X. Enhancing the teleportation of quantum Fisher information by weak measurement and environment-assisted measurement. Quan Inf Process (2021) 20:55. doi:10.1007/s11128-021-02998-1

CrossRef Full Text | Google Scholar

26. Caruso F, Giovannetti V, Lupo C, Mancini S. Quantum channels and memory effects. Rev Mod Phys (2014) 86:1203–59. doi:10.1103/RevModPhys.86.1203

CrossRef Full Text | Google Scholar

27. Macchiavello C, Palma GM. Entanglement-enhanced information transmission over a quantum channel with correlated noise. Phys Rev A (2002) 65:050301. doi:10.1103/PhysRevA.65.050301

CrossRef Full Text | Google Scholar

28. D’Arrigo A, Benenti G, Falci G. Quantum capacity of dephasing channels with memory. New J Phys (2007) 9:310. doi:10.1088/1367-2630/9/9/310

CrossRef Full Text | Google Scholar

29. Plenio MB, Virmani S. Spin chains and channels with memory. Phys Rev Lett (2007) 99:120504. doi:10.1103/PhysRevLett.99.120504

PubMed Abstract | CrossRef Full Text | Google Scholar

30. D’Arrigo A, Benenti G, Falci G, Macchiavello C. Classical and quantum capacities of a fully correlated amplitude damping channel. Phys Rev A (2013) 88:042337. doi:10.1103/PhysRevA.88.042337

CrossRef Full Text | Google Scholar

31. Xiao X, Yao Y, Xie YM, Wang XH, Li YL. Protecting entanglement from correlated amplitude damping channel using weak measurement and quantum measurement reversal. Quan Inf Process (2016) 15:3881–91. doi:10.1007/s11128-016-1356-2

CrossRef Full Text | Google Scholar

32. Huang ZM, Zhang C. Protecting quantum correlation from correlated amplitude damping channel. Braz J Phys (2017) 47:400–5. doi:10.1007/s13538-017-0509-9

CrossRef Full Text | Google Scholar

33. He Z, Zeng HS. Enhancing entanglement of assistance using weak measurement and quantum measurement reversal in correlated amplitude damping channel. Quan Inf Process (2020) 19:299. doi:10.1007/s11128-020-02791-6

CrossRef Full Text | Google Scholar

34. Li YL, Zu CJ, Wei DM. Enhance quantum teleportation under correlated amplitude damping decoherence by weak measurement and quantum measurement reversal. Quan Inf Process (2019) 18:2. doi:10.1007/s11128-018-2114-4

CrossRef Full Text | Google Scholar

35. Werner RF. Quantum states with Einstein-Podolsky-Rosen correlations admitting a hidden-variable model. Phys Rev A (1989) 40:4277–81. doi:10.1103/PhysRevA.40.4277

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Yeo Y, Skeen A. Time-correlated quantum amplitude-damping channel. Phys Rev A (2003) 67:064301. doi:10.1103/PhysRevA.67.064301

CrossRef Full Text | Google Scholar

37. Nielesen MA, Chuang IL. Quantum computation and quantum information. Cambridge: Cambridge University Press (2000).

Google Scholar

38. Arshed N, Toor AH. Entanglement-assisted capacities of time-correlated amplitude-damping channel (2013). arXiv:1307.5403.

Google Scholar

39. Zhong W, Sun Z, Ma J, Wang XG, Nori F. Fisher information under decoherence in Bloch representation. Phys Rev A (2013) 87:022337. doi:10.1103/PhysRevA.87.022337

CrossRef Full Text | Google Scholar

40. Koashi M, Ueda M. Reversing measurement and probabilistic quantum error correction. Phys Rev Lett (1999) 82:2598–601. doi:10.1103/PhysRevLett.82.2598

CrossRef Full Text | Google Scholar

41. Kim YS, Lee JC, Kwon O, Kim YH. Protecting entanglement from decoherence using weak measurement and quantum measurement reversal. Nat Phys (2012) 8:117–20. doi:10.1038/nphys2178

CrossRef Full Text | Google Scholar

42. Xiao X. Protecting qubit-qutrit entanglement from amplitude damping decoherence via weak measurement and reversal. Phys Scr (2014) 89:065102. doi:10.1088/0031-8949/89/6/065102

CrossRef Full Text | Google Scholar

43. Zhao X, Hedemann SR, Yu T. Restoration of a quantum state in a dephasing channel via environment-assisted error correction. Phys Rev A (2013) 88:022321. doi:10.1103/PhysRevA.88.022321

CrossRef Full Text | Google Scholar

44. Wang K, Zhao X, Yu T. Environment-assisted quantum state restoration via weak measurements. Phys Rev A (2014) 89:042320. doi:10.1103/PhysRevA.89.042320

CrossRef Full Text | Google Scholar