Abstract
Nonreciprocal microwave devices are key components of communication platforms. Nonreciprocity can arise in chiral systems, where chirality refers to a fixed handedness that is preserved under time reversal. Chiral excitations (quasiparticles) provide opportunities for the realization of miniaturized microwave components with directional properties. In particular, surface acoustic waves that propagate in magnetic media are chiral and can display pronounced nonreciprocal character. Because surface acoustic waves are an established technological platform, hybrid surface acoustic wave/spin wave devices have great application potential. In this mini-review, we introduce the general concept of chiral and nonreciprocal magnetoacoustic waves. We discuss a widely employed phenomenological model based on magnetoelastic coupling and magneto-rotation that quantitatively accounts for many experimental findings and give a brief overview over selected experiments and advances in this emerging research field.
Introduction
Information transport and processing at microwave frequencies are central to modern information processing applications. Gigahertz-frequency free-space radio waves are a cornerstone of our communication platforms. The centimeter-scale wavelength of the corresponding microwave photons, however, makes the miniaturization of signal processing components challenging. Such a miniaturization is crucial for many applications, in particular for mobile devices. A possible route for downscaling is the interconversion of photons to phonons with micrometer-scale wavelength at microwave frequencies and corresponding miniaturization of signal processing components. In this spirit, surface acoustic wave (SAW) devices are widely employed as frequency filters for mobile communication [1–7]. Efficient excitation and detection of SAWs is possible on piezoelectric substrates with metallic grating structures - so-called interdigital transducers (IDTs) - via the piezoelectric effect [8], as schematically shown in Figure 1A. In general, these acoustic devices benefit from a small footprint, mass fabrication capabilities, and high adjustability of the transmission characteristics [1, 5, 7]. Magnons in ferromagnetic materials can provide a similar miniaturiziation as phonons. Complimentary research thus also pursuits the use of magnonic devices for miniaturized logic circuits and field-controllable microwave components, such as phase shifters [9–12].
FIGURE 1
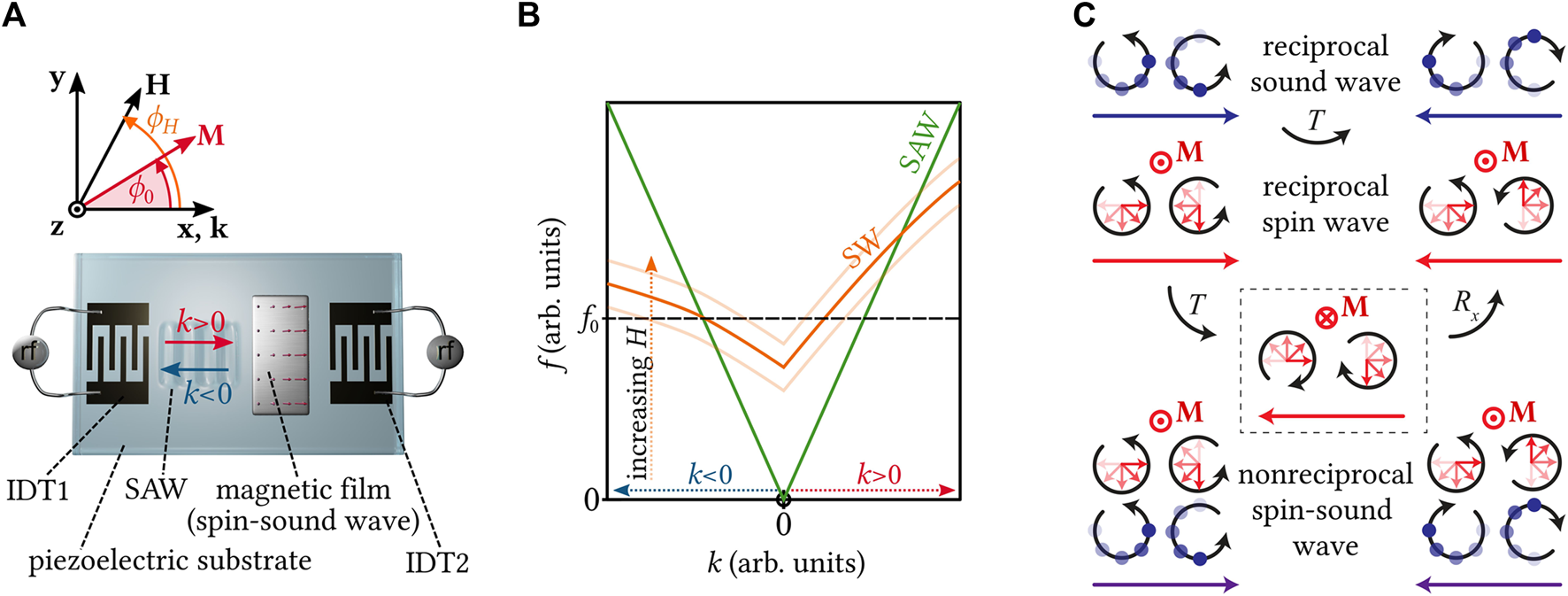
(A) Illustration of the investigated piezoelectric-ferromagnetic hybrid device. Nonreciprocal effects are characterized by studying the transmission of counter-propagating SAWs with wave vectors k > 0 and k < 0. (B) The dispersion relation is reciprocal for SAWs but can be nonreciprocal for SWs because of dissimilar interfaces on the opposite sides of the magnetic thin film. If the SAW is excited at a fixed frequency f0 (dashed line), resonant SAW-SW coupling is only possible for the magnetoacoustic waves propagating to the left side (k < 0), and a large nonreciprocal transmission is expected. The SW dispersion is tuned by the magnitude H and angle ϕH of the external magnetic field. (C) Nonreciprocal spin-sound waves can arise from the interaction of individually reciprocal sound and spin waves. The lattice motion (magnetization precession) at two different lattice sites along the x-axis propagation direction of the sound wave (spin wave) is schematically depicted by the blue dots (red arrows) and the black circles represent the circular motion and its phase shift. The reciprocal counter-propagating waves can be transformed into each other by time reversal T and rotation Rx operations. No symmetry operation exists for the nonreciprocal spin-sound wave.
Such phononic and magnonic devices each have their individual strengths and weaknesses. While phonons can have much longer lifetimes than magnons, they lack the additional symmetry breaking caused by the magnetization degree of freedom. As discussed in detail in Section 3, SAWs are thus generally reciprocal with respect to the acoustic propagation direction, even though they have chiral properties [13]. The helicity of the lattice rotation thereby switches with SAW propagation direction inversion. Spin waves (SWs) are generally achiral [14], unless the symmetry is broken orthogonal to their propagation direction, such as at a surface or interface [15–19]. The helicity of the spin precession is given by the sign of the gyromagnetic ratio and is independent of the SW propagation direction. By combining individually reciprocal SAWs and SWs, chiral and nonreciprocal magnetoacoustic waves can emerge. These magnetoacoustic waves are similar to chiral magnons in their nonreciprocal properties, while still profiting from the long acoustic lifetimes. In such magnetoacoustic devices, if we interchange the location of the sound source and receiver, the transmitted signal will not be the same [20]. In this mini review article we summarize the recent advances in SAW-SW coupling with a focus on nonreciprocal effects. More general reviews about phonon-magnon coupling can be found in references [20–24].
Phenomenology of the magnetoacoustic interaction
Because of spin-orbit interaction, excitations of the lattice atoms from their equilibrium positions that impact the electronic orbitals will cause a concomitant spin excitation. Here, we briefly discuss the resulting magnetoelastic interaction of SAWs and SWs in magnetic thin films based on a phenomenological model that dates back to C. Kittel [25]. To this end, we only consider the Rayleigh-type SAW, which has most often been studied in magnetoacoustic experiments. The retrograde elliptical lattice motion on the substrate surface causes nonzero strain components ɛkl=xx,zz,xz ≠ 0 in a magnetic thin film deposited on top of a substrate [4, 26, 27], as shown in Figure 1A. Additionally, the Rayleigh-SAW features a lattice rotation ωxz ≠ 0. Here, we consider the case where the equilibrium magnetization direction M is aligned in the plane of the magnetic thin film and encloses the angle ϕ0 with the x-axis. Because of magnetoelastic coupling to ɛkl and magneto-rotation coupling to ωxz [28–30], the free energy of the magnetic thin film is modulated with the frequency ω = 2πf and wave vector of the SAW [27, 31]. More general situations, including the out-of-plane orientation of M and other SAW modes, are discussed in references [27, 32–34].
The resulting magnetization dynamics can be described in terms of effective magnetoacoustic driving fields [27, 29–31]. For magnetic thin films with cubic crystal structure, the driving field reads aswhereby hoop (hip) is the out-of-plane (in-plane) projection normal to the equilibrium orientation of M, b1,2 are the magnetoelastic coupling constants [27, 35], and Meff = Ms − Hk is the effective magnetization with the saturation magnetization Ms and out-of-plane anisotropy field Hk. It is noteworthy that the magneto-rotation coupling does not require spin-orbit interaction, as Meff = Ms is obtained from the thin film shape anisotropy alone. Magneto-rotation is thus also active in materials with vanishing magnetostriction, such as NiFe [36] or in ultrathin films with vanishing ɛxz [29]. Furthermore, spin-rotation coupling [37–39] and gyromagnetic coupling [40] can contribute to the magnetoacoustic driving field h. To obtain the impact of h on the magnetization dynamics, one needs to solve the Landau–Lifshitz–Gilbert equation to find the solution with the Polder susceptibility . The SAW transmission can be experimentally determined with a second receiver IDT and is often modeled by considering the absorbed acoustic power [31]where w, d, l are width, thickness, and length of the magnetic film and h*(x) is the complex conjugate of h(x). From Eq. 2 it can be seen that in resonance the energy Pabs of the SAW is transferred to the magnetic system to excite SWs. If Pabs is a significant fraction of the initial power P0 of the SAW, the exponential decay of the amplitude h(x) in x-direction must be taken into account [30], otherwise h(x) = h can be assumed. Moreover, the strain and driving fields are assumed to be approximately constant along the thin film thickness (kd ≲ 1).
If SAW and SW have identical wave vectors k and frequencies f, resonant magnetoacoustic interaction is possible and hybrid magnetoacoustic waves form [29, 30, 41]. The dispersion of the SAWis defined by the propagation velocity cSAW ≈ 3500 m/s [4] and is reciprocal. For magnetic thin films with no in-plane anisotropy (ϕ0 = ϕH) the SW dispersion is [19, 42]with the gyromagnetic ratio γ, orientation ϕH, and magnitude H of the external magnetic field H. Furthermore, the dipolar SW term [43] is and the magnetic exchange term with the exchange constant A is defined as . In presence of the Dzyaloshinskii-Moriya interaction (DMI), the SW dispersion becomes nonreciprocal with the thickness-averaged effective DMI constant Deff. The dispersions of a SAW and nonreciprocal SW are schematically depicted in Figure 1B.
In experiments, ϕH and H are usually changed to manipulate the SW dispersion. Because the transfer function of an acoustic delayline shows a typical pass-band behavior [2–4], f and k of the SAW are conventionally fixed and correspond to the maxima of the transfer function. Hereby, the IDTs are often operated at higher harmonic resonance frequencies n = 1, 3, 5, … and p is the periodicity of the IDT. Nevertheless, quasi wide-band characterization of nonreciprocal magnetoacoustic waves with IDTs has also been demonstrated [30, 36]. In addition to the IDT-based excitation and detection of magnetoacoustic waves discussed above, the coupling between electrically or thermally excited SAWs with SWs has been characterized by optical measures such as Brillouin light scattering (BLS) [44–47], Faraday rotation [48], magneto-optic Kerr effect (MOKE) [49–51], and x-ray magnetic circular dichroism (XMCD) [52].
Nonreciprocity and chirality
Chirality refers to the situation where an object and its mirror image cannot be superimposed by translation and spatial rotations [14, 53]. Examples are our hands or more general objects that are described by three orthogonal vectors. For chiral excitations, it is additionally required that their chirality remains unchanged under time reversal. Nonreciprocity of propagating waves such as magnons or phonons requires that counter-propagating waves cannot be superimposed by any combination of time reversal, rotation and translation operations. Not all chiral excitations are nonreciprocal. As an example, we consider a sound wave in a solid propagating along x, specifically a circularly polarized wave, viz. a combined shear ɛxz and tensile ɛxx wave, such as found in the Rayleigh SAW. In Figure 1C (top row) we sketch the lattice displacement of one atom that follows an elliptical motion in the xz plane. Since the strain components ɛxx and ɛxz are phase-shifted by ±90◦ for ± k, the helicity of the elliptical trajectory of lattice atoms inverts when k is inverted. While a Rayleigh-SAW is chiral because it can be described by three orthogonal vectors which are defined by its helicity, propagation direction, and evanescent contribution along the surface normal [13], it is reciprocal since a time reversal operation T that inverts time t → −t maps the counter-propagating waves, as indicated in Figure 1C (top row).
In a similar fashion, we consider a spin wave as sketched in Figure 1C (middle row). Here, the helicity of spin-precession is fixed and does not invert if the propagation direction of the SW is inverted. The counter-propagating SW is obtained by a combination of a time reversal operation T (t → −t and M → −M) and a rotation Rx around the direction of propagation x that transforms (Mx, My, Mz) → (Mx, − My, − Mz). Thus, SWs are achiral and reciprocal if the rotation operation Rx is not prohibited by additional symmetry breaking. Examples for such a symmetry breaking are dissimilar interfaces on the opposite sides of a thin film or the interface to vacuum at the sample edge [18, 19, 42, 54] that simultaneously introduces chirality and nonreciprocity.
If we finally consider a combined spin-sound wave, as sketched in Figure 1C (bottom row), there exists no symmetry operation that can map the counter-propagating spin-sound wave. Given an interaction between the magnetic and elastic degrees of freedom, spin-sound waves are thus nonreciprocal. The spin-sound waves are chiral if symmetry along z is broken, as is the case for Rayleigh waves.
Surface acoustic wave-Spin wave helicity mismatch effect
Here, we specifically consider the case where individually reciprocal spin waves and sound waves are coupled to form nonreciprocal magnetoacoustic (spin-sound) waves. In magnetic media, the SAW causes a magnetoacoustic driving field h, as defined in Eq. 1. The magnetoacoustic field has a rotational sense which inverts under inversion of SAW propagation direction together with the concomitant inversion of displacement helicity, as depicted in Figure 1C. Because the magnetization precession direction has a fixed right-handed rotational sense, the efficiency of acoustic SW excitation differs for counter-propagating SAWs which gives rise to nonreciprocal SAW absorption. In the following, we call this effect, SAW-SW helicity mismatch effect“.
The SAW-SW helicity mismatch effect was initially observed in yttrium iron garnets [55] and later in nickel [27, 56]. More recently, for a Ta(10 nm)/Co20Fe60B20(1.6 nm)/MgO(2 nm) magnetic thin film Xu et al. observed a large nonreciprocal SAW transmission at 6.1 GHz and ϕH = 10°, as shown in Figure 2A [29]. The absorbed power Pabs differs for counter-propagating waves mainly due to the SAW-SW helicity mismatch effect. Because the nonreciprocity is significantly stronger than expected from pure magnetoelastic coupling, other non-magnetoelastic coupling mechanisms, which enlarge the helicity of the magnetoacoustic driving fields must be present. Since magneto-rotation coupling [28–30], spin-rotation coupling [37–39], and gyromagnetic coupling [40] induce additional driving fields with the same symmetry as the shear strain magnetoelastic driving field hoop, it is difficult to separate these individual contributions [29, 36]. Nevertheless, it was demonstrated that good agreement between experiment and simulation is achieved by solely considering magnetoelastic and magneto-rotation coupling for CoFeB magnetic thin films [29, 36]. Besides that, the helicity of the magnetoacoustic driving field and thus the transmission nonreciprocity can be enhanced in magnetic thin films with thick nonmagnetic capping layers [57] or magnetic bilayers [36].
FIGURE 2
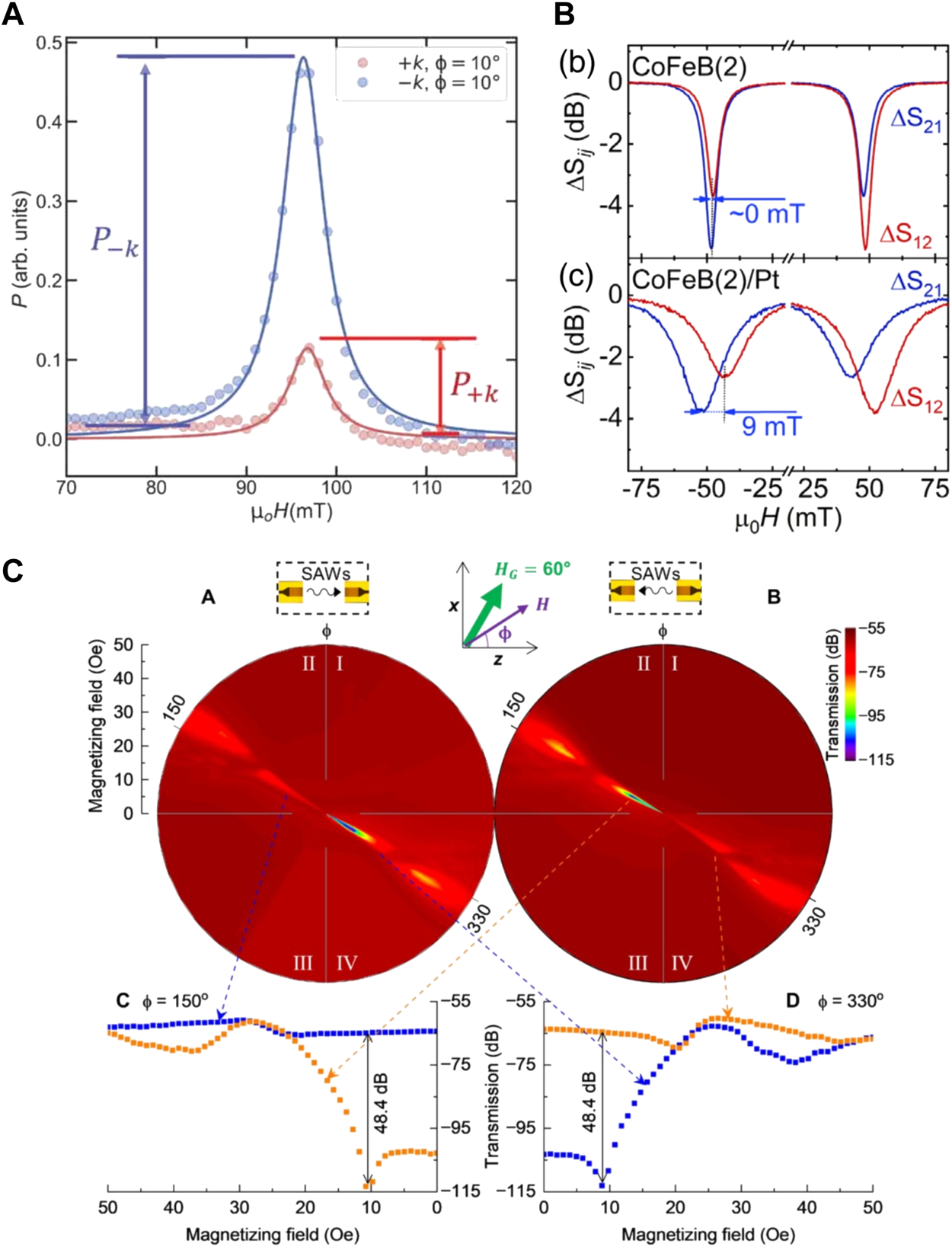
Experimental results of nonreciprocal magnetoacoustic surface waves propagating in inverted directions k > 0 and k < 0 (or + k and − k). (A) The SAW-SW helicity mismatch effect in Ta(10 nm)/Co20Fe60B20(1.6 nm)/MgO(2 nm) is enhanced by magneto-rotation coupling and causes at 6.1 GHz and ϕH = 10° a pronounced nonreciprocity of the absorbed power P±k. (B) The resonance fields are solely nonreciprocally shifted for Co40Fe40B20(2 nm)/Pt (3 nm), but not for Co40Fe40B20(2 nm), since interfacial DMI is mediated by the Pt layer. The background corrected SAW transmission ΔS21,12 for counter-propagating SAWs with k < 0 and k > 0 was measured at 6.9 GHz and ϕH = 64.8°. Adapted from reference [30]. (C) The magnetic dipolar fields of the SW cause nonreciprocally shifted resonance fields in the magnetic bilayer FeGaB(20 nm)/Al2O3(5 nm)/FeGaB(20 nm) at 1.4 GHz. The upper two panels show the SAW transmission as a function of the external magnetic field magnitude H and orientation ϕH for counter-propagating waves. The two diagrams below depict line cuts at ϕH = 150, 330° for k > 0 (blue) and k < 0 (orange). (A,C) From [29, 72]. ⓒ The Authors, some rights reserved; exclusive licensee AAAS. Distributed under a CC BY-NC 4.0 license “http://creativecommons.org/licenses/by-nc/4.0/”. Reprinted with permission from AAAS.
Additionally to the nonreciprocal magnetoacoustic excitation efficiency, magnetic thin film systems with tailored nonreciprocal dispersion of chiral SWs can be used to further increase the overall transmission nonreciprocity, as schematically shown in Figure 1B. Two approaches have so far been discussed in the literature: Interfacial DMI and dipolar fields in magnetic bilayers.
Dzyaloshinskii-Moriya interaction
The DMI at a ferromagnetic–heavy metal interface energetically favors spin structures with a fixed chirality, which is fundamentally responsible for the formation of magnetic skyrmions [58]. Counter-propagating SWs have opposite spatial helicity, as shown in Figure 1C, and are thus non-degenerate in the presence of DMI [15, 19, 42, 59]. The SW dispersion in Eq. 4 causes therefore shifted resonance frequencies for k > 0 and k < 0 at a fixed external field, as depicted in Figure 1B. Vice versa, shifted resonance fields for a fixed SAW excitation frequency f0 in magnetoacoustic transmission measurements are expected. This nonreciprocal shift was studied by Küß et al. for two magnetic films Co40Fe40B20(2 nm) and Co40Fe40B20(2 nm)/Pt (3 nm) at 6.9 GHz and ϕH = 64.8° [30]. Figure 2B shows the background corrected SAW transmission signal ΔS21 and ΔS12 for counter-propagating SAWs with k > 0 and k < 0. Only the sample with the heavy metal Pt capping layer shows nonreciprocally shifted resonance fields of 9 mT because of DMI. Unfortunately, the ferromagnetic–heavy metal interface additionally results in linewidth broadening via the magnetic spin-pumping effect [60]. Thus, the nonreciprocal field shift is not high enough to separate the resonances for counter-propagating SAWs, which limits the overall transmission nonreciprocity. Further information about the potential and behavior of nonreciprocal magnetoacoustic waves with DMI can be found in references [29, 61].
Dipolar fields in magnetic bilayers
It has been known for many years that the dipolar fields of SWs cause a nonreciprocal SW dispersion in magnetic bi- and multilayers because the dynamic dipolar-interaction energy differs for counter-propagating SWs [62–67]. Analytical formulas for the SW dispersion of symmetric magnetic bilayers in antiparallel magnetization configuration can be found in references [67–69]. The potential of nonreciprocal magnetoacoustic waves in synthetic antiferromagnets was initially theoretically discussed by Verba et al. for wide-band nonreciprocal transmission [70] and later for magnetoacoustic circulators [71]. In reference [36], it is experimentally demonstrated that SAWs can magnetoacoustically couple with nonreciprocal optical and acoustic SW modes in magnetic bilayers with parallel alignment of the magnetization. An extremely high nonreciprocity of the SAW transmission magnitude of about 48 dB at a low excitation frequency of 1.4 GHz was observed by Shah et al. for FeGaB(20 nm)/Al2O3(5 nm)/FeGaB(20 nm) [72]. These results are shown in Figure 2C for a bilayer sample with a mutually prepared in-plane anisotropy field HG at 60° with respect to the x-axis. The huge nonreciprocity of the SW dispersion is attributed on the one hand to the specific alignment of the equilibrium direction of the saturation magnetization, which results from antiferromagnetic coupling of both magnetic layers, the in-plane anisotropy, and external magnetic field at ϕH = 150°. On the other hand, large magnetoelastic coupling constants and low SW damping constant enhance the overall SAW-SW coupling and thus the SAW transmission nonreciprocity.
Discussion, conclusion and outlook
For the last years, the potential technological application of nonreciprocal SWs in chiral materials [73, 74], chiral domain walls [75–79], magnetic films with additional symmetry breaking at the interfaces via DMI [15, 17, 59, 80], and magnetic multilayers [16, 67, 81, 82] as nonreciprocal microwave devices has stimulated extensive research activities. In comparison to SWs, coupled SAW-SWs additionally benefit from long propagation lengths [31, 52] and nonreciprocity in these material systems. Thus, magnetoacoustic waves could be a good alternative to SWs for most proposed nonreciprocal applications in magnonics [17, 75, 76, 83]. The magnetoelastic driving field of a horizontal shear-type SAW is in contrast to the Rayleigh-type SAW (Eq. 1) at its maximum for the most interesting geometries for magnonics [33], which are the backward volume (ϕ0 = 0°) and Damon-Eshbach geometry (ϕ0 = ±90◦) [10].
The chirality of SAW-SW can easily be switched because the helicity of the lattice atoms is controlled by the SAW propagation direction and the orientation of the magnetization by the external magnetic field. This potentially allows encoding information in the chiral degree of freedom offered by magnetoacoustic surface waves. Moreover, instead of using unidirectional IDTs [4, 84, 85], the chirality of SAW-SWs makes unidirectional pumping of phonons by magnetization dynamics possible [86].
The pronounced nonreciprocal transmission of magnetoacoustic waves opens an avenue to build new types of miniaturized and energy-efficient microwave components, such as acoustic isolators or circulators [23, 36, 71, 72, 87]. A good magnetoacoustic isolator shows at the same time a low insertion loss IL and a high transmission nonreciprocity ΔS. Since ΔS for the so far realized devices is already very high (ΔS ≈ 50 dB, IL ≲−55 dB [72]) in comparison to state of the art rf-isolators (ΔS ≈ 20 dB, IL ≈ 1 dB), the main challenge in the future lays in reducing IL. A reduction of the insertion loss of the acoustic delay line can be achieved by using impedance-matched unidirectional IDTs [4, 84, 85]. For example, a low IL of about 6 dB at 4 GHz was demonstrated for acoustic delay lines without magnetic thin films [84]. Furthermore, the undesired IL related to the nonresonant magnetoacoustic interaction can become vanishingly small (≲0.8 dB) [29, 36]. Because interfacial DMI is restricted to magnetic thin films and comes with large linewidth broadening due to spin pumping [30], magnetic bi- and multilayers appear to be the more promising and more flexible approach for the realization of magnetoacoustic isolators [36, 54, 70, 71]. Interfacial DMI in magnetic bi- and multilayers can be used to further enhance the SW nonreciprocity [16]. Furthermore, acoustic isolators, which work in zero external magnetic field, can potentially be realized by using magnetic thin films with exchange-bias [88] or/and tailored anisotropies [72, 89]. Switching the magnetization by electrical currents via e.g. Oersted fields, spin-transfer, or spin-orbit torques might be a possible route towards all-electrical reconfigurable acoustic isolators [67, 90].
Moreover, the amplitude and phase of magnetoacoustic waves are characteristically modulated as a function of the external magnetic field. This was used to build low-noise magnetic field sensors [91–93]. For future acoustic magnetic field sensors, it should be additionally possible to determine the sign of the magnetic field if the transmission of the magnetoacoustic wave is nonreciprocal.
Finally, it is possible to characterize SWs in magnetic films [29, 30], bi-, and multilayers [36] via magnetoacoustic transmission measurements. Because the overall transmission depends on the helicities of the driving fields and magnetization precession in the individual layers, the SAW-SW helicity mismatch effect gives insight into the type of the excited SW-mode [36, 70].
Statements
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This work is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—project numbers 391592414 and 492421737.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The handling editor declared a past co-authorship with one of the authors MW.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1.
Hartmann C Bell D Rosenfeld R . Impulse model design of acoustic surface-wave filters. IEEE Trans Microw Theor Tech (1973) 21:162–75. 10.1109/TMTT.1973.1127967CrossRef Full Text | Google Scholar
2.
Campbell C . Surface acoustic wave devices and their signal processing applications. Boston: Academic Press (1989). Google Scholar
3.
Campbell C . Surface acoustic wave devices for mobile and wireless communications. Academic Press (1998). Google Scholar
4.
Morgan DP . Surface acoustic wave filters: With applications to electronic communications and signal processing. 2nd ed.. Amsterdam, London: Academic Press (2007). Google Scholar
5.
Ruppel CCW . Acoustic wave filter technology–A review. IEEE Trans Ultrason Ferroelectr Freq Control (2017) 64:1390–400. 10.1109/TUFFC.2017.2690905PubMed Abstract | CrossRef Full Text | Google Scholar
6.
Hashimoto K . Surface acoustic wave devices in telecommunications. Berlin, Heidelberg: Springer Berlin Heidelberg (2000). 10.1007/978-3-662-04223-6CrossRef Full Text | Google Scholar
7.
Mahon S . The 5G effect on RF filter technologies. IEEE Trans Semicond Manufact (2017) 30:494–9. 10.1109/TSM.2017.2757879CrossRef Full Text | Google Scholar
8.
White RM Voltmer FW . Direct piezoelectric coupling to surface elastic waves. Appl Phys Lett (1965) 7:314–6. 10.1063/1.1754276CrossRef Full Text | Google Scholar
9.
Chumak AV Vasyuchka VI Serga AA Hillebrands B . Magnon spintronics. Nat Phys (2015) 11:453–61. 10.1038/nphys3347CrossRef Full Text | Google Scholar
10.
Serga AA Chumak AV Hillebrands B . YIG magnonics. J Phys D Appl Phys (2010) 43:264002. 10.1088/0022-3727/43/26/264002CrossRef Full Text | Google Scholar
11.
Au Y Dvornik M Dmytriiev O Kruglyak VV . Nanoscale spin wave valve and phase shifter. Appl Phys Lett (2012) 100:172408. 10.1063/1.4705289CrossRef Full Text | Google Scholar
12.
Khitun A Bao M Wang KL . Magnonic logic circuits. J Phys D Appl Phys (2010) 43:264005. 10.1088/0022-3727/43/26/264005CrossRef Full Text | Google Scholar
13.
Yu T Luo Z Bauer GEW . Chirality as generalized spin-orbit interaction in spintronics. arxiv (2022). 10.48550/ARXIV.2206.05535CrossRef Full Text | Google Scholar
14.
Cheong SW Xu X . Magnetic chirality. Npj Quan Mater (2022) 7:40. 10.1038/s41535-022-00447-5CrossRef Full Text | Google Scholar
15.
Nembach HT Shaw JM Weiler M Jué E Silva TJ . Linear relation between Heisenberg exchange and interfacial Dzyaloshinskii–Moriya interaction in metal films. Nat Phys (2015) 11:825–9. 10.1038/nphys3418CrossRef Full Text | Google Scholar
16.
Franco AF Landeros P . Enhancement of the spin-wave nonreciprocity in antiferromagnetically coupled multilayers with dipolar and interfacial Dzyaloshinskii-Moriya interactions. Phys Rev B (2020) 102:184424. 10.1103/PhysRevB.102.184424CrossRef Full Text | Google Scholar
17.
Brächer T Boulle O Gaudin G Pirro P . Creation of unidirectional spin-wave emitters by utilizing interfacial Dzyaloshinskii-Moriya interaction. Phys Rev B (2017) 95:064429. 10.1103/PhysRevB.95.064429CrossRef Full Text | Google Scholar
18.
Gladii O Haidar M Henry Y Kostylev M Bailleul M . Frequency nonreciprocity of surface spin wave in permalloy thin films. Phys Rev B (2016) 93:054430. 10.1103/PhysRevB.93.054430CrossRef Full Text | Google Scholar
19.
Moon JH Seo SM Lee KJ Kim KW Ryu J Lee HW et al Spin-wave propagation in the presence of interfacial Dzyaloshinskii-Moriya interaction. Phys Rev B (2013) 88:184404. 10.1103/PhysRevB.88.184404CrossRef Full Text | Google Scholar
20.
Rasmussen C Quan L Alù A . Acoustic nonreciprocity. J Appl Phys (2021) 129:210903. 10.1063/5.0050775CrossRef Full Text | Google Scholar
21.
Camley R . Nonreciprocal surface waves. Surf Sci Rep (1987) 7:103–87. 10.1016/0167-5729(87)90006-9CrossRef Full Text | Google Scholar
22.
Bozhko DA Vasyuchka VI Chumak AV Serga AA . Magnon-phonon interactions in magnon spintronics (Review article). Low Temperature Phys (2020) 46:383–99. 10.1063/10.0000872CrossRef Full Text | Google Scholar
23.
Yang WG Schmidt H . Acoustic control of magnetism toward energy-efficient applications. Appl Phys Rev (2021) 8:021304. 10.1063/5.0042138CrossRef Full Text | Google Scholar
24.
Li Y Zhao C Zhang W Hoffmann A Novosad V . Advances in coherent coupling between magnons and acoustic phonons. APL Mater (2021) 9:060902. 10.1063/5.0047054CrossRef Full Text | Google Scholar
25.
Kittel C . Interaction of spin waves and ultrasonic waves in ferromagnetic crystals. Phys Rev (1958) 110:836–41. 10.1103/PhysRev.110.836CrossRef Full Text | Google Scholar
26.
Rayleigh L . On waves propagated along the plane surface of an elastic solid. Proc Lond Math Soc (1885) s1-17:4–11. 10.1112/plms/s1-17.1.4CrossRef Full Text | Google Scholar
27.
Dreher L Weiler M Pernpeintner M Huebl H Gross R Brandt MS et al Surface acoustic wave driven ferromagnetic resonance in nickel thin films: Theory and experiment. Phys Rev B (2012) 86:134415. 10.1103/PhysRevB.86.134415CrossRef Full Text | Google Scholar
28.
Maekawa S Tachiki M . Surface acoustic attenuation due to surface spin wave in ferro- and antiferromagnets. AIP Conf Proc (1976) 29:542–3. 10.1063/1.30437CrossRef Full Text | Google Scholar
29.
Xu M Yamamoto K Puebla J Baumgaertl K Rana B Miura K et al Nonreciprocal surface acoustic wave propagation via magneto-rotation coupling. Sci Adv (2020) 6:eabb1724. 10.1126/sciadv.abb1724PubMed Abstract | CrossRef Full Text | Google Scholar
30.
Küß M Heigl M Flacke L Hörner A Weiler M Albrecht M et al Nonreciprocal Dzyaloshinskii–Moriya magnetoacoustic waves. Phys Rev Lett (2020) 125:217203. 10.1103/PhysRevLett.125.217203PubMed Abstract | CrossRef Full Text | Google Scholar
31.
Weiler M Dreher L Heeg C Huebl H Gross R Brandt MS et al Elastically driven ferromagnetic resonance in nickel thin films. Phys Rev Lett (2011) 106:117601. 10.1103/PhysRevLett.106.117601PubMed Abstract | CrossRef Full Text | Google Scholar
32.
Thevenard L Gourdon C Prieur JY von Bardeleben HJ Vincent S Becerra L et al Surface-acoustic-wave-driven ferromagnetic resonance in (Ga, Mn)(As, P) epilayers. Phys Rev B (2014) 90:094401. 10.1103/PhysRevB.90.094401CrossRef Full Text | Google Scholar
33.
Küß M Heigl M Flacke L Hefele A Hörner A Weiler M et al Symmetry of the magnetoelastic interaction of Rayleigh and shear horizontal magnetoacoustic waves in nickel thin films on LiTaO3. Phys Rev Appl (2021) 15:034046. 10.1103/PhysRevApplied.15.034046CrossRef Full Text | Google Scholar
34.
Küß M Porrati F Hörner A Weiler M Albrecht M Huth M et al Forward volume magnetoacoustic spin wave excitation with micron-scale spatial resolution (2022). 10.48550/arXiv.2208.05205CrossRef Full Text | Google Scholar
35.
Chikazumi S Graham CD Chikazumi S . Physics of ferromagnetism. No. 94 in the international series of monographs on physics. Oxford, New York: Clarendon Press; Oxford University Press (1997). Google Scholar
36.
Küß M Heigl M Flacke L Hörner A Weiler M Wixforth A et al Nonreciprocal magnetoacoustic waves in dipolar-coupled ferromagnetic bilayers. Phys Rev Appl (2021) 15:034060. 10.1103/PhysRevApplied.15.034060CrossRef Full Text | Google Scholar
37.
Matsuo M Ieda J Saitoh E Maekawa S . Effects of mechanical rotation on spin currents. Phys Rev Lett (2011) 106:076601. 10.1103/PhysRevLett.106.076601PubMed Abstract | CrossRef Full Text | Google Scholar
38.
Matsuo M Ieda J Harii K Saitoh E Maekawa S . Mechanical generation of spin current by spin-rotation coupling. Phys Rev B (2013) 87:180402. 10.1103/PhysRevB.87.180402CrossRef Full Text | Google Scholar
39.
Kobayashi D Yoshikawa T Matsuo M Iguchi R Maekawa S Saitoh E et al Spin current generation using a surface acoustic wave generated via spin-rotation coupling. Phys Rev Lett (2017) 119:077202. 10.1103/PhysRevLett.119.077202PubMed Abstract | CrossRef Full Text | Google Scholar
40.
Kurimune Y Matsuo M Nozaki Y . Observation of gyromagnetic spin wave resonance in NiFe films. Phys Rev Lett (2020) 124:217205. 10.1103/PhysRevLett.124.217205PubMed Abstract | CrossRef Full Text | Google Scholar
41.
Gowtham PG Moriyama T Ralph DC Buhrman RA . Traveling surface spin-wave resonance spectroscopy using surface acoustic waves. J Appl Phys (2015) 118:233910. 10.1063/1.4938390CrossRef Full Text | Google Scholar
42.
Cortés-Ortuño D Landeros P . Influence of the Dzyaloshinskii–Moriya interaction on the spin-wave spectra of thin films. J Phys : Condens Matter (2013) 25:156001. 10.1088/0953-8984/25/15/156001PubMed Abstract | CrossRef Full Text | Google Scholar
43.
Kalinikos BA Slavin AN . Theory of dipole-exchange spin wave spectrum for ferromagnetic films with mixed exchange boundary conditions. J Phys C: Solid State Phys (1986) 19:7013–33. 10.1088/0022-3719/19/35/014CrossRef Full Text | Google Scholar
44.
Vincent B Krüger JK Elmazria O Bouvot L Mainka J Sanctuary R et al Imaging of microwave-induced acoustic fields in LiNbO3 by high-performance Brillouin microscopy. J Phys D Appl Phys (2005) 38:2026–30. 10.1088/0022-3727/38/12/026CrossRef Full Text | Google Scholar
45.
Zhao C Zhang Z Li Y Zhang W Pearson JE Divan R et al Direct imaging of resonant phonon-magnon coupling. Phys Rev Appl (2021) 15:014052. 10.1103/PhysRevApplied.15.014052CrossRef Full Text | Google Scholar
46.
Babu NKP Trzaskowska A Graczyk P Centała G Mieszczak S Głowiński H et al The interaction between surface acoustic waves and spin waves: The role of anisotropy and spatial profiles of the modes. Nano Lett (2021) 21:946–51. 10.1021/acs.nanolett.0c03692PubMed Abstract | CrossRef Full Text | Google Scholar
47.
Geilen M Nicoloiu A Narducci D Mohseni M Bechberger M Ender M et al Fully resonant magneto-elastic spin-wave excitation by surface acoustic waves under conservation of energy and linear momentum. Appl Phys Lett (2022) 120:242404. 10.1063/5.0088924CrossRef Full Text | Google Scholar
48.
Janušonis J Chang CL Jansma T Gatilova A Vlasov VS Lomonosov AM et al Ultrafast magnetoelastic probing of surface acoustic transients. Phys Rev B (2016) 94:024415. 10.1103/PhysRevB.94.024415CrossRef Full Text | Google Scholar
49.
Yahagi Y Harteneck B Cabrini S Schmidt H . Controlling nanomagnet magnetization dynamics via magnetoelastic coupling. Phys Rev B (2014) 90:140405. 10.1103/PhysRevB.90.140405CrossRef Full Text | Google Scholar
50.
Kuszewski P Duquesne JY Becerra L Lemaître A Vincent S Majrab S et al Optical probing of Rayleigh wave driven magnetoacoustic resonance. Phys Rev Appl (2018) 10:034036. 10.1103/PhysRevApplied.10.034036CrossRef Full Text | Google Scholar
51.
Yahagi Y Berk C Hebler B Dhuey S Cabrini S Albrecht M et al Optical measurement of damping in nanomagnet arrays using magnetoelastically driven resonances. J Phys D Appl Phys (2017) 50:17LT01. 10.1088/1361-6463/aa6472CrossRef Full Text | Google Scholar
52.
Casals B Statuto N Foerster M Hernández-Mínguez A Cichelero R Manshausen P et al Generation and imaging of magnetoacoustic waves over millimeter distances. Phys Rev Lett (2020) 124:137202. 10.1103/PhysRevLett.124.137202PubMed Abstract | CrossRef Full Text | Google Scholar
53.
Cheong SW Talbayev D Kiryukhin V Saxena A . Broken symmetries, non-reciprocity, and multiferroicity. NPJ Quan Mater (2018) 3:19. 10.1038/s41535-018-0092-5CrossRef Full Text | Google Scholar
54.
Barman A Gubbiotti G Ladak S Adeyeye AO Krawczyk M Gräfe J et al The 2021 magnonics roadmap. J Phys : Condens Matter (2021) 33:413001. 10.1088/1361-648X/abec1aCrossRef Full Text | Google Scholar
55.
Lewis MF Patterson E . Acoustic-surface-wave isolator. Appl Phys Lett (1972) 20:276–8. 10.1063/1.1654147CrossRef Full Text | Google Scholar
56.
Sasaki R Nii Y Iguchi Y Onose Y . Nonreciprocal propagation of surface acoustic wave in Ni/LiNbO3. Phys Rev B (2017) 95:020407. 10.1103/PhysRevB.95.020407CrossRef Full Text | Google Scholar
57.
Tateno S Nozaki Y . Highly nonreciprocal spin waves excited by magnetoelastic coupling in a Ni/Si bilayer. Phys Rev Appl (2020) 13:034074. 10.1103/PhysRevApplied.13.034074CrossRef Full Text | Google Scholar
58.
Mühlbauer S Binz B Jonietz F Pfleiderer C Rosch A Neubauer A et al Skyrmion lattice in a chiral magnet. Science (2009) 323:915–9. 10.1126/science.1166767PubMed Abstract | CrossRef Full Text | Google Scholar
59.
Di K Zhang VL Lim HS Ng SC Kuok MH Yu J et al Direct observation of the Dzyaloshinskii-Moriya interaction in a Pt/Co/Ni film. Phys Rev Lett (2015) 114:047201. 10.1103/PhysRevLett.114.047201PubMed Abstract | CrossRef Full Text | Google Scholar
60.
Tserkovnyak Y Brataas A Bauer GEW . Enhanced Gilbert damping in thin ferromagnetic films. Phys Rev Lett (2002) 88:117601. 10.1103/PhysRevLett.88.117601PubMed Abstract | CrossRef Full Text | Google Scholar
61.
Verba R Lisenkov I Krivorotov I Tiberkevich V Slavin A . Nonreciprocal surface acoustic waves in multilayers with magnetoelastic and interfacial Dzyaloshinskii-Moriya interactions. Phys Rev Appl (2018) 9:064014. 10.1103/PhysRevApplied.9.064014CrossRef Full Text | Google Scholar
62.
Camley R Maradudin A . Magnetostatic interface waves in ferromagnets. Solid State Commun (1982) 41:585–8. 10.1016/0038-1098(82)90946-2CrossRef Full Text | Google Scholar
63.
Grünberg P Schreiber R Pang Y Brodsky MB Sowers H . Layered magnetic structures: Evidence for antiferromagnetic coupling of Fe layers across Cr interlayers. Phys Rev Lett (1986) 57:2442–5. 10.1103/PhysRevLett.57.2442PubMed Abstract | CrossRef Full Text | Google Scholar
64.
Grünberg P . Some ways to modify the spin-wave mode spectra of magnetic multilayers (invited). J Appl Phys (1985) 57:3673–7. 10.1063/1.334985CrossRef Full Text | Google Scholar
65.
Zhang PX Zinn W . Spin-wave modes in antiparallel magnetized ferromagnetic double layers. Phys Rev B (1987) 35:5219–25. 10.1103/PhysRevB.35.5219PubMed Abstract | CrossRef Full Text | Google Scholar
66.
Binasch G Grünberg P Saurenbach F Zinn W . Enhanced magnetoresistance in layered magnetic structures with antiferromagnetic interlayer exchange. Phys Rev B (1989) 39:4828–30. 10.1103/PhysRevB.39.4828PubMed Abstract | CrossRef Full Text | Google Scholar
67.
Gallardo R Schneider T Chaurasiya A Oelschlägel A Arekapudi S Roldán-Molina A et al Reconfigurable spin-wave nonreciprocity induced by dipolar interaction in a coupled ferromagnetic bilayer. Phys Rev Appl (2019) 12:034012. 10.1103/PhysRevApplied.12.034012CrossRef Full Text | Google Scholar
68.
Grünberg P . Magnetostatic spin-wave modes of a heterogeneous ferromagnetic double layer. J Appl Phys (1981) 52:6824–9. 10.1063/1.328636CrossRef Full Text | Google Scholar
69.
Wintz S Tiberkevich V Weigand M Raabe J Lindner J Erbe A et al Magnetic vortex cores as tunable spin-wave emitters. Nat Nanotechnol (2016) 11:948–53. 10.1038/nnano.2016.117PubMed Abstract | CrossRef Full Text | Google Scholar
70.
Verba R Tiberkevich V Slavin A . Wide-band nonreciprocity of surface acoustic waves induced by magnetoelastic coupling with a synthetic antiferromagnet. Phys Rev Appl (2019) 12:054061. 10.1103/PhysRevApplied.12.054061CrossRef Full Text | Google Scholar
71.
Verba R Bankowski EN Meitzler TJ Tiberkevich V Slavin A . Phase nonreciprocity of microwave-frequency surface acoustic waves in hybrid heterostructures with magnetoelastic coupling. Adv Electron Mater (2021) 7:2100263. 10.1002/aelm.202100263CrossRef Full Text | Google Scholar
72.
Shah PJ Bas DA Lisenkov I Matyushov A Sun NX Page MR . Giant nonreciprocity of surface acoustic waves enabled by the magnetoelastic interaction. Sci Adv (2020) 6:eabc5648. 10.1126/sciadv.abc5648PubMed Abstract | CrossRef Full Text | Google Scholar
73.
Iguchi Y Uemura S Ueno K Onose Y . Nonreciprocal magnon propagation in a noncentrosymmetric ferromagnet LiFe5O8. Phys Rev B (2015) 92:184419. 10.1103/PhysRevB.92.184419CrossRef Full Text | Google Scholar
74.
Seki S Okamura Y Kondou K Shibata K Kubota M Takagi R et al Magnetochiral nonreciprocity of volume spin wave propagation in chiral-lattice ferromagnets. Phys Rev B (2016) 93:235131. 10.1103/PhysRevB.93.235131CrossRef Full Text | Google Scholar
75.
Lan J Yu W Wu R Xiao J . Spin-wave diode. Phys Rev X (2015) 5:041049. 10.1103/PhysRevX.5.041049CrossRef Full Text | Google Scholar
76.
Xing X Zhou Y . Fiber optics for spin waves. NPG Asia Mater (2016) 8:e246. 10.1038/am.2016.25CrossRef Full Text | Google Scholar
77.
Buijnsters F Ferreiros Y Fasolino A Katsnelson M . Chirality-dependent transmission of spin waves through domain walls. Phys Rev Lett (2016) 116:147204. 10.1103/PhysRevLett.116.147204PubMed Abstract | CrossRef Full Text | Google Scholar
78.
Hämäläinen SJ Madami M Qin H Gubbiotti G van Dijken S . Control of spin-wave transmission by a programmable domain wall. Nat Commun (2018) 9:4853. 10.1038/s41467-018-07372-xPubMed Abstract | CrossRef Full Text | Google Scholar
79.
Henry Y Stoeffler D Kim JV Bailleul M . Unidirectional spin-wave channeling along magnetic domain walls of Bloch type. Phys Rev B (2019) 100:024416. 10.1103/PhysRevB.100.024416CrossRef Full Text | Google Scholar
80.
Gallardo R Cortés-Ortuño D Schneider T Roldán-Molina A Ma F Troncoso R et al Flat bands, indirect gaps, and unconventional spin-wave behavior induced by a periodic Dzyaloshinskii-Moriya interaction. Phys Rev Lett (2019) 122:067204. 10.1103/PhysRevLett.122.067204PubMed Abstract | CrossRef Full Text | Google Scholar
81.
Albisetti E Tacchi S Silvani R Scaramuzzi G Finizio S Wintz S et al Optically inspired nanomagnonics with nonreciprocal spin waves in synthetic antiferromagnets. Adv Mater (2020) 32:1906439. 10.1002/adma.201906439PubMed Abstract | CrossRef Full Text | Google Scholar
82.
Gallardo RA Alvarado-Seguel P Kákay A Lindner J Landeros P . Spin-wave focusing induced by dipole-dipole interaction in synthetic antiferromagnets. Phys Rev B (2021) 104:174417. 10.1103/PhysRevB.104.174417CrossRef Full Text | Google Scholar
83.
Jamali M Kwon JH Seo SM Lee KJ Yang H . Spin wave nonreciprocity for logic device applications. Sci Rep (2013) 3:3160. 10.1038/srep03160PubMed Abstract | CrossRef Full Text | Google Scholar
84.
Yamanouchi K Lee C Yamamoto K Meguro T Odagawa H . GHz-range low-loss wide band filter using new floating electrode type unidirectional transducers. In: IEEE 1992 Ultrasonics Symposium Proceedings; Tucson, AZ, USA (1992). p. 139–42. 10.1109/ULTSYM.1992.276049CrossRef Full Text | Google Scholar
85.
Ekström MK Aref T Runeson J Björck J Boström I Delsing P . Surface acoustic wave unidirectional transducers for quantum applications. Appl Phys Lett (2017) 110:073105. 10.1063/1.4975803CrossRef Full Text | Google Scholar
86.
Zhang X Bauer GE Yu T . Unidirectional pumping of phonons by magnetization dynamics. Phys Rev Lett (2020) 125:077203. 10.1103/PhysRevLett.125.077203PubMed Abstract | CrossRef Full Text | Google Scholar
87.
Matsumoto H Kawada T Ishibashi M Kawaguchi M Hayashi M . Large surface acoustic wave nonreciprocity in synthetic antiferromagnets. Appl Phys Express (2022) 15:063003. 10.35848/1882-0786/ac6da1CrossRef Full Text | Google Scholar
88.
Stamps RL . Mechanisms for exchange bias. J Phys D Appl Phys (2000) 33:R247–68. 10.1088/0022-3727/33/23/201CrossRef Full Text | Google Scholar
89.
Duquesne JY Rovillain P Hepburn C Eddrief M Atkinson P Anane A et al Surface-acoustic-wave induced ferromagnetic resonance in Fe thin films and magnetic field sensing. Phys Rev Appl (2019) 12:024042. 10.1103/PhysRevApplied.12.024042CrossRef Full Text | Google Scholar
90.
Ishibashi M Shiota Y Li T Funada S Moriyama T Ono T . Switchable giant nonreciprocal frequency shift of propagating spin waves in synthetic antiferromagnets. Sci Adv (2020) 6:eaaz6931. 10.1126/sciadv.aaz6931PubMed Abstract | CrossRef Full Text | Google Scholar
91.
Chiriac H Pletea M Hristoforou E . Magneto-surface-acoustic-waves microdevice using thin film technology: Design and fabrication process. Sensors Actuators A: Phys (2001) 91:107–11. 10.1016/S0924-4247(01)00500-3CrossRef Full Text | Google Scholar
92.
Kittmann A Durdaut P Zabel S Reermann J Schmalz J Spetzler B et al Wide band low noise love wave magnetic field sensor system. Sci Rep (2018) 8:278. 10.1038/s41598-017-18441-4PubMed Abstract | CrossRef Full Text | Google Scholar
93.
Müller C Durdaut P Holländer RB Kittmann A Schell V Meyners D et al Imaging of love waves and their interaction with magnetic domain walls in magnetoelectric magnetic field sensors. Adv Electron Mater (2022) 8:2200033. 10.1002/aelm.202200033CrossRef Full Text | Google Scholar
Summary
Keywords
magnetoelastic coupling, magneto-rotation, surface acoustic waves, spin waves, chirality, nonreciprocity, Dzyaloshinskii-Moriya interaction, magnetization dynamics
Citation
Küß M, Albrecht M and Weiler M (2022) Chiral Magnetoacoustics. Front. Phys. 10:981257. doi: 10.3389/fphy.2022.981257
Received
29 June 2022
Accepted
25 July 2022
Published
31 August 2022
Volume
10 - 2022
Edited by
Akashdeep Kamra, Autonomous University of Madrid, Spain
Reviewed by
Markus Weissenhofer, University of Konstanz, Germany
Richard Schlitz, ETH Zürich, Switzerland
Updates
Copyright
© 2022 Küß, Albrecht and Weiler.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Matthias Küß, matthias.kuess@physik.uni-augsburg.de
This article was submitted to Condensed Matter Physics, a section of the journal Frontiers in Physics
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.