Abstract
A new adaptive iterative learning control (AILC) scheme is proposed to solve the finite-time hybrid function projective synchronization (HFPS) problem of chaotic systems with unknown periodic time-varying parameters. Fourier series expansion (FSE) is introduced to deal with the problem of uncertain time-varying parameters. The bound of the expanded remaining items is unknown. A typical convergent series is used to deal with the unknown bound in the design process of the controller. The adaptive iterative learning synchronization controller and parameter update laws are designed. Two different chaotic systems are synchronized asymptotically according to different proportional functions on a finite time interval by Lyapunov stability analysis. The simulation example proves the feasibility and effectiveness of the proposed method.
Introduction
Chaos synchronization has a wide range of applications in physical systems, biological networks, and secure communications [1]. However, due to the unpredictability, pseudo-randomness, and extreme sensitivity to initial values of chaotic systems [2], hybrid function projection synchronization of chaotic systems is widely concerned. In 1990, the pioneer workers Pecora and Carroll first proposed the concept of chaos synchronization and solved the synchronization problem of two identical chaotic systems under different initial conditions [3]. Since then, chaos synchronization control has become a very active research topic [4–16], for example, projective synchronization control and hybrid function projective synchronization control. Many control methods have been used to synchronize different chaotic systems, such as feedback linearization method [17], optimal control [18], and neural network control [19–24]. However, few people study the problem of chaos synchronization on a finite time interval.
When studying chaos synchronization, the problem of system parameter uncertainty will be encountered. The adaptive control method is often used to solve this problem and improve control performance [25–27]. Chaotic systems are vulnerable to encounter the problem of uncertain parameters due to external interference. These uncertain parameters may disrupt synchronization. Therefore, this is an important problem to study the synchronization of chaotic systems with unknown time-varying parameters.
The adaptive iterative learning control method can solve the finite-time tracking control problem of uncertain non-linear systems [28] by modifying the input information according to the previous output data. This ensures that the output of the system tracks the given trajectory on a finite time interval accurately. This is one of the most effective control methods of the non-linear systems’ repetitive tracking control. Because synchronization is similar to tracking, the synchronization problem of chaotic systems on a finite time interval can be solved by adaptive iterative learning control [29, 30]. Achieving finite-time hybrid function projection synchronization control of chaotic systems with time-varying parameters is an interesting topic.
This paper proposes a new adaptive iterative learning control method to solve the HFPS problem of chaotic systems with uncertain periodic time-varying parameters. FSE is introduced to deal with the problem of uncertain parameters. Convergent series is used to deal with the unknown upper bounds of uncertain parameters. The parameter updating laws and AILC law are designed to synchronize the states of two chaotic systems according to different proportion functions asymptotically. The simulation example illustrates the correctness and effectiveness of the research results in this paper.
The main contributions of this paper are listed as follows:
(1) The problem of chaos synchronization on a limited time interval is very important. We proposed an adaptive iterative learning control scheme to solve the finite-time hybrid function projective synchronization of chaotic systems with unknown periodic time-varying parameters.
(2) The problem of system parameter uncertainty of chaos synchronization must be solved. Fourier series expansion (FSE) is introduced to solve the problem of time-varying parameters.
(3) The residual term after expansion is bounded, but the bound is unknown. Based on the author’s previous work, a typical convergent series is used to deal with the remaining items after expansion.
System specification and synchronization controller design
System specification
Consider the following continuous time chaotic systems with unknown time-varying parameters:where is the state. is the coefficient matrix which is linear.is the non-linear part. is the uncertain parameter vector. is the number of iterations. Here, is the nominal value of is a time-varying parameter. System (1) is a driving system, and the response system containing controller is shown in system (2):where is the state. is the matrix. is the non-linear function of (2) which is continuous. is the control vector. Here, suppose is an uncertain function with a known period , then . This assumption is reasonable because many things in nature occur periodically, so the parameters of the system often exist periodically.
According to the Fourier series expansion, the continuous period vector can be expressed as shown in (3):where is composed of the first parameters in the FSE of . is the truncation error and . , where , , , and their th derivative are smooth and bounded. Take ,, , and . Then, by substituting (3) into system (1), system (1) can be rewritten as follows:
According to (3), , suppose the upper bound is an unknown parameter.
Define the synchronization error asHere, is the scale matrix and is a bounded non-zero continuous differentiable function.
The control objective of this paper is to design an appropriate controller and related parameter adaptive laws for response system 2) on the finite time , so that response system 2) can synchronize with drive system 1) using different scale functions as asymptotically. That is to say, .
Design of the adaptive iterative learning synchronization controller
In the process of controller design, the following definition and lemma of the convergence series sequence will be used.
Definition1[31]: The sequence is defined asThis sequence is a convergence series. Here, and are parameters to be designed, .
Lemma1 [31]: For the sequence , the following conclusion holds:The specific design process of the controller is as follows:From system (4) and system (2), it is easy to get (8)From (8), the following controller is designed:Here, is a positive feedback gain matrix, . , and are estimates of , , and , respectively.Select the following parameter update laws:where is a positive definite diagonal gain matrix of the appropriate dimension.The initial conditions satisfy the following relations: for any , when , .
Stability analysis
According to the aforementioned controller design process, the following theorem is given in this paper:
For the given scaling function , designing the control law 9) and parameter update laws (10) for response system (2) can obtain that all closed-loop signals are bounded on , and .
ProofFor convergence analysis, the following Lyapunov functions are selected:where .According to the assumptions, definition, and lemma, it is easy to prove that the conclusion of Theorem 1 is true.The derivation process of according to system 8) is as follows:Substituting (9) and (10) into (12), we getwhere for any .According to the initial conditions, we have . By (11), we getSubstituting (12) into (14), we getTaking , formula (15) is rewritten asFrom (7), we get , which is bounded, and . Therefore,From (11), for any k, we have . Substituting (12), we getBy (17), is bounded. According to Definition 1, when is bounded. So is bounded and . From (11), for any , is bounded; is bounded. When is bounded, is also bounded. According to 9), is bounded. By (8), is bounded, so is uniformly continuous. According to the aforementioned parameters, we can draw the conclusion .
Simulation analysis
Consider the hybrid function projection synchronization of the following two systems. The specific system is as follows:
The drive system is the Lorenz system:
The response system is the Chen system:By comparing system (19) and system (20) with system (1) and system (2), we can getwhere the uncertain parameters are , , and . During the simulation, the parameters are chosen as , , , , , , and . The proportional functions are chosen as , , and . The initial values of the drive system and response system are chosen as and , respectively.
According to controller 9) and adaptive iterative learning laws (10) given in this paper, the results of Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, and Figure 6 can be obtained. It can be seen from Figure 1 and Figure 2 that there will be large errors between the drive signals and the response signals (Figures 2A–C) when there is no iteration, but in the 10th iteration, their errors tend to zero (Figures 1A–C) basically. It can be seen that the synchronization errors decrease as the number of iterations increases. Therefore, this method can realize synchronization using different scale functions between two different chaotic systems, which proves the correctness and effectiveness of the proposed method.
FIGURE 1
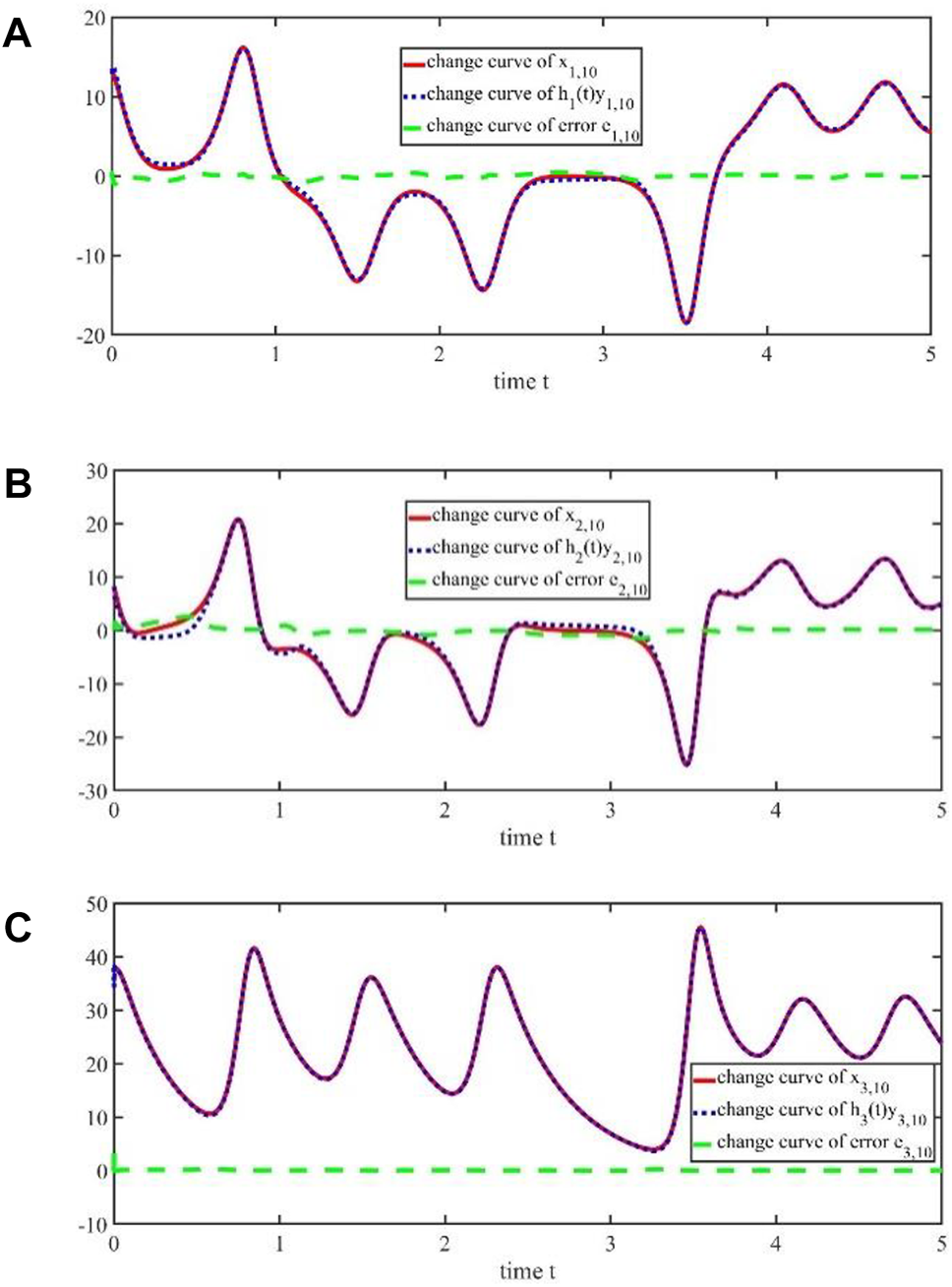
(A) Change of the 10th iteration trajectories and error on time t; (B) Change of the 10th iteration trajectories and error on time t; (C) Change of the 10th iteration trajectories and error on time t.
FIGURE 2
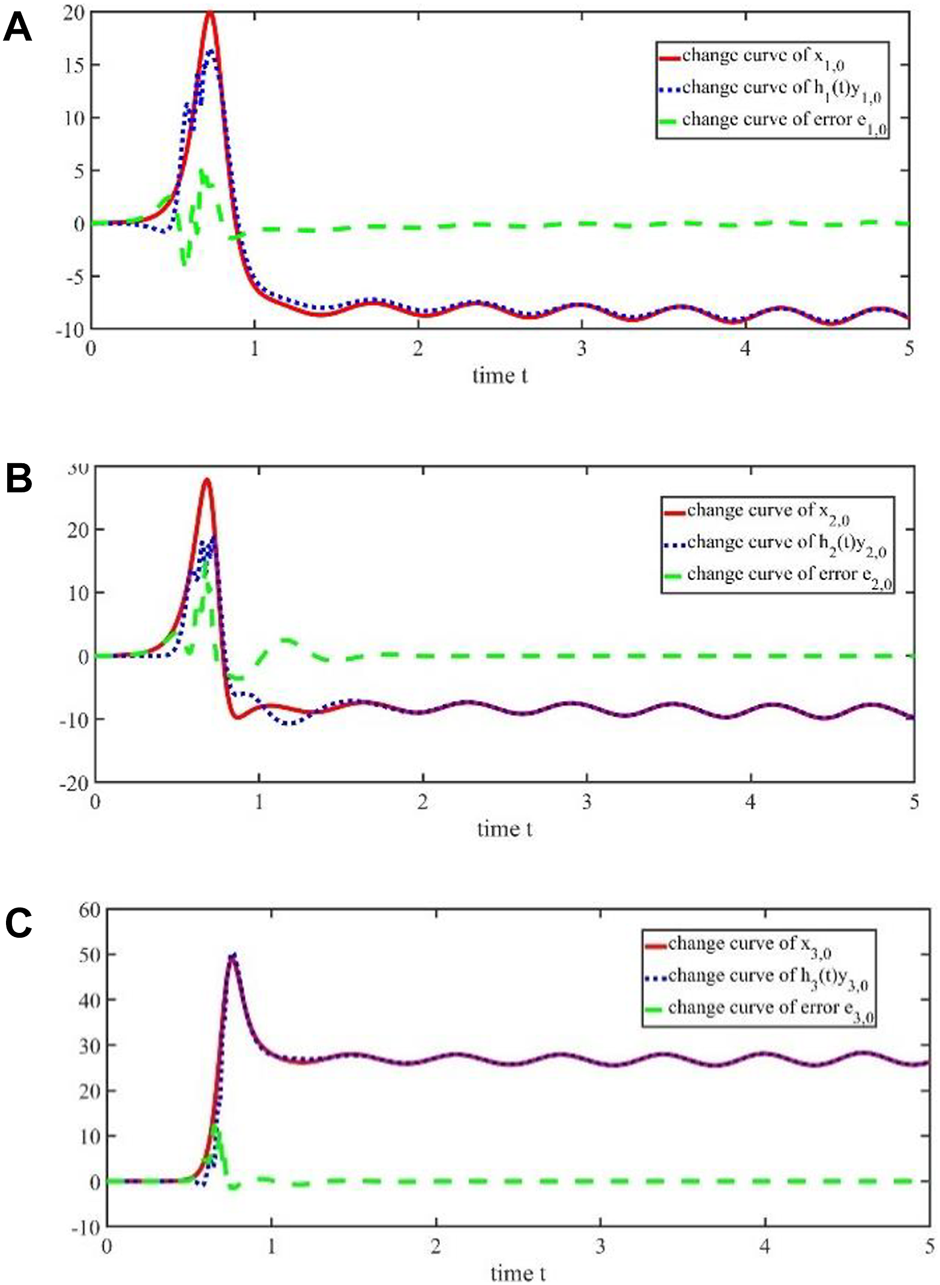
(A) Change of trajectories and error without iteration on time ; (B) Change of trajectories and error without iteration on time ; (C) Change of trajectories and error without iteration on time .
FIGURE 3
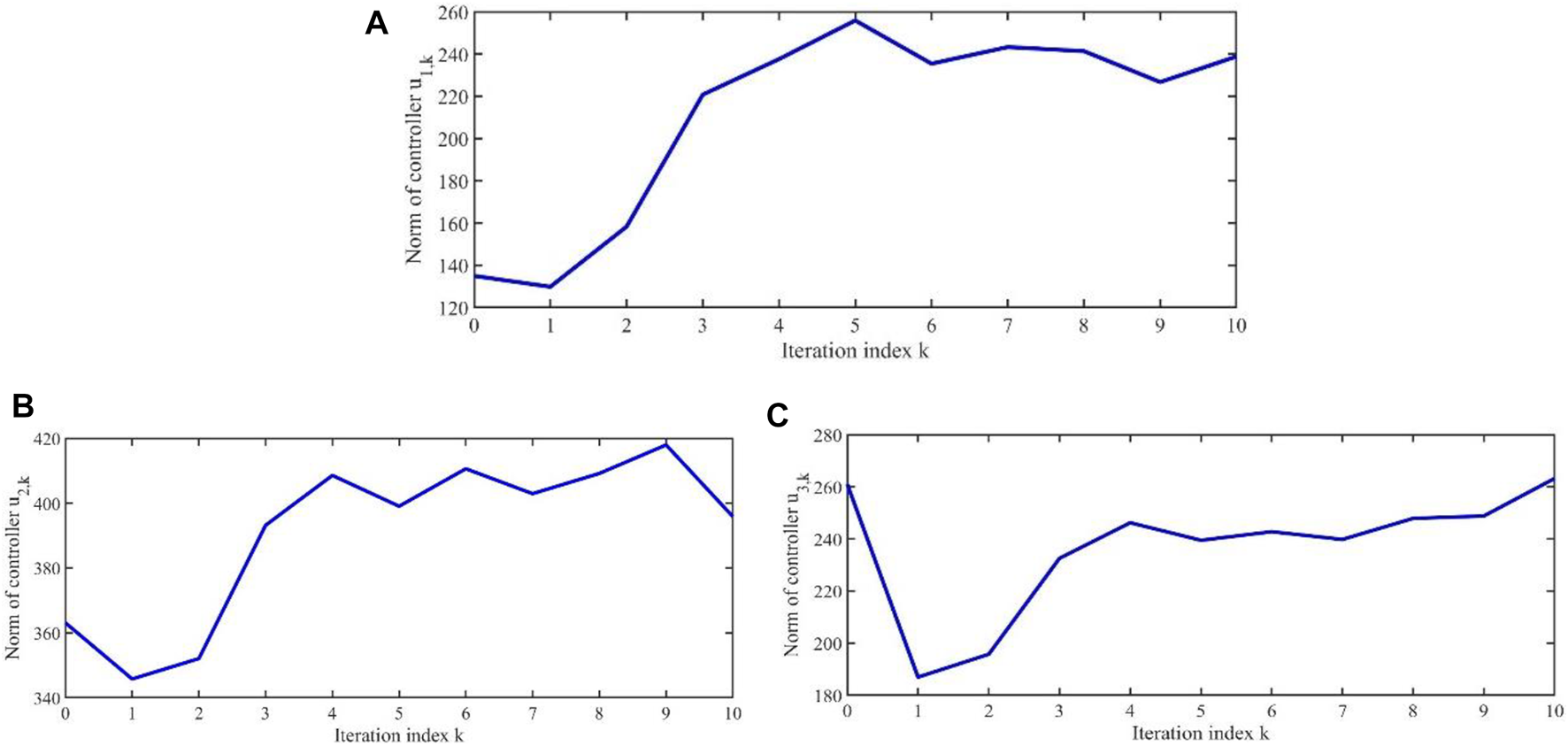
Norm variation curve of controller with iteration .
FIGURE 4
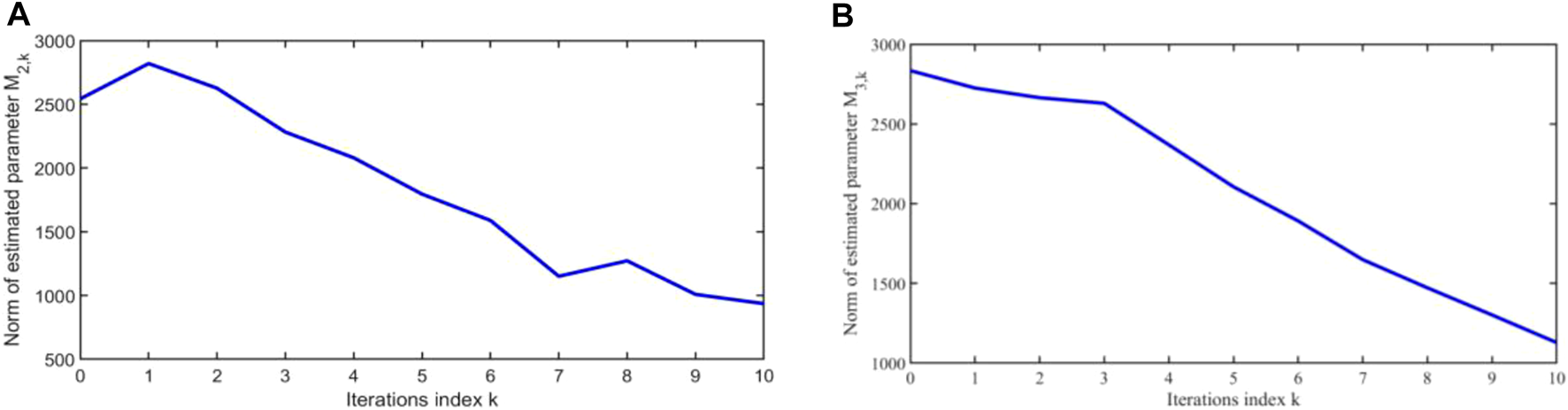
Norm variation curve of parameter with iteration .
FIGURE 5
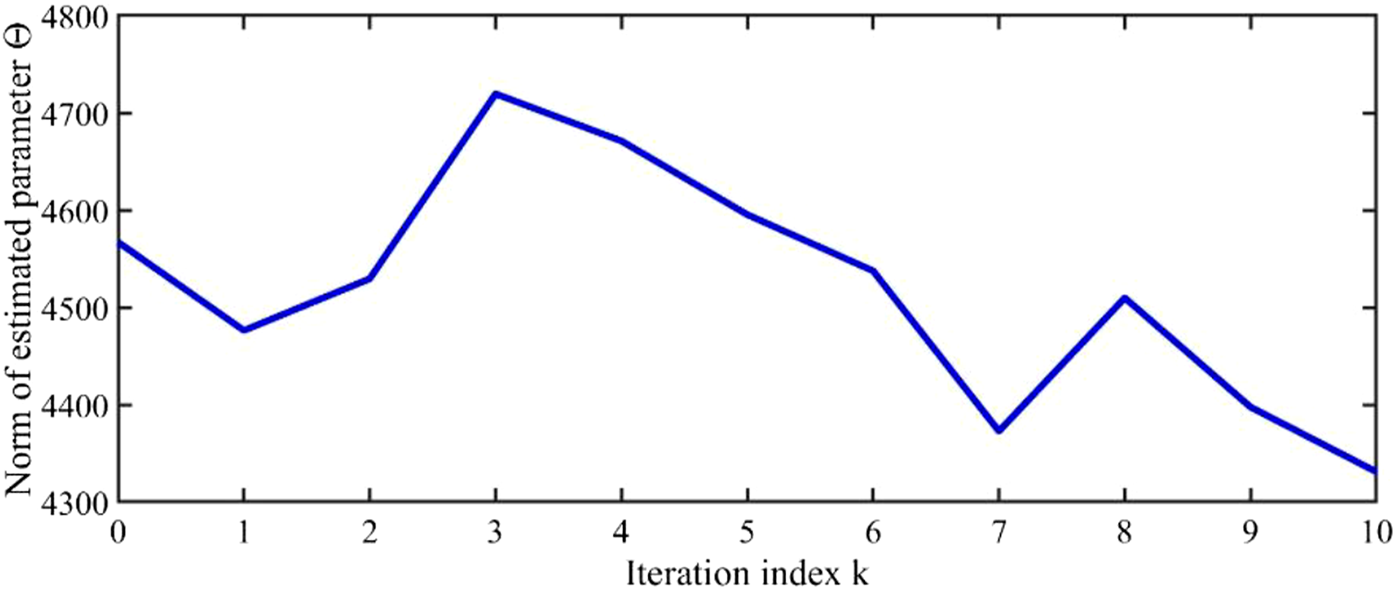
Variation curve of parameter with iteration .
FIGURE 6
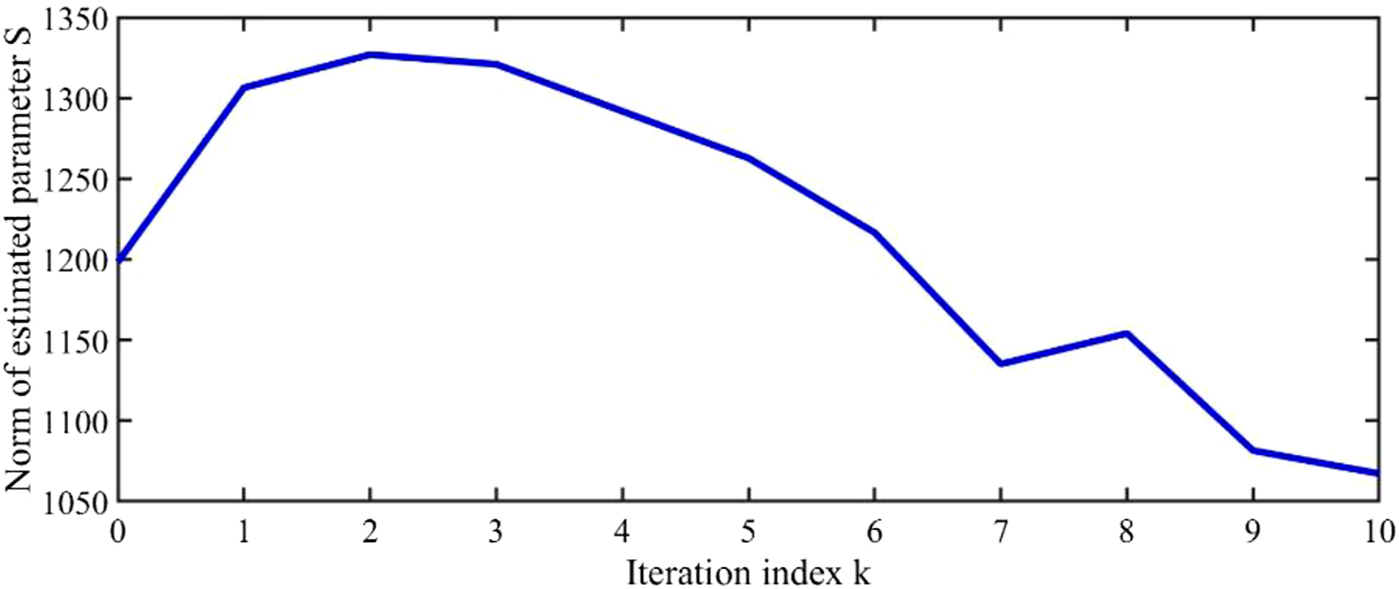
Variation curve of parameter with iteration .
At the same time, it can be seen from Figure 3 to Figure 6 that as the number of iterations increases, the controllers and the estimated system parameters will remain within a certain range, which ensures the boundedness of system parameters , and . This also satisfies the content of the theorem.
Conclusion
The AILC method is proposed to solve the different proportional synchronization problems on finite time interval with uncertain parameters. The adaptive iterative learning controller and parameter update laws make the drive system and the response system synchronize along different scale functions asymptotically. The proposed controller solves the problem of hybrid function projection synchronization between the Lorenz system and Chen system successfully. The correctness of the method is verified by theory and numerical simulation. Further work is needed on how to realize the finite-time synchronization between hyper-chaotic systems with time-varying parameters or chaotic systems with different dimensions. As far as the author knows, these studies are very difficult and interesting topics in the field of chaos synchronization control.
Statements
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
Conceptualization, CZ; methodology, CZ; software, LY; validation, LY, YG, and KL.; writing—original draft preparation, LY; writing—review and editing, CZ and WW; visualization, DW; supervision, LZ. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by National Natural Science Foundation (NNSF) of China (Grant 61603296 and Grant 62073259) and supported by the Natural Science Basis Research Plan in Shaanxi Province of China (Program No. 2023-JC-QN-0752, 2023-JC-YB-533 and 2022JQ-609). This work is also supported by Key Laboratory of complex system control and intelligent information processing in Shaanxi Province.
Conflict of interest
KL, DW, and LZ were employed by State Grid Xi’an Electric Power Supply Company.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1.
SamimiMHassan MajidiMKhorashadizadehS. Secure communication based on chaos synchronization using brain emotional learning. J Int J Elect Commun (2020) 127:153424. 10.1016/j.aeue.2020.153424
2.
NiuYZhangX. A novel plaintext-related image encryption scheme based on chaotic system and pixel permutation. J IEEE Access (2020) 8:22082–93. 10.1109/ACCESS.2020.2970103
3.
PecoraLMCarrollTL. Synchronization in chaotic systems. J Phys Rev Lett (1990) 64:821–4. 10.1103/physrevlett.64.821
4.
LiZXuD. A secure communication scheme using projective chaos synchronization. Chaos J Solitons Fractals (2004) 22:477–81. 10.1016/j.chaos.2004.02.019
5.
TanFZhouLLuJQuanHLiuK. Adaptive quantitative control for finite time synchronization among multiplex switched nonlinear coupling complex networks. Eur J Control (2022) 100764. 10.1016/j.ejcon.2022.100764
6.
LiXZhouLTanF. An image encryption scheme based on finite-time cluster synchronization of two-layer complex dynamic networks. Soft Comp (2022) 26:511–25. 10.1007/s00500-021-06500-y
7.
CheeCYXuD. Secure digital communication using controlled projective synchronisation of chaos. J Chaos Solitons Fractals (2005) 23:1063–70. 10.1016/s0960-0779(04)00366-2
8.
ZhouLTanFYuF. A robust synchronization-based chaotic secure communication scheme with double-layered and multiple hybrid networks. IEEE Syst J (2020) 14(2):2508–19. 10.1109/jsyst.2019.2927495
9.
TanFZhouL. Analysis of random synchronization under bilayer derivative and nonlinear delay networks of neuron nodes via fixed time policies. ISA Trans (2022) 129:114–27. 10.1016/j.isatra.2022.01.023
10.
LiGH. Modified projective synchronization of chaotic system. J Chaos, Solitons Fractals (2007) 32:1786–90. 10.1016/j.chaos.2005.12.009
11.
TanFZhouLLuJChuYLiY. Fixed-time outer synchronization under double-layered multiplex networks with hybrid links and time-varying delays via delayed feedback control. Asian J Control (2022) 24:137–48. 10.1002/asjc.2420
12.
ZhouLTanFLiXZhouL. A fixed-time synchronization-based secure communication scheme for two-layer hybrid coupled networks. Neurocomputing (2021) 433:131–41. 10.1016/j.neucom.2020.12.033
13.
LinHWangCCuiLSunYXuCFeiY. Brain-like initial-boosted hyperchaos and application in biomedical image encryption. IEEE Trans Ind Inform (2022) 18(12):8839–50. 10.1109/tii.2022.3155599
14.
ZhouLTanFFeiYLiuW. Cluster synchronization of two-layer nonlinearly coupled multiplex networks with multi-links and time-delays. Neurocomputing (2019) 359:264–75. 10.1016/j.neucom.2019.05.077
15.
LinHWangCXuCZhangXHerbertHC. A memristive synapse control method to generate diversified multi-structure chaotic attractors. IEEE Trans Computer-Aided Des Integrated Circuits Syst (2022) 1. 10.1109/TCAD.2022.3186516
16.
ZhouLTanF. A chaotic secure communication scheme based on synchronization of double-layered and multiple complex networks. Nonlinear Dynamic (2019) 96:869–83. 10.1007/s11071-019-04828-7
17.
LiuLWangJLiuC. Fast synergetic control for chaotic oscillation in the power system based on input-output feedback linearization. J Math Probl Eng Theor Methods Appl (2021) 2021:1–14. 10.1155/2021/8404192
18.
LetellierCBarbotJ-P. Optimal flatness placement of sensors and actuators for controlling chaotic systems. J Nonlinear Sci (2021) 31(10):103114. 10.1063/5.0055895
19.
YuFShenHYuQKongXSharmaPKCaiS. Privacy protection of medical data based on multi-scroll memristive hopfield neural network. IEEE Trans Netw Sci Eng (2022) 1–14. 10.1109/TNSE.2022.3223930
20.
RabahKLadaciS. A fractional adaptive sliding mode control configuration for synchronizing disturbed fractional-order chaotic systems. J Circuits, Syst Signal Process (2020) 39(3):1244–64. 10.1007/s00034-019-01205-y
21.
YuFKongXMokbelAAMYaoWCaiS. Complex dynamics, hardware implementation and image encryption application of multiscroll memeristive hopfield neural network with a novel local active memeristor. IEEE Trans Circuits Systems--II: Express Briefs (2022) 70:326–30. 10.1109/TCSII.2022.3218468
22.
ShenHYuFWangCSunJCaiS. Firing mechanism based on single memristive neuron and double memristive coupled neurons. Nonlinear Dyn (2022) 110:3807–22. 10.1007/s11071-022-07812-w
23.
TanFZhouLXiaJ. Adaptive quantitative exponential synchronization in multiplex Cohen-Grossberg neural networks under deception attacks. J Franklin Inst (2022) 359(18):10558–77. 10.1016/j.jfranklin.2022.09.020
24.
LinHWangCSunYWangT. Generating -scroll chaotic attractors from a memristor-based magnetized hopfield neural Network<i/>. IEEE Trans Circuits Systems--II: Express Briefs (2023) 70:311–5. 10.1109/TCSII.2022.3212394
25.
SepestanakiMABarhaghtalabMHMobayenSJalilvandAFekihASkruchP. Chattering-free terminal sliding mode control based on adaptive barrier function for chaotic systems with unknown uncertainties. J IEEE Access (2022) 10:103469–84. 10.1109/access.2022.3209993
26.
YanMSongJZuoLYangP. Neural adaptive sliding-mode control of a vehicle platoon using output feedback. J Energies (2017) 10(11):1906. 10.3390/en10111906
27.
ZhangCLiJ. Adaptive iterative learning control of non-uniform trajectory tracking for strict feedback nonlinear time-varying systems with unknown control direction. Appl Math Model (2015) 39:2942–50. 10.1016/j.apm.2014.10.070
28.
QiangHLinZZZouXGSunCLuW. Synchronizing non-identical time-varying delayed neural network systems via iterative learning control. C Neurocomputing (2020) 411:406–15. 10.1016/j.neucom.2020.05.053
29.
ChengCKChaoPCP. Chaos synchronization between Josephson junction and classical chaotic system via iterative learning control. In: 2018 IEEE International Conference on Applied System Invention (ICASI); April 2018; Chiba, Japan (2018). p. 1232–1235. 10.1109/ICASI.2018.8394512
30.
ZhuSSunM-XHeXX. Iterative learning control of strict-feedback nonlinear time-varying systems. J ACTA AUTOMATICA SINICA (2010) 36(3):454–8. 10.3724/sp.j.1004.2010.00454
31.
ZhangCLiJ. Hybrid function projective synchronization of chaotic systems with uncertain time-varying parameters via fourier series expansion. Int J Automation Comput (2012) 9(4):388–94. 10.1007/s11633-012-0659-8
Summary
Keywords
hybrid function projective synchronization, chaotic systems, adaptive iterative learning control, Fourier series expansion, finite time
Citation
Zhang C, Yan L, Gao Y, Wang W, Li K, Wang D and Zhang L (2023) A new adaptive iterative learning control of finite-time hybrid function projective synchronization for unknown time-varying chaotic systems. Front. Phys. 11:1127884. doi: 10.3389/fphy.2023.1127884
Received
20 December 2022
Accepted
06 January 2023
Published
30 January 2023
Volume
11 - 2023
Edited by
Fei Yu, Changsha University of Science and Technology, China
Reviewed by
Fei Tan, Xiangtan University, China
Ciyan Zheng, Guangdong Polytechnic Normal University, China
Updates
Copyright
© 2023 Zhang, Yan, Gao, Wang, Li, Wang and Zhang.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Chunli Zhang, gaozhangchunli@163.com
This article was submitted to Interdisciplinary Physics, a section of the journal Frontiers in Physics
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.