The shifted parity and delayed time-reversal symmetry-breaking solutions for the (1+1)-dimensional Alice–Bob Boussinesq equation

The integrable Alice–Bob system with the shifted parity and delayed time reversal is presented through the Lax pair for the (1 + 1)-dimensional Boussinesq equation. After introducing an extended Bäcklund transformation, this system shows abundant exact solutions with the auxiliary functions consisting of hyperbolic functions or rational functions. The corresponding soliton structures contain line solitons, breathers, and lumps, all which satisfied the shifted parity and delayed time-reversal symmetry for the states of Alice A and Bob B. In particular, some lower-order circumstances can be expressed through their explicit solutions and their dynamic structures.

1 Introduction

For one (1 + 1)-dimensional model, except for identity transformation, there are the shifted parity ${\widehat{P}}_s$ and delayed time-reversal ${\widehat{T}}_d$ transformations for the spatial variable x and time variable t, respectively. In other words,

$x^{\prime }=-x+x_0\equiv {\widehat{P}}_{s}x,t^{\prime }=-t+t_0\equiv {\widehat{T}}_{d}t,(1)$

with x₀ and t₀ being arbitrary constants [1, 2]. However, the Alice–Bob system, which can be successively used to describe two-place physical problems, may be entangled with each other through the following relation:

$B=\widehat{f}A=A^{\widehat{f}},(2)$

with the state of Alice A ≡ A(x, t) and the Bob’s state B ≡ B(x′, t′); $\widehat{f}$ is a suitable operator (such as ${\widehat{f}}^2=1$ or $\widehat{f}\in \mathrm{\Theta }\equiv \{1,{\widehat{P}}_s,{\widehat{T}}_d,{\widehat{P}}_s{\widehat{T}}_d\}$) [3–7]. Usually, this intrinsic Alice–Bob system is non-local since {x′, t′} is far away from {x, t}. However, for one Alice–Bob system, through the ${\widehat{P}}_s{\widehat{T}}_d$ transformation, there indeed exist some types of multiple soliton structures with symmetry-breaking solutions according to Lou’s research. In other words, by applying the operator ${\widehat{P}}_s{\widehat{T}}_d$ on one solution S, one can find ${\widehat{P}}_s{\widehat{T}}_{d}S\ne S$.

For an illustrated model, the (1 + 1)-dimensional Boussinesq equation has the following form:

$w_{tt}+w_{xx}-{\left(w^2\right)}_{xx}-\frac{1}{3}{w}_{\mathit{xxxx}}=0,(3)$

or

$w_{tt}=-w_{xx}+2w_x^2+2w{w}_{xx}+\frac{1}{3}{w}_{\mathit{xxxx}},(4)$

where $w_{tt}\equiv \frac{{\partial }^2}{\partial t^2}w,w_{ix}\equiv \frac{{\partial }^i}{\partial x^i}w$. Eq. 3 is an integrable equation as it has the following Lax pair:

${\psi }_{\mathit{xxx}}=\frac{3}{4}\left(\mathrm{I}\int w_t\mathrm{d}x-w_x\right)\psi +\left(\frac{3}{4}-\frac{3}{2}w\right){\psi }_x,(5)$

${\psi }_t=\frac{\mathrm{I}}{4}\left(4w-1\right)\psi +\mathrm{I}{\psi }_{xx},(6)$

and its adjoint version is as follows:

${\psi }_{\mathit{xxx}}=\frac{3}{4}\left(-\mathrm{I}\int w_t\mathrm{d}x-w_x\right)\psi +\left(\frac{3}{4}-\frac{3}{2}w\right){\psi }_x,(7)$

${\psi }_t=-\frac{\mathrm{I}}{4}\left(4w-1\right)\psi -\mathrm{I}{\psi }_{xx},(8)$

where I is an imaginary unit.

In non-linear science, this equation is one of the important prototypic models. It can be used to study the dynamics of thin inviscid layers with a free surface, the non-linear string, and the propagation of waves in elastic rods and in the continuum limit of lattice dynamics or coupled electrical circuits. Multiple complex soliton solutions through multiple exponential function schemes, interactions between solitons and cnoidal periodic waves using the truncated Painlevé expansion method, and soliton solutions by the extended Kudryashov’s approach can all be presented [8–10].

Except for the former works where the physical quantity $\frac{A+B}{2}$ is taken directly, we derive the Alice–Bob system of Eq. 3 through its Lax pair and the dark parameterization approach [11–13].

After adopting the $\widehat{f}={\widehat{P}}_{s}x{\widehat{T}}_{d}t$ symmetry principle through $B=\widehat{f}A=A^{\widehat{f}}$, the Boussinesq Eq. 3 can be induced into the following Alice–Bob system:

$A_{tt}={\left(AB-A+\frac{3}{2}{A}^2-\frac{1}{2}{B}^2\right)}_{xx}+\frac{1}{3}{A}_{\mathit{xxxx}},(9)$

$B_{tt}={\left(AB-B+\frac{3}{2}{B}^2-\frac{1}{2}{A}^2\right)}_{xx}+\frac{1}{3}{B}_{\mathit{xxxx}}.(10)$

The corresponding Lax pairs of Eqs 5, 6areas follows:

${\mathrm{\Psi }}_{\mathit{xxx}}=\frac{3}{4}\left(\mathrm{I}\int W_t\mathrm{d}x-W_x\right)\mathrm{\Psi }+\left(\frac{3}{4}E-\frac{3}{2}W\right){\mathrm{\Psi }}_x,(11)$

${\mathrm{\Psi }}_t=\frac{\mathrm{I}}{4}\left(4W-E\right)\mathrm{\Psi }+\mathrm{I}{\mathrm{\Psi }}_{xx},(12)$

with

$\mathrm{\Psi }=\left(\begin{array}{c}\hfill {\psi }_1\hfill \\ \hfill {\psi }_2\hfill \end{array}\right),W=\left(\begin{array}{cc}\hfill w\hfill & \hfill \sigma v\hfill \\ \hfill v\hfill & \hfill w\hfill \end{array}\right),E=\left(\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right),(13)$

and we can obtain the following coupled equations:

$w_{tt}+w_{xx}-{\left(w^2\right)}_{xx}-\frac{1}{3}{w}_{\mathit{xxxx}}=0,(14)$

$v_{tt}+v_{xx}-2{\left(wv\right)}_{xx}-\frac{1}{3}{v}_{\mathit{xxxx}}=0,(15)$

when σ = 0. After letting w = A+ B and v = A− B, the non-local systems (9) and (10) are a direct result from Eqs 14, 15.

Another method to derive the non-local systems (9) and (10) is the dark parameterization approach [14–17]. For the coupling Boussinesq system,

$w_{i,tt}=-w_{i,xx}+2\sum _{j=0}^i\left(w_{j,x}{w}_{i-j,x}+w_j{w}_{i-j,xx}\right)+\frac{1}{3}{w}_{i,xxxx},\left(i=\mathrm{0,1,2},\dots ,n\right).(16)$

w₀ is the usual solution of Eq. 3; when taking w = u + vα (α is a dark parameter) and n = 1, the coupled equations are as follows:

$u_{tt}+u_{xx}-{\left(u^2\right)}_{xx}-\frac{1}{3}{u}_{\mathit{xxxx}}=0,(17)$

and

$v_{tt}+v_{xx}-2{\left(uv\right)}_{xx}-\frac{1}{3}{v}_{\mathit{xxxx}}=0.(18)$

These equations can directly derive the non-local systems (9) and (10) through u = A+ B and v = A− B.

The rest of this paper is organized as follows: in Section 2, after introducing an extended Bäcklund transformation, the Hirota bilinear form is presented through an undetermined function f, which may contain some soliton solutions for the Alice–Bob systems (9) and (10) of the (1 + 1)-dimensional Boussinesq Eq. 3. Then, the hyperbolic function solution and the rational solution for this system are shown subsequently. In order to illustrate more clearly, three kinds of explicit solutions and their corresponding soliton structures are given for the lower-order circumstances. All of these results satisfy the symmetry of $B={\widehat{P}}_s{\widehat{T}}_{d}A$. A short summary is given in Section 3.

2 The symmetry-breaking solutions

We first introduce an extended Bäcklund transformation:

$A={\left[\ln \left(f\right)+b\ln {\left(f\right)}_x+c\ln {\left(f\right)}_t\right]}_{xx},B={\left[\ln \left(f\right)-b\ln {\left(f\right)}_x-c\ln {\left(f\right)}_t\right]}_{xx},(19)$

with b and c being two constants; f ≡ f (x, t) is an undetermined function and satisfies the following conditions:

$f=\widehat{f}f=f^{\widehat{f}}.(20)$

By substituting Eq. 19 into the non-local systems (9) and (10), we obtain the following bilinear form:

$\left(D_t^2+D_x^2-\frac{1}{3}{D}_x^4\right)\left(f\cdot f\right)=0,(21)$

where Hirota’s bilinear derivative operators $D_t^2,D_x^2$ and $D_x^4$ are written as [18, 19]

$D_x^m{D}_t^n\left(f\cdot g\right)={\left(\frac{\partial }{\partial x}-\frac{\partial }{\partial x^{\prime }}\right)}^m{\left(\frac{\partial }{\partial t}-\frac{\partial }{\partial t^{\prime }}\right)}^{n}f\left(x,t\right)\cdot g\left(x^{\prime },t^{\prime }\right){|}_{x^{\prime }=x,t^{\prime }=t}.(22)$

Eq. 21 also has the following explicit expression:

$f_{tt}=\frac{1}{3f}\left(3f_t^2+3f_x^2-3f{f}_{xx}+3f_{xx}^2-4f_x{f}_{\mathit{xxx}}+f{f}_{\mathit{xxxx}}\right).(23)$

2.1 The hyperbolic function solutions and their soliton structures

Through the bilinear form (21) or Eq. 23, the function f exists in the following form of the hyperbolic function for the Boussinesq Eq. 3 [4–6].

$f=f_N=\sum _{\left\{\nu \right\}}{K}_{\left\{\nu \right\}}\cosh \left(\sum _{i=1}^N{\nu }_i{\xi }_i\right),{\xi }_i=k_{i}x+{\omega }_{i}t,{\omega }_i=\frac{{\delta }_i{k}_i}{3}\sqrt{12k_i^2-9},{\delta }_i^2=1,(24)$

where {ν} = {ν_i = ±1} and k_i(i = 1, 2, ⋅⋅⋅, N) are arbitrary constants, and

$K_{\left\{\nu \right\}}=\prod _{i<j}^N{a}_{ij},a_{ij}=\sqrt{3{\delta }_i{\delta }_j\sqrt{\left(4k_i^2-3\right)\left(4k_j^2-3\right)}-24k_i^2-36{\nu }_i{\nu }_j{k}_i{k}_j-24k_j^2+9},(25)$

where (i, j = 1, 2, ⋅⋅⋅, N, i ≠ j).

When N = 1, Eq. 24 has the following simple form:

$f=\cosh \left({\xi }_1\right),{\xi }_1=k_{1}x+{\omega }_{1}t,{\omega }_1=\frac{{\delta }_1{k}_1}{3}\sqrt{12k_1^2-9},{\delta }_1^2=1.(26)$

After substituting this form into the Bäcklund transformation (19), the non-local solution of Eqs 9, 10 can be derived as follows:

$A=-2k_1^2\left[\left(b{k}_1+c{\omega }_1\right)\tanh \left({\xi }_1\right)-1\right]{\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}}^2\left({\xi }_1\right),(27)$

$B=2k_1^2\left[\left(b{k}_1+c{\omega }_1\right)\tanh \left({\xi }_1\right)+1\right]{\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}}^2\left({\xi }_1\right).(28)$

This single-soliton solution satisfies the condition of ${\widehat{P}}_s{\widehat{T}}_d$ symmetry $B=\widehat{f}A=A(-x,-t)$. By introducing Eq. 26, the Alice–Bob system is the coupling form of two solitary waves. The two solitary waves move along the X-axis at the speed $\frac{\sqrt{12k_1^2-9}}{3}$; the direction is determined by δ₁, and the amplitude and wave width are determined by k₁, b, and c, which is also confirmed by Eqs 27, 28. Figure 1 shows this structure when the related parameters are taken as follows:

$b=1,c=1,k_1=\frac{3}{2},{\delta }_1=1,{\omega }_1=1.(29)$

FIGURE 1

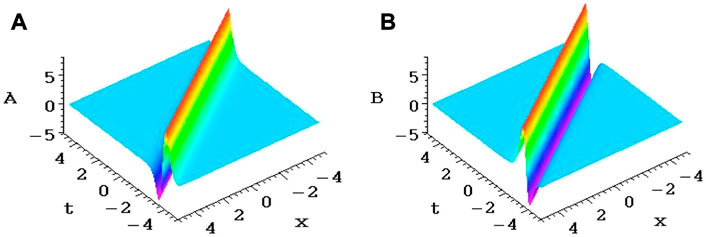
FIGURE 1. (A,B) are single soliton structures of Eqs 27, 28, respectively, when the parameters taken as Eq. 29.

When N = 2, Eq. 24 becomes as follows:

$f=K_{\left\{0\right\}}\cosh \left[\left(k_1+k_2\right)x+\left({\omega }_1+{\omega }_2\right)t\right]+K_{\left\{1\right\}}\cosh \left[\left(k_1-k_2\right)x+\left({\omega }_1-{\omega }_2\right)t\right],(30)$

with

$K_{\left\{0\right\}}=\sqrt{3{\delta }_1{\delta }_2\sqrt{\left(4k_1^2-3\right)\left(4k_2^2-3\right)}-24k_1^2+36k_1{k}_2-24k_2^2+9},(31)$

$K_{\left\{1\right\}}=\sqrt{3{\delta }_1{\delta }_2\sqrt{\left(4k_1^2-3\right)\left(4k_2^2-3\right)}-24k_1^2-36k_1{k}_2-24k_2^2+9}.(32)$

The corresponding two-soliton solution can be obtained by substituting Eq. 30 with Eqs 31, 32 into Eq. 19. From the perspective of algebra, it is natural to consider the simplification of the function of Eq. 30 by quantifying the double variables of the hyperbolic function into single variables, that is, k₁ = ±k₂, ω₁ = ±ω₂. These four cases may produce the corresponding soliton or breather solutions for the Alice–Bob system, respectively. Two typical cases are presented here for N = 2. Figure 2 presents this structure when the related parameters are taken through the real constants as follows:

$b=1,c=1,k_1=1,k_2=1,{\delta }_1=1,{\delta }_2=-1,{\omega }_1=\frac{\sqrt{3}}{3},{\omega }_2=-\frac{\sqrt{3}}{3}.(33)$

Therefore,

$K_{\left\{0\right\}}=\sqrt{6}\mathrm{I},K_{\left\{1\right\}}=\sqrt{78}\mathrm{I},f=\sqrt{6}\mathrm{I}\cosh \left(2x\right)+\sqrt{78}\mathrm{I}\cosh \left(\frac{2\sqrt{3}}{3}t\right).(34)$

FIGURE 2

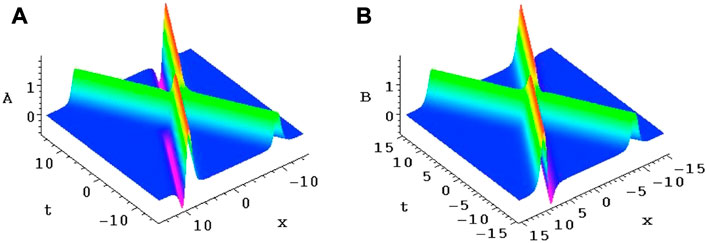
FIGURE 2. (A,B) are the two-soliton structures of the Alice-Bob systems (9) and (10), respectively through Eq. 19 after selecting the conditions are Eqs 33, 34.

It is not difficult to find that Eq. 34 is coupled by two hyperbolic functions similar to Eq. 26, and its image also shows this phenomenon.

On the other hand, by restricting the parameters k₁, k₂ to the assumed units on the two-soliton solution, the breather can be obtained. For example, by setting the following parameters

$b=1,c=1,k_1=\mathrm{I},k_2=\mathrm{I},{\delta }_1=1,{\delta }_2=-1,{\omega }_1=-\frac{\sqrt{21}}{3},{\omega }_2=\frac{\sqrt{21}}{3},(35)$

the following equation can be derived:

$K_{\left\{0\right\}}=\sqrt{42},K_{\left\{1\right\}}=\sqrt{114},f=\sqrt{42}\cos \left(2x\right)+\sqrt{114}\cosh \left(\frac{2\sqrt{21}}{3}t\right).(36)$

Here, the cosine part of Eq. 36 makes the Alice–Bob system periodic, and the corresponding breather structure is obtained, as shown in Figure 3.

FIGURE 3

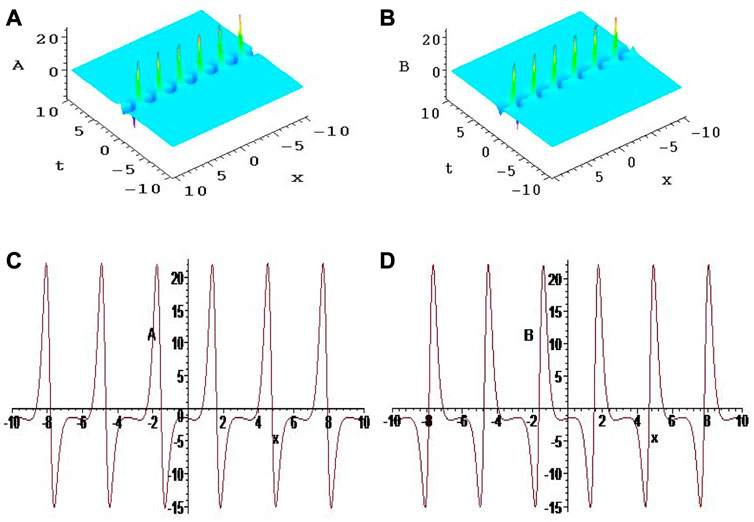
FIGURE 3. Breather structures of the Alice–Bob system (9) and (10) through Eq. 19 after selecting the conditions are Eqs 35, 36. (C,D) are the corresponding sectional plots of (A,B) at t =0, respectively.

When N = 3, Eq. 24 has the following more complicated situation:

$f=K_{\left\{0\right\}}\cosh \left({\xi }_1+{\xi }_2+{\xi }_3\right)+K_{\left\{1\right\}}\cosh \left({\xi }_1-{\xi }_2-{\xi }_3\right)+K_{\left\{2\right\}}\cosh \left({\xi }_1-{\xi }_2+{\xi }_3\right)+K_{\left\{3\right\}}\cosh \left({\xi }_1+{\xi }_2-{\xi }_3\right),(37)$

with

$K_{\left\{0\right\}}=3\sqrt{{\delta }_1{\delta }_2\sqrt{\left(4k_1^2-3\right)\left(4k_2^2-3\right)}-24k_1^2+36k_1{k}_2-24k_2^2+9},$

$\sqrt{\left[3{\delta }_1{\delta }_3\sqrt{\left(4k_1^2-3\right)\left(4k_3^2-3\right)}-24k_1^2+36k_1{k}_3-24k_3^2+9\right]\left[3{\delta }_2{\delta }_3\sqrt{\left(4k_2^2-3\right)\left(4k_3^2-3\right)}-24k_2^2+36k_2{k}_3-24k_3^2+9\right]},$

$K_{\left\{1\right\}}=3\sqrt{{\delta }_1{\delta }_2\sqrt{\left(4k_1^2-3\right)\left(4k_2^2-3\right)}-24k_1^2-36k_1{k}_2-24k_2^2+9}$

$\sqrt{\left[3{\delta }_1{\delta }_3\sqrt{\left(4k_1^2-3\right)\left(4k_3^2-3\right)}-24k_1^2-36k_1{k}_3-24k_3^2+9\right]\left[3{\delta }_2{\delta }_3\sqrt{\left(4k_2^2-3\right)\left(4k_3^2-3\right)}-24k_2^2+36k_2{k}_3-24k_3^2+9\right]},$

$K_{\left\{2\right\}}=3\sqrt{{\delta }_1{\delta }_2\sqrt{\left(4k_1^2-3\right)\left(4k_2^2-3\right)}-24k_1^2-36k_1{k}_2-24k_2^2+9},$

$\sqrt{\left[3{\delta }_1{\delta }_3\sqrt{\left(4k_1^2-3\right)\left(4k_3^2-3\right)}-24k_1^2+36k_1{k}_3-24k_3^2+9\right]\left[3{\delta }_2{\delta }_3\sqrt{\left(4k_2^2-3\right)\left(4k_3^2-3\right)}-24k_2^2-36k_2{k}_3-24k_3^2+9\right]},$

$K_{\left\{3\right\}}=3\sqrt{{\delta }_1{\delta }_2\sqrt{\left(4k_1^2-3\right)\left(4k_2^2-3\right)}-24k_1^2+36k_1{k}_2-24k_2^2+9},$

$\sqrt{\left[3{\delta }_1{\delta }_3\sqrt{\left(4k_1^2-3\right)\left(4k_3^2-3\right)}-24k_1^2-36k_1{k}_3-24k_3^2+9\right]\left[3{\delta }_2{\delta }_3\sqrt{\left(4k_2^2-3\right)\left(4k_3^2-3\right)}-24k_2^2-36k_2{k}_3-24k_3^2+9\right]},$

and

${\xi }_i=k_{i}x+{\omega }_{i}t,{\omega }_i=\frac{{\delta }_i{k}_i}{3}\sqrt{12k_i^2-9},{\delta }_i^2=1\left(i=\mathrm{1,2,3}\right).$

Based on the selecting parameters b, c, k₁, k₂, δ₁, and δ₂ of Eqs 33, 35, two kinds of interactions for the solitons can be constructed by considering the following equation:

$k_3=\frac{11}{10},{\delta }_3=1,{\omega }_3=\frac{11\sqrt{138}}{150},(38)$

and

$k_3=\frac{3}{2},{\delta }_3=1,{\omega }_3=\frac{3\sqrt{2}}{2}.(39)$

For this time, K_{i}(i = 0, 1, 2, 3) are expressed as follows:

$K_{\left\{0\right\}}=-\frac{9\sqrt{146}\text{I\hspace{0.17em}}}{25},K_{\left\{1\right\}}=-\frac{\sqrt{17296578-2316600\sqrt{46}}\mathrm{I}}{25},$

$K_{\left\{2\right\}}=-\frac{\sqrt{17296578+2316600\sqrt{46}\mathrm{I}}}{25},K_{\left\{3\right\}}=-\frac{63\sqrt{6594}\mathrm{I}}{25},(40)$

and

$K_{\left\{0\right\}}=3\left[\sqrt{21\left(-233+13\sqrt{697}\right)}-\sqrt{21\left(233+13\sqrt{697}\right)}\mathrm{I}\right],K_{\left\{1\right\}}=3\sqrt{114\left(415-36\sqrt{42}\right)},$

$K_{\left\{2\right\}}=3\sqrt{114\left(415+36\sqrt{42}\right)},K_{\left\{3\right\}}=3\left[\sqrt{21\left(-233+13\sqrt{697}\right)}+\sqrt{21\left(233+13\sqrt{697}\right)}\mathrm{I}\right].(41)$

The corresponding functions of Eq. 37 are expressed as follows:

$f=K_{\left\{0\right\}}\cosh \left(\frac{31}{10}x+\frac{11\sqrt{138}}{150}t\right)+K_{\left\{1\right\}}\cosh \left[-\frac{11}{10}x+\left(\frac{2\sqrt{3}}{3}-\frac{11\sqrt{138}}{150}\right)t\right]$

$+K_{\left\{2\right\}}\cosh \left[\frac{11}{10}x+\left(\frac{2\sqrt{3}}{3}+\frac{11\sqrt{138}}{150}\right)t\right]-K_{\left\{3\right\}}\cosh \left(-\frac{9}{10}x+\frac{11\sqrt{138}}{150}t\right),(42)$

and

$f=6\left[\sqrt{21\left(233+13\sqrt{697}\right)}\sin \left(2x\right)\sinh \left(\frac{3}{2}x+\frac{3\sqrt{2}}{2}t\right)+6\sqrt{21\left(-233+13\sqrt{697}\right)}\cos \left(2x\right)\cosh \left(\frac{3}{2}x+\frac{3\sqrt{2}}{2}t\right)\right.$

$+3\sqrt{114\left(415+36\sqrt{42}\right)}\cosh \left[\frac{3}{2}x+\left(\frac{3\sqrt{2}}{2}-\frac{2\sqrt{21}}{3}\right)t\right]+3\sqrt{114\left(415-36\sqrt{42}\right)}\cosh \left[\frac{3}{2}x+\left(\frac{3\sqrt{2}}{2}-\frac{2\sqrt{21}}{3}\right)t\right].(43)$

Figure 4 and Figure 5 show two interaction structures of the Alice–Bob systems (9) and (10) through Eqs 42, 43.

FIGURE 4

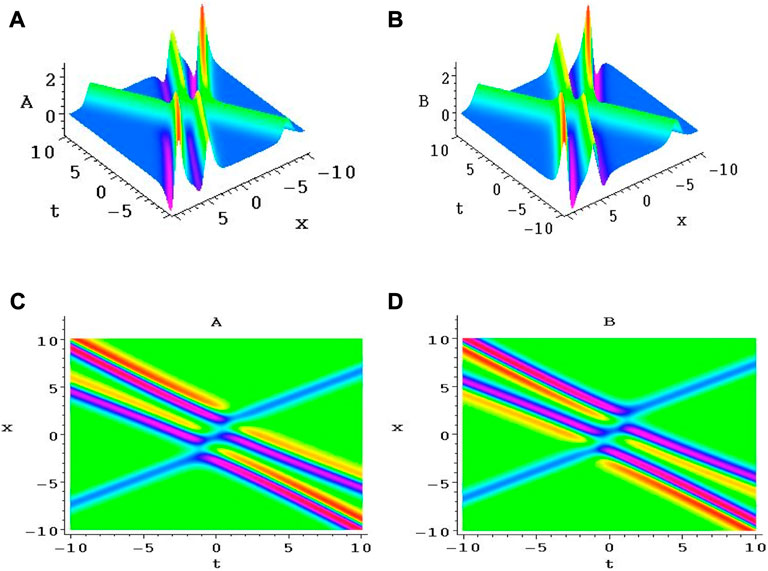
FIGURE 4. (A,B) are the interaction structures of three solitons for the Alice–Bob systems (9) and (10) through Eq. 42. (C,D) are the corresponding density plots of (A,B), respectively.

FIGURE 5

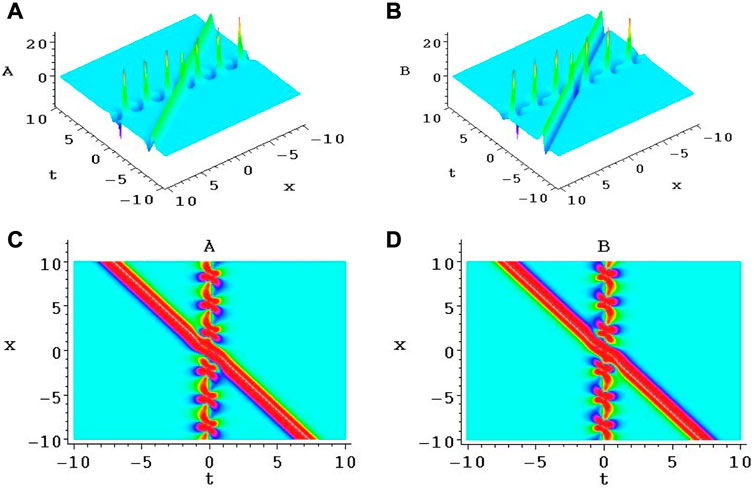
FIGURE 5. (A,B) are the interaction structures between the breather and one-soliton structures for the Alice–Bob systems (9) and (10) through Eq. 43. (C,D) are the corresponding density plots of (A,B), respectively.

2.2 The rational solutions and lump structures

The Alice–Bob systems (9) and (10) have a series of rational solutions and hence contain the corresponding lump structures. For this purpose, we introduce the following polynomial function:

$f=f_N=\sum _{m=0}^{\frac{1}{2}N\left(N+1\right)}\left[\sum _{j=0}^m{a}_{j,m}{x}^{2\left(m-j\right)}{t}^{2j}\right],(44)$

where $a_{j,m}(j=\mathrm{0,1,2},\dots ,m,m=\mathrm{0,1,2},\dots ,\frac{1}{2}N(N+1),N=\mathrm{1,2},\cdots )$ are constants determined by the powers of the variables x and t [20, 21].

When N = 1, Eq. 44 has the following simple form:

$f=a_{\mathrm{0,0}}+a_{\mathrm{0,1}}{x}^2+a_{\mathrm{1,1}}{t}^2.(45)$

When

$b=c=a_{\mathrm{0,0}}=a_{\mathrm{0,1}}=a_{\mathrm{1,1}}=1,(46)$

the lump solution of the Alice–Bob systems (9) and (10) has the following rational form:

$A=\frac{2\left(1-6x-2t+2t^2+2x^3+6x^{2}t-6x{t}^2-2t^3-x^4+t^4\right)}{{\left(1+x^2+t^2\right)}^3},(47)$

$B=\frac{2\left(1+6x+2t+2t^2-2x^3-6x^{2}t+6x{t}^2+2t^3-x^4+t^4\right)}{{\left(1+x^2+t^2\right)}^3},(48)$

which is obtained through the Bäcklund transformation (19) (Figure 6).

FIGURE 6

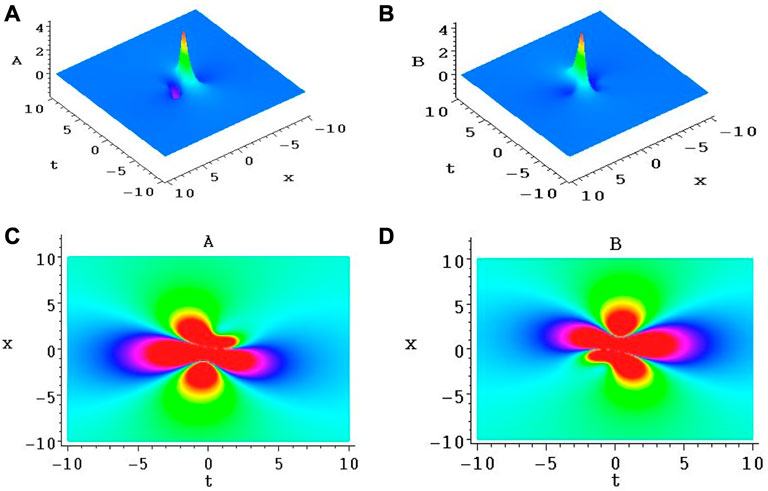
FIGURE 6. (A,B) are two lump structures of A and B from Eqs 47, 48. (C,D) are the corresponding density plots of (A,B), respectively.

When N = 2, Eq. 44 has the following function form:

$f=a_{\mathrm{0,0}}+a_{\mathrm{0,1}}{x}^2+a_{\mathrm{0,2}}{x}^4+a_{\mathrm{0,3}}{x}^6+a_{\mathrm{1,1}}{t}^2+a_{\mathrm{1,2}}{x}^2{t}^2+a_{\mathrm{1,3}}{x}^4{t}^2+a_{\mathrm{2,2}}{t}^4+a_{\mathrm{2,3}}{x}^2{t}^4+a_{\mathrm{3,3}}{t}^6.(49)$

A pair of lumps of A and B for the Alice–Bob systems (9) and (10) can be shown after the constants are taken as b = c = a_0,0 = 1, just as Eq. 46, while

$a_{\mathrm{0,1}}=-\frac{1}{5},a_{\mathrm{0,2}}=\frac{3}{25},a_{\mathrm{0,3}}=\frac{9}{625},a_{\mathrm{1,1}}=-\frac{19}{25},a_{\mathrm{1,2}}=\frac{54}{125},a_{\mathrm{1,3}}=\frac{27}{625},$

$a_{\mathrm{2,2}}=\frac{57}{625},a_{\mathrm{2,3}}=\frac{27}{625},a_{\mathrm{3,3}}=\frac{9}{625}.(50)$

These two pairs of lumps for the Alice–Bob systems (9) and (10) through Eq. 19, Eq. 49, and Eq. 50 are shown in Figure 7.

FIGURE 7

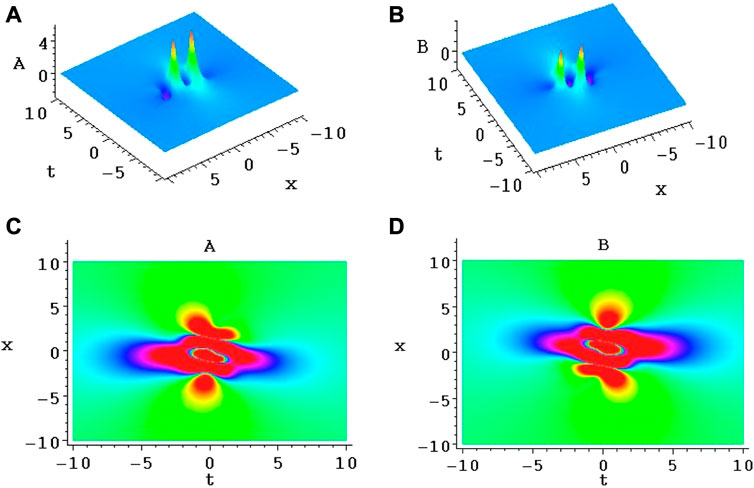
FIGURE 7. (A,B) are two pairs of lumps for the Alice–Bob systems (9) and (10) through Eqs 19, 49, 50. (C,D) are the corresponding density plots of (A,B), respectively.

When N = 3, Eq. 44 has the more complicated function form:

$f=a_{\mathrm{0,0}}+a_{\mathrm{0,1}}{x}^2+a_{\mathrm{0,2}}{x}^4+a_{\mathrm{0,3}}{x}^6+a_{\mathrm{0,4}}{x}^8+a_{\mathrm{0,5}}{x}^{10}+a_{\mathrm{0,6}}{x}^{12}+a_{\mathrm{1,1}}{t}^2+a_{\mathrm{1,2}}{x}^2{t}^2+a_{\mathrm{1,3}}{x}^4{t}^2+a_{\mathrm{1,4}}{x}^6{t}^2+a_{\mathrm{1,5}}{x}^8{t}^2+a_{\mathrm{1,6}}{x}^{10}{t}^2+a_{\mathrm{2,2}}{t}^4+a_{\mathrm{2,3}}{x}^2{t}^4+a_{\mathrm{2,4}}{x}^4{t}^4+a_{\mathrm{2,5}}{x}^6{t}^4+a_{\mathrm{2,6}}{x}^8{t}^4+a_{\mathrm{3,3}}{t}^6+a_{\mathrm{3,4}}{x}^2{t}^6+a_{\mathrm{3,5}}{x}^4{t}^6+a_{\mathrm{3,6}}{x}^6{t}^6+a_{\mathrm{4,4}}{t}^8+a_{\mathrm{4,5}}{x}^2{t}^8+a_{\mathrm{4,6}}{x}^4{t}^8+a_{\mathrm{5,5}}{t}^{10}+a_{\mathrm{5,6}}{x}^2{t}^{10}+a_{\mathrm{6,6}}{t}^{12}.(51)$

The lumps of A and B for the Alice–Bob systems (9) and (10) can also be constructed after the constants b = c = a_0,0 = 1; therefore, the following equations are obtained:

$a_{\mathrm{0,1}}=\frac{18}{11},a_{\mathrm{0,2}}=\frac{135}{847},a_{\mathrm{0,3}}=\frac{324}{46585},a_{\mathrm{0,4}}=\frac{2187}{3587045},a_{\mathrm{0,5}}=\frac{4374}{17935225},a_{\mathrm{0,6}}=\frac{6561}{878826025},$

$a_{\mathrm{1,1}}=-\frac{2610}{847},a_{\mathrm{1,2}}=\frac{486}{9317},a_{\mathrm{1,3}}=\frac{43740}{717409},a_{\mathrm{1,4}}=\frac{55404}{3587045},a_{\mathrm{1,5}}=\frac{301806}{175765205},a_{\mathrm{1,6}}=\frac{39366}{878826025},$

$a_{\mathrm{2,2}}=\frac{361287}{717409},a_{\mathrm{2,3}}=-\frac{2916}{717409},a_{\mathrm{2,4}}=\frac{156006}{5021863},a_{\mathrm{2,5}}=\frac{8748}{2282665},a_{\mathrm{2,6}}=\frac{19683}{175765205},$

$a_{\mathrm{3,3}}=\frac{1849068}{25109315},a_{\mathrm{3,4}}=\frac{67068}{2282665},a_{\mathrm{3,5}}=\frac{638604}{175765205},a_{\mathrm{3,6}}=\frac{26244}{175765205},$

$a_{\mathrm{4,4}}=\frac{632043}{175765205},a_{\mathrm{4,5}}=\frac{249318}{175765205},a_{\mathrm{4,6}}=\frac{19683}{175765205},$

$a_{\mathrm{5,5}}=\frac{126846}{878826025},a_{\mathrm{5,6}}=\frac{39366}{878826025},a_{\mathrm{6,6}}=\frac{6561}{878826025}.(52)$

These lump structures of the Alice–Bob systems (9) and (10) obtained through Eqs 19, 51, and 52 are shown in Figure 8.

FIGURE 8

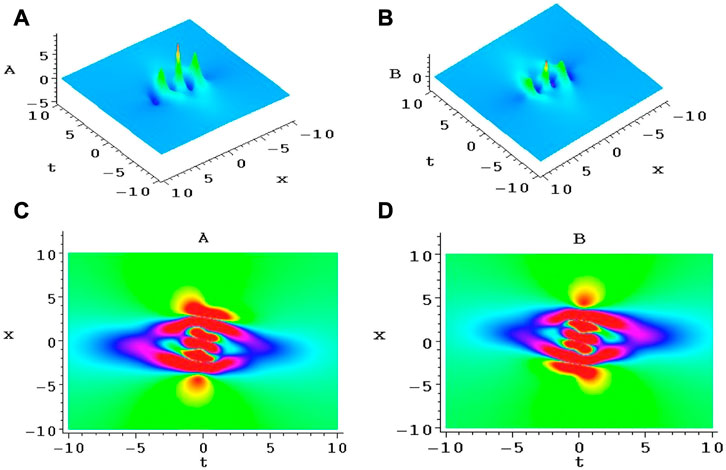
FIGURE 8. (A,B) are lump structures of A and B from Eqs 9, 10 through Eqs 19, 51, and 52. (C,D) are the corresponding density plots of (A,B), respectively.

3 Summary

In this paper, according to the (1 + 1)-dimensional Boussinesq Eq. 3, the Alice–Bob systems (9) and (10) for this equation are first derived through the Lax pair and the dark parameterization approach. This non-local system owns the bilinear form and may exist in the explicit solution. Therefore, the N-soliton solutions of the Alice–Bob systems (9) and (10) are presented with the aid of an undetermined function f after introducing an extended Bäcklund transformation. Typically, the auxiliary function can be taken as the hyperbolic function or rational function. These two kinds of functions induce the system having solutions that satisfy $B={\widehat{P}}_s{\widehat{T}}_{d}A$. The lower-order circumstances for N = 1, 2, 3 are presented through their auxiliary functions, and the symmetry-breaking solutions can be constructed. With the special parameters, the antisymmetric local structures are depicted, which contain line solitons, breathers, and lumps. Whether the induced Alice–Bob systems (9) and (10) of the (1 + 1)-dimensional Boussinesq Eq. 3 or the derived results through the hyperbolic and rational functions satisfy the symmetry of $B={\widehat{P}}_s{\widehat{T}}_{d}A$ is first shown here for our understanding. We believe that this approach is important to solve the Alice–Bob system for one integrable equation, which may possess rich local structures.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

PD: writing—original draft and software. Z-YM: supervision and funding acquisition. J-XF: conceptualization and software. W-PC: formal analysis and investigation.

Funding

This work was supported by the National Natural Science Foundation of China (11775104) and the Zhejiang Province Natural Science Foundation of China (2022SJGYZC01).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Bender CM, Boettcher S. Real spectra in non-hermitian Hamiltonians HavingPTSymmetry. Phys Rev Lett (1998) 80:5243–6. doi:10.1103/physrevlett.80.5243

CrossRef Full Text | Google Scholar

2. Ablowitz MJ, Musslimani ZH. Integrable nonlocal nonlinear Schrödinger equation. Phys Rev Lett (2013) 110:064105–5. doi:10.1103/physrevlett.110.064105

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Lou SY. Alice-Bob systems, $\widehat{P}-\widehat{\mathit{T}}-\widehat{C}$ symmetry invariant and symmetry breaking soliton solutions. J Math Phys 2018;59:083507–20. doi:10.1063/1.5051989

CrossRef Full Text | Google Scholar

4. Lou SY. Prohibitions caused by nonlocality for nonlocal Boussinesq-KdV type systems. Stud Appl Math (2019) 142:1–16. doi:10.1111/sapm.12265

CrossRef Full Text | Google Scholar

5. Li H, Lou SY. Multiple soliton solutions of Alice-Bob Boussinesq equations. Chin Phys Lett (2019) 36:050501–5. doi:10.1088/0256-307x/36/5/050501

CrossRef Full Text | Google Scholar

6. Zhao QL, Lou SY, Jia M. Solitons and soliton molecules in two nonlocal Alice-Bob Sawada-Kotera systems. Commun Theor Phys (2020) 72:085005–7. doi:10.1088/1572-9494/ab8a0e

CrossRef Full Text | Google Scholar

7. Jia M, Lou SY. Exact P_sT_d invariant and P_sT_d symmetric breaking solutions, symmetry reductions and Bäcklund transformations for an AB-KdV system. Phys Lett A (2018) 382:1157–66. doi:10.1016/j.physleta.2018.02.036

CrossRef Full Text | Google Scholar

8. Wazwaz AM. Multiple soliton solutions and multiple complex soliton solutions for two distinct Boussinesq equations. Nonlinear Dyn (2016) 85:731–7. doi:10.1007/s11071-016-2718-0

CrossRef Full Text | Google Scholar

9. Yang D, Lou SY, Yu WF. Interactions between solitons and cnoidal periodic waves of the Boussinesq equation. Commun Theor Phys (2013) 60:387–90. doi:10.1088/0253-6102/60/4/01

CrossRef Full Text | Google Scholar

10. Adem AR, Yildirim Y, Yasar E. Soliton solutions to the non-local Boussinesq equation by multiple exp-function scheme and extended Kudryashov’s approach. Pramana-j Phys (2019) 92:24–11. doi:10.1007/s12043-018-1679-x

CrossRef Full Text | Google Scholar

11. Fei JX, Ma ZY, Cao WP. Controllable symmetry breaking solutions for a nonlocal Boussinesq system. Sci Rep-uk (2019) 9:19667–14. doi:10.1038/s41598-019-56093-8

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Cao WP, Fei JX, Li JY. Symmetry breaking solutions to nonlocal Alice-Bob Kadomtsev-Petviashivili system. Chaos Soliton Fract (2021) 144:110653–8. doi:10.1016/j.chaos.2021.110653

CrossRef Full Text | Google Scholar

13. Wu WB, Lou SY. Exact solutions of an Alice-Bob KP equation. Commun Theor Phys (2019) 71:629–32. doi:10.1088/0253-6102/71/6/629

CrossRef Full Text | Google Scholar

14. Lou SY. Dark parameterizations, equivalent partner fields and integrable systems. Commun Theor Phys (2011) 55:743–6. doi:10.1088/0253-6102/55/5/02

CrossRef Full Text | Google Scholar

15. Peng L, Yang XD, Lou SY. Integrable KP coupling and its exact solution. Commun Theor Phys (2012) 58:1–4. doi:10.1088/0253-6102/58/1/01

CrossRef Full Text | Google Scholar

16. Cao WP, Fei JX, Ma ZY, Liu Q. Bosonization and new interaction solutions for the coupled Korteweg-de Vries system. Wave Random Complex (2020) 30:130–41. doi:10.1080/17455030.2018.1489565

CrossRef Full Text | Google Scholar

17. Fei JX, Cao WP, Ma ZY. Dark parameterization approach to the Benjamin Ono equation. Int J Mod Phys B (2020) 34:2050247–8. doi:10.1142/s0217979220502471

CrossRef Full Text | Google Scholar

18. Hirota R. Exact solution of the Korteweg-de Vries equation for multiple collisions of solitons. Phys Rev Lett (1971) 27:1192–4. doi:10.1103/physrevlett.27.1192

CrossRef Full Text | Google Scholar

19. Hirota R. The direct method in soliton theory. Cambridge: Cambridge University Press (2004).

Google Scholar

20. Clarkson PA, Dowie E. Rational solutions of the Boussinesq equation and applications to rogue waves. Trans Math Appl (2017) 1:1–26. doi:10.1093/imatrm/tnx003

CrossRef Full Text | Google Scholar

21. Ma YL, Li BQ. Analytic rogue wave solutions for a generalized fourth-order Boussinesq equation in fluid mechanics. Math Meth Appl Sci (2019) 42:39–48. doi:10.1002/mma.5320

CrossRef Full Text | Google Scholar