- 1Key Laboratory of Atomic and Molecular Physics and Functional Materials of Gansu Province, College of Physics and Electronic Engineering, Northwest Normal University, Lanzhou, China
- 2School of Mathematics and Physics, Lanzhou Jiaotong University, Lanzhou, China
Terahertz generation from atoms driven by two color linearly polarized (LP) and circularly polarized (CP) laser fields have been well investigated. In this work, based on the photocurrent model, we investigate theoretically the intensity and polarization characteristics of terahertz waves radiated by the bi-elliptical polarized two-color laser fields with orthogonal or parallel major axes. We show that polarization-controlled, including circularly polarized terahertz waves with sufficient intensity comparable to that of co-rotating CP or parallel LP laser field, can be generated by using a longer-wavelength few-cycle bi-elliptical field. Our simulations also show that THz energy and ellipticity can be dramatically improved with dual-color elliptical field with tiny or large ellipticity, compared with that with two-color orthogonal LP field and counter-rotating CP laser field, respectively. Bi-elliptical polarized laser field provides a huge parameter space allowing for far-reaching control of THz emission.
1 Introduction
Due to its unique performance, such as high coherence, high intensity, broadband and high orientation, terahertz (THz) wave has brought profound influence to the fields of communications, electronic countermeasures, electromagnetic weapons, radar, astronomy, medical imaging, and so on [1–7]. At present, there are many ways to generate THz radiation, such as free electron lasers [8], vacuum electronics THz sources [9], THz quantum cascade lasers [10], and ultrafast laser pumped photoconductance THz sources [11]. With the development of ultra-short and ultra-strong laser pulse technology, the interaction of intense femtosecond laser with gas target has also become an important way to generate high power, broad THz radiation [12, 13]. How to obtain THz sources with higher strength and controllable polarization is still a challenge of the current THz research.
In the scheme of interaction of intense laser field with gases, the commonly used driving field is a combination of a fundamental linearly polarized pulse and its second harmonic [14, 15], for the linearly polarized THz generation. In order to enhance the THz radiation intensity, the duration of the pump pulse [16, 17], phase delay [14, 15, 18, 19] and intensity ratio between two pulses [20, 21], should be carefully optimized. With these efforts, the THz pulse energy can be increased by at least one order of magnitude. Besides, adjusting the frequency ratio between two components [22, 23], and increasing the number of combing pulses [24, 25], can also increase THz yield. The polarization of pump laser also influences the generated THz pulse energy [26–28]. The recent experimental results of Meng et al. [26] and Tu et al. [28] show that the THz power produced by two-color circularly polarized with the same helicity (CP-S) laser fields is about 5 times (from a thin get) or 8 times (from an air filament) higher than that produced by parallel linearly polarized (LP-P) laser fields. In contrast, the THz radiation from two-color CP-C (circularly polarized pulses with counter helicity) laser fields, which has a much weaker THz yield, is on par with the THz power provided by the orthogonal linearly polarized fields (LP-O).
In some THz applications, effective control of their polarization states is a prerequisite. For example, in materials science, the polarization direction of THz waves plays a key role in optical excitation [29], spectral diagnosis [30, 31], and THz information technology [32, 33]. At the same time, the ellipticity of THz wave is an important parameter in birefringent material imaging [34], and its chirality is very important for the study of chiral rotation of organic molecules and spin dynamics in solid materials [35, 36]. Therefore, it has been an important subject to achieve flexible control of the polarization state of THz pulses over wide band. To this end, many driving laser schemes have been proposed to generate elliptically or circularly polarized THz radiation, such as monochromatic circularly polarized laser pulses [37], combination of circularly polarized and linearly polarized beams [38, 39], and so on. For the attractive CP-S field, the generated THz radiation is always linearly polarized when pulse duration is relatively long, namely, exceeding tens of femtoseconds for 800-nm wavelength. One of our recent works show that CP-S laser pulses can generate elliptically and circularly polarized THz radiations by increasing the wavelength [40].
Compared with linearly and circularly polarized driving fields, the investigation on the THz generation by two-color elliptically polarized driving field are still scarce [27, 41–44], which draws our interest in this work. We focus on whether the strong and polarization-controllable THz waves can be generated with this kind of pump field. In addition, we are curious about how THz radiation changes when a tiny ellipticity is introduced into a LP-O or CP-C laser field. We find that when taking different laser ellipticity, the THz energy generated is comparable with those produced by LP-P or CP-S fields. More importantly, THz radiation with high ellipticity or even circularly polarized can be obtained with longer-wavelength co-rotating bi-elliptical laser fields. Laser ellipticity, intensity ratio and phase difference together constitute a larger parameter space for THz polarization control, compared with other driving field. When an imperfect LP-O or CP-C field is considered, some counterintuitive results are obtained. These results can be partly understood in terms of the generated electric current.
2 Theoretical method
The simulations in this paper are based on the photocurrent model [14, 15]. When the laser pulse interacts with the gas, the electrons in the gas atoms undergo tunneling ionization. The produced free electrons are accelerated by the laser fields. Assuming that the initial density of gas is
The tunneling ionization rate
Then the electron accelerates under laser field to form the transverse current
where e is the electron charge and
Finally, time-dependent photocurrent
where
3 Results and discussion
The two-color
where
3.1 Co-rotating BEOTC and BEPTC fields
3.1.1 800 nm + 400 nm
First, we make a comparison of THz strength radiated by co-rotating BEOTC driving lasers with various ellipticity from 0.1 to 0.9. Figure 1A shows the dependence of THz yields (0.1–10 THz) generated by laser fields with different ellipticity interacting with Ar atoms on relative phase
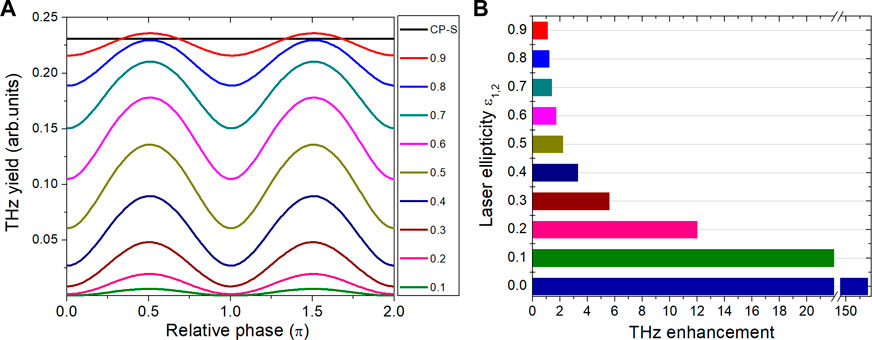
FIGURE 1. Dependence of THz radiation strength on the ellipticity and phase
Simulation results show that the ionization level at the end of BEOTC laser pulse increases with the increasing of laser ellipticity, and depends weakly on the relative phase. For
Take
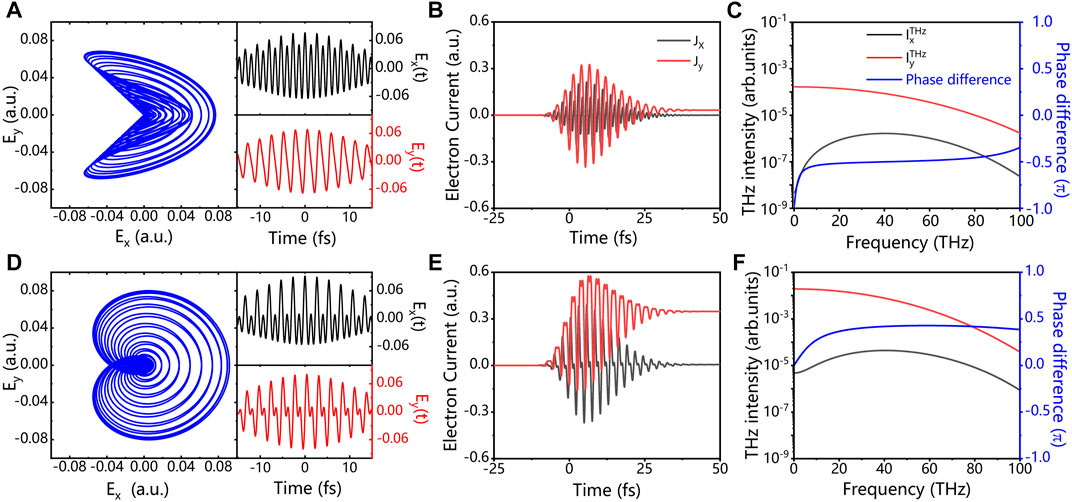
FIGURE 2. Comparisons between
When the two major axes of 800-nm and 400-nm elliptical fields are parallel, different THz energy dependence on the laser ellipticity and relative laser phase is observed, which is shown in Figure 3. At
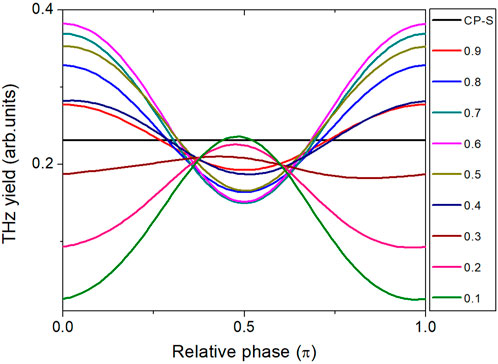
FIGURE 3. The same as Figure 1A, but for co-rotating BEPTC laser field.
Figure 4 compares the electric field of BEPTC fields with phase
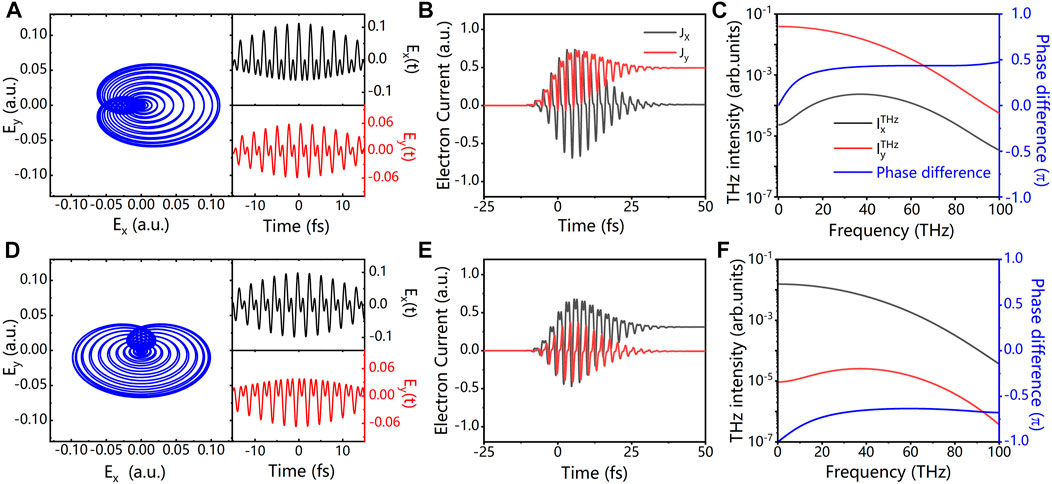
FIGURE 4. Comparisons of the waveforms of BEPTC laser field (left column) with ellipticity of 0.6, and generated electric currents (middle column), THz radiation (right column) for
From the THz spectra shown in Figures 2, 4, we can learn that THz radiation in the whole frequency range should be nearly lineally polarized, due to the huge strength difference in two orthogonal directions. To get the THz polarization information generated by bi-elliptical laser field more intuitively, Figure 5A shows the 30 THz electric field waveform changes with more relative phase
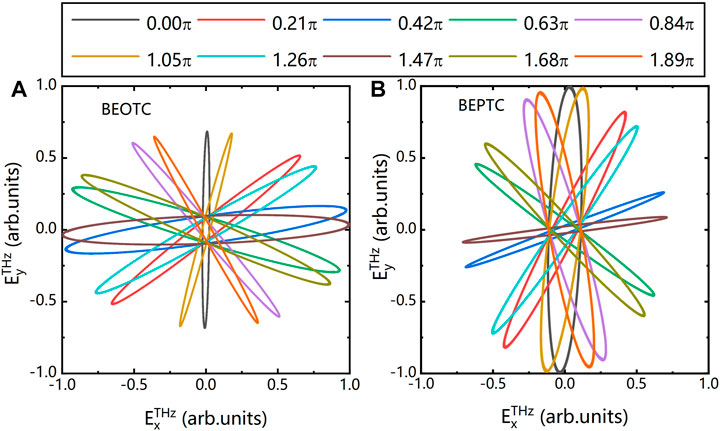
FIGURE 5. Dependence of 30-THz radiation field on the phase
3.1.2 1600 nm + 3200 nm
To further improve THz ellipticity generated by co-rotating bi-elliptical field, we increase the wavelength
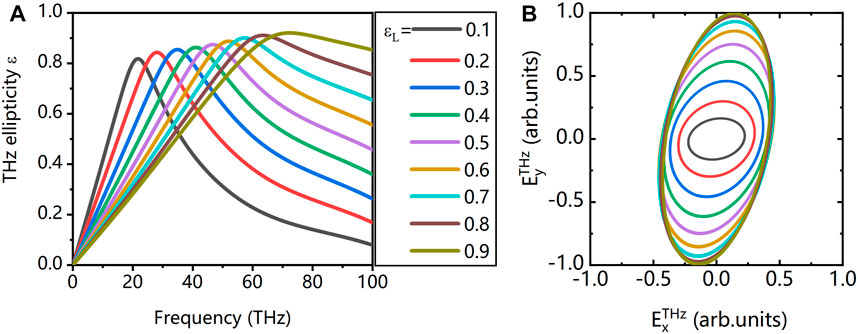
FIGURE 6. (A) The ellipticity of THz waves generated by 20-fs 1600 nm + 3200 nm co-rotating BEOTC laser fields varies with laser ellipticity. (B) 30-THz THz wave electric field.
Such control over THz polarization can also be achieved when the two major polarization axes of the bi-elliptical laser fields are parallel. Take
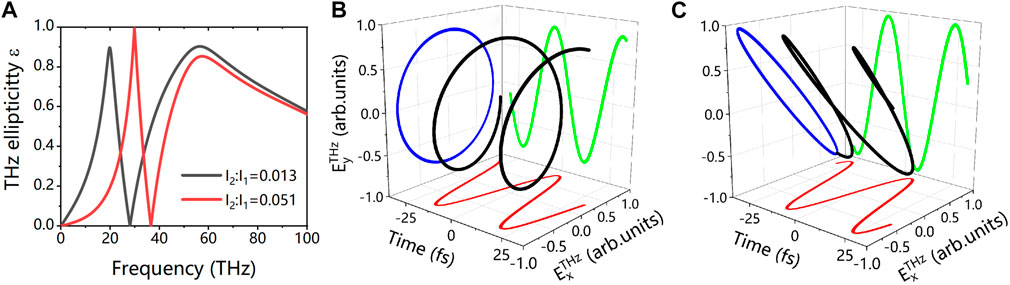
FIGURE 7. THz polarization characteristics radiated by 20 fs, 1600 nm + 3200 nm BEPTC laser fields. (A) THz ellipticity varies with the THz frequency for two laser intensity ratios of 0.013 and 0.051 at
3.2 Influence of the small fluctuation of ellipticity of LP-O and CP-C fields on the THz radiation
3.2.1 Non-perfect LP-O field
It is depressing that the THz intensity generated by LP-O field is very low, and these radiations can only be lineally polarized. In surprise, we find that a co-rotating BEOTC laser with a very small ellipticity (<0.1), i.e., an imperfect LP-O field, can improve the performance. In Figure 8A, we give the 30-THz THz electric field waveforms for bicolor laser fields with
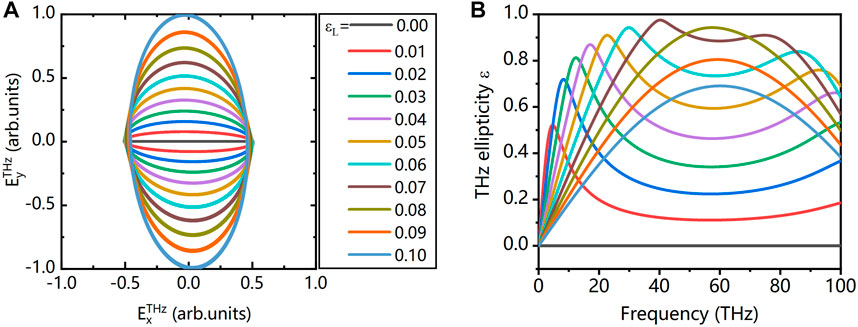
FIGURE 8. (A) Electric field evolution of 30-THz THz waves generated by BEOTC fields with laser ellipticities of
Such sensitivity of THz polarization and intensity on the small fluctuation of ellipticity of driving laser is incomprehensible. However, we note that similar phenomenon has also been observed in other strong field process, namely, the generation of high order harmonics [48, 49]. In Milošević et al simulations, they observe a dramatic dependence of harmonic ellipticity on the ellipticity of BEOTC field even in a level of one part in one thousand. The explanation behind these phenomena is difficult. Here, we give a qualitative analysis from the view of residual current. In Figure 9 we show the laser waveforms with the ellipticity
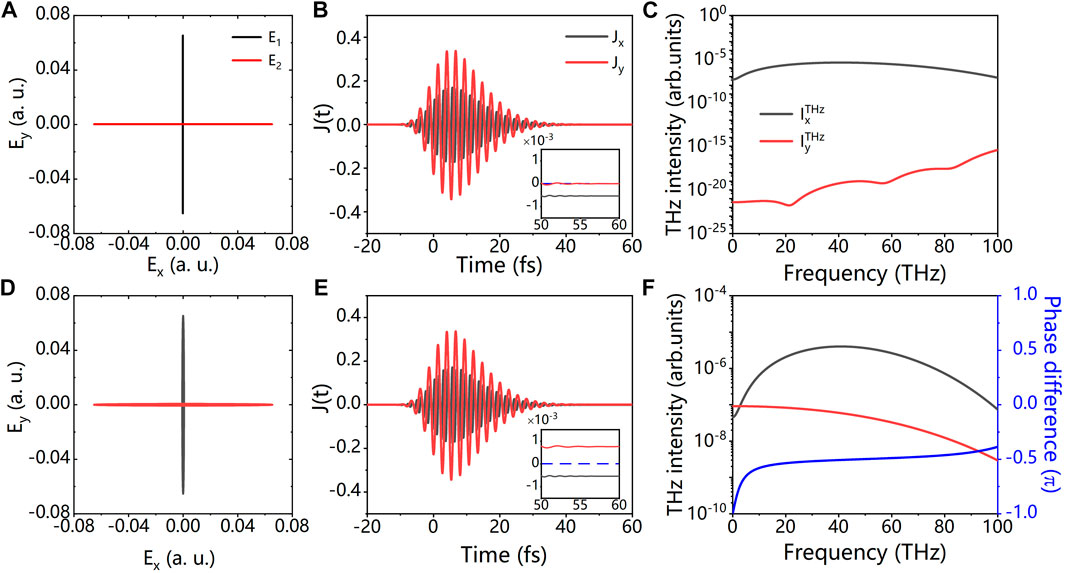
FIGURE 9. Waveforms of laser fields (left column), the electric currents (middle column, where the inset shows an enlarged view of the residual current), and generated THz radiation (right column) for LP-O (upper row) and BEOTC laser fields with
3.2.2 Counter-rotating bi-elliptical polarized laser fields with high ellipticity—imperfect CP-C field
For a CP-C driving laser field, it can produce high-ellipticity THz waves, but the intensity of the THz emission is very weak. Tailliez et al [44] has showed that a very small departure from an ideal CP-C configuration, that is, a BEOTC field with high ellipticity may lead to a substantial increase in the THz energy. Here, we give a similar demonstration with BEPTC field. We find that such a small deviation could lead to recovering THz performances comparable with those reached with a LP-P or CP-S field. Figure 10 compares the laser field waveforms, electric currents, and radiated THz spectra of the CP-C and the counter-rotating 800 nm + 400 nm BEPTC laser field with ellipticity
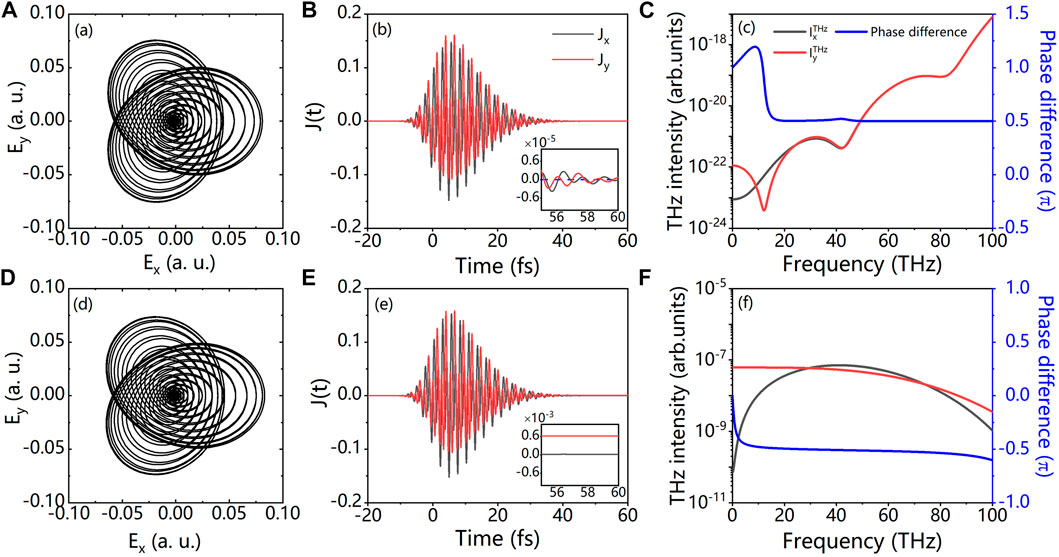
FIGURE 10. Waveforms of laser fields (left column), the electric currents (middle column), and generated THz radiation (right column) for CP-C field (upper row) and counter-rotating BEPTC field with
For the polarization state, Figure 10C indicates that THz radiations above 20 THz are nearly circularly polarized for the CP-C field, while they are elliptically polarized with high ellipticity at most frequencies with elliptical field [Figure 10F]. In Figure 11, we further show that we can control the THz polarization by adjusting the intensity ratio of a counter-rotating bi-elliptical field. Obviously, elliptical and circular THz field can be generated with the optimization.
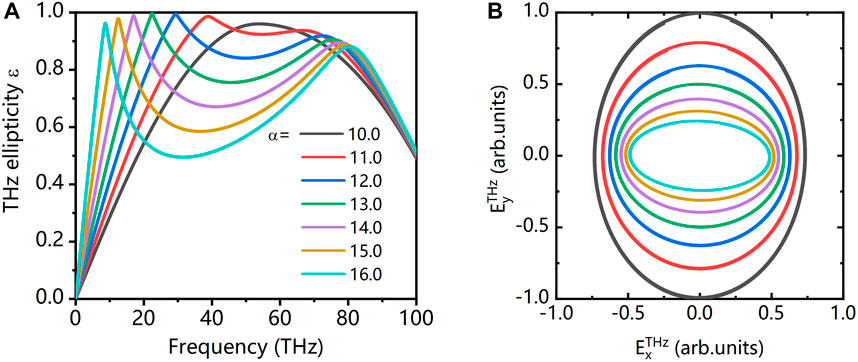
FIGURE 11. (A) The ellipticity of THz waves varies with the intensity ratio
4 Conclusion
In conclusion, we have shown that the bi-elliptical
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This work was supported by the National Natural Science Foundation of China (Nos. 12164044 and 11864037) and the Industrial Support and Guidance Project of Universities in Gansu Province, China (No. 2022CYZC-06).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Clough B, Dai J, Zhang X-C. Laser air photonics: Beyond the terahertz gap. Mater Today (2012) 15:50–8. doi:10.1016/s1369-7021(12)70020-2
2. Fu X, Liu Y, Chen Q, Fu Y, Cui J. Applications of terahertz spectroscopy in the detection and recognition of substances. Front Phys (2022) 10:869537. doi:10.3389/fphy.2022.869537
3. Kürner T, Priebe S. Towards THz communications-status in research, standardization and regulation. J Infrared Millim Te (2014) 35:53–62. doi:10.1007/s10762-013-0014-3
4. Hafez HA, Chai X, Ibrahim A, Mondal S, Férachou D, Ropagnol X, et al. Intense terahertz radiation and their applications. J Opt (2016) 18:093004. doi:10.1088/2040-8978/18/9/093004
5. Federici JF, Schulkinl B, Huang F, Gary D, Barat R, Oliveira F, et al. THz imaging and sensing for security applications-explosives, weapons and drugs. Semicond Sci Tech (2005) 20:S266–80. doi:10.1088/0268-1242/20/7/018
6. Ashish YP, Deepak DS, Kiran BE, Deelip VD. Terahertz technology and its applications. Drug Invent Today (2013) 5:157–63. doi:10.1016/j.dit.2013.03.009
7. Wu H, Guo Q, Tu Y, Lyu Z, Wang X, Li Y, et al. Polarity reversal of terahertz electric field from heavily p-doped silicon surfaces. Chin Phys Lett (2021) 38:074201. doi:10.1088/0256-307X/38/7/074201
8. Tan P, Huang J, Liu K, Xiong Y, Fan M. Terahertz radiation sources based on free electron lasers and their applications. Sci China Inf Sci (2012) 55:1–15. doi:10.1007/s11432-011-4515-1
9. Vitiello MS, Scalari G, Williams B, Natale PD. Quantum cascade lasers: 20 years of challenges. Opt Express (2015) 23:5167–82. doi:10.1364/oe.23.005167
10. Booske JH, Dobbs RJ, Joye CD, Kory CL, Neil GR, Park GS, et al. Vacuum electronic high power terahertz sources. IEEE Trans Terahertz Sci Technol (2011) 1:54–75. doi:10.1109/tthz.2011.2151610
11. Berry CW, Wang N, Hashemi MR, Unlu M, Jarrahi M. Significant performance enhancement in photoconductive terahertz optoelectronics by incorporating plasmonic contact electrodes. Nat Commun (2013) 4:1622. doi:10.1038/ncomms2638
12. Cook DJ, Hochstrasser RM. Intense terahertz pulses by four-wave rectification in air. Opt Lett (2000) 25:1210–2. doi:10.1364/ol.25.001210
13. Kreß M, Löffler T, Thomson MD, Dörner R, Gimpel H, Zrost K, et al. Determination of the carrier-envelope phase of few-cycle laser pulses with terahertz-emission spectroscopy. Nat Phys (2006) 2:327–31. doi:10.1038/nphys286
14. Kim K-Y, Glownia JH, Taylor AJ, Rodriguez G. Terahertz emission from ultrafast ionizing air in symmetry-broken laser fields. Opt Express (2007) 15:4577–84. doi:10.1364/oe.15.004577
15. Kim K-Y, Taylor AJ, Glownia JH, Rodriguez G. Coherent control of terahertz supercontinuum generation in ultrafast laser-gas interactions. Nat Photon (2008) 2:605–9. doi:10.1038/nphoton.2008.153
16. Lu C, He T, Zhang L, Zhang H, Yao Y, Li S, et al. Effect of two-color laser pulse duration on intense terahertz generation at different laser intensities. Phys Rev A (2015) 92:063850. doi:10.1103/physreva.92.063850
17. Wang T, Chen Y, Marceau C, Théberge F, Châteauneuf M, Dubois J, et al. High energy terahertz emission from two-color laser-induced filamentation in air with pump pulse duration control. Appl Phys Lett (2009) 95:131108. doi:10.1063/1.3242024
18. Kim K-Y. Generation of coherent terahertz radiation in ultrafast laser-gas interactions. Phys Plasmas (2009) 16:056706. doi:10.1063/1.3134422
19. Zhang D, Lü Z, Meng C, Du X, Zhou Z, Zhao Z, et al. Synchronizing terahertz wave generation with attosecond bursts. Phys Rev Lett (2012) 109:243002. doi:10.1103/PhysRevLett.109.243002
20. Dai H, Liu J. Terahertz emission dependence on the intensity ratio of 400-800 nm in generating terahertz waves from two-color laser-induced gas plasma. Photonic Nanostruct (2012) 10:191–5. doi:10.1016/j.photonics.2011.12.005
21. Lu C, Zhang S, Yao Y, Xu S, Jia T, Ding J, et al. Effect of two-color laser pulse intensity ratio on intense terahertz generation. RSC Adv (2015) 5:1485–90. doi:10.1039/c4ra12556h
22. Zhang L, Wang W, Wu T, Zhang R, Zhang S, Zhang C, et al. Observation of terahertz radiation via the two-color laser scheme with uncommon frequency ratios. Phys Rev Lett (2017) 119:235001. doi:10.1103/physrevlett.119.235001
23. Wang W, Sheng Z, Li Y, Zhang Y, Zhang J. Terahertz emission driven by two-color laser pulses at various frequency ratios. Phys Rev A (2017) 96:023844. doi:10.1103/physreva.96.023844
24. González de Alaiza Martínez P, Babushkin I, Bergé L, Skupin S, Cabrera-Granado E, Köhler C, et al. Boosting terahertz generation in laser-field ionized gases using a sawtooth wave shape. Phys Rev Lett (2015) 114:183901. doi:10.1103/physrevlett.114.183901
25. Vaicaitis V, Balachninaite O, Morgner U, Babushkin I. Terahertz radiation generation by three-color laser pulses in air filament. J Appl Phys (2019) 125:173103. doi:10.1063/1.5078683
26. Meng C, Chen W, Wang X, Lü Z, Huang Y, Liu J, et al. Enhancement of terahertz radiation by using circularly polarized two-color laser fields. Appl Phys Lett (2016) 109:131105. doi:10.1063/1.4963883
27. Dai J, Karpowicz N, Zhang X-C. Coherent polarization control of terahertz waves generated from two-color laser-induced gas plasma. Phys Rev Lett (2009) 103:023001. doi:10.1103/PhysRevLett.103.023001
28. Tu Y, Meng C, Sun X, Wu H, Song P, Meng C, et al. Enhancement of terahertz radiation from a filament by using circularly polarized two-color laser fields. J Opt Soc Am B (2022) 39:83–8. doi:10.1364/JOSAB.446156
29. Cocker TL, Jelic V, Gupta M, Molesky SJ, Burgess JAJ, Reyes GDL, et al. An ultrafast terahertz scanning tunnelling microscope. Nat Photon (2013) 7:620–5. doi:10.1038/nphoton.2013.151
30. Zhu J, Ma Z, Sun W, Ding F, He Q, Zhou L, et al. Ultra-broadband terahertz metamaterial absorber. Appl Phys Lett (2014) 105:021102. doi:10.1063/1.4890521
31. Wang BX, Wang LL, Wang GZ, Huang WQ, Li XF, Zhai X. A simple design of ultra-broadband and polarization insensitive terahertz metamaterial absorber. Appl Phys A (2014) 115:1187–92. doi:10.1007/s00339-013-8158-5
32. Baierl S, Hohenleutner M, Kampfrath T, Zvezdin AK, Kimel AV, Huber R, et al. Nonlinear spin control by terahertz-driven anisotropy fields. Nat Photon (2016) 10:715–8. doi:10.1038/nphoton.2016.181
33. Zhang L, Zhang D, Hu F, Xu X, Zhao Q, Sun X, et al. Generation and control of ultrafast circular photon drag current in multilayer PtSe2 revealed via terahertz emission. Adv Opt Mater (2023) 11:2201881. doi:10.1002/adom.202201881
34. Katletz S, Pfleger M, Puhringer H, Mikulics M, Vieweg N, Peters O, et al. Polarization sensitive terahertz imaging: Detection of birefringence and optical axis. Opt Express (2012) 20:23025. doi:10.1364/oe.20.023025
35. Hoshina H, Morisawa Y, Sato H, Minamide H, Noda I, Ozakib Y, et al. Polarization and temperature dependent spectra of poly(3-hydroxyalkanoate)s measured at terahertz frequencies. Phys Chem Chem Phys (2011) 13:9173–9. doi:10.1039/c0cp02435j
36. Tonouchi M. Cutting-edge terahertz technology. Nat Photon (2007) 1:97–105. doi:10.1038/nphoton.2007.3
37. Song L, Bai Y, Xu R, Li C, Liu P, Li R, et al. Polarization control of terahertz waves generated by circularly polarized few-cycle laser pulses. Appl Phys Lett (2013) 103:261102. doi:10.1063/1.4856495
38. Zhang Z, Chen Y, Cui S, He F, Chen M, Zhang Z, et al. Manipulation of polarizations for broadband terahertz waves emitted from laser plasma filaments. Nat Photon (2018) 12:554–9. doi:10.1038/s41566-018-0238-9
39. Li Y, Wang G, Zhang L, Jiao Z, Zhao S, Zhou X. Generating the polarization-controllable THz radiations by incommensurate two-color femtosecond laser fields. Phys Plasmas (2019) 26:073109. doi:10.1063/1.5093145
40. Wang G, Qi H, Li Y, Jiao Z, Zhao S, Zhang L. Polarization-controlled terahertz generation by bicircular longer-wavelength laser fields. J Opt Soc Am B (2022) 39:1370–7. doi:10.1364/JOSAB.456066
41. Yousef-Zamanian A, Neshat M. Investigation of polarization state of terahertz radiation from compact laser-induced plasma in air. J Mod Opt (2017) 64:300–8. doi:10.1080/09500340.2016.1230235
42. Rylyuk VM. Multiphoton ionization of atoms in two-color laser field and coherent polarization control of terahertz waves. Laser Phys (2018) 28:116001. doi:10.1088/1555-6611/aada40
43. Rylyuk VM. Multiphoton ionization of atoms in two-color laser field and coherent polarization control of terahertz waves. Int J Mod Phys B (2020) 34:116001. doi:10.1088/1555-6611/aada40
44. Tailliez C, Stathopulos A, Skupin S, Buožius D, Babushkin I, Vaicaitis V, et al. Terahertz pulse generation by two-color laser fields with circular polarization. New J Phys (2020) 22:103038. doi:10.1088/1367-2630/abb863
45. Corkum PB. Plasma perspective on strong field multiphoton ionization. Phys Rev Lett (1993) 71:1994–7. doi:10.1103/physrevlett.71.1994
46. Rae SC, Burnett K. Detailed simulations of plasma-induced spectral blue shifting. Phys Rev Lett (1992) 46:1084–90. doi:10.1103/physreva.46.1084
47. Yuan K, Bandrauk AD. High-order elliptically polarized harmonic generation in extended molecules with ultrashort intense bichromatic circularly polarized laser pulses. Phys Rev A (2010) 81:063412. doi:10.1103/physreva.81.063412
48. Miloševic DB, Becker W. High-order harmonic generation by bi-elliptical orthogonally polarized two-color fields. Phys Rev A (2020) 102:023107. doi:10.1103/physreva.102.023107
Keywords: terahertz generation, bi-elliptical polarized laser field, photocurrent, polarization, terahertz intensity
Citation: Liu Y-M, Li Y-N, Zhang L, Jiao Z-H, Zhao S-F and Wang G-L (2023) Strong polarization-controlled terahertz generation by bi-elliptical polarized laser fields. Front. Phys. 11:1222665. doi: 10.3389/fphy.2023.1222665
Received: 15 May 2023; Accepted: 17 July 2023;
Published: 28 July 2023.
Edited by:
Li Li, Harbin Institute of Technology, ChinaReviewed by:
Dong-Wen Zhang, National University of Defense Technology, ChinaSunil Kumar, Indian Institute of Technology Delhi, India
Copyright © 2023 Liu, Li, Zhang, Jiao, Zhao and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Guo-Li Wang, d2FuZ2dsQG53bnUuZWR1LmNu; Lei Zhang, emxfbHpqdHVAMTI2LmNvbQ==
 Yan-Mei Liu
Yan-Mei Liu Ya-Ning Li1
Ya-Ning Li1 Song-Feng Zhao
Song-Feng Zhao Guo-Li Wang
Guo-Li Wang