Development of a parallel multiscale 3D model for thrombus growth under flow

1 Introduction

Thrombosis is a pathological process that results in the formation of blood clots within the vascular system. These clots can lead to serious health consequences, such as heart attacks and strokes. Platelets are the primary cellular components involved in arterial thrombosis. Platelet activation and aggregation are complex processes that depend on a variety of factors, including local blood flow conditions and the surrounding biochemical environment. In turn, the structure and size of platelet aggregates affect blood flow as well as the release and transport of various biochemical species that couple back to platelet activation. The formation of a thrombus therefore is a complex and multiscale process that involves interactions across multiple length scales, ranging from the cellular level (sub-micron) to the macroscopic clot scale (∼1 mm) [1]. Consequently, computational modeling, specifically multiscale modeling has emerged as a powerful tool for investigating the underlying mechanisms of thrombus growth under flow [2–15]. Several of these models make use of a continuum approach where platelets, platelet agonists, and coagulation factors are treated as chemical species that obey the convection-diffusion-reaction equation for species transport [11–15]. This approach overcomes the significant computational burden associated with explicitly resolving individual blood cells and accounting for molecular-level interactions between these cells. However, certain key aspects are neglected, such as the ability to capture the stochastic nature of clot formation.

To overcome this limitation, we developed a fully three-dimensional multiscale model for platelet aggregation under flow and validated model predictions against experimental observations in prior work [9]. The model consists of four modules: a neural network (NN) model for platelet calcium signaling and activation, a lattice kinetic Monte Carlo (LKMC) module to track platelet motion and deposition on a growing clot mass under flow, a finite volume method (FVM) solver for computing agonist species concentration fields (ADP, thromboxane A₂) described by a convection-diffusion-reaction equation, and a lattice Boltzmann (LB) method solver for tracking and updating the fluid velocity field as the clot grows (see Figure 1). This model falls under the class of hybrid multiscale models where blood velocity and platelet agonists are treated as continuum fields while platelets are resolved explicitly [2–10]. As a result, the model has the ability to predict the structure of the clot at the resolution of an individual platelet. However, a key challenge in utilizing this model to simulate thrombosis in physiologically important settings such as the coronary vessels is the rather high computational cost involved, motivating the need to parallelize the overall model.

FIGURE 1

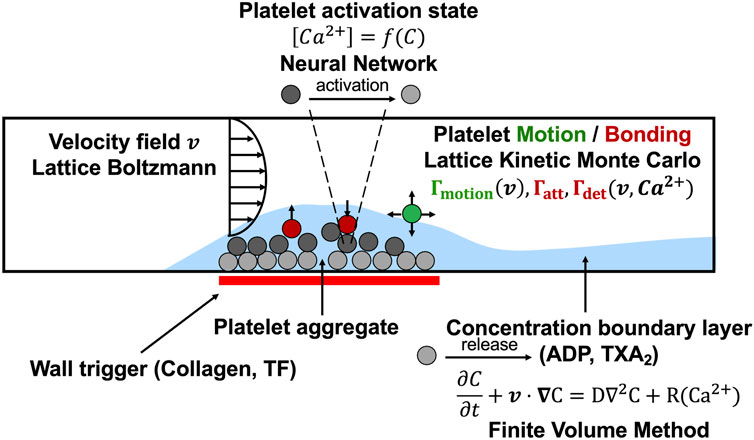
FIGURE 1. The multiscale simulation of thrombus growth under flow required simultaneous solution of the instantaneous velocity field over a complex and evolving platelet boundary by LB, concentration fields of ADP and TXA₂ by FVM, individual intracellular platelet state ([Ca²⁺]_i) and release reactions (R) for ADP and TXA₂ by NN, and all platelet positions and adhesion/detachment by LKMC.

In this paper, we present the strategies used to parallelize each module of the computational framework. We use parallel open-source software where applicable: Palabos (LB) [16], OpenFOAM (FVM) [17], and Multiscale universal Interface [18] for module coupling. Parallel versions of LKMC and NN were achieved by employing a novel parallel particle decomposition approach, which is a key topic of this paper. Using examples, we demonstrate that the parallelized framework enables simulations of systems approaching clinically relevant length scales and may be used to provide insights into the underlying mechanisms of thrombus growth and to predict the risk of thrombotic events in different clinical scenarios. The remainder of the paper is organized as follows. In Section 2, we describe the numerical methods and parallelization strategies used in each of the model components. In Section 3, we present results that validate our parallel model against a serial version, provide a benchmark example simulation, and evaluate the parallel performance of our model. Finally, in Section 4 we provide a discussion of the implications and limitations of our work.

2 Materials and methods

In this section, we outline each individual module of the multiscale framework, and discuss the parallelization and module coupling strategies. A more detailed description of the biological underpinnings of each component of the multiscale model, along with a list of model parameters is available in Ref. [9].

2.1 Neural network for platelet signaling

Upon exposure to biochemical stimuli that are either soluble species or cell surface-linked, platelet signal transduction results in calcium mobilization, which is a marker of platelet activation. Our model accounts for platelet activation via a neural network (NN) model trained in previous work using multicomponent agonist exposure data to determine a unique patient-specific, intra-platelet calcium mobilization response [19, 20]. The NN predicts the intracellular calcium concentration for any platelet, ${\left[C{a}^{2+}\right]}_i\left(t\right)$, based on the feedback vector (containing information from 1, 2, 4, 8, 16, 32, 64, and 128 s prior to the current instant) and the current concentration input of six agonists, namely ADP, TXA₂, collagen, thrombin, nitric oxide donor GSNO, and prostacyclin analog iloprost. The intracellular calcium concentration is then employed to determine the extent of integrin activation and adhesiveness of each platelet, ${\xi }_i\left(t\right)$, given by

${\xi }_i\left(t\right)={\displaystyle \underset{0}{\overset{t}{\int }}}\left({\left[C{a}^{2+}\right]}_i\left(t\right)-\left[C{a}^{2+}\right]\left(0\right)\right)dt,(1)$

where $\left[C{a}^{2+}\right]\left(0\right)$ is the basal level intracellular calcium ion concentration (100 nM) within a platelet. Detailed information on the NN architecture, training, and validation is available in Supplementary Section S1.

The Hill function is used to normalize the cumulative and recent-history calcium integrals between the basal and maximal levels of activation, α_min and α_max, to determine a time-dependent extent of inside-out signaling and integrin activation, F, given by

$F\left({\xi }_i\right)={\alpha }_{\mathit{min}}+\left({\alpha }_{\mathit{max}}-{\alpha }_{\mathit{min}}\right)\frac{{\xi }_i^n}{{\xi }_i^n+{\xi }_{50}^n},(2)$

where n is the Hill coefficient and ${\xi }_{50}$ is the critical value of ${\xi }_i$ for 50% activation.

Since NN computations of intracellular calcium concentration need to be carried out for each individual platelet within the simulation, we employ parallel particle decomposition to efficiently parallelize the NN module (see Section 2.2 for more details on the particle decomposition algorithm).

2.2 Lattice kinetic Monte Carlo solver for platelet motion and bonding

To track individual platelets as they move across the domain, aggregate to, or detach from the blood clot, we use the lattice kinetic Monte Carlo (LKMC) method [7–9]. The input for a LKMC simulation is a rate database for all possible events in the system at any given time. In the present case, the possible events include platelet motion (in the ± x, ± y, or ± z directions), bonding, and detachment. The rate of platelet motion in direction $i$ is given by Ref. [21]

${\mathrm{\Gamma }}_{motion,i}=\frac{D_{platelet}}{h_{LKMC}^2}+\max \left(0,\frac{\mathit{v}\cdot {\mathit{e}}_{\mathit{i}}}{h_{LKMC}}\right),(3)$

where $D_{platelet},h_{LKMC},$ and $\mathit{v}$ are the platelet diffusion coefficient in blood, the LKMC lattice spacing (1.5 μm), and local blood flow velocity vector, respectively.

The rates of platelet bonding/detachment are directly/inversely proportional to the extent of inside-out signaling, F (defined in Eq. 2), respectively. Furthermore, the role of the local shear rate in the shear-dependent breakage of ligand-receptor bonds and the effect of von Willebrand factor (VWF) are accounted for in the bonding and detachment rates. Detailed expressions for the bonding and detachment rates are available in Ref. [9].

With the specified rate database at system time t, the time step of the next event is chosen as

$\Delta t_{LKMC}=-\frac{\ln u}{{\mathrm{\Gamma }}_{total}},(4)$

where ${\mathrm{\Gamma }}_{total}$ is the total rate of all events currently accessible in the system and u is a random number drawn from the uniform distribution in the interval (0, 1). The probability $P_i$ that event i with rate ${\mathrm{\Gamma }}_i$ will be the next event is given by

$P_i=\frac{{\mathrm{\Gamma }}_i}{{\mathrm{\Gamma }}_{total}}.(5)$

While there exist parallel open-source LKMC implementations in the literature, their applicability to model particle motion and aggregation in complex geometries is limited either by restrictions placed on domain geometries, or by limitations on the types of events that can be simulated [22, 23]. More importantly, they employ spatial domain decomposition, which would not be an efficient parallelization strategy for the present simulations. The reason for this is that the distribution of events, i.e., platelet motion, bonding, and detachment, with high propensities is extremely spatially heterogeneous; motion events are directly proportional to the local velocity field which is highly variable across the domain (see Eq. 3), and bonding/detachment events are restricted to a small portion of the domain. Since spatial decomposition parallel algorithms for LKMC involve cores performing events in their respective subdomains, and the LKMC time step is inversely proportional to the aggregate rate, a single core can end up being a bottleneck because time is advanced much slowly on that core [24]. Therefore, to efficiently parallelize the LKMC method with spatially heterogeneous (and time varying) event distributions, we have developed a custom in-house C++ code based on the message passing interface (MPI) library for inter-core communication that employs parallel particle decomposition instead of spatial domain decomposition. Here, each core is assigned a subset of particles, irrespective of their spatial locations, such that the sum of event rates is approximately uniform across cores. Moreover, to maintain this balance over time, new particles entering the simulation domain are assigned randomly among the cores. A schematic that illustrates the advantages of particle-based decomposition over domain decomposition is shown in Figure 2.

FIGURE 2

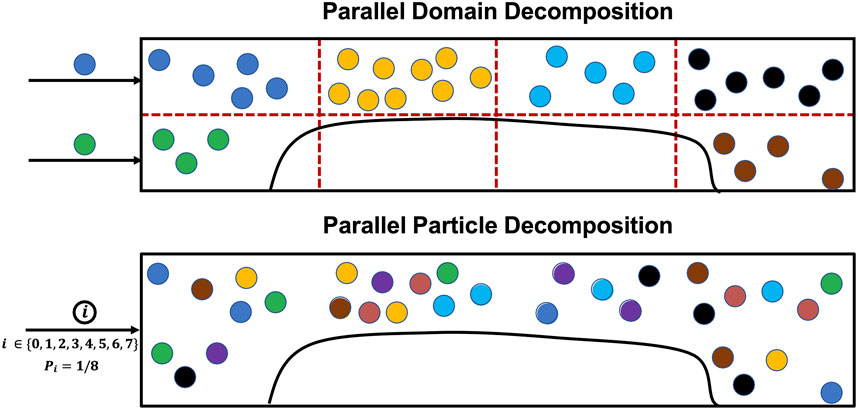
FIGURE 2. Comparison between parallel spatial domain decomposition and parallel particle decomposition for LKMC. An example decomposition is presented using 8 cores for the two cases. The ownership of particles to different cores is color coded for illustration. Assuming equal rates associated with each particle, spatial domain decomposition would advance time 2.25 × slower than parallel particle decomposition because it is bottlenecked by the core owning yellow-colored particles.

We have adapted the synchronous parallel kinetic Monte Carlo method developed by Martinez et al. for our parallel LKMC module [25, 26]. In the parallel algorithm, we first divide the system by distributing the particles equally among K cores. Then, the aggregate rate of all possible events on each core $k$, ${\mathrm{\Gamma }}_{total,k}$ is calculated, and the highest aggregate rate ${\mathrm{\Gamma }}_{\mathit{max}}$ is communicated to all cores, where

${\mathrm{\Gamma }}_{\mathit{max}}\ge \underset{k=1,\dots ,K}{\max }{\mathrm{\Gamma }}_{total,k}.(6)$

A null event is assigned to each core with a rate ${\mathrm{\Gamma }}_{0,k}$ given by the difference between the highest aggregate rate and the total rate on that core, i.e.,

${\mathrm{\Gamma }}_{0,k}={\mathrm{\Gamma }}_{\mathit{max}}-{\mathrm{\Gamma }}_{total,k}.(7)$

A null event is a “do-nothing” event where the system configuration remains unchanged. The introduction of these null events helps achieve time synchronicity, since each core now has the same total rate (${\mathrm{\Gamma }}_{\mathit{max}}$) that determines the time step associated with an LKMC event. Each core now executes an LKMC event in parallel and independently of other cores, with time step and event probabilities according to Eqs 4, 5, respectively.

It can be readily seen that the parallel efficiency in the case of domain decomposition would be suboptimal due to the high fraction of null events in most cores (see also Figure 2), while parallel particle decomposition is designed to provide excellent load balancing. While load balancing is readily enforceable in particle-based decomposition, the chief drawback of this approach is that communication across cores becomes more challenging to execute because of the lack of well-defined inter-core boundaries. Ideally, any two particles assigned to different cores must not occupy the same lattice site, or perform lattice hops to or bonding events at the same lattice site. Strictly ensuring this condition after every event would require global communication across all cores after each LKMC event is executed, which is undesirable due to the high communication overhead costs entailed by this operation. However, here we take advantage of the fact that bulk platelets (i.e., free platelets that are not a part of a clot) exist in low concentrations in flowing blood (<1% of occupied LKMC sites). We therefore treat bulk platelets as tracer particles that interact only with aggregated platelets comprising a clot but are otherwise noninteracting with other bulk platelets. In other words, a platelet assumes an excluded volume only after it becomes a part of a clot via a bonding event. This assumption is reasonable (and later will be quantitatively validated by comparison to a serial reference simulation) because the probability is low that any two bulk platelets on different cores execute simultaneous hops resulting in an overlapping configuration. To minimize the impact of overlapping bulk platelets, a periodic scan is performed for platelets occupying the same lattice site, and if found, one of the overlapping platelets is deleted from the system. At any instant of time, the previously known clot configuration is available to all cores. We define an update frequency, F, which is the number of LKMC moves after which a global call is initiated to update the clot configuration in each core. Additionally, we only make global calls to update ${\mathrm{\Gamma }}_{\mathit{max}}$ after every F LKMC moves by specifying ${\mathrm{\Gamma }}_{\mathit{max}}$ to a value slightly higher than the highest total rate to account for any fluctuations in the highest total rate (e.g., a platelet entering the system will increase the total rate). The choice of F therefore determines the trade-off between accuracy and computational cost of the algorithm. For all the simulations presented in this paper, we set F to be three times the average number of bulk platelets on a core. In other words, bulk platelets perform on average three lattice hops between successive updates of the aggregated platelet configuration. We maintain good parallel efficiency by making use of these assumptions and approximations to avoid global calls without compromising the accuracy of the parallel model when compared to the results of the serial model (see Section 3).

2.3 Finite volume method solver for agonist concentration fields: OpenFOAM

Soluble platelet agonist concentration fields C_j(x,y,z,t) (where j = ADP, TXA₂) were determined using the FVM solution to the convection-diffusion-reaction equations:

$\frac{\partial C_j}{\partial t}+\mathit{v}\cdot \nabla C_j=D_j{\nabla }^2{C}_j+R_j(8)$

where D_j and R_j are the diffusion coefficients and the volumetric release rates of ADP and TXA₂, respectively, and v is the local blood flow velocity. The open-source software package OpenFOAM was used to carry out our FVM computations of spatiotemporal agonist concentration profiles [17]. OpenFOAM is an open-source C++ library that with parallel FVM implementations based on MPI, and has been widely used in both academic and industrial settings. OpenFOAM deploys a spatial domain decomposition approach for parallelization, where the simulation domain is divided among the cores. The mesh and fields were decomposed using the decomposePar utility provided in OpenFOAM. Starting from an initial coarse mesh, the dynamicRefineFvMesh utility provided by OpenFOAM was used to perform topological refinements to the mesh. At mesh locations where platelets become sufficiently activated for dense granule release, the mesh spacing was refined to 1.5 μm. In such a scenario, a single platelet overlapped several FVM cells, so the cell at the center of the activated platelet was treated as the source element for the PDE calculation. The time derivative was approximated using the Crank Nicolson scheme with a time step of 0.01 s.

2.4 Lattice Boltzmann method solver for blood flow field: Palabos

To model the blood flow velocity profile across the simulation domain, we use the lattice Boltzmann (LB) method, which has been used extensively in blood flow modelling [27–32]. Importantly, LB lends itself well to parallel computing [33]. Specifically, we carry out our LB simulations using Palabos, which is an open-source computational fluid dynamics solver based on the LB method [16]. Palabos has been demonstrated to exhibit excellent parallel efficiencies for benchmark computational fluid dynamics calculations [16]. It is designed in C++ with parallel features using spatial domain decomposition and MPI for communication between neighboring cores.

We assume that blood is an incompressible Newtonian fluid that satisfies the Navier-Stokes equations. However, instead of solving these equations directly, LB models the fluid with fictive particles. The fundamental quantity underpinning LB is the density distribution function, $f_i\left(\mathit{x},t\right)$, in phase space, $\left(\mathit{x},{\mathit{c}}_{\mathit{i}}\right)$, where $t$ denotes time and ${\mathit{c}}_{\mathit{i}}$ denotes the lattice velocity along direction i. The evolution of the density distribution function is governed by a discretization of the Boltzmann equation, given by

$f_i\left(\mathit{x}+{\mathit{c}}_{\mathit{i}},t+1\right)-f_i\left(\mathit{x},t\right)=\frac{1}{\tau }\left(f_i^{eq}-f_i\left(\mathit{x},t\right)\right),(9)$

where $f_i^{eq}$ is the equilibrium distribution function based on the current distribution along direction i and $\tau$ is the relaxation parameter. The simplest incompressible Bhatnagar-Gross-Krook (BGK) scheme is used for relaxation to equilibrium via collisions between the molecules of a fluid [34], given by

$f_i^{eq}=w_i\rho \left(1+3{\mathit{c}}_{\mathit{i}}\cdot \mathit{v}+\frac{9}{2}{\left({\mathit{c}}_{\mathit{i}}\cdot \mathit{v}\right)}^2-\frac{3}{2}\mathit{v}\cdot \mathit{v}\right).(10)$

The fluid density $\rho$ and velocity $v$ in scaled LB units are computed as

$\rho ={\displaystyle \sum _i}{f}_i,(11)$

$\rho \mathit{v}={\displaystyle \sum _i}{f}_i{\mathit{c}}_{\mathit{i}} .(12)$

The fluid kinematic viscosity in scaled LB units, ${\nu }_{LB}$, is related to the relaxation parameter $\tau$ as

${\nu }_{LB}=c_s^2\left(\tau -\frac{1}{2}\right)=\frac{1}{3}\left(\tau -\frac{1}{2}\right).(13)$

In all LB simulations reported in this paper, the fluid domain is discretized using a uniform D3Q19 lattice [$i=1,\dots ,19$]; see Ref. [33]. The 3D lattice for carrying out our simulations is obtained from a stereolithography (STL) file surface mesh describing the computational domain. Palabos is then used to discretize the domain, i.e., convert the surface description of the domain into a volumetric description by identifying which fluid nodes (or voxels) lie inside the domain. This discretization is done internally in Palabos and is fully parallelized. Moreover, parallel domain decomposition is carried out automatically in Palabos using a homogeneous volume mesh. For all LB simulations presented in this work, the lattice spacing was set to 3 μm. During each LB time step, the density distribution function, $f_i\left(\mathit{x},t\right)$, is updated according to Eq 9. At locations in the domain where there are bound/aggregated platelets, no-slip (bounce-back) boundary conditions are applied [35]. For more details on implementation of the LB model, the exact form of the equilibrium distribution, and LB unit conversion, see Refs. [16, 33, 34].

2.5 Module coupling: multiscale universal interface

The multiscale framework described in this work is composed of several modules that require periodic exchange of information, with individual modules each having their respective open-source libraries or routines. To facilitate the coupling between different modules at each coupling time, we use the Multiscale universal Interface (MUI) [18]. MUI is a C++ library that makes use of non-blocking MPI messages to achieve data exchange between each module with minimal modifications to individual module source codes. The flow of information between modules and a schematic of the time stepping alignment across modules is shown in Figures 3, 4 respectively. LKMC provides the positions of all platelets in the domain and the bonding state of each platelet. LKMC requires the velocity field of the fluid from LB to calculate convective rates of motion and the activation state of each platelet from NN to determine the bonding and detachment rates. The NN provides the activation state of each platelet and the input to the NN requires the concentration fields of soluble agonists from FVM. The LB method provides the velocity field and requires the location of all aggregated platelets from LKMC for the location of the no-slip surfaces. FVM provides the concentration field and requires the release rate of platelets, which depends on the location of platelets obtained from LKMC, activation states from NN, and the velocity field from LB. To interpolate the values of velocity fields at locations required by another module, a trilinear interpolation scheme using field values at the 8 nearest available points is used, while a nearest-neighbor sampler is used for interpolating agonist concentration fields and the mapping of platelet locations to mesh cells in LB/FVM.

FIGURE 3

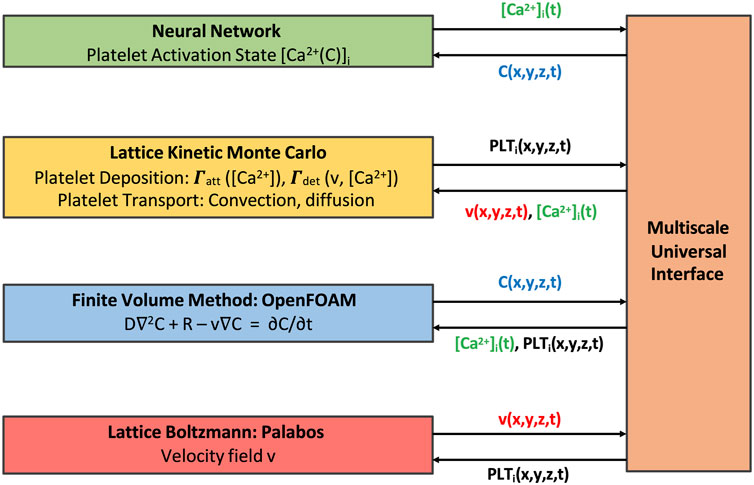
FIGURE 3. Multiscale model coupling scheme illustrating the exchange of information between individual modules.

FIGURE 4

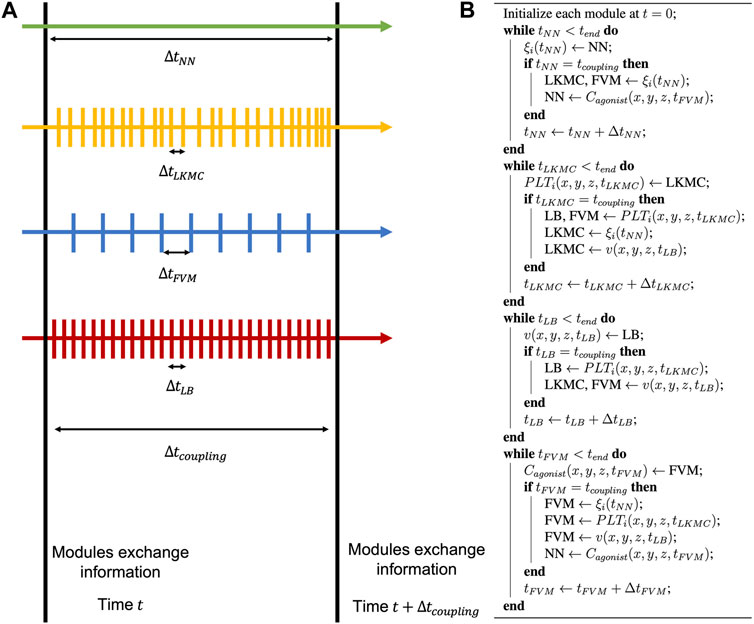
FIGURE 4. Model time stepping. (A) Each individual module is advanced in time independently until the next coupling time is reached. (B) During this update, all modules share information, and this process is repeated until the end of the simulation.

Coupling of the individual models occurs after time intervals of $\Delta t_{coupling}=0.1s$. At the start of the simulation LKMC, LB, FVM, and the NN are all specified by the initial condition for each method. Each method is stepped forward in time until the first coupling time is reached. During this update, all modules share information: LKMC updates the positions of all platelets and the bound states of all platelets in FVM and LB; LB updates the velocity field in LKMC and FVM; FVM updates the concentration field in NN; and NN updates the activation state in FVM and LKMC. This process is repeated until the end of the simulation. The timescale for velocity field relaxation is generally $\ll \Delta t_{coupling}$, i.e., the velocity field reaches steady state in LB significantly before the next update time. Consequently, the LB calculation is performed in a quasi-static mode in which it is evolved only until steady state is achieved for a given particle configuration.

3 Results

3.1 Parallel multiscale model validation

To validate our coupled parallel multiscale model of thrombus growth against serial computations, we considered the dynamics of platelet deposition and aggregation in two case studies. In the first case study we considered a cylindrical domain as shown in Figure 5 (inset). The simulation domain was 0.5 mm long with a diameter of 0.12 mm. A semicylindrical reactive collagen surface patch of diameter 0.12 mm and length 0.25 mm that represents an injury was located at the center of the domain. A constant wall shear rate of 200 s⁻¹ that is typical for venous flow was maintained at the inlet. In the second case study, we considered a 1 mm-long stenotic vessel with an inlet diameter of 0.12 mm. In the central 0.5 mm of the vessel, we introduced a narrowing of the vessel that corresponded to a 75% reduction in flow area as shown in Figure 6 (inset). The stenotic area was assumed to express collagen that extends up to half the circumference and represents the region of injury that triggers platelet aggregation, as shown in Figure 6 (inset). The inlet and outlet of the vessel were maintained at a constant pressure drop that corresponds to an initial inlet wall shear rate of ∼1000s^-1, typical of arterial flow conditions [36]. In both case studies, the bulk platelet concentration was set at 1.5 × 10⁵ μL^-1.

FIGURE 5

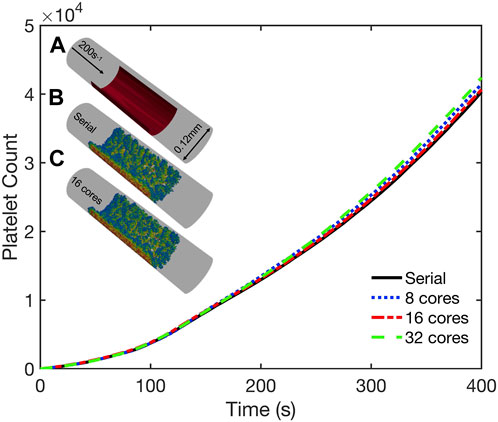
FIGURE 5. Validation simulations of the parallel multiscale model for thrombus growth in a cylindrical vessel. Observed dynamics of aggregated platelet count as a function of time for simulations using 1, 8, 16, and 32 cores. Inset: (A) Schematic of the geometry. Inlet flow: 200s⁻¹; reactive collagen surface: red bar. Platelet activation (blue indicates inactivated and red, highly activated) and deposition after 400 s simulated using (B) serial model and (C) parallel model using 16 cores.

FIGURE 6

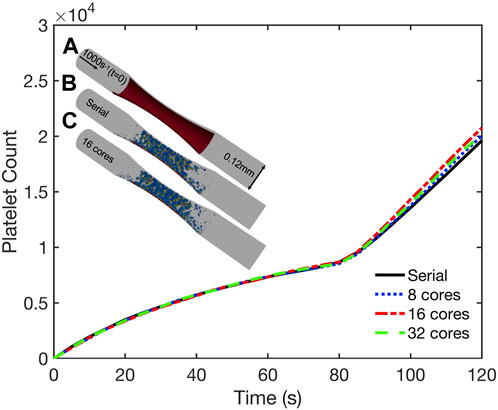
FIGURE 6. Validation simulations of the parallel multiscale model for thrombus growth in a stenotic vessel. Observed dynamics of aggregated platelet count as a function of time for simulations using 1, 8, 16, and 32 cores. Inset: (A) Schematic of the geometry. Inlet and outlet of the vessel maintained at a constant pressure drop across the length of the geometry that corresponded to an initial inlet wall shear rate of 1000s⁻¹. Surface collagen: red bar. Platelet activation (blue indicates inactivated and red, highly activated) and deposition after 120 s simulated using (B) serial model and (C) parallel model using 16 cores.

Both case studies were first simulated in serial (i.e., on a single core) and the dynamics of platelet deposition used to validate results from corresponding parallel simulations using 8, 16, and 32 cores. As shown in Figures 5, 6, the platelet counts (defined as the number of aggregated platelets that are part of a clot) as a function of time predicted by the parallel runs agree well with those predicted by the serial run. Also shown in Figures 5, 6 (insets) are snapshots of the platelet aggregates generated in both the serial and parallel cases. Histograms of deposited platelet counts placed in bins along the axial location in the domain showed identical results for simulations using 1, 8, 16, and 32 cores (see Supplementary Figure S2). Consequently, the serial and parallel models can be considered functionally equivalent.

3.2 Benchmark simulation of human stenotic thrombus growth from initial platelet deposition to full occlusion

Following validation of our parallel multiscale algorithm, we next considered a benchmark simulation in an idealized cylindrical blood vessel 2 mm long with a diameter of 0.24 mm. We imposed a stenosis with a 75% reduction in lumen area in the central 1 mm of the vessel, as shown in Figure 7A. The inlet and outlet of the stenosis were maintained under a constant pressure drop that correspond to an initial inlet wall shear rate of ∼1,000 s⁻¹. The entire stenotic area was assumed to express collagen and trigger platelet activation and deposition. Again, the platelet inlet concentration was set at 1.5 × 10⁵ μL⁻¹. Under these conditions, we simulated the first 180 s of the formation and subsequent growth of the thrombus using our parallelized code running on 64 CPU cores.

FIGURE 7

FIGURE 7. Benchmark parallel simulation of thrombus growth in a stenotic vessel. Inlet and outlet of the stenosis maintained at a constant pressure drop across the length of the geometry that corresponded to an initial inlet wall shear rate of 1000s⁻¹. Collagen is expressed along the stenotic surface. (A) Schematic of the geometry along with a snapshot of the aggregated platelets (blue indicates inactivated and red, highly activated) after 180 s. (B) Observed dynamics of aggregated platelet count and change in inlet volumetric flow rate versus time. (C) Platelet activation and deposition in the presence of released (D) ADP, (E) TXA₂ and (F) velocity field contours plotted along a central slice of the geometry after 180 s.

The simulation predicted a rapid rate of thrombus growth after an initial lag time of about 80s from ∼0.1 million platelets to ∼0.5 million platelets at 180 s; see Figures 7A, B. This lag time corresponds to the time at which the first monolayer of platelets adhered to the collagen surface become sufficiently activated to release platelet agonists. The inlet volumetric flow rate dropped to ∼10% of its initial value in 180s due to the flow resistance caused by the growing platelet aggregates. A plot of the aggregated platelet count and the change in inlet flow rate as a function of time is provided in Figure 7B. We also present a snapshot of the deposited platelet mass, the concentration profiles of soluble platelet agonists ADP and thromboxane, and the velocity profile along a central slice of the stenosis after 180⁻s in Figures 7C–F. We note that platelet aggregation is significantly higher near the apex of the stenosis where the observed shear rates experienced by the platelets are highest, a feature that is consistent with prior published computational models and experimental observations [6, 9, 15, 37–39]. This observation is due to the role of VWF in mediating platelet adhesion at high shear rates. At pathological shear rates greater than 3000s^-1, VWF undergoes structural changes from a globular conformation to a stretched conformation, increasing the number of exposed ligands [40–42]. To account for this effect in our platelet adhesion model we included an enhancement factor for the platelet adhesion rates as a function of the local shear rate [9].

3.3 Parallel performance

The parallel performance of the code was examined using the benchmark case considered in Section 3.2. All simulations were carried out on the Bridges-2 system at the Pittsburgh Supercomputing Center [43]. Parallel performance was analyzed using the observed speedup and the parallel scaling efficiency. For a strong scaling study, the speedup is defined as $S\left(K\right)=\frac{t_0}{t_K}$, where $t_0$ refers to the simulation time for a reference simulation on $N_0$ cores, and $t_K$ refers to the simulation time for a parallel simulation using K cores. Here, $N_0$ was defined as 4 cores. The parallel efficiency is obtained from the measured speedup as $\eta \left(K\right)=S\left(K\right)\frac{N_0}{K}.$

The strong scaling performance was analyzed at an intermediate simulation time of t = 120s following the initiation of thrombus growth. This time was chosen because it provided a representative snapshot of the system where there is sufficient platelet aggregation leading to a spatially heterogeneous distribution of platelets. We note here that the parallel efficiencies of individual modules and the overall code vary as the simulation progresses in time because they are dependent on the number of platelets considered at any instant for LKMC and NN, the number of LB time steps needed to reach steady flow, and the number of FVM cells. For the system under consideration at t = 120s, the LKMC and NN models accounted for ∼0.2 million platelets, the LB model considered an 82 $\times$ 82 $\times$ 669 lattice (corresponding to a lattice spacing of 3 µm), and the FVM model considered ∼1.5 million mesh cells. The coupled multiscale code was run to simulate 0.1⁻s of clotting and the time taken by each individual module of the code was recorded. During this period, the coupled solver performed ∼10 million LKMC updates, ∼3,000 LB time steps ($\Delta t_{LB}=1.25\times {10}^{-8}s$) until LB achieved steady state, and 10 FVM time steps ($\Delta t_{FVM}=0.01s$). The observed speedup and parallel efficiency as a function of the number of cores used is shown in Figure 8 for each individual module and the overall coupled code.

FIGURE 8

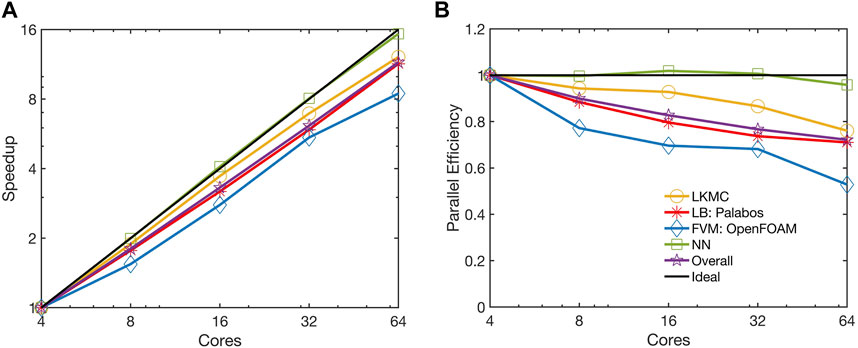
FIGURE 8. Observed (A) speedup and (B) parallel efficiency of the parallelized multiscale code. The strong scaling of the benchmark simulation is considered from 4 to 64 cores.

The NN module is essentially embarrassingly parallel as it requires negligible communication overhead. Moreover, the parallel particle decomposition LKMC method used to distribute platelets across cores ensures a homogeneous load distribution across different cores. The parallel efficiency of the LKMC module remained at 0.76 despite the spatial heterogeneity in the distribution of platelets. While most platelets are a part of the thrombus and do not appreciably influence the total rate, it is worth noting that they would contribute quite significantly to the spatial heterogeneity in the distribution of rates in the domain. This is because the rates of platelet motion are dependent on the local velocity field which is higher in regions where there is flow narrowing caused by deposited platelets. Consequently, spatial domain decomposition would be a poor choice for parallelizing LKMC. The observed parallel efficiency of the FVM module was 0.53 on 64 cores, while the efficiency of the LB module remained at 0.71 on 64 cores. The parallel efficiency of the overall code was observed to mirror that of the LB module was 0.72 on 64 cores.

A breakdown of the overall computational cost is provided in Figure 9 for the simulation on 64 cores. We observed that the NN and FVM modules contribute negligible computational expense compared to the LB and LKMC modules. The computational expense involved in interpolating and exchanging solutions between different modules using MUI was also found to be negligible. The LB module most significantly dictated the overall computational cost of the model, especially at the later stages of the simulation (at times close to full vessel occlusion) for the present system. This explains why the overall parallel efficiency of the framework was observed to mirror that of the LB module. We note that while these computational times have been obtained for a specific set of physiological and technical parameters, we expect the high parallel efficiency of the overall code to remain robust to changes in platelet density or the mesh resolutions of individual solvers. This is because Palabos (LB) and OpenFOAM (FVM) have demonstrated excellent parallel performance for different benchmark computations [16, 17]. The LKMC code also demonstrated excellent performance over a range of platelet densities in a weak scaling analysis (see Supplementary Figure S4).

FIGURE 9

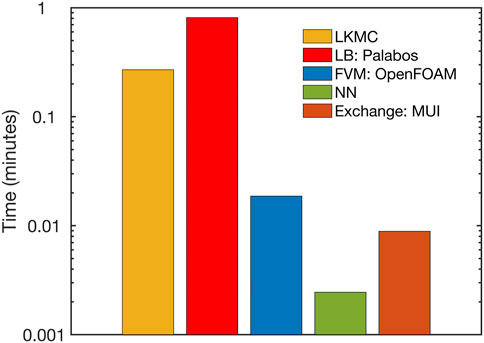
FIGURE 9. Breakdown of the computational expense of each individual module within the parallel multiscale model.

4 Discussion

In this study, we demonstrated the effectiveness of a parallelized multiscale model of thrombus growth under flow. To validate the parallelized model, we used two case studies to compare predictions with those obtained using a serial version of the model. We found that the parallelized model produced similar results to the serial model, indicating that the parallelization strategies and the accompanying approximations did not compromise the accuracy of the simulations. We also evaluated the parallel performance of the model by measuring the speedup achieved with increasing numbers of cores. Our results showed that the model achieved a parallel efficiency of ∼70% on 64 cores for vessels of size ∼1 mm.

A key aspect of our multiscale framework is its modularity, which enables the easy incorporation of additional components into the model. For example, our model can be coupled to patient-specific models of coronary, carotid, or cerebral circulation that would supply time-varying inlet velocity and outlet pressure boundary conditions to simulate thrombus growth in patient-specific vasculatures [44, 45]. Another feature that can be added to the model is a full PDE-based description of the coagulation cascade that can be integrated seamlessly into the FVM solver to study, for example, the inhibitory effect of a novel anticoagulant on the rate of thrombus growth [46]. Moreover, the individual modules of the framework are designed to be independent, meaning that they can be updated or modified without disrupting the overall functionality of the model. For example, the LB model may be replaced with an equivalent direct computational fluid dynamics solver if desired by the user. This modular design allows for the flexible integration of new components as they are developed, improving the accuracy and robustness of the model over time.

The model has some limitations that could be incorporated in future work. At present, we are yet to incorporate the effects of collective detachment of platelets from the thrombus (emboli) and their subsequent transport and interaction with the blood. Another limitation of the model is that we do not model blood vessel wall deformation. The deformation of the blood vessel wall can influence thrombus formation and growth by altering the flow dynamics in the vessel. Still, diseased vessels are generally more rigid compared to compliant healthy vessels. Therefore, our model assumes a rigid blood vessel wall, which greatly reduces the computational cost of the simulation but may not capture the full range of physiological conditions.

In conclusion, the simulations presented in this work represent a significant advancement in the state-of-the-art in multiscale modeling of thrombus growth under flow. Specifically, we demonstrated the ability to simulate length scales up to ∼1 mm using modest parallel computing resources. The ability to simulate large systems with single-platelet resolution has important implications for understanding the mechanisms of thrombus growth and predicting the risk of thrombotic events in different clinical scenarios. For example, the model could be used to investigate the impact of vascular geometry, blood rheology, and different drug treatments on thrombus formation and growth. This information could be used to develop patient-specific evaluations of cardiovascular risk or response to therapy. Looking ahead, even larger length and timescale simulations will require additional computational strategies, such as further optimization of parallelization algorithms, the use of novel massively parallel hardware architectures (e.g., GPUs), or the use of non-uniform adaptive grids for the LKMC and LB modules [16, 47].

Data availability statement

The original contributions presented in the study are publicly available. This data can be found here: https://github.com/kaushikns/3d-multiscale-thrombosis-solver.

Author contributions

KS: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Software, Validation, Visualization, Writing–original draft, Writing–review and editing. SD: Conceptualization, Funding acquisition, Methodology, Project administration, Resources, Supervision, Writing–review and editing. TS: Conceptualization, Funding acquisition, Methodology, Project administration, Resources, Supervision, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was funded by NIH R01 HL-103419 (SD and TS) and American Heart Association Predoctoral Fellowship Award #908962 (KS).

Acknowledgments

This work used the Bridges-2 system at the Pittsburgh Supercomputing Center (PSC) through allocation #BIO220017 from the Advanced Cyberinfrastructure Coordination Ecosystem: Services & Support (ACCESS) program, which is supported by National Science Foundation grants #2138259, #2138286, #2138307, #2137603, and #2138296.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2023.1256462/full#supplementary-material

References

1. Grande Gutiérrez N, Shankar KN, Sinno T, Diamond SL. Thrombosis and hemodynamics: External and intrathrombus gradients. Curr Opin Biomed Eng (2021) 19:100316. doi:10.1016/j.cobme.2021.100316

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Bouchnita A, Volpert V. A multiscale model of platelet-fibrin thrombus growth in the flow. Comput Fluids (2019) 184:10–20. doi:10.1016/j.compfluid.2019.03.021

CrossRef Full Text | Google Scholar

3. Xu Z, Chen N, Kamocka MM, Rosen ED, Alber M. A multiscale model of thrombus development. J R Soc Interf (2008) 5:705–22. doi:10.1098/rsif.2007.1202

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Wang P, Sheriff J, Zhang P, Deng Y, Bluestein D. A multiscale model for shear-mediated platelet adhesion dynamics: Correlating in silico with in vitro results. Ann Biomed Eng (2023) 51:1094–105. doi:10.1007/s10439-023-03193-2

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Liu ZL, Ku DN, Aidun CK. Mechanobiology of shear-induced platelet aggregation leading to occlusive arterial thrombosis: A multiscale in silico analysis. J Biomech (2021) 120:110349. doi:10.1016/j.jbiomech.2021.110349

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Yazdani A, Li H, Humphrey JD, Karniadakis GE. A general shear-dependent model for thrombus formation. Plos Comput Biol (2017) 13:e1005291. doi:10.1371/journal.pcbi.1005291

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Flamm MH, Colace TV, Chatterjee MS, Jing H, Zhou S, Jaeger D, et al. Multiscale prediction of patient-specific platelet function under flow. Blood (2012) 120:190–8. doi:10.1182/blood-2011-10-388140

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Lu Y, Lee MY, Zhu S, Sinno T, Diamond SL. Multiscale simulation of thrombus growth and vessel occlusion triggered by collagen/tissue factor using a data-driven model of combinatorial platelet signalling. Math Med Biol (2016) 34:523–46. doi:10.1093/imammb/dqw015

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Shankar KN, Zhang Y, Sinno T, Diamond SL. A three-dimensional multiscale model for the prediction of thrombus growth under flow with single-platelet resolution. Plos Comput Biol (2022) 18:e1009850. doi:10.1371/journal.pcbi.1009850

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Yazdani A, Deng Y, Li H, Javadi E, Li Z, Jamali S, et al. Integrating blood cell mechanics, platelet adhesive dynamics and coagulation cascade for modelling thrombus formation in normal and diabetic blood. J R Soc Interf (2021) 18:20200834. doi:10.1098/rsif.2020.0834

CrossRef Full Text | Google Scholar

11. Leiderman K, Fogelson AL. Grow with the flow: a spatial-temporal model of platelet deposition and blood coagulation under flow. Math Med Biol (2011) 28:47–84. doi:10.1093/imammb/dqq005

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Wu W-T, Zhussupbekov M, Aubry N, Antaki JF, Massoudi M. Simulation of thrombosis in a stenotic microchannel: The effects of vWF-enhanced shear activation of platelets. Int J Eng Sci (2020) 147:103206. doi:10.1016/j.ijengsci.2019.103206

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Wang Y, Luo K, Qiao Y, Fan J. An integrated fluid-chemical model toward modeling the thrombus formation in an idealized model of aortic dissection. Comput Biol Med (2021) 136:104709. doi:10.1016/j.compbiomed.2021.104709

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Montgomery D, Municchi F, Leiderman K. clotFoam: An open-source framework to simulate blood clot formation under arterial flow. SoftwareX (2023) 23:101483. doi:10.1016/j.softx.2023.101483

CrossRef Full Text | Google Scholar

15. Zhussupbekov M, Méndez Rojano R, Wu W-T, Antaki JF. von Willebrand factor unfolding mediates platelet deposition in a model of high-shear thrombosis. Biophysical J (2022) 121:4033–47. doi:10.1016/j.bpj.2022.09.040

CrossRef Full Text | Google Scholar

16. Latt J, Malaspinas O, Kontaxakis D, Parmigiani A, Lagrava D, Brogi F, et al. Palabos: Parallel lattice Boltzmann solver. Comput Math Appl (2021) 81:334–50. doi:10.1016/j.camwa.2020.03.022

CrossRef Full Text | Google Scholar

17. Jasak H. OpenFOAM: Open source CFD in research and industry. Int J Naval Architecture Ocean Eng (2009) 1:89–94. doi:10.2478/IJNAOE-2013-0011

CrossRef Full Text | Google Scholar

18. Tang Y-H, Kudo S, Bian X, Li Z, Karniadakis GE. Multiscale universal interface: A concurrent framework for coupling heterogeneous solvers. J Comput Phys (2015) 297:13–31. doi:10.1016/j.jcp.2015.05.004

CrossRef Full Text | Google Scholar

19. Chatterjee MS, Purvis JE, Brass LF, Diamond SL. Pairwise agonist scanning predicts cellular signaling responses to combinatorial stimuli. Nat Biotechnol (2010) 28:727–32. doi:10.1038/nbt.1642

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Lee MY, Diamond SL. A human platelet calcium calculator trained by pairwise agonist scanning. Plos Comput Biol (2015) 11:e1004118. doi:10.1371/journal.pcbi.1004118

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Flamm MH, Diamond SL, Sinno T. Lattice kinetic Monte Carlo simulations of convective-diffusive systems. J Chem Phys (2009) 130:094904. doi:10.1063/1.3078518

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Mitchell JA, Abdeljawad F, Battaile C, Garcia-Cardona C, Holm EA, Homer ER, et al. Parallel simulation via SPPARKS of on-lattice kinetic and Metropolis Monte Carlo models for materials processing. Model Simul Mater Sci Eng (2023) 31:055001. doi:10.1088/1361-651X/accc4b

CrossRef Full Text | Google Scholar

23. Leetmaa M, Skorodumova NV. KMCLib: A general framework for lattice kinetic Monte Carlo (kmc) simulations. Comp Phys Commun (2014) 185:2340–9. doi:10.1016/j.cpc.2014.04.017

CrossRef Full Text | Google Scholar

24. Shim Y, Amar JG. Semirigorous synchronous sublattice algorithm for parallel kinetic Monte Carlo simulations of thin film growth. Phys Rev B (2005) 71:125432. doi:10.1103/PhysRevB.71.125432

CrossRef Full Text | Google Scholar

25. Martínez E, Marian J, Kalos MH, Perlado JM. Synchronous parallel kinetic Monte Carlo for continuum diffusion-reaction systems. J Comput Phys (2008) 227:3804–23. doi:10.1016/j.jcp.2007.11.045

CrossRef Full Text | Google Scholar

26. Martínez E, Monasterio PR, Marian J. Billion-atom synchronous parallel kinetic Monte Carlo simulations of critical 3D Ising systems. J Comput Phys (2011) 230:1359–69. doi:10.1016/j.jcp.2010.11.006

CrossRef Full Text | Google Scholar

27. Afrouzi HH, Ahmadian M, Hosseini M, Arasteh H, Toghraie D, Rostami S. Simulation of blood flow in arteries with aneurysm: Lattice Boltzmann Approach (LBM). Comp Methods Programs Biomed (2020) 187:105312. doi:10.1016/j.cmpb.2019.105312

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Krafczyk M, Cerrolaza M, Schulz M, Rank E. Analysis of 3D transient blood flow passing through an artificial aortic valve by Lattice–Boltzmann methods. J Biomech (1998) 31:453–62. doi:10.1016/S0021-9290(98)00036-0

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Sun C, Munn LL. Lattice-Boltzmann simulation of blood flow in digitized vessel networks. Comput Math Appl (2008) 55:1594–600. doi:10.1016/j.camwa.2007.08.019

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Ouared R, Chopard B. Lattice Boltzmann simulations of blood flow: Non-Newtonian rheology and clotting processes. J Stat Phys (2005) 121:209–21. doi:10.1007/s10955-005-8415-x

CrossRef Full Text | Google Scholar

31. Clausen JR, Reasor DA, Aidun CK. Parallel performance of a lattice-Boltzmann/finite element cellular blood flow solver on the IBM Blue Gene/P architecture. Comp Phys Commun (2010) 181:1013–20. doi:10.1016/j.cpc.2010.02.005

CrossRef Full Text | Google Scholar

32. Spieker CJ, Závodszky G, Mouriaux C, Van Der Kolk M, Gachet C, Mangin PH, et al. The effects of micro-vessel curvature induced elongational flows on platelet adhesion. Ann Biomed Eng (2021) 49:3609–20. doi:10.1007/s10439-021-02870-4

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Succi S. The lattice Boltzmann equation for fluid dynamics and beyond. Oxford : New York: Clarendon Press ; Oxford University Press (2001).

Google Scholar

34. Qian YH, D’Humières D, Lallemand P. Lattice BGK models for Navier-Stokes equation. Europhys Lett (1992) 17:479–84. doi:10.1209/0295-5075/17/6/001

CrossRef Full Text | Google Scholar

35. Ziegler DP. Boundary conditions for lattice Boltzmann simulations. J Stat Phys (1993) 71:1171–7. doi:10.1007/BF01049965

CrossRef Full Text | Google Scholar

36. Diamond SL. Systems analysis of thrombus formation. Circ Res (2016) 118:1348–62. doi:10.1161/CIRCRESAHA.115.306824

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Mehrabadi M, Casa LDC, Aidun CK, Ku DN. A predictive model of high shear thrombus growth. Ann Biomed Eng (2016) 44:2339–50. doi:10.1007/s10439-016-1550-5

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Westein E, Van Der Meer AD, Kuijpers MJE, Frimat J-P, Van Den Berg A, Heemskerk JWM. Atherosclerotic geometries exacerbate pathological thrombus formation poststenosis in a von Willebrand factor-dependent manner. Proc Natl Acad Sci USA (2013) 110:1357–62. doi:10.1073/pnas.1209905110

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Li M, Hotaling NA, Ku DN, Forest CR. Microfluidic thrombosis under multiple shear rates and antiplatelet therapy doses. PLoS ONE (2014) 9:e82493. doi:10.1371/journal.pone.0082493

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Schneider SW, Nuschele S, Wixforth A, Gorzelanny C, Alexander-Katz A, Netz RR, et al. Shear-induced unfolding triggers adhesion of von Willebrand factor fibers. Proc Natl Acad Sci USA (2007) 104:7899–903. doi:10.1073/pnas.0608422104

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Casa LDC, Ku DN. Thrombus Formation at high shear rates. Annu Rev Biomed Eng (2017) 19:415–33. doi:10.1146/annurev-bioeng-071516-044539

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Kim D, Bresette C, Liu Z, Ku DN. Occlusive thrombosis in arteries. APL Bioeng (2019) 3:041502. doi:10.1063/1.5115554

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Brown ST, Buitrago P, Hanna E, Sanielevici S, Scibek R, Nystrom NA. Bridges-2: A platform for rapidly-evolving and data intensive research. In: Practice and experience in advanced research computing. Boston MA USA: ACM (2021). p. 1. doi:10.1145/3437359.3465593

CrossRef Full Text | Google Scholar

44. Grande Gutiérrez N, Sinno T, Diamond SL. A 1D–3D hybrid model of patient-specific coronary hemodynamics. Cardiovasc Eng Tech (2022) 13:331–42. doi:10.1007/s13239-021-00580-5

CrossRef Full Text | Google Scholar

45. Pfaller MR, Pham J, Verma A, Pegolotti L, Wilson NM, Parker DW, et al. Automated generation of 0D and 1D reduced-order models of patient-specific blood flow. Numer Methods Biomed Eng (2022) 38:e3639. doi:10.1002/cnm.3639

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Anand M, Rajagopal K, Rajagopal KR. A model for the formation, growth, and lysis of clots in quiescent plasma. A comparison between the effects of antithrombin III deficiency and protein C deficiency. J Theor Biol (2008) 253:725–38. doi:10.1016/j.jtbi.2008.04.015

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Lee YK, Sinno T. Analysis of the lattice kinetic Monte Carlo method in systems with external fields. J Chem Phys (2016) 145:234104. doi:10.1063/1.4972052

PubMed Abstract | CrossRef Full Text | Google Scholar