- Department of Physics and Astronomy, Hearne Institute of Theoreticale Physics, Louisiana State University, Baton Rouge, LA, United States
We report results for the superconducting transition temperature and anisotropic energy gap for pure niobium based on Eliashberg’s equations and electron and phonon band structures computed from density functional theory. The electronic band structure is used to construct the Fermi surface and calculate the Fermi velocity at each point on the Fermi surface. The phonon bands are in excellent agreement with inelastic neutron scattering data. The corresponding phonon density of states and electron–phonon coupling define the electron–phonon spectral function, α2F(p, p′; ω), and the corresponding electron–phonon pairing interaction, which is the basis for computing the superconducting properties. The electron–phonon spectral function is in good agreement with existing tunneling spectroscopy data except for the spectral weight of the longitudinal phonon peak at ℏωLO = 23 meV. We obtain an electron–phonon coupling constant of λ = 1.057, renormalized Coulomb interaction μ⋆ = 0.218, and transition temperature Tc = 9.33 K. The corresponding strong-coupling gap at T = 0 is modestly enhanced, Δ0 = 1.55 meV, compared to the weak-coupling BCS value
1 Introduction
The electronic properties of niobium (Nb) and its alloys are central to the development of superconducting radio frequency (SRF) cavity technology for particle accelerators, as well as applications to device technologies for quantum computing and sensing applications [1, 2]. In particular, the role of disorder in the low-power quantum limit for the performance of superconducting Nb SRF cavities is an active area of research [3, 4]. Nitrogen-doped (N-doped) Nb, with quality factors of order Q ≈ 1011 and accelerating gradients as high as 45 MV/m, is also the superconductor of choice for SRF cavities used for high-energy accelerators [5]. However, even for state-of-the-art cavities, there is room for improved performance, both in terms of the quality factor as well as the maximum accelerating gradient. Impurities and structural defects, nano-scale inclusions, and two-level tunneling centers all impact the electromagnetic response of the current-carrying region near the vacuum-superconducting interface, sometimes in counter-intuitive ways [6]. In order to obtain a deeper understanding of the multiple roles in which impurities and defects impact the performance of Nb superconducting cavities, films, and devices, we develop the theory of moderately disordered superconducting Nb starting from first-principles theory of pure Nb informed by experimental data for the metallic and superconducting properties of high-purity bulk Nb. This report focusses on the zero-field equilibrium superconducting properties of pure Nb obtained from Eliashberg’s theory for electron–phonon-mediated superconductivity [7] with electronic structure, phonon structure, and the electron–phonon coupling obtained from density functional theory (DFT) [8, 9]. We then investigate the effects of impurity disorder on N-doped Nb.
The anisotropy of the electron–phonon coupling, angle-resolved density of states, and thus, the pairing amplitude for different momenta on the Fermi surface, combined with quasiparticle-impurity scattering, leads to violation of Anderson’s theorem [10] and, thus, a suppression of the superconducting transition temperature that increases with the impurity scattering rate. The suppression of Tc by non-magnetic impurity disorder on conventional anisotropy superconductors such as Nb provides an excellent diagnostic of the impurity scattering rate in films and cavities. In a separate report, we build these results into a theory for the microwave response of Nb with impurity and surface disorder [11].
2 Eilenberger/Eliashberg theory
The results reported here are based on the strong-coupling theory of electron–phonon-mediated superconductivity in metallic alloys as formulated by Eliashberg, Eilenberger, and Larkin and Ovchinnikov [7, 12–14]. We use the notation of [15] which includes development of the theory from the formal quantum field theoretical equations for interacting Fermi systems. For equilibrium states of superconductors, a central object of the theory is the 4 × 4 Nambu matrix propagator.
The diagonal element is the 2 × 2 quasiparticle propagator,
The off-diagonal element,
2.1 Eilenberger’s equations
The quasiparticle and anomalous pair propagators, organized into 4 × 4 Nambu matrices, obey Gorkov’s equations [16]. Eilenberger transformed Gorkov’s equations into a matrix transport-type equation for the matrix propagator [13]:
In contrast to Gorkov’s equation, which is a second-order differential equation with a unit source term originating from the Fermion anti-commutation relations, Eilenberger’s equation is a homogeneous, first-order differential equation describing the evolution of the matrix propagator along classical trajectories in phase space (p, r) defined by the Fermi velocity, vp = ∇pɛp, where ɛp is the excitation energy of a normal-state electronic quasiparticle relative to the Fermi energy. Eilenberger’s transport equation determines the equilibrium propagator, including inhomogeneous states generated by an external magnetic field and/or a spatially varying pairing self-energy,
which enforces the spectral weight implied by the source term in Gorkov’s equation. The physical properties of a particular superconducting material are encoded in the self-energy functional,
The leading order contributions to the electronic self-energy for elemental superconductors like Nb are shown in Figure 1. The diagram in Figure 1A shows the leading order self-energy,
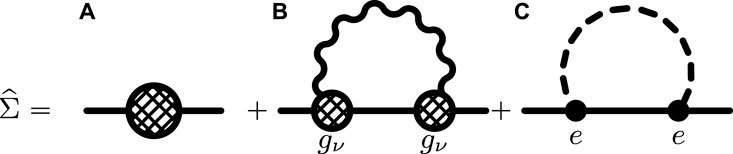
FIGURE 1. The leading order electronic self-energy diagram (A) determines the Fermi surface, Fermi velocity, and electronic contribution to the effective mass. Next to leading order: (B) Diagram showing this exchange of a branch ν phonon of momentum q and energy ων(q) represented by the phonon propagator,
2.1.1 Electron–phonon self-energy
The electron–phonon self-energy in Figure 1B provides the attractive interaction, leading to superconductivity in most elemental superconductors [7, 20]. Phonon-mediated interactions are retarded in time, and as a consequence, the self-energy,
We use the short-hand notation p to denote a point on the Fermi surface, which, in general, will have multiple sheets within the first Brillouin zone (FBZ), ∫dp(…) ≡∫dSp n(p) (…), where the integral is over the area of the Fermi surface and n(p) is the anisotropy of the normal-state density of states normalized to ∫dp(1) ≡ 1. For conventional spin-singlet pairing, and neglecting spin-dependent interactions, the electron–phonon self-energy reduces to
The diagonal and off-diagonal self-energies are given by
where the phonon-mediated electron–electron interaction,
is determined by the electron–phonon coupling,
where
is the angle-resolved electron–phonon spectral function. Equation 10 is the generalization of the Eliashberg function, α2F(ω), for anisotropic electron–phonon interactions. The latter can be defined as the Fermi-surface-averaged spectral function,
and is the spectral function that is often obtained from the analysis of tunneling conductance data for strong-coupling superconductors [21–23].
2.1.2 Electronic pairing self-energy
The leading order contribution to the electron–electron self-energy is represented by the diagram in Figure 1C, which is generated by the renormalized Coulomb interaction, Vee(p, p′; ɛn, ɛn′), and it represents electron–electron scattering contributions to the self-energy in both the particle–hole (Landau) and particle–particle (Cooper) channels. The renormalized electron–electron interaction that defines the electron–electron self-energy,
The renormalized electron–electron interaction in the Cooper channel can be expressed in terms of dimensionless interaction potentials,
that separate into spin-singlet (total spin S = 0) and spin-triplet (S = 1) channels, labeled by superscripts, (s, t), with corresponding interactions between pairs of quasiparticles with zero total momentum, μ(s)(p, p′) and μ(t)(p, p′), respectively. For Nb, the triplet pairing channel is at best sub-dominant to the singlet channel. Thus, we ignore triplet pairing correlations for the homogeneous equilibrium state of Nb. As a result, the electron–electron anomalous propagator and off-diagonal self-energy have the spin-singlet form:
where
In the absence of retardation resulting from the coupling to long-lived collective excitations, e.g., spin fluctuations, then to leading order in
For electron–phonon-mediated superconductors like Nb, the Cooper instability is in the “conventional” spin-singlet, A1g, channel. Thus, we need retain only the spin singlet, A1g, component of μ(s)(p, p′). The corresponding renormalized electron–electron interaction is repulsive and competes with the attractive electron–phonon-mediated pairing interaction, suppressing the instability temperature to superconductivity.
In what follows, we neglect the angular dependence of the renormalized electron–electron interaction, in which case μ(s)(p, p′) → μ represents the isotropic average of the static screened Coulomb interaction. The accurate calculation of Coulomb interaction is beyond DFT, but it is estimated from the static screened Coulomb interaction for an electron–ion plasma, defined here as μ = NfVee. The cutoff that regulates the electron–electron contribution to the gap equation is Ω ∼ Ef ≫ ℏωD, where Ef is the Fermi energy and ωD is the Debye frequency. However, the cutoff, ωc, that we introduce to regulate the electron–phonon contribution to the gap equation is ωD < ωc ≪Ω. In Section 4.1, we describe the procedure used to determine the low energy cutoff ωc, which includes renormalization of the Coulomb interaction, μ → μ⋆, such that we obtain a single gap equation for Δ with the low-energy cutoff ωc.
The spatially homogeneous solution to Eqs 2, 3 for the Nambu matrix propagator reduces to
with the renormalized Matsubara energy and pairing self-energy defined by
If the anisotropy of the pairing self-energy is negligible, then we can simplify Eqs 17, 18 by averaging the electron–phonon spectral function to obtain Eq. 11, and the reduction of Eqs 17, 18 to the simpler set of integral-sum equations gives
where the electron–phonon coupling function averaged over the Fermi surface is
with α2F(ω) defined by Eqs 11, 10. Isotropic Eliashberg’s equations are the correct limiting equations for strong-coupling superconductors in the extreme dirty limit, 1/τ > ωD, where the diffusive motion of electrons averages the electron–phonon interaction over the Fermi surface and the full bandwidth, ωD, of the phonon spectrum [17]. In Section 4.3, we examine the effect of scattering by a random impurity potential and calculate Tc in anisotropic superconducting Nb as a function of the quasiparticle-impurity scattering rate for disorder with 1/τ ≪ωD. Our theory for the suppression of Tc is expected to be accurate for disorder in the weak up to dirty limit, ℏ/2πτkBTc ≲ 1, with corrections of order 1/ωDτ ≪ 1.
3 Electronic structure
The electronic structure and the superconducting state of Nb have been the subject of considerable theoretical, computational, and experimental investigation [22, 26–35]. Accurate results for the energy levels and dispersion relations for electrons and phonons, as well as the interaction between electrons and phonons, are essential for calculating the superconducting properties of Nb [17]. We first obtain the electronic band structure and phonon dispersion relations for Nb using Quantum ESPRESSO (QE) which is an integrated suite of open-source computer codes for electronic structure calculations and material modeling at the atomic scale. QE is based on DFT, plane waves, and pseudo-potentials [18, 19]. From the electronic band structure data, we then construct the Fermi surface and calculate the Fermi velocity at each point on the Fermi surface. The anisotropy of the Fermi velocity plays a central role in determining the anisotropy of the upper critical field of Nb [36, 37]. We obtain the electron–phonon interaction and phonon spectral function and use Eliashberg theory to calculate the superconducting order parameter (“gap function”) as a function of momentum on the Fermi surface and for energies within the phonon bandwidth of attraction.
Gap anisotropy plays a key role in pair-breaking processes associated with impurity and boundary scattering. In particular, the combination of branch conversion scattering induced by impurity scattering leads to suppression of the superconducting transition temperature. We compute the suppression of Tc using self-consistent T-matrix theory for quasiparticle-impurity scattering for the broad class of anisotropic superconductors and use the result to predict the suppression of Tc of Nb doped with non-magnetic impurities. We compare our results with reports of the suppression of Tc for N-doped Nb SRF cavities as well as disordered Nb films in Section 4.3.
Bulk single crystals of Nb have the BCC lattice structure with lattice constant a = 3.3 Å and atomic weight of M = 92.906. The electron configuration of the Nb atom is [Kr]4d45s1, which generates 24 electronic bands. Superconductivity develops from pairing of electrons and holes in a narrow band of energies near the Fermi surface. An accurate calculation of the superconducting order parameter (“gap”) requires numerical integration over fine grids in momentum space for the energy levels of electrons and phonons. A direct calculation of the electron and phonon band structures, as well as the electron–phonon coupling and spectral function, on fine grids is computationally demanding. A more efficient approach was developed in [38–41]. The method is to calculate the electronic bands on a coarse grid in momentum space, but over a wider bandwidth around the Fermi surface, then Fourier transform to coordinate space and find maximally localized Wannier functions. The wider energy bandwidth results in more accurate Wannier functions. Once determined, one can Fourier transform back to a finer grid in momentum space.
Figure 2 shows the two lowest-energy electronic bands of Nb that cross the Fermi energy (defined as zero) for the course grid of k = 183 points in the FBZ calculated using QE. The right panel of Figure 2 shows the electronic density of states (DOS) for the same low-energy bandwidth. Using the band structure calculated for a uniform k-grid and the value of the Fermi energy output from QE Ef = 18.096 eV, we construct the Fermi surface using the marching cube algorithm to identify the Fermi surface in momentum space [42]. The result is shown in Figure 3 for two sheets of the Fermi surface using a grid of k = 983. The left panel of Figure 3 shows the Fermi surface sheet referred to as the “jack” centered at the Γ point, while the right panel shows the open Fermi sheet referred to as the “jungle gym,” also centered at the Γ point, and the “ellipsoids” centered on the N points.
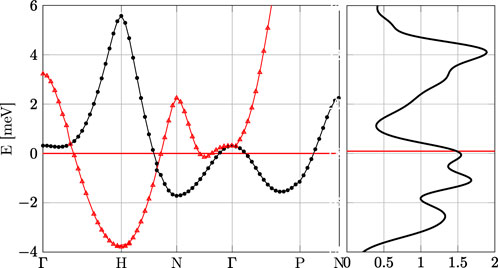
FIGURE 2. The red line is the Fermi energy which we define as zero energy. Shown are the two electronic bands of niobium within the phonon bandwidth that cross the Fermi energy. The right panel shows the electronic density of states in units of eV−1 per atom. The total DOS at the Fermi level is Nf ≃ 1.49 eV−1 per atom.
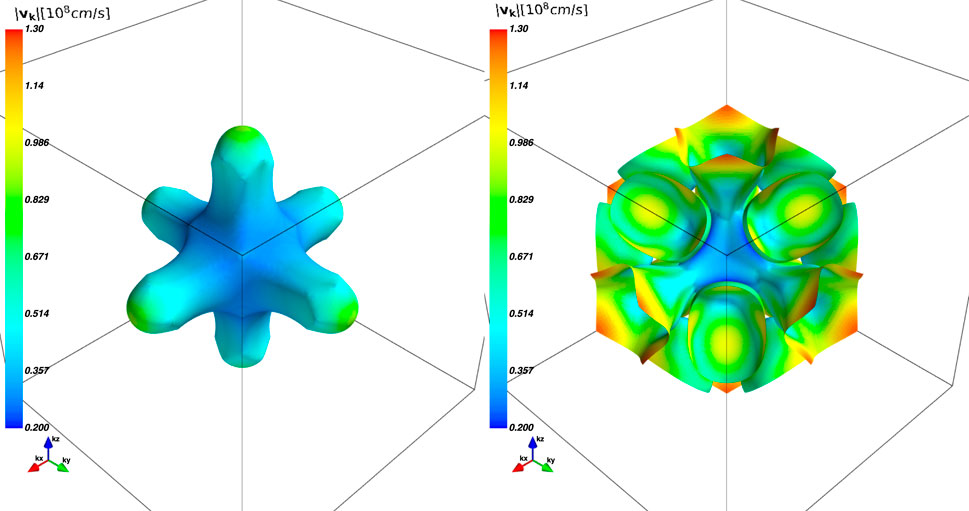
FIGURE 3. Anisotropy of the Fermi velocity shown on the two sheets of the Fermi surface. The box spans [−π/2a, π/2a] in k-space along each direction for the first sheet (left panel) and [−π/a, π/a] for the second sheet (right panel).
From the band dispersions near the Fermi energy, we calculated the group velocity, vp = ∇pεp, evaluated at the Fermi energy, i.e., the Fermi velocity, at each point on the Fermi surface. The color map shown in Figure 3 indicates the magnitude of Fermi velocity at each point on the Fermi surface. There is substantial anisotropy of the Fermi velocity with a maximum velocity of
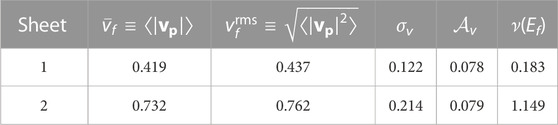
TABLE 1. Mean Fermi velocity, the rms Fermi velocity, and the standard deviation of the distribution of Fermi velocities, in units of 108 cm/s. In addition, the dimensionless anisotropy parameter,
3.1 Phonon band structure
The phonon band structure is calculated based on the electronic structure calculations and the Born–Oppenheimer approximation. For the purposes of calculating the phonon energy levels and band structure, this allows one to decouple the dynamics of the electronic subsystem from the lattice dynamics. Thus, the ground state energy of the electronic system is calculated for the fixed ionic positions. The resulting total energy of the electronic system, Eel(R1, R2, … , RN), serves as a potential energy function for the ionic Hamiltonian. By displacing the atoms by small amounts, {ui, i = 1, .., N}, relative to the Bravais lattice sites, the electronic ground state for displaced ions is calculated. The ionic lattice energy is then expanded in displacements of the ions relative to their equilibrium BCC lattice configuration. The first derivatives of the energy functional vanish, and the set of second derivatives provides a matrix of interactions between displaced ions. The Fourier transform of this matrix with respect to relative displacements gives the dynamical matrix whose eigenvalues determine the phonon energies, ων(q), where ν is the phonon branch index and q is the phonon wavevector. The dynamical matrix is calculated using the QE code for a discrete grid of wavevectors q belonging to the unit cell in reciprocal space [9]. Since the dynamical matrix is a smooth function of q, it is usually sufficient to evaluate the matrix on a sparse grid in reciprocal space, then perform a discrete Fourier transform to the position space, restrict the inter-atomic forces to a few lattice spacings, and finally, transform back to momentum space to obtain the dynamical matrix on a much finer grid in reciprocal space. The eigenvalues of the resulting dynamical matrix generate the phonon dispersion relations evaluated on the dense grid in reciprocal space [9]. Figure 4 shows the results of our calculation of the phonon modes based on an electronic grid of k = 183 and a phonon grid of q = 63 and the comparison with the mode frequencies obtained from inelastic neutron scattering [31].
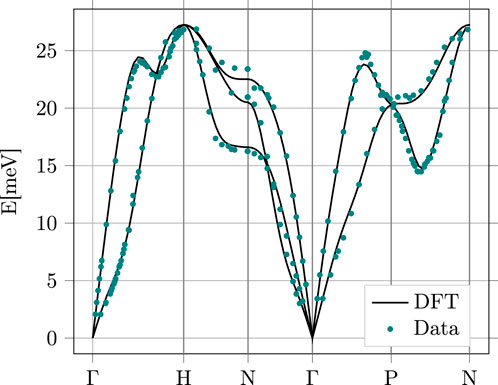
FIGURE 4. Calculated phonon energies (solid lines) for Nb based on QE along various directions in the FBZ. The green data points are the phonon energies obtained from inelastic neutron scattering [31].
3.2 Electron–phonon coupling
The retarded electron–phonon interaction defined by Eqs 9 and 10 depends on the electron–phonon matrix element,
The self-consistent electron–nucleus interaction potential, V(r − R), is calculated for small ion displacements, u = R − RBL, where RBL is an equilibrium Bravais lattice site. The directional derivative in Eq. 23 is defined by the polarization vector of the phonon,
4 Results
We use EPW, which is an integral part of QE, to compute the electron–phonon matrix elements. The calculation of these quantities requires dense grids in reciprocal space. To achieve such dense grids, it is efficient to Fourier transform the Kohn–Sham orbitals to position space, construct optimally localized Wannier functions, and then, Fourier transform back to obtain a dense grid in momentum space [43–45].
From the electron–phonon matrix elements and the phonon spectrum, the electron–phonon spectral function and pairing interaction function are computed using Eqs 9, 10. The corresponding Fermi-surface-averaged quantities, Eqs 11, 21, are calculated by averaging over the Fermi surface.
4.1 Isotropic Eliashberg theory
The isotropic electron–phonon spectral function, α2F(ω), is related to the differential conductance for NIS tunneling into strong-coupling superconductors [22, 29, 30, 32, 46]. For comparison, we show the results reported in [23] for Nb in Figure 5 in comparison with our result for the calculated spectral function using EPW. The low-frequency values are in reasonable agreement with the data from tunneling experiments; however, there are deviations for the phonon modes near the zone boundary, particularly the high-frequency longitudinal phonon near ℏωLO = 23 meV. The transverse phonon peak is calculated to be slightly higher in frequency than the experimental peak at 15.75 meV. Previous ab initio calculations also report higher spectral weight for the longitudinal phonon peak than that obtained from tunneling spectroscopy [33, 47]. As other authors have noted, determination of α2F(ω) from tunneling spectroscopy is subject to a number of interface effects that may complicate an accurate inversion of the tunneling data for the electron–phonon coupling function [22, 23, 32, 33].
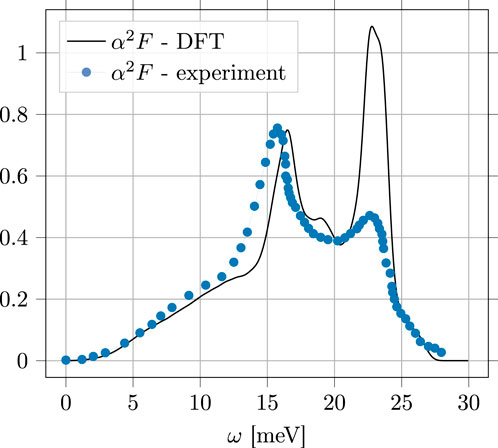
FIGURE 5. Calculated Fermi-surface-averaged α2F(ω) as a function of phonon frequency (solid line) and experimental data (blue dots and line) derived from tunneling spectroscopy [23].
From the calculated result for α2F(ω) shown in Figure 5, the average electron–phonon coupling is calculated to be
This result compares with the value of 1.14 obtained in [48] based on de Hass–van Alphen measurements, as well as tunneling spectroscopy, 1.04 from [49] and 0.98 from [46].
The Fermi-surface-averaged electron–phonon spectral function α2F(ω) is used to calculate the superconducting order parameter and Tc from the isotropic Eliashberg equations, Eqs 19, 20, as a function of energy within the phonon bandwidth and as a function of temperature. For pure Nb with a transition temperature of Tc = 9.33 K and momentum grids of k = q = 513, we obtain a renormalized Coulomb interaction of μ⋆ = 0.218 for a cutoff of ωc = 3ωD. This value of μ⋆ is close to the experimentally determined value of 0.24 based on the analysis of de Hass–van Alphen data [48]. The theoretical value might be slightly smaller as μ⋆ tends to decrease for finer momentum grids. In particular, for a coarser grid with k = q = 363, we obtain μ⋆ = 0.260 with no change in Δ(T).
Figure 6 shows the calculated gap function for T = 1 K as a function of Matsubara frequency (smooth black curve), as well as both real and imaginary components of ΔR(ɛ) obtained by analytic continuation to the real frequency axis. The QE code calculates ΔR(ɛ) from the gap equation analytically continued to the real axis, as well as by numerical continuation using Padé approximates of Δ(ɛn) defined on Matsubara frequencies. The results are shown in Figure 6.
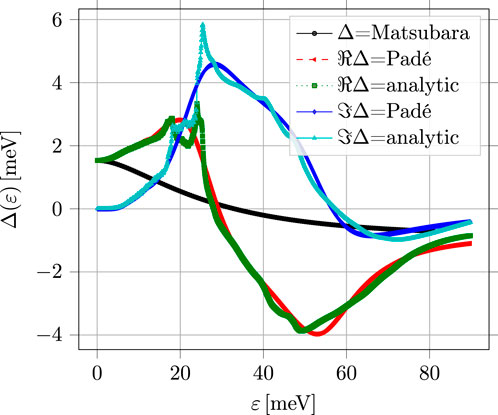
FIGURE 6. Superconducting gap Δ(ɛ) at T =1.0 K as a function of Matsubara energy ɛn (black circles). The real and imaginary parts of the gap function calculated from the gap equation defined on the real energy axis are labeled ‘analytic.’ The same functions obtained by numerical continuation of the Matsubara gap function using Padé approximates are labeled ‘Padé.’
For strong-coupling superconductors, the gap obtained using tunneling conductance spectroscopy is identified with Δ(ɛn → πkBT). Figure 7 shows the tunneling gap as a function of the temperature. The value of the gap at zero temperature is Δ0 = 1.55 meV and a transition temperature of Tc = 9.33 K. This result is also in reasonable agreement with the value of 1.5 meV reported by several independent studies based on tunneling spectroscopy [23, 26, 50]. This corresponds to a modest enhancement of the zero-temperature gap compared to the weak-coupling BCS prediction of

FIGURE 7. Superconducting gap as a function of temperature (dots and solid line) for momentum grids of k = 513, q = 513 and μ⋆ = 0.218. The dashed line is the result for the gap calculated using the weak-coupling BCS theory.
The low-energy cutoff, ωc, is chosen such that the solution of the Eliashberg equation for
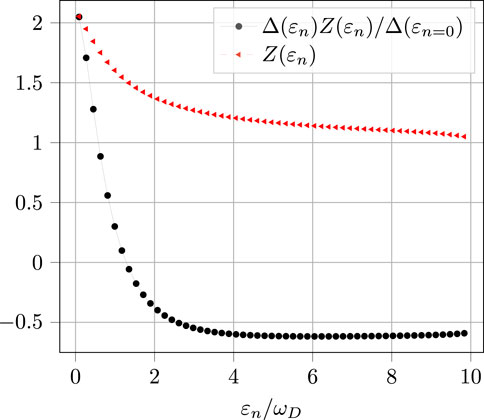
FIGURE 8. Diagonal and off-diagonal self-energy function, derived by solving Eliashberg equations, as a function of ɛn/ωD, where ɛn = (2n + 1)πkBT is the Matsubara frequency.
4.2 Anisotropic Eliashberg theory
Anisotropy of the electron–phonon coupling function, λ(p, p′; ωm), and, thus, the superconducting gap function, Δ(p; ɛn), is an important and widely discussed topic [36, 51–58]. Our analysis implies measurable gap anisotropy for pure Nb and shows that the electron–phonon matrix element and phonon density of states are anisotropic functions of the momenta on the Fermi surface. The anisotropy of α2F(p, p′; ω) generates an anisotropic pairing self-energy, Δ(p; ɛn), obtained using EPW as the solution of anisotropic Eliashberg Eqs 17, 18. The EPW code calculates ΔR(p; ɛ) in an energy shell of order δɛ = 1 eV around the Fermi surface. This rather thick shell is required in order to obtain accurate results for the self-energies. We then determine the Fermi momentum and Δ(p; ɛn) on the Fermi surface by linear interpolation.
Our results for the magnitude of the gap evaluated at the lowest Matsubara frequency, Δ(p) ≡Δ(p; ɛ0 = πkBT), are shown in Figure 9 for T = 3.0 K, λ = 1.057, and μ⋆ = 0.218 for both sheets of the Fermi surface. The gap varies from Δmin = 1.09 meV to Δmax = 2.20 meV. However, the maximum and minimum gap values are confined to rather small regions of the Fermi surface. Table 2 provides a measure of the distribution of gap values on the Fermi surface. At low temperatures, the mean value of the gap averaged over the Fermi surface is dominated by band 2 with
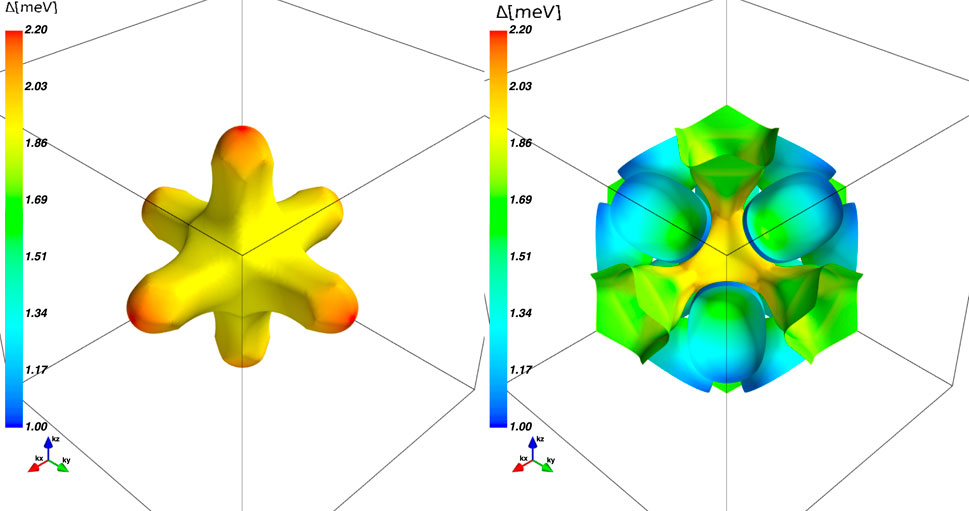
FIGURE 9. The color map indicates the value of Δ(p) at T = 3.0 K at each point of the Fermi surface for the two sheets. The box spans [−π/2a, π/2a] in k-space along each direction for the first sheet (left panel) and [−π/a, π/a] for the second sheet (right panel). The average gap, rms average gap, and the dimensionless gap anisotropy parameter are given in Table 2.
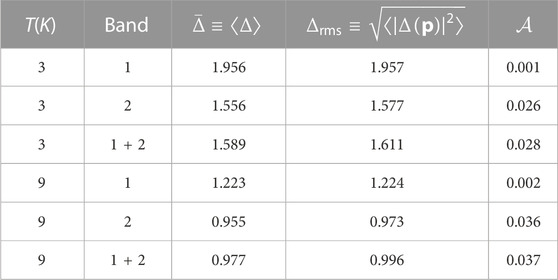
TABLE 2. The average gap,
It should be noted that this measure of the gap anisotropy varies from 0.028 at T = 3.0 K to 0.037 for T = 9.0 K, consistent with the expectation based on Eq. 18 that the anisotropy is maximum for
4.3 Anisotropy, disorder, and pair-breaking
Elemental metals such as Al, Nb, Pb, Sn, and Hg are conventional superconductors in the sense that the order parameter, Δ(p), reflects the symmetry of the Fermi surface or equivalently the point group symmetry of the normal metallic phase. Anisotropy of the gap function, Δ(p), for momenta on the Fermi surface is, in principle, observable in a number of physical properties: anisotropy of the upper critical field, anisotropy of Meissner screening currents with respect to surface and crystal orientation, and more generally, the a.c. electromagnetic response.
Elastic scattering by a random potential such as a dilute concentration of impurities embedded in the metal leads to finite lifetimes for the momentum of ballistic quasiparticles and to charge diffusion after several scattering events. For non-magnetic impurities, the transition temperature and excitation gap are unmodified in isotropic (“s-wave”) superconductors. This result, widely referred to as “Anderson’s theorem,” is derived from the common renormalization of the spectrum of quasiparticles and Cooper pairs for elastic scattering by the random potential. However, anisotropy of the pairing interaction, and, thus, the Cooper pair wave function on the Fermi surface, leads to pair-breaking and violation of the Anderson theorem even for non-magnetic impurities. This effect was first studied by Markowitz and Kadanoff [59], Hohenberg [60], and Maier [61] for Born scattering by impurities. These authors obtained approximate results for the change in Tc with impurity scattering rate in several limits. Experimental studies of gases, in particular oxygen and nitrogen, dissolved in Nb showed the suppression of Tc for concentrations below a few percent [62, 63] (c.f. Figure 4 in [63]). The analyses we report further provide quantitative predictions for the pair-breaking suppression of Tc by non-magnetic impurities in anisotropic superconductors and are restricted to neither the Born limit for quasiparticle-impurity scattering nor weak anisotropy.
The theory of superconducting alloys, as originally formulated by A. Abrikosov and L. Gorkov [64] and by P. W. Anderson [10], is a generalization of S. Edwards’ theory of dilute random impurities in metals [65]. Disorder is treated as a statistical ensemble of random, homogeneously distributed, uncorrelated impurities. Thus, to calculate the effects of quasiparticle scattering by a dilute concentration of impurities on the properties of Nb, we consider the scattering of quasiparticles and pairs by a static impurity, i.e., the processes represented diagrammatically in Figure 10, corresponding to the Bethe–Salpeter equation,
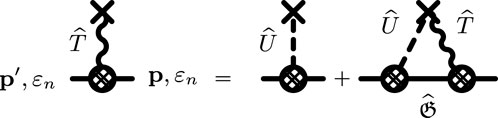
FIGURE 10. Leading order impurity scattering T-matrix. The internal propagator is the self-consistently determined Nambu propagator.
The equation for the Nambu T-matrix describes multiple scattering by a single impurity, with the intermediate states defined by the self-consistently determined Nambu matrix propagator. The leading order electron-impurity self-energy is then given by the T-matrix evaluated in the forward-scattering limit,
and the mean impurity density, ns. This mean-field impurity self-energy omits contributions from intermediate states involving scattering off more than one impurity. These terms are higher order in the small parameter, s = ℏ/pfℓei, where ℓei = vfτei is the mean-free path for elastic scattering of normal-state quasiparticles by impurities.
For “point-like” impurities, only the s-wave scattering channel contributes significantly to the T-matrix,
where U0 is the s-wave matrix element of the impurity potential. The term proportional to the unit matrix does not contribute to static equilibrium properties, and the prefactor of the term proportional to
where the second equality is the expression for the scattering rate in terms of the normal-state s-wave scattering phase shift, δ0, with
In what follows, we neglect retardation effects of the electron–phonon coupling. For Nb with kBTc/ωc ≈ 0.07 [32], retardation effects are relatively small, which includes the electromagnetic response of Nb at microwave frequencies, ℏω ≪ 2Δ0 [11]. At much higher frequencies, phonons are observable in the optical absorption spectrum for frequencies just above the gap [15, 66]. Thus, for the purposes of calculating the effects of disorder on the superconducting transition, we replace λ(p, p′; ɛn − ɛn′) → λ(p, p′; 0)Θ(ωc − |ɛn|)Θ(ωc − |ɛn′|).
The anisotropy of the gap function is determined by the momentum dependence of the electron–phonon coupling and angle-resolved quasiparticle density of states at the Fermi energy via the linearized gap equation.
where
where λΓ is the strength of the pairing interaction in the channel labeled by Γ. The most attractive interaction determines the highest instability temperature and, thus, the superconducting transition temperature, Tc. The corresponding eigenfunctions determine the pairing symmetry and gap anisotropy.
In Eq. 31, the renormalized Matsubara energy and pairing self-energy reduce to
where 1/τ is the normal-state quasiparticle-impurity scattering rate and ⟨(…)⟩ = ∫dp(…) is the average over the Fermi surface.
We project out the dominant pairing channel and set
It should be noted that for conventional superconductors, the superconducting order parameter is in general anisotropic but retains the full symmetry of the crystal point group; i.e.,
It is useful to cast the linearized gap equation as an equation for Tc as a function of 1/τ and the transition temperature,
which is the dimensionless measure of the gap anisotropy at Tc. For an isotropic “s-wave” superconductor,
Thus, in general, anisotropy of the pairing interaction combined with elastic scattering off the disorder potential leads to suppression of the superconducting transition, which is obtained from the solution of Eq. 36 with
For weak pair-breaking,
It should be noted that the pair-breaking parameter,
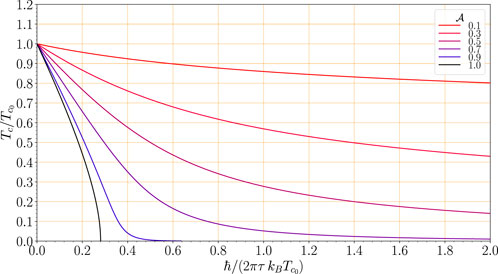
FIGURE 11. Suppression of Tc by disorder over a wide range of possible gap anisotropy values. It should be noted that for
For anisotropic conventional superconductors with
4.4 Tc versus disorder in Nb
The suppression of Tc for Nb with the anisotropy ratio calculated from the anisotropic Eliashberg theory using EPW is shown in Figure 12. The combination of scattering by the disorder potential and anisotropy of the electron–phonon coupling can suppress Tc from

FIGURE 12. Suppression of Tc by disorder from Eq. 36 for Nb with gap anisotropy parameter
5 Conclusion
A first-principles calculation of superconducting properties of pure Nb single crystals depends on accurate determination of the electron–phonon coupling solutions of the anisotropic Eliashberg equations. We used the QE code for BCC Nb to obtain the electron–phonon spectral function that best agrees with available tunneling experiment data. Our result for α2F(ω) is in good agreement with existing tunneling spectroscopy data except for the spectral weight of the longitudinal phonon peak at ℏωLO = 23 meV. We obtain an electron–phonon coupling constant of λ = 1.057, renormalized Coulomb interaction, μ⋆ = 0.218 for a transition temperature of Tc = 9.33 K. The corresponding strong-coupling gap at T = 0 is modestly enhanced, Δ0 = 1.55 meV, compared to the weak-coupling BCS value
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
MZ: Data curation, Formal Analysis, Investigation, Methodology, Software, Validation, Visualization, Writing–review and editing. HU: Formal Analysis, Investigation, Methodology, Writing–review and editing. JS: Conceptualization, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Software, Supervision, Visualization, Writing–original draft, Writing–review and editing.
Funding
The authors declare financial support was received for the research, authorship, and/or publication of this article. The work of MZ was supported by National Science Foundation Grant PHY-1734332. The work of HU and JS was supported by the U.S. Department of Energy, Office of Science, National Quantum Information Science Research Centers, Superconducting Quantum Materials and Systems Center (SQMS), under contract number DE-AC02-07CH11359.
Acknowledgments
The authors thank Drs. D. Bafia, A. Grassellino, and A. Romanenko of Fermilab for discussions and for sharing their results on high-Q SRF cavities which motivated this study.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The authors declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1For simplicity and relevance to conventional superconductors such as Nb, we consider only one-dimensional irreps.
2γE ≃ 0.577216 … is the Euler–Mascheroni constant.
References
1. Gurevich A. Superconducting radio-frequency fundamentals for particle accelerators. Rev Accelerator Sci Technol (2012) 5:119–46. doi:10.1142/S1793626812300058
2. Reagor M, Pfaff W, Axline C, Heeres RW, Ofek N, Sliwa K, et al. Quantum memory with millisecond coherence in circuit QED. Phys Rev B (2016) 94:014506. doi:10.1103/PhysRevB.94.014506
3. Romanenko A, Schuster DI. Understanding quality factor degradation in superconducting niobium cavities at low microwave field amplitudes. Phys Rev Lett (2017) 119:264801. doi:10.1103/PhysRevLett.119.264801
4. Lee J, Sung Z, Murthy AA, Reagor M, Grassellino A, Romanenko A. Discovery of Nb hydride precipitates in superconducting qubits (2022). https://arxiv.org/abs/2108.10385. doi:10.48550/arXiv.2108.10385
5. Grassellino A, Romanenko A, Trenikhina Y, Checchin M, Martinello M, Melnychuk OS, et al. Unprecedented quality factors at accelerating gradients up to 45 MVm−1 in niobium superconducting resonators via low temperature nitrogen infusion. Supercond Sci Tech (2017) 30:094004. doi:10.1088/1361-6668/aa7afe
6. Ngampruetikorn V, Sauls JA. The effect of inhomogeneous surface disorder on the superheating field of superconducting RF cavities. Phys Rev Res (2019) 1:012015. doi:10.1103/PhysRevResearch.1.012015
7. Eliashberg GM. Temperature green’s function for electrons in a superconductor. Sov Phys JETP (1961) 12:1000–2.
8. Kohn W, Sham LJ. Self-consistent equations including exchange and correlation effects. Phys Rev (1965) 140:A1133–A1138. doi:10.1103/PhysRev.140.A1133
9. de Gironcoli S. Lattice dynamics of metals from density-functional perturbation theory. Phys Rev B (1995) 51:6773–6. doi:10.1103/PhysRevB.51.6773
10. Anderson PW. Theory of dirty superconductors. J Phys Chem Sol (1959) 11:26–30. doi:10.1016/0022-3697(59).90036-8
11. Ueki H, Zarea M, Sauls JA. The frequency shift and Q of disordered superconducting RF cavities. Phys Rev Res Submitted (2022) 1–11. doi:10.48550/arXiv.2207.14236
12. Eliashberg GM. Interactions between electrons and lattice vibrations in a superconductor. Sov Phys JETP (1960) 11:696–702.
13. Eilenberger G. Transformation of Gorkov’s equation for type II superconductors into transport-like equations. Zeit F Physik (1968) 214:195. doi:10.1007/BF01379803
14. Larkin AI, Ovchinnikov YN. Quasiclassical method in the theory of superconductivity. Sov Phys JETP (1969) 28:1200–5.
15. Rainer D, Sauls JA. Strong-coupling theory of superconductivity. In: Superconductivity: from basic Physics to new developments. Singapore: World Scientific (2018). p. 45–78. doi:10.48550/arXiv.1809.05264
16. Gorkov LP. On the energy spectrum on superconductors. Zh Eskp Teor Fiz English: Sov. Phys. JETP (1958) 7:505–508.
17. Rainer D. Principles of ab initio calculations of superconducting transition temperatures. Amsterdam, Netherlands: Elsevier Science Publishers B.V. (1986). p. 371–424. doi:10.1016/S0079-6417(08)60024-4
18. Giannozzi P, Baroni S, Bonini N, Calandra M, Car R, Cavazzoni C, et al. Quantum espresso: a modular and open-source software project for quantum simulations of materials. J Phys Cond Matt (2009) 21:395502. doi:10.1088/0953-8984/21/39/395502
19. Giannozzi P, Andreussi O, Brumme T, Bunau O, Buongiorno Nardelli M, Calandra M, et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J Phys Cond Matt (2017) 29:465901. doi:10.1088/1361-648X/aa8f79
20. Migdal A. Superfluidity and the moments of inertia of nuclei. Nucl Phys (1959) 13:655–74. doi:10.1016/.0029-5582(59)90264-0
21. McMillan WL, Rowell JM. Lead phonon spectrum calculated from superconducting density of states. Phys Rev Lett (1965) 14:108–12. doi:10.1103/PhysRevLett.14.108
22. Wolf E, Zasadzinski J, Osmun J, Arnold GB. Proximity electron tunneling spectroscopy I. Experiments on Nb. J Low Temp Phys (1980) 40:19–50. doi:10.1007/BF00115980
23. Arnold GB, Wolf E, Zasadzinski J, Osmun J. Proximity electron tunneling spectroscopy II. Effects of the induced N-metal pair potential on calculated S-metal properties. J Low Temp Phys (1980) 40:225–46. doi:10.1007/BF00117117
24. Morel P, Anderson PW. Calculation of the superconducting state parameters with retarded electron-phonon interaction. Phys Rev (1962) 125:1263. doi:10.1103/PhysRev.125.1263
25. Scalapino D, Schrieffer JR, Wilkins J. Strong-coupling superconductivity I. Phys Rev (1966) 148:263–79. doi:10.1103/.PhysRev.148.263
26. Townsend P, Sutton J. Investigation by electron tunneling of the superconducting energy gaps in Nb, Ta, Sn, and Pb. Phys Rev (1962) 128:591. doi:10.1103/PhysRev.128.591
27. McMillan WL. Transition temperature of strong-coupled superconductors. Phys Rev (1968) 167:331–44. doi:10.1103/.PhysRev.167.331
28. Mattheiss L. Electronic structure of niobium and tantalum. Phys Rev B (1970) 1:373. doi:10.1103/PhysRevB.1.373
29. Bostock J, Diadiuk V, Cheung W, Lo K, Rose R, MacVicar M. Does strong-coupling theory describe superconducting Nb? Phys Rev Lett (1976) 36:603. doi:10.1103/PhysRevLett.36.603
30. Butler W, Smith H, Wakabayashi N. Electron-phonon contribution to the phonon linewidth in Nb: theory and experiment. Phys Rev Lett (1977) 39:1004. doi:10.1103/PhysRevLett.39.1004
31. Powell B, Martel P, Woods A. Phonon properties of niobium, molybdenum, and their alloys. Can J Phys (1977) 55:1601–12. doi:10.1103/PhysRev.171.727
32. Daams J, Carbotte JP. Thermodynamic properties of superconducting niobium. J Low Temp Phys (1980) 40:135–54. doi:10.1007/BF00115987
33. Savrasov SY, Savrasov DY. Electron-phonon interactions and related physical properties of metals from linear-response theory. Phys Rev B (1996) 54:16487. doi:10.1103/PhysRevB.54.16487
34. Saunderson TG, Annett JF, Újfalussy B, Csire G, Gradhand M. Gap anisotropy in multiband superconductors based on multiple scattering theory. Phys Rev B (2020) 101:064510. doi:10.1103/PhysRevB.101.064510
35. Tidholm J, Hellman O, Shulumba N, Simak SI, Tasnádi F, Abrikosov IA. Temperature dependence of the Kohn anomaly in bcc Nb from first-principles self-consistent phonon calculations. Phys Rev B (2020) 101:115119. doi:10.1103/.PhysRevB.9.888
36. Seidl E, Weber HW, Teichler H. Hc2 anisotropy in the system of Niobium-Nitrogen. J Low Temp Phys (1978) 30:273–88. doi:10.1007/BF00114954
37. Arai M, Kita T. Ab initio Calculations of Hc2 for Nb, NbSe2, and MgB2. J Phys Soc Jpn (2004) 73:2924–7. doi:10.1143/JPSJ.73.2924
38. Pizzi G, Vitale V, Arita R, Blügel S, Freimuth F, Géranton G, et al. Wannier90 as a community code: new features and applications. J Phys Cond Matt (2020) 32:165902. doi:10.1088/1361-648X/ab51ff
39. Marzari N, Vanderbilt D. Maximally localized generalized Wannier functions for composite energy bands. Phys Rev B (1997) 56:12847. doi:10.1103/PhysRevB.56.12847
40. Souza I, Marzari N, Vanderbilt D. Maximally localized Wannier functions for entangled energy bands. Phys Rev B (2001) 65:035109. doi:10.1103/PhysRevB.65.035109
41. Ptok A, Kapcia KJ, Piekarz P, Oleś AM. The ab initio study of unconventional superconductivity in CeCoIn5 and FeSe. New J Phys (2017) 19:063039. doi:10.1088/1367-2630/aa6d9d
42. Lorensen WE, Cline HE. Marching cubes: a high resolution 3D surface construction algorithm. ACM siggraph Comput graphics (Acm) (1987) 21:163–9. doi:10.1145/37402.37422
43. Poncé S, Margine E, Verdi C, Giustino F. EPW: electron–phonon coupling, transport and superconducting properties using maximally localized Wannier functions. Comp Phys Commun (2016) 209:116–33. doi:10.1016/j.cpc.2016.07.028
44. Giustino F, Cohen ML, Louie SG. Electron-phonon interaction using Wannier functions. Phys Rev B (2007) 76:165108. doi:10.1103/PhysRevB.76.165108
45. Margine ER, Giustino F. Anisotropic Migdal-Eliashberg theory using Wannier functions. Phys Rev B (2013) 87:024505. doi:10.1103/PhysRevB.87.024505
46. Robinson B, Rowell J. A superconducting tunnelling measurement of the annealing characteristics of the transition metals Nb and V. Transition metals. Toronto, Canada: University of Toronto (1978).
47. Butler WH, Pinski FJ, Allen PB. Phonon linewidths and electron-phonon interaction in Nb. Phys Rev B (1979) 19:3708–21. doi:10.1103/PhysRevB.19.3708
48. Scott GB, Springford M. The Fermi surface in niobium. Proc R Soc Lond Ser A, Math Phys Sci (1970) 320:115–30. doi:10.1098/rspa.1970.0200
49. Wolf EL. Principles of electron tunneling spectroscopy. Oxford, United Kingdom: Oxford University Press (2012).
50. Sherrill MD, Edwards HH. Superconducting tunneling on bulk niobium. Phys Rev Lett (1961) 6:460–1. doi:10.1103/PhysRevLett.6.460
51. Shen LYL, Senozan N, Phillips NE. Evidence for two energy gaps in high-purity superconducting Nb, Ta, and V. Phys Rev Lett (1965) 14:1025. doi:10.1103/PhysRevLett.14.1025
52. MacVicar M, Rose R. Anisotropic energy-gap measurements on superconducting niobium single crystals by tunneling. J Appl Phys (1968) 39:1721–7. doi:10.1063/1.1656421
53. Sellers G, Anderson A, Birnbaum H. The anomalous heat capacity of superconducting niobium. Phys Lett A (1973) 44:173–4. doi:10.1016/0375-9601(73)90870-0
54. Bostock J, Agyeman K, Frommer M, MacVicar M. Determining accurate superconducting tunneling energy gaps: anisotropy in single-crystal Nb. J Appl Phys (1973) 44:5567–9. doi:10.1063/1.1662197
55. Butler W, Allen P. Gap anisotropy and Tc enhancement: general theory, and calculations for Nb using Fermi surface harmonics. In: Superconductivity in d-and f-Band Metals. Berlin, Germany: Springer (1976). p. 73–120.
56. Crabtree GW, Dye DH, Karim DP, Koelling DD, Ketterson JB. Anisotropic many-body effects in the quasiparticle velocity of Nb. Phys Rev Lett (1979) 42:390–3. doi:10.1103/PhysRevLett.42.390
57. Butler W. Upper critical field of Nb: calculated temperature dependence and anisotropy. Phys Rev Lett (1980) 44:1516. doi:10.1103/PhysRevLett.44.1516
58. Peter M, Ashkenazi J, Dacorogna M. Unrestricted solution of the Eliashberg equations for Nb. Helvetica Physica Acta (1977) 50:267–78.
59. Markowitz D, Kadanoff LP. Effect of impurities upon critical temperature of anisotropic superconductors. Phys Rev (1963) 131:563–75. doi:10.1103/PhysRev.131.563
60. Hohenberg P. Anisotropic superconductors with nonmagnetic impurities. Sov Phys JETP (1964) 18:834.
61. Maier T, Graser S, Scalapino D, Hirschfeld P. Origin of gap anisotropy in spin fluctuation models of the iron pnictides. Phys Rev B (2009) 79:224510. doi:10.1103/PhysRevB.79.224510
62. DeSorbo W. Effect of dissolved gases on some superconducting properties of niobium. Phys Rev (1963) 132:107–21. doi:10.1103/PhysRev.132.107
63. Koch C, Scarbrough J, Kroeger D. Effects of interstitial oxygen on the superconductivity of niobium. Phys Rev B (1974) 9:888. doi:10.1103/PhysRevB.9.888
64. Abrikosov AA, Gorkov LP. Superconducting alloys at finite temperatures. Sov Phys JETP (1959) 9:220.
65. Edwards SF. A new method for the evaluation of the electrical conductivity in metals. Phil Mag (1958) 3:1020. doi:10.1080/14786435808243244
66. Lee W, Rainer D, Zimmermann W. Holstein effect in the far-infrared conductivity of high Tc superconductors. Physica C (1989) 159:535–44. doi:10.1016/0921-4534(89)91284-7
67. Bafia D, Checchin M, Grassellino A, Melnychuk OS, Romanenko AS, Sergatskov DA, et al. Investigation of frequency behavior near Tc of niobium superconducting radio-frequency cavities. Geneva, Switzerland): JACoW Publishing (2019). p. 112–7. doi:10.18429/JACoW-SRF2019-MOP031
68. Bafia D, Grassellino A, Checchin M, Zasadzinski J, Romanenko A. The anomalous resonant frequency variation of microwave superconducting niobium cavities near Tc (2021). https://arxiv.org/abs/2103.10601. doi:10.48550/arXiv.2103.10601
Keywords: electronic structure, phonon structure, first-principles DFT calculations, Eliashberg theory, electron–phonon-mediated superconductivity, anisotropic superconductors, impurity scattering, pair-breaking
Citation: Zarea M, Ueki H and Sauls JA (2023) Effects of anisotropy and disorder on the superconducting properties of niobium. Front. Phys. 11:1269872. doi: 10.3389/fphy.2023.1269872
Received: 31 July 2023; Accepted: 06 October 2023;
Published: 30 October 2023.
Edited by:
Pashupati Dhakal, Jefferson Lab (DOE), United StatesReviewed by:
Nathan Sitaraman, Cornell University, United StatesKonrad Jerzy Kapcia, Adam Mickiewicz University, Poland
Copyright © 2023 Zarea, Ueki and Sauls. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: J. A. Sauls, c2F1bHNAbHN1LmVkdQ==
 Mehdi Zarea
Mehdi Zarea Hikaru Ueki
Hikaru Ueki J. A. Sauls
J. A. Sauls