Double-edged sword role of reinforcement learning based decision-makings on vaccination behavior

Pre-emptive vaccination has been proven to be the most effective measure to control influenza outbreaks. However, when vaccination behavior is voluntary, individuals may face the vaccination dilemma owing to the two sides of vaccines. In view of this, many researchers began to use evolutionary game theory to model the vaccination decisions of individuals. Many existing models assume that individuals in networks use the Fermi function based strategy to update their vaccination decisions. As we know, human beings have strong learning capability and they may continuously search for the optimal strategy based on the surrounding environments. Hence, it is reasonable to use the reinforcement learning (RL) strategy to reflect the vaccination decisions of individuals. To this end, we here explore a mixed updating strategy for the vaccination decisions, specifically, some individuals called intelligent agents update their vaccination decisions based on the RL strategy, and the other individuals called regular agents update their decisions based on the Fermi function. We then investigate the impact of RL strategy on the vaccination behavior and the epidemic dynamics. Through extensive experiments, we find that the RL strategy plays a double-edged sword role: when the vaccination cost is not so high, more individuals are willing to choose vaccination if more individuals adopt the RL strategy, leading to the significant suppression of epidemics. On the contrary, when the vaccination cost is extremely high, the vaccination coverage is dramatically reduced, inducing the outbreak of the epidemic. We also analyze the underlying reasons for the double-edged sword role of the RL strategy.

1 Introduction

The spreading of large-scale epidemics, such as the Severe Acute Respiratory Syndrome (SARS), Avian influenza and Corona Virus Disease 2019 (COVID-19), not only seriously endangers human health, but also causes huge economic losses. Therefore, how to develop effective strategies to suppress the spreading of epidemics has always been an important issue. It has been proven that vaccination is the most successful intervention against the spread of epidemics, increasing life expectancy, and decreasing morbidity [1,2]. When considering the voluntary vaccination principle, an individual’s vaccination decision may depend on the perceived risk of infection, cost of infection, cost of vaccination, and the vaccination behaviors of other individuals [3–5]. Thus, whether to take vaccination or not represents a dilemma: vaccination protects not only those who are vaccinated but also their neighbors. In this case, many others in the community can also be benefited, so they have less incentive to be vaccinated. This scenario naturally leads to the “free-riding” problem commonly observed in public goods studies [6–8].

Inspired by these facts, researchers have investigated the impacts of vaccination behaviors on the epidemiological models within the game-theoretical framework [9–12]. For instance, Bauch et al. [9,10] analyzed the collective behavior of voluntary vaccination for various childhood diseases within a game-theoretic framework, and found that this voluntary strategy can not lead to the group-level optimum due to the risk perception pertaining to the vaccine and the effect of “herd immunity”. The imitation dynamics inherent in the strategy-updating process was considered in the game-based vaccination model in Ref. [13], where the oscillations of vaccine uptake can emerge under some specific conditions, such as the change of disease prevalence or a high perceived risk of vaccine. Vardavas et al. [14] studied the effects of voluntary vaccination on the prevalence of influenza based on a minority game, and they demonstrated that severe epidemics could not be prevented unless vaccination programs offer incentives.

Since complex network provides an ideal and effective tool to describe the spreading of epidemics among populations, more works begun to study the voluntary vaccination behaviors within the network science framework [15–18]. For example, Perisic et al. studied the interplay of epidemic spreading dynamics and individual vaccination behavior on social contact networks. Compared to the homogeneously mixing model, they observed that increasing the neighborhood size of the contact network can eliminate the disease if individuals decide whether to vaccinate by accounting for infection risks from neighbors [19]. Mbah et al. considered the effects of both imitation behavior and contact heterogeneity on vaccination coverage and disease dynamics, and they found that the imitation behavior may impede the eradication of infectious diseases [20]. Fu et al. developed a network-based model to explore the effects of individual adaptation behavior and network structure on vaccination coverage as well as final epidemic size. Their findings indicate that the network structure can improve vaccination coverage when cost of vaccination is small; conversely, the network structure inhibits vaccination coverage when cost of vaccination is large [12]. Recently, a great deal of study has also focused on the impacts of various factors on individual vaccination behavior, such as perception [21], stubborn [22], social influence [23], different subsidy strategies [16,24,25], strategy conformity [15,26], anti-social behavior [27], hypergraph structure [28] and so on.

Given that individuals may have no complete information of the entire network and are not completely rational, the Fermi function based rule is often used to characterize the vaccination decision of individuals, i.e., the probability that individual i adopts individual j’s strategy is determined by their current payoff differences and the rationality level of individuals [12,16]. Nevertheless, the Fermi function based rule only considers the difference of the current payoffs, without fully considering the strong learning capability of human beings. In fact, individuals can continuously interact with the environment and then search for the best policy for themselves. Reinforcement learning (RL) is an aspect of machine learning where an agent tries to maximize the total amount of reward it receives when interacting with a complex, uncertain environment, and it utilizes a Q-table to record and update the values for each state-action pair [29]. In practical scenarios, the number of state-action pairs is not fixed, so the deep reinforcement learning (DRL) was proposed to solve the problem [30]. As a pioneering work of DRL, the deep Q-network (DQN) algorithm is a representative method and has garnered widespread attention in recent years [31,32].

Motivated by the above considerations, in this work, we consider a mixed updating strategy for vaccination decision of individuals composed of Fermi function strategy and RL strategy, and then study the impact of such a mixed strategy on the vaccination behaviors and epidemic dynamics. Specifically, we divide individuals in networks into two categories: one group of individuals update their vaccination decisions based on Fermi function (referred to as regular agents), while the other group of individuals update their vaccination decisions based on RL strategy (referred to as intelligent agents). Since each individual’s local information is flexible and dynamically changing, such as the number of neighbors, vaccinated neighbors or infected neighbors, we utilize DQN algorithm to update the decisions of intelligent agents. Experiments demonstrate that the RL strategy plays a double-edged sword role in vaccination behavior as well as epidemic dynamics. When the vaccination cost is not very high, a higher proportion of intelligent agents promotes vaccination coverage, leading to a dramatic reduction in the epidemic. However, when the vaccination cost is very high, the presence of intelligent agents can hinder the willingness to vaccinate, leading to an outbreak of the epidemic.

The rest of this paper is structured as follows. In Sec. 2, the descriptions of our model are introduced. In Sec. 3, main experimental results are presented and analyzed. Finally, the conclusions are summarized in Sec. 4.

2 Proposed model

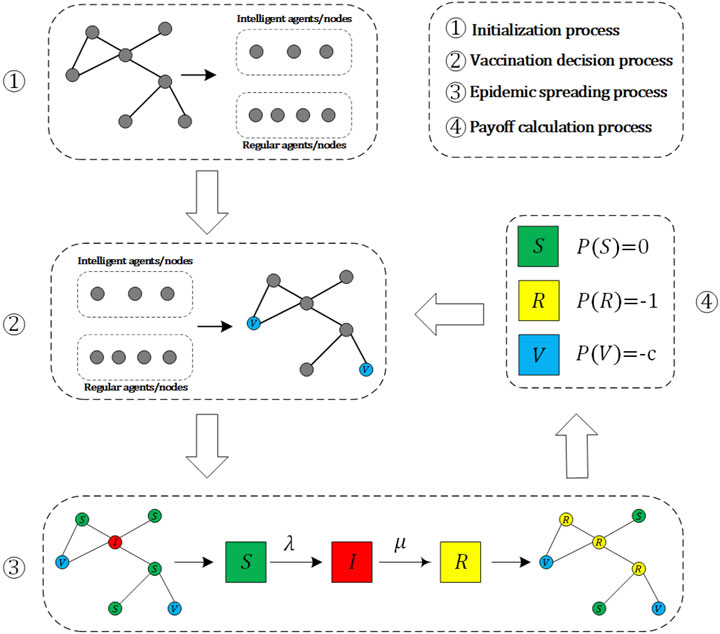
We study the vaccination dynamics for the prevention of the flu-like disease, in which individuals in networks must make vaccination decision before the onset of each epidemic season. Due to the periodic outbreaks of flu-like diseases and the limited validity of the vaccines, individuals who receive vaccinations can only gain immunity to the disease during the current season. In this situation, we also model the vaccination dynamics as a two-stage iterative process [12]: the first stage is a public vaccination campaign, in which individuals determine whether to vaccinate or not based on the previous season’s conditions. The second stage is the epidemic season stage, where vaccinated individuals cannot be infected, while unvaccinated individuals face a certain probability of being infected. In previous studies, individuals within social networks relied on the Fermi function to decide whether to vaccinate or not. In this work, we assume that some individuals update their vaccination decisions using the DQN method. As illustrated in Figure 1, the overall architecture of our proposed model can be subdivided into four steps: the initialization process, the decision-making process, the epidemic spreading process, and the payoff calculation process, where the last three steps repeatedly iterate until convergence or a given number of iterations. It should be noted that, the step 2 and step 4 correspond to the first stage of the two-stage iterative process, i.e., public vaccination campaign, where individuals make decisions based on the calculated payoffs. The step 3 is the epidemic season stage of the two-stage iterative process, after this step the payoff of each node can be calculated. Below, we provide detailed explanations for each of them.

FIGURE 1

FIGURE 1. Overall architecture of the proposed model.

2.1 Initialization process

In initialization phase, a proportion ρ of the total number of nodes in the network is randomly selected as the intelligent agents/nodes (i.e., updating vaccination decision based on DQN), and the other nodes are the regular agents/nodes (i.e., updating vaccination decision based on Fermi function). Once the categories of these nodes are established, they remain unchanged throughout the entire process. Meanwhile, we randomly select one-third of nodes to be vaccinated to begin the iterative process. After that, individuals need to use Fermi function or DQN method to decide whether to vaccinate or not based on the prior season’s information, such as the vaccination status, epidemic infection situation, payoffs of individuals, and so forth.

2.2 Decision-making process

Since we consider a mixed updating strategy composed of the Fermi function and the DQN method, we will respectively introduce the details of them.

2.2.1 Fermi function based strategy

The regular nodes determine whether to vaccinate or not based on the Fermi function. In detail, for a regular node i, updates his/her vaccination decision by randomly choosing one of its immediate neighbors, say j, compares their costs, and adopts the strategy of j with the following probability [16]:

${\pi }_{i\to j}=\frac{1}{1+e^{-\beta \left(P_j\left(t\right)-P_i\left(t\right)\right)}}(1)$

where P_i(t) defined in Eq. 5 represents the payoff of individual i in the previous season, and β quantifies the uncertainty in the decision-making process [12]. In this work, we fix β = 10. Node i will adopt the strategy of neighbor j with a probability π_i→j, and it will retain its own strategy with a probability 1 − π_i→j.

2.2.2 DQN based strategy

The intelligent nodes decide whether to vaccinate or not based on the DQN method. The specific steps are illustrated in Figure 2. We employ an ϵ − greedy strategy, which means randomly selecting an action with a probability of ϵ and choosing the action with the highest Q-value with a probability of 1 − ϵ.

FIGURE 2

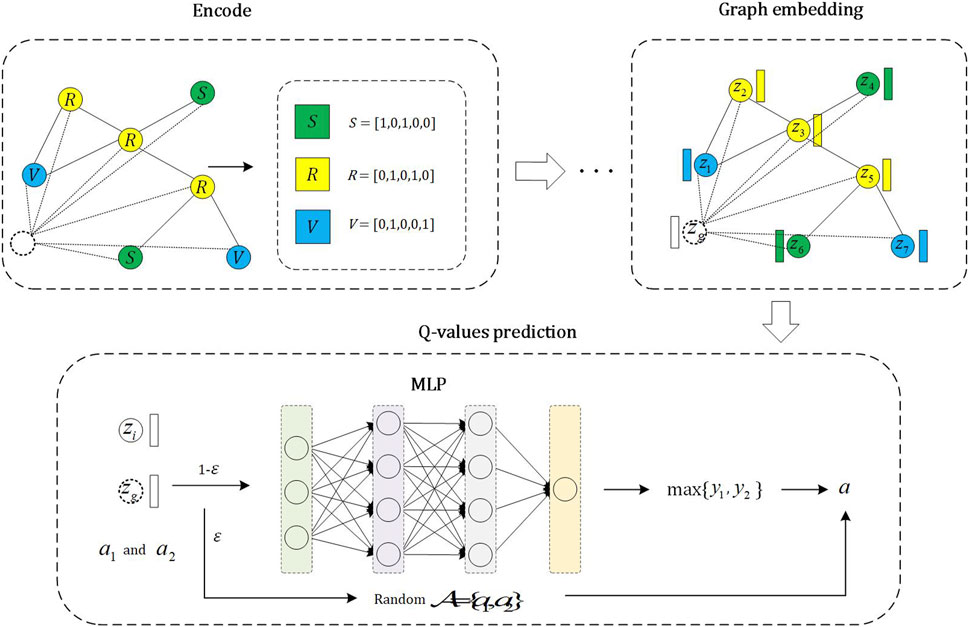
FIGURE 2. The whole process of Q-network. The encode module is to encode nodes in the network. The graph embedding module is responsible for representing both local and global information related to nodes through graph embeddings. The Q-values prediction module predicts the Q-values for an node’s states and actions, allowing the selection of the action with the highest Q-value for the node’s current state.

The overall process of predicting the Q-values for actions can be divided into three steps. In the first step, all intelligent agents are encoded, and they can be categorized into three types: a) vaccinated and get immunity; b) unvaccinated and not being infected; c) unvaccinated and being infected. We encode these three categories as (1, 0, 1, 0, 0), (0, 1, 0, 0, 1), (0, 1, 0, 1, 0) respectively. The first two digits of the code represent vaccination status, while the following three digits represent immunity, infection, and non-infection, respectively. It is important to emphasize that the encoding method for intelligent agents is not unique. Similar to Ref. [33], we also define a virtual node to represent the global information of the network. And the encoding with the largest number of individuals in three categories (i.e., a, b and c) is defined as the encoding of the virtual node, meanwhile, the neighborhood of the virtual node is the entire network.

In the second step, we utilize a Graph Neural Network (GNN) to generate their embedding representations for the encoded intelligent agents. The specific process is defined as follows [34]:

$h_{N\left(v\right)}^{\left(l-1\right)}=\sum _{j\in N\left(v\right)}{h}_j^{\left(l-1\right)}(2)$

and

$h_v^{\left(l\right)}=ReLU\left(\left[W_1\cdot h_v^{\left(l-1\right)},W_2\cdot h_{N\left(v\right)}^{\left(l-1\right)}\right]\right),(3)$

where $h_{N(v)}^{(l-1)}$ represents the aggregated features of the neighbors of node v at the (l − 1) − th convolutional layer, with N(v) being the neighborhood set of node v. ReLU represents the non-linear activation function. Eq. 2, 3 represent a single layer of graph convolution. During the convolution process, the virtual node aggregates information from its neighbors, its neighbors do not aggregate information from the virtual node.

In the last step, we need to predict the Q-values for the actions that intelligent agents may potentially undertake in a given state. Let [z_i, z_g] be the state of intelligent node i, where z_i and z_g represent the embeddings of node i and the virtual node, respectively. z_i and z_g also represent the local information of node i and global information, respectively. There are two situations in which node i may take action: taking vaccination or not. We encode it as A = {a₁, a₂} = {[1, 0], [0, 1]}. We then input the state and action into a Multilayer Perceptron (MLP) to predict the current state of node i and the Q-values of potential actions, namely,:

$y=W_4^T\cdot ReLU\left(W_3^T\cdot \left[z_i,z_g,a_j\right]\right),(4)$

where a_j (j = 1 or 2) represents the actions that intelligent node i may take, and W_i (i = 1, 2, 3, 4) in Eq. 3, 4 are the learnable parameters. The action with the highest Q-value prediction result among all possible actions is chosen. The training process and loss function of DQN are defined in Sub Section 2.5.

2.3 Epidemic spreading process

We use the Susceptibility-Infection-Recovery (SIR) model to simulate the epidemic spread process, with a transmission rate of λ and a recovery rate of μ [35]. In the beginning of each epidemic season, a small proportion of unvaccinated individuals are randomly selected as initial infection seeds I₀. Vaccinated individuals will not be infected in the upcoming season. The epidemic evolves until there are no more newly infected individuals.

2.4 Payoff calculation process

When the epidemic season ends, it is necessary to calculate the payoffs of individuals in the previous season. Let C_V and C_I be the cost of vaccination and infection, respectively. Without loss of generality, one can set c = C_V/C_I as the relative cost of vaccination with 0 < c < 1. Namely, the cost of infection is 1. Further let P_i(t) be the payoffs of node i in the t − th season, according to the costs of vaccination and infection, one has

$P_i\left(t\right)=\left\{\begin{array}{c}-c,\text{vaccination};\hfill \\ -1,\text{infected};\hfill \\ 0,\text{free}-\text{rider}.\hfill \end{array}\right.(5)$

2.5 DQN training process and loss function

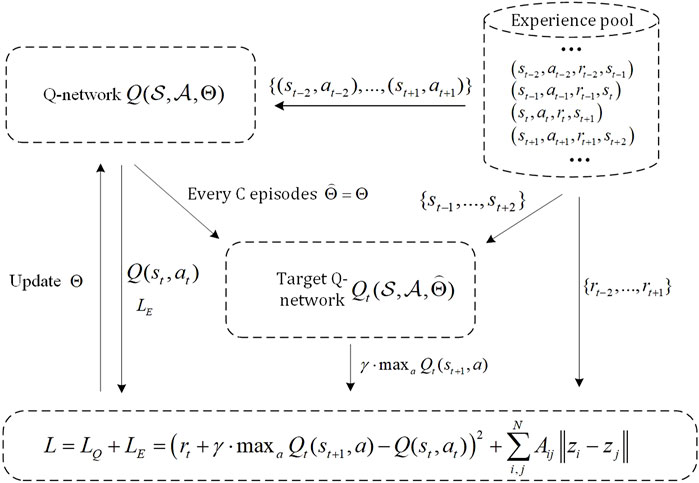
Next, we will introduce the training process and loss function of DQN. The overall training process of DQN is depicted in Figure 3. Intelligent agents can obtain the current season’s state s_t and the chosen action a_t based on the previous season’s infection situation. Meanwhile, each intelligent agent can obtain its payoff according to their vaccination decision and whether to be infected or not, i.e., as defined in Eq. 5, which can be treated as the reward value r_t for (s_t, a_t). Similarly, based on the current season’s infection situation, we can obtain the state s_t+1 for the next season, and this process continues iteratively. We define (s_t, a_t, r_t, s_t+1) as an experience and store it in a fixed-size experience pool. We regard the experience of five seasons as an episode of DQN.

FIGURE 3

FIGURE 3. Training process of DQN.

We need to define two identical models: one is the Q-network, and the other is the Target Q-network. After a fixed number of C episodes, the parameters of the Q-network are copied to the Target Q-network. To update the parameters of the Q-network, small batches of experiences from the experience pool are randomly selected. We then need to compute the loss for each experience and then update the parameters of the Q-network through the Back-Propagation algorithm. The loss function consists of two components. The first component is the network embedding loss, which is defined as:

$L_E=\sum _{i,j}^N{A}_{ij}\Vert z_i-z_j\Vert =2tr\left(Z^{T}LZ\right),(6)$

where N and A_ij are the size and the adjacency matrix of the network, respectively. z_i and Z represent the embedding vector of node i and the matrix formed by embedding vectors of all nodes, respectively, and L is the Laplacian matrix. tr(⋅) denotes the trace of a matrix.

The second part is the Q-value prediction loss. For each experience, the objective of the Q-value prediction loss is to minimize the reward error between the predicted and actual values, which is described as:

$L_Q={\left(r_t+\gamma \cdot \underset{a\in A}{\max }{Q}_t\left(s_{t+1},a\right)-Q\left(s_t,a_t\right)\right)}^2,(7)$

where the predicted reward value Q(s_t, a_t) is predicted by the Q-network based on the state and action, and the current reward value r_t plus γ ⋅ max_a∈AQ_t(s_t+1, a) from the Target Q-network is regarded as the actual reward value. γ represents the reward discount factor, which is used to balance the importance of future and current rewards. The overall loss for each experience is defined as a combination of L_E and L_Q with a balancing parameter α, i.e.,

$L=L_Q+\alpha \cdot L_E.(8)$

The specific steps of the above process are outlined in Algorithm 1. The first line represents the initialization process for classifying individuals into intelligent or regular agents. Lines 3–14 depict how nodes with different categories decide whether to take vaccination based on various decision rules. Lines 15–16 simulate the epidemic season, in which SIR model is used to model the spreading of epidemic, and line 17 indicates the payoff calculation process.

Algorithm 1. Algorithm for the model.

Input: The intelligent agents proportion ρ, the initial infection seed I₀ = 5, the season number 2000; 

Output: The fraction of vaccination/infection/free-riders;

1: Number N ⋅ ρ of nodes are randomly selected as the intelligent agents, and the rest are the regular agents;

2: for t = 1 to 2000 do

3:  if node is intelligent agents then

4:   if t < = 1500 then

5:    Decide whether to vaccinate according to Q-network, and the parameter Θ of Q-network is updated;

6:   else if t > 1500 then

7:    Decide whether to vaccinate according to Target Q-network;

8:   end if

9:  else if node is regular agents then

10:   The decision rule is the Fermi function, as shown in Eq. (1);

11:  end if

12:  if t%50 == 0 then

13:   The parameter of Target Q-network is updated as $\widehat{\mathrm{\Theta }}=\mathrm{\Theta }$;

14:  end if

15:  The unvaccinated individuals are randomly selected as initial infection seeds I₀;

16:  epidemic spreads via the SIR model until there are no new infected individuals;

17:  The payoffs of individuals are calculated;

18: end for

19: Calculate the fraction of vaccination/infection/free-riders based on the Target Q-network.

3 Experiment

In this section, we investigate the impacts of different proportions of intelligent agents on the vaccination behaviors and the epidemic dynamics.

3.1 Experimental setup

Our experiments are employed on three types of networks: the Barabási-Albert (BA) network with m = 3 (number of edges with which a new node attaches to existing nodes) and N = 2000 [36], the Erdős-Rényi (ER) random network with average degree ⟨k⟩ = 6 and N = 2000 [37], and a real-world Email network [38]. The GNN has 2 embedding layers with a dimensionality of 64 for the embeddings. As in Ref. [33,39], the reward discount factor γ, the size of the experience pool, and the ϵ for ϵ − greedy strategy are set as 0.99, 10000, and 0.05, respectively. We conduct a total of 2000 seasons, with the initial 1500 seasons designated for model training, followed by the subsequent 500 seasons for testing. Meanwhile, the Q-network’s parameters are copied to the Target Q-network for every fixed 50 seasons. In all experiments, without specification, the balancing parameter is α = 0.01, the recovery rate is μ = 0.25 and the initial infection seed I₀ = 5.

3.2 Experimental results

Figure 4 presents the heatmap results regarding ρ and c on the BA network, demonstrating their impacts on the fraction of vaccination (Figures 4A, C) and the fraction of infection (Figures 4B, D). Several observations can be concluded from Figure 4: Firstly, when the cost of vaccination c is not so high, such as c < 0.6 for λ = 0.10 (Figures 4A, B) and c < 0.8 for λ = 0.18 (Figures 4C, D), the fraction of vaccination increases with the value of ρ, leading to the reduction of the infection. In particular, when ρ is close to 1, almost all nodes take vaccination, giving rise to the complete extinction of epidemic; Secondly, when the cost of vaccination c is very high, such as c = 0.9, the opposite phenomenon happens, larger value of ρ induces lower level of vaccination, yielding higher level of infection. The result is also universal for different values of λ. Based on the two observations, one can conclude that the RL based strategy plays a double-edge sword role in the vaccination behavior and the epidemic dynamics. Thirdly, by comparing Figure 4A with Figure 4C, it is found that the fraction of vaccination for the case of λ = 0.18 is generally higher than that of λ = 0.10 when the values of ρ and c are not so large. That is to say, higher risk of infection encourages more individuals to take vaccination.

FIGURE 4

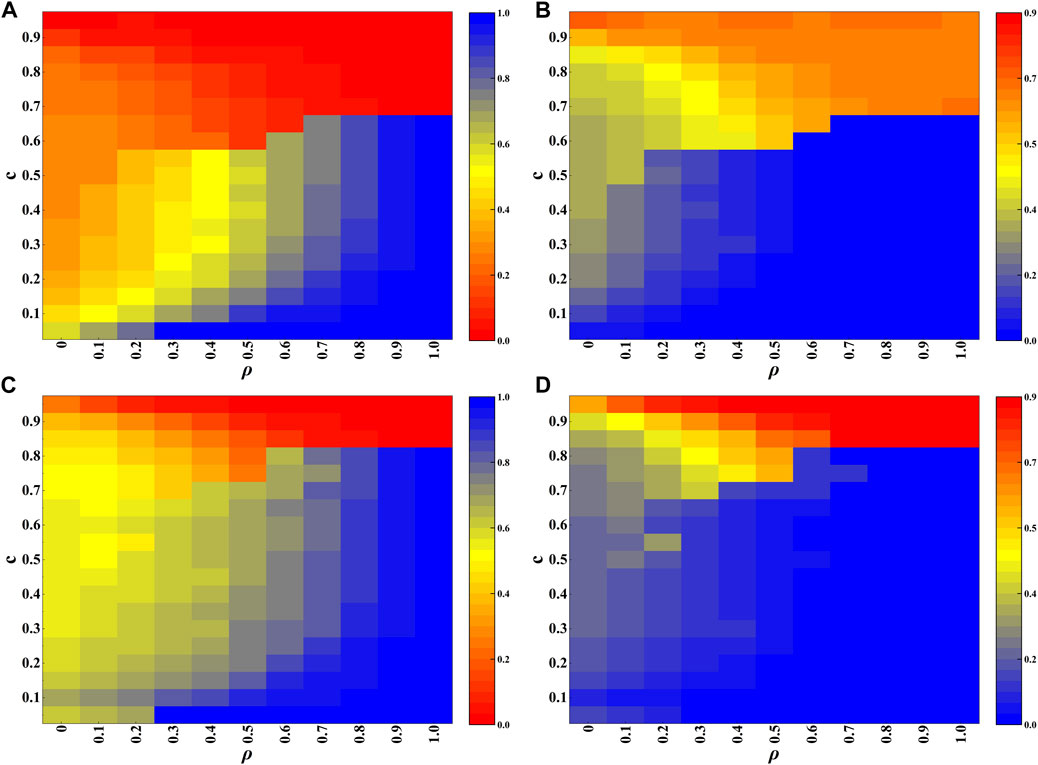
FIGURE 4. Experimental results on the BA network. (A, B) are heatmaps depicting the fractions of vaccination and infection, respectively, with transmission rate λ = 0.10. (C, D) are heatmaps depicting the fractions of vaccination and infection, respectively, with transmission rate λ = 0.18.

To validate the universality of our observations, we conduct experiments on the ER network (Figures 5A–C) and the Email network (Figure 5D–F) as well. To reflect the double-edge sword role of RL based strategy more clear, the fraction of vaccination, infection and free-riders as the function of ρ are shown in Figure 5. Similar to the results on the BA network, the double-edge sword role of RL based strategy can be observed in Figure 5. In other words, the existence of the intelligent agents has a beneficial impact on suppressing the spreading of epidemic when the cost of vaccination is not very high, whereas, it has a detrimental effect otherwise. As we know, taking vaccination is a better choice when the cost of vaccination is low, however, taking vaccination is almost unnecessary when the cost of vaccination is also equal to the cost of infection. Under different situations, intelligent agents prefer to select so-called “better choice” for themselves, therefore, the double-edge sword role of RL strategy is explainable.

FIGURE 5

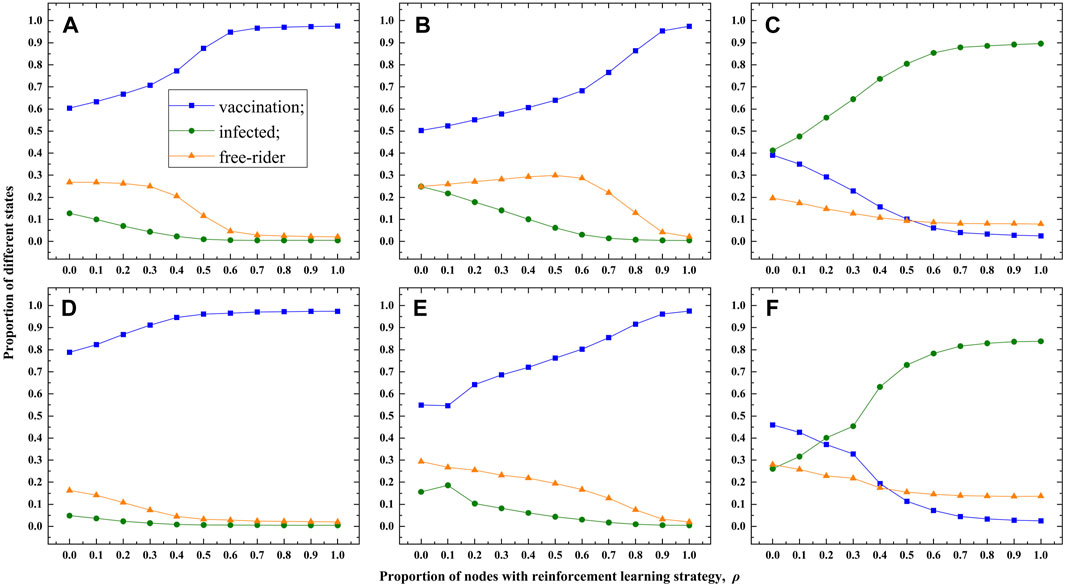
FIGURE 5. Experimental results on the ER and Email networks. (A–C) show the results for the ER network with vaccination cost set to c =0.1, 0.5, and 0.9, respectively. (D–F) display the results for the Email network with vaccination cost set to c = 0.1, 0.5, and 0.9, respectively. The transmission rate is λ = 0.18.

To further elucidate the findings, we define V(k) as the vaccination ratio among nodes with degree k, and let P_V(k), P_N(k) and P_A(k) be the average payoffs of vaccinated nodes, unvaccinated nodes, and of all nodes with degree k, respectively. First, the experimental results for λ = 0.18 and c = 0.1 (low vaccination cost) on the BA network are presented in Figure 6. When ρ = 0 (i.e., without intelligent agents), Figure 6A indicates that the vaccination ratio V(k) is proportional to the degree k. The reason is that the nodes with a higher degree are more susceptible to infection since they have a greater number of neighbors, thus nodes with higher degrees exhibit a greater inclination towards choosing vaccination. When ρ = 0.5, a notable increase in the vaccination ratio is observed compared to Figure 6A, especially for nodes with lower degrees (Figure 6B). Because the majority of nodes in the BA network are of low degree, it leads to a significant improvement in the vaccination coverage. When ρ = 1.0, it can be observed that all nodes have a high probability of vaccination, all exceeding 0.95 (Figure 6C). This results in a high overall vaccination coverage in the entire network. Figures 6D–F display the average payoffs of nodes with different degree k in various states. Overall, the average payoffs of unvaccinated nodes decreases with degree k, it is because nodes with lower degrees have a lower probability of being infected. Furthermore, the payoffs of vaccinated nodes significantly surpass unvaccinated nodes. As a result, individuals are more willing to get vaccination. This also explains why, in situations with a relatively low vaccination cost, the introduction of intelligent agents can encourage more nodes to take vaccination. Figures 6D–F also demonstrate that the average payoff of all nodes P_A(k) increases with ρ, which indicates that the presence of intelligent agents also contributes to an overall increase in group benefits when c is relatively small.

FIGURE 6

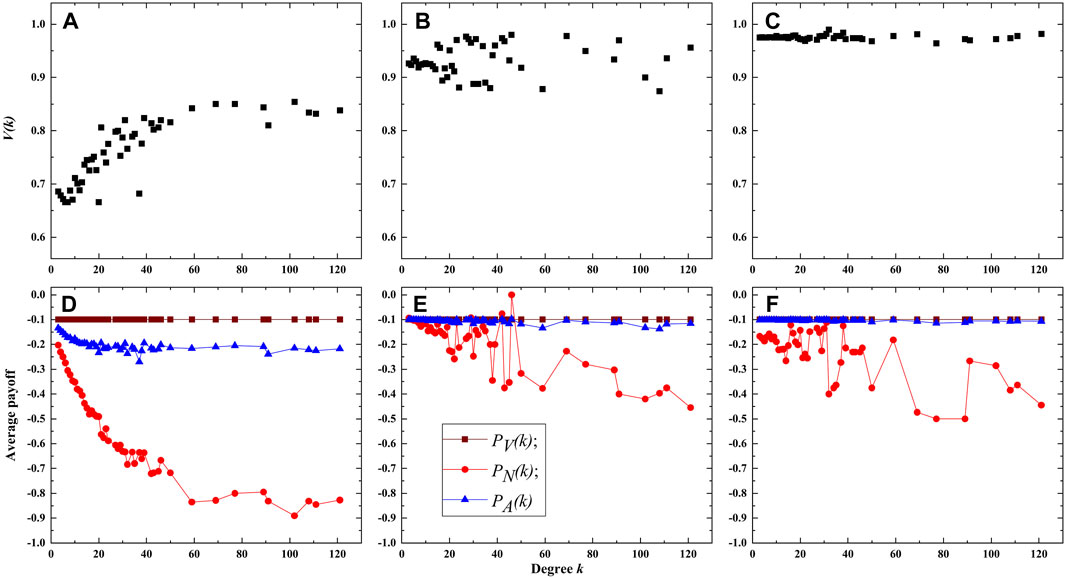
FIGURE 6. Vaccination ratio and payoffs of nodes with different degrees. (A–C) are the vaccination proportion V(k) for ρ = 0.0,0.5 and 1.0 respectively. (D–F) are the average payoffs of nodes in different states for ρ = 0.0, 0.5 and 1.0 respectively. The cost of vaccination is c = 0.1.

Figure 7 displays the experimental results for λ = 0.18 and c = 0.9 (high cost of vaccination) in the BA network. When ρ = 0 (Figure 7A), the vaccination ratio V(k) still increases with the degree k, however, owing to the higher cost of vaccination, its growth trend is slower than that shown in Figure 6A. In addition, the vaccination ratio V(k) decreases dramatically as ρ increases to 0.5 (Figure 7B) and further to 1.0 (Figure 7B), especially for the case of ρ = 1, the values of V(k) are almost equal to zero for different degree k. The observations imply that the presence of intelligent agents further lower the vaccination proportion when the vaccination cost is extremely high. The average payoffs of nodes with different degrees in different states are further illustrated in Figures 7D–F, they also imply that the average payoffs of unvaccinated nodes decrease with degree k. However, differing from the scenario with low vaccination cost, the average payoff of unvaccinated nodes with lower degrees, such as degree value is 3 or 4, is higher than that of vaccinated nodes. It is because the vaccination cost is extremely high (i.e., average payoff is very low), while the average payoff of unvaccinated nodes with lower degrees is not very small owing to the lower infection risk of them. One can also observe that the average payoff of all nodes P_A(k) decreases with the value of ρ. This indicates that in scenarios with high vaccination cost, the presence of intelligent agents not only reduces the vaccination coverage but also leads to a decrease in overall group benefits.

FIGURE 7

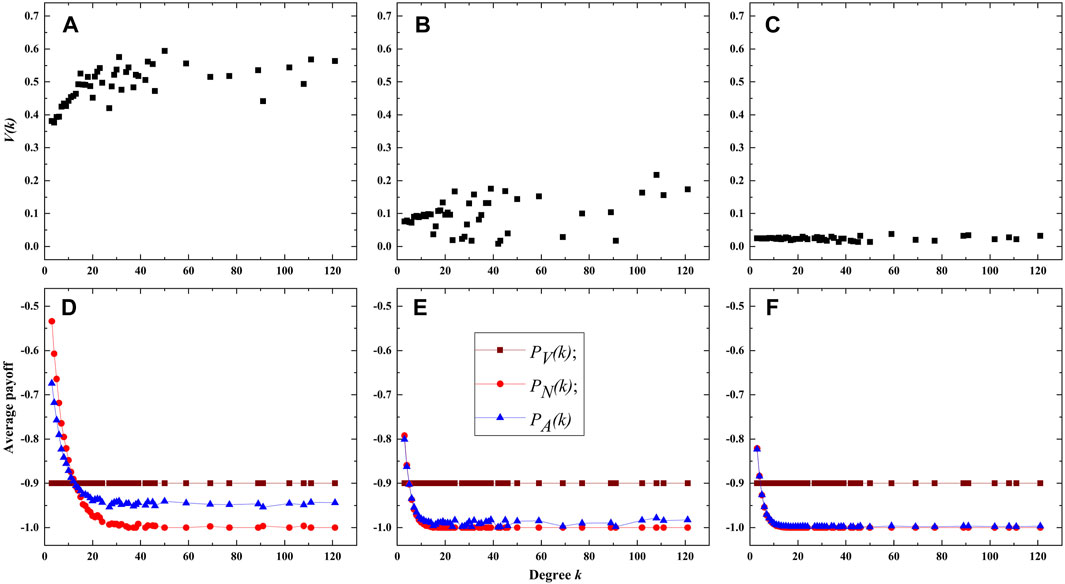
FIGURE 7. Vaccination ratio and payoffs of nodes with different degrees. (A–C) are the vaccination proportion V(k) for ρ = 0.0,0.5 and 1.0 respectively. (D–F) are the average payoffs of nodes in different states for ρ = 0.0, 0.5 and 1.0 respectively. The cost of vaccination is c = 0.9.

Finally, we conduct the sensitivity analysis regarding the balancing parameter α, and the experimental results are shown in Figure 8. By varying the values of α from 1 to 1e-4, and one can observe that different values of α have minor impact on the fraction of vaccination, no matter c = 0.1 (Figure 8A) or c = 0.9 (Figure 8B). This indicates that the double-edged sword role of RL based strategy is robust to the value of α.

FIGURE 8

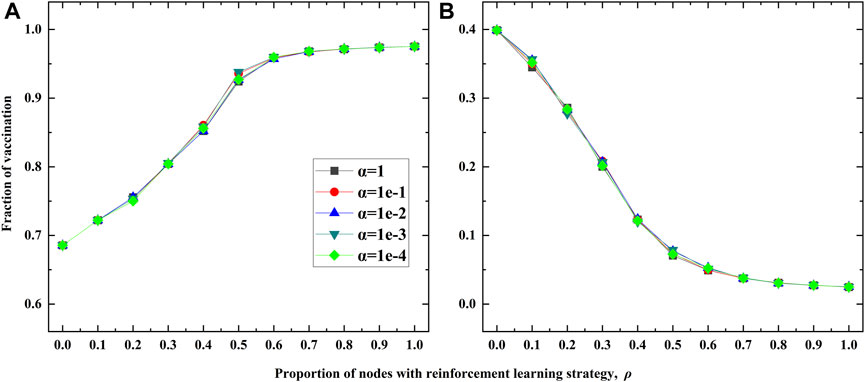
FIGURE 8. Sensitivity analysis of the balancing parameter α on the BA network. (A) is for c =0.1. (B) is for c = 0.9. Here the transmission rate is λ = 0.18.

4 Conclusion

In this work, considering the strong learning capability of human beings, we introduced a mixed updating strategy for the vaccination decision of individuals. Specifically, we categorized individuals in the social networks into two groups: regular agents make vaccination decisions based on the Fermi function, primarily considering the difference in current payoffs, while intelligent agents’ vaccination decisions are determined by the RL strategy, which relies on local and global information. Since individuals’ local information in the network is flexible and dynamic, we have further integrated the DQN algorithm into the RL strategy for intelligent agents. By varying the proportion of intelligent agents in networks, we found that under appropriate vaccination cost, increasing the proportion of intelligent agents can lead to a significant improvement of vaccination and an effective suppression of epidemic, also inducing an increase of the group benefits. Nevertheless, when the vaccination cost is extremely high, we observed an inverse relationship between the proportion of intelligent agents and vaccination coverage, which consequently leads to a decrease in the group benefits. That is to say, intelligent agents have a double-edged sword effect on vaccination behaviors and group benefits in pursuit of maximizing their own utilization. The findings enrich our understanding on the interplay of the human behavioral responses and epidemic spreading, and may also provide some insights for policymakers regarding the protection and control of epidemics.

There are a number of ways our methods can be extended in future work. For instance, we can consider more decision options for individuals, the incomplete effectiveness of vaccines, the subsidy of vaccines, the distinct structures of epidemic transmission and the vaccination decision updating process, and so on. In addition, we mainly focus on the repeated season model, namely, the vaccination decision should be repeatedly made before each epidemic season. In many situations, the decisions of individuals are often made before or during one emerging diseases. In this case, we should adjust our model to characterize the interplay of the vaccination behavior and the epidemic dynamics for the single season model [40].

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

J-QK: Validation, Writing–original draft, Writing–review and editing. FZ: Validation, Writing–original draft, Writing–review and editing. H-FZ: Conceptualization, Supervision, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work is supported by the National Natural Science Foundation of China (61973001) and the Key Project of Natural Science Research of Education Department of Anhui Province (KJ2021A0896).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Stöhr K, Esveld M. Will vaccines be available for the next influenza pandemic? Science (2004) 306:2195–6. doi:10.1126/science.1108165

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Wang Z, Bauch CT, Bhattacharyya S, d’Onofrio A, Manfredi P, Perc M, et al. Statistical physics of vaccination. Phys Rep (2016) 664:1–113. doi:10.1016/j.physrep.2016.10.006

CrossRef Full Text | Google Scholar

3. Yin Q, Wang Z, Xia C, Bauch CT. Impact of co-evolution of negative vaccine-related information, vaccination behavior and epidemic spreading in multilayer networks. Commun Nonlinear Sci Numer Simulation (2022) 109:106312. doi:10.1016/j.cnsns.2022.106312

CrossRef Full Text | Google Scholar

4. Wang W, Liu Q-H, Liang J, Hu Y, Zhou T. Coevolution spreading in complex networks. Phys Rep (2019) 820:1–51. doi:10.1016/j.physrep.2019.07.001

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Kabir KA, Kuga K, Tanimoto J. The impact of information spreading on epidemic vaccination game dynamics in a heterogeneous complex network-a theoretical approach. Chaos, Solitons & Fractals (2020) 132:109548. doi:10.1016/j.chaos.2019.109548

CrossRef Full Text | Google Scholar

6. Wu B, Fu F, Wang L. Imperfect vaccine aggravates the long-standing dilemma of voluntary vaccination. PLoS One (2011) 6:e20577. doi:10.1371/journal.pone.0020577

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Chen X, Fu F. Imperfect vaccine and hysteresis. Proc R Soc B (2019) 286:20182406. doi:10.1098/rspb.2018.2406

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Chang SL, Piraveenan M, Pattison P, Prokopenko M. Game theoretic modelling of infectious disease dynamics and intervention methods: a review. J Biol Dyn (2020) 14:57–89. doi:10.1080/17513758.2020.1720322

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Bauch CT, Galvani AP, Earn DJ. Group interest versus self-interest in smallpox vaccination policy. Proc Natl Acad Sci (2003) 100:10564–7. doi:10.1073/pnas.1731324100

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Bauch CT, Earn DJ. Vaccination and the theory of games. Proc Natl Acad Sci (2004) 101:13391–4. doi:10.1073/pnas.0403823101

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Ndeffo Mbah ML, Liu J, Bauch CT, Tekel YI, Medlock J, Meyers LA, et al. The impact of imitation on vaccination behavior in social contact networks. PLoS Comput Biol (2012) 8:e1002469. doi:10.1371/journal.pcbi.1002469

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Fu F, Rosenbloom DI, Wang L, Nowak MA. Imitation dynamics of vaccination behaviour on social networks. Proc R Soc B: Biol Sci (2011) 278:42–9. doi:10.1098/rspb.2010.1107

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Bauch CT. Imitation dynamics predict vaccinating behaviour. Proc R Soc B: Biol Sci (2005) 272:1669–75. doi:10.1098/rspb.2005.3153

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Vardavas R, Breban R, Blower S. Can influenza epidemics be prevented by voluntary vaccination? PLoS Comput Biol (2007) 3:e85. doi:10.1371/journal.pcbi.0030085

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Wang X, Jia D, Gao S, Xia C, Li X, Wang Z. Vaccination behavior by coupling the epidemic spreading with the human decision under the game theory. Appl Math Comput (2020) 380:125232. doi:10.1016/j.amc.2020.125232

CrossRef Full Text | Google Scholar

16. Zhang H-F, Shu P-P, Wang Z, Tang M, Small M. Preferential imitation can invalidate targeted subsidy policies on seasonal-influenza diseases. Appl Math Comput (2017) 294:332–42. doi:10.1016/j.amc.2016.08.057

CrossRef Full Text | Google Scholar

17. Han D, Sun M. An evolutionary vaccination game in the modified activity driven network by considering the closeness. Physica A: Stat Mech its Appl (2016) 443:49–57. doi:10.1016/j.physa.2015.09.073

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Han D, Wang X. Vaccination strategies and virulent mutation spread: a game theory study. Chaos, Solitons & Fractals (2023) 176:114106. doi:10.1016/j.chaos.2023.114106

CrossRef Full Text | Google Scholar

19. Perisic A, Bauch CT. Social contact networks and disease eradicability under voluntary vaccination. PLoS Comput Biol (2009) 5:e1000280. doi:10.1371/journal.pcbi.1000280

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Mbah MLN, Liu J, Bauch CT, Tekel YI, Medlock J, Meyers LA, et al. The impact of imitation on vaccination behavior in social contact networks. PLoS Comput Biol (2012) 8:e1002469. doi:10.1371/journal.pcbi.1002469

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Feng X, Wu B, Wang L. Voluntary vaccination dilemma with evolving psychological perceptions. J Theor Biol (2018) 439:65–75. doi:10.1016/j.jtbi.2017.11.011

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Fukuda E, Tanimoto J. Effects of stubborn decision-makers on vaccination and disease propagation in social networks. Int J Automation Logistics (2016) 2:78–92. doi:10.1504/ijal.2016.074909

CrossRef Full Text | Google Scholar

23. Xia S, Liu J. A computational approach to characterizing the impact of social influence on individuals’ vaccination decision making. PLoS One (2013) 8:e60373. doi:10.1371/journal.pone.0060373

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Zhang H-F, Wu Z-X, Xu X-K, Small M, Wang L, Wang B-H. Impacts of subsidy policies on vaccination decisions in contact networks. Phys Rev E (2013) 88:012813. doi:10.1103/physreve.88.012813

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Wang J, Zhang H, Jin X, Ma L, Chen Y, Wang C, et al. Subsidy policy with punishment mechanism can promote voluntary vaccination behaviors in structured populations. Chaos, Solitons & Fractals (2023) 174:113863. doi:10.1016/j.chaos.2023.113863

CrossRef Full Text | Google Scholar

26. An T, Wang J, Zhou B, Jin X, Zhao J, Cui G. Impact of strategy conformity on vaccination behaviors. Front Phys (2022) 10:972457. doi:10.3389/fphy.2022.972457

CrossRef Full Text | Google Scholar

27. Utsumi S, Arefin MR, Tatsukawa Y, Tanimoto J. How and to what extent does the anti-social behavior of violating self-quarantine measures increase the spread of disease? Chaos, Solitons & Fractals (2022) 159:112178. doi:10.1016/j.chaos.2022.112178

CrossRef Full Text | Google Scholar

28. Nie Y, Su S, Lin T, Liu Y, Wang W. Voluntary vaccination on hypergraph. Commun Nonlinear Sci Numer Simulation (2023) 127:107594. doi:10.1016/j.cnsns.2023.107594

CrossRef Full Text | Google Scholar

29. Kaelbling LP, Littman ML, Moore AW. Reinforcement learning: a survey. J Artif Intelligence Res (1996) 4:237–85. doi:10.1613/jair.301

CrossRef Full Text | Google Scholar

30. Arulkumaran K, Deisenroth MP, Brundage M, Bharath AA. Deep reinforcement learning: a brief survey. IEEE Signal Process. Mag (2017) 34:26–38. doi:10.1109/msp.2017.2743240

CrossRef Full Text | Google Scholar

31. Mnih V, Kavukcuoglu K, Silver D, Rusu AA, Veness J, Bellemare MG, et al. Human-level control through deep reinforcement learning. Nature (2015) 518:529–33. doi:10.1038/nature14236

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Hafiz A (2022). A survey of deep q-networks used for reinforcement learning: state of the art. Intell Commun Tech Virtual Mobile Networks: Proc ICICV 2022, 393–402.

CrossRef Full Text | Google Scholar

33. Fan C, Zeng L, Sun Y, Liu Y-Y. Finding key players in complex networks through deep reinforcement learning. Nat Machine Intelligence (2020) 2:317–24. doi:10.1038/s42256-020-0177-2

CrossRef Full Text | Google Scholar

34. Wu Z, Pan S, Chen F, Long G, Zhang C, Philip SY. A comprehensive survey on graph neural networks. IEEE Trans Neural Networks Learn Syst (2020) 32:4–24. doi:10.1109/tnnls.2020.2978386

CrossRef Full Text | Google Scholar

35. Pastor-Satorras R, Castellano C, Van Mieghem P, Vespignani A. Epidemic processes in complex networks. Rev Mod Phys (2015) 87:925–79. doi:10.1103/revmodphys.87.925

CrossRef Full Text | Google Scholar

36. Barabási A-L, Albert R. Emergence of scaling in random networks. Science (1999) 286:509–12. doi:10.1126/science.286.5439.509

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Erdös P, Rényi A. On the evolution of random graphs. Publ Math Inst Hung Acad Sci (1960) 5:43.

Google Scholar

38. Rossi RA, Ahmed NK (2015). The network data repository with interactive graph analytics and visualization, West Lafayette: Purdue University

Google Scholar

39. Yan D, Xie W, Zhang Y, He Q, Yang Y. Hypernetwork dismantling via deep reinforcement learning. IEEE Trans Netw Sci Eng (2022) 9:3302–15. doi:10.1109/tnse.2022.3174163

CrossRef Full Text | Google Scholar

40. Tanimoto J. Sociophysics approach to epidemics, 23. Berlin, Germany: Springer (2021).

Google Scholar