- 1Theoretical Division, Los Alamos National Laboratory, Los Alamos, NM, United States
- 2Accelerator Operations and Technology Division, Los Alamos National Laboratory, Los Alamos, NM, United States
Understanding the underlying factors responsible for higher-than-anticipated local field enhancements required to trigger vacuum breakdown on pristine metal surfaces is crucial for the development of devices capable of withstanding intense operational fields. In this study, we investigate the behavior of nominally flat copper electrode surfaces exposed to electric fields of hundreds of MV/m. Our novel approach considers curvature-driven diffusion processes to elucidate the formation of sharp breakdown precursors. To do so, we develop a mesoscale finite element model that accounts for driving forces arising from both electrostatic and surface-tension-induced contributions to the free energy. Our findings reveal a dual influence: surface tension tends to mitigate local curvature, while the electric field drives mass transport toward regions of high local field density. This phenomenon can trigger the growth of sharper protrusions, ultimately leading to a rapid enhancement of local fields and, consequently, to a runaway growth instability. We delineate supercritical and subcritical regimes across a range of initial surface roughness. Our numerical results are in qualitative agreement with experimentally reported data, indicating the potential practical relevance of field-driven diffusion in the formation of breakdown precursors.
1 Introduction
Strong electric fields are often encountered on solid material surfaces of high voltage and field-emission devices used in a broad range of applications, including high gradient accelerators [1–6]. One of the key challenges in maintaining and improving the functionality of such devices at high fields is related to the control of field-induced breakdown [7–10] or vacuum arc generating events [11]. As breakdown is routinely observed at fields that are much lower than those required for strong emission at flat clean surface [12, 13], the formation of sharp surface features which can locally enhance the applied field by factors of 50–100x is broadly assumed [2, 14]. Indeed, the development of breakdown from sharp emitter geometries is now well understood to follow from thermal runaway following from strong field emission currents [15]. The process of partial melting followed by plasma/vacuum arc formation have been described via a multiphysics and multiscale modeling approaches [16]. Overall, plasma-driven and ejection mechanisms [17, 18] during localized high current-induced Joule heating explain formation of micro craters in cathodes during vacuum arcs, under nominal electric fields (e.g., in the range of 100 s of MV/m). In these models, the presence of a sharp emitter tip has proved to be an essential trigger of breakdown [19, 20].
Since the observed surface roughness of polished surfaces is generally not thought to be compatible with the field-enhancement factors required to trigger spontaneous breakdown, the formation of precursors through some surface deformation mechanisms have to be invoked. To date, unraveling the precise mechanisms governing the formation of such sharp field-enhancing precursors has remained elusive, these are often destroyed in the breakdown process Therefore, understanding the physical mechanisms through which the material surface couples and dynamically evolves under experimentally relevant field to form breakdown precursors is paramount to design ultra-high gradient systems including the next-generation of compact accelerators. Several hypotheses have been proposed to explain the formation of such precursors [15, 21, 22]. These hypotheses have been guided by the notion that real electrodes deviate significantly from ideal materials. Material imperfections, such as point defects, voids, dislocations, slip extrusions, preexisting surface features, are proposed to interact with electric fields, resulting in localized field-enhancement factors. For example, the role of dislocation mediated plasticity [21] has been explored to address the formation of possible stress-concentrators [23] through slips interacting with free metal surfaces. However, both fully-atomistic [24] and hybrid continuum-atomistic [21] approaches suggest that fields on the order tens of GV/m (i.e., 2 orders of magnitude larger than typical experimental breakdown fields) are required to trigger substantial defect activity, unless these processes are assisted by other driving forces (e.g., thermo-elastic stresses caused by Joule heating [25]). Effect of electric field gradients on diffusion rates of metal emitter surfaces has been atomistically probed [26]. However, the long-range, long-time consequences of such biased diffusion on breakdown precursor formation was not directly elucidated. As of now, these models remain difficult to directly validate experimentally, so the precise mechanisms leading to the formation of breakdown precursors at electric fields on the order of hundreds of MV/m remains incompletely understood.
In this paper, we introduce a simple surface evolution model driven by surface tension and applied electric fields. Our findings underscore the interplay between these forces: while surface tension tends to diminish local curvature, the electric field drives mass transport towards regions with heightened field strengths. This dynamic leads to the formation of sharper protrusions, further intensifying local fields and ultimately resulting in a tip-growth instability and potentially in breakdown. Our investigation reveals a crucial aspect: the critical fields for instability exhibit a rapid increase with the growing aspect ratio of the initial surface morphology. For instance, in the case of a typical copper surface featuring a micron-scale roughness [27], our numerical modeling suggests that diffusive surface evolution can indeed lead to the formation of breakdown precursors at experimentally-relevant fields without invoking the presence of very specific microstructural features. Our investigation also reveals a crucial aspect: the critical fields for instability exhibit a rapid decrease with the growing aspect ratio of the initial surface morphology, as well as a slow but consequential decrease with increasing perturbation wavelength.
The paper is organized as follows: first in Section 2 we describe the mesoscale finite element model of morphological evolution of surfaces under electric fields. We then analyze the subcritical and supercritical regimes and identify fields associated with unstable growth of surface perturbations into sharp protrusions in Section 3. Finally, Section 4 puts these results in relation with previous experimental findings and discusses possible extensions of the model.
2 Mesoscale curvature-driven growth model
Surface kinetics–Our computational model follows conventional descent dynamics where the system evolves to minimize its free energy. Such models where first put forth by Herring [28, 29] and Mullins [30], and have since proven successful at predicting several surface and interface evolution phenomena [31] e.g., grain boundary grooving [32], electromigration-driven void collapse [33] in electronic interconnects, diffusive surface crack nucleation [34] and instability in stressed solids [35] etc. In our setting, atomic migration is assumed to occur only at the free surface and to be governed by a driving force that is given by the surface-gradient of free energy density (per-unit volume, g)
Depending on its wavelength (λ), a small-amplitude perturbation on the surface can either decay or grow based on competition between effective contribution to free-energy density from surface tension (Wsurf–which tends to stabilize flat surfaces) and any external driving mechanisms (Wext—potentially leading to growth of curvature). We further assume the flux of mass (js) to be proportional to the driving forces (Figure 1), i.e.,
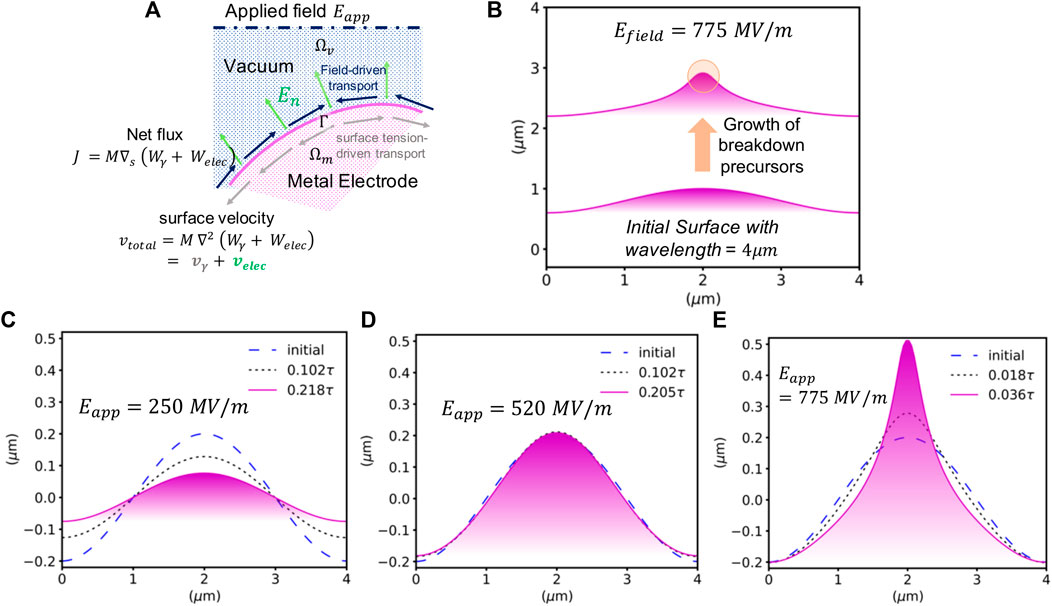
FIGURE 1. Curvature-driven growth of electrode surfaces under fields: (A) A metal electrode (magenta) is exposed to an applied electric field imposed at some distance in the vacuum (blue). Surface tension and electrostatic energies drive surface diffusion fluxes which leads to the evolution of the surface. (B) Breakdown precursor formation at a nominally flat electro-polished copper surface perturbed at a wavelength (λ) 4 μm [27] with a low aspect ratio (h0/λ ∼ 0.1) under Eapplied = 775 MV/m. (C–E) illustrates the morphological evolution of a sinusoidal perturbation of aspect ratio 0.1 under various dynamical regimes. Under a subcritical field of 250 MV/m, the perturbation decays back toward a flat surface (C) Under a critical field of 520 MV/m, the surface perturbation remains stable. (D) Under a super-critical field (775 MV/m), a sharp tip quickly grows (E).
Here, M is the mobility of surface atoms which is related to surface self-diffusivity (
γ is the surface tension, and h(x) is the surface height at position x. In the following, Wext accounts for the coupling of the system with an externally applied electric field (hence, Wext = Welec).
Invoking conservation of mass, a continuity equation for the flux leads to the evolution of velocity (vn) normal to the surface,
Summarizing from Eqs 1–5, the total velocity
For the vertical (y) component of the total velocity,
Where vy is the local vertical velocity of the surface (Eq. 7) such that for a surface profile h(x),
Electrostatics–Consider a domain as shown in Figure 1A which has a vacuum (Ωv) and an electrode material component (Ωm) which is assumed to be a perfect conductor. We obtain the electrostatic potential ϕ and the electric field E = −∇ϕ) through the solution of the Poisson equation:
with Eapplied (Eq. 10) the macroscopically-applied field. The electrostatic contribution to the free energy density at the surface is then obtained as
The discretized solution space of Eq. 11 is a mixed space
In a staggered solution approach, the electrostatics (Eq. 8) is first solved to evaluate Welec on the coinciding nodes of the meshes of the domains Ωv and Γ, the surface profile h (x, t) is then evolved using a small timesteps Δt. As the electrostatic solution changes slowly on the timescale Δt required for numerical stability of the integration of the surface kinetic equations, the electrostatic solution is updated less frequently. A frequency ratio of 100–200 was found to give good results.
In the resulting model, termed SurFE-XD Surface curvature-driven Finite Elements model for Diffusion under eXtreme conditions, the variational forms are specified in the FEniCS workflow [36] in the high-level Python-based Unified Form Language (UFL). These forms are then automatically compiled [37] and executed through high-performance computational kernels using the finite element library DOLFIN [38].
3 Results
First, we demonstrate and verify our simulation results for a periodic sinusoidal profile (
In Figures 1A–D, a critical field of 520 MV/m is identified below which surface tension dominates, leading to the gradual decrease in amplitude of the initial surface profile. Above the critical field, the electric field drives mass transport towards the tip, leading to the emergence of a sharp surface feature that has the characteristics of an efficient breakdown precursor (Figure 1E).
At low aspect ratio, one can compare the numerical results with growth/decay rates obtained from linear-stability analysis with an initial profile, say e.g.,
Our simulation results are in close agreement with the predictions of this linear stability analysis. One of the key limitations of this approximation is that is it only valid in the limit of small aspect ratios, i.e., A0/λ ≪ 1. Outside of this regime, explicit numerical solutions like that provided by (SurFE-XD) is essential. It is important to note that the critical field is inversely proportional to the square root of the wavelength λ, and so could be higher or lower depending on the physical scale of the surface roughness. In particular, longer wavelengths lead to a lowering of the critical field. E.g., for copper, a wavelength of 100 μm would correspond to a critical field to 100 MV/m. The specific values cited should therefore be taken as indicative of the order of magnitude of the critical fields, but can be expected to vary with the specifics of each surface finish.
In order to understand the effect of strong electric fields on the growth dynamics of nominally flat (h0/λ ∼ 0.1) copper surfaces, we analyze their evolution under a near-critical (775 MV/m) and stronger supercritcal (1.5 GV/m) regimes. Figure 2A shows that, at slightly super-critical fields, precursor formation occurs by long-range mass transport towards the hillock region. As the field are further increased into the super-critical regime, the growth becomes much more localized, leading to the formation of sharp emitter (Figure 2B). The growth speed of the initial perturbation is also observed to be strongly dependent on the applied field. At 775 MV/m, the timescale required for growth up to an amplitude of 0.5 μm in the orders of
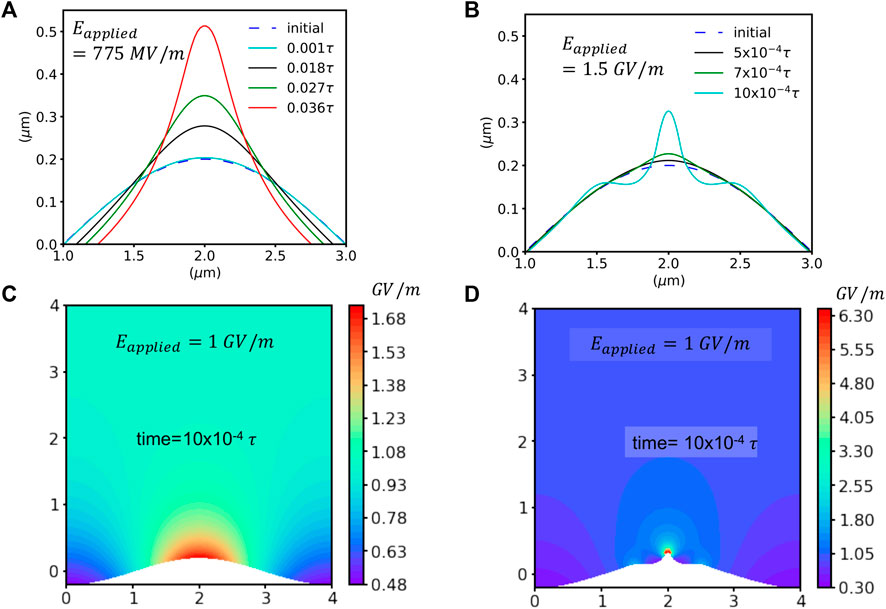
FIGURE 2. Breakdown precursor formation under strong e-fields: Surface evolution at 775 MV/m (A) and 1.5 GV/m (B). Field-enhancement at a particular time instance, e.g., t = 10 × 10−4τ (cyan surface profiles in (A,B)) is compared through the corresponding spatial distribution of the local electric field magnitude under an applied field of 1 GV/m in (C) (case a.) and (D) (case b).
Figures 2C, D shows that the electric field localizes at the hillock regions while it is being partially shielded at the trough or valley regions. In the near critical regime (e.g., 775 MV/m), the contribution of surface tension towards mass transport is of similar order with that of the electric field. Hence, while local enhancement at the hillock region drives the curvature to grow, active mass transport from the valley towards the hillock lead to long-range mass transport. On the other hand, at 1.5 GV/m, the electrostatic driving force completely overwhelms surface tension in the hillock, leading to a localized and rapid growth of a very sharp tip. The rapid nonlinear growth towards instability is accelerated by local field enhancement in highly-curved regions.
To further probe the effect of local geometry on field induced breakdown precursor formation, we model the evolution of isolated Gaussian-shaped features (
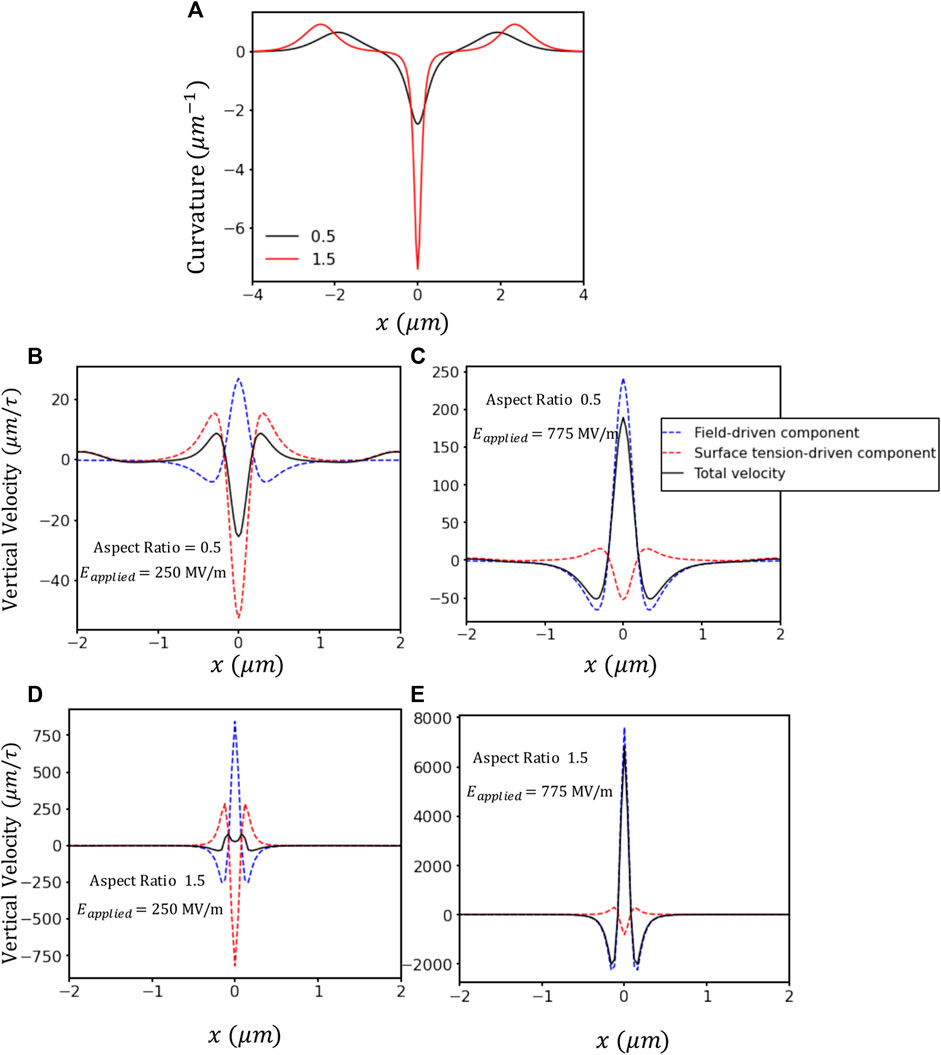
FIGURE 3. Effect of the initial aspect ratio on the relative contributions of surface tension and electric fields. (A) Curvature (κ(x)) of Gaussian surface profiles with aspect ratio 0.5 and 1.5. Middle panel (B,C) with aspect ratio 0.5 and lower panel (D,E) with 1.5 show spatial variation of individual and total velocity contributions from electric field and surface tension driven forces under fields 250 MV/m (B,D) and 775 MV/m at t = 0 (C,E).
For a fixed width of 4μm, the individual contributions of surface tension (vγ) and electrostatics (velec) again act in opposite directions, as shown in Figures 3B–E. Under a field of 250 MV/m, for a surface feature with a modest aspect-ratio (0.5), (Figure 3B) surface tension slightly dominates over the electrostatic driving force at the tip location (x = 0), leading to the decay of the initial protrusion. This trend is completely reversed at a field of 775 MV/m for the same aspect ratio 0.5 (Figure 3C); here the electric-field-induced velocity drives the growth of the tip resulting in the rapid growth of sharp feature that could act as a breakdown precursor.
At even higher aspect ratios (1.5, c.f. Figure 3D) the local field enhancement at highly curved regions magnifies the electro-static driving forces for diffusion, inducing tip growth at fields that were previously sub-critical for smaller protrusions. E.g., at field of 250 MV/m, the electrostatics contributions slightly exceed the restoring tendency of the surface tension, resulting in a net positive velocity at tip. This is in contrast with the much higher linear stability estimation of 520 MV/m reported above. We note that two effects are at play: first, field enhancement is more efficient at isolated protrusions due to the lack of interactions between tips (however note that in our simulations, periodic boundary conditions remain in the lateral direction so tip-tip interactions are not totally absent, but they are smaller in magnitude); second, non-linear interactions between modes invalidate the predictions obtained in the linear regime.
The respective contributions of surface tension and electric fields is further analyzed in Figure 4, which presents the ratio of the different velocity contributions (
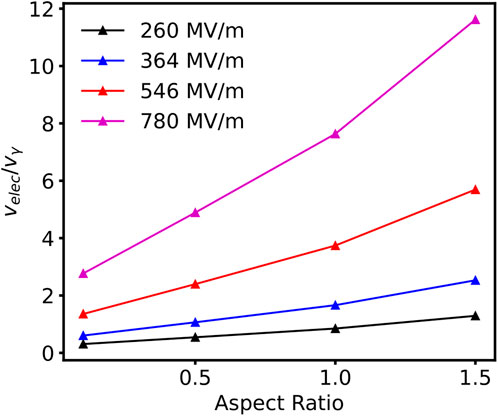
FIGURE 4. Ratio of the vertical surface velocity contributions stemming from electrostatics and surface tension at the location of the tip as a function of aspect ratio for a Gaussian protrusion of 4 μm in width.
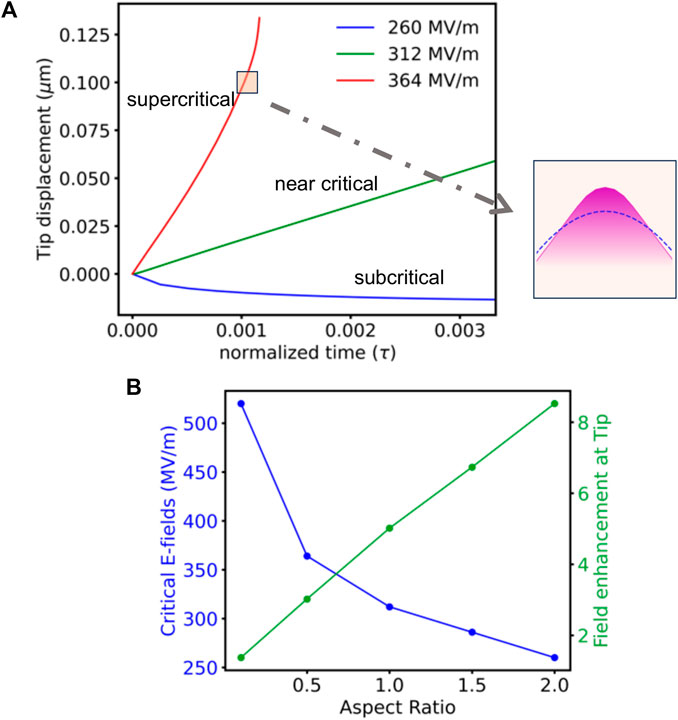
FIGURE 5. Time evolution of precursor growth for identifying critical electric fields: (A) For an aspect-ratio of 1.0, subcritical (260 MV/m), near-critical (312 MV/m) and supercritical (364 MV/m) regimes of tip-displacement evolution. Inset Sharpening of tip (magenta fill) at supercrtical (364 MV/m) compared to initial tip geometry in blue dashed line. (B) Critical e-fields (blue) decrease with increasing aspect ratio while field enhancement at the tip (green) linearly increases.
4 Discussion
A key factor that should be quantified in order to assess the efficiency of this mechanism is the timescale over which the growth of such surface features can be expected to occur. The time-unit in the simulation τ is estimated as:
Considering Cu parameters (c.f. Section 2)
Further, the simulations have shown that breakdown precursors can be expected to spontaneously form through surface transport at fields in low hundreds of MV/m, depending on the initial roughness of the surface. This mechanism can therefore potentially contribute to the spontaneous formation of breakdown-inducing features in application-relevant conditions. Indeed, the conditions investigated here are consistent with experiments carried on for breakdown with DC pulses with Copper electrodes [12]. These experiments have shown that i) the spatial location of the breakdown events is highly correlated, with a high fraction of craters overlapping, and ii) the breakdown events occurred preferentially close to the edge of the electrode. The first point is consistent with the observation that breakdown events leave craters and debris behind [12, 45]. As shown above, these surface features can couple efficiently with the electric field, potentially leading to fast tip-growth instabilities and to further breakdown events occurring in close proximity and in rapid succession, consistent with experimental results [45, 46]. Second, the edge of the cathode will be exposed to additional macroscopic field gradients which can also drive surface diffusion. This effect has been observed in nanoscale experiments on gold surfaces where electric field gradients at the edge of the electrode led to enhanced formation of ridge and tip-like features [47]. Both these observations are consistent with the hypothesis that breakdown was there mediated by surface diffusion driven by electric fields.
Finally, our simulations show that the mechanism investigated here can lead to very-fast runaway instabilities. Indeed, Figure 5A shows that tip growth proceeds in two stages: an initial stage where the tip grows roughly linearly in time, and a second runaway stage where exponential growth is observed. This suggests that directly observing these sharp precursors in experiments can be expected to be very challenging, as the onset of runaway growth occurs at relatively modest aspect ratios and then unfolds very rapidly, leading to the destruction of the tip during the breakdown process. During short-time scanning probe investigations of surface roughness of electrodes in vacuum under moderate electric fields, sharp features leading to high field-enhancement factors were rarely observed [48]. This is consistent with a mechanism where sharp breakdown precursors form only shortly before breakdown occurs.
While field-driven surface diffusion appears to be a viable mechanism to explain the formation of breakdown precursors, other phenomena could contribute. For example, theoretical treatments typically assume clean surfaces free of contamination. Any contaminants could potentially affect surface evolution in complex fashion. Second, many high-field applications occur in high-frequency AC settings [2, 13]. In this case, losses through Joule heating induce thermo-elastic stresses. These introduce an additional driving force for surface deformation [34] and can also lead to the formation of surface roughness through thermal fatigue [25]. Other mechanisms could therefore “seed” the tip-growth process by introducing surface features, which would then grow and sharpen through the diffusive mechanism discussed here. The contributions of thermo-elastic stresses on surface evolution are considered in a follow-on paper, where significant reductions in critical fields are observed for temperature rises on the order of tens of degrees [49]. We also ote that the present study mostly focuses with micron-scale roughnesses in metal electrodes as observed in electropolished surfaces. A different polishing approach (e.g., “mirror-polish”) might lead to submicron wavelengths. Furthermore, postmortem investigations of high-gradient breakdown surfaces in rf cavities revealed that pristine roughness conditions might be greatly modified by the presence of micron-scale debris or adsorbates, which could further affect the coupling with the electric field [50].
Finally, our study focuses only on early-stages of precursor formation, before runaway mechanisms that dissipate large amounts of energy are activated. Once they do so, several other mechanisms related to plasma formation e.g., ion-desorption [17], droplet ejection and emission-current induced heat transport [18] will become relevant in the intermediate stages of breakdown once field-induced surface instability has triggered localized emission [51, 52]/melting [16]. We have also neglected any effects on mass loss due to vaporization, which are not expected to be significant in the early stages of precursor formation, but would become significant once the runaway process begins.
5 Conclusion
In this study, the evolution of metallic surfaces exposed to strong electric fields was modeled using a surface diffusion model driven by surface tension and electro-static driving forces. The numerical results are consistent with the prediction of linear stability analysis in the regime small aspect-ratio perturbations on the surface. Non-linearities in the growth process start to emerge with high aspect-ratio surface features as well as under stronger electric fields. Our results show that exposure to electric fields in the low hundreds of MV/m can trigger the spontaneous formation of sharp surface features that can act as precursors for breakdown. These fields are of the same order of magnitude as those experimentally observed to lead to breakdown, suggesting that field-driven transport is a plausible mechanism for precursor formation, acting either alone, or in concert with other surface deformation mechanisms.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary materials, further inquiries can be directed to the corresponding author.
Author contributions
SB: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Software, Validation, Visualization, Writing–original draft, Writing–review and editing. ES: Funding acquisition, Project administration, Resources, Supervision, Validation, Writing–original draft, Writing–review and editing. DP: Conceptualization, Investigation, Project administration, Resources, Supervision, Validation, Writing–original draft, Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the Laboratory Directed Research and Development program of Los Alamos National Laboratory under project number 20230011DR. Los Alamos National Laboratory is operated by Triad National Security, LLC, for the National Nuclear Security Administration of U.S. Department of Energy (Contract No. 89233218CNA000001).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Sicking E, Ström R. From precision physics to the energy frontier with the Compact Linear Collider. Nat Phys (2020) 16:386–92. doi:10.1038/s41567-020-0834-8
2. Simakov EI, Dolgashev VA, Tantawi SG. Advances in high gradient normal conducting accelerator structures. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2018) 907:221–30. doi:10.1016/j.nima.2018.02.085
3. Schneider M, Dolgashev V, Lewellen JW, Tantawi SG, Nanni EA, Zuboraj M, et al. High gradient off-axis coupled C-band Cu and CuAg accelerating structures. Appl Phys Lett (2022) 121. doi:10.1063/5.0132706
4. Nanni EA, Breidenbach M, Li Z, Vernieri C, Wang F, White G, et al. Status and future plans for C3 R&D. J Instrumentation (2023) 18:P09040. doi:10.1088/1748-0221/18/09/p09040
5. Schulte R, Johnstone C, Boucher S, Esarey E, Geddes CG, Kravchenko M, et al. Transformative technology for FLASH radiation therapy. Appl Sci (2023) 13:5021. doi:10.3390/app13085021
6. Kutsaev S. Novel technologies for compact electron linear accelerators (review). Instr Exp Tech (2021) 64:641–56. doi:10.1134/s0020441221050079
8. Dolgashev VA, Tantawi S. G., Higashi Y, Tsukuba KEK. Proc LINAC Tsukuba, Japan, September, 2010(2010) 1043.
9. Dolgashev VA, Tantawi SG, Yeremian AD, Higashi Y, Spataro B. Proc IPAC, Kyoto, Japan, May, 2010, (2010) 3810.
10. Grudiev A, Calatroni S, Wuensch W. New local field quantity describing the high gradient limit of accelerating structures. Phys Rev Spec Topics-Accelerators Beams (2009) 12:102001. doi:10.1103/physrevstab.12.102001
11. Hopkins MM, Jindal AK, Bussmann E, Ohta T, Berg M, Thomas C, et al. Employing nanoscale surface characterizations in a field emission model. Albuquerque, NM, United States: Sandia National Lab.SNL-NM (2020).
12. Saressalo A, Kyritsakis A, Djurabekova F, Profatilova I, Paszkiewicz J, Calatroni S, et al. Classification of vacuum arc breakdowns in a pulsed dc system. Phys Rev Acc Beams (2020) 23:023101. doi:10.1103/physrevaccelbeams.23.023101
13. Dal Forno M, Dolgashev V, Bowden G, Clarke C, Hogan M, McCormick D, et al. Rf breakdown tests of mm-wave metallic accelerating structures. Phys Rev Acc Beams (2016) 19:011301. doi:10.1103/physrevaccelbeams.19.011301
14. Descoeudres A, Ramsvik T, Calatroni S, Taborelli M, Wuensch W. Dc breakdown conditioning and breakdown rate of metals and metallic alloys under ultrahigh vacuum. Phys Rev Spec topics-accelerators beams (2009) 12:032001. doi:10.1103/physrevstab.12.032001
15. Nordlund K, Djurabekova F. Defect model for the dependence of breakdown rate on external electric fields. Phys Rev Spec Topics-Accelerators Beams (2012) 15:071002. doi:10.1103/physrevstab.15.071002
16. Kyritsakis A, Veske M, Eimre K, Zadin V, Djurabekova F. Thermal runaway of metal nano-tips during intense electron emission. J Phys D: Appl Phys (2018) 51:225203. doi:10.1088/1361-6463/aac03b
17. Uimanov I, Shmelev D, Oks E, Yushkov GY, Barengolts S. Cathode and plasma phenomena in vacuum-arc sources of hydrogen isotope ions: I. Desorption of hydrogen isotopes during the operation of vacuum arc cathode spots. Plasma Sourc Sci Tech (2020) 29:015021. doi:10.1088/1361-6595/ab62da
18. Kaufmann H, Cunha M, Benilov M, Hartmann W, Wenzel N. Detailed numerical simulation of cathode spots in vacuum arcs: interplay of different mechanisms and ejection of droplets. J Appl Phys (2017) 122. doi:10.1063/1.4995368
19. Eimre K, Parviainen S, Aabloo A, Djurabekova F, Zadin V. Application of the general thermal field model to simulate the behaviour of nanoscale Cu field emitters. J Appl Phys (2015) 118:033303. doi:10.1063/1.4926490
20. Jansson V, Baibuz E, Kyritsakis A, Vigonski S, Zadin V, Parviainen S, et al. Growth mechanism for nanotips in high electric fields. Nanotechnology (2020) 31:355301. doi:10.1088/1361-6528/ab9327
21. Pohjonen A, Djurabekova F, Nordlund K, Kuronen A, Fitzgerald S. Dislocation nucleation from near surface void under static tensile stress in Cu. J Appl Phys (2011) 110. doi:10.1063/1.3606582
22. Engelberg EZ, Ashkenazy Y, Assaf M. Stochastic model of breakdown nucleation under intense electric fields. Phys Rev Lett (2018) 120:124801. doi:10.1103/physrevlett.120.124801
23. Zadin V, Pohjonen A, Aabloo A, Nordlund K, Djurabekova F. Electrostatic-elastoplastic simulations of copper surface under high electric fields. Phys Rev Spec Topics-Accelerators Beams (2014) 17:103501. doi:10.1103/physrevstab.17.103501
24. Bagchi S, Perez D. Atomistic modeling of the coupling between electric field and bulk plastic deformation in fcc metals. Phys Rev Acc Beams (2022) 25:033101. doi:10.1103/physrevaccelbeams.25.033101
25. Laurent L, Tantawi S, Dolgashev V, Nantista C, Higashi Y, Aicheler M, et al. Experimental study of rf pulsed heating. Phys Rev Spec topics-accelerators beams (2011) 14:041001. doi:10.1103/physrevstab.14.041001
26. Kimari J, Wang Y, Kyritsakis A, Zadin V, Djurabekova F. Biased self-diffusion on Cu surface due to electric field gradients. J Phys D: Appl Phys (2022) 55:465302. doi:10.1088/1361-6463/ac91dd
27. Pendyala P, Bobji M, Madras G. Evolution of surface roughness during electropolishing. Tribology Lett (2014) 55:93–101. doi:10.1007/s11249-014-0336-x
28. Herring C. Effect of change of scale on sintering phenomena. J Appl Phys (1950) 21:301–3. doi:10.1063/1.1699658
29. Herring C. Fundamental contributions to the continuum theory of evolving phase interfaces in solids: a collection of reprints of 14 seminal papers. Berlin, Germany: Springer (1999). p. 33–69.
30. Mullins WW. Flattening of a nearly plane solid surface due to capillarity. J Appl Phys (1959) 30:77–83. doi:10.1063/1.1734979
32. Sun B, Suo Z, Yang W. A finite element method for simulating interface motion—I. Migration of phase and grain boundaries. Acta materialia (1997) 45:1907–15. doi:10.1016/s1359-6454(96)00323-0
33. Xia L, Bower AF, Suo Z, Shih C. A finite element analysis of the motion and evolution of voids due to strain and electromigration induced surface diffusion. J Mech Phys Sol (1997) 45:1473–93. doi:10.1016/s0022-5096(97)00013-6
34. Yang WH, Srolovitz DJ. Surface morphology evolution in stressed solids: surface diffusion controlled crack initiation. J Mech Phys Sol (1994) 42:1551–74. doi:10.1016/0022-5096(94)90087-6
35. Srolovitz DJ. On the stability of surfaces of stressed solids. Acta metallurgica (1989) 37:621–5. doi:10.1016/0001-6160(89)90246-0
36. Langtangen HP, Logg A. Solving PDEs in python: the FEniCS tutorial I. Berlin, Germany: Springer Nature (2017).
37. Kirby RC, Logg A. A compiler for variational forms. ACM Trans Math Softw (Toms) (2006) 32:417–44. doi:10.1145/1163641.1163644
38. Logg A, Wells GN. DOLFIN: automated finite element computing. ACM Trans Math Softw (Toms) (2010) 37:1–28. doi:10.1145/1731022.1731030
39. Kumykov V, Sergeev I, Sozaev V, Gedgagova M. Surface tension of copper in solid phase. Bull Russ Acad Sci Phys (2017) 81:357–9. doi:10.3103/s1062873817030236
40. Simon N, Drexler E, Reed RP. Properties of copper and copper alloys at cryogenic temperatures. Final report. Boulder, CO, United States: National Inst. of Standards and Technology MSEL (1992).
41. Karimi M, Tomkowski T, Vidali G, Biham O. Diffusion of Cu on Cu surfaces. Phys Rev B (1995) 52:5364–74. doi:10.1103/physrevb.52.5364
42. Schulze Icking-Konert G, Giesen M, Ibach H. Decay of Cu adatom islands on Cu(111). Surf Sci (1998) 398:37–48. doi:10.1016/s0039-6028(98)80009-5
43. Kallinteris G, Evangelakis G, Papanicolaou N. Molecular dynamics study of the vibrational and transport properties of copper adatoms on the (111) copper surface; comparison with the (001) face. Surf Sci (1996) 369:185–98. doi:10.1016/s0039-6028(96)00920-x
44. Evangelakis G, Papageorgiou D, Kallinteris G, Lekka C, Papanicolaou N. Self-diffusion processes of copper adatom on Cu(110) surface by molecular dynamics simulations. Vacuum (1998) 50:165–9. doi:10.1016/s0042-207x(98)00039-6
45. Timko H, Djurabekova F, Nordlund K, Costelle L, Matyash K, Schneider R, et al. Mechanism of surface modification in the plasma-surface interaction in electrical arcs. Phys Rev B (2010) 81:184109. doi:10.1103/physrevb.81.184109
46. Wuensch W, Degiovanni A, Calatroni S, Korsbäck A, Djurabekova F, Rajamäki R, et al. Statistics of vacuum breakdown in the high-gradient and low-rate regime. Phys Rev Accel Beams (2017) 20:011007. doi:10.1103/physrevaccelbeams.20.011007
47. Gill V, Guduru P, Sheldon B. Electric field induced surface diffusion and micro/nano-scale island growth. Int J Sol Structures (2008) 45:943–58. doi:10.1016/j.ijsolstr.2007.09.010
48. Hopkins MM, Bussmann E, Smith S, Scrymgeour D, Brumbach MT, Hjalmarson HP, et al. Vacuum field emission models measurements and simulations. Albuquerque, NM, United States: Sandia National Lab.SNL-NM (2017).
49. Shinohara R, Bagchi S, Simakov E, Baryshev SV, Perez D. Thermal and electric field driven breakdown precursor formation on metal surfaces (2023). https://arxiv.org/abs/2311.02519. (Accessed 29 February 2024).
50. Nusinovich G, Kashyn D, Antonsen T. Possible role of rf melted microparticles on the operation of high-gradient accelerating structures. Phys Rev Spec Topics-Accelerators Beams (2009) 12:101001. doi:10.1103/physrevstab.12.101001
51. Kyritsakis A, Xanthakis J. Extension of the general thermal field equation for nanosized emitters. J Appl Phys (2016) 119. doi:10.1063/1.4940721
Keywords: breakdown, precursor formation, mesoscale surface diffusion, electrodiffusion, field induced behavior, field-enhancment mechanisms
Citation: Bagchi S, Simakov E and Perez D (2024) Formation of field-induced breakdown precursors on metallic electrode surfaces. Front. Phys. 12:1353658. doi: 10.3389/fphy.2024.1353658
Received: 11 December 2023; Accepted: 20 February 2024;
Published: 11 March 2024.
Edited by:
Andreas Kyritsakis, University of Tartu, EstoniaReviewed by:
Kristinn Torfason, Reykjavík University, IcelandChris Moore, Sandia National Laboratories (DOE), United States
Copyright © 2024 Bagchi, Simakov and Perez. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Soumendu Bagchi, c291bWVuZHViYWdjaGlAZ21haWwuY29t, YmFnY2hpc0Bvcm5sLmdvdg==
†Present address: Soumendu Bagchi, Center for Nanophase Materials Sciences, Oak Ridge National Laboratory, Oak Ridge, TN, United States
 Soumendu Bagchi
Soumendu Bagchi Evgenya Simakov2
Evgenya Simakov2