Abstract
Total reaction, interaction, and charge-changing cross sections, which are kinds of cross sections standing for total nuclear collision probability in medium-to high-energy region from a few to several hundred MeV, have been extensively utilized to probe nuclear sizes especially for unstable nuclei. In this mini review, experimental techniques and recent findings from these cross sections are briefly overviewed. Additionally, two new methods to extract neutron skin thickness solely from the above cross sections are explained: One is utilizing the energy and isospin dependence of the total reaction cross sections, and the other is the combination of the total reaction and charge-changing cross section measurements.
1 Introduction
In neutron-rich nuclei, a thick neutron skin forms, reflecting both the nuclear structure and the bulk properties of nuclear matter. The neutron skin thickness , which is defined as the difference between the root-mean-square (RMS) radii of the point-neutron and point-proton density distributions, and :This quantity is particularly anticipated as a promising observable to determine the slope parameter, , of the symmetry energy at the saturation density in the equation of state (EoS) of nuclear matter [1], where is the density. This parameter is defined as playing a crucial role in extrapolating the EOS for symmetric nuclear matter to that for asymmetric nuclear matter. Although significant efforts have been made to determine the neutron skin thickness, , in neutron-rich stable nuclei using various experimental techniques [2–16], a consistent value for has not yet been determined. Recent compilations report the range of values as MeV [17], MeV [18], and 40–60 MeV [19].
Determining of neutron-rich unstable nuclei has the advantage of constraining the parameter , as a thicker neutron skin is expected [20–23]. There are some measurements in neutron-rich unstable nuclei using the low-lying dipole resonance [24] and electric dipole polarizability [25–27]. Compared to the above experimental methods, the total reaction , interaction , and charge-changing cross sections , which will be focused in this paper are powerful tools for determining the size properties and of neutron-rich unstable nuclei far from the stability line. The and are sensitive to the matter radius , which is the RMS radius of the nucleon density distribution, . Therefore, if is precisely obtained via or , one can determine by combining with from another method, such as isotope shift measurements [28, 29], using Equation 1 together with the relation of , where , , and are the mass, atomic, and neutron numbers of the nucleus of interest.
Furthermore, recent developments using and/or , mentioned in Section 5, offer new ways to determine solely from these total cross sections. Compared to other major nuclear reaction measurement techniques using RI beams [30], these total cross sections can be measured even with extremely low radioactive-isotope (RI) beam intensities of, e.g., around 0.1 particles/sec, making it possible to extract of very neutron-rich nuclei. In this paper, we briefly review recent studies regarding these total cross sections, with a particular focus on advances related to the neutron skin.
2 Overview of experimental techniques
The and are defined as the total cross sections for all inelastic reactions and all reactions that change the nuclides, respectively. At energies above approximately 200 MeV/nucleon, is generally assumed in Glauber-model analyses (Section 3) because the inelastic scattering where the projectile nucleus remains in the ground state hardly occurs. Theoretical studies have indicated that the ratio of this inelastic scatteing cross section to , , is typically 2%–3% at energies above 200 MeV/nucleon, increasing to around 5% as energy decreases to several tens MeV/nucleon [31, 32]. The values for Mg isotopes on 12 at 240 MeV/nucleon were experimentally estimated to be around 2% [33].
The is often measured using the transmission method [34] represented bywhere is the number of target nuclei per unit area, and are the nonreaction rates for measurements with and without the target. The and in Equation 2 are obtained by counting the number of incident particles and that of outgoing nonreaction ones, respectively. This method has lower experimental uncertainty compared to the associate- method [35], which assumes that all inelastic scatterings necessarily emit rays.
At energies above 200 MeV/nucleon, is often measured instead of . This is because the “nonreaction particle” for represents the particle that has not changed nuclide species, which is easier to identify experimentally. Conversely, at energies below around 100 MeV/nucleon, where cannot be ignored, are often measured. The definition of “nonreaction particle” of includes the “elastically scattered particle.” Therefore, in addition to the identification of nuclide species, energy or momentum measurements are required downstream of the target. The are practically estimated from the tail of the energy or momentum distribution [33, 36], while that peculiarly from the inelastic excitations to bound states is sometimes estimated from counting de-exciting rays [37, 38].
The charge-changing cross section, , mentioned in Section 5.2, is also measured by the transmission method. This is the total cross section of atomic-number-changing reactions of the projectile nucleus, so that particles with the same number as the projectile ones downstream of the target are counted as “nonreaction particles.” Note that some studies treated products with a larger than projectile nuclei as nonreaction particles because an increase in is not considered to result from the fragmentation reaction [39–41]. For example, in C isotopes [39, 42], that contribution was comparable or less to the experimental uncertainty of (around 1%).
3 Glauber model
There are several approaches to theoretically describe the relationship between (or ) and the RMS radii of colliding nuclei, such as the black sphere model [31, 43–45] and the folding model with optical potentials [46–55]. Among these, the Glauber theory [56] has frequently been used. In the Glauber formalism, is expressed aswhere is the impact parameter vector, is the phase-shift function for the elastic scattering between the projectile and target nuclei. The in Equation 3 is given by the ground-state wave functions of the projectile and target nuclei, and , respectively:where the subscripts “” and “” denote the isospin of nucleons of the projectile and target nuclei, the superscripts “P” and “T” the projectile and target nuclei, respectively, is the incident energy per nucleon, and are the two-dimensional vectors of the ()-th nucleon’s cordinates () in the plane perpendicular to the beam axis. The nucleon-nucleon profile function , obtained by a Fourier transform of the nucleon-nucleon scattering amplitude, is typically parameterized as [57].where is the nucleon-nucleon total cross section [58] (Figure 1A), the ratio of the real to the imaginary part of the nucleon-nucleon scattering amplitude, and the slope parameter of the nucleon-nucleon elastic differential cross section representing the range of nucleon-nucleon interaction.
FIGURE 1
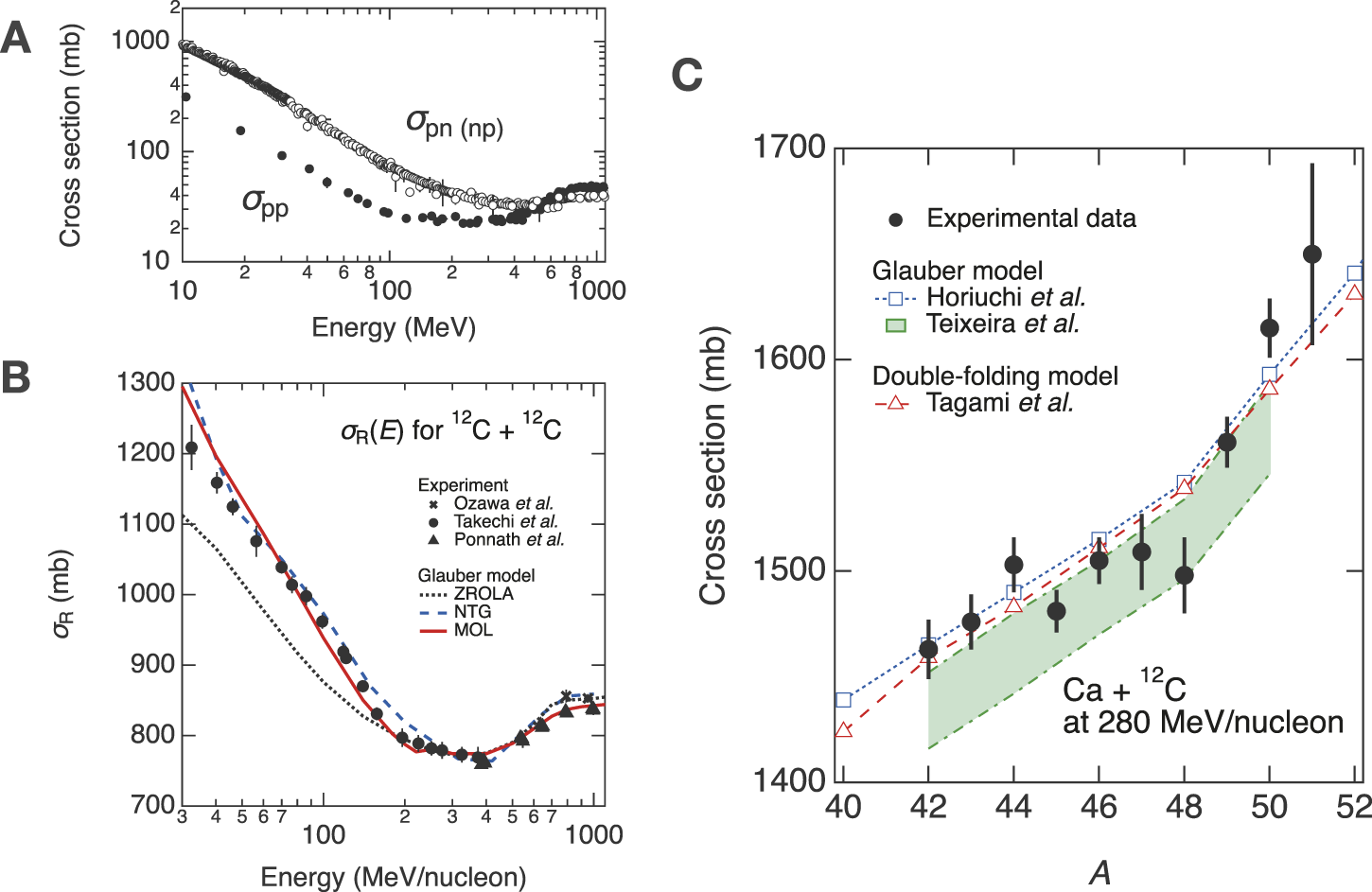
Properties regarding total-reaction cross sections or interaction cross sections (A) Energy dependence of proton–proton and proton–neutron (or neutron–proton) total cross sections, (closed circles) and (open circles), which are fundamental inputs of the Glauber-model calculations. The experimental values are taken from Ref. [58]. (B) Energy dependence of reaction cross section . Crosses [78], closed circles [64], and closed triangles [72] show experimental data, and the dotted black, dashed blue, and solid red lines represent the Glauber-model calculations under the zero-range OLA, NTG [63], and MOL [64] formalisms. (C) Comparison between experimental data [70] and theoretical calculations of for Ca isotopes on 12 at 280 MeV/nucleon. Open blue squares connected by a dotted line represent the Glauber-model calculation under the NTG approximation with density distributions of Ca isotopes obtained from the Hartree–Fock calculation using the SLy4 interaction [71], dot-dashed green lines with the shaded band the Glauber-model calculations considering several effects with the density distributions obtained from the Hartree–Fock–Bogoliubov (HFB) or relativistic mean field calculations using 31 different interactions [69], respectively. For comparison, the double-folding-model calculation with the Gogny-D1S HFB with the angular momentum projection (GHFB + AMP) is also shown by open red triangles connected by a dashed line [50].
To calculate in Equation 4, multiple integrals of the wave functions of the projectile and target nuclei are required, which can be performed using the Monte Carlo integration technique [59, 60]. However, approximations are generally applied to avoid the complexity of the calculations. One of the simplest and most frequently used approximations is the optical-limit approximation (OLA):Here, represents the density distribution of the projectile (target) nucleus. Using the OLA, can be calculated given the density distributions of projectile and target nuclei and . However, this approximation does not account for various possible multiple-scattering effects. To incorporate them effectively, is extended to the nucleon-target profile function, [61, 62], which is called the “nucleon-target formalism in the Glauber model” (NTG) [63] or “modified OLA” (MOL) [64]:Here, although Equation 7 also incorporate the isospin dependence and similar to those in Equation 6, these isospin notations are omitted for the sake of simplicity. Note that a modified version of this equation that satisfies symmetry regarding the exchange between projectile and target components is usually used [61, 62]. Other various effects have been also considered: the energy dependendent parameters of and in [63, 65–68], Fermi-motion effect [64], and Pauli blocking [69]. Although these frameworks have minor differences, each is constructed to effectively reproduce the benchmark dataset (e.g., the energy dependence of for 12 on 12 shown in Figure 1B). Then, measured results are analyzed based on these evaluated theoretical framework. As an example, Figure 1C shows for Ca isotopes on 12 at 280 MeV/nucleon [70] together with the calculations using the Glauber model [69, 71] as well as the double-folding model [50] employing theoretical density distributions. To improve the Glauber formalism much more, there are recent experimental contributions, such as high-precision data for 12 on 12 at energies of 400–1,000 MeV/nucleon [72] and for 17 and 17 on a solid hydrogen target [73] at energies of 50–450 MeV/nucleon [74, 75].
4 Progress of total-reaction and interaction cross section studies
4.1 Progress in recent 20 years
After the pioneering work of measurements by Tanihata et al. [76, 77], and have been extensively measured at the RI-beam facilities. Here, the progress of studies related to and achieved after the 2001 review paper [78] is outlined.
Regarding nuclei near the neutron dripline, 22C [38, 79] and 29F [80] were newly identified as halo nuclei through measurements, and the structure of these nuclei and neighboring 31 were also investigated theoretically [60, 81–84]. The measurements for 22,23 found that the structure of 23 can be understood within the model consisting of a 22 core and a valence neutron [85]. Systematic measurements for F [86], Ne [87], Na [88], and Mg [33] isotopes at RIBF, which accessed more neutron-rich ones compared to previous measurements at GSI [89, 90], have significantly contributed to revealing the area consisting of islands of inversion around and 28. Additionally, these systematic data showed that 29,31 and 37 were found to have the halo structure induced by the strong deformation [91, 92]. The mechanisms of these phenomena were further investigated by various theoretical studies [46–48, 93–95]. The measurements, especially below 100 MeV/nucleon, have been extensively conducted to probe the details of density profiles near the nuclear surface [74, 96–109] because at lower energy than 200 MeV/nucleon are more sensitive to the dilute density of nuclei due to the large values [36, 110–113] (Figure 1A).
In the heavier region, other halo nuclei and islands of inversion have been predicted theoretically [114–116]. Regarding experimental progress in this region, measurements for Cl and Ar [37], Ca [70], and Kr isotopes [117] have been conducted mainly to discuss the evolution of neutron (proton) skins, which are reviewed separately below.
4.2 Studies on neutron skins
After revealing thick neutron skins in 6,8 from and neutron-removal cross sections [118], the first direct observation of neutron-skin growth along a long chain including unstable nuclei was conducted in Na isotopes by combining results [119] with the from the isotope-shift measurements [120]. The deduced of Na isotopes, as well as those of Cl and Ar isotopes [37], show a monotonic dependence on the difference between one-neutron and one-proton separation energies, [119]. In contrast to these isotopes, the trend of in Kr isotopes was different, implying that only the valence nucleons are responsible for the trend [117].
Recent measurements revealed a substantial growth of neutron skin in Ca isotopes across the neutron magic number [70], which is different from the isotopes mentioned above. It has been known that the trend of (charge radii) shows a sudden slope change against globally at the neutron magic numbers, which is called a “kink” [28, 29]. The experimental values determined from for 42–51 [70] (Figure 1C) also show a kink structure at similar to that of [121]. Interestingly, the magnitude of the kink in is much larger than that in , resulting in the emergence of the kink also in the evolution. Various mechanisms have been proposed for the possible origins behind the kink structure in (e.g., see Ref. [122]).
The evolution of neutron skin in Ca isotopes provides new insight also into the bulk properties of nuclear matter. The Hartree–Fock calculations have pointed out that the kink structure occurs depending on the properties of the occupying valence single-neutron states to minimize the energy loss resulting from the saturation of the densities in the internal region of the nucleus [71, 116]. Evaluating the contribution of caused by the surface difference between and is also important for determining the EOS parameter . Decomposing into the bulk part , which is sensitive to , and the surface part within the incompressible droplet model has clarified that the neutron-skin kink appears when the trend of changes [23, 123–126]. Thus, while the neutron skin is sensitive to the parameter as mentioned in the introduction, the neutron-skin kink itself plays a different role in identifying the effect of on determining .
In addition to the approach with the total collision cross sections described above and below, methods only using nucleon removal cross sections have been proposed [127].
5 Extraction of neutron skin thickness solely from collision cross sections
Recently, two novel methods have been developed to derive solely from nuclear collision cross sections. One method utilizes the energy and target dependence of (Section 5.1), and the other combines and (Section 5.2) [128–131].
5.1 Total reaction cross sections utilizing its energy and isospin dependence
This method [126, 132] utilizes the isospin and energy dependence of nucleon-nucleon total cross sections, [58]. As shown in Equation 5, the shown in Figure 1A is a fundamental input for Glauber model calculations, leading to the energy dependence of . The ratio of the proton-neutron to proton-proton (or neutron-neutron) total cross sections is at 100 MeV/nucleon, and decreases as the energy increases, then reaches unity at around 600 MeV/nucleon. At higher incident energies, although becomes slightly larger than , remains around unity. Therefore, proton targets and nuclear targets such as 12C, which contain equal numbers of protons and neutrons, are expected to have a different sensitivity to .
Horiuchi et al. analyzed the correlation between and through the Glauber-model calculation using the density distributions obtained from Skyrme-Hartree-Fock (SHF) theory [126]. In this analysis, the “reaction radius” was introduced in regard to , namely, , where and are the neutron and atomic numbers of the projectile nucleus, is the reaction energy, and is the label of the target species. The correlation between and the difference in obtained from at different energies, , shows global consistency over all isotopes of O, Ne, Mg, Si, S, Ca, and Ni isotopes examined here. For carbon targets, is almost independent of , whereas for proton targets, the plot of versus shows a clear non-zero slope. Especially, the trends including 100 MeV/nucleon data have a higher sensitivity to . To further investigate the effectiveness of on , was parameterized as the empirical formula ofwhere , , and are energy- and target-dependent parameters. The parameter , representing the effect of , shows prominent energy and target (isospin) dependence: is independent of energy for carbon targets, whereas strongly dependent for proton targets. Therefore, it is possible to extract by measuring at multiple energies and/or targets having different . Furthermore, to enhance sensitivity to , it is desirable to use a combination of proton and neutron targets that are completely isospin asymmetric pair. The use of deuteron targets has been proposed as an alternative to a neutron target [133].
The sensitivity of for separating density distributions of proton and neutron, and , using these properties was demonstrated experimentally in halo nuclei. The experimental values for 11Be and 8B on proton targets at 50–120 MeV/nucleon were consistent only with calculations assuming neutron and proton tails, respectively [134]. The and of 11Li were determined solely from the energy dependence of the experimental values on proton and carbon targets [103].
5.2 Charge-changing cross sections
The measurements aiming to derive have been conducted for isotopes up to Fe, particularly since 2010 [39, 40, 65, 135–147]. By analogy with the relationship between and , is expected to be sensitive to . The relationship between and is usually treated in the following Glauber-model-like formalism [65, 135, 136]:where is obtained from Equation 6 by omitting of the projectile nucleus, that is, only is adopted for Equation 6 [148]. In the case of , the situation appears to be less straightforward than that of due to the potential influence of neutrons in the incident nucleus. Here, for the sake of subsequent expressions, the calculated value from this equation is denoted as . There are several treatments to depict based on Equation 8. First, Yamaguchi et al. introduced an energy-dependent phenomenological correction factor into Equation 8 with the zero-range optical-limit approximation (ZROLA) to reproduce data for 28 on 12 at energies of 100–600 MeV/nucleon [135], as shown in Figure 2A. It has been shown that this calculation with explains the experimental values for Be to O isotopes on 12 at 300 MeV/nucleon with 3% standard deviation [136]. Second, the experimental of stable B, C, N, and O isotopes on 12 at around 900 MeV/nucleon were well reproduced by the finite-range optical-limit approximation (FROLA) calculations without [39–41, 141]. For 10,11B, the ratio of the experimental values to the calculated ones is 1.01(2) [141]. Third, Tran et al. determined profile-function parameters with the FROLA calculation common to reproduce both and for 12 on 12 over the range of 10–2,100 MeV/nucleon [65]. However, this calculation still underestimates at around 300 MeV/nucleon. Thus, although the consistency over respective treatments is not necessarily guaranteed, the reliability is ensured by locally normalizing with well-known data.
FIGURE 2

(A)Energy dependence of for 28 on a carbon target [135]. The dashed and dotted lines represent the ZROLA calculations of (Equation 8) and , respectively. The solid line shows the ZROLA calculation of with the empirical correction factor . (B) dependence of for Ca isotopes on a carbon target at around 280 MeV/nucleon (bottom figure), and the corresponding values (top figure). The black solid and green dashed lines represent calculations using Equation 8 with and without the empirical correction factor , respectively. The thin-dashed lines, red-solid lines with shaded bands, and dotted lines show calculations from Equation 9 with different values of 20, , and 70 MeV, respectively. Figures in (A, B) were reprinted from Ref. [135] and Ref. [144], respectively.
Contrary to the description by Equation 8, it has been suggested that considering the contribution of of the projectile nucleus is crucial to describe [148–151]. Tanaka et al. demonstrated that the trend of the experimental data can be explained by explicitly incorporating the contribution of of the projectile nucleus [144] based on the abrasion-ablation model [152, 153]. In this framework, the contribution of the cross section , which accounts for the charge-changing process of the projectile nucleus caused by the evaporation of charged particles following neutron removal reactions, was introduced in addition to the ZROLA calculation of Equation 8:The is calculated using the contribution probability of the neutron-removal reaction to , . The depends on the applied value of the parameter , which represents the maximum excitation energy of the prefragment produced after a one-nucleon removal reaction (Figure 2B). Using MeV, this calculation consistently explains existing data on 12 at around 300 MeV/nucleon over a wide mass region from C to Fe isotopes, with 1.6% standard deviation [144]. Figure 2B represents measured results for Ca isotopes on 12 together with several caluculated cross sections explained in this subsection (see caption). This framework also reproduces new experimental results for C, N, and O isotopes on 12 at 300 MeV/nucleon [146] as well as one of two datasets of for N isotopes on 12 at around 900 MeV/nucleon [40]. The framework of Equation 9; Figure 2B indicates that the majority of provides information on of the projectile nucleus and the contribution of decreases as of the projectile nucleus increases. Thus, in very neutron-rich region, the assumption of Equation 8 works well. The sensitivity of to becomes much larger.
A proton target has been adopted in measurements, as in the cases of 30, 32,33 [139], and 34–36 [142]. Suzuki et al. emphasized the necessity of considering the contribution of of the projectile nucleus peculiarly in on a proton target [154]. The FROLA calculation of Equation 8 underestimates the experimental values by 10%–20% for C isotopes on a proton target at around 900 MeV/nucleon. They found that this discrepancy can be explained by introducing the “p-n exchange” effect, in which a part of the proton flux of the target is converted to the neutron flux by neutrons of the projectile, contributing to .
To derive the EOS parameter , the difference in the charge radii of mirror nuclei, , has been used [155–160]. Similarly, the relationship between and the difference in of mirror nuclei, , was demonstrated to show a good linear correlation [161]. The degree of this linear correlation is equivalent to the ones between and or .
6 Summary
This paper has reviewed recent advancements in the total reaction , interaction , and charge-changing cross sections , with a special emphasis on the neutron skin and corresponding nuclear radii. The framework describing the relationship between these cross sections and the size properties of atomic nuclei has been well investigated, providing the advantage to probe nuclear sizes of neutron-rich unstable nuclei, where a thick neutron skin is expected. The review has also highlighted two novel methods for extracting from the total collision cross sections: one utilizing the energy and isospin dependence of , and the other combining with . These advancements lead to more accurate constraining the slope parameter in the symmetry energy term of the EoS of nuclear matter through of unstable nuclei in very neutron-rich region.
Statements
Author contributions
MT: Writing–original draft, Writing–review and editing. WH: Writing–review and editing. MF: Writing–review and editing.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1.
BrownBA. Neutron radii in nuclei and the neutron equation of state. Phys Rev Lett (2000) 85:5296–9. 10.1103/PhysRevLett.85.5296
2.
TsangMBStoneJRCameraFDanielewiczPGandolfiSHebelerKet alConstraints on the symmetry energy and neutron skins from experiments and theory. Phys Rev C (2012) 86:015803. 10.1103/physrevc.86.015803
3.
TrzcińskaAJastrzȩbskiJLubińskiPHartmannFJSchmidtRvon EgidyTet alNeutron density distributions deduced from antiprotonic atoms. Phys Rev Lett (2001) 87:082501. 10.1103/physrevlett.87.082501
4.
KlosBTrzcinskaAJastrzebskiJCzosnykaTKisielinskiMLubinskiPet alNeutron density distributions from antiprotonic 208Pb and 209Bi atoms. Phys Rev C (2007) 76:014311. 10.1103/physrevc.76.014311
5.
TerashimaSSakaguchiHTakedaHIshikawaTItohMKawabataTet alProton elastic scattering from tin isotopes at 295 MeV and systematic change of neutron density distributions. Phys Rev C (2008) 77:024317. 10.1103/physrevc.77.024317
6.
ZenihiroJSakaguchiHMurakamiTYosoiMYasudaYTerashimaSet alNeutron density distributions of 204,206,208Pb deduced via proton elastic scattering at = 295 MeV. Phys Rev C (2010) 82:044611. 10.1103/physrevc.82.044611
7.
ZenihiroJUesakaTSagawaHYoshidaS. Proton density polarization of the doubly magic 40Ca core in 48Ca and EoS parameters. Prog Theor Exp Phys (2021) 2021. 023D05. 10.1093/ptep/ptab001
8.
KrasznahorkayABacelarJBordewijkJABrandenburgSBudaAvan ’tHGet alExcitation of the isovector giant dipole resonance by inelastic alpha scattering and the neutron skin of nuclei. Phys Rev Lett (1991) 66:1287–90. 10.1103/PhysRevLett.66.1287
9.
KrasznahorkayAFujiwaraMvan AarlePAkimuneHDaitoIFujimuraHet alExcitation of isovector spin-dipole resonances and neutron skin of nuclei. Phys Rev Lett (1999) 82:3216–9. 10.1103/physrevlett.82.3216
10.
TamiiAPoltoratskaIvon Neumann-CoselPFujitaYAdachiTBertulaniCAet alComplete electric dipole response and the neutron skin in 208Pb. Phys Rev Lett (2011) 107:062502. 10.1103/PhysRevLett.107.062502
11.
HashimotoTKrumbholzAMReinhardPGTamiiAvon Neumann-CoselPAdachiTet alDipole polarizability of 120Sn and nuclear energy density functionals. Phys Rev C (2015) 92:031305. 10.1103/physrevc.92.031305
12.
BirkhanJMiorelliMBaccaSBassauerSBertulaniCAHagenGet alElectric dipole polarizability of 48Ca and implications for the neutron skin. Phys Rev Lett (2017) 118:252501. 10.1103/physrevlett.118.252501
13.
FearickRWvon Neumann-CoselPBaccaSBirkhanJBonaitiFBrandhermIet alElectric dipole polarizability of 40Ca. Phys Rev Res (2023) 5:L022044. 10.1103/PhysRevResearch.5.L022044
14.
AbrahamyanSAhmedZAlbatainehHAniolKArmstrongDSArmstrongWet alMeasurement of the neutron radius of 208Pb through parity violation in electron scattering. Phys Rev Lett (2012) 108:112502. 10.1103/PhysRevLett.108.112502
15.
AdhikariDAlbatainehHAndroicDAniolKArmstrongDSAverettTet alAccurate determination of the neutron skin thickness of 208Pb through parity-violation in electron scattering. Phys Rev Lett (2021) 126:172502. 10.1103/PhysRevLett.126.172502
16.
CREX CollaborationAdhikariDAlbatainehHAndroicDAniolKAArmstrongDSAverettTet alPrecision determination of the neutral weak form factor of 48Ca. Phys Rev Lett (2022) 129:042501. 10.1103/PhysRevLett.129.042501
17.
LiBAHanX. Constraining the neutron–proton effective mass splitting using empirical constraints on the density dependence of nuclear symmetry energy around normal density. Phys Lett B (2013) 727:276–81. 10.1016/j.physletb.2013.10.006
18.
OertelMHempelMKlähnTTypelS. Equations of state for supernovae and compact stars. Rev Mod Phys (2017) 89:015007. 10.1103/revmodphys.89.015007
19.
TewsILattimerJMOhnishiAKolomeitsevEE. Symmetry parameter constraints from a lower bound on neutron-matter energy. Astrophys J (2017) 848:105. 10.3847/1538-4357/aa8db9
20.
OyamatsuKIidaK. Saturation of nuclear matter and radii of unstable nuclei. Progr Theoret Phys (2003) 109:631–50. 10.1143/ptp.109.631
21.
ChenLWKoCMLiBAXuJ. Density slope of the nuclear symmetry energy from the neutron skin thickness of heavy nuclei. Phys Rev C (2010) 82:024321. 10.1103/physrevc.82.024321
22.
IidaKOyamatsuK. Symmetry energy, unstable nuclei and neutron star crusts. Eur Phys J (2014) 50:42. 10.1140/epja/i2014-14042-9
23.
HoriuchiWEbataSIidaK. Neutron-skin thickness determines the surface tension of a compressible nuclear droplet. Phys Rev C (2017) 96:035804. 10.1103/physrevc.96.035804
24.
RossiDMAdrichPAksouhFAlvarez-PolHAumannTBenlliureJet alMeasurement of the dipole polarizability of the unstable neutron-rich nucleus 68Ni. Phys Rev Lett (2013) 111:242503. 10.1103/physrevlett.111.242503
25.
AdrichPKlimkiewiczAFallotMBoretzkyKAumannTCortina-GilDet alEvidence for pygmy and giant dipole resonances in 130Sn and 132Sn. Phys Rev Lett (2005) 95:132501. 10.1103/physrevlett.95.132501
26.
CollaborationLANDKlimkiewiczAPaarNAdrichPFallotMBoretzkyKet alNuclear symmetry energy and neutron skins derived from pygmy dipole resonances. Phys Rev C (2007) 76:051603. 10.1103/physrevc.76.051603
27.
WielandOBraccoACameraFBenzoniGBlasiNBrambillaSet alSearch for the pygmy dipole resonance in 68Ni at 600 MeV/nucleon. Phys Rev Lett (2009) 102:092502. 10.1103/physrevlett.102.092502
28.
AngeliIMarinovaKP. Table of experimental nuclear ground state charge radii: an update. At. Data Nucl Data Tables (2013) 99:69–95. 10.1016/j.adt.2011.12.006
29.
LiTLuoYWangN. Compilation of recent nuclear ground state charge radius measurements and tests for models. At. Data Nucl Data Tables (2021) 140:101440. 10.1016/j.adt.2021.101440
30.
NakamuraTSakuraiHWatanabeH. Exotic nuclei explored at in-flight separators. Prog Part Nucl Phys (2017) 97:53–122. 10.1016/j.ppnp.2017.05.001
31.
KohamaAIidaKOyamatsuK. Difference between interaction cross sections and reaction cross sections. Phys Rev C (2008) 78:061601. 10.1103/physrevc.78.061601
32.
HatakeyamaSHoriuchiW. Complete Glauber calculations for proton–nucleus inelastic cross sections. Nucl Phys A (2019) 985:20–37. 10.1016/j.nuclphysa.2019.02.004
33.
TakechiMSuzukiSNishimuraDFukudaMOhtsuboTNagashimaMet alEvidence of halo structure in 37Mg observed via reaction cross sections and intruder orbitals beyond the island of inversion. Phys Rev C (2014) 90:061305. 10.1103/physrevc.90.061305
34.
KoxSGampAPerrinCArvieuxJBertholetRBruandetJFet alTrends of total reaction cross sections for heavy ion collisions in the intermediate energy range. Phys Rev C (1987) 35:1678–91. 10.1103/physrevc.35.1678
35.
MittigWChouvelJMLongZWBianchiLCunsoloAFernandezBet alMeasurement of total reaction cross sections of exotic neutron-rich nuclei. Phys Rev Lett (1987) 59:1889–91. 10.1103/physrevlett.59.1889
36.
FukudaMMiharaMFukaoTFukudaSIshiharaMItoSet alDensity distribution of 8B studied via reaction cross sections. Nucl Phys A (1999) 656:209–28. 10.1016/s0375-9474(99)00308-5
37.
OzawaABaumannTChulkovLCortinaDDattaUFernandezJet alMeasurements of the interaction cross sections for Ar and Cl isotopes. Nucl Phys A (2002) 709:60–72. 10.1016/s0375-9474(02)01071-0
38.
ToganoYNakamuraTKondoYTostevinJASaitoATGibelinJet alInteraction cross section study of the two-neutron halo nucleus 22C. Phys Lett B (2016) 761:412–8. 10.1016/j.physletb.2016.08.062
39.
KanungoRHoriuchiWHagenGJansenGRNavratilPAmeilFet alProton distribution radii of 12-19C illuminate features of neutron halos. Phys Rev Lett (2016) 117:102501. 10.1103/physrevlett.117.102501
40.
BagchiSKanungoRHoriuchiWHagenGMorrisTDStrobergSRet alNeutron skin and signature of the shell gap found from measured proton radii of 17-22N. Phys Lett B (2019) 790:251–6. 10.1016/j.physletb.2019.01.024
41.
KaurSKanungoRHoriuchiWHagenGHoltJDHuBSet alProton distribution radii of 16–24O: signatures of new shell closures and neutron skin. Phys Rev Lett (2022) 129:142502. 10.1103/physrevlett.129.142502
42.
TanihataITerashimaSKanungoRAmeilFAtkinsonJAyyadYet alObservation of large enhancements of charge exchange cross sections with neutron-rich carbon isotopes. Prog Theor Exp Phys (2016) 2016:043D05. 10.1093/ptep/ptw034
43.
KohamaAIidaKOyamatsuK. Reaction cross section described by a black sphere approximation of nuclei. Phys Rev C (2005) 72:024602. 10.1103/physrevc.72.024602
44.
IidaKKohamaAOyamatsuK. Formula for proton–nucleus reaction cross section at intermediate energies and its application. J Phys Soc Jpn (2007) 76:044201. 10.1143/jpsj.76.044201
45.
SihverLKohamaAIidaKOyamatsuKHashimotoSIwaseHet alCurrent status of the “hybrid kurotama model†for total reaction cross sections. Nucl Instrum Methods Phys Res B (2014) 334:34–9. 10.1016/j.nimb.2014.04.021
46.
MinomoKSumiTKimuraMOgataKShimizuYRYahiroM. Deformation effect on total reaction cross sections for neutron-rich ne isotopes. Phys Rev C (2011) 84:034602. 10.1103/physrevc.84.034602
47.
MinomoKSumiTKimuraMOgataKShimizuYRYahiroM. Determination of the structure of 31Ne by a fully microscopic framework. Phys Rev Lett (2012) 108:052503. 10.1103/physrevlett.108.052503
48.
WatanabeSMinomoKShimadaMTagamiSKimuraMTakechiMet alGround-state properties of neutron-rich Mg isotopes. Phys Rev C (2014) 89:044610. 10.1103/physrevc.89.044610
49.
BonaccorsoACarstoiuFCharityRJ. Imaginary part of the 9C–9Be single-folded optical potential. Phys Rev C (2016) 94:034604. 10.1103/physrevc.94.034604
50.
TagamiSTanakaMTakechiMFukudaMYahiroM. Chiral matrix folding-model approach to reaction cross sections for scattering of Ca isotopes on a C target. Phys Rev C (2020) 101:014620. 10.1103/physrevc.101.014620
51.
MoumeneIBonaccorsoA. Localization of peripheral reactions and sensitivity to the imaginary potential. Nucl Phys (2021) 1006:122109. 10.1016/j.nuclphysa.2020.122109
52.
TagamiSWakasaTMatsuiJYahiroMTakechiM. Neutron skin thickness of 208Pb determined from the reaction cross section for proton scattering. Phys Rev C (2021) 104:024606. 10.1103/physrevc.104.024606
53.
MatsuzakiMTagamiSYahiroM. Neutron skin thickness of 208Pb, 116,120,124Sn, and 40Ca determined from reaction cross sections of 4He scattering. Phys Rev C (2021) 104:054613. 10.1103/physrevc.104.054613
54.
MoumeneIBonaccorsoA. Optical potentials and nuclear reaction cross sections for n C and N C scattering. Phys Rev C (2023) 108:044609. 10.1103/physrevc.108.044609
55.
WakasaTTagamiSMatsuiJTakechiMYahiroM. Neutron-skin values and matter and neutron radii determined from reaction cross sections of proton scattering on 12C, 40,48Ca, 58Ni, and 208Pb. Phys Rev C (2023) 107:024608. 10.1103/PhysRevC.107.024608
56.
GlauberRJBrittinWEDunhamLG (1959) Lectures in theoretical physics, 1. Interscience.
57.
RayL. Proton-nucleus total cross sections in the intermediate energy range. Phys Rev C (1979) 20:1857–72. 10.1103/physrevc.20.1857
58.
Particle Data GroupTanabashiMHagiwaraKHikasaKNakamuraKSuminoYTakahashiFet alReview of particle physics. Phys Rev D (2018) 98:030001. 10.1103/PhysRevD.98.030001
59.
VargaKPieperSCSuzukiYWiringaRB. Monte Carlo integration in Glauber model analysis of reactions of halo nuclei. Phys Rev C (2002) 66:034611. 10.1103/physrevc.66.034611
60.
NagahisaTHoriuchiW. Examination of the 22C radius determination with interaction cross sections. Phys Rev C (2018) 97:054614. 10.1103/physrevc.97.054614
61.
Abu-IbrahimBSuzukiY. Utility of nucleon-target profile function in cross section calculations. Phys Rev C (2000) 61:051601. 10.1103/physrevc.61.051601
62.
Abu-IbrahimBSuzukiY. Scatterings of complex nuclei in the Glauber model. Phys Rev C (2000) 62:034608. 10.1103/physrevc.62.034608
63.
HoriuchiWSuzukiYAbu-IbrahimBKohamaA. Systematic analysis of reaction cross sections of carbon isotopes. Phys Rev C (2007) 75:044607. 10.1103/physrevc.75.044607
64.
TakechiMFukudaMMiharaMTanakaKChindaTMatsumasaTet alReaction cross sections at intermediate energies and fermi-motion effect. Phys Rev C (2009) 79:061601. 10.1103/physrevc.79.061601
65.
TranDTOngHJNguyenTTTanihataIAoiNAyyadYet alCharge-changing cross-section measurements of 12-16C at around MeV and development of a Glauber model for incident energies MeV. Phys Rev C (2016) 94:064604. 10.1103/physrevc.94.064604
66.
Abu-IbrahimBHoriuchiWKohamaASuzukiY. Reaction cross sections of carbon isotopes incident on a proton. Phys Rev C (2008) 77:034607. 10.1103/physrevc.77.034607
67.
Abu-IbrahimBHoriuchiWKohamaASuzukiY. Erratum: reaction cross sections of carbon isotopes incident on a proton [Phys. Rev. C 77, 034607 (2008)]. Phys Rev C (2009) 80:029903. 10.1103/physrevc.80.029903
68.
Abu-IbrahimBHoriuchiWKohamaASuzukiY. Publisher’s Note: reaction cross sections of carbon isotopes incident on a proton [Phys. Rev. C77, 034607 (2008)]. Phys Rev C (2010) 81:019901. 10.1103/physrevc.81.019901
69.
TeixeiraEAAumannTBertulaniCACarlsonBV. Nuclear fragmentation reactions as a probe of neutron skins in nuclei. The Eur Phys J A (2022) 58:205. 10.1140/epja/s10050-022-00849-w
70.
TanakaMTakechiMHommaAFukudaMNishimuraDSuzukiTet alSwelling of doubly magic 48Ca core in Ca isotopes beyond. Phys Rev Lett (2020) 124:102501. 10.1103/physrevlett.124.102501
71.
HoriuchiWInakuraT. Core swelling in spherical nuclei: an indication of the saturation of nuclear density. Phys Rev C (2020) 101:061301. 10.1103/physrevc.101.061301
72.
PonnathLAumannTBertulaniCAGernhäuserRHeilMAlmusidiTet alMeasurement of nuclear interaction cross sections towards neutron-skin thickness determination. Phys Lett B (2024) 855:138780. 10.1016/j.physletb.2024.138780
73.
MoriguchiTIshimotoSIgarashiSOzawaAAbeYIshibashiYet alDevelopments of a thick and large solid hydrogen target for radioisotope beams. Nucl Instrum Methods Phys Res A (2010) 624:27–32. 10.1016/j.nima.2010.09.005
74.
MoriguchiTAmanoMOzawaAHoriuchiWAbeYFujiiTet alEnergy dependence of total reaction cross sections for 17Ne on a proton target. Nucl Phys A (2020) 994:121663. 10.1016/j.nuclphysa.2019.121663
75.
MoriguchiTKagesawaROzawaAHoriuchiWAbeYAmanoMet alInvestigation of total reaction cross sections for proton-dripline nuclei 17F and 17Ne on a proton target. Phys Rev C (2024) 110:014607. 10.1103/physrevc.110.014607
76.
TanihataIHamagakiHHashimotoONagamiyaSShidaYYoshikawaNet alMeasurements of interaction cross sections and radii of He isotopes. Phys Lett B (1985) 160:380–4. 10.1016/0370-2693(85)90005-x
77.
TanihataIHamagakiHHashimotoOShidaYYoshikawaNSugimotoKet alMeasurements of interaction cross sections and nuclear radii in the light p-shell region. Phys Rev Lett (1985) 55:2676–9. 10.1103/physrevlett.55.2676
78.
OzawaASuzukiTTanihataI. Nuclear size and related topics. Nucl Phys A (2001) 693:32–62. 10.1016/s0375-9474(01)01152-6
79.
TanakaKYamaguchiTSuzukiTOhtsuboTFukudaMNishimuraDet alObservation of a large reaction cross section in the drip-line nucleus 22C. Phys Rev Lett (2010) 104:062701. 10.1103/physrevlett.104.062701
80.
BagchiSKanungoRTanakaYKGeisselHDoornenbalPHoriuchiWet alTwo-neutron halo is unveiled in 29F. Phys Rev Lett (2020) 124:222504. 10.1103/physrevlett.124.222504
81.
HoriuchiWSuzukiY. 22C: an s-wave two-neutron halo nucleus. Phys Rev C (2006) 74:034311. 10.1103/physrevc.74.034311
82.
SinghJCasalJHoriuchiWFortunatoLVitturiA. Exploring two-neutron halo formation in the ground state of 29F within a three-body model. Phys Rev C (2020) 101:024310. 10.1103/physrevc.101.024310
83.
FortunatoLCasalJHoriuchiWSinghJVitturiA. The 29F nucleus as a lighthouse on the coast of the island of inversion. Commun Phys (2020) 3:132–5. 10.1038/s42005-020-00402-5
84.
MasuiHHoriuchiWKimuraM. Two-neutron halo structure of 31F and a novel pairing antihalo effect. Phys Rev C (2020) 101:041303. 10.1103/physrevc.101.041303
85.
KanungoRProchazkaAUchidaMHoriuchiWHagenGPapenbrockTet alExploring the anomaly in the interaction cross section and matter radius of 23O. Phys Rev C (2011) 84:061304. 10.1103/physrevc.84.061304
86.
HommaATakechiMOhtsuboTNishimuraDFukudaMSuzukiTet alMeasurements of interaction cross sections for 19-27F isotopes. JPS Conf Proc (2017) 14:021010. 10.7566/jpscp.14.021010
87.
TakechiMOhtsuboTFukudaMNishimuraDKubokiTSuzukiTet alInteraction cross sections for Ne isotopes towards the island of inversion and halo structures of 29Ne and 31Ne. Phys Lett B (2012) 707:357–61. 10.1016/j.physletb.2011.12.028
88.
SuzukiSTakechiMOhtsuboTNishimuraDFukudaMKubokiTet alMeasurements of interaction cross sections for 22-35Na isotopes. EPJ Web of Conferences (2014) 66:03084. 10.1051/epjconf/20146603084
89.
SuzukiTGeisselHBochkarevOChulkovLGolovkovMFukunishiNet alNuclear radii of Na and Mg isotopes. Nucl Phys A (1998) 630:661–77. 10.1016/s0375-9474(98)00799-4
90.
KanungoRProchazkaAHoriuchiWNociforoCAumannTBoutinDet alMatter radii of 32-35Mg. Phys Rev C (2011) 83:021302. 10.1103/physrevc.83.021302
91.
NakamuraTKobayashiNKondoYSatouYAoiNBabaHet alHalo structure of the island of inversion nucleus 31Ne. Phys Rev Lett (2009) 103:262501. 10.1103/physrevlett.103.262501
92.
KobayashiNNakamuraTKondoYTostevinJAUtsunoYAoiNet alObservation of a p-wave one-neutron halo configuration in 37Mg. Phys Rev Lett (2014) 112:242501. 10.1103/physrevlett.112.242501
93.
HoriuchiWSuzukiYCapelPBayeD. Probing the weakly-bound neutron orbit of 31Ne with total reaction and one-neutron removal cross sections. Phys Rev C (2010) 81:024606. 10.1103/physrevc.81.024606
94.
HoriuchiWInakuraTNakatsukasaTSuzukiY. Glauber-model analysis of total reaction cross sections for Ne, Mg, Si, and S isotopes with Skyrme-Hartree-Fock densities. Phys Rev C (2012) 86:024614. 10.1103/physrevc.86.024614
95.
TakatsuRSuzukiYHoriuchiWKimuraM. Microscopic study of the deformed neutron halo of 31Ne. Phys Rev C (2023) 107:024314. 10.1103/physrevc.107.024314
96.
ZhangHYShenWQRenZZMaYGJiangWZZhuZYet alMeasurement of reaction cross section for proton-rich nuclei at intermediate energies. Nucl Phys A (2002) 707:303–24. 10.1016/S0375-9474(02)01007-2
97.
ZhengTYamaguchiTOzawaAChibaMKanungoRKatoTet alStudy of halo structure of 16C from reaction cross section measurement. Nucl Phys A (2002) 709:103–18. 10.1016/S0375-9474(02)01043-6
98.
FangDQYamaguchiTZhengTOzawaAChibaMKanungoRet alOne-neutron halo structure in 15C. Phys Rev C (2004) 69:034613. 10.1103/physrevc.69.034613
99.
YamaguchiYWuCSuzukiTOzawaAFangDQFukudaMet alDensity distribution of 17B from a reaction cross-section measurement. Phys Rev C (2004) 70:054320. 10.1103/physrevc.70.054320
100.
OzawaACaiYZChenZQChibaMFangDQGuoZGet alMeasurements of the interaction cross-sections for 14Be and 14,15B as projectiles with a new scheme at RIBLL. Nucl Instrum Methods Phys Res B (2006) 247:155–60. 10.1016/j.nimb.2006.01.054
101.
TanakaKFukudaMMiharaMTakechiMNishimuraDChindaTet alDensity distribution of 17Ne and possible shell-structure change in the proton-rich sd-shell nuclei. Phys Rev C (2010) 82:044309. 10.1103/physrevc.82.044309
102.
YamaguchiTTanakaKSuzukiTOzawaAOhtsuboTAibaTet alNuclear reactions of 19,20C on a liquid hydrogen target measured with the superconducting TOF spectrometer. Nucl Phys A (2011) 864:1–37. 10.1016/j.nuclphysa.2011.05.095
103.
MoriguchiTOzawaAIshimotoSAbeYFukudaMHachiumaIet alDensity distributions of 11Li deduced from reaction cross-section measurements. Phys Rev C (2013) 88:024610. 10.1103/physrevc.88.024610
104.
MoriguchiTOzawaAIshimotoSAbeYFukudaMHachiumaIet alDensity distribution of 14Be from reaction cross-section measurements. Nucl Phys A (2014) 929:83–93. 10.1016/j.nuclphysa.2014.06.003
105.
FanGWFukudaMNishimuraDCaiXLFukudaSHachiumaIet alStructure of 8Li from a reaction cross-section measurement. Phys Rev C (2014) 90:044321. 10.1103/physrevc.90.044321
106.
FukudaMMoritaYNishimuraDTakechiMIwamotoKWakabayashiMet alNucleon density distribution of the proton drip-line nucleus 12N studied via reaction cross sections. JPS Conf Proc (2015) 6:030103. 10.7566/jpscp.6.030103
107.
TanakaMFukudaMNishimuraDSuzukiSTakechiMMiharaMet alReaction cross sections for 8He and 14B on proton target for the separation of proton and neutron density distributions. JPS Conf Proc (2015) 6:020026. 10.7566/JPSCP.6.020026
108.
NishizukaKTakechiMOhtsuboTNishimuraDFukudaMAokiKet alMeasurements of reaction cross sections for 9-11C. JPS Conf Proc (2017) 14:021015. 10.7566/JPSCP.14.021015
109.
TanakaMFukudaMNishimuraDTakechiMSuzukiSDuHet alReaction cross sections for 13-15B and one-neutron halo in 14B. Acta Phys Pol B (2017) 48:461. 10.5506/aphyspolb.48.461
110.
FukudaMIchiharaTInabeNKuboTKumagaiHNakagawaTet alNeutron halo in 11Be studied via reaction cross sections. Phys Lett B (1991) 268:339–44. 10.1016/0370-2693(91)91587-l
111.
TanihataIKobayashiTSuzukiTYoshidaKShimouraSSugimotoKet alDetermination of the density distribution and the correlation of halo neutrons in 11Li. Phys Lett B (1992) 287:307–11. 10.1016/0370-2693(92)90988-g
112.
NegoitaFBorceaCCarstoiuFLewitowiczMSaint-LaurentMGAnneRet al8B proton halo via reaction and breakup cross section measurements. Phys Rev C (1996) 54:1787–97. 10.1103/physrevc.54.1787
113.
TakechiMFukudaMMiharaMChindaTMatsumasaTMatsubaraHet alReaction cross-sections for stable nuclei and nucleon density distribution of proton drip-line nucleus 8B. Eur Phys J (2005) 25:217–9. 10.1140/epjad/i2005-06-078-0
114.
HoriuchiWInakuraTMichimasaS. Large enhancement of total reaction cross sections at the edge of the island of inversion in ti, cr, and fe isotopes. Phys Rev C (2022) 105:014316. 10.1103/physrevc.105.014316
115.
HoriuchiWSuzukiYShalchiMATomioL. Possible halo structure of 62,72Ca by forbidden-state-free locally peaked Gaussians. Phys Rev C (2022) 105:024310. 10.1103/physrevc.105.024310
116.
HoriuchiWInakuraT. Pairing core swelling effect in Pb isotopes at. Phys Rev C (2022) 105:044303. 10.1103/physrevc.105.044303
117.
YamaguchiTSuzukiTOhnishiTBeckerFFukudaMGeisselHet alNuclear matter radii of neutron-deficient Kr isotopes. Phys Rev C (2008) 77:034315. 10.1103/physrevc.77.034315
118.
TanihataIHirataDKobayashiTShimouraSSugimotoKTokiH. Revelation of thick neutron skins in nuclei. Phys Lett B (1992) 289:261–6. 10.1016/0370-2693(92)91216-v
119.
SuzukiTGeisselHBochkarevOChulkovLGolovkovMHirataDet alNeutron skin of Na isotopes studied via their interaction cross sections. Phys Rev Lett (1995) 75:3241–4. 10.1103/physrevlett.75.3241
120.
HuberGTouchardFBüttgenbachSThibaultCKlapischRDuongHTet alSpins, magnetic moments, and isotope shifts of 21-31Na by high resolution laser spectroscopy of the atomic line. Phys Rev C (1978) 18:2342–54. 10.1103/physrevc.18.2342
121.
Garcia RuizRFBissellMLBlaumKEkströmAFrömmgenNHagenGet alUnexpectedly large charge radii of neutron-rich calcium isotopes. Nat Phys (2016) 12:594–8. 10.1038/nphys3645
122.
MinamisonoKRossiDMBeerwerthRFritzscheSGarandDKloseAet alCharge radii of neutron deficient 52,53Fe produced by projectile fragmentation. Phys Rev Lett (2016) 117:252501. 10.1103/physrevlett.117.252501
123.
IidaKOyamatsuK. Surface tension in a compressible liquid-drop model: effects on nuclear density and neutron skin thickness. Phys Rev C (2004) 69:037301. 10.1103/physrevc.69.037301
124.
WardaMVinasXRoca-MazaXCentellesM. Neutron skin thickness in the droplet model with surface width dependence: indications of softness of the nuclear symmetry energy. Phys Rev C (2009) 80:024316. 10.1103/physrevc.80.024316
125.
WardaMCentellesMVinasXRoca-MazaX. Influence of the single-particle structure on the nuclear surface and the neutron skin. Phys Rev C (2014) 89:064302. 10.1103/physrevc.89.064302
126.
HoriuchiWSuzukiYInakuraT. Probing neutron-skin thickness with total reaction cross sections. Phys Rev C (2014) 89:011601. 10.1103/physrevc.89.011601
127.
FangDQMaYGCaiXZTianWDWangHW. Effects of neutron skin thickness in peripheral nuclear reactions. Chin Phys. Lett. (2011) 28:102102. 10.1088/0256-307x/28/10/102102
128.
FangDQMaYGCaiXZTianWDWangHW. Neutron removal cross section as a measure of neutron skin. Phys Rev C (2010) 81:047603. 10.1103/physrevc.81.047603
129.
MaCWWeiHLYuM. Reexamination of the neutron skin thickness using neutron removal cross sections. Phys Rev C (2010) 82:057602. 10.1103/physrevc.82.057602
130.
AumannTBertulaniCASchindlerFTypelS. Peeling off neutron skins from neutron-rich nuclei: constraints on the symmetry energy from neutron-removal cross sections. Phys Rev Lett (2017) 119:262501. 10.1103/physrevlett.119.262501
131.
BertulaniCAValenciaJ. Neutron skins as laboratory constraints on properties of neutron stars and on what we can learn from heavy ion fragmentation reactions. Phys Rev C (2019) 100:015802. 10.1103/physrevc.100.015802
132.
HoriuchiWHatakeyamaSEbataSSuzukiY. Extracting nuclear sizes of medium to heavy nuclei from total reaction cross sections. Phys Rev C (2016) 93:044611. 10.1103/physrevc.93.044611
133.
HoriuchiWSuzukiYUesakaTMiwaM. Total reaction cross section on a deuteron target and the eclipse effect of the constituent neutron and proton. Phys Rev C (2020) 102:054601. 10.1103/physrevc.102.054601
134.
NishimuraDFukudaMTakechiMMiharaMIshikawaDKomurasakiJet alDistinction between proton-neutron density distribution of halo nuclei at the nuclear surface via reaction cross sections. Nucl Phys A (2010) 834:470c–2c. 10.1016/j.nuclphysa.2010.01.067
135.
YamaguchiTFukudaMFukudaSFanGWHachiumaIKanazawaMet alEnergy-dependent charge-changing cross sections and proton distribution of si 28. Phys Rev C (2010) 82:014609. 10.1103/physrevc.82.014609
136.
YamaguchiTHachiumaIKitagawaANamihiraKSatoSSuzukiTet alScaling of charge-changing interaction cross sections and point-proton radii of neutron-rich carbon isotopes. Phys Rev Lett (2011) 107:032502. 10.1103/physrevlett.107.032502
137.
YamakiSYamaguchiTKounoJSatoKIchihashiNSuzukiTet alSystematic study of individual charge-changing cross sections of intermediate-energy secondary beams. Nucl Instrum Methods Phys Res B (2013) 317:774–8. 10.1016/j.nimb.2013.05.057
138.
YamakiSKounoJNishimuraDNagashimaMTakechiMSatoKet alCharge-changing interactions probing point-proton radii of nuclei. EPJ Web of Conferences (2014) 66:03099. 10.1051/epjconf/20146603099
139.
OzawaAMoriguchiTOhtsuboTAoiNFangDQFukudaNet alCharge-changing cross sections of 30Ne, 32,33Na with a proton target. Phys Rev C (2014) 89:044602. 10.1103/physrevc.89.044602
140.
TerashimaSTanihataIKanungoREstradeAHoriuchiWAmeilFet alProton radius of 14Be from measurement of charge-changing cross sections. Prog Theor Exp Phys (2014) 2014:101D02. 10.1093/ptep/ptu134
141.
EstradéAKanungoRHoriuchiWAmeilFAtkinsonJAyyadYet alProton radii of 12–17B define a thick neutron surface in 17B. Phys Rev Lett (2014) 113:132501. 10.1103/physrevlett.113.132501
142.
SawahataKOzawaASaitoYAbeYIchikawaYInabaNet alInvestigations of charge-changing processes for light proton-rich nuclei on carbon and solid-hydrogen targets. Nucl Phys A (2017) 961:142–53. 10.1016/j.nuclphysa.2017.02.012
143.
TranDTOngHJHagenGMorrisTDAoiNSuzukiTet alEvidence for prevalent Z = 6 magic number in neutron-rich carbon isotopes. Nat Commun (2018) 9:1594. 10.1038/s41467-018-04024-y
144.
TanakaMTakechiMHommaAProchazkaAFukudaMNishimuraDet alCharge-changing cross sections for 42–51Ca and effect of charged-particle evaporation induced by neutron-removal reactions. Phys Rev C (2022) 106:014617. 10.1103/physrevc.106.014617
145.
WangCJGuoGOngHJSongYNSunBHTanihataIet alCharge-changing cross section measurements of 300 MeV/nucleon 28Si on carbon and data analysis. Chin Phys C (2023) 47:084001. 10.1088/1674-1137/acd366
146.
ZhaoJWSunBHTanihataITerashimaSProchazkaAXuJYet alIsospin-dependence of the charge-changing cross-section shaped by the charged-particle evaporation process. Phys Lett B (2023) 847:138269. 10.1016/j.physletb.2023.138269
147.
ZhaoJWSunBHTanihataIXuJYZhangKYProchazkaAet alCharge radii of 11–16C, 13–17N and 15–18O determined from their charge-changing cross-sections and the mirror-difference charge radii. Phys Lett B (2024) 858:139082. 10.1016/j.physletb.2024.139082
148.
BhagwatAGambhirYK. Microscopic investigations of mass and charge changing cross sections. Phys Rev C (2004) 69:014315. 10.1103/physrevc.69.014315
149.
AkaishiTHaginoK. Analysis of charge changing cross sections with the Glauber-Abrasion-Ablation model. JPS Conf Proc (2015) 6:030097. 10.7566/JPSCP.6.030097
150.
FanGWZhanX. Influence of neutrons on charge-changing cross-sections. Int J Mod Phys E (2019) 28:1950070. 10.1142/s0218301319500708
151.
Abdul-MageadIAMAbu-IbrahimB. Contribution of the projectile neutrons to the total charge-changing cross sections. Nucl Phys (2020) 1000:121804. 10.1016/j.nuclphysa.2020.121804
152.
GaimardJJSchmidtKH. A reexamination of the abrasion-ablation model for the description of the nuclear fragmentation reaction. Nucl Phys A (1991) 531:709–45. 10.1016/0375-9474(91)90748-u
153.
ScheidenbergerCPshenichnovIASümmereKVenturaABondorfJPBotvinaASet alCharge-changing interactions of ultrarelativistic Pb nuclei. Phys Rev C (2004) 70:014902. 10.1103/physrevc.70.014902
154.
SuzukiYHoriuchiWTerashimaSKanungoRAmeilFAtkinsonJet alParameter-free calculation of charge-changing cross sections at high energy. Phys Rev C (2016) 94:011602. 10.1103/physrevc.94.011602
155.
WangNLiT. Shell and isospin effects in nuclear charge radii. Phys Rev C (2013) 88:011301. 10.1103/physrevc.88.011301
156.
BrownBA. Mirror charge radii and the neutron equation of state. Phys Rev Lett (2017) 119:122502. 10.1103/physrevlett.119.122502
157.
YangJPiekarewiczJ. Difference in proton radii of mirror nuclei as a possible surrogate for the neutron skin. Phys Rev C (2018) 97:014314. 10.1103/physrevc.97.014314
158.
GaidarovMKMoumeneIAntonovANKadrevDNSarrigurenPMoya de GuerraE. Proton and neutron skins and symmetry energy of mirror nuclei. Nucl Phys A (2020) 1004:122061. 10.1016/j.nuclphysa.2020.122061
159.
BrownBAMinamisonoKPiekarewiczJHergertHGarandDKloseAet alImplications of the 36Ca–36S and 38Ca–38Ar difference in mirror charge radii on the neutron matter equation of state. Phys Rev Res (2020) 2:022035. 10.1103/physrevresearch.2.022035
160.
PinedaSVKönigKRossiDMBrownBAIncorvatiALantisJet alCharge radius of neutron-deficient 54Ni and symmetry energy constraints using the difference in mirror pair charge radii. Phys Rev Lett (2021) 127:182503. 10.1103/PhysRevLett.127.182503
161.
XuJYLiZZSunBHNiuYFRoca-MazaXSagawaHet alConstraining equation of state of nuclear matter by charge-changing cross section measurements of mirror nuclei. Phys Lett B (2022) 833:137333. 10.1016/j.physletb.2022.137333
Summary
Keywords
total reaction cross sections, interaction cross sections, charge-changing cross sections, root-mean-square radii, neutron skin thickness, unstable nuclei
Citation
Tanaka M, Horiuchi W and Fukuda M (2024) Unveiling radii and neutron skins of unstable atomic nuclei via nuclear collisions. Front. Phys. 12:1488428. doi: 10.3389/fphy.2024.1488428
Received
30 August 2024
Accepted
13 November 2024
Published
10 December 2024
Volume
12 - 2024
Edited by
Masayuki Matsuzaki, Fukuoka University of Education, Japan
Reviewed by
Nobuo Hinohara, University of Tsukuba, Japan
Updates
Copyright
© 2024 Tanaka, Horiuchi and Fukuda.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Masaomi Tanaka, mtanaka@artsci.kyushu-u.ac.jp
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.